Abstract
We present a comparative study of high carrier density transport in mono-, bi-, and trilayer graphene using electric double-layer transistors to continuously tune the carrier density up to values exceeding 1014 cm-2. Whereas in monolayer the conductivity saturates, in bi- and trilayer filling of the higher-energy bands is observed to cause a nonmonotonic behavior of the conductivity and a large increase in the quantum capacitance. These systematic trends not only show how the intrinsic high-density transport properties of graphene can be accessed by field effect, but also demonstrate the robustness of ion-gated graphene, which is crucial for possible future applications.
The investigation of transport through graphene layers has been focusing almost exclusively on the low carrier density regime (n ∼ 1012 cm-2), where electrons behave as chiral particles and unexpected physical phenomena occur (1, 2). Despite exciting theoretical predictions (possible occurrence of superconductivity; refs. 3–5) and its clear relevance for technological applications (transparent electrodes for flat panel displays, ref. 6, supercapacitors, ref. 7, and biosensors, ref. 8), the high carrier density regime (n ∼ 1014 cm-2) has remained vastly unexplored due to the limited amount of carrier density accessible in conventional solid-state field-effect transistors (9, 10). The recent development of so-called ionic-liquid gates, in which the coupling between gate electrode and transistor channel is effectively realized through moving ions that form an electric double layer (EDL) at the liquid/channel interface (Fig. 1A), is now changing the situation. The gate voltage applied—up to several volts—drops across a very large geometrical EDL capacitance of approximately 1-nm thick. As a result, the induced carrier density can easily exceed n2D ≈ 1014 cm-2, more than one order of magnitude larger than that in conventional solid-state field-effect transistors (FETs). Such a very strong field effect is valuable for technological applications (for instance, in organic FETs, ref. 11, where it enables low-voltage operation) and as a versatile and effective tool to tune electronic states in a rich variety of systems (by modulating metal insulator transition, ref. 12, magnetoresistance, ref. 13, and by inducing superconductivity at the surface of insulators, refs. 14 and 15).
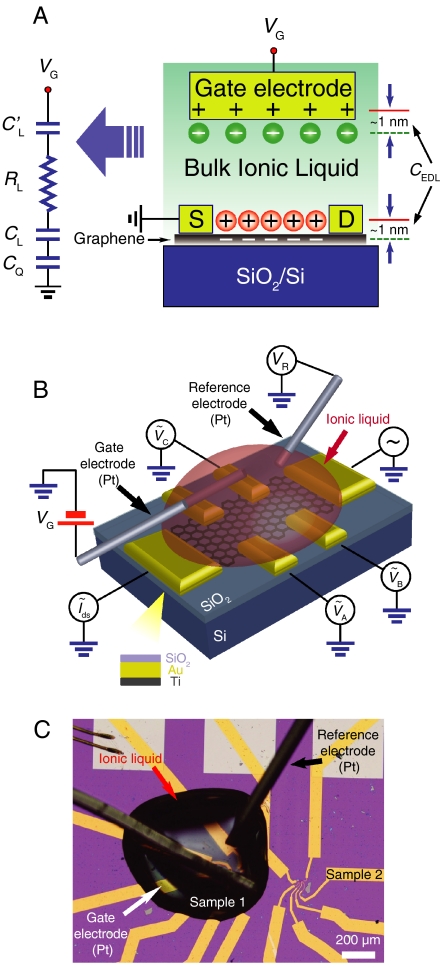
Fig. 1.
Electric double-layer graphene devices. (A) A schematic cross-section of our graphene EDLTs, together with the equivalent electrical circuit describing its operation. In the equivalent circuit, 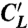 is the capacitance between Pt gate and liquid, RL is the electrical resistance of the bulk of the ionic liquid, where transport is mediated by ions, CL and CQ, are the geometrical capacitance of double layer/graphene interface and the quantum capacitance of graphene associated with the finite density of states. (B) A schematic representation of a device including the bias configuration used in the electrical measurements. (C) Optical microscope image of an actual device (the white bar in the right bottom corner is 200 μm long). In fact, two separate graphene flakes are visible on the substrate, but only one of them is immersed in the ionic liquid. Also clearly visible are the two Pt wires immersed in the ionic liquid, acting as gate and quasi-reference electrodes.
is the capacitance between Pt gate and liquid, RL is the electrical resistance of the bulk of the ionic liquid, where transport is mediated by ions, CL and CQ, are the geometrical capacitance of double layer/graphene interface and the quantum capacitance of graphene associated with the finite density of states. (B) A schematic representation of a device including the bias configuration used in the electrical measurements. (C) Optical microscope image of an actual device (the white bar in the right bottom corner is 200 μm long). In fact, two separate graphene flakes are visible on the substrate, but only one of them is immersed in the ionic liquid. Also clearly visible are the two Pt wires immersed in the ionic liquid, acting as gate and quasi-reference electrodes.
Recent works show that ion gating can also be used in combination with graphene. Experiments (e.g., Raman spectroscopy, ref. 16, quantum capacitance, ref. 17, transport, refs. 18 and 19, etc.) have focused almost exclusively on properties of monolayer, but no characteristic high carrier density features in the transport properties were identified. Here, as an efficient strategy to reveal these characteristic features, we perform a comparative study of transport in ion-gated mono-, bi-, and trilayer graphene at high carrier density of approximately 1014 cm-2. The motivation for this strategy is twofold. First, when n2D exceeds values of several 1013 cm-2, differences between monolayer and bi-/trilayer are expected, because in the latter systems the higher-energy split-off bands start to be populated, which can provide an effective way to identify signatures of the intrinsic properties characteristic of the layers of different thickness. Second, in bi- and trilayer, the regime in which higher-energy bands are populated has not yet been studied, and it is currently unknown how the opening of parallel transport channels affects the conductivity of these systems. As we now proceed to discuss, our strategy enables the observation of conductivity saturation in monolayer graphene, as well as a nonmonotonic density dependence of the conductivity in bi- and trilayer graphenes, and provide the information necessary to determine the origin of these phenomena. Although a precise quantitative analysis of our data in terms of theoretical calculations capturing all the details of the graphene systems investigated is beyond present capabilities—because of the microscopic complexity of the graphene/ionic-liquid interface—we also discuss a simple model which captures the important qualitative features of our data and reproduces the correct order of magnitude of the measured quantities.
Experiments
Mono-, bi-, and trilayer graphene devices were fabricated on SiO2/Si substrates by exfoliating graphite (see Materials and Methods and Fig. S1) (9). A small droplet of ionic liquid was applied onto the devices, covering the graphene layer, the gate, and a quasi-reference electrode, as shown in Fig. 1 B and C. The droplet can be easily removed and substituted with a different ionic liquid, enabling the comparison of electric double-layer transistors (EDLTs) realized on the same graphene layer, with different ionic liquids (see Materials and Methods and Fig. S2A): This is important to check that the features observed in the experiments are not artifacts caused by the specific ionic liquid chosen. For all devices, the longitudinal sheet resistivity ρxx, and Hall coefficient RH were simultaneously measured at room temperature, in a Hall bar configuration, as a function of VG - Vref. [VG is the voltage applied on the Pt gate electrode and Vref is the voltage measured on the quasi-reference electrode as shown in Fig. 1B. We found Vref ≈ 0 over the whole sweep range of VG (see Fig. S2B), which ensured almost all the applied VG dropped at the liquid/graphene interface.] The measurements were performed in a limited gate voltage range, to avoid the occurrence of chemical reactions between the ionic liquid and graphene, as it is necessary to obtain reproducible and reversible results (Fig. S3 and S4). Despite this limitation, charge density as large as n2D ≈ 2 × 1014 cm-2 could be reached.
Results
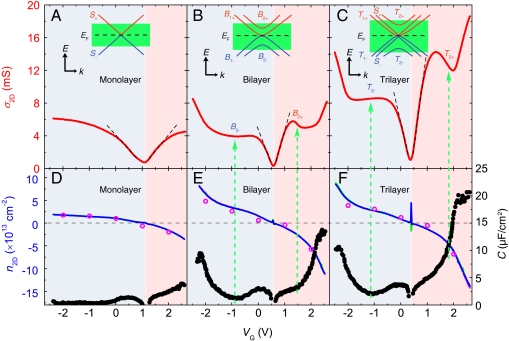
Fig. 2 shows the VG dependence of the sheet conductivity σ2D = 1/ρxx for mono-, bi-, and trilayer graphene devices fabricated using 1-allyl-3-butylimidazolium bis-(trifluoromethanesulfonyl)-imide (ABIM-TFSI) as ionic gate. For monolayer graphene (Fig. 2A), a linear increase of σ2D is observed upon accumulating either electrons or holes, within a voltage window of ΔVG ≈ ± 1 V from the charge neutrality point. For larger (in modulus) VG, σ2D exhibits a pronounced saturation (20). The onset of a trend toward conductivity saturation is normally seen in conventional SiO2-based monolayer graphene FETs with sufficient high mobility (21). Here, the use of EDLTs makes the phenomenon unambiguously clear, owing to the much larger carrier density range spanned. The behavior of bi- and trilayer graphenes (see Fig. 2 B and C) differs from that of monolayer. In particular, the linear increases of σ2D appear within a narrower voltage range of ΔVG ≈ ± 0.5 V near the charge neutrality point. More distinctly, outside this range, the σ2D exhibits a nonmonotonic behavior—both for electrons and holes—before continuing to increase further at higher VG.
Fig. 2.
Electrical properties of mono-, bi-, and trilayer graphene EDLT devices. (A–C) The conductivity σ2D of mono-, bi-, and trilayer graphene, respectively, measured as a function of applied gate voltage VG, in devices using ABIM-TFSI ionic liquid gate. The black dashed lines indicate the linear VG dependence of the σ2D near the charge neutrality point (whose position is marked by the vertical white lines). For the monolayer (A), σ2D exhibits a very pronounced saturation with increasing VG (i.e., carrier density). The saturation is absent in the bi- and trilayer, which instead show a nonmonotonic dependence of σ2D. In all cases, the asymmetry between positive and negative voltage is associated with the properties of the ionic liquid, and it is in large part due to the fact that positive and negative ions have different size (leading to different thicknesses of the EDL; see also Fig. 3 and Fig. S3A). (D–F) Hall effect measurements of the carrier density n2D for the graphene layers of different thickness. Three curves (overlapped) measured by fixing magnetic field while scanning VG and the pink dots measured by fixing VG while scanning the magnetic field show perfectly consistent data (see also Fig. S3B). D–F also show the capacitance C of the layers, obtained by deriving the accumulated n2D with respect to VG. In E and F, the vertical arrows show that the features observed in the conductivity occur at the same gate voltage as the features in the measured capacitance. This result is expected because these features indicate the starting of carrier accumulation in the higher-energy bands of bi- and trilayer. The insets of A–C illustrate schematically the main aspects of the band structure of mono-, bi-, and trilayer graphene, respectively. The green shaded areas illustrate the range within which the Fermi level can be shifted in the three cases.
Because charge accumulation in graphene EDLT devices is not simply described by a geometrical capacitance (see below), it is necessary to determine the electron density as a function of gate voltage independently, in order to interpret the conductivity data. To this end, we have simultaneously measured the Hall resistance as a function of VG. The blue lines in Fig. 2 D–F display the sheet carrier density n2D derived for devices fabricated on layers of different thickness. As expected, at the value of VG corresponding to the conductivity minimum n2D changes sign, confirming the shift of Fermi level EF across the charge neutrality point (Fig. S3). Using the carrier density determined from Hall measurements, we can directly extract the mobility of the devices. We find maximum values of 5.5, 3.5, and 9 × 103 cm2/Vs close to the neutrality point, for mono-, bi-, and trilayer graphene, respectively; similar mobility values are also observed using other ionic liquid, for instance N,N-diethyl-N-(2-methoxyethyl)-N-methylammonium bis-(trifluoromethylsulfonyl)-imide (DEME-TFSI) (Fig. S5).
Having determined the density of carriers, we can directly extract the total capacitance of the devices, defined as 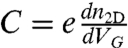 , from the data shown in Fig. 2 D–F. A strong asymmetry between electrons and holes is clearly present, in sharp contrast to what happens in conventional transistors based on solid dielectrics. As electron-hole symmetry is known to approximately hold in graphene on the studied energy scale, we attribute the asymmetries observed to the properties of the EDLs. In large part, they originate from the different size of the positive and negative ions forming the ionic liquid, which are responsible for different thickness of the EDL for opposite polarities of the gate voltage. Indeed, the details of the asymmetry are different for different ionic liquids, as can be seen in Fig. 3A where the characteristics of a bilayer graphene device realized using ABIM-TFSI, DEME-TFSI, and 1-ethyl-3-methylimidazolium tetrafluoroborate (EMIM-BF4) are shown. More importantly, however, the devices based on different liquids exhibit a fairly good agreement in the main features of the conductivity, including the absolute values of conductivity, the nonmonotonic behavior, and the position of the features as a function of carrier density. This observation is important because it indicates that the features in the conductivity are intrinsic to graphene.
, from the data shown in Fig. 2 D–F. A strong asymmetry between electrons and holes is clearly present, in sharp contrast to what happens in conventional transistors based on solid dielectrics. As electron-hole symmetry is known to approximately hold in graphene on the studied energy scale, we attribute the asymmetries observed to the properties of the EDLs. In large part, they originate from the different size of the positive and negative ions forming the ionic liquid, which are responsible for different thickness of the EDL for opposite polarities of the gate voltage. Indeed, the details of the asymmetry are different for different ionic liquids, as can be seen in Fig. 3A where the characteristics of a bilayer graphene device realized using ABIM-TFSI, DEME-TFSI, and 1-ethyl-3-methylimidazolium tetrafluoroborate (EMIM-BF4) are shown. More importantly, however, the devices based on different liquids exhibit a fairly good agreement in the main features of the conductivity, including the absolute values of conductivity, the nonmonotonic behavior, and the position of the features as a function of carrier density. This observation is important because it indicates that the features in the conductivity are intrinsic to graphene.
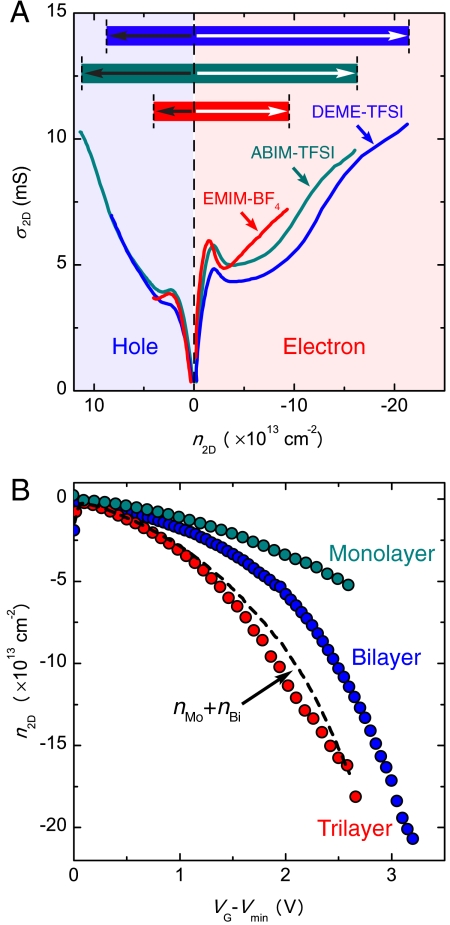
Fig. 3.
Comparison of different ionic liquids. (A) The conductivity σ2D of bilayer graphene devices fabricated using three different ionic liquids (green, ABIM-TFSI; blue, DEME-TFSI; red, EMIM-BF4) as a function of carrier density n2D (measured from the Hall effect). It is apparent that all the main features observed in the conductivity (linear increase at low n2D, nonmonotonic behavior at intermediate n2D, and increase at a very large n2D) are essentially identical, irrespective of the specific ionic liquid used. This observation indicates that these features are intrinsic properties of bilayer graphene, not influenced by the specific ionic liquid used. Similar experiments were performed on mono- and trilayer and showed a similar insensitivity to the ionic liquid. Note also that, when plotted as a function of n2D, the asymmetry between electron and hole side in the conductivity appears to be much smaller than in the plots as a function of gate voltage (see Fig. 2). This result is indeed what should be expected if the asymmetry originates from the geometrical capacitance of the EDL that is different for the two different polarities (owing to the different physical size of positive and negative ions). The inset illustrates the maximum value of n2D for electrons (white arrows) and for holes (black arrows) accessible by means of the different ionic liquids. The largest carrier density that has been accessed in this study is 2 × 1014 cm-2 using DEME-TFSI. (B) The dependence of carrier density n2D on gate voltage VG (measured from the charge neutrality point) for mono-, bi-, and trilayer graphene devices, using DEME-TSFI as ionic liquid. The dashed black line is the sum of n2D of mono- and bilayer graphene, which compares well to the n2D measured in the trilayer. This relationship is approximately expected from the known band structure of these materials, because the two lowest energy bands of trilayer roughly correspond to the lowest energy band of mono- and bilayer.
It is apparent from Fig. 2 that the capacitance depends very strongly on VG, because the total capacitance C measured experimentally is given by  , where CL is the “geometrical” capacitance of the EDL, and CQ is the so-called quantum capacitance associated to the finite density of states of graphene. Owing to the large geometrical capacitance of EDLs (several tens of μF/cm2) (17), CQ dominates the total capacitance, which is why the position of the Fermi energy EF can be tuned by applying only small values of VG. (In conventional graphene FETs with solid gate dielectrics, except close to the Dirac point, the quantum capacitance is normally negligible, because the geometrical capacitance is three orders of magnitude smaller than for EDLs—typically, for a 300-nm SiO2 layer, ca. 12 nF/cm-2.) The dominant role of the quantum capacitance naturally explains why the amount of carrier density accumulated in the graphene of different layers (at the same gate voltage and using a same ionic liquid) is very different, as a direct consequence of the different density of states in graphene layers of different thickness.
, where CL is the “geometrical” capacitance of the EDL, and CQ is the so-called quantum capacitance associated to the finite density of states of graphene. Owing to the large geometrical capacitance of EDLs (several tens of μF/cm2) (17), CQ dominates the total capacitance, which is why the position of the Fermi energy EF can be tuned by applying only small values of VG. (In conventional graphene FETs with solid gate dielectrics, except close to the Dirac point, the quantum capacitance is normally negligible, because the geometrical capacitance is three orders of magnitude smaller than for EDLs—typically, for a 300-nm SiO2 layer, ca. 12 nF/cm-2.) The dominant role of the quantum capacitance naturally explains why the amount of carrier density accumulated in the graphene of different layers (at the same gate voltage and using a same ionic liquid) is very different, as a direct consequence of the different density of states in graphene layers of different thickness.
We now proceed to discuss the microscopic origin of our observations. The insets of Fig. 2 A–C illustrate the main features of the band structures of graphene mono-, bi-, and trilayer. Whereas in monolayer only two (valence and conduction) linearly dispersing bands S2± touching at zero energy are present, bi- and trilayer graphenes have additional bands at higher energy. The first of these bands starts at around 0.4 (B2±) and 0.5 ∼ 0.6 eV (T2±) from the charge neutrality point, for bi- and trilayer, respectively (SI Theoretical simulation and quantum capacitance); filling of these bands is expected to occur when the carrier density approximately exceeds 2 and 7 × 1013 cm-2 in these two cases (these estimates are based on the known band structure, but they are approximated by neglecting changes in the band structure itself, induced by the perpendicular electric field generated by the gate voltage). Indeed, the “anomalies” (i.e., the nonmonotonic behavior) in the conductivity occur at density values—larger for trilayer than for bilayer—close to the ones estimated above. We therefore attribute the anomaly in conductivity to the presence of an additional scattering channel—interband scattering—that opens when the higher bands are filled, and that, as it is known from conventional semiconductors (22), can strongly reduce the carrier mobility. In contrast, no anomaly is seen in the monolayer, because no higher-energy band is present in its band structure in a reasonable energy scale.
The interpretation of the conductivity anomalies in terms of interband scattering is further supported by the observed behavior of the capacitance of bi- and trilayer graphene (Fig. 2 E and F), which exhibits a sharp increase concomitant with the conductivity anomalies. This increase is precisely what should be expected, because when the Fermi level enters the B2± or T2± bands, the density of states increase in a step-like manner and so does the quantum capacitance (in the experiments, the step-like increase is broadened by disorder). Finally, Fig. 3B shows the relation between n2D and VG for mono-, bi-, and trilayer devices, from which we find that the carrier density for the trilayer closely matches the sum of the densities in the mono- and bilayer. Such a relation is expected to approximately hold from the theoretical band structure of these systems, because the two lowest energy bands in trilayer correspond approximately to the linear band of monolayer and the lowest energy quadratic band of bilayer (SI Theoretical simulation and quantum capacitance).
Discussion and Conclusion
To substantiate all the considerations just made, we have analyzed the high-density electronic properties of mono-, bi-, and trilayer graphene in terms of a simple, well-defined theoretical model (20). As our only goal at this stage is to show that all the main features observed in the conductivity and capacitance measurements naturally arise from a formally correct theoretical framework, for simplicity we have included only the effect of weak short-range scattering (20) and adopted a self-consistent Born approximation scheme (23, 24). For a quantitative analysis, other scattering mechanisms should be included as well—e.g., to capture the effect of long-range Coulomb potential (25), resonant scattering (26, 27), as well as ripples (28). However, such a precise quantitative analysis is far from straightforward, because the graphene layers are in close proximity (approximately 1-nm distance) with very high-density molecular ions in the ionic-liquid gate. These nearby charges generate large electrostatic potential fluctuations—much larger than in the case of SiO2 substrates—and are certainly expected to smear all sharp features that are calculated using models where disorder has limited amplitude. Because of these sources of uncertainty, the model is only expected to give a qualitative picture of the charge accumulation in graphene (multi)layers. Indeed, on the experimental side, the broad features observed in the data prevent a precise quantitative determination of the absolute values of parameters, such as the carrier density required for the band filling. It is clear that the experimental data, although having the correct orders of magnitude, can certainly be affected by a large uncertainty at the quantitative level.
The experimental data for devices realized using ABIM-TFSI are compared with theory in Fig. 4. At a qualitative level, theory reproduces the trends seen in both σ2D vs. n2D and C vs. n2D curves, for the graphene layers of different thickness. This consistency includes the trend toward conductivity saturation in the monolayer, and the features in the conductivity and in the capacitance in bi- and trilayer. In particular, the nonmonotonic behavior of the calculated conductivity in bi- and trilayer can be traced back to the presence of interband scattering, which agrees with our initial interpretation and confirms the relevance of this process at high carrier density. Note, finally, that in the model, we have not included the modification of the band structure due to the perpendicular electric field generated by the gate (i.e., the opening of a gap in bilayer, ref. 29, and the modification of the band overlap in trilayer, ref. 30). Inclusion of these effects is important for a more quantitative analysis (in particular, to achieve a more precise quantitative agreement for the values of carrier density at which higher-energy bands are populated in bi- and trilayer). Nevertheless their omission does not change the qualitative trends and most of the quantitative discrepancies between model and calculations originate from the very large potential fluctuations associated with the discreteness and random position of the nearby molecular ions in the ionic-liquid gate.
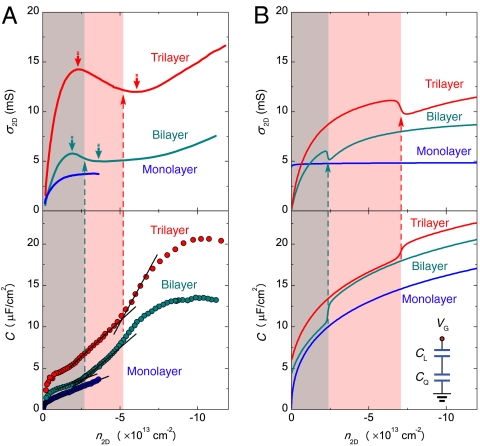
Fig. 4.
Theoretical interpretation of the carried density dependence. (A) The experimental data of conductivity σ2D and capacitance 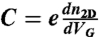 as a function of carrier density n2D for mono-, bi-, and trilayer graphene. The red and cyan pair of arrows point to the conductivity anomaly (nonmonotonic dependence of σ2D on n2D). The dashed lines indicate how the range of densities, at which the conductivity anomalies are observed in bi- and trilayer, corresponds to the values of density where the measured capacitance increases. (B) The results of theoretical simulations for the same quantities plotted in A. In the theoretical calculations, the features observed in the conductivity and in the capacitance are much sharper than that in the experimental data, because of large potential fluctuations in the ionic-liquid gate (due to the presence of high-density molecular ions that are only approximately 1 nm away from the graphene layers) that are not included in the theoretical model. The inset shows the configuration of the total capacitance between ionic liquid and graphene, which consists of the geometrical and quantum capacitances connected in series. To analyze the data theoretically, we have chosen for the geometrical capacitance a realistic value of CL = 40 μF/cm2. Overall, all the qualitative features and trends observed in the experiments are reproduced by the calculations.
as a function of carrier density n2D for mono-, bi-, and trilayer graphene. The red and cyan pair of arrows point to the conductivity anomaly (nonmonotonic dependence of σ2D on n2D). The dashed lines indicate how the range of densities, at which the conductivity anomalies are observed in bi- and trilayer, corresponds to the values of density where the measured capacitance increases. (B) The results of theoretical simulations for the same quantities plotted in A. In the theoretical calculations, the features observed in the conductivity and in the capacitance are much sharper than that in the experimental data, because of large potential fluctuations in the ionic-liquid gate (due to the presence of high-density molecular ions that are only approximately 1 nm away from the graphene layers) that are not included in the theoretical model. The inset shows the configuration of the total capacitance between ionic liquid and graphene, which consists of the geometrical and quantum capacitances connected in series. To analyze the data theoretically, we have chosen for the geometrical capacitance a realistic value of CL = 40 μF/cm2. Overall, all the qualitative features and trends observed in the experiments are reproduced by the calculations.
From the results obtained, we conclude that ionic-liquid gating is an effective and reliable technique to accumulate very large amounts of carriers in graphene-based materials. Although our investigations have mainly focused on basic aspects of the electronic properties that can be directly related to the graphene band structure, the technique has the potential to have a much broader impact, both to disclose phenomena of fundamental interest and for possible future applications. For instance, the carrier densities that have been achieved in this study are not far from those for which superconductivity is observed in graphite intercalated compounds (e.g., KC8 corresponding to a carrier density of 5 × 1014 cm-2) and, indeed, superconductivity in graphene at high carrier density has been predicted theoretically (3–5). Accessing these higher carrier densities appears to be within experimental reach, by biasing the gate at lower temperature (approximately 220 K, just above the freezing point of the ionic liquid) to prevent the occurrence of chemical reaction (whose rate decreases exponentially with lowering temperature) over a much broader gate voltage range (15, 31). For applications, ionic gating allows to boost the conductivity of graphene, as it is required, for instance, for the practical realization of transparent electrodes in flat panel displays (6). (Indeed, it is believed that graphene has the potential to replace the commonly used—and expensive—indium tin oxide; note that the ionic liquids themselves are also transparent.) The use of liquid gates is also crucial for the application of graphene in supercapacitors (7) and, possibly, in biosensors (8). At the current stage, it appears that all the ingredients necessary for a rapid progress in directions of fundamental and technological interest that combine the unique properties of graphene and ionic-liquid gates are already available.
Materials and Methods
Graphene flakes were cleaved from bulk graphite using an adhesive tape. All data shown were collected on natural graphite; we checked that the same behavior is observed also when starting from Kish graphite. Graphene layers of different thickness were transferred onto a heavily doped Si substrate covered by 300-nm-thick, thermally grown SiO2 (9, 32). To identify the layer thickness, we used both the analysis of the optical intensity in the green channel from images taken under an optical microscope, as well as Raman spectroscopy (Fig. S1).
To contact the flakes selected for the experiments, electrodes were attached into a Hall bar configuration using conventional microfabrication techniques (electron-beam lithography, electron-beam evaporation, and liftoff). The electrodes consisted in a multilayer Ti/Au/SiO2 (10/50/30 nm), with Ti providing good electrical contacts to graphene and SiO2 minimizing the direct contact area between the electrodes and the ionic liquids (Fig. 1B). The electrical properties of a same graphene device were measured using different ionic liquids under identical conditions, to facilitate a direct comparison of the effect of the different ionic liquids used [we have worked with three different ionic liquids: DEME-TFSI, ABIM-TFSI, and EMIM-BF4).
Because of the sensitivity of the ionic liquid to moisture (humidity present in the liquid can significantly increase the tendency to chemical reactions when the gate voltage is applied), the part of device preparation involving ionic liquid was performed inside a glove box. The devices were then quickly transferred to the vacuum chamber of the measurement system (a cryostat equipped with a 9T magnet) and left under vacuum for several hours before starting the measurements.
Experiments were performed by measuring simultaneously the longitudinal and transverse voltage, Vxx and Vxy as a function of gate voltage bias VG applied on the Pt gate electrode (Fig. 1 B and C, and Fig. S2B). Most transport experiments were repeated several times to ensure the reproducibility of the data, and exclude the occurrence of chemical reactions between the ionic liquid and graphene, which would result in irreversible device degradation.
Supplementary Material
Acknowledgments.
We thank D. Chiba, Y. Ohno, F. Matsukura, and H. Ohno for providing the electron-beam lithography facility at Laboratory for Nanoelectronics and Spintronics, Research Institute of Electrical Communication, Tohoku University. M.F.C., S.R., and A.F.M. thank S. Tarucha for support and for a collaboration during which this work has started. This research is funded by MEXT (Ministry of Education, Culture, Sports, Science, Technology) and JST (Japan Science and Technology Agency). A.F.M. gratefully acknowledges MaNEP (Materials with Novel Electronic Properties) and the Swiss National Science Foundation (project 200021_121569) for financial support.
Footnotes
The authors declare no conflict of interest.
*This Direct Submission article had a prearranged editor.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1018388108/-/DCSupplemental.
References
- 1.Du X, Skachko I, Duerr F, Luican A, Andrei EY. Fractional quantum Hall effect and insulating phase of Dirac electrons in graphene. Nature. 2009;462:192–195. doi: 10.1038/nature08522. [DOI] [PubMed] [Google Scholar]
- 2.Bolotin KI, Ghahari F, Shulman MD, Stormer HL, Kim P. Observation of the fractional quantum Hall effect in graphene. Nature. 2009;462:196–199. doi: 10.1038/nature08582. [DOI] [PubMed] [Google Scholar]
- 3.Gonzalez J, Guinea F, Vozmediano MAH. Electron-electron interactions in graphene sheets. Phys Rev B. 2001;63:134421. [Google Scholar]
- 4.Kopnin NB, Sonin EB. BCS superconductivity of Dirac electrons in graphene layers. Phys Rev Lett. 2008;100:246808. doi: 10.1103/PhysRevLett.100.246808. [DOI] [PubMed] [Google Scholar]
- 5.Uchoa B, Neto AHC. Superconducting states of pure and doped graphene. Phys Rev Lett. 2007;98:146801. doi: 10.1103/PhysRevLett.98.146801. [DOI] [PubMed] [Google Scholar]
- 6.Lee B, et al. Modification of electronic properties of graphene with self-assembled monolayers. Nano Lett. 2010;10:2427–2432. doi: 10.1021/nl100587e. [DOI] [PubMed] [Google Scholar]
- 7.Stoller MD, Park SJ, Zhu YW, An JH, Ruoff RS. Graphene-based ultracapacitors. Nano Lett. 2008;8:3498–3502. doi: 10.1021/nl802558y. [DOI] [PubMed] [Google Scholar]
- 8.Ohno Y, Maehashi K, Yamashiro Y, Matsumoto K. Electrolyte-gated graphene field-effect transistors for detecting pH protein adsorption. Nano Lett. 2009;9:3318–3322. doi: 10.1021/nl901596m. [DOI] [PubMed] [Google Scholar]
- 9.Novoselov KS, et al. Electric field effect in atomically thin carbon films. Science. 2004;306:666–669. doi: 10.1126/science.1102896. [DOI] [PubMed] [Google Scholar]
- 10.Geim AK, Novoselov KS. The rise of graphene. Nat Mater. 2007;6:183–191. doi: 10.1038/nmat1849. [DOI] [PubMed] [Google Scholar]
- 11.Cho JH, et al. High-capacitance ion gel gate dielectrics with faster polarization response times for organic thin film transistors. Adv Mater. 2008;20:686–690. [Google Scholar]
- 12.Shimotani H, et al. Insulator-to-metal transition in ZnO by electric double layer gating. Appl Phys Lett. 2007;91:082106. [Google Scholar]
- 13.Dhoot AS, Israel C, Moya X, Mathur ND, Friend RH. Large electric field effect in electrolyte-gated manganites. Phys Rev Lett. 2009;102:136402–136405. doi: 10.1103/PhysRevLett.102.136402. [DOI] [PubMed] [Google Scholar]
- 14.Ueno K, et al. Electric-field-induced superconductivity in an insulator. Nat Mater. 2008;7:855–858. doi: 10.1038/nmat2298. [DOI] [PubMed] [Google Scholar]
- 15.Ye JT, et al. Liquid-gated interface superconductivity on an atomically flat film. Nat Mater. 2010;9:125–128. doi: 10.1038/nmat2587. [DOI] [PubMed] [Google Scholar]
- 16.Das A, et al. Monitoring dopants by Raman scattering in an electrochemically top-gated graphene transistor. Nature Nanotechnol. 2008;3:210–215. doi: 10.1038/nnano.2008.67. [DOI] [PubMed] [Google Scholar]
- 17.Xia JL, Chen F, Li JH, Tao NJ. Measurement of the quantum capacitance of graphene. Nature Nanotechnol. 2009;4:505–509. doi: 10.1038/nnano.2009.177. [DOI] [PubMed] [Google Scholar]
- 18.Chen F, Qing Q, Xia JL, Li JH, Tao NJ. Electrochemical gate-controlled charge transport in graphene in ionic liquid and aqueous solution. J Am Chem Soc. 2009;131:9908–9909. doi: 10.1021/ja9041862. [DOI] [PubMed] [Google Scholar]
- 19.Efetov DK, Kim P. Controlling electron-phonon interactions in graphene at ultrahigh carrier densities. Phys Rev Lett. 2010;105:256805. doi: 10.1103/PhysRevLett.105.256805. [DOI] [PubMed] [Google Scholar]
- 20.Shon NH, Ando T. Quantum transport in two-dimensional graphite system. J Phys Soc Jpn. 1998;67:2421–2429. [Google Scholar]
- 21.Chen JH, et al. Charged-impurity scattering in graphene. Nat Phys. 2008;4:377–381. [Google Scholar]
- 22.Appel J. Interband electron-electron scattering and transport phenomena in semiconductors. Phys Rev. 1962;125:1815–1823. [Google Scholar]
- 23.Koshino M, Ando T. Transport in bilayer graphene: Calculations within a self-consistent Born approximation. Phys Rev B. 2006;73:245403. [Google Scholar]
- 24.Koshino M. Electronic transport in bilayer graphene. New J Phys. 2009;11:095010. [Google Scholar]
- 25.Adam S, Hwang EH, Galitski VM, Das Sarma S. A self-consistent theory for graphene transport. Proc Natl Acad Sci USA. 2007;104:18392–18397. doi: 10.1073/pnas.0704772104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Stauber T, Peres NMR, Guinea F. Electronic transport in graphene: A semiclassical approach including midgap states. Phys Rev B. 2007;76:205423. [Google Scholar]
- 27.Ostrovsky PM, Gornyi IV, Mirlin AD. Electron transport in disordered graphene. Phys Rev B. 2006;74:235443. [Google Scholar]
- 28.Katsnelson MI, Geim AK. Electron scattering on microscopic corrugations in graphene. Philos Trans R Soc A. 2008;366:195–204. doi: 10.1098/rsta.2007.2157. [DOI] [PubMed] [Google Scholar]
- 29.Oostinga JB, Heersche HB, Liu XL, Morpurgo AF, Vandersypen LMK. Gate-induced insulating state in bilayer graphene devices. Nat Mater. 2007;7:151–157. doi: 10.1038/nmat2082. [DOI] [PubMed] [Google Scholar]
- 30.Craciun MF, et al. Trilayer graphene is a semimetal with a gate-tunable band overlap. Nat Nanotechnol. 2009;4:383–388. doi: 10.1038/nnano.2009.89. [DOI] [PubMed] [Google Scholar]
- 31.Yuan HT, et al. High-density carrier accumulation in ZnO field-effect transistors gated by electric double layers of ionic liquids. Adv Funct Mater. 2009;19:1046–1053. [Google Scholar]
- 32.Novoselov KS, et al. Two-dimensional atomic crystals. Proc Natl Acad Sci USA. 2005;102:10451–10453. doi: 10.1073/pnas.0502848102. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.