Evolution of direct reciprocity under uncertainty can explain human generosity in one-shot encounters

Abstract

Are humans too generous? The discovery that subjects choose to incur costs to allocate benefits to others in anonymous, one-shot economic games has posed an unsolved challenge to models of economic and evolutionary rationality. Using agent-based simulations, we show that such generosity is the necessary byproduct of selection on decision systems for regulating dyadic reciprocity under conditions of uncertainty. In deciding whether to engage in dyadic reciprocity, these systems must balance (i) the costs of mistaking a one-shot interaction for a repeated interaction (hence, risking a single chance of being exploited) with (ii) the far greater costs of mistaking a repeated interaction for a one-shot interaction (thereby precluding benefits from multiple future cooperative interactions). This asymmetry builds organisms naturally selected to cooperate even when exposed to cues that they are in one-shot interactions.

Human behavior in all known cultures is densely interpenetrated by networks of reciprocity or exchange (to use the terms of biologists and economists, respectively). Fueled by these observations, biologists and game theorists developed models that outlined how the fitness benefits to be reaped from gains in trade can, under the right envelope of conditions, drive the evolution of decision-making adaptations for successfully engaging in direct reciprocity (1–5). Indeed, a broad array of experimental and neuroscientific evidence has accumulated over the last two decades supporting the hypothesis that our species’ decision-making architecture includes both cognitive and motivational specializations whose design features are specifically tailored to enable gains through direct reciprocity (e.g., detection of defectors and punitive sentiment toward defectors) (6–16).

The most important condition necessary for the evolution of direct reciprocity is that interactions between pairs of agents be sufficiently repeated (2). For reciprocity to operate, after one agent delivers a benefit, the partner must forgo the immediate gain offered by cheating—that is, of not incurring the cost involved in returning a comparable benefit. In general, selection can only favor forgoing this gain and incurring the cost of reciprocating when the net value to the partner of the future series of exchange interactions (enabled by reciprocation) exceeds the benefit of immediate defection (which would terminate that future series). If there were no future exchanges—if an interaction was one-shot—then the equilibrium strategy would be always defect. However, both direct observations and the demographic conditions that characterize hunter–gatherer life indicate that large numbers of repeat encounters, often extending over decades, was a stable feature of the social ecology of ancestral humans (17).

Despite this close fit between theory and data for direct reciprocity, problems emerged in closely related issues. In particular, when experimentalists began using laboratory economic games to test theories of preferences and cooperation, they uncovered some serious discrepancies between observed experimental behavior and the predictions of traditional economic models of rationality and self-interest (18–21). Some of these results have proven equally challenging to biologists, because they seem to violate the expectations of widely accepted models of fitness maximization that predict selfishness in the absence of either (i) genetic relatedness, (ii) conditions favoring reciprocity, or (iii) reputation enhancement (22).

The most glaring anomaly stems from the fact that, according to both evolutionary and economic theories of cooperation, whether an interaction is repeated or one-shot should make a crucial difference in how agents act. The chance of repeated interactions offers the only possibility of repayment for forgoing immediate selfish gains when the interactants are not relatives and the situation precludes reputation enhancement in the eyes of third parties. Specifically, in an anonymous one-shot interaction, where (by definition) there will be no future interactions or reputational consequences, it seems both well-established and intuitive that rational or fitness-maximizing agents ought to choose the higher payoff of behaving selfishly (defecting) over cooperating. In one-shot games, cooperative or other altruistic choices were theoretically expected to vanish (2, 23).

Empirically, however, individuals placed in anonymous, one-shot experimental games seem far more altruistic than biologists, economists, and game theorists predicted (18–22). To explain these anomalies, a proliferating series of alternative economic, evolutionary, cultural, and psychological explanations has been advanced, many proposing major revisions to the foundations of economic theory and to standard views of how social evolution typically works (24–30). These explanations have ranged from reconceptualizations of economic rationality and proposals of generalized other-regarding preferences to accounts of altruism produced variously through genetic group selection, cultural group selection, or gene–culture coevolution.

Whatever the merit of these hypotheses (31–36), however, they all start from the widely accepted assumption that the highest paying (or most rational) decision procedure is: If you are in a one-shot interaction, always defect. However, a number of questions arise when one dissects this assumption as part of an attempt to turn it into decision-making procedures that an evolved agent operating in the real world could actually carry out: How much evidence should ideally be required before categorizing an interaction as one-shot? Given uncertainty about this categorization, is Always defect when the interaction has been categorized as one-shot truly the payoff-maximizing strategy? We argue that once these questions are addressed, it becomes clear that the strategy If you are in a one-shot interaction, always defect is either defective or inapplicable to evolved cooperative architectures, such as those found in the human mind. Using agent-based simulations, we show that a propensity to make contributions in one-shot games (even those without reputational consequences) evolves as a consequence of including in the architecture an overlooked computational step necessary for guiding cooperative decisions: the discrimination of one-shot from repeated interactions.

One-shot discrimination, like cheater detection (37), enables cooperative effort to be directed away from unproductive interactions. However, to behave differently in one-shot vs. repeated interactions requires the capacity to distinguish them, a judgment that must be made under uncertainty. These simulations explore the impact on cooperative decision-making architectures (or equivalently, on cooperative strategies) of evolving in conditions of uncertainty—conditions in which the discrimination of one-shot from repeated interactions can be better or worse, but never perfect and error-free.*

Imperfect discrimination is the biologically realistic case because real computational systems, such as human minds, cannot know with certainty whether an interaction is one-shot at the time the decision about cooperating must be made. Indeed, given the stochastic nature of the world, it might be correct to say that, at the time of the interaction, the interaction is not determinately either one-shot or repeated. Instead, an interaction only becomes one-shot retroactively at events that uniquely preclude additional interactions, such as the death of one of the parties. Of course, certain situations or persons may exhibit cues that lead a decision-maker to judge that an interaction is highly likely to be one-shot, but that probability can never reach certainty: While both parties live, there is always a nonzero probability of a repeated encounter, whether through error, intent, or serendipity. This logic applies with special force to the small-scale world of our ancestors, where travel was on foot and population sizes were small. In such a world, a first encounter with someone suggests a nonzero probability of encountering them again.

To judge whether an interaction is likely to be repeated or one-shot, decision-making designs engineered by evolution must use probabilistic information available in the social ecology—cues that differentially predict the two types of interactions. These cues can be present in the situation (e.g., you are traveling far from home), in the person encountered (e.g., the interactant speaks with your accent), or in both (e.g., the interactant marries into your band). In the real world, however, no cue will be perfectly predictive, and the presence of several cues may entail conflicting implications (even in laboratory experiments, verbal assurances from an experimenter may compete with situational cues suggesting that other interactants are members of one's community). Consequently, each choice is a bet, and even an ideal Bayesian observer will make errors. Therefore, agents face a standard Neyman–Pearsonian decision problem (38) with two types of possible errors: false positives and misses. A false-positive error occurs when the agent decides that (or acts as if) an interaction will be repeated, but it turns out to be one-shot. A miss occurs when the agent decides that (or acts as if) the interaction will be one-shot, but it turns out to be repeated.

Under uncertainty, decision architectures (or strategies) cannot simultaneously eliminate both types of errors; making fewer errors of one type must be paid for with more errors of the other type. If the two errors inflict costs of different magnitudes, selection will favor a betting strategy that buys a reduction in the more expensive error type with an increase in the cheaper type (13, 39, 40). We show here that the costs to the architecture of the two types of errors will be different under nearly all conditions. Defecting has the modest upside of gaining from a single instance of benefit-withholding (if it is a one-shot interaction) and a downside equal to the summed value of the future series of benefit–benefit interactions precluded by defection (if the interaction turns out to be repeated, but the partner withdraws her cooperative effort in response to the initial defection). In social ecologies where repeat interactions are numerous enough to favor the evolution of reciprocation, the value of such a forfeited benefit series will generally be large compared with expending a single retrospectively unnecessary altruistic act. Overall, these asymmetric costs evolutionarily skew decision-making thresholds in favor of cooperation; as a result, fitter strategies will cooperate “irrationally” even when given strong evidence that they are in one-shot interactions.

Model

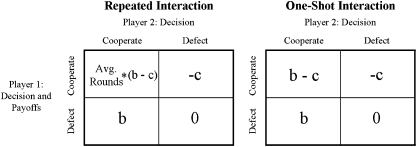
To investigate the effect of selection on cooperative decision-making in a world where organisms can only imperfectly discriminate one-shot from repeated interactions, we conducted simulations^† of agents interacting in two-player prisoner's dilemmas (PDs). (An analytic exploration is in SI Text.) PDs, the most common model for cooperative decision-making, can have one or more rounds of interaction. Within a round, defection always pays more than cooperation, regardless of the other player's actions. However, the relative costs and benefits are arranged such that mutual cooperation is better than mutual defection (Fig. 1). Agents face two types of PDs: one-shot PDs consisting of a single round, and indefinitely repeated PDs consisting of a first round and a stochastic number of subsequent rounds. Agents are not given perfect knowledge of which type of PD they are in, but only a probabilistic cue.

Fig. 1.

Under realistic parameter values, the largest possible benefits occur when both players cooperate in a repeated interaction. This figure shows payoffs in a two-player PD as a function of players’ strategies and whether the interaction is one-shot or repeated. Payoffs assume that cooperation entails playing TIT-for-TAT or GRIM, and defection entails defecting forever (SI Text). Avg. Rounds, average number of rounds of the PD in repeated interactions; b, within-round benefit delivered to partner by cooperation; c, cost of delivering within-round benefit.

Agents can commit two types of errors. One error is to cooperate in a one-shot interaction, paying the cost of cooperating without increasing the benefits received (Fig. 1 Right, upper right square). A second error is to defect in a repeated interaction, missing the associated opportunity for long-term, mutually beneficial exchange. This error is typically far more costly. As shown in Fig. 1 Left, upper left square, when (i) the net within-round benefits of cooperation and (ii) the number of rounds become large enough, this payoff will be much larger than any other payoff.

In each simulation, all agents have identical rules for deciding when to cooperate or defect; the only component of their psychology that can vary is the value of a regulatory variable that is consulted by these rules. Before their interactions, they observe a cue value that probabilistically—but imperfectly—reflects the type of PD that they face. The decision rule then operates on the cue with procedures that are calibrated by an evolvable regulatory variable to produce a decision of whether to cooperate or defect. Described more fully below (SI Text), these variables determine how likely agents are to cooperate or defect based on the cues that they perceive. We allow the magnitudes of these decision-regulating variables to evolve by natural selection based on their fitness consequences. To explore how broad or narrow the conditions are that favor cooperation in one-shot interactions, across simulations we parametrically varied (i) the relative frequency of one-shot vs. repeated interactions, (ii) the average length of indefinitely repeated interactions, and (iii) the within-round benefits of cooperation.

Our goal is to determine whether agents evolve to cooperate as opposed to defect in one-shot interactions; it is not to determine exactly which of the many cooperative strategies discussed in the literature would ultimately prevail in our simulated social ecology. Thus, as a representative strategy, our main simulations use the well-known, conditionally cooperative TIT-for-TAT strategy to represent an agent's choice to cooperate. TIT-for-TAT cooperates on the first round of an interaction and thereafter copies its partner's behavior from the previous round (2). (Using a contingently cooperative strategy is important because noncontingent, pure cooperation cannot evolve, even if all interactions are indefinitely repeated.) When an agent chooses to cooperate, it does so by playing TIT-for-TAT. When it chooses to defect instead, it defects on all rounds of an interaction, regardless of its partner's behavior. We also checked whether our main results are robust against the possibility of behavioral errors (accidental defections) by using a contingently cooperative strategy that is much less forgiving than TIT-for-TAT, permanently shutting down cooperation after even a single act of defection (see below).

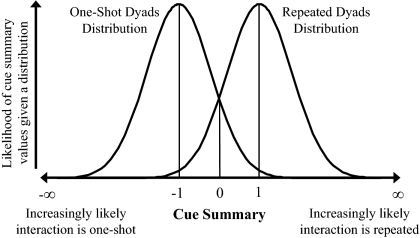
In the real world, agents can perceive multiple cues that probabilistically predict whether their interaction with a partner will be one-shot or repeated. Some of these cues involve personal characteristics of the partner, whereas other cues involve characteristics of the situation. Although the perception and use of such cues is surely an independent target of selection, such complexity is orthogonal to the scope of this investigation. Rather, we simply model this informational ecology by assuming that all cues, situational and personal, could be collapsed into a single number—a cue summary—that is associated with a partner. Cue summaries are modeled as two normally distributed random variables, one for each type of PD (Fig. 2). Larger observed cue summaries imply a greater chance that the interaction is repeated. The fourth and final exogenous parameter varied in our simulations is the distance between the cue summary distributions. A greater distance makes it easier to correctly discriminate one-shot from repeated interactions.

Fig. 2.

The distributions of cue summary values showing that repeated interactions are associated with larger-valued cue summaries. Agents are paired and randomly assigned to be part of one-shot or repeated interactions irrespective of genotype. Moreover, given the interaction that they face, agents are randomly assigned cue summaries from the appropriate cue summary distribution, irrespective of their genotype.

Within a simulation, each generation of 500 agents was sorted into dyads, and dyads were assigned to be one-shot or repeated, both randomly with respect to genotype. Each member of a dyad independently and randomly with respect to genotype drew a cue summary from the one-shot distribution (if they had been assigned to a one-shot dyad) or from the repeated distribution (if they had been assigned to a repeated dyad) (Fig. 2). Thus, agents’ strategies (i.e., the evolvable variables embedded in their decision rules) are completely uncorrelated with which type of PD they face and the value of their cue summary. Of course, cue summaries and types of PDs are necessarily—although imperfectly—correlated. Within each generation, agents behaved in accordance with their decision rules, accrued fitness based on their PD's outcome, reproduced asexually in proportion to their fitness, and then died. This cycle occurred through 10,000 generations for each simulation run. Each run had fixed parameter values, and four replicate runs were conducted for each fixed parameter set.

As a clarifying idealization, one can partition a behavior-regulating architecture (or strategy) into components concerned with representing states of the world (cognitive components) and components that transform such representations into decisions about what actions to take (motivational components). The strategy most often articulated in standard models—Defect when you are in a one-shot interaction—can be mapped into these components as follows:

• i) Cognitive component: Compute your beliefs about whether you are in a one-shot or repeated interaction as accurately as possible.

• ii) Motivational component: Given the state of your beliefs, be motivated to act in a manner consistent with your beliefs—that is, act to give yourself the highest payoff, assuming your belief is true. This logic reduces to: If you believe that you are in a one-shot interaction, defect; If you believe that you are in repeated interaction, cooperate.

Each of these decision-making components embodies canonically rational decision-making methods, and jointly, they prescribe what is typically believed to be ideal strategic behavior in PDs. Here, we show that neither of these forms of rationality produces the fittest or best-performing strategic choice when there is uncertainty about whether an interaction is one-shot or repeated. That is, when key aspects of these decision-making rules are subjected to mutation and selection, better performing alternatives evolve.

In a first set of simulations, the motivational component is allowed to evolve, whereas the cognitive component is fixed. Here, the agents’ cognitive component specifies that they use Bayesian updating to form ideally rational beliefs to discriminate the kind of interaction that they face. The motivational component, however, references an evolvable regulatory variable: Cooperation Probability_One-Shot. This variable specifies the probability of cooperation given a belief that the interaction is one-shot. Instead of being fixed at what is typically assumed to be the optimal value—0% cooperation (i.e., 100% defection)—in these simulations, the probability of cooperation given a one-shot belief is left free to evolve.

In a second set of simulations, the motivational component is fixed such that organisms never cooperate given a belief the interaction is one-shot and always cooperate given a belief the interaction is repeated. Now, the cognitive component references an evolvable regulatory variable, a decision threshold; this variable sets the weight of evidence required for the agent to conclude that it is in a one-shot interaction.

In the human case, of course, both cognitive and motivational elements might have been simultaneously shaped by these selection pressures, leaving an infinite set of candidate cooperative architectures to consider. The two architectures explored here, however, bracket the spectrum of possible architectures, allowing us to separately test the performance of each component of standard rationality (more discussion is in SI Text).

Results

Simulation Set 1.

Given accurate belief formation, how will selection shape the motivation to cooperate? Starting with a common assumption in economics and psychology, in this set of simulations, agents’ decision rules use Bayesian updating to form optimally rational beliefs (23, 41). Using Bayesian updating, agents compute the (posterior) probabilities that their interaction is one-shot or repeated by integrating their partner's cue summary with the relative frequencies of one-shot and repeated PDs in their environment. For simplicity, we assume that our agents have innate and perfect knowledge of these base rates (this works against our hypothesis by giving agents the most accurate beliefs possible). Given these updated probabilities, if it is more likely that the interaction is one-shot, then the agent believes that it is one-shot; otherwise, the agent believes that it is repeated.

Unlike standard models of cooperation, however, there is no direct mapping between belief and action in this simulation. Agents with one-shot beliefs do not necessarily defect; agents with repeated beliefs do not necessarily cooperate. Instead, agents access one of two inherited motivational variables: Cooperation Probability_One-Shot and Cooperation Probability_Repeated. Because these variables are subject to mutation and selection, and hence can evolve, it is possible for selection to move one or both to any value between zero and one.

In contrast to previous accounts, our analysis predicts that Cooperation Probability_One-Shot will evolve to be larger than zero—generating cooperation even when agents have one-shot beliefs—because the costs of missing repeated cycles of mutually beneficial cooperation outweigh the costs of mistaken one-shot cooperation. We test this prediction by setting the regulatory variables of the first generation such that beliefs and actions are perfectly consistent—optimal on the standard view. First-generation agents always cooperate when they believe the interaction is repeated (Cooperation Probability_Repeated ≈ 1) and never cooperate with a one-shot belief (Cooperation Probability_One-Shot ≈ 0) (SI Text). If the canonically rational decision rules were in fact optimal, then selection should not change these values.

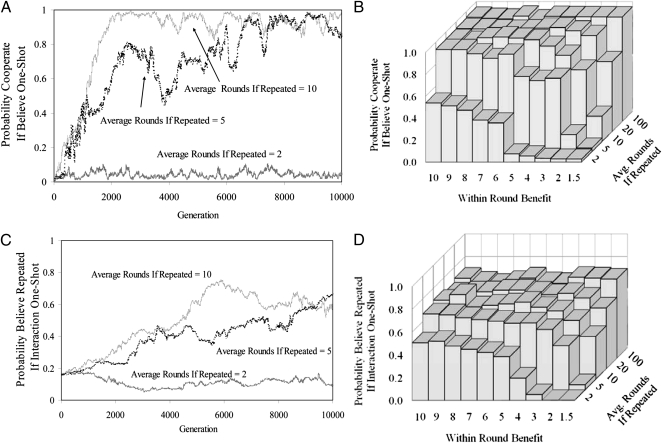
We ran 3,000 simulations in this set (SI Text). Fig. 3A shows how Cooperation Probability_One-Shot evolves in several typical runs. For these examples, half of the dyads are one-shot, and the distance between the cue summary distributions is two (the middle value of the distances that we examined). The benefit to cost ratio within a PD round is 3:1, a relatively small value. Given these parameters, if an agent believes that she is facing a one-shot PD, there is only a 16% chance that she is wrong and instead faces a repeated PD. Nonetheless, when the average length of a repeated interaction is 5 or 10 rounds—relatively short interaction lengths—agents with a one-shot belief nonetheless evolve to cooperate a remarkable 87% or 96% of the time, respectively. When discrimination is even easier—when the distance between distributions is three—there is only a 7% chance that an agent with a one-shot belief is actually facing a repeated interaction. In this case, when the average number of interactions is only 10, then agents with a one-shot belief evolve to cooperate 47% of the time, despite the fact that such interactions will turn out to be repeated only 7% of the time (SI Text).

Fig. 3.

One-shot cooperation evolves when interactions are moderately long and benefits are moderately large. (A) Example evolutionary dynamics showing that the probability of cooperation, given a rational (ideal Bayesian) belief that an interaction is one-shot, evolves to be high when the motivational architecture is allowed to evolve based on its fitness consequences. (B) Aggregated final stabilized values across all runs where the motivational architecture is free to evolve and half of all interactions are repeated; this example shows that the probability of cooperating despite a rational belief that an interaction is one-shot evolves to be high except when the benefits of cooperating and the average length of repeated interactions are both small. (C) Example evolutionary dynamics showing that agents evolve to become highly resistant to concluding that interactions are one-shot, even in the face of strong evidence that interactions are one-shot, when the weight of evidence required by the cognitive architecture is allowed to evolve. These stringent thresholds to conclude the interaction is one-shot results in a high probability of cooperating, even when the interaction is actually one-shot. (D) Aggregated final stabilized values across all runs where the cognitive architecture is free to evolve and one half of all interactions are repeated. These data show that the probability of cooperating when the interaction is one-shot evolves to be high, except when benefits of cooperating and the average length of repeated interaction are both small. For A and C, the benefit to cost ratio is 3:1, half of all interactions are repeated, and the distance between cue summary distributions (a measure of the ease of discriminating one-shot from repeated interactions) is 2 SDs. Traditionally, it has been assumed that the highest paying strategy is to cooperate 0% of the time whenever an interaction is likely to be one-shot.

Fig. 3B summarizes the values that Cooperation Probability_One-Shot evolves to as a function of (i) the benefits that can be gained in a single round of cooperation and (ii) the average length of repeated interactions, with the other parameters fixed. As predicted, Cooperation Probability_One-Shot evolves to higher values when either of these variables increases. When benefit size and interaction length parameters exceed those used in the examples above, Cooperation Probability_One-Shot evolves to be extremely high. In many cases, the regulatory variables evolve such that agents almost always cooperate, even with an explicit belief that their interaction is one-shot (Fig. 3B, Figs. S1 and S2, and Table S1).

Simulation Set 2.

Given behavior that is consistent with belief, how will selection shape the formation of such beliefs? We conducted an additional set of simulations to explore this case, where the cognitive rule, but not the motivational rule, was allowed to evolve. The motivational rule was fixed at what is conventionally considered to be optimal: Defect if you believe that the interaction is one-shot; Otherwise, cooperate. Here, agents do not form optimally rational beliefs by Bayesian updating. Instead, agents execute a fast and frugal heuristic (42); agents simply observe their partner's cue summary, compare it with an evolvable decision threshold value, and believe the interaction is repeated or not based on that comparison. This threshold value can be seen as the level of evidence that the agent requires before it believes that an interaction is repeated and chooses to cooperate. As before, to work against our hypothesis, we set the average threshold values for first-generation agents at the value that equalized the rates of the two error types (e.g., a threshold of 0 when the base rates of one-shot and repeated dyads are both 0.5).

Paralleling the previous results, here, agents also typically evolve to cooperate, despite strong evidence that the interaction is one-shot. For example, with the same parameter values used in the upper lines of Fig. 3A (i.e., where cooperation has only modest benefits), Fig. 3C shows that agents evolve to have belief thresholds that lead them to cooperate ∼60% of the time when their interaction is actually one-shot. In contrast, given these thresholds, agents will only defect 1% of the time when their interaction is actually repeated.

Again, paralleling the previous results, Figs. 3D, Figs. S3 and S4 and Table S2 demonstrate that, across multiple simulation runs, greater within-round benefits to cooperation and longer interactions cause the evolution of agents who are increasingly likely to cooperate, even when given evidence that they are in a one-shot interaction. This move to increasing cooperativeness is accomplished by creating a cognitive rule that requires very high levels of evidence before it will conclude that the interaction is one-shot. As expected, the cognitive architecture evolves to make fewer expensive errors (defecting in repeated interactions) at the cost of a higher frequency of the cheaper errors (cooperating in one-shot interactions). Cognitive architectures that are highly resistant to concluding that interactions are one-shot are favored by selection over architectures that are cognitively more accurate.

It is important to ensure that these two sets of results are not fragilely predicated on specific assumptions of our formalizations. We checked the robustness of these two parallel results in several ways. First, we reran both sets of simulations but allowed agents to erroneously defect when their strategy specifies cooperation on a given round. Errors have been shown to have important consequences for evolutionary dynamics, revealing hidden assumptions in models that, once removed, can prove evolutionarily fatal to certain strategies (43). In these simulations, we used the GRIM strategy, because it militates against our hypothesis. Although including such errors necessarily lowers the average benefits of repeated cooperation—because the GRIM strategy shuts down cooperation after a single experience of defection—the qualitative dynamics of our simulations remain unchanged. Agents still robustly evolve to cooperate in one-shot interactions (SI Text and Figs. S2 and S4).

As a final check, we created a simple, nondynamic, best-response analytic model of ideal behavior in this kind of uncertain ecology. Paralleling the simulation results, this model shows that agents will be designed to cooperate when they believe that the interaction is one-shot if interactions are sufficiently long and within-round benefits sufficiently large. Indeed, when the benefits of repeated cooperation are sufficiently large, agents should always cooperate, even when presented evidence that they face a one-shot interaction (SI Text, Eqns. S1 and S2). Regardless of the method used, cooperation in one-shot encounters is a robust result of selection for direct reciprocity, once the necessary step of discriminating one-shot from repeat encounters is explicitly included as part of the decision problem.

Discussion

Despite the fact that cooperation in one-shot interactions is viewed as both biologically maladaptive and economically irrational, it is nonetheless behaviorally widespread in our species. This apparent anomaly has posed a challenge to well-established theories in biology and economics, and it has motivated the development of a diverse array of alternatives—alternatives that seem to either conflict with known selection pressures or sensitively depend on extensive sets of untested assumptions.

These alternatives all assume that one-shot cooperation is an anomaly that cannot be explained by the existence of cooperative architectures that evolved for direct reciprocity. Our main results show that this assumption is false: organisms undergoing nothing but a selective regime for direct reciprocity typically evolved to cooperate even in the presence of strong evidence that they were in one-shot interactions. Indeed, our simulated organisms can form explicit beliefs that their interactions are one-shot and, nonetheless, be very likely to cooperate. By explicitly modeling the informational ecology of cooperation, the decision-making steps involved in operating in this ecology, and selection for efficiently balancing the asymmetric costs of different decision errors, we show that one-shot cooperation is the expected expression of evolutionarily well-engineered decision-making circuitry specialized for effective reciprocity.

This cooperation-elevating effect is strong across broad regions of parameter space. Although it is difficult to precisely map parameters in simplified models to real-world conditions, we suspect that selection producing one-shot generosity is likely to be especially strong for our species. The human social world—ancestrally and currently—involves an abundance of high-iteration repeat interactions and high-benefit exchanges. Indeed, when repeated interactions are at least moderately long, even modest returns to cooperation seem to select for decision architectures designed to cooperate even when they believe that their interaction will be one-shot. We think that this effect would be even stronger had our model included the effects of forming reputations among third parties. If defection damages one's reputation among third parties, thereby precluding cooperation with others aside from one's current partner, defection would be selected against far more strongly (44). Therefore, it is noteworthy that cooperation given a one-shot belief evolves even in the simple case where selection for reputation enhancement cannot help it along. It is also worth noting that a related selection pressure—defecting when you believe your partner will not observe you—should be subject to analogous selection pressures. Uncertainty and error attach to judgments that one's actions will not be observed, and the asymmetric consequences of false positives and misses should shape the attractiveness of defection in this domain as well.

In short, the conditions that promote the evolution of reciprocity—numerous repeat interactions and high-benefit exchanges—tend to promote one-shot generosity as well. Consequently, one-shot generosity should commonly coevolve with reciprocity. This statement is not a claim that direct reciprocity is the only force shaping human cooperation—only that if reciprocity is selected for (as it obviously was in humans), its existence casts a halo of generosity across a broad variety of circumstances.

According to this analysis, generosity evolves because, at the ultimate level, it is a high-return cooperative strategy. Yet to implement this strategy at the proximate level, motivational and representational systems may have been selected to cause generosity even in the absence of any apparent potential for gain. Human generosity, far from being a thin veneer of cultural conditioning atop a Machiavellian core, may turn out to be a bedrock feature of human nature.