Abstract
Parallel transmission (PTX) has emerged as an efficient means for implementing multidimensional and/or spatially-selective radiofrequency excitation pulses. To date, most theoretical and experimental work on PTX RF pulse design is based on the small-tip-angle (STA) approximation to the Bloch equation. The STA, while mathematically compact, is not an exact solution and leads to significant errors when large-tip-angle pulses are designed. Methods have been proposed to overcome the limitations of the STA using regularized least-square optimization or optimal controls algorithms. These methods, however, are based on further approximations to the Bloch equation or require using computationally prohibitive techniques that provide no physical input to the pulse design. In this paper, a novel algorithm for large-tip-angle PTX pulse design is proposed. The algorithm relies on a perturbation analysis (PTA) of the Bloch equation and it depicts the relationship between the excited magnetization, its deviation from the target pattern and the desired pulses. Simulations and experiments are used to validate the proposed method on a 7T 8-channel transmit array. The results demonstrate that the PTA algorithm provides a faster and more accurate approach for multidimensional large-tip-angle pulse design than previously existing methods, especially when large acceleration factors and/or echo-planar trajectories are used.
Keywords: RF pulse design, parallel transmission, ultra-high field
INTRODUCTION
Parallel excitation (PTX) (1, 2) provides an effective and comprehensive means to implement complex tailored radiofrequency (RF) excitation for a wide range of MRI applications. While the fundamental framework for the design of complex RF excitations was introduced many years ago (3), the resulting RF pulses were too long for practical implementation on multidimensional selective excitation (4, 5, 6). In PTX, the use of multiple simultaneous RF channels allows shortening the duration of the RF pulse by a factor that increases with the number of independent RF channels being used. This leads to practical RF pulse designs that can be used as the foundation for improved imaging applications.
Under the Small Tip Angle (STA) approximation (3) the relationship between the desired excitation pattern and the required RF pulses can be easily estimated using the methodology introduced by Grissom et al. (7). This methodology provides an analytic expression relating the desired excitation pattern to each of the independent RF pulses in the design. The solution of the ensuing set of equations can be obtained by a variety of means, though typically methods such as the conjugate gradient yield an acceptable solution. The STA-based method (7, 8) can only be applied under the STA approximation, and it is not very effective for the design of large tip angle excitations, such as inversion and refocusing, in which case it often yields significant errors in the excitation profile (7, 9).
When the desired flip angle is large, the simple analytic expression quoted above no longer yields adequate results and other means of solution are required. One approach is to use non-linear optimization algorithms to essentially “search” through the parameter space for a solution based on the minimization of a cost functional reflecting some of the desired properties in the excitation profile and the RF pulses (10). Another approach is the so-called additive angle (AA) technique (11) in which the difference between the target magnetization profile and that produced by the STA is used to drive an iterative algorithm.
In this work, we evaluate the use of a new approach for PTX pulse design that is based on a perturbation analysis of the Bloch equation and is recently reported as PTA method (12). In this approach, the difference between the target magnetization profile and that produced by the STA can be analytically expressed as a function of the applied RF pulses. This analytical expression can then be used to calculate corrections for the applied RF pulse in an iterative fashion. We demonstrate with simulations as well as experimental results that this approach leads to fast convergence and improved excitation quality during PTX pulse design.
THEORY
Analytic Framework
In the rotating frame, for a multidimensional spatial selective excitation, the Bloch equation, without relaxation terms, and including the radiofrequency (RF) B1(t) = B1,x (t) + iB1, y (t) and gradient fields G(t) = [Gx(t) Gy(t) Gz(t)]T simultaneously applied can be written as follows:
| [1] |
where [Mx My Mz]T represents the x, y, z components of the magnetization vector at spatial location r = [x y z]T at time t and γ is the gyromagnetic ratio of the excited nucleus. This equation can be used to determine the magnetization state following a RF excitation for given an initial magnetization state . The goal of RF pulse design is to develop methods for designing RF pulses that rotate magnetization from an initial state at the beginning of the RF pulse, to a desired state at the end of the RF pulse.
The proposed method is derived directly from a perturbation analysis to the Bloch equation and it is analogous in concept to the ‘Additive Angle’ method of Grissom et al. (11). We first write the transverse magnetization in complex form, Mxy = Mx + iMy, and use the excitation k-space notation introduced by Pauly et al. (3) to obtain the following “formal” solution to the Bloch equation:
| [2] |
| [3] |
where “×” in “Mxy (r, t)×b1 (t)” is the cross product operator for vectors. Combining Eq. [2] and Eq. [3], we can write the transverse magnetization as follows,
| [4] |
Equation [4] readily illustrates the inherent non-linear dependence of the Bloch equation on the excitation RF and can also be used to illustrate the errors introduced when the STA method (3) is used. Essentially, the contribution of the non-linear term in equation [4] is neglected. A corollary of this expression is that the expected error when the STA is used can also be estimated by calculating an upper bound for the second term in equation [4].
In the context of parallel transmission (PTX), the equation above is modified to include the spatially weighted transmit sensitivity map S(r),
| [5] |
This equation is the starting point for the perturbation analysis (PTA) used in this work. If we denote by MD the desired transverse magnetization and by Mp the excited transverse magnetization at spatial position r created by RF pulses B1{b1,…,bR} and respectively, where satisfies equation [7], then we have,
| [6] |
| [7] |
Subtract Eq. [7] from Eq. [6], and denote ΔM = MD − MP and we then obtain
| [8] |
where represents the longitudinal magnetization created by , k(t) is the excitation k-space trajectory as defined in Ref. (3). Note that by making (small-tip-angle approximation) and keeping only the first term in equation [8], the formula used in the AA method (11) is obtained.
Numerical Solution
In the PTA approach, equation [8] is used for designing RF pulses by minimizing the following cost function,
| [9] |
| [10] |
where (j denotes the iteration number) is the difference between the longitudinal magnetization created by and by . The matrix A incorporates the Fourier kernel exp(i2πkr) for the k-space traversal and field map corresponding to B0 inhomogeneity. The W is a spatial error weighting mask that can be used to specify a region of interest (ROI). The regularization parameter β is used to compromise RF power and excitation error. The minimization problem can be solved by using the Conjugate Gradient (CG) method. Because no approximations are applied, the proposed method is not restricted by flip angles and k-space trajectories.
In the algorithm considered here, we use an initial set of RF pulses calculated via the STA parallel pulse design method in Ref. (7), to excite an initial transverse magnetization. The difference between this initial magnetization and the target magnetization profile is then calculated and used as the driving term in equation [8]. The “corrected” RF pulse, , is then used to drive a Bloch equation solver so that the required time-dependent terms in equation [8] are calculated and the process is repeated until convergence is achieved. During the iterative solution, it is not necessary to constraint the phase of the transverse magnetization since the phase information is already incorporated in the expression for the transverse magnetization. During the iterations, the regularization parameter β effectively balances the excitation accuracy and RF power, and, therefore, cannot be set in an arbitrary fashion. Specifically, the regularization parameter β is adjusted for each iteration using the ‘L-curve’ method (13), albeit at the expense of an increase in the computational time. This computational time, however, can be effectively managed by allowing the regularization parameter to be constrained within a prescribed range.
METHODS
B1+ Mapping
One of the more important ingredients for effective PTX pulses design is the rapid and accurate mapping of the B1+ profiles of the transmit coil array in both experimental phantoms and humans. A technique similar to the method proposed by Kerr et al. (14) was employed to estimate the B1+ profiles. This technique relied on RF transmission via slice-selective excitation for a set of voltages, namely, 30V, 60V, 90V, 120V and 150V, and fitting of the resulting sinusoidal signal intensity on pixel-by-pixel basis. A standard nonlinear fitting algorithm in the MATLAB toolbox was employed to perform the aforementioned fit and the desired B1+ profiles were extracted from the “apparent” frequency of the sinusoid. The saturated double angle method proposed by Cunningham et al. (15) was also used whenever a reduction in scan time was desired, albeit at the expense of a minor decrease in mapping accuracy. An example of the B1+ profiles obtained in this fashion is presented in Figure. 1 (a).
Figure 1.

Magnitude of water phantom B1+ map (a) and field map (b) used in the simulations of eight-channel parallel excitation
Main Field Inhomogeneity Mapping
A FLASH sequence with TE1=3.7 ms and TE2=4.7 ms, respectively, was used to estimate the B0 map, and incorporate its value into the RF pulse design (7, 11, 16) and reduce the effects of magnetic field inhomogeneities while improving the robustness of the RF pulse design. This B0 compensation proved particularly useful during the use of high acceleration in PTX. The measured B0 map is shown in Figure. 1 (b).
Pulse Design
Two-dimensional RF pulses were designed using the STA (7), AA (11) and PTA methods, respectively, and the results compared using computer simulations as well as experimental data. The desired pattern was a rectangle of 4.5 × 9 cm2 on a 64 × 64 grid, within a FOV of 20 × 20 cm2. The RF pulses were smoothed with a Gaussian filter in order to reduce Gibbs ringing in the excitation patterns. When evaluating the performance of the RF pulse designs, the difference between the target and excited magnetizations was computed over the entire excited slice. Maximizing the spin excitation within the excited patterns and minimizing the spin excitation everywhere else were simultaneously implemented. We used the Root-mean-square error (RMSE) defined as with ROI masked between the desired and excited patterns to evaluate the accuracy. Both additive angle design and perturbation analysis design were initialized with small tip angle designed pulses, with the same tip angle and with 50 CG iterations. Regularization parameter β of 10 was chosen. All pulse designs and simulations were performed in MATLAB 2009a (Mathworks, Natick, MA).
Computer Simulations
RF pulses were designed using spiral (SP) and echo-planar (EP) excitation k-space trajectories, respectively. Spiral trajectories were outward with maximum gradient amplitude of 40 mT/m and a maximum slew rate of 150 mT/m/ms. PTX acceleration was achieved by undersampling the k-space trajectories in the radial direction. The EP trajectories were designed using the using a maximum gradient amplitude of 36mT/m and maximum slew rate of 120 mT/m/ms. For the EP trajectories, acceleration was achieved by undersampling along the phase-encoding dimension. In all cases, the acceleration factor (R) was defined as the number of interleaved trajectories. To test the effectiveness of the proposed methodologies acceleration factors of 2, 3, 4, 5 and 6 for both spiral and EP trajectories were used. Likewise, excitation patterns with tip angles of 90 and 180 degrees were also used. Inversion as well as refocusing pulses was designed. The initial magnetization was set along the +z and +y axes for the inversion and refocusing pulses, respectively.
Experimental Data Acquisition
All experiments were performance on a Siemens 7T Magnetom scanner (Erlangen, Germany) equipped with an 8-channel parallel transmit (PTX) RF system and a gradient set capable with a maximum amplitude of 40mT/m and a maximum slew rate of 170 mT/m/ms. An 8-channel transmit/receive volume birdcage coil was used for all experiments. The phantom used for the experimental data acquisition consisted an 8cm diameter sphere filled with 1.25 g/liter of nickel sulfate and 5 g/liter of sodium chloride.
For experimental data acquisition, SP designs with acceleration factors of 2, 4 and 6, were used. The nominal flip angle was 90° for all experiments. The data were acquired with a 2D gradient recalled echo (GRE) sequence using the following parameters: matrix= 64 × 64, FOV= 20 × 20 cm2, voxel resolution =3.125 × 3.125 mm2. Repetition time (TR) =700 ms, echo time (TE) =2.41 ms, slice thickness = 5.0 mm and bandwidth =300 Hz/pixel. In order to minimize scanning time, we employed partial Fourier on both phase and slice directions (6/8 partial Fourier). Variable density SP designs (17) with a undersampling factor of 2 were also used to reduce the SAR and allow achieving the transmission voltages to remain within the limits required by the RF coil.
For each method of pulse design (i.e., STA, AA and PTA) transmission voltages were calibrated through non-linear fitting of the sinusoidal signal intensity in a data set with varying excitation (30V, 60V, 90V, 120V and 150V) in an experimental phantom. The transmission voltages for different methods were obtained by simply scaling the RF pulses. The estimated voltages for a 90° flip angle were 70V, 118V and 132V for STA, AA and PTA, respectively.
RESULTS
Computer Simulations
Figure 2 shows simulated excitation pattern produced by a selective 90° excitation pulses for a SP trajectory using the STA, AA and PTA methods with various acceleration factors (R= 2, 4, 6). At low acceleration (R=2, Figs. 2a, 2d and 2g), the STA-designed pulses yield an inaccurate pattern both in excitation strength and spatial orientation. By contrast, the excitation patterns produced by AA and PTA methods are very close to the desired targets. At medium acceleration (R=4, Figs. 2b, 2e and 2h), the excited pattern produced by AA begins to show evidence of decreased homogeneity that is not apparent on the results from the PTA technique. At high acceleration (R=6, Figs 2c, 2f and 2i), the pattern excited by STA pulses is severely distorted. For this acceleration the inhomogeneity in the AA results has increased with obvious excitation errors clearly present outside the target excitation region as well. By contrast, the PTA method is still able to yield satisfactory results despite the reduction in RF pulse length.
Figure 2.

2D selective 90° excitation pulses for a spiral trajectory with various acceleration factors R= 2, 4, 6, respectively. a-c: The transverse magnetization produced by Small Tip Angle (STA) method. d-f: The transverse magnetization produced by Additive Angle (AA) method. g-i: The transverse magnetization produced by Perturbation Analysis (PTA) method.
When the EP trajectory is used, the resulting excitation pattern is well behaved along the readout direction (left to right). However, excitation errors are readily apparent along the phase encoding direction. This is especially obvious at high acceleration (R=6) in Fig .3 (c, f, i), where even for the additive angle method there are large excitation errors. Use of the PTA approach under these conditions leads to improved results.
Figure 3.
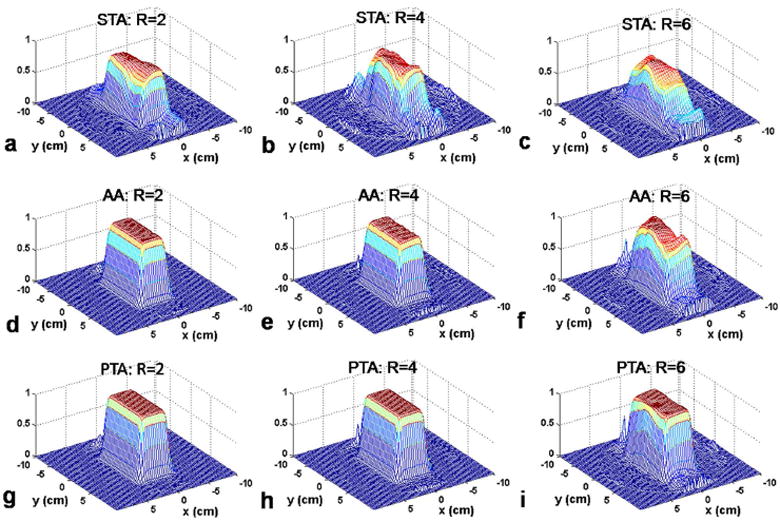
2D selective 90° excitation pulses for an EP trajectory with various acceleration factors R= 2, 4, 6, respectively. a-c: The transverse magnetization produced by Small Tip Angle (STA) method. d-f: The transverse magnetization produced by Additive Angle (AA) method. g-i: The transverse magnetization produced by Perturbation Analysis (PTA) method.
A more in-depth depiction of the quality of the excitation patterns is presented on the line plots of Figure 2 and 3. Here, a comparison of the profiles along the midline of the excitation patterns is presented for all the results. Notably, the STA designed pulses yield consistently poor profiles for both the spiral and EP trajectories. Improvements to the STA approach are clearly achieved using the AA method, though the bandwidth narrowing effect previously described by Grissom et al (11) and Pauly et al (18) is clearly present along the phase encoding direction (Fig. 4b). Excitation errors due to inaccuracies in the field map on the superior aspect of the phantom are also clearly depicted in Fig. 3(e, h). In all cases, marked improvements in excitation accuracy are obtained through the use of the PTA technique.
Figure 4.
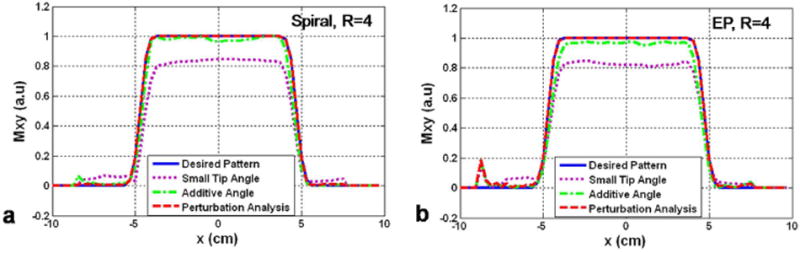
Transverse magnetization profiles taken through the center of the excited patterns in Figure 1 for spiral trajectory (a) and in Figure 2 for EP trajectory (b) with acceleration factor R=4 using Small Tip Angle method, Additive Angle method and Perturbation Analysis method, respectively.
Figure 5 presents a comparison of excitation accuracy and peak RF magnitude for the AA and PTA methods over a range of acceleration factors. In Fig. 5a, it is shown that smaller RMSE can be achieved with the PTA method for both spiral and EP trajectories over the entire range of acceleration factors. In Fig. 5b, the graphs demonstrate that the peak magnitudes for the pulses designed by the AA and PTA methods at different acceleration factors are almost identical when the spiral trajectory is used; however, the PTA method yields pulses with slightly higher than the AA technique. Consequently, the RF pulses designed with the PTA method achieve lower excitation errors without a significant increase in peak magnitude over the entire range of acceleration factors.
Figure 5.

Comparison of excitation accuracy (a) and peak RF magnitude (b) between 90° excitation pulses designed Additive Angle method and Perturbation Analysis method at various acceleration factors R=2, 3, 4, 5, 6.
Figure 6 presents selective 180° inversion pulses intended to invert the rectangle pattern used above when using spiral and EP trajectories with acceleration factor R=4. The initial magnetization vector is along +z direction at all spatial locations. Fig. 6a-c show the Mx, My and Mz magnetization profiles excited by the inversion pulses designed using the AA method with a spiral trajectory. The Mx component stays close to zero at most regions, but some magnetization flips over to Mx leading to large excitation errors. For the My component, most of the magnetization is kept close to zero over the entire field of view (Except near the edge of the pattern). The Mz component is well inverted inside the desired pattern despite the small distortions within the target pattern. These distortions are almost completely corrected by the PTA method (Fig. 6d-f), though there are only minor improvements for the Mx, My components for both methods.
Figure 6.
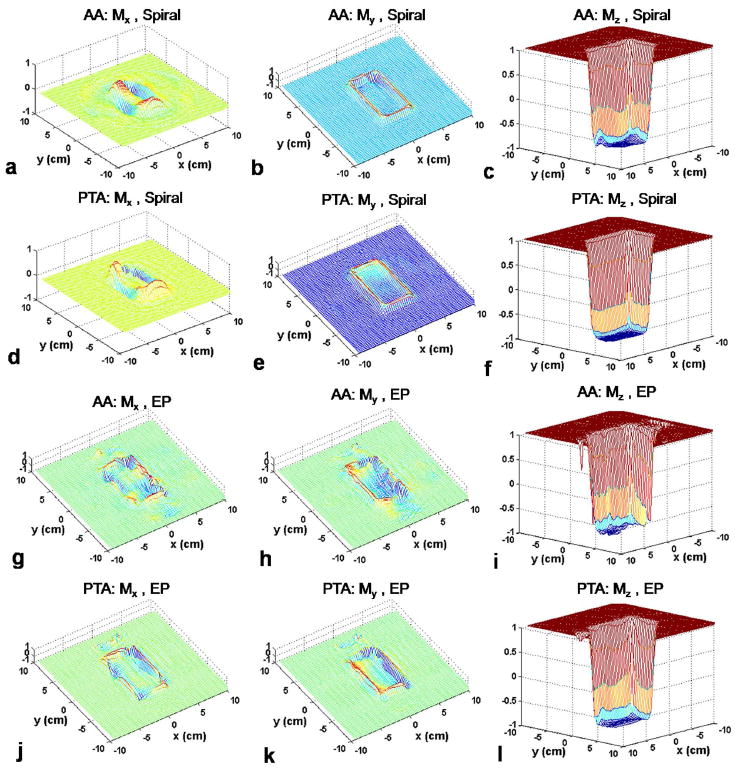
2D selective 180° inversion pulses for spiral and EP trajectories with acceleration factor R=4. a-f: Mx, My and Mz components of magnetization profiles produced by Additive Angle (AA) method and Perturbation Analysis (PTA) method for a spiral trajectory. g-l: Mx, My and Mz components of magnetization profiles produced by Additive Angle (AA) method and Perturbation Analysis (PTA) method for an EP trajectory.
The excited Mx and My components have very similar behavior using the RF pulses designed by the AA and PTA methods when an EP trajectory is used (Fig. 6g, h, j, and k). However, the Mz component generated by the AA and PTA techniques (Fig. 6i) suffers from more severe distortions than the one when the spiral trajectory (Fig. 6c) is used. A minor improvement in these distortions is clearly obtained when the PTA method is used.
Theoretically, an ideal refocusing pulse rotates the transverse component of the magnetization by 180 degrees (e.g., a magnetization pointing along +y direction is transformed into one pointing along −y direction) (10, 19). Fig. 7a-b presents a comparison of 180° refocusing pulses for a spiral trajectory with an acceleration factor of 4 designed with the AA and PTA methods, respectively. Just as in the aforementioned example, some of the excitation errors obtained with the AA method (e.g., non-uniformity within the target block) are corrected through the use of the PTA techniques. The plot presented in Fig. 7c provides a more quantitative depiction of these variations in the form of a line profile through the centerline of the 2D excitation pattern for both methods.
Figure 7.
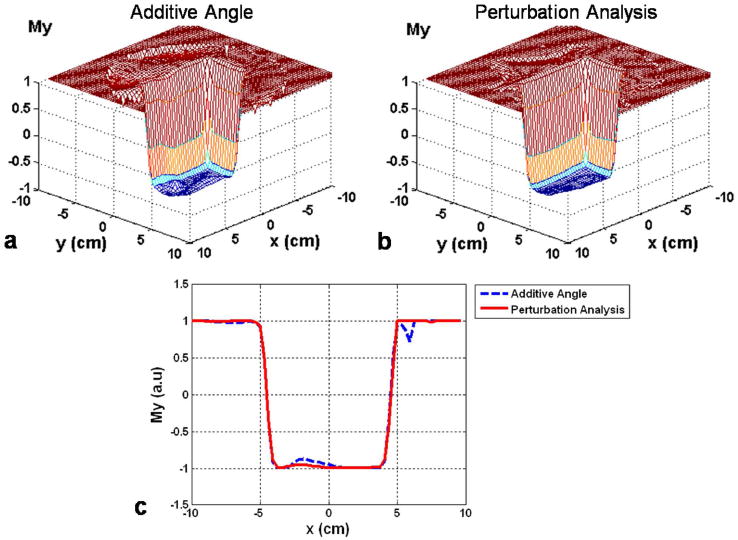
2D selective 180° refocusing pulses for a spiral trajectory with acceleration factor R=4 designed using Additive Angle method (a) and Perturbation Analysis method (b). c: Transverse magnetization profiles taken through the center of the excited patterns from (a) and (b).
Experimental Results
Figure 8 shows the experimental results obtained on the water phantom. Excitation patterns for the same target magnetization as in the simulations above are presented when the STA, AA and PTA methods are used with acceleration factors R=2, 4 and 6. The corresponding line profiles are also shown in the right panels of this figure (Figs. 8d, h and l). For low acceleration (R=2, Figs. 8a-c), the pattern excited by the STA pulses shows the same tilt observed in the simulation results (Figs. 2a-c). Likewise, the magnetization amplitude is lower than that of the desired pattern. As in the simulation results, for low accelerations, there is virtually no difference in the excitation patterns produced by the AA and PTA methods. At medium acceleration (R=4, Figs. 8e-g), the STA excitation pattern is still tilted and the magnetization amplitude deviates further from that the target pattern. Use of the AA method improves the amplitude of the magnetization although there are noticeable inhomogeneities within the target area. These inhomogeneities are successfully corrected through the use of the PTA technique (Fig. 8h). At high acceleration (R=6, Figs. i-k), the excited magnetization profile by the STA method is severely distorted. These distortions are only partially corrected by the AA method and are further improved through the use the PTA technique. Examination of the line profiles shown in Figs. 8d, h and l, further illustrates that the magnetization amplitude obtained by all three methods is always lower than its target value when high acceleration are used. This is as expected since the excitation errors increase with the acceleration factors due to a lower tolerance for errors in the experimental parameters not fully controlled during the experiments (B1, B0, gradient imperfections, etc)
Figure 8.
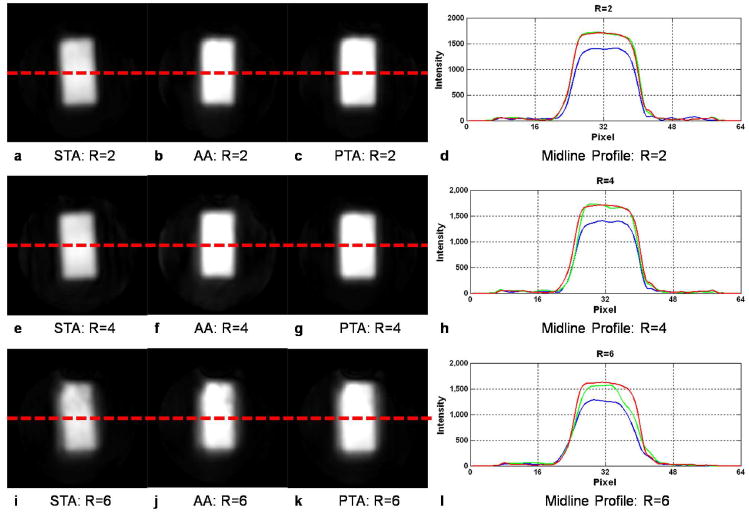
Experimental results of magnitude images of the water phantom excited via Small Tip Angle method (a, e, i), Additive Angle method (b, f, j) and Perturbation Analysis method (c, g, k) for a spiral trajectory with corresponding transverse magnetization profiles (d, h, l) taken through the midline of the excited patterns with acceleration factors R=2, 4, 6, respectively.
Discussion
We have successfully presented a new method for slice-selective large flip angle parallel RF excitation and demonstrated its use for large tip angle gradient echo imaging, inversion-recovery is imaging and spin-echo imaging for parallel transmission at ultra-high field (i.e., 7T). The technique presented here is similar in concept to the AA technique introduced by Grissom et al (11), but yields improved results at higher acceleration factors for the same computational time (number of iterations) due to its exact analytical nature. In this work, we have chosen to implement the solution to the PTA equations using an iterative algorithm for the sake of computational efficiency. However, other means to seek the solution, such as using nonlinear optimization techniques (e.g., Optimal Control method (10, 20)) can also be used, albeit at the expense of much increased computational time. For the iterative method used here, we have found that the regularization parameter has a significant effect on excitation accuracy and that specifically, in order to maintain the same excitation error the number of iterations must be increased when large regularization parameters are used.
Another feature of the method presented above is that by evaluating the second term of equation [7], the deviations from nonlinearity could be prospectively evaluated and used as a guide for the selection of the appropriate numerical technique used during its solution. Linearization schemes will yield improved results when the nonlinear component of the equation is small and nonlinear optimization technique could be preferred when this is not the case. The effect of trajectory design could also be evaluated in this fashion. This particular observation is useful when interpreting the improved performance of all methods when spiral trajectories are used since this trajectory choice leads to linear-class conditions (21, 22) that are well-suited for the iterative techniques used here. When the EP trajectories are used this conditions are not met leading to decreased excitation accuracy when any of the methods presented here are used. Consequently, a nonlinear optimization approach for the solution of equation [7] might be a better numerical choice under such conditions.
The pulses calculated here often lead to high peak RF magnitudes that might not be well-suited practical routine implementations on human subjects. During the numerical solution of the problem using the iterative techniques shown above, the regularization parameter can be used effectively to reduce the peak RF magnitudes, however, the excitation errors will increase leading to longer computational times (more iterations) in order to constrain size of these excitation errors. Lee et al (23) has successfully extened the variable-rate selective excitation (VERSE) (24) for the reduction of peak RF magnitude, albeit at the expense of increased pulse durations. The use of this approach for PTX SAR reduction needs to be carefully evaluated since with increased pulse length the effects of eddy current and off-resonance must be prospectively mitigated (25). Also, because VERSE increases the sampling density near the center of k-space, the effective acceleration factor for PTX is lower than its nominal value. Therefore, further detailed work is needed in order to develop fast and effective algorithms for mitigating SAR concerns while at the same time achieving low excitation errors during large tip angle PTX pulse design.
CONCLUSIONS
We have demonstrated an exact formulation for the inversion of the Bloch equation during PTX RF pulse design. Through the use of iterative solution of the resulting equations we have demonstrated using simulated, as well experimental results, that the proposed formulation can be used to obtain improved excitation patterns relative to other existing iterative pulse design techniques. Experimental results agreed well with the theoretical calculations and demonstrated the improvements in excitation patterns that can be obtained through a complete account of the intervening terms in the solution of the Bloch equations
Acknowledgments
Work Supported in part by PHS Grant NIH CA106840 and Siemens Medical Systems
References
- 1.Katscher U, Bornert P, Leussler C, van den Brink JS. Transmit SENSE. Magn Reson Med. 2003;49:144–150. doi: 10.1002/mrm.10353. [DOI] [PubMed] [Google Scholar]
- 2.Zhu Y. Parallel excitation with an array of transmit coils. Magn Reson Med. 2004;51:775–784. doi: 10.1002/mrm.20011. [DOI] [PubMed] [Google Scholar]
- 3.Pauly J, Nishimura D, Macovski A. A k-space analysis of small-tip angle excitation. J Magn Reson. 1989;81:43–56. doi: 10.1016/j.jmr.2011.09.023. [DOI] [PubMed] [Google Scholar]
- 4.Hardy CJ, Cline HE. Spatial localization in two dimensions using NMR designer pulses. J Magn Reson. 1989;82:647–654. [Google Scholar]
- 5.Bottomley PA, Hardy CJ. Two-dimensional spatially selective spin inversion and spin-echo refocusing with a single nuclear magnetic resonance pulse. J Appl Phys. 1987;62:4284–4290. [Google Scholar]
- 6.Hardy CJ, Cline HE. Broadband nuclear magnetic resonance pulses with two-dimensional spatial selectivity. J Appl Phys. 1989;66:1513–1516. [Google Scholar]
- 7.Grissom W, Yip CY, Zhang Z, Stenger VA, Fessler JA, Noll DC. Spatial domain method for the design of RF pulses in multicoil parallel excitation. Magn Reson Med. 2006;56:620–629. doi: 10.1002/mrm.20978. [DOI] [PubMed] [Google Scholar]
- 8.Setsompop K, Wald LL, Alagappan V, Gagoski BA, Adalsteinsson E. Magnitude least squares optimization for parallel radio frequency excitation design demonstrated at 7 tesla with eight channels. Magn Reson Med. 2008;59:908–915. doi: 10.1002/mrm.21513. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Katscher U, Bornert P, van den Brink JS. Theoretical and numerical aspects of transmit SENSE. IEEE Trans Med Imaging. 2004;23:520–525. doi: 10.1109/TMI.2004.824151. [DOI] [PubMed] [Google Scholar]
- 10.Xu D, King KF, Zhu Y, McKinnon GC, Liang ZP. Designing multichannel, multidimensional, arbitrary flip angle RF pulses using an optimal control approach. Magn Reson Med. 2008;59:547–560. doi: 10.1002/mrm.21485. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Grissom W, Yip CY, Wright SM, Fessler JA, Noll DC. Additive-angle method for fast large-tip-angle RF pulse design in parallel excitation. Magn Reson Med. 2008;59:779–787. doi: 10.1002/mrm.21510. [DOI] [PubMed] [Google Scholar]
- 12.Zheng H, Zhao TJ, Ibrahim T, Boada FE. Fast and Accurate Large-Tip-Angle RF Pulse Design for Parallel Excitation Using a Perturbation Analysis of the Bloch Equation. Proceedings of the 18th Annual Meeting of ISMRM; Stockholm, Sweden. 2010. Abstract 100. [Google Scholar]
- 13.Lin F, Kwong KK, Belliveau JW, Wald LL. Parallel imaging reconstruction using automatic regularization. Magn Reson Med. 2004;51:559–567. doi: 10.1002/mrm.10718. [DOI] [PubMed] [Google Scholar]
- 14.Kerr AB, Cunningham CH, Pauly JM, Piel JE, Giaquinto RO, Watkins RF, Zhu Y. Accelerated B1 mapping for parallel excitation. Proceedings of the 15th Annual Meeting of ISMRM; Berlin, Germany. 2007. Abstract 1092. [Google Scholar]
- 15.Cunningham CH, Pauly JM, Krishna NS. Saturated double-angle method for rapid B1+ mapping. Magn Reson Med. 2006;55:1326–1333. doi: 10.1002/mrm.20896. [DOI] [PubMed] [Google Scholar]
- 16.Setsompop K, Zelinski AC, Alagappan V, Nistler J, Hebrank F, Fontius U, Schmitt F, Wald LL, Adalsteinsson E. In vivo parallel RF excitation with B0 correction. Proceedings of the 15 Annual Meeting of ISMRM; Berlin, Germany. 2007. abstract 671. [Google Scholar]
- 17.Kim DH, Adalsteinsson E, Spielman DM. Simple analytic variable density spiral design. Magn Reson Med. 2003;50:214–219. doi: 10.1002/mrm.10493. [DOI] [PubMed] [Google Scholar]
- 18.Pauly JM, Spielman D, Macovski A. Echo-planar spin-echo and inversion pulses. Magn Reson Med. 1993;29:776–782. doi: 10.1002/mrm.1910290609. [DOI] [PubMed] [Google Scholar]
- 19.Conolly S, Nishimura D, Macovski A. Optimal control solution to the magnetic resonance selective excitation problem. IEEE Trans Med Imaging. 1986;5:106–115. doi: 10.1109/TMI.1986.4307754. [DOI] [PubMed] [Google Scholar]
- 20.Grissom W, Xu D, Kerr AB, Fessler JA, Noll DC. Fast large-tip-angle multidimensional and parallel RF pulse design in MRI. IEEE Trans Med Imag. 2009;28:1548–1559. doi: 10.1109/TMI.2009.2020064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Pauly JM, Nishimura DG, Macovski A. A linear class of large-tip-angle selective excitation pulses. J Magn Reson. 1989;82:571–587. [Google Scholar]
- 22.Xu D, King KF, Zhu Y, McKinnon GC, Liang ZP. A noniterative method to design large-tip-angle multidimensional spatially-selective radio frequency pulses for parallel transmission. Magn Reson Med. 2007;58:326–334. doi: 10.1002/mrm.21314. [DOI] [PubMed] [Google Scholar]
- 23.Lee D, Lustig M, Grissom W, Pauly JM. Time-optimal design for multidimensional and parallel transmit variable-rate selective excitation. Magn Reson Med. 2009;61:1471–1479. doi: 10.1002/mrm.21950. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Conolly S, Nishimura DG, Macovski A, Glover G. Variable-rate selective excitation. J Magn Reson. 1988;78:440–458. [Google Scholar]
- 25.Zheng H, Zhao T, Ibrahim T, Boada FE. Eddy current compensated RF pulse design for parallel excitation. Proceedings of the 18th Annual Meeting of ISMRM; Stockholm, Sweden. 2010. Abstract 4923. [Google Scholar]


