The Impact of Research Grant Funding on Scientific Productivity

Abstract

In this paper, we estimate the impact of receiving an NIH grant on subsequent publications and citations. Our sample consists of all applications (unsuccessful as well as successful) to the NIH from 1980 to 2000 for standard research grants (R01s). Both OLS and IV estimates show that receipt of an NIH research grant (worth roughly $1.7 million) leads to only one additional publication over the next five years, which corresponds to a 7 percent increase. The limited impact of NIH grants is consistent with a model in which the market for research funding is competitive, so that the loss of an NIH grant simply causes researchers to shift to another source of funding.

1. Introduction

Governments devote considerable resources to subsidize R&D, either through tax policy or direct investment. In the United States, for example, the National Institutes of Health (NIH) and the National Science Foundation (NSF) allocate over $30 billion annually for basic and applied research in the sciences. Despite the magnitude of this investment and its importance for long-run economic growth, there is surprisingly little evidence regarding the effectiveness of government expenditures in R&D (Jaffe, 2002).

There are at least two reasons why understanding the impact of government expenditure is critical. First, it is not obvious that such expenditures are effective. Waste or inefficiency may result in the unproductive use of government resources, and public support for R&D may crowd out private support (David et al., 2000). Second, the efficient allocation of government expenditures requires an understanding of the circumstances under which investment is likely to be most productive.

In this analysis, we utilize a quasi experimental research design to identify the causal effect of receiving an NIH grant on the subsequent research output of individual researchers. Unlike the NSF and most foundations, the NIH allocates research funding in a largely formulaic way on the basis of priority scores derived from independent scientific reviews. We first show that there is a highly nonlinear relationship between a proposal’s priority score and the likelihood it is funded. We then use this nonlinearity in an instrumental variables framework to estimate the effect of funding on a variety of outcomes, including publications, citations, and future research funding.

We find that receipt of a specific NIH research grants has at most a small effect on the research output of the marginal applicants. The average award amount for a research grant in our sample is $1.7 million. OLS and IV estimates suggest that grant receipt is associated with only about 1.2 publications (and only .20 first-author publications) over the next five years, and roughly double this over the 10 years following the grant. Given a baseline of 14 publications over a typical five-year period for unsuccessful applicants, this represents a relative effect of only 7 percent.

This relatively small impact is consistent with a model of multiple funding agencies and a competitive market for research funding, so that the loss of an NIH grant simply causes researchers to shift to another source of funding. This displacement phenomenon is analogous to that by which public R&D expenditures may crowd out private investments in R&D. We provide some evidence suggesting that such displacement may explain our results in part.

In addition, the small effects we document here may be, at least in part, a consequence of the research design itself. As with a standard regression discontinuity analysis, our strategy identifies the impact of research funding for marginal applicants, which may be lower than that for the average successful applicant. In addition, however, the existence of multiple potential sources of funding, means that we are identifying the impact of funding on marginal applications which would not have withstood additional scrutiny (i.e., been able to obtain funding from non-NIH funding sources). It is likely that the treatment effect for this group is small even relative to marginal NIH applications as a whole. Note that this would be true even if one could observe all sources of grant funding an individual receives and thus completely characterize the extent and nature of displacement.

2. Prior Literature

The analysis presented below fits within a large literature on the economics of science (see, for example, Stephan, 1996), but is particularly related to prior studies on the determinants of research output and the impact of research funding on scientific publications.

Prior research has documented the relationship between various demographic factors, such as age and gender, and scientific publications (see, for example, Cole and Cole, 1973, Levin and Stephan, 1991, 1992, and Long and Fox, 1995). Other work has emphasized the importance of institutional factors in the productivity of individual scientists (Stephan, 1996). Yet other work emphasizes the importance of social networks or spillovers. Seminal work by Jaffe (1989) and Jaffe et al. (1993) document the importance of knowledge spillovers from academia to industry. Arora and Gambardella (2005) find that location in certain regions and affiliation with specific elite institutions are positively associated with future publication output, even after controlling for past publications and other proxies for researcher quality. In a recent paper, Azoulay et al. (2010) explore the nature of professional interactions among scientists by studying how the premature and unexpected death of specific academic superstars affects the productivity of their prior collaborators. They find that superstar extinction leads to a 5 to 8 percent lasting decline in the collaborator publication rates.¹

Another prominent stream of the literature focuses on the impact of funding on research output. For example, various studies have evaluated the effects of government sponsored commercial R&D using matched comparison groups (Branstetter and Sakakibara, 2002; Irwin and Klenow, 1996; Lerner, 1999). While these studies generally suggest that government funding can increase productivity, Klette et al. (2000) note that all of these studies are susceptible to serious selection biases. In a review of fiscal incentives for R&D, Hall and Van Reenen (2000) conclude a dollar of tax credit induces a dollar worth of additional R&D.

Several studies examine the relationship between funding and research output at the level of the university or department. Adams and Griliches (1998), for example, find constant returns to scale in research funding at the aggregate level, but some diminishing returns to scale at individual universities. Looking at longitudinal data on 68 universities, they could not reject the contention that the positive correlation between funding and output is due solely to differences across schools. Building on this study, Payne and Siow (2003) examine the impact of federal research funding on university-level research output, instrumenting for funding with the alumni representation on U.S. Congressional appropriations committees. They find that $1 million in federal research funding is associated with 10 more articles and .2 more patents.

Other studies that examine the funding-output link at the level of the individual researcher tend to find small positive effects (Arora and Gambardella, 2005; Averch, 1987, 1989). However, these studies recognize the potential for selection bias, which would lead them to overstate the true impact of grant receipt. For example, Arora and Gambardella (2005) find that past productivity and other observable researcher characteristics such as institution quality are correlated with NSF award selection even after controlling for reviewer score, suggesting that their estimates may be biased upward. ²

A few earlier studies have examined the effect of research funding provided by NIH in particular. In their evaluation of NIH career development awards, for example, Carter et al. (1987) compare successful versus unsuccessful applicants, controlling for a linear measure of the applicant’s priority score. They find that the award may increase future grant funding slightly, but that it does not appear to increase publication-based measures of research productivity. While the strategy leverages the intuition behind a regression discontinuity design, the implementation of the analysis suffers from several shortcomings and the study does not include the standard research grants (R01s).

3. Institutional Background

The NIH allocates $31.2 billion per year for research and training,³ with approximately one third of this funding devoted to standard research grants for specific projects, also known as R01s. These grants can be awarded for up to five years, are renewable and generally provide substantial funding (e.g., the average R01 funded by the National Cancer Institute in 2000 awarded researchers $1.7 million over 3.1 years).

Grant applications can be submitted three times during the year.⁴ All applications are subject to non-blind peer review on the basis of five criteria: significance, approach, innovation, investigator, and environment. Reviewers assign each application a priority score on a scale of 1.0 to 5.0, with 1 being the highest quality. The average of these scores is calculated and multiplied by 100 to obtain the priority score. Typically about half of the lowest quality applications, as determined by the reviewers, do not receive a priority score. Because funding decisions are made within institutes and review groups examine applications from different institutes, the NIH normalizes scores such that each research grant applications are assigned a percentile score relative to other applications in the same review group.

Funding decisions are often, though not always, awarded by units within an institute (e.g., divisions, programs, branches). The number of grants funded depends on decision-making unit’s budget for the fiscal year. Generally, grants are awarded solely on the basis of priority score. This does not always occur, however. Institute directors have the discretion to fund applications out of order on the basis of their subjective judgment of application quality, or other factors such as how an application fits with the institute’s mission or whether there were a large number of applications submitted on a similar topic. Moreover, as noted above, institutes may also choose to fund applications on their last evaluation cycle instead of newly submitted applications that can be reconsidered later.

Researchers whose applications receive a poor score and do not receive funding have the ability to respond to the criticisms raised by reviewers and submit an amended application. Amended applications are treated in the same manner as new applications for the purposes of evaluation and funding.

4. Data

This study relies on several data sources. Information on NIH applicants and applications, including priority scores, are drawn from the Consolidated Grant Applicant File (CGAF). The outcomes we examine include publications and citations, future NIH funding, and future NSF funding.

The NIH files utilize a unique individual identifier, enabling us to match applicants in any given year, institute, and mechanism to past and future funding information. Unfortunately, matching is more difficult for our other outcomes. Our basic approach is to match NIH applicants to publications and using first initial and last name. Of course, this will likely result in a number of false positives. Therefore, we utilize a variety of different strategies to minimize the incidence of bad matches (for a complete discussion, see Appendix C). For example, when matching to publication information, we exclude matches to journals in the humanities and several other fields under the assumptions that these are likely bad matches.

While we believe that we have eliminated the vast majority of bad matches in our sample, some clearly remain. Regardless of the nature or extent of the measurement error, it is important to keep in mind that it will not affect the consistency of our estimates (except the constant) as long as the measurement error is not correlated with priority scores in the same nonlinear fashion as the funding cutoff. In our case, there is no reason to believe that applicants just above the cutoff are any more or less likely to have bad matches than applicants who score just below the cutoff (or that the likelihood of bad matches is correlated with the nonlinear term of one’s priority score). Consequently, that there is no reason to believe that the measurement error will bias our results.

The presence of measurement error in the dependent variable will, however, reduce the statistical power of the analysis. To remedy this, we limit our analysis to a sample of individuals with uncommon names (for more details, see Appendix D). Since name frequency is unlikely to be correlated with whether an individual is above or below the funding cutoff (conditional on flexible controls for her priority score) this restriction will not influence the consistency of our estimates. However, if this group of researchers is different than the overall pool of applicants in important ways, this strategy may change the interpretation of our estimates. In order to assess the external validity of our estimates, we compared NIH applicants with common and uncommon names on a variety of observable characteristics. The results, reported in Appendix Table D2, suggest that those with uncommon names are quite comparable to those with more common names.

4.1 Sample

We start with all R01 applications submitted to NIH between 1980 and 2000. We exclude all applications that were solicited (in a Request for Proposal or RFP) and focus exclusively on new grant applications or competing continuations (i.e., applications that propose to continue an existing grant, but nonetheless must compete against other applications).⁵ To minimize measurement error, we focus on the 45 percent of applications in which the applicants have uncommon names, defined as those whose last name was associated with 10 or fewer unique NIH applicants during our time period.⁶

Summary statistics for our analysis sample are shown in Table 1.⁷ Recall that the unit of observation is an application. The final sample contains 54,741 observations, reflecting 18,135 unique researchers covering 20 years and 18 different institutes. Note that over 90 percent of applicants have at least one publication in the first five years following their application, suggesting that most individuals in our sample are at least somewhat engaged in the research process regardless of whether or not they are successful in obtaining the NIH grant. Moreover, the variance of outcomes is extremely large. For example, among researchers who published at least once, the standard deviation of publications in the five years following application is 16.⁸ The corresponding measure for citations is 820. To see what fraction of the variation is due to false matches, we identified a set of false positives for a set of NIH applicants with uncommon names. This allows us to estimate the standard deviation of true publications and citations, which are 15.7 and 817 respectively.

Table 1.

Summary Statistics for Analysis Sample

Application Characteristics	All applications	Awarded Applications	Non-Awarded Applications
Normalized score	0.813	−38.791	101.558
Awarded	0.508	0.708	0.000
Ever awarded	0.718	1.000	0.000
Applicant’s Background
Female	0.177	0.177	0.175
Age	45.817	45.837	45.767
Married	0.629	0.626	0.640
Divorced	0.353	0.355	0.349
Number of Dependents	0.480	0.476	0.491
Name frequency	2.220	2.233	2.187
Has PhD	0.542	0.546	0.531
Has MD	0.338	0.341	0.333
Has PhD & MD	0.079	0.080	0.075
Rank of graduate institution in terms of NIH funding	114.368	112.817	118.457
Rank of current institution in terms of NIH funding	78.963	77.249	83.495
Productivity Measures
Years 1–5 prior to the application
Any NIH funding	0.781	0.802	0.728
Amount of NIH funding (/$100,000)	7.436	7.826	6.342
Any publications	0.911	0.909	0.916
Number of publications	16.427	16.825	15.423
Years 1–5 following the application
Any NIH funding (excluding reference application)	0.716	0.760	0.606
Amount of NIH funding ($/100,000) (excluding reference application)	12.650	12.690	12.525
Any publications	0.907	0.908	0.905
Number of publications	18.661	19.445	16.660
Any citations	0.906	0.907	0.903
Number of citations	643.375	678.729	552.975
Any NSF funding	0.083	0.076	0.101
Amount of NSF ($/100,000)	2.786	2.632	3.093
Years 6–10 following the application
Any NIH funding (excluding reference application)	0.654	0.725	0.493
Amount of NIH funding ($/100,000) (excluding reference application)	20.567	21.327	17.901
Any publications	0.886	0.896	0.861
Number of publications	18.843	19.552	16.993
Any citations	0.857	0.867	0.833
Number of citations	446.992	462.263	406.569
Any NSF funding	0.072	0.070	0.077
Amount of NSF funding ($/100,000)	3.202	3.141	3.332
Number of observations	54,741	39,294	15,447

Notes: Sample includes applicants with uncommon names (name frequency <=10) who scored within +/− 200 points. Name frequency reflects the number of other NIH applicants who share the same last name. The unit of observation is a grant application. Estimates of amount of NIH or NSF funding include zeroes for those who received no funding. Marital status, number of dependents, and rank of graduate institution are frequently missing (in 47, 56, and 53 percent of cases respectively). Other variables have coverage of 87 percent or better. The coverage rates are similar for the sample of eventual winners and losers. Adjusted publications and citations take into account the average number of false matches.

5. Methodology

If research grants were randomly allocated to researchers, one could identify the causal effect of receiving a specific grant by comparing the output of successful and unsuccessful applicants. However, it seems likely that successful applicants are more productive or have superior project proposals than unsuccessful applicants, so that funding is likely to be positively correlated with the unobserved characteristics of the applicant. To the extent that this is true, naïve comparisons of successful and unsuccessful applicants may be biased upwards.

We will attempt to deal with the non-random assignment of grants to applications in two ways. First, we will use the abundant information available to us regarding the quality of the grant application and prior productivity of the researcher to control for the expected output of the researcher in the absence of the grant. More specifically, we will estimate a regression of the following form:

$$y_{it+1}=\beta {\mathit{funded}}_{it}+f(n_{it})+X_{it}B+{\epsilon }_{it+1}.$$ (1)

where y_i,t+1 is a measure of research output of individual i in period t+1, funded_it indicates whether the researcher’s application was ultimately successful, n_it is the priority score of the researcher’s application normalized relative to the grant funding cutoff (described in more detail below), f() is a smooth function, X_it is a vector of researcher-level covariates, and ε_i,t+1 is a mean zero residual. While we are able to control for a much richer set of researcher and project characteristics than in prior research, we recognize that the OLS estimates from (1) may still be biased upward. However, because these estimates (shown below) are generally quite small, this estimator provides an informative upper bound on the true causal impact of grant receipt.

Our second approach relies upon the fact that NIH funding is awarded on the basis of observable priority scores, and that there is a highly nonlinear relationship between this score and the probability of funding. This strategy leverages the intuition underlying a regression discontinuity design (RDD) that applications just above and just below the funding cutoff will be unlikely to differ in any unobservable determinants of the research output but will experience a large difference in the likelihood of receiving funding.⁹

There is no pre-determined cutoff for funding that applies universally across the NIH. Instead, the realized cutoff in each situation depends on the level of funding for a particular institute, year, and mechanism, along with the number and quality of applications submitted. This political reality actually provides significant advantages for our identification since it essentially establishes dozens of different cutoffs that we can exploit and reduces the concern that a single cutoff might coincide with some other factor that is correlated with research output.

The dotted line in Figure 1 shows the probability that a grant application is funded as a function of the normalized priority scores for researchers within our sample.¹⁰ Note that while the probability of funding is a highly nonlinear function of the normalized application score, there is clearly evidence of out-of-order funding. In our sample, 4 percent of individuals who scored above the cutoff received the grant, while 9 percent of those below the cutoff did not receive a grant or declined the award.

Figure 1.

Relationship between Normalized Priority Score and Award Status

Notes: Data is smoothed using a lowess estimator with a bandwidth of .03.

The solid line in Figure 1 shows the probability that an award is eventually funded as a function of the current application’s score, and thus accounts for the fact that many unsuccessful applicants with marginal scores choose to resubmit their application.¹¹ Relative to the dotted line, we see that the relationship between current grant score and eventual grant funding becomes much less sharp. While the probability of current award drops rapidly in the vicinity of the cutoff, the probability of eventual award continues to decline more gradually a fair distance from the cutoff. While 96 percent of applicants with a score below the cutoff are awarded a grant, 24 percent of those above the cutoff are also awarded a grant at some point.

While the existence of out-of-order funding, rejected awards, and reapplication makes a standard RDD infeasible, it is still possible to leverage the nonlinear relationship between normalized priority score and the probability of eventual grant receipt to identify the causal impact of research funding. We do so using instrumental variables. In this framework, the second stage of our IV estimation is represented by equation (1). Our first stage equation is given by

$${\mathit{funded}}_{it}={\gamma }_1\mathit{below}\_{\mathit{cut}}_{it}+{\gamma }_2\mathit{below}\_{\mathit{cut}}_{it}\ast n_{it}+g(n_{it})+X_{it}\mathrm{\Gamma }+{\eta }_{it+1},$$ (2)

where below _ cut_it is a binary variable indicating that the normalized score was below the imputed funding cutoff and the other variables are as described earlier. This specification not only allows for a discrete increase in the probability of funding in the vicinity of the cutoff, but also takes into account that the relationship between the application score and the probability of being funded changes at the cutoff.

Note that our strategy differs from a standard regression discontinuity design in that identification comes from two sources: (a) changes in output associated with being below the cutoff, conditional on a smooth function of the normalized priority score, and (b) changes in the slope of the relationship between the normalized priority score and subsequent productivity above versus below the cutoff. Because a lower priority score has little impact on the probability of grant receipt below the cutoff, if research funding does indeed increase output, we should see a weaker relationship between normalized priority score and output below the cutoff relative to above the cutoff. As a robustness check, however, we estimate a model that relies only on variation due to jumps at the cutoff (analogous to a standard RDD) and find comparable results.

Figure 2 shows the relationship between the normalized priority score and subsequent publication rates. Because publication rates are noisy, we show publication residuals instead of the raw rates. These residuals are calculated by regressing an applicant’s number of publications on prior productivity measures as well as demographics and institutional characteristics. We do not control for subsequent productivity or application score.

Figure 2.

Relationship between Normalized Priority Score, Eventual Award, and Publication Residuals

Notes: Data is smoothed using a lowess estimator with a bandwidth of .03. Publication residuals are calculated by regressing five year publication rates on researcher demographics and prior productivity measures.

In Figure 2, we see that publication residuals are negatively correlated with the normalized priority score, which is what we would expect if higher quality applications received the lowest score and were funded first. If receiving a grant had a large causal effect on subsequent research output, we would expect publication residuals to rise rapidly as one approached the cutoff from above and then level out below the cutoff. We see no evidence of such a relationship, suggesting at most a small impact of grant receipt on subsequent research output. Note that even if the full rise in publication rates associated with having a lower score is attributable to the increase probability of grant receipt, the implied impact of grant receipt is still only about 2.5 publications over five years.

As in any empirical analysis, our estimates rely on several important assumptions. The exclusion restriction for our IV estimates assumes that, conditional on the low-order polynomial control for priority score and other covariates, the non-linear function of the prior score we use as an instrument is not correlated with research outcomes other than through grant receipt. One way that this assumption could be violated is if researchers could manipulate their priority score in a targeted way around the cutoff. A second way in which this assumption could be violated is if our smooth function of the priority score does not adequately control for the baseline relationship between application quality and researcher output.

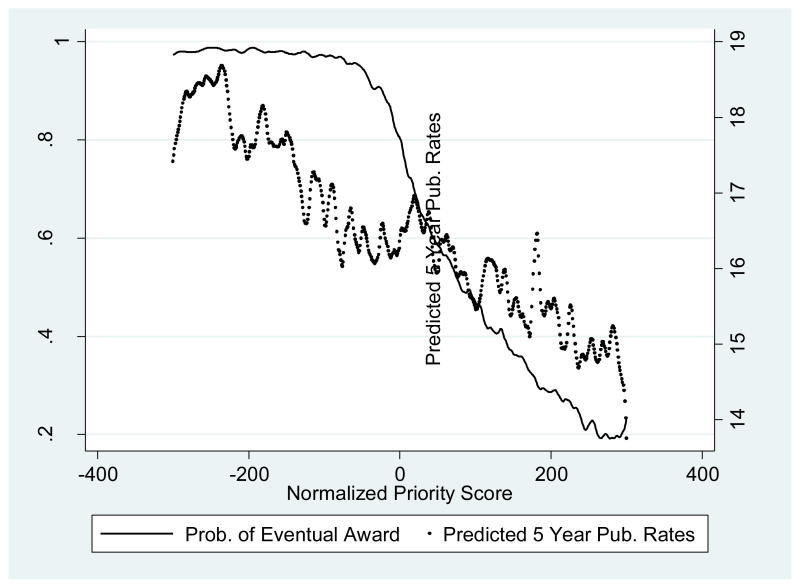
Fortunately, we can shed empirical light on these issues by examining how the observable characteristics of applicants change in the vicinity of the cutoff. Figure 3 shows predicted publications in the five years subsequent to grant application as a function of the applicant’s pre-application characteristics. This predicted value is not based on the priority score of the application or whether an applicant received an award. It serves as an index of observable characteristics. Examining the figure, we see that the characteristics of applicants just below the cutoff and hence eligible for funding appear a bit worse than those of applicants just above the cutoff. This suggests that our instruments may also be negatively correlated to the residual biasing downwards our estimates. We examine this issue in more depth when we discuss our empirical results.

Figure 3.

Relationship between Normalized Priority Score, Eventual Award, and Predicted Publication Rates

Notes: Data is smoothed using a lowess estimator with a bandwidth of .03. Predicted publication rates are calculated by regressing five year publication rates on researcher demographics and prior productivity measures.

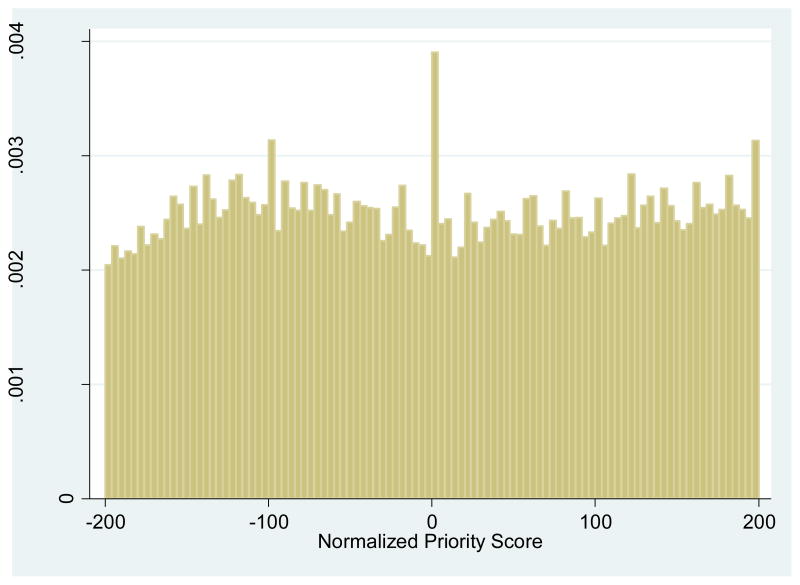
Figure 4 shows the distribution of priority scores. We see a spike right at the cutoff. With a predetermined cutoff, this would generally be considered evidence of strategic behavior. In our case, however, it simply reflects how we constructed the funding line. The cutoff is defined as the score of the last application that would be funded if funding decisions were made in order. Hence, in each institute*year combination, there is always at least one applicant at the cutoff, generating the spike. We show later that our results are robust to dropping observations at the cutoff. Additionally, there do not appear to be any other suspicious spikes in the neighborhood of the cutoff.

Figure 4.

Histogram of Normalized Priority Scores

Notes: The figure shows a histogram of normalized priority scores. The spike at zero is due to the fact that we define the cutoff empirically as the score of the application that would be funded if funding decisions were made in strict order according to priority score.

6. Findings

Table 2 presents a series of OLS estimates. For all outcomes, row 1 shows unconditional estimates and rows 2–4 include progressively more controls. Robust standard errors that cluster by researcher are shown in parenthesis beneath the estimates. In columns 1 and 2, we see that grant receipt is positively associated with future publications and citations, although the introduction of a rich set of controls reduces the point estimates by over 50 percent. Interestingly, the point estimates continue to decline with the inclusion of background characteristics in rows 3 and 4, even after conditioning for application priority score. This reflects the prevalence of successful resubmissions for R01 awards. More specifically, a strong applicant with an initially poor priority score is more likely to successfully resubmit an improved application and eventually receive funding than a weak applicant. Column 3 demonstrates that individuals who receive an R01 award will, on average, receive $251,000 more NIH funding in years 6 to 10 following the original grant submission.

Table 2.

OLS Estimates of the Impact of NIH Funding on Research and Funding Outcomes

Specification	Pubs in Yrs 1–5	Citations in Yrs 1–5	NIH Funding in Yrs 6–10 (/$100,000)
(1) No controls	2.58** (0.19))	116.58** (8.85)	6.63** (0.25)
(2) Quadratic priority score + institute and year fixed effects	1.61** (0.22)	75.95** (10.28)	3.80** (0.29)
(3) = (2) + applicant characteristics	1.40** (0.21)	61.66** (9.93)	3.27** (0.28)
(4) = (3) + Measures of prior publications, funding	1.17** (0.14)	49.01** (8.56)	2.51** (0.25)
Control group mean (s.d)	14.49 (15.04)	487.32 (735.31)	9.15 (18.05)
R-squared from model in row 4	0.62	0.36	0.35
Number of obs	54,741	54,741	44,859

Notes: Each cell in rows 1–4 of this table represents the coefficient (s.e.) from a separate OLS regression where the dependent variable is shown at the top of the column and the set of control variables are described under “Specification” in the first column. The unit of observation is an application. In each case, the estimate shown is the coefficient (s.e.) on a binary indicator for eventual NIH grant receipt. The sample size in column 3 is smaller because we only have NIH funding information through 2003, thus we cannot calculate measures for years 6–10. For measures of years 1–5, we interpolate some values as described in the text. The control variables include fixed effects for institute, year of award, name frequency, name frequency squared, age and age squared at time of award, binary indicators for female, married and divorced, a linear measure for the number of dependents, binary indicators for region (West, Central and South, with East omitted), binary indicators for degree type (MD, and MD/PhD with PhD as the omitted category), binary indicators for field (social sciences, physical sciences and other, with biological sciences as the omitted category), binary indicators for organization type (research institute, hospital with university as the omitted category), binary indicators for unit within organization which only applies to universities (hospital, arts and sciences, school of public health, institute, or other with medical/dental school omitted), linear and quadratic terms for the rank of the applicant’s current and graduate institutions where rank is measured in terms of amount of NIH funding received in prior years, and linear and quadratic terms for a host of prior productivity measures including number of publications in years 1–5 prior to application, number of publications in years 6–10 prior to application, research direction in years 1–5 prior to application, research direction in years 6–10 prior to application, amount of NSF funding in years 1–5 prior to application, amount of NSF funding in years 6–10 prior to application, amount of NIH funding in years 1–5 prior to application, and amount of NIH funding in years 6–10 prior to application. The control group means and standard deviations for the publication and citation columns are adjusted to account for the presence of false positive matches, as described in the text. Standard errors are clustered by researcher.

^**indicates statistical significance at the 5 percent level;

^*indicates significance at the 10 percent level.

The OLS estimates suggest that the receipt of an NIH research grant increases publications. However, the evident selection on observables raises concern that selection on unobservable characteristics may still bias the estimates. To address this concern, we estimate the IV model described above.

Table 3 presents the results from the IV estimation. The first column shows the results of the first stage estimates from equation (1). We see that receiving a priority score below the cutoff is associated with a 16 percentage point increase in the probability of grant receipt. The interaction term between the priority score and the “below cutoff” indicator variable is significantly positive. This reflects the fact that above the cutoff the relationship between the priority score and probability of eventual award is negative, while below the cutoff it is virtually zero. The F-statistic of 315 on our excluded instruments (shown in column 1) indicates considerable power in the first-stage model, suggesting that our estimates do not suffer from weak instruments bias.

Table 3.

IV Estimates of the Relationship Between NIH Funding and Research Output

	First-Stage Estimates	Second-Stage Estimates
	Publication Measures 1–5 Years Following Grant Application						Future NIH Funding (excluding reference grant)
	Received Grant (1)	Pubs (2)	Normalized Pubs (3)	First- Author Pubs (4)	Non First- Author Pubs (5)	Citations (6)	NIH funding in yrs 1–5 (/$100,000) (7)	NIH funding in yrs 6–10 (/$100,000) (8)
Below the cutoff	0.16** (0.01)
Below cutoff* priority score	0.002** (0.000)
F-statistic of instruments [p-value]	315.22 [0.00]
OLS estimates		1.17** (0.14)	0.36** (0.04)	0.20** (0.05)	0.97** (0.13)	49.01** (8.56)	−1.17** (0.14)	2.51** (0.25)
IV estimates		0.79 (0.98)	0.27 (0.29)	0.60* (0.33)	0.19 (0.91)	33.79 (62.18)	2.27** (1.09)	6.48** (1.79)
Diff: IV - OLS		−0.33 (0.93)	−0.08 (0.28)	0.40 (0.40)	−0.73 (0.88)	−11.34 (60.04)	3.44** (0.92)	3.99** (1.51)
Control group mean (s.d.)	0.48 (0.50)	14.49 (15.04)	4.16 (4.08)	2.72 (3.58)	11.77 (13.44)	487.32 (735.31)	7.68 (13.89)	9.15 (18.05)

Notes: The estimates are derived from specifications (1) and (2) in the text. Normalized publications are calculated by dividing each publication by the total number of authors on the publication prior to summing across years. First-author publications reflect the number of normalized publications in which the author was first author. Each regression includes the full set of control variables described in the notes to Table 3. The control group means and standard deviations for the publication and citation columns are adjusted to account for the presence of false positive matches, as described in the text. Standard errors are clustered by researcher.

^**indicates statistical significance at the 5 percent level;

^*indicates significance at the 10 percent level.

The remaining columns in Table 3 show the second-stage estimates for different outcome measures. All models include the full set of controls as well as a quadratic in priority score. Standard errors clustered by applicant are shown in parentheses below the estimates. For each outcome, row 4 shows the OLS estimate, row 5 shows the corresponding IV estimate and row 6 shows the difference between the OLS and IV estimates. Because we cluster correct the standard errors at the researcher level, a conventional Hausman test is inappropriate. Hence, to examine whether the differences between the OLS and IV estimates are statistically different, we block bootstrap (at the researcher level) the difference between the OLS and IV estimates and calculate the corresponding standard error.

The results suggest that NIH research grants do not have a substantial impact on total publications or citations. The point estimates of 0.79 and 0.36 in columns 2 and 3 are quite small relative to their respective means of 14.5 and 4.2,¹² and are not statistically different from zero. Similarly, the point estimate for citations of 33 is only 7 percent of the control mean of 487. In addition, it is worth noting that our estimates are relatively precise. For example, the IV confidence interval for publications ranges from −1.13 to +2.71. This means that we can rule out positive impacts larger than .18 standard deviations with over 95 percent confidence.

Table 3 also shows the OLS and IV impacts of grant receipt on a number of other outcomes. Not surprisingly, receiving a grant has a smaller impact on normalized publications, since each publication is divided by the number of authors. The OLS estimates suggest a smaller impact on first-author publications than non-first-author publications. This is consistent with the head of labs often being listed as the final author. In the IV estimates, we see a larger impact of grant receipt on first author publications, though this is only marginally different from zero and statistically indistinguishable from the OLS point estimate. The OLS indicates that grant receipt is associated with an increase in subsequent citations, while the IV yields statistically insignificant estimates. Finally, receiving an NIH grant is associated with an additional $227,000 in NIH funding (i.e., funding not attributable to the reference grant application) in the five years following the reference application. Looking further into the future, we find that receiving an NIH grant is associated with a roughly $648,000 more NIH funding in years 6–10 following the initial application. This is consistent with the “Matthew Principle” that “success begets success” in scientific funding (Merton, 1968).

6.1 Sensitivity Analysis

To test whether the exclusion restriction holds in our IV model, we re-estimate the baseline models using various pre-treatment measures outcomes. We know that a NIH grant cannot have a causal impact on publications prior to the award of the grant. Hence, any “effect” we find is an indication that receipt of the award, even after we condition on a continuous function of the priority score, is correlated with some unobservable factor that also determines research output.

Table 4 presents IV estimates of NIH grants on a variety of “pre-treatment” characteristics, including prior publications and funding. Note that these models include a quadratic in the priority score along with institute and year fixed effects, but none of the other covariates that are included in the earlier models (since these variables are the outcomes in this analysis). In order to account for the fact that many of these pre-treatment measures are correlated within researcher, we estimate a Seemingly Unrelated Regression (SUR) that allows us to test the joint significance of the treatment effects that takes this correlation into account.¹³

Table 4.

Effects of NIH Funding on Pre-Treatment Outcomes

Specification	Coefficient (Standard Error)	Specification	Coefficient (Standard Error)
Number of publications in five previous years	−3.26** (1.29)	Has MD	0.01 (0.04)
NIH funding in five previous years	−2.27** (0.97)	Rank of graduate institution	48.22** (18.89)
Name frequency	0.06 (0.25)	Rank of current institution	12.69 (8.90)
Female	0.02 (0.04)	Biological sciences department	0.02 (0.04)
Age	0.41 (0.87)	Physical sciences department	0.03 (0.02)
Married	0.03 (0.05)	Social sciences department	−0.02 (0.02)
Divorced	0.02 (0.04)	Research institute	−0.04 (0.03)
Number of Dependents	0.01 (0.04)	Hospital	0.01 (0.03)
Has PhD	0.05 (0.05)	F-Statistic [p-value] of joint significance of excluded instruments for all outcomes listed above	53.69 [0.03]

Notes: These specifications were estimated using IV in which we control only for institute and year fixed effects as well as linear and quadratic measures of either of the normalized priority scores. Instruments include whether the priority score was below the cutoff and normalizes priority score interacted with a below cutoff indicator variable. Standard errors are clustered by researcher.

^**indicates statistical significance at the 5 percent level;

^*indicates significance at the 10 percent level.

We see that researchers who were awarded a grant because they scored just below the cutoff had lower productivity prior to the grant application. For example, R01 grant recipients had 3.3 fewer publications in the five years prior to the grant application compared with similar peers. They also had less NIH funding over the same period. These results, which are consistent with the graphical evidence in Figure 3, suggest that the nonlinear measure of priority score that we are using as an instrument may be negatively correlated with observables that influence future output. In this case, one should view the IV estimates presented above as lower bounds on any positive impacts of NIH grant receipt. As noted earlier, the results in Table 2 suggest that the OLS estimates are likely biased upward.

Hence, together the OLS and IV estimates provide likely bounds to the causal impact of grant receipt. Given that the magnitude of the OLS estimates are at best modest and quite small in many cases, the sensitivity analyses presented here do not change the overall interpretation of the findings. It still appears that receipt of an NIH grant has at most a small positive impact on future publications and citations.

Table 5 shows a series of additional sensitivity analyses. The first row reproduces the IV estimates from the baseline model. Row 2 presents IV estimates with no covariates other than institute and year fixed effects and a quadratic in the priority score. Row 3 shows our findings when we include institutes regardless of the size or frequency of out of order funding. In Row 4, we further restrict our sample to include institutes with very low levels of out of order funding. In Row 5, we drop observations at the cutoff. Rows 6 through 9 replicate the analysis using narrower and wider ranges of priority scores. Rows 10 and 11 show the results with linear and cubic terms in the rating variable instead of the baseline quadratic term. In Row 12 we implement a more standard regression discontinuity approach. In particular, we control in the second stage for a linear measure of priority score which is allowed to vary above and below the cutoff. Our instrument is only a dummy variable for whether the application score is below the cutoff. Hence we only use variation associated with crossing the funding threshold.

Table 5.

Sensitivity Analyses

Specification	Pubs in Yrs 1–5	Citations in Yrs 1–5	NIH funding in Yrs 6–10 (/$100,000)
(1) Baseline	0.79 (0.98)	33.79 (62.18)	6.48** (1.79)
(2) No covariates	−2.29 (1.51)	−79.20 (73.80)	4.57** (2.03)
(3) Including Institutes with Few Grants or Higher Error Rates	0.84 (0.98)	33.10 (62.41)	6.73** (1.82)
(4) Restricting Sample to Institutes with Lower Error Rates	0.45 (1.21)	5.36 (80.40)	7.43** (2.12)
(5) Dropping Observations at Cutoff	0.62 (0.91)	7.65 (59.24)	6.49** (1.68)
(6) Using Observations within 100 Points of Cutoff	0.67 (2.72)	353.93** (177.08)	14.62** (4.84)
(7) Using Observations within 150 Points of Cutoff	0.81 (1.44)	61.64 (90.63)	6.03** (2.58)
(8) Using Observations within 250 Points of Cutoff	0.63 (0.72)	−9.17 (45.73)	5.46** (1.33)
(9) Using Observations within 300 Points of Cutoff	0.68 (0.57)	−45.15 (36.75)	4.21** (1.03)
(10) Including only linear term in the rating	−0.30 (0.66)	−164.06** (44.03)	0.04 (1.30)
(11) Including 3rd order polynomials in the rating	0.14 (1.86)	85.65 (120.56)	7.42** (3.37)
(12) Only using Variation Attributable to Cutoff	1.00 (1.03)	43.10 (66.10)	6.90** (1.87)

Notes: The specifications are identical to those in Table 3 except as indicated.

^**indicates statistical significance at the 5 percent level;

^*indicates significance at the 10 percent level.

Table 6 examines the impact of NIH grants on different subgroups. Due to the lack of precision associated with the IV estimates, we focus on the OLS results. While the number of comparisons suggests that one should be cautious in interpreting any differences, several interesting patterns emerge. First, R01 grants appear have a larger impact on the research output of researchers under the age of 45 compared with older researchers. Second, whether or not a researcher has received a prior NIH award is unrelated to the effect size of R01 grant receipt on subsequent publications and citations. ¹⁴ The impact on subsequent NIH funding, however, is larger for researchers with no prior funding than for researchers with prior funding. Third, there is evidence that NIH grants may impact men and women differently, although the evidence is somewhat mixed. On one hand, receipt of an NIH grant appears to have a bigger impact on the citations of male researchers. On the other hand, grant receipt has a larger impact on future NIH funding for women.

Table 6.

Heterogeneity of Effects

Specification	Publications in Yrs 1–5	Citations in Yrs 1–5	NIH funding in Yrs 6–10 (/$100,000)
Baseline	1.17** (0.14)	49.01** (8.56)	2.51** (0.25)
Researcher Demographics
Younger researchers	1.34** (0.18)	76.93** (12.52)	3.21** (0.31)
Older researchers	0.92** (0.20)	15.26 (11.34)	1.63** (0.38)
Chi-Square Test of Equal Coefficients [p-value]	2.38 [0.12]	13.33 [0.00]	10.46 [0.00]
No prior awards	1.29** (0.28)	50.54** (18.01)	3.48** [0.38]
Prior awards	1.15** (0.16)	49.13** (9.69)	2.28** [0.29]
Chi-Square Test of Equal Coefficients [p-value]	0.17 [0.68]	0.00 [0.95]	6.22 [0.01]
Female researchers	1.12** (0.24)	18.24 (15.43)	3.84** (0.55)
Male researchers	1.17** (0.16)	55.58** (10.10)	2.26** (0.28)
Chi-Square Test of Equal Coefficients [p-value]	0.03 [0.86]	4.11 [0.04]	6.69 [0.01]
Department Type
Social science	0.62 (0.42)	26.60 (26.47)	2.88** (1.01)
Physical science	0.67 (0.58)	−10.75 (35.56)	0.53 (0.54)
Biological science	1.26** (0.15)	61.30** (9.64)	2.68** (0.28)
Chi-Square Test of Equal Coefficient [p-value]	2.87 [0.23]	4.95 [0.08]	12.88 [0.00]
Organization Type
University	1.06** (0.15)	42.91** (8.94)	2.44** (0.26)
Research Institute	1.10** (0.50)	20.28 (36.36)	3.25** (0.93)
Hospital	2.47** (0.50)	147.21** (35.14)	2.46** (1.05)
Chi-Square Test of Equal Coefficient [p-value]	7.26 [0.03]	8.87 [0.01]	0.69 [0.71]
Has a PhD	1.03** (0.17)	41.42** (10.75)	2.67** (0.31)
Has an MD	1.31** (0.27)	63.33** (17.08)	2.66** (0.53)
Chi-Square Test of Equal Coefficients [p-value]	0.76 (0.38)	1.18 [0.28]	0.00 [0.98]
Time Period
1980–1989	1.19** (0.19)	57.02** (13.52)	1.66** (0.23)
1990–2000	1.14** (0.19)	34.45** (10.41)	3.69** (0.46)
Chi-Square Test of Equal Coefficients [p-value]	0.03 [0.87]	1.60 [0.19]	15.51 [0.00]
By Overall NIH Funding Levels
High funding point (1985–87)	1.04** (0.33)	49.23** (21.40)	1.15** (0.37)
Low funding point (1993–94)	1.55** (0.44)	55.95** (26.57)	4.96** (0.80)
Chi-Square Test of Equal Coefficients [p-value]	0.85 [0.36]	0.04 [0.84]	18.86 [0.00]

Notes: These estimates are based on OLS regressions similar to those presented in row 4 of Table 3. Younger researchers are defined as those less than 30 and 45 years of age in the F and R samples respectively.

^**indicates statistical significance at the 5 percent level;

^*indicates significance at the 10 percent level.

There are also some interesting differences across discipline and grant type. NIH funding has a significantly greater impact on researchers in the biological than on those in the physical or social sciences, consistent with the fact that NIH funding constitutes a larger share of total available funding in the biological sciences relative to the other disciplines.¹⁵ Similarly, the impact of NIH funding is larger among researchers based in hospitals relative to researchers in universities or research institutes who arguably have greater sources of funding outside of NIH.

The final panels in this table examine whether the impact of NIH funding varies over time. The results for the 1980s vs. the 1990s are somewhat mixed. Winning an NIH grant in the 1980s resulted in roughly the same number of publications and citations as winning a grant in the 1990s, but grant receipt in the 1990s had a larger impact on subsequent NIH funding. One reason for this may have been the relative scarcity of funding in the 1990s. To examine the effect of NIH funding in periods of high versus low overall funding, we compare the impact of receiving an R01 grant from 1985 to 1987 (the funding high point in our sample) to the impact from 1993 and 1994 (the funding low point). The point estimates suggest that grant receipt had a larger impact on researcher output in the low-funding period, although only the effect on subsequent NIH funding is statistically significant.

7. Discussion

The analysis above suggests that standard NIH research grants have at most a relatively small effect on the number of publications and citations of the marginal applicants.¹⁶ In this section, we describe an economic model of research funding and production that is consistent with these findings (Appendix E provides a more formal model of this phenomenon.) Our framework suggests that there is likely to be little variation in the funding status of the best applications. Indeed, with the possibility to resubmit grant applications to the NIH or other funding agencies, it is likely we will only be able to identify the impact of grant receipt on funded applications which would not have withstood additional scrutiny. Finally, NIH funding may displace other sources of funding. There are several ways in which unsuccessful researchers might obtain funding to continue their research: (1) they might obtain funding from another source, such as the NSF, a private foundation, or their home institution; (2) they might collaborate with another researcher who was successful at obtaining NIH funding; or (3) they might collaborate with another researcher who was successful at obtaining non-NIH funding.

To develop some intuition regarding the interpretation of our findings, it is helpful to first consider a scenario in which the NIH was the only source of funding in a particular field. If the NIH awarded grants to maximize the amount of research produced, funding would be allocated in order to applications based on perceived productivity of the project. In this case, the comparison of funded and non-funded applications near the funding line would identify the impact of grant receipt for the marginal applicant, which is likely to be lower than the impact of the best applicants.

However, the fact that applicants can submit revised applications changes the interpretation of the local average treatment effect (LATE). Consider applicants in the vicinity of the funding line. Some applicants respond to rejection by submitting an amended application that is successful. Being above the funding cutoff generates no variation in these individuals’ eventual funding status, and so their experience is not reflected in our LATE. Other applicants, in the case of rejection, submit an amended application that is again rejected or fail to reapply funding. Being above the cutoff generates variation in these applicants’ funding status so they are captured in our LATE. Because the impact of funding can only be identified for an adversely selected set of applications which scored poorly (i.e., at least slightly below the funding threshold) in all reviews, we may expect the identified treatment effect to be small relative to the average impact of grant receipt.

Unsuccessful researchers may also choose to apply for funding for a different project from the NIH or submit an application to a different funding agency with similar funding objectives. We can observe NIH and NSF funding as long as the researcher is listed as the principal investigator on the grant. It may be, however, that the researcher receives NIH or NSF funding from a grant for which she is not the principal investigator. Furthermore, we cannot observe funding received from other sources including the researcher’s institution or private funding agencies. When receipt of an NIH grant displaces funding from alternative sources, the size of the grant overstates the impact of grant receipt on the amount of financial resources available to a researcher. Hence, the apparent impact of government funding (that is, the impact we can estimate in the framework above) could be quite small. This problem grows with the number of funding agencies that have similar research objectives as the NIH.

In the context of our framework, a positive impact of NIH funding implies that there is a positive marginal impact of funding on productivity and that at least some NIH applicants would not otherwise have been able to fund productive projects. Conversely, observing an impact of NIH funding close to zero is consistent with the existence of a competitive market for research funding and/or a zero marginal impact of funding for applicants whose projects would have been funded only by the NIH. In other words, one would expect that the causal impact of receiving a particular grant on subsequent research to be quite small, even if the average impact of funding were large and positive.

7.1 Evidence Regarding the Displacement Hypothesis

Consistent with our model, we find larger impacts among researchers who are arguably more reliant on NIH funding, thus diminishing the possibility of displacement. Though the differences are not always statistically significant we find that younger researchers, researchers in the biological sciences, those located in hospitals, and those individuals who have not received NIH funding in the past enjoy relatively large benefits from grant receipt. In addition, we find that the impact of an NIH grant is larger in years when overall NIH funding is lower.¹⁷

To examine the existence of displacement more directly, one would ideally like to examine how a NIH-grant receipt influences the application for (and subsequent receipt of) other NIH grants as well as funding from other entities. In Table 3, we saw that receipt of an NIH grant is associated with an increase of $227,000 in NIH funding over the next five years (excluding the reference grant). In results not shown here, we found that receiving an R01 grant is associated a decline of $25,000 in NSF funding. Given the an average R01 grant is $1.7 million, these results suggest that other NIH and NSF grants do not appear to be a primary source of displacement.

However, as discussed above, researchers may receive support from a variety of other sources, including their home institutions or foundations. Perhaps more importantly, they may receive funding as a co-investigator on a NIH or NSF grant that a colleague receives. In order to explore how receipt of NIH funding impacts other sources of funding, we collected more complete funding information for a randomly selected sub-sample of researchers in our data.

Using the funding information listed in the acknowledgement section of randomly chosen papers for our sub-sample as outcome measures, we re-estimate the specifications from row 4 of Table 2. We find that while published papers of unsuccessful applicants are less likely to be funded by the NIH, they are no less likely to have at least one funding source. Furthermore, the difference in the total number of funding sources between grant winners and losers is not statistically significant. This is consistent with the hypothesis that high-value projects are funded regardless of the success of any particular grant. For a more in-depth discussion of the data and analysis described here, see online Appendix F.

Together, these results provide some evidence that researchers are insured by coauthors, smaller funding agencies, or their own institutions against the possibility that their most productive research projects are not funded. We do not view the evidence presented here as a definitive test of displacement, but do believe that they suggest that displacement may be at least a partial explanation of the relatively small impacts we find.

8. Conclusions

In this paper, we use plausibly exogenous variation in grant receipt generated by the nonlinear funding rules in the NIH to examine the impact of funding on research output. We find that receipt of an NIH grant has at most a small relative effect on the research output of the marginal applicants. There are a number of reasons why these small effects are likely to understate the average productivity of research funding. First, because applicants can reapply for funding, we only observe variation in the funding status of researchers whose applications were funded but would not have been able to withstand further scrutiny. These projects are likely to be less fruitful than the average funded application. Second, researchers who are rejected for funding by the NIH may receive research support from an alternative funding agency, their institution, or a coauthor. These limitations are likely to generalize to the evaluation of any program in which applicants have access to services from a variety of providers.

It is important to recognize that despite the apparent small impact on the marginal applicant, if overall funding is in fixed supply, then NIH research support may increase the amount of R&D in the aggregate. There are relatively few empirical studies on such general equilibrium effects of research funding. Prior research on the labor market for scientists demonstrates that the supply of individuals into depends on a variety of market forces including R&D expenditures and the prevailing salaries in the scientific field and in alternative occupations (see Ehrenberg, 1991, 1992, Freeman, 1975, and Leslie and Oxaca, 1993 for surveys of this literature). However, a recent paper by Freeman and Van Reenen (2009) documents substantial adjustment problems after Congress doubled NIH spending in the bio-medical sciences between 1998 and 2003.¹⁸

Our analysis represents an early step toward examining the effectiveness of government expenditures in R&D. Given the importance of technological innovation for economic growth and the considerable public resources devoted to R&D, considerably more research is warranted.

Research Highlights.

• We employ a regression discontinuity design to identify the impact of NIH grant receipt on subsequent research productivity and finding.

• Receiving an award is associated with only modest increases in applicant research productivity.

• We find little impact that an award displaces other NIH to the applicant.

• Results may reflect that researchers have access to other funding sources for high quality projects.