Bayesian gene set analysis for identifying significant biological pathways

Summary

We propose a hierarchical Bayesian model for analyzing gene expression data to identify pathways differentiating between two biological states (e.g., cancer vs. non-cancer and mutant vs. normal). Finding significant pathways can improve our understanding of biological processes. When the biological process of interest is related to a specific disease, eliciting a better understanding of the underlying pathways can lead to designing a more effective treatment. We apply our method to data obtained by interrogating the mutational status of p53 in 50 cancer cell lines (33 mutated and 17 normal). We identify several significant pathways with strong biological connections. We show that our approach provides a natural framework for incorporating prior biological information, and it has the best overall performance in terms of correctly identifying significant pathways compared to several alternative methods.

1 Introduction

1.1 Motivation

Complex diseases such as cancer involve gene or protein groups functioning in concert. Therefore, it is beneficial not only to identify individual genes related to the disease, but also to understand the underlying pathways (i.e., sets of interconnected genes) that drive the disease process. This would help us improve our understanding of the disease mechanism and to design more effective treatments. We propose a hierarchical Bayesian model for analyzing high-throughput biological experiments, such as gene expression microarrays, in order to identify pathways that are differentially expressed between two (or more) biological states (e.g., cancer vs. non-cancer and mutant vs. normal).

Recent studies have demonstrated that evaluating changes in expression across predefined sets of interconnected genes (e.g., pathways) often increases statistical power and produces more robust results (Virtaneva et al., 2001; Pavlidis et al., 2002; Mootha et al., 2003; Smyth, 2004; Rahnenfuhrer et al., 2004; Subramanian et al., 2005; Barry et al., 2005; Zahn et al., 2006; Efron and Tibshirani, 2007; Muller et al., 2008). Ignoring the interconnectivity among genes on the other hand can result in lack of statistical power and low reproducibility (i.e., there is little overlap between findings from different research groups working on the same biological system). Moreover, it is not uncommon for traditional genomic studies, which focus on individual genes, to produce a large list of significant candidate genes with no unifying biological theme (Subramanian et al., 2005).

In general, gene sets are defined based on prior biological information such as biochemical pathways or similarity of gene sequences. Throughout this paper, we primarily assume that biological pathways are used to form gene sets. Therefore, we use the terms gene sets and pathways interchangeably. The information regarding pathways to define gene sets is available from databases such as the Gene Ontology (http://www.geneontology.org), Kyoto Encyclopedia of Genes and Genomes (http://www.genome.jp/kegg), and the Molecular Signatures Database (http://www.broadinstitute.org/gsea/msigdb/index.jsp). Using the available biological information on interconnectivity among genes, we aim to discover pathways that are associated with a specific biological process. More specifically, in this paper, we aim to identify pathways that are associated with the mutation status of the p53 gene, which plays an important role in many cancers (Harris and Levine, 2005).

1.2 Data

The p53 gene and its network of genes and proteins respond to a variety of signals that regulate DNA replication, chromosome segregation, and cell division (Vogelstein et al., 2000). After DNA damage occurs in a cell, the p53 responsive proteins can aid directly in DNA repair processes. The activation of p53 and its network of genes initiates an elaborate process of autoregulatory-positive or autoregulatory-negative feedback loops, which connect the p53 pathway to other signaling pathways in the cell. Within each pathway the activity (i.e., expression) of some genes may go up while the activity of some other genes may go down. The combination of these activities in concert determine outcome of the cell (to be repaired, to enter cell cycle, or to undergo apoptosis).

To identify pathways involved with p53, we use the publicly available data from http://www.broadinstitute.org/gsea/datasets.jsp. The biological data were obtained based on interrogating the mutation status of p53 in cancer cell lines from the NCI-60 collection (Ross et al., 2000), which was created to explore gene expression in 60 cell lines using DNA microarrays prepared by robotically spotting 9,703 human cDNAs on glass microscope slides. The cDNAs included approximately 8,000 different genes. Subramanian et al. (2005) used the NCI-60 collection to identify targets of the transcription factor p53. Using the IARC TP53 database (Olivier et al., 2002), they found the mutational status of the p53 gene for 50 of the NCI-60 cell lines. Out of 50 cell lines (n = 50), 17 were classified as normal and the remaining 33 were classified as carrying mutations in the p53 gene. Our goal is to identify pathways that are differentially expressed between cell lines with mutated and normal p53 genes.

1.3 Gene set analysis

In recent years, several methods have been proposed for finding significant (differentially expressed) pathways using microarray gene expression data (Virtaneva et al., 2001; Pavlidis et al., 2002; Mootha et al., 2003; Smyth, 2004; Rahnenfuhrer et al., 2004; Subramanian et al., 2005; Barry et al., 2005; Newton et al., 2007; Efron and Tibshirani, 2007). These methods produce inferences on predefined sets of genes as opposed to individual genes. Typically, gene set analysis methods start with a collection of gene sets , , 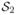…, 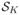defined based on some prior information. Then, for each individual gene, a statistic, z, (e.g., two sample t-statistic), is calculated to measure the amount of support for its corresponding hypothesis. Then, for each gene set 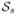, a set-level statistic T_s is calculated as a function of individual statistics z_s = {z_s1, z_s2, …, z_sℓs}, where ℓ_s is the number of genes assigned to that set. The significance of T_s is assessed by using a permutation test where the class labels are repeatedly permuted.

One of the most widely used methods for analyzing gene sets is Gene Set Enrichment Analysis (GSEA). The gene-level test statistic, z, in GSEA is calculated using t-test when the analysis involves two classes (e.g., treatment vs. control). The set-level statistic for the set 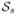is defined as a signed Kolmogorov-Smirnov (KS) statistic based on the distribution of z_s and that of its complement, ${\mathbf{z}}_{\mathbf{s}}^{\mathbf{c}}$, which includes all genes that are not 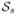. Recall that the KS statistic quantifies the distance between the empirical cumulative distribution function of a sample (here, z_s) and that of a reference sample (here, ${\mathbf{z}}_{\mathbf{s}}^{\mathbf{c}}$). The sign represents the direction of shift in the distribution.

The GSEA method poses several statistical concerns (Damian and Gorfine, 2004; Efron and Tibshirani, 2007). For example, Efron and Tibshirani (2007) argue that while GSEAs dependence on KS is reasonable, it is not necessarily the best choice since KS is sensitive to change in the distribution of z scores across the whole distribution, whereas we are interested mainly in changes in lower and upper distribution tails, where genes are statistically significant. Efron and Tibshirani (2007) propose an alternative approach, Gene Set Analysis (GSA), that has a significant power advantage over GSEA. Their method uses a new statistic called maxmean. For each gene set, maxmean is calculated by first separating negative and positive z-scores (i.e., separating downregulated and upregulated genes within the set). Then, we set the positive z-scores to 0 and take the average over all scores (zeros included). We denote this average as T⁻. Next, we set all negative z-scores to 0 and take the average over all scores (zeros included). We denote this average as T⁺. The maxmean statistic, T_max, is the larger average in absolute value: T_max = max(|T⁻¹|, |T⁺|).

Efron and Tibshirani (2007) show that the maxmean statistic can detect shift of location and scale change in the distribution of z-values. Assuming z_i ~ N (L, S²), they show that maxmean has reasonable power against shift alternatives, L ≠ 0, and scale alternatives, S > 1, where H₀ : (L, S) = (0, 1).

Efron and Tibshirani also argue that any method for assessing gene sets should compare a given gene set score not only to scores from permutations of the sample labels, but also to scores from sets formed by random selections of genes. To illustrate this concept, they generated data on 1000 genes and 50 samples, with each consecutive non-overlapping block of 20 genes considered to be a gene set. The first 25 samples are the control group, and the second 25 samples are the treatment group. First they generated each data value independently from N(0, 1), and then they increased the expression values for the treatment group by the constant 2.5 for the first 10 genes in each gene set. This way, all of the maxmean scores look significantly large compared to the permutation values. But they argue that given the way that the data were generated, there seems to be nothing special about any one gene set. To address this issue, they propose restandardization, where they center and scale the maxmean statistic by its mean and standard deviation under the randomization of genes among gene sets.

Although the maxmean statistic has several advantages (mainly, higher statistical power) over other statistics, it has some limitations. More specifically, we believe that the maxmean statistic performs well when almost all significant candidate genes in a set are either upregulated or down-regulated, since it captures the dominating change (up or down) in gene expression. This method might not work well in situations when some genes within the gene set change in different directions. To illustrate this, consider two gene sets, 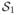and 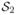, each with 100 genes. In the first set, 50 genes have z-scores equal to −2, and the z-scores of the remaining genes are zero. The second gene set also has 50 z-scores of −2; however, the remaining genes have z-scores equal to 1.5. While it is possible that for a given experiment one might regard 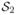as a more significant gene set compared to 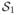, the maxmean score for both gene sets is 1.

As mentioned above, it is not uncommon that within a significant biological pathway, some significant genes are upregulated, while other significant genes are downregulated. For example, when a cell is exposed to ionizing radiation, DNA damage is induced and the p53 pathway is activated. In this case, p53 functions through ataxia telangiectasia (ATM). ATM is a protein kinase that stimulates DNA repair while simultaneously blocking cell cycle progression. Using the p53 gene expression data set, we find that in the ATM pathway, the genes CDKN1A and MDM2 are substantially downrequlated (with z-scores equal to −4.7 and −4.0 respectively) in the cell lines with mutant p53, while two other genes, RELA and CHEK1, are substantially upregulated (with z-scores equal to 2.1 and 2.0 respectively).

In this paper, we propose an alternative approach based on hierarchical Bayesian models for gene set analysis. In the next section, we describe our method in detail. Section 3 shows the results from applying our model to the p53 data. In Section 4, we use simulated data to evaluate the performance of our model. We compare our model to several other approaches including GSEA (Subramanian et al., 2005) and GSA (Efron and Tibshirani, 2007). Finally, Section 5 is devoted to discussion and future directions.

2 Bayesian analysis of gene sets

We denote the i^th observed expression value of gene g in set s as y_sgi. Given the class label x_i, where x_i ∈ {0, 1} (i.e., normal=0, mutant=1), we assume the following model for y_sgi :

$$\begin{array}{lll}{y}_{\mathit{sgi}}\hfill & =\hfill & {\alpha }_{sg}+{\beta }_{sg}{x}_i+{\epsilon }_{\mathit{sgi}}g=1,2,\dots ,{\ell }_s\hfill \\ {\epsilon }_{\mathit{sgi}}\hfill & \sim \hfill & N(0,{\sigma }_{sg}^2)\hfill \end{array}$$

Here, α_sg is the overall mean of expression values for gene g in set s, and β_sg is the expected change in the expression of this gene between the two groups. The model therefore can be considered as a simple linear mixed-effects model, where β_sg are the random effects associated with the class variable. We could therefore use a mixed effects ANOVA model to evaluate the overall significance of a gene set, where the null hypothesis is defined as H₀ : β_s1 = … = β_sℓs= 0. Alternatively, assuming that ${\beta }_{sg}\sim N(0,{\tau }_s^2)$, we have H₀ : ${\tau }_s^2=0$. Standard computer packages such as nlme and lme4 in R could be used for such analysis. Note however that the clustering of observations is based on genes (i.e., variables) as opposed to subjects (which is more common in mixed-effects models).

2.1 A hierarchical Bayesian model

A simple mixed-effects model with a fixed intercept and a random effect parameter is equivalent to a simple hierarchical Bayesian model with uniform prior on the intercept and a normal prior (with mean 0 and unknown variance) on the random effect parameter. However, compared to mixed-effects models, hierarchical Bayesian models are more flexible and can easily handle more complex data structure (e.g., overlaps between gene sets). Using appropriately informative (i.e., reasonably broad) hyperpriors, these models can also accommodate shrinkage of β’s and their corresponding variance ${\tau }_s^2$ towards zero when the gene set as a whole is not significant. This way, they avoid strong influences of one or two differentially expressed genes on the overall measure of significance for the set. Moreover, by using more flexible priors, such as the mixture prior proposed in Section 2.2, we can mitigate the negative effect of wrong model assumptions. Therefore, we believe that models with random effects are more naturally discussed within the hierarchical Bayesian framework where by default all parameters are considered to be random (in general, there is no fixed effect). Here, we use the following prior distributions for the parameters of our model:

$$\begin{array}{lll}\hfill {\sigma }_{sg}^2\mid \xi ,\eta & \sim \hfill & \text{Inv}-{\chi }^2(\xi ,{\eta }^2)\hfill \\ \hfill {\alpha }_{sg}\mid \gamma & \sim \hfill & N(0,{\gamma }^2)\hfill \\ \hfill {\beta }_{sg}\mid \tau & \sim \hfill & N(0,{\tau }_s^2)\hfill \end{array}$$

Note that the priors for ${\sigma }_{sg}^2$ and α_sg are the same for all genes regardless of their associated gene sets. We could set ξ, η and γ to some constant values such that the resulting distributions are appropriately broad so they give reasonable prior probability to the set of possible values. For simplicity, however, we use non-informative priors for these parameters. To this end, we assume $P({\alpha }_{sg},{\sigma }_{sg}^2)\propto 1/{\sigma }_{sg}^2$. For ${\sigma }_{sg}^2$, this is equivalent to setting ξ = 0 and η = 1. For α_sg, this is equivalent to the limit of the normal distribution when we take γ² → ∞.

For the prior of β_sg, we regard ${\tau }_s^2$ as a hyperparameter with its own hyperprior, ${\tau }_s^2\sim \text{Inv}-{\chi }^2(\nu ,{\phi }^2)$. Note that ${\tau }_s^2$ is shared by all genes in the set 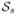. (Throughout this paper, we assume that gene expression values are normalized.) The role of ${\tau }_s^2$ is to adjust the distribution of β’s within a gene set. If a gene is not differentially expressed, its corresponding β_sg moves close to zero in posterior. This would be accommodated by small values of ${\tau }_s^2$. If a large number of genes in a set are not differentially expressed (i.e., negligible amounts of shift are observed), the hyperparameter ${\tau }_s^2$, which is shared by all the genes in the set, would shrink towards zero. If a gene is in fact significant, we expect a large shift in its expression values between the two groups. This in turn makes the posterior distribution of β_sg to move away from zero. When the gene set includes a large number of significant genes, ${\tau }_s^2$ becomes larger in posterior to allow for large values of β_sg. Therefore, we can evaluate the overall significance of a gene set based on the posterior distribution of ${\tau }_s^2$: for a less significant gene set, the posterior distribution of ${\tau }_s^2$ shrinks towards zero, whereas for a significant gene set, the posterior distribution would give higher probabilities to large values of ${\tau }_s^2$. Similarly, we can evaluate the significance of individual genes within a set using the posterior distribution of their corresponding β_sg: the posterior distribution of β_sg for a more significant gene would be away from zero. We can quantify the significance of a gene by measuring the posterior tail probability of zero.

To illustrate the above approach, we use a simple example. We first generate a dataset with 1000 candidate genes and 30 samples such that the first 15 samples are assigned to the control group, and the rest to the treatment group. We assume that each consecutive non-overlapping block of 20 genes forms a set; that is, there are 50 gene sets in total. The values for all genes are first sampled independently from N(0, 1). To make a gene significant, we add the constant 1 to the expression values for the treatment group. In Set 1 we make all 20 genes significant. In Set 2, we make only half of the genes (i.e., 10) significant. We reduce the number of significant genes to 5 for Set 3 and to 2 for Set 4. We keep the remaining 46 gene sets (i.e., Sets 5–50) non significant. Therefore, the significance of gene sets reduces from Set 1 to Set 4, and there is no association between the class variable and Sets 5–50. We use our hierarchical Bayesian method to evaluate the significance of these gene sets.

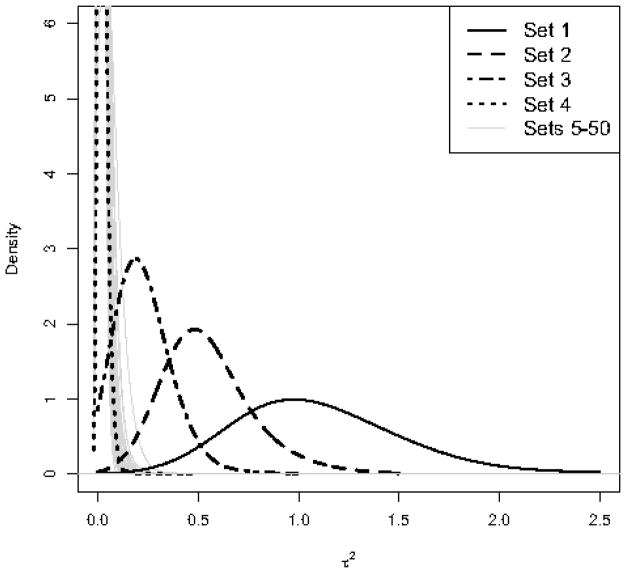
Figure 1 shows the posterior distribution of ${\tau }_s^2$ for the 50 gene sets. As we can see, there is a clear separation between the posterior distribution of ${\tau }_s^2$ for Set 1 (solid black curve) and the posterior distributions of ${\tau }_s^2$ for Sets 5–50. As the number of significant genes reduces from Set 1 to Set 4, the posterior distribution of ${\tau }_s^2$ shrinks towards 0. The posterior distribution of ${\tau }_s^2$ for Set 4 (where only 2 genes out of 20 are significant) is very similar to the posterior distribution of ${\tau }_s^2$ for Sets 5–50. The posterior expectations of ${\tau }_s^2$ for Sets 1 to 4 are 1.11, 0.55, 0.23, and 0.02 respectively. The posterior expectation of ${\tau }_s^2$ for Sets 5–50 ranges from 0.02 to 0.05.

Figure 1.

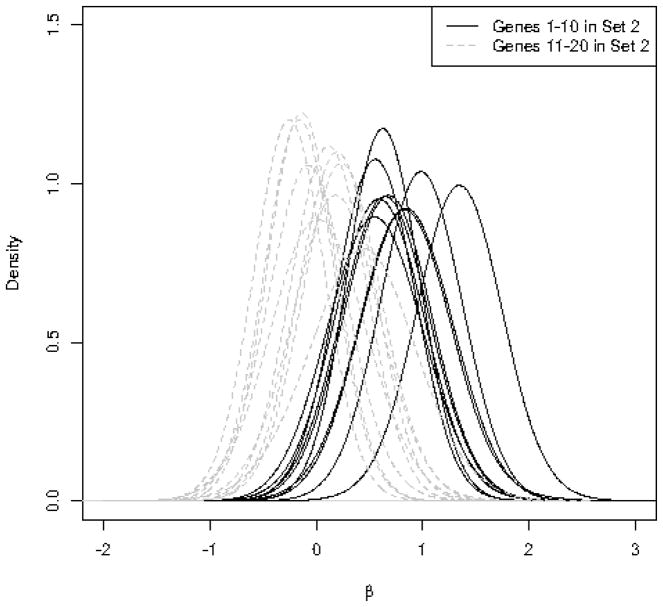
Left panel: Posterior distribution of the hyperparameter ${\tau }_s^2$ for 50 simulated gene sets. Sets 1–4 have 20, 10, 5, and 2 significant genes respectively. Sets 5–50 contain no significant genes. Right panel: Posterior distribution of β_sg for individual genes in Set 2, where the first 10 genes are significantly upregulated (the constant 1 is added to the expression values for the treatment group). The remaining 10 genes in this set are non-significant (β_sg = 0).

As mentioned above, we can use the posterior distribution of β_sg to evaluate the significance of individual genes. The right panel of Figure 1 shows the posterior distribution of β_sg for individual genes in Set 2, where only 10 genes out of 20 are significant. For the significant genes, the posterior distributions of β_sg moves away from 0.

2.2 Gene set selection via mixture priors

The above approach could be useful for ranking gene sets in terms of their significance based on, for example, posterior expectations of ${\tau }_s^2$: the higher the posterior expectation of ${\tau }_s^2$, the more significant the gene set. However, in many practical problems, an automatic mechanism for selecting significant gene sets (or genes) is required. For linear mixed-effects models, we could obviously use p-values with a cutoff that has been adjusted to control the family-wise error rate (i.e., the chance of making at least one type I error) or false discovery rate (i.e., the expected proportion of false positives among the rejected null hypotheses). For our model, we do this by using a mixture prior similar to that of George and McCulloch (1993) and Ishwaran and Rao (2005); instead of a simple scaled-inv-χ² distribution as the prior of ${\tau }_s^2$, we use the following prior:

$${\tau }_s^2\sim (1-\lambda )F_0+\lambda F_1,$$

where F₀ and F₁ are the distributions of ${\tau }_s^2$ under the null and alternative hypotheses respectively, and λ is the probability that ${\tau }_s^2$ is generated under the alternative. As mentioned above, under the null hypothesis of no relationship between a gene set and the class variable, we have ${\tau }_s^2=0$. Therefore, we could assume that under the null F₀ ≡ δ₀ (i.e., point mass distribution at 0). However, making such assumption is appropriate if we are using the correct model (e.g., all the relevant factors are included in the model), and data in fact conform with the model assumptions. This rarely happens in reality. A more reasonable assumption is that under the null ${\tau }_s^2$ are quite small and close to zero. Therefore, we assume the following mixture prior for ${\tau }_s^2$:

$$\begin{array}{lll}\hfill {\tau }_s^2\mid \lambda ,{\phi }_0,{\phi }_1& \sim \hfill & (1-\lambda )\text{Inv}-{\chi }^2(\nu ,{\phi }_0^2)+\lambda \text{Inv}-{\chi }^2(\nu ,{\phi }_0^2+{\phi }_1^2)\hfill \\ \hfill {\phi }_0^2,{\phi }_1^2& \sim \hfill & \text{Gamma}(1,1)\hfill \\ \hfill \nu & \sim \hfill & \text{Gamma}(1,1)\hfill \\ \hfill \lambda & \sim \hfill & \text{Beta}(a,b)\hfill \end{array}$$

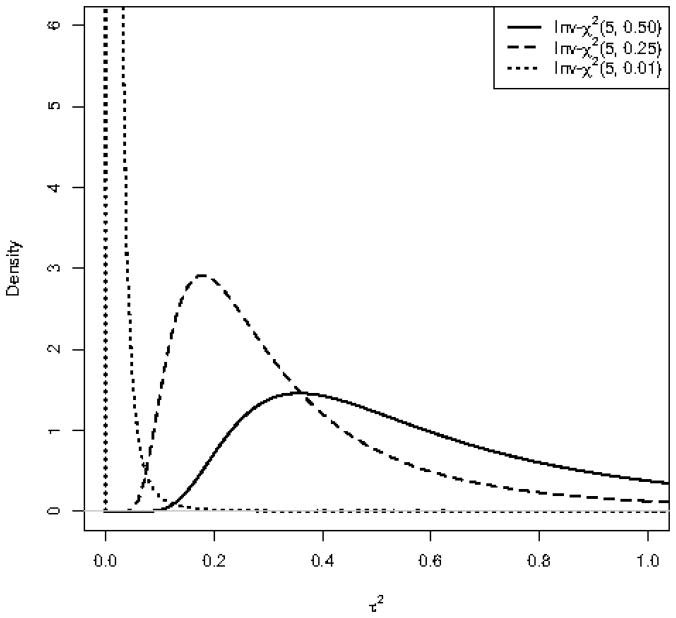
This way, the distribution of ${\tau }_s^2$ are assumed to come from two different distributions: a scaled-inv-χ² distribution with a relatively small scale parameter ${\phi }_0^2$, and a scaled-inv-χ² with a relatively larger scale parameter ${\phi }_0^2+{\phi }_1^2$. As shown in Figure 2, for given degrees of freedom, as the scale parameter increases, scaled-inv-χ² distribution gives higher probability to large values of random variable (i.e., the distribution moves to the right). Therefore, we separate ${\tau }_s^2$ into two groups. One group includes small values of ${\tau }_s^2$ with $\text{Inv}-{\chi }^2(\nu ,{\phi }_0^2)$ prior distribution. These ${\tau }_s^2$ are assumed to be generated under the null hypothesis. The second group includes large values of ${\tau }_s^2$ with $\text{Inv}-{\chi }^2(\nu ,{\phi }_0^2+{\phi }_1^2)$ prior distribution. These ${\tau }_s^2$ are assumed to be generated under the alternative hypothesis.

Figure 2.

Three scaled-inv-χ² distributions with the same degrees of freedom and different scale parameters. As the scale parameter increases, the distribution moves to the right giving higher probabilities to large values of ${\tau }_s^2$.

For λ, we use a conjugate Beta(1, 1) prior (i.e., a = b = 1), which is equivalent to the Uniform(0, 1) distribution. In practice, we might expect that only a small number of gene sets are significant and use more informative priors such as Beta(1, 10).

To facilitate posterior sampling, we use the data augmentation approach (Tanner and Wong, 1987) by introducing binary latent variables v_s ~ Bernoulli(λ) such that

$${\tau }_s^2\mid v_s,{\phi }_0,{\phi }_1\sim (1-v_s)\text{Inv}-{\chi }^2(\nu ,{\phi }_0^2)+v_s\text{Inv}-{\chi }^2(\nu ,{\phi }_0^2+{\phi }_1^2).$$

Alternatively, we can write the above prior as

$$\{\begin{array}{l}{\tau }_s^2\mid v_s=0,\nu ,{\phi }_0\sim \text{Inv}-{\chi }^2(\nu ,{\phi }_0^2)\hfill \\ {\tau }_s^2\mid v_s=1,\nu ,{\phi }_0,{\phi }_1\sim \text{Inv}-{\chi }^2(\nu ,{\phi }_0^2+{\phi }_1^2)\hfill \end{array}$$

Note that we can use the posterior distribution of v_s given the observed data, D, to evaluate the significance of each gene set. To this end, we use p̂₀ = 1 −E(v_s|D), where E(v_s|D) is the posterior expectation of the latent variable v_s, as our point estimate for the posterior probability of H₀ given the data, P(H₀|D).

We refer to the above method as Bayesian Gene Set Analysis (BGSA). We applied the BGSA model to the simulated data discussed above. For Sets 1–4, the estimated values p̂₀ are 0.002, 0.008, 0.06, and 0.99 respectively. For Sets 5–50 (non significant genes sets), p̂₀ ranges from 0.96 to 1.

2.3 Posterior sampling

The priors used in this paper are all conditionally conjugate except for the priors used for scale parameters of scaled-inv-χ² distributions (i.e., ν, ${\phi }_0^2$ and ${\phi }_1^2$). Using conjugate priors make posterior sampling easier since posterior distributions are conditionally tractable so we can use the Gibbs sampler. The posterior distributions for ${\sigma }_{sg}^2$ and α_sg given all other parameters are as follows:

$$\begin{array}{lll}{\sigma }_{sg}^2\mid ·\hfill & \sim \hfill & \text{Inv}-{\chi }^2\left(n,\frac{{\sum }_{i=1}^n{(y_{\mathit{sgi}}-{\alpha }_{sg}-{\beta }_{sg}{x}_i)}^2}{n}\right),\hfill \\ {\alpha }_{sg}\mid ·\hfill & \sim \hfill & N\left(\frac{{\sum }_i^n(y_{\mathit{sgi}}-{\beta }_{sg}{x}_i)}{n},\frac{{\sigma }_{sg}^2}{n}\right).\hfill \end{array}$$

Samples from the posterior distribution of β_sg obtained given the updated values of the above parameters as well as the current value of ${\tau }_s^2$,

$${\beta }_{sg}\mid ·\sim N\left(\frac{\frac{1}{{\sigma }_{sg}^2}{\sum }_i^n(y_{\mathit{sgi}}-{\alpha }_{sg})x_i}{\frac{t}{{\tau }_s^2}+\frac{{\sum }_i^n{x}_i}{{\sigma }_{sg}^2}},{\left[\frac{1}{{\tau }_s^2}+\frac{{\sum }_i^n{x}_i}{{\sigma }_{sg}^2}\right]}^{-1}\right)$$

The posterior distribution of ${\tau }_s^2$ has a closed form given the current values of β’s, v_s, ν, ${\phi }_0^2$ and ${\phi }_1^2$,

$$\{\begin{array}{l}{\tau }_s^2\mid v_s=0,\nu ,{\phi }_0^2,\beta \sim \text{Inv}-{\chi }^2\left(\nu +{\ell }_s,\frac{\nu {\phi }_0^2+{\sum }_{g=1}^{{\ell }_s}{\beta }_{sg}^2}{\nu +{\ell }_s}\right),\hfill \\ {\tau }_s^2\mid v_s=1,\nu ,{\phi }_0^2,{\phi }_1^2,\beta \sim \text{Inv}-{\chi }^2\left(\nu +{\ell }_s,\frac{\nu ({\phi }_0^2+{\phi }_1^2)+{\sum }_{g=1}^{{\ell }_s}{\beta }_{sg}^2}{\nu +{\ell }_s}\right).\hfill \end{array}$$

We sample v_s from a Bernoulli distribution with the following probability:

$$P(v_s=1\mid {\tau }_s^2,\nu ,{\phi }_0^2,{\phi }_1^2,\lambda )=\frac{\lambda f({\tau }_s^2\mid \nu ,{\phi }_0^2,{\phi }_1^2)}{(1-\lambda )f({\tau }_s^2\mid v,{\phi }_0^2)+\lambda f({\tau }_s^2\mid \nu ,{\phi }_0^2,{\phi }_1^2)},$$

where $f({\tau }_s^2\mid \nu ,{\phi }_0^2)$ and $f({\tau }_s^2\mid \nu ,{\phi }_0^2,{\phi }_1^2)$ are densities for scaled-inv-χ² distributions with ${\phi }_0^2$ and ${\phi }_0^2+{\phi }_1^2$ scale parameters respectively. The conditional posterior distribution of λ also has a closed form,

$$\lambda \sim \text{Beta}(a+\sum _s^K{v}_s,b+K-\sum _s^K{v}_s).$$

Here, a = b = 1 and K is the total number of gene sets.

Because priors for ν, ${\phi }_0^2$ and ${\phi }_1^2$ are not conditionally conjugate, we cannot use the Gibbs sampler for these parameters. However, the computational burden is negligible since the number of these parameters is small. To sample from the posterior distribution of ν, ${\phi }_0^2$ and ${\phi }_1^2$, we use single-variable slice sampling (Neal, 2003). At each iteration, we use the “stepping out” procedure to find the interval around the current point and the “shrinkage” procedure for sampling from the interval.

3 Results for the p53 data

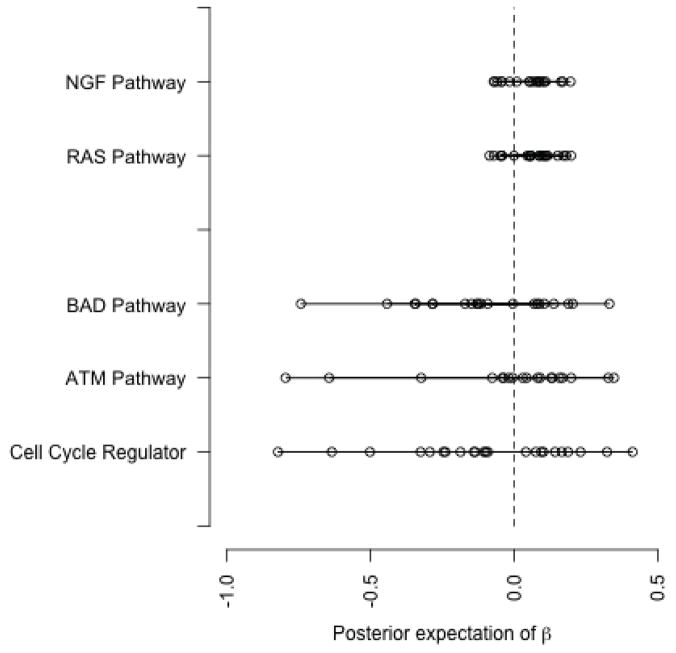
We apply our BGSA model to the p53 data set, which is publicly available from http://www.broadinstitute.org/gsea/datasets.jsp. As discussed above, our goal is to identify the pathways that are significantly associated with p53 mutation status. Using the curated gene sets available from the Molecular Signatures Database (MSigDB), we allocate genes into 522 gene sets. We ran the MCMC simulation for 2000 iterations of which the first 500 were discarded. Table 1 shows the selected pathways by setting the cutoff for p̂₀ at 0.1. While many of these pathways are also identified as significant by GSEA and GSA, there are notable differences between the results based on these methods. For example, Cell Cycle Regulator, ATM, and BAD pathways, which appear in Table 1, are not selected as significant by Efron and Tibshirani (2007) and Subramanian et al. (2005). On the other hand, some pathways such as RAS and NGF are identified as significant by GSA but not by BGSA. Figure 3 compares these pathways based on the posterior expectation of β_sg. The pathways are presented on the y axis. Each point shows the posterior expectation of β_sg for an individual gene in a pathway. As we can see, the three pathways identified by our model present a substantial location shift (from zero) as well as scale change compared to RAS and NGF. For the ATM pathway, the two downregulated genes shown on the far left (with the posterior expectation of β_sg equal to −0.80 and −0.64) are CDKN1A and MDM2, and the two upregulated genes on the far right (with the posterior expectation of β_sg equal to 0.35 and 0.33) are RELA and CHEK1 as discussed in Section 1.3.

Table 1.

List of significant gene sets in p53 dataset based on the BGSA model. The sets are selected by setting the cutoff for p̂₀ at 0.1.

Gene set	Number of genes	E(τ2|D)	p̂0
p53 Pathway	16	0.34	0.004
Radiation Sensitivity	26	0.26	0.004
p53 Hypoxia Pathway	20	0.28	0.011
p53 Up	40	0.28	0.016
Cell Cycle Regulator	23	0.19	0.023
DNA Damage Signaling	90	0.15	0.047
ATM Pathway	19	0.19	0.079
g2 Pathway	23	0.17	0.091
BAD Pathway	21	0.15	0.098

Figure 3.

Comparing the pathways which are not common between the results based on BGSA and GSA. “Cell Cycle Regulator”, “ATM pathway”, and “BAD pathway” are selected by BGSA only. RAS and NGF, on the other hand, are identified as significant by the GSA method. Each point shows the posterior expectation of β_sg for an individual gene in the pathway.

Both ATM and BAD are strongly involved with p53. ATM encodes a protein kinase that acts as a tumor suppressor, and its activation via IR damage to DNA stimulates DNA repair and blocks cell cycle progression. One mechanism through which this occurs is ATM dependent phosphorylation of p53, which causes growth arrest of the cell at a checkpoint to allow for DNA damage repair. It can also cause the cell to undergo apoptosis if the damage cannot be repaired. BAD, as a member of the BCL2 family, is also involved with the p53 pathway. BAD physically interacts with cytoplasmic p53 thereby preventing p53 from entering the nucleus. BAD mRNA and protein are increased in response to the upregulated expression of wild-type p53 but not the mutant p53 in cell lines.

One main concern about gene set analysis methods is how the size of gene sets influences the result. For our method, there is no strong relationship (the correlation coefficient is 0.07) between the number of genes in a gene set and p̂₀.

4 Results for simulated datasets

We conduct three simulation studies in order to evaluate the performance of our approach in terms of identifying significant pathways. More specifically, we compare our model, BGSA, to a linear mixed-effects (LME) model, GSEA (Subramanian et al., 2005), maxmean statistic (Efron and Tibshirani, 2007), and two other summary statistics based on the mean of z_i and the mean of |z_i|, which we refer to as Mean.z and Mean.abs.z respectively. For the BGSA model, we ran 2000 Markov chain Monte Carlo (MCMC) iterations, and obtained the posterior distributions after discarding the first 500 samples (i.e., from pre-convergence iterations). The convergence of MCMC was evaluated based on hyperparameters ν, ${\phi }_0^2,{\phi }_1^2$ and ${\tau }_s^2$. For the LME model, we use lme4 package in R. For GSEA, we use the publicly available R package (http://www.broad.mit.edu/gsea) called R-GSEA. Maxmean, Mean.z and Mean.abs.z statistics are obtained using the GSA software available from http://www-stat.stanford.edu/~tibs/GSA/index.html. The computer programs for all the above models along with the R script to simulate data are available online at http://www.ics.uci.edu/~babaks/Homepage/Codes.html.

To make sure our simulations closely resemble real situations (hence, making the simulation studies aligned to the application), we simulate data using the p53 data set discussed in the previous section. That is, we use the actual gene expression values and the class labels from real biological data. Of course, we need to know which gene sets are in fact related to the class variable, x, so we can evaluate different models based on their ability to identify the significant gene sets. To this end, we start by randomly re-allocating genes among the 522 gene sets. (522 is the actual number of gene sets obtained from MSigDB.) This way, the grouping of genes among gene sets is random; hence, no gene set should be selected as significant, except by chance. Next, we randomly select five gene sets and make them significant. For this, we use t-tests for individual genes (i.e., regardless of their corresponding gene sets), identify the top 20 genes with the lowest p-values, and randomly allocate them among the five selected gene sets. (On average, each selected gene set would include four highly significant genes.) A reasonable gene set analysis method should identify these five gene sets as significant.

For the first simulation, we make the gene sets mutually exclusive, i.e., each gene belongs to one gene set only. For the second simulation, we relax this assumption for all genes, except the top 20 genes assigned to the five selected significant gene sets. In this scenario, significant gene sets could share common genes with non-significant gene sets. This could make them less distinguishable. Therefore, compared to the first simulation, we expect that identifying the significant gene sets becomes more difficult. In the third simulation, we allow gene sets to share common genes, including the top 20 genes. In this scenario, finding the five significant gene sets will become even more difficult, since the top 20 genes (which could only belong to the five selected gene sets in simulations 1 and 2) can now randomly appear in non-significant gene sets, making them appear significant by chance. We repeat each simulation 100 times. At each iteration, we randomize genes among the 522 gene sets, randomly select five gene sets, and allocate the top 20 genes among them.

The sample size for the p53 data set is n = 50. Typical microarray data sets tend to have smaller sample size. To make simulated data sets more comparable to real situations, we randomly select a subset of samples such that the sample size would be between 10 and 20. The sample size itself is chosen randomly and varies from one simulated data set to another.

The performance of each model is evaluated using the ROC curve which allows for simultaneous consideration of power (i.e., sensitivity) and type I error (i.e., 1-specificity) without setting an arbitrary cut-off for significance level. Each point on the curve represents the number of correctly identified significant gene sets (vertical axis) compared to the number of times a model identified a non significant gene set as significant (horizontal axis) for different cut-offs. A more accurate model will have an ROC curve further away from the diagonal line (random model) with perfect prediction corresponding to the (0, 1) point. The Area under the ROC curve (AUC) is used as a summary statistic to compare models. For a perfect model, the AUC is equal to 100%. For each simulation, we regard the five selected gene sets as true positive and all other sets as true negative. Table 2 shows the average (over 100 repetitions) of AUC values for alternative methods under different simulation settings. The corresponding standard errors are presented in parentheses. As we can see, our hierarchical Bayesian model provides the best overall performance. Also, our results show that Maxmean outperforms GSEA in all three simulations. This is consistent with the findings of Efron and Tibshirani (2007).

Table 2.

Comparing our hierarchical Bayesian model to alternative approaches based on the average AUC (presented in percentage) over 100 simulated data sets for each simulation. The numbers in parentheses show the corresponding standard errors.

	GSEA	Mean.z	Mean.abs.z	Maxmean	LME	BGSA
Simulation 1	60.0 (0.71)	65.3 (0.98)	67.7 (1.20)	80.9 (0.97)	80.8 (1.16)	87.2 (0.87)
Simulation 2	60.4 (0.74)	61.0 (0.92)	65.8 (1.00)	68.9 (1.08)	76.3 (1.14)	79.1 (1.10)
Simulation 3	60.2 (0.76)	61.2 (0.84)	64.7 (0.97)	68.7 (1.03)	74.8 (1.11)	77.0 (1.08)

5 Discussion and future directions

We have proposed a new method for evaluating the significance of biological pathways using a hierarchical Bayesian model. In this approach, the prior distributions of β_sg (where β_sg measures the effect of the gene g associated with the pathway s), for g = 1, …, ℓ_s, share a common hyperparameter, ${\tau }_s^2$; that is, ${\beta }_{sg}\mid {\tau }_s^2\sim N(0,{\tau }_s^2)$. In prior, β_sg, for g = 1, …, ℓ_s, are conditionally independent given the value of ${\tau }_s^2$. Marginally, however, sharing the common hyperprameter ${\tau }_s^2$ introduces prior dependence among the magnitudes (i.e., |β_sg|) of gene effects for genes in the pathway s. (Note that two genes within the same pathway can be either positively related if they are upregulated or downregulated together, or they can be negatively related if they move in opposite directions.) For large values of ${\tau }_s^2$, the magnitudes of β_sg tend to be large. As ${\tau }_s^2$ decreases, the magnitudes of gene effects decrease so β_sg will be concentrated near zero. Therefore, if the pathways are defined properly, we expect that the informative prior incorporated in our model results in better performance in terms of identifying significant pathways.

In our model, we use $N(0,{\tau }_s^2)$ as the prior for β_sg. Alternatively, one could use $N({\mu }_s,{\tau }_s^2)$, which is a more flexible prior since the mean of the distribution is not fixed at zero. However, this complicates our inference regarding the significance of gene sets since with this prior, μ_s captures the location of the distribution of β_sg, while ${\tau }_s^2$ captures its variance. For example, suppose all β_sg are equal to 1. Then, the posterior distribution of μ_s would be concentrated around one, while the posterior distribution of ${\tau }_s^2$ shrinks towards zero since the actual variance of β’s is zero. On the other hand, if half of β’s are 1 and the other half are −1, then μ_s becomes concentrated around zero in posterior, while ${\tau }_s^2$ becomes large to accommodate the relatively larger variation among β_sg. Therefore, to have power against both shift and scale alternatives, we have to take both hyperparameters μ_s and ${\tau }_s^2$ into account. Our prior (with the mean fixed at zero) on the other hand, captures both location shift and scale change in the distribution of β_sg using one hyperparameter, ${\tau }_s^2$. This is clear for the example where half of β_sg are 1 and the other half are −1. For the example where all β’s are 1, since the mean is fixed at zero, ${\tau }_s^2$ has to become large to accommodate values of β_sg away from zero.

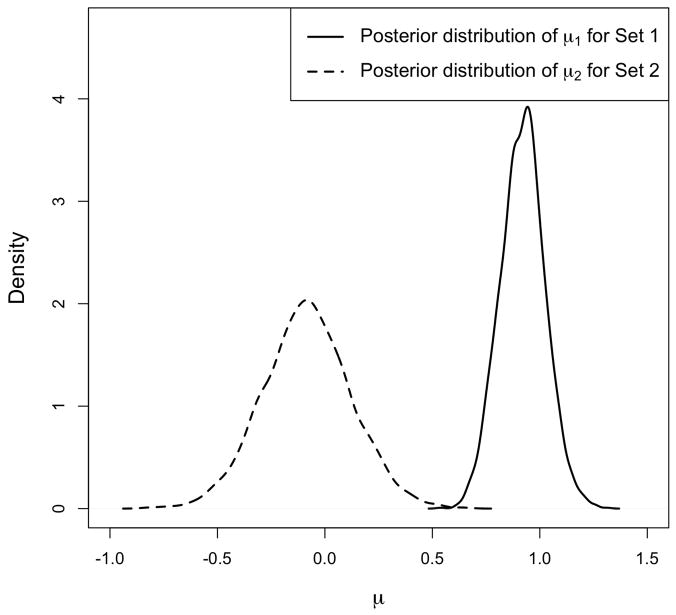
To illustrate this concept, we generate a dataset with two gene sets each with 20 genes. We set the sample size n = 30, where the first 15 samples are assigned to the control group, and the rest to the treatment group. The values for all genes are first sampled independently from N(0, 1). For the genes in the first set, we add the constant 1 to the expression values for the treatment group. For the first 10 genes in the second set, we add the constant −1 to the expression values for the treatment group, and for the remaining 10 genes, we add the constant 1 instead. We first run our model using ${\beta }_{sg}\sim N({\mu }_s,{\tau }_s^2)$ prior. Figure 4 shows the posterior distribution of μ_s and ${\tau }_s^2$ for the two sets. Notice that the location shift (away from zero) of β_sg for the first set is clear from comparing μ₁ to μ₂, while the relatively larger variance of β_sg in the second set is clear from comparing ${\tau }_2^2$ to ${\tau }_1^2$.

Figure 4.

Posterior distribution of hyperparameters, μ_s and ${\tau }_s^2$, if we assume ${\beta }_{sg}\sim N({\mu }_s,{\tau }_s^2)$. The simulated data includes two gene sets, each with 20 genes. For the first gene set, we set the actual values of β_sg to 1, for g = 1, …, 20. For the second gene set, β_sg is set to −1 for half of the genes and to 1 for the remaining genes. The left panel shows the posterior distribution of μ₁ and μ₂ for Set 1 and Set 2. The right panel shows the posterior distribution of ${\tau }_1^2$ and ${\tau }_2^2$ for the two sets. Notice that the location shift in the distribution of β_sg for Set 1 is captured by μ₁, while the relatively larger variance of β_sg for Set 2 is captured by ${\tau }_2^2$.

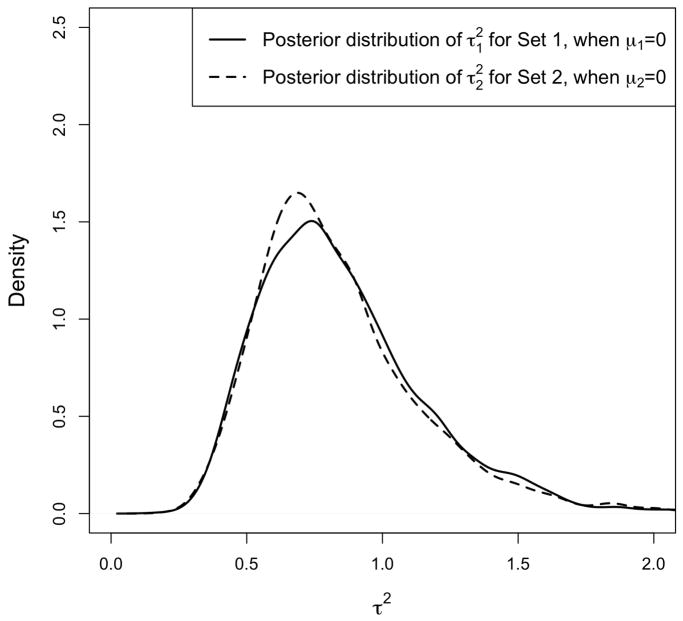
Next, we run our model using ${\beta }_{sg}\sim N(0,{\tau }_s^2)$ prior. Figure 5 shows the posterior distribution of ${\tau }_1^2$ and ${\tau }_2^2$ for Set 1 and Set 2 respectively. (μ₁ and μ₂ are fixed at zero.) As we can see, the posterior distributions are quite similar for the two sets. That is, ${\tau }_s^2$ has captured the location shift in the distribution of β_sg for the first set, and the scale change for the second set. Therefore, by fixing μ_s at zero and using the posterior distribution of ${\tau }_s^2$ for inference, our method has power against both shift and scale alternatives.

Figure 5.

Posterior distribution of ${\tau }_s^2$ assuming ${\beta }_{sg}\sim N(0,{\tau }_s^2)$. The simulated data includes two gene sets, each with 20 genes. For the first gene set, we set the actual values of β_sg to 1, for g = 1, …, 20. For the second gene set, β_sg is set to −1 for half of the genes and to 1 for the remaining genes. The Posterior distribution of ${\tau }_1^2$ and ${\tau }_2^2$ for Set 1 and Set 2 are similar. Therefore, the hyperparameter ${\tau }_s^2$ has captured the location shift in the distribution of β_sg for Set 1, and the scale change for Set 2.

One advantage of our model is that it automatically performs a form of restandardization that proposed by Efron and Tibshirani (2007). To show this, we generate data similar to the illustrative example in Section 2.1, but this time we increase the expression values for the treatment group by 1 unit for half of the genes in every gene set. This way, we make half of the genes in each set upregulated, but there is nothing special about any of the gene sets. In this case, the estimated values p̂₀ for the 50 gene sets are close to 0.5 ranging from 0.29 to 0.77. This is consistent with the fact that no set is special.

Our hierarchical Bayesian model could also be extended for problems with multiple samples (e.g., several experimental conditions). For such problems, we can modify the prior for β’s as follows:

$${\beta }_{\mathit{sgc}}\sim N(0,{\tau }_s^2),c=1,\dots ,C,$$

where c is the index for the groups (e.g., experimental conditions), and β_sgc is the effect parameter associated with class c. Note that the control group with c = 0 is considered as the baseline, and x_i is now a vector of dummy variables. In this setting, all β’s in a set are still controlled by one hyperparameter, ${\tau }_s^2$. Alternatively, we could have an additional hyperparameter for each gene

$${\beta }_{\mathit{sgc}}\sim N(0,{\tau }_s^2{\rho }_{sg}^2)$$

This way, ρ_sg controls all β’s associated with gene g in set s. This setting makes it easier for the variance of β_sg to shrink towards zero if a gene is not significant (i.e., its corresponding β’s are small) while other genes in the set seem to be significant. If the set as a whole is not signifiant, the posterior distribution of ${\tau }_s^2$ will shrink towards zero making all β’s associated with set s small simultaneously.

While simulation studies show that our approach outperforms other methods, our BGSA model is more computationally intensive compared to GSA and GSEA. Using an implementation of R script on a Linux CentOS 5.3 machine with 2191 MHz processor speed, 2000 iterations of posterior sampling for p53 dataset takes approximately 20 minutes to run. This is much slower than, for example, the GSA model, which runs for 25 seconds on the same dataset (with 100 permutations).

Currently, our method does not take into account possible overlaps between gene sets. In reality, the gene sets are not mutually exclusive. Our approach could easily be extended to take into account the overlaps between gene sets. We could, for example, modify our prior such that gene sets that include common genes share common hyperparameters. Without loss of generality, consider two gene sets 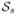= {G₁, G₂, …, G_q, G_s,q+1, G_s,q+2, …, G_sℓs} and 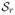= {G₁, G₂, …, G_q, G_r,q+1, G_r,q+2, …, G_rℓr} that share q genes: {G₁, …, G_q}. We can use the following priors for β’s to account for the overlap:

$$\begin{array}{lll}\hfill {\beta }_1,\dots ,{\beta }_q\mid {\tau }_{rs}& \sim \hfill & N(0,{\tau }_{rs}^2)\hfill \\ \hfill {\beta }_{s,q+1},\dots ,{\beta }_{s{\ell }_s}\mid {\tau }_{rs},{\tau }_s& \sim \hfill & N(0,{\tau }_s^2+{\tau }_{rs}^2)\hfill \\ \hfill {\beta }_{r,q+1},\dots ,{\beta }_{r{\ell }_r}\mid {\tau }_{rs},{\tau }_r& \sim \hfill & N(0,{\tau }_r^2+{\tau }_{rs}^2)\hfill \end{array}$$

This way, if the common genes are not significant, their corresponding hyperparameter, ${\tau }_{rs}^2$, shrinks towards zero, and the significance of sets 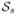and 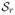would depend solely on the non-overlapping genes. However, if the common genes are in fact significant, ${\tau }_{rs}^2$ moves away from zero and contributes to the overall significance of both gene sets.

Similar to GSEA and GSA, our method regards the gene sets as known and fixed. Therefore, none of these methods take into account the uncertainty regarding the grouping of genes. In reality, there are many ways to group genes depending on which biological aspect we consider. A similar concern is recently discussed by Shen and West (2008). Our hierarchical Bayesian model could address this issue by assuming multiple grouping schemes each with its own separate set of hyperparameters.

While the main motivating application for our proposed model is identifying signaling pathways (each pathway is associated with a collection of interconnected genes), our method could be applied to a wide range of problems, for which a large number of hypotheses are grouped into subsets of related hypotheses according to some prior information. One such problem is functional neuroimaging for human brain mapping, to study normal versus pathological brain functions. A typical experiment in this area involves assessing a large number of pixels (each pixel representing a small area of brain tissue). It is possible to group pixels such that each subset of pixels represents a different brain region. Another possible application for our method is analysis of single-nucleotide polymorphisms (SNPs) in genome-wide association studies, where the objective is to identify and characterize genetic variants related to complex diseases. These studies commonly focus on haplotypes (a set of statistically associated SNPs that are transmitted together as a block) on a single chromatid. More recently, there have been suggestions to focus on pathways in genome-wide association studies (see for example, Luan and Li, 2008).