A Sharp-Interface Immersed Boundary Method with Improved Mass Conservation and Reduced Spurious Pressure Oscillations

Abstract

A method for reducing the spurious pressure oscillations observed when simulating moving boundary flow problems with sharp-interface immersed boundary methods (IBMs) is proposed. By first identifying the primary cause of these oscillations to be the violation of the geometric conservation law near the immersed boundary, we adopt a cut-cell based approach to strictly enforce geometric conservation. In order to limit the complexity associated with the cut-cell method, the cut-cell based discretization is limited only to the pressure Poisson and velocity correction equations in the fractional-step method and the small-cell problem tackled by introducing a virtual cell-merging technique. The method is shown to retain all the desirable properties of the original finite-difference based IBM while at the same time, reducing pressure oscillations for moving boundaries by roughly an order of magnitude.

1. Introduction

Immersed Boundary methods (IBM)[1] are a highly versatile approach for the simulation of flows around moving/deforming bodies with complex geometrical shapes. One undesirable property of IBMs being reported for the dealing with such moving/deforming bodies on a fixed, non-body conformal computational grid is, unphysical, temporal oscillation of the pressure fields[2, 3, 4, 5, 6, 7, 8]. These spurious pressure oscillations are observed virtually for all type of IBMs including flow-reconstruction based methods[2, 3, 4] as well as discrete[5, 6] and distributed[7, 8] forcing methods. Other immersed boundary based approaches also show spurious oscillations in the forces exerted on the moving body[9]. As will be shown here, the primary source for this error is that for moving boundary problems, the role of some grid cells (or grid points) in the computational domain changes in time leading to spurious mass sources/sinks. For example, in an IBM based on the sharp-interface treatment[2], the governing equations (mass and momentum conservation) are solved only on the cells in the fluid domain and for moving immersed boundaries, this leads to the generation of fresh cells (cells that go from being inside the solid to being in the fluid) and dead cells (cells that go from being inside the fluid to being inside the solid). Luo et al.[3] mentioned that the abrupt change of the stencils for the flow reconstruction and a finite-differencing of the governing equations associated with these cells causes spurious oscillations in the pressure. Similarly, in IBMs using the forcing method [5, 6, 7, 8], numerical stencils for applying forcing terms are changing with the boundary motion. Lee et al.[5] identified two sources of the pressure oscillations in a discrete-forcing IBM; one source is the spatial discontinuity in the pressure across the immersed boundary caused by the fresh cells, and the other is the temporal discontinuity in the velocity at the dead cell. For diffuse-interface IBMs such as distributed forcing methods[7, 8, 10, 11], spurious pressure oscillations are diminished by spreading and smoothing out of the forcing term[8]. On the other hand, in sharp-interface IBMs, the pressure oscillation error is manifested more severely and it is more difficult to control, since these methods have no intrinsic smoothing mechanism at the immersed boundaries. A few remedies have been proposed for sharp-interface IBMs: for instance, pressure oscillations are reduced by applying the flow reconstruction[3, 4] or forcing[6] on cells that at inside as well as outside of the immersed body. Such treatments, however, reduce the sharpness of the immersed boundary and may diminish the advantage of sharp interface methods.

In the present study, we have analyzed the pressure oscillations due to the boundary motion in a sharp-interface immersed boundary method and made the case that the major source for the pressure oscillations is found to be the violation of local mass conservation near the immersed boundary. The mass conservation error is in-fact primarily due to violation of the geometric conservation law (GCL), a concept that is well established in body-fitted grid methods[12]. In order to reduce the spurious pressure oscillations, we propose a method that significantly improves local mass-conservation. The proposed approach employs ideas from the cut-cell approach but avoids some significant complexities associated with a cut-cell discretization. Tests are carried out to demonstrate the effectiveness and accuracy of the current approach.

2. Source of Pressure Field Oscillation

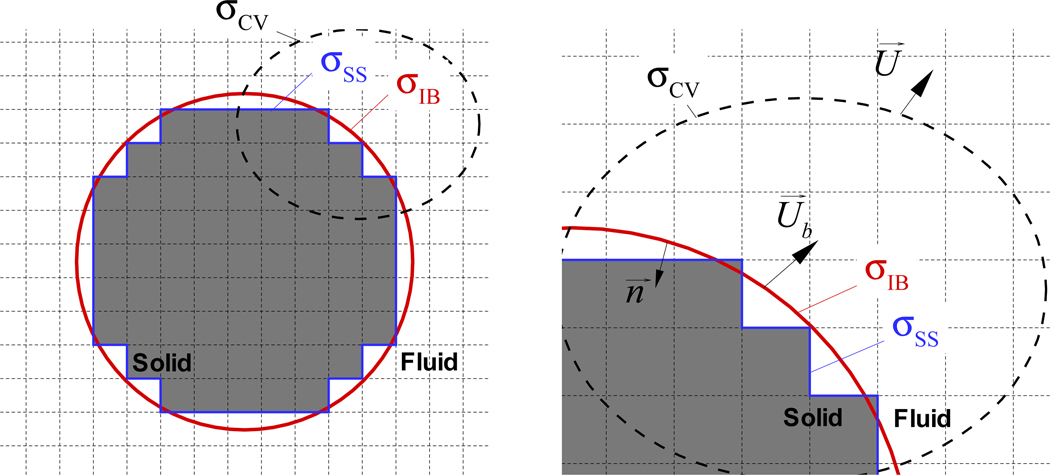
Consider a rigid moving, immersed boundary on a fixed, non-body conformal grid (Fig.1). For the class of immersed boundary methods of particular interest here, the boundary conditions, which include no-slip, no-penetration for velocity and appropriate Neumann boundary condition for pressure, are imposed to some order of accuracy (typically between 1st and 2nd order) on σ_IB. This imposition may be through the use of direct flow reconstruction by interpolation[3, 4] or extrapolation[2], or through the introduction of a discrete forcing term[5, 6] in the momentum equations. Thus, the boundary conditions are imposed at a finite number of points that are located precisely on the surface of the immersed boundary and this leads to a “sharp-interface” representation of the immersed boundary. For an incompressible fluid, the fluid volume inside the computational domain should be conserved through the satisfaction of the following condition:

$${\displaystyle {\int }_{{\sigma }_{\mathit{\text{IB}}}}}{\overrightarrow{U}}_b·\overrightarrow{n}\mathit{\text{dA}}+{\displaystyle {\int }_{{\sigma }_{\mathit{\text{CV}}}}}\overrightarrow{U}·\overrightarrow{n}\mathit{\text{dA}}=0,$$ (1)

where σ_IB and σ_CV are the surfaces of the immersed body and the control volume, respectively (see Fig.1), U⃗_b is the boundary velocity on the immersed boundary, and n⃗ is the surface normal unit vector. Here we assume that the solid boundary is a non-porous, no-slip wall which allows no relative velocity between the fluid and the body. Using divergence theorem on the first term, the above equation can be rewritten as

$$-\frac{{d\mathbf{V}}_{\mathit{\text{IB}}}}{\mathit{\text{dt}}}+{\displaystyle {\int }_{{\sigma }_{\mathit{\text{CV}}}}}\overrightarrow{U}·\overrightarrow{n}\mathit{\text{dA}}=0,$$ (2)

where V_IB is the volume enclosed by immersed boundary surface, σ_IB. The fluid control volume is defined by (V_IB^c ∩ V_CV). For stationary bodies, the total fluid volume should be unchanged in time. In projection-method based solution algorithms, mass (volume) conservation is imposed when solving the pressure Poisson equation. In the finite-difference based, sharp-interface IBMs, the pressure Poisson equation is solved for the cells inside the fluid domain and the local mass conservation is satisfied by enforcing the following condition;

$$\nabla ·{\overrightarrow{U}}^{n+1}=0,$$ (3)

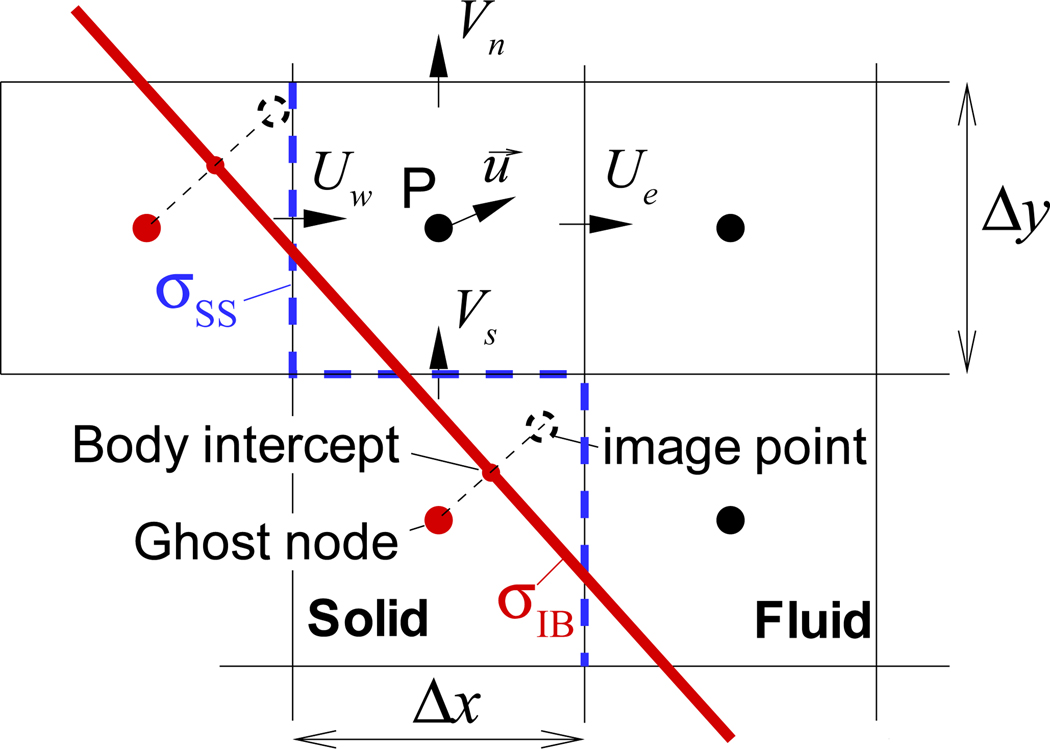
where U⃗ⁿ⁺¹ is the face-velocity at the new time level. In a finite-difference based method, the above local mass conservation can be written as (e.g. using the second-order central differencing, see Fig. 2)

$$\frac{U_e-U_w}{\mathrm{\Delta }x}+\frac{V_n-V_s}{\mathrm{\Delta }y}+\frac{W_f-W_b}{\mathrm{\Delta }z}=0.$$ (4)

Figure 1.

Immersed boundary in a fixed, non-body conformal Cartesian grid. σ_IB: Immersed boundary surface, σ_SS: Surface of stair-step representation of solid body, σ_CV : Control volume surface, and Grayed: Computational cells inside the immersed boundary.

Figure 2.

Sharp interface immersed boundary method based on a finite difference method. The velocity on the ghost node is obtained by extrapolation with the fluid velocity on the image point and the booundary velocity on the body-intercept point.

Now consider the situation for a cell that is intersected by the immersed boundary such as cell ‘P’ shown in Fig. 2. For such a cell, even though the velocities are carefully imposed using a second-order accurate ghost-cell based prescription of the velocity on the immersed boundary surface (in this case at the adjacent body-intercept points), the control volume of such a cell remains cuboidal with volume equal to ΔV = Δx · Δy · Δz, regardless of how the immersed body “cuts” this cell. For example, on Fig. 2, the face velocity, V_s is computed using the velocity on the ghost node which is evaluated with the fluid velocity on the image point and the boundary velocity on the body-intercept point. The mass conservation for this boundary cell is however still written by Eq. (4) for a cell volume ΔV. Additionally, the mass conservation for the ghost cells (the cell-center of which is inside the immersed body) is not considered at all although it contains some part of the fluid volume. In this case, the fluid control volume is considered to be (V_SS^c ∩ V_CV). As a result, the global conservation law applied in the current (as well as all other) sharp-interface IBM is effectively replaced by the following equation:

$$-\frac{\mathrm{\Delta }V}{\mathrm{\Delta }t}(q^{n+1}-q^n)+{\displaystyle {\int }_{{\sigma }_{\mathit{\text{SS}}}}}{\overrightarrow{U}}_f·\overrightarrow{n}\mathit{\text{dA}}+{\displaystyle {\int }_{{\sigma }_{\mathit{\text{CV}}}}}\overrightarrow{U}·\overrightarrow{n}\mathit{\text{dA}}=0,$$ (5)

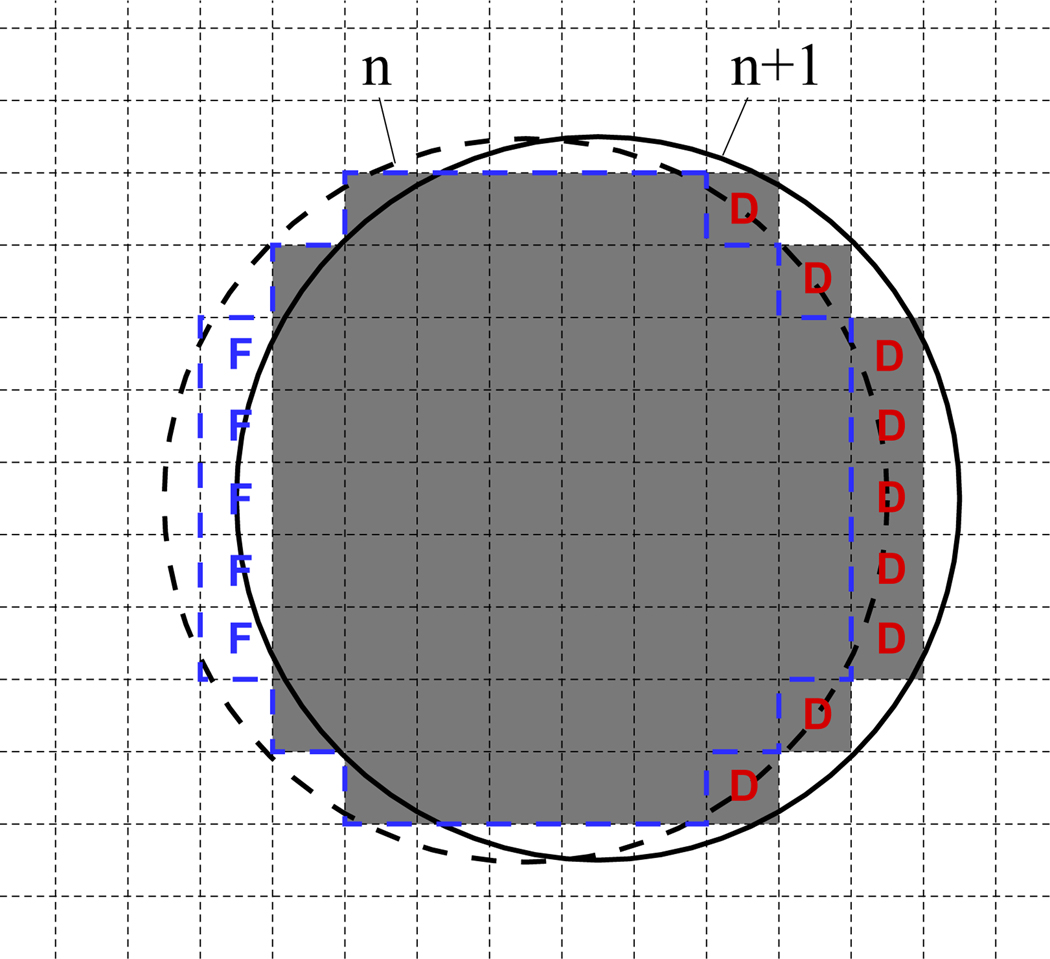
where q^k corresponds to the total number of solid cells at time level k, ΔV is the volume of each of these cells, Δt is the time step size, and subscript f denotes the value on the cell faces of the “stair-step” boundary, σ_SS associated with the immersed body. The first term is associated with the fact that the volume enclosed by a “stair-step” shaped boundary changes abruptly with the appearance of ‘fresh cells’ and ‘dead cells’ as shown in Fig. 3. The second term represents the “transpiration” mass flux through the boundary which, as we will show presently, is also generally non-zero even when the original immersed boundary has no transpiration. In order to estimate overall mass conservation error associated with the sharp-IBM treatment, the above equation is re-written as:

$$-\frac{{d\mathbf{V}}_{\mathit{\text{IB}}}}{\mathit{\text{dt}}}+{\displaystyle {\int }_{{\sigma }_{\mathit{\text{CV}}}}}\overrightarrow{U}·\overrightarrow{n}\mathit{\text{dA}}=\frac{\mathrm{\Delta }V}{\mathrm{\Delta }t}(q^{n+1}-q^n)+[{\displaystyle {\int }_{{\sigma }_{\mathit{\text{IB}}}}}{\overrightarrow{U}}_b·\overrightarrow{n}\mathit{\text{dA}}-{\displaystyle {\int }_{{\sigma }_{\mathit{\text{SS}}}}}{\overrightarrow{U}}_f·\overrightarrow{n}\mathit{\text{dA}}],$$ (6)

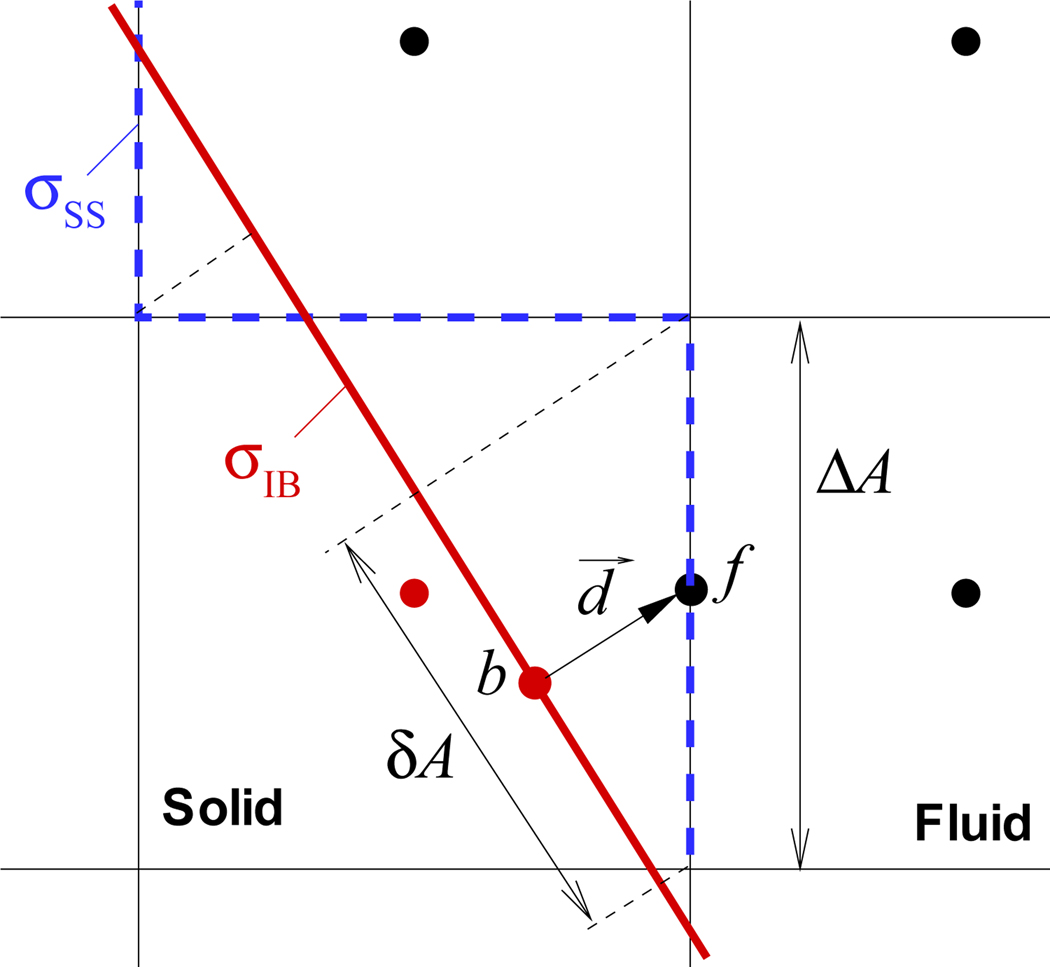
where the right-hand side terms represent the error in mass conservation. The terms inside the bracket can be estimated as follows (see Fig. 4):

$${\displaystyle {\int }_{{\sigma }_{\mathit{\text{IB}}}}}{\overrightarrow{U}}_b·\overrightarrow{n}\mathit{\text{dA}}-{\displaystyle {\int }_{{\sigma }_{\mathit{\text{SS}}}}}{\overrightarrow{U}}_f·\overrightarrow{n}\mathit{\text{dA}}={\displaystyle \sum _{\mathit{\text{face}}}}({\overrightarrow{U}}_b·{\overrightarrow{n}}_b\delta A-{\overrightarrow{U}}_f·{\overrightarrow{n}}_f\mathrm{\Delta }A)=\mathrm{\Delta }A{\displaystyle \sum _{\mathit{\text{face}}}}({\overrightarrow{U}}_b·{\overrightarrow{n}}_b({\overrightarrow{n}}_f·{\overrightarrow{n}}_b)-[{\overrightarrow{U}}_b+(\overrightarrow{d}·\overrightarrow{\nabla })\overrightarrow{U}+\cdots ]·{\overrightarrow{n}}_f)=-\mathrm{\Delta }A{\displaystyle \sum _{\mathit{\text{face}}}}{\overrightarrow{U}}_b·({\overrightarrow{n}}_f-{\overrightarrow{n}}_b({\overrightarrow{n}}_f·{\overrightarrow{n}}_b))-\mathrm{\Delta }A{\displaystyle \sum _{\mathit{\text{face}}}}(\overrightarrow{d}·\overrightarrow{\nabla })\overrightarrow{U}·{\overrightarrow{n}}_f.$$ (7)

Figure 3.

Boundary motion on a fixed Cartesian grid from time level n to n + 1. ‘F’ and ‘D’ denote fresh and dead cells generated by the boundary motion.

Figure 4.

Projection of face areas on to the immersed boundary surface; ΔA: face area, ΔA: area projected on the boundary surface, f: face-center point, and b: projected point on the boundary surface.

As depicted in Fig. 4, each cell face is projected on to the immersed boundary surface and the face-velocity is evaluated by a Taylor series expansion from the boundary velocity. In the above analysis, ΔA is the cell face area, δA is projected area on to the boundary surface, and n⃗_f and n⃗_b are the unit normal vectors of the cell face and the boundary surface, respectively. Consequently, the conservation statement that is actually enforced in finite-difference based sharp-interface IBM solvers is

$$-\frac{{d\mathbf{V}}_{\mathit{\text{IB}}}}{\mathit{\text{dt}}}+{\displaystyle {\int }_{{\sigma }_{\mathit{\text{CV}}}}}\overrightarrow{U}·\overrightarrow{n}\mathit{\text{dA}}=\underset{S_V}{\underbrace{\frac{\mathrm{\Delta }V}{\mathrm{\Delta }t}(q^{n+1}-q^n)}}-\underset{S_{\sigma }}{\underbrace{\mathrm{\Delta }A{\displaystyle \sum _{\mathit{\text{face}}}}{\overrightarrow{U}}_b({\overrightarrow{n}}_f-{\overrightarrow{n}}_b({\overrightarrow{n}}_f·{\overrightarrow{n}}_b))-\mathrm{\Delta }A{\displaystyle \sum _{\mathit{\text{face}}}}(\overrightarrow{d}·\overrightarrow{\nabla })\overrightarrow{U}·{\overrightarrow{n}}_f}}.$$ (8)

The right-hand side terms are essentially geometric conservation errors. The first term in the right-hand side (S_V) corresponds to a spurious source of fluid volume and this source is associated with the fresh and dead cells as shown in Fig. 3. On the other hand, the second and third terms (S_σ) are associated with the transpiration error through the surface area. The second term is caused by the geometrical (shape and size) difference between the immersed boundary and the stair-step boundary. As a simple example consider the fact that, for a circular immersed body of radius R, the surface area of the immersed boundary is ∫_σIB dA = 2πR whereas the surface area of a corresponding ‘stair-step’ boundary is given by ∫_σSS dA = 8R + O(Δ). For a stationary boundary, the first and second terms become zero, since q is unchanged in time and U⃗_b=0. The third term is associated with the mismatch in the location of the actual immersed boundary and the boundary on which the conservation statement is enforced; it is proportional to the velocity gradients near the immersed boundary and is non-zero even for a stationary boundary. It should be noted that while the third term is of a higher order in grid spacing than the second term (due to the fact that d = O(Δ)), the actual magnitude of this term is difficult to determine a-priori since the velocity gradient in the vicinity of the immersed boundary can be large.

Because the first term is associated with the sudden changes in fluid volume due to the fresh and dead cells, this error would show a highly discontinuous variation in time. In contrast, the second and third terms, that are associated with the shape change of the stair-step boundary relative to the immersed boundary are expected to vary more smoothly in time since U⃗_b, n⃗_b, n⃗_f and d⃗ are all expected to vary smoothly in time. Shape changes associated with the appearance of fresh and dead cells contribute only a small fraction to these error terms and should not affect the temporal smoothness of these terms significantly.

We also note that if we reduce the control volume size down to that of an individual fresh or dead cell, the volume conservation error can be written as

$$\left|\frac{\mathrm{\Delta }V}{\mathrm{\Delta }t}-{\overrightarrow{U}}_b·{\overrightarrow{A}}_n\right|=\frac{\mathrm{\Delta }V}{\mathrm{\Delta }t}|1-{\mathit{\text{CFL}}}_b|,$$ (9)

where A⃗_n is the normal area vector of the boundary surface segmented by the cell and CFL_b = ΔtU⃗_b · A⃗_n/ΔV. Thus, it is expected that the dominant component of the pressure oscillation error is proportional to the grid area (volume in 3D), and inversely proportional to the size of the time-step. This implies that one should choose the grid and time step size carefully to reduce the pressure oscillation error. Lee et al.[5] have investigated the effect of time step size, grid spacing, and CFL number on the pressure oscillation error for several test cases.

In order to demonstrate the generation of spurious pressure oscillations in a moving boundary problem and investigate its relation to the volume conservation error, we devise a simple test problem; a circular cylinder with center located at x_c and of diameter D, which oscillates sinusoidally in the x-direction .i.e.

$$x_c(t)=x_c(0)+X_o[1-\text{cos}(2\mathrm{\pi }{f}_{0}t)],u_c(t)=U_o\text{sin}(2\mathrm{\pi }{f}_{0}t),$$ (10)

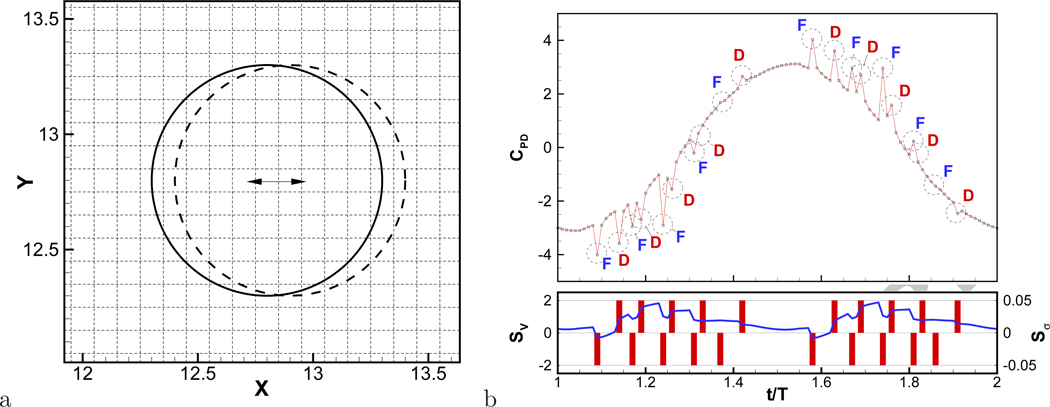
where U₀ = 2πf₀X₀ and the period of oscillation is T = 1/f₀. For this case, we choose X₀ = 0.05D. The Reynolds number defined as Re = U₀D/ν is set at 31, and the Strouhal number is St = f₀D/U₀ = 3.2. The Neumann type boundary conditions with zero gradients are applied for the pressure and velocities at the outer boundaries. A relatively coarse grid with Δx = Δy = 0.1D is employed and this corresponds to the cylinder being covered by 10 × 10 cells (see Fig. 5a). Furthermore, a small time-step corresponding to Δt = 0.01T, (CFL = U₀Δt/Δx = 0.0314) is used. In keeping with Eq. (9), the combination of a large grid spacing and small time-step should produce large and noticeable spurious pressure oscillations. Furthermore, while the cylinder motion for this case produces both fresh and dead cells, they do not occur at the same time, and this allows us to distinguish the effect of these different cells on the pressure oscillations.

Figure 5.

a) Geometry and computational grid for fundamental oscillating body test problem. Bodies are resolved by about 10 by 10 grid points and oscillation amplitude is 1Δx. b) Time history of pressure drag coefficient. ‘F’ and ‘D’ mark time instances where fresh and dead cells are created respectively. The bar graph below represents the first term on the right hand side of Eq. (8), (S_V), and the solid line is the sum of the second and third terms, (S_σ).

The total pressure drag on the body is given by

$$C_{\mathit{\text{PD}}}=\frac{{\displaystyle \int }p(\overrightarrow{n}·\overrightarrow{i})\mathit{\text{dA}}}{(1/2){\rho }_0{D}^3{f_0}^2},$$ (11)

where C_PD is a pressure drag coefficient, n⃗ is a unit surface normal vector, and i⃗ is a x-direction unit vector, is a good measure of the instantaneous pressure around the body and we estimate this using the trapezoidal rule. The time histories of C_PD are plotted in Fig. 5b, and one can see several peaks in the pressure force. The first term on the right hand side source of Eq. (8) denoted by S_V (bar graph) and other two terms denoted by S_σ (solid line) are also plotted at the bottom. It clearly shows that the volume source/sink error caused by fresh and dead cells, (S_V) is much larger (by a factor of about 40) than the transpiration error through the surface, (S_σ). It is therefore not surprising that the oscillations on the pressure force is correlated well with the S_V plot. By comparing the two plots, it is clear that the pressure peaks appear when fresh or dead cells occur, and the peaks caused by fresh cells and dead cells are marked with ‘F’ and ‘D’, respectively. Also note that dead and fresh cells are created at different times for this problem. Figure 5b, therefore, clearly shows that the dominant source of pressure oscillations is connected with the spurious mass source/sinks caused by the creation of fresh and dead cells. It should be noted that in general, both dead and fresh cells may be created at a given time-step but the individual effects still do not cancel out since they occur at different locations around the body. Figure 5b confirms that the errors associated with the change in the shape of the stair-step boundary (second and third terms on the right hand side of Eq.(8)) are smaller in magnitude and also vary more smoothly in time than the volume change error.

In order to further assess the effect of grid spacing and time-step size on the pressure oscillation, we solve the oscillating cylinder problem with larger oscillation amplitude, X₀ = 0.125D, on four different grids (with grid spacing, Δx = Δy = D/16, D/32, D/48, and D/64) and a fixed Δt equal to 0.002T (CFL =0.025, 0.05, 0.1, and 0.2). We also solve the problem for different time-step sizes (Δt/T = 0.002, 0.004, 0.008, and 0.016) for a fixed grid spacing of Δx = Δy = D/16 (CFL =0.025, 0.05, 0.1, and 0.2). In order to quantify the amplitude of the pressure oscillations we define a 2δ-discontinuity in the temporal variation of a quantity F as

$$F^{2\delta }=|F^{n+1}-2F^n+F^{n-1}|,$$ (12)

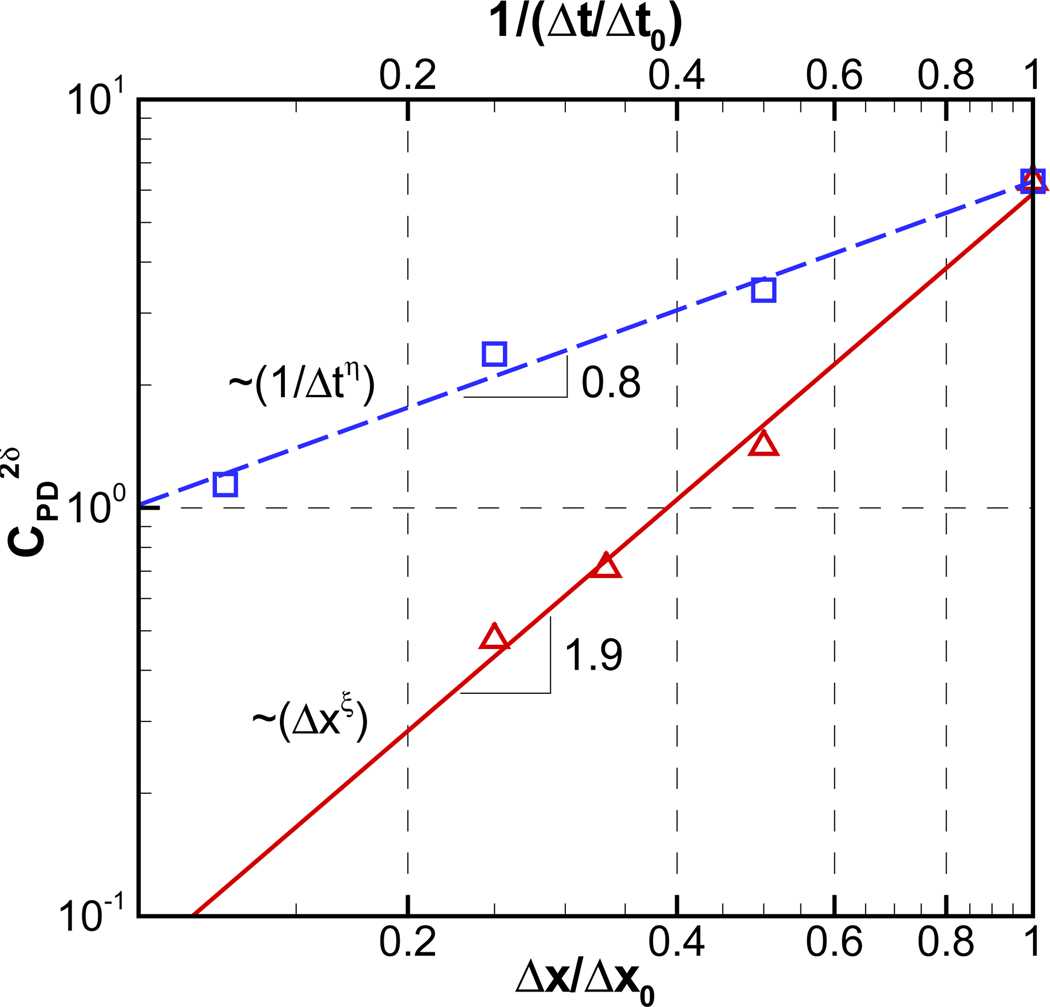
where n is time-step index. The root-mean-squared (RMS) values of $C_{\mathit{\text{PD}}}^{2\delta }$ are plotted in Fig. 6 as a function of grid spacing and time-step size. As expected (and predicted by Eq. (9)) the pressure oscillations decrease with decreasing grid spacing and increase with decreasing time-step. This tendency has also been confirmed in previous studies[3, 4, 5]. A best-fit power-law though the points in Fig. 6 indicates that the pressure oscillations as quantified by $C_{\mathit{\text{PD}}}^{2\delta }$ scale as

$$C_{\mathit{\text{PD}}}^{2\delta }\sim \frac{{(\mathrm{\Delta }x)}^{1.9}}{{(\mathrm{\Delta }t)}^{0.8}}.$$ (13)

Figure 6.

RMS of 2δ-discontinuity in pressure drag coefficient ($C_{\mathit{\text{PD}}}^{2\delta }$) for an oscillating circular cylinder. The results are shown for different grid (solid, triangles) and time-step sizes (dashed, squares). Lines are power-law fitting, $C_{\mathit{\text{PD}}}^{2\delta }\sim {(\mathrm{\Delta }x)}^{\xi }\text{ and }{C}_{\mathit{\text{PD}}}^{2\delta }\sim {(1/\mathrm{\Delta }t)}^{\eta }$, where ξ = 1.9 and η = 0.8. (Δx₀ = 1/16, Δt₀ = 0.002)

This is very much in line with Eq. (9) which predicts that $C_{\mathit{\text{PD}}}^{2\delta }$ would scale as (Δx)²/(Δt) for a two-dimensional problem. It should be noted that for the present test case, the second term of Eq. (9) is negligible, since the maximum CFL number based on the body velocity is 0.025 ~ 0.2 and therefore much smaller than 1. Interestingly, for a solid body moving with constant uniform speed U₀, if the local grid size and time step size satisfy the condition, CFL = U₀Δt/Δx = 1, our analysis suggests that the conservation error terms vanish and the regional(or global) volume conservation error (Eq. 8) is smooth in time (since qⁿ⁺¹ = qⁿ and the shape of ‘stair-step’ boundary is un-changed). We have tested such a case and observed no noticeable pressure oscillations. These tests therefore provide strong support for our hypothesis that the pressure oscillations are caused primarily by violation of the geometric conservation law which introduces local mass sources and sinks. It should also be pointed out that some past studies have focused primarily on the pressure oscillations caused by fresh cells[13]. The current analysis shows that dead cells are equally important sources of spurious oscillations.

It is useful to point out that for diffuse-interface methods which include the discrete-delta function based implementation[7, 8] or penalization based methods[14, 15], the interface is normally described by a discretized delta function, which is spread smoothly over a set of local grid points. For example, the immersed boundary velocity is distributed by

$${\overrightarrow{u}}_b(\overrightarrow{x})={\overrightarrow{U}}_b·{\delta }^{*}(\overrightarrow{x}-{\overrightarrow{x}}_b),$$ (14)

where δ^* is a discretized delta function which varies smoothly in space, and x⃗_b is the position vector of immersed boundary. The smoothing of the interface can be viewed conceptually as leading to the following modified local volume conservation error:

$$\left|\frac{{d\mathbf{V}}_{\delta }}{\mathit{\text{dt}}}-\frac{{d\mathbf{V}}_{\mathit{\text{IB}}}}{\mathit{\text{dt}}}\right|\simeq {\overrightarrow{U}}_b·{\overrightarrow{A}}_n|{\delta }^{*}(\overrightarrow{x}-{\overrightarrow{x}}_b)-1|=\frac{\mathrm{\Delta }V}{\mathrm{\Delta }t}{\mathit{\text{CFL}}}_b|{\delta }^{*}(\overrightarrow{x}-{\overrightarrow{x}}_b)-1|,$$ (15)

where V_δ is the smoothed solid volume. Smoothing of interface therefore leads to a smoother temporal variation of the error. This is the reason why the pressure oscillation can be reduced by these diffuse-interface treatments. In fact, Yang et al.[8] have shown that the pressure oscillations can be suppressed by introducing smoother discrete delta functions. Also, in the diffused-interface IBM of Taira & Colonius [10, 11], they claimed that the global mass is conserved well and there were no temporal oscillation errors on the body force for a moving boundary problem. Note however that the smoothing of this form reduces pressure oscillations without mitigating the underlying conservation error.

Based on the above analysis it is therefore clear that the pressure oscillations can be suppressed by reducing the errors associated with the geometric conservation law. One way to satisfy the geometric conservation law and local mass conservation accurately is through the use of a Cartesian cut-cell method[16, 17]. In this method, the boundary cells which are cut by the immersed boundary are reconstituted into non-rectangular control-volumes and a finite-volume method used to ensure strict satisfaction of GCL as well as local and global mass (and momentum) conservation. Due to these conservative properties, the Cartesian cut-cell method produces no significant spurious pressure oscillations for moving boundary problems[17]. However, there are two main challenges with cut-cell methods. First the cell cutting procedure for a 3D geometry can produce seven different polyhedral control volumes (if the cell is cut by only one surface) and handling all these different cell topologies in a single solver is highly challenging. Even state-of-the-art finite-volume solvers typically handle at most two different cell topologies. The second issue is the formation of arbitrarily small cells which can lead to excessive stability constraints and problems with convergence of elliptic equations such as the pressure Poisson equation. In order to avoid the formation of very small cut-cells, a geometric cell-merging approach can be adopted[16, 17]. Unfortunately, not only are these merging schemes highly complex, they introduce additional cell topologies, and this severely complicates the discretization process as well as the solution methodology. Consequently, the extension of these methods to 3D problems has been very difficult. To resolve the small cut-cell problem in a 3D Cartesian cut-cell method, Kirkpatrick et al.[18] used ‘cell-linking’ technique instead of ‘merging’, and Meyer et al.[19] proposed a ‘momentum-exchange’ technique which is a type of ‘virtual’ cell merging. Recently, a 3D cut-cell method which allows multiple small cell linking has been reported[20] for the viscous compressible flows, but the efficiency of the method and its ability to address highly complex geometries remains to be established.

In the present study, we propose a method to reduce the pressure oscillations for sharp-interface IBMs by adopting the conservative properties of the Cartesian cut-cell method. However, two strategies are employed in order to preserve the efficiency and simplicity of the finite-difference method; first, the cut-cell methodology is applied only to mass (and not to momentum) conservation, and second, the small cell-merging/linking process is simplified by introducing the “virtual” merging technique of Meyer et al.[19]. This allows us to avoid all the significant complexities associated with geometric cell merging/linking. The details of our approach and the numerical procedure are given in the following section.

3. Numerical Method

The immersed boundary method used in this study is the sharp-interface IBM described by Mittal et al.[2]. The method uses a ghost-cell method which is second-order accurate in space and a detailed description of this method can be found in the original paper of Mittal et al.[2]. The incompressible Navier-Stokes equations are solved by a fractional-step method based algorithm and we provide a very brief description of this method here. In the first sub-step of the fractional step method, the intermediate, cell-center velocity is computed by

$${\overrightarrow{u}}^{*}={\overrightarrow{u}}^n+\mathrm{\Delta }t·\left[\right(\frac{3}{2}{C}^n-\frac{1}{2}{C}^{n-1})+\frac{1}{2}(D^n+D^{*})],$$ (16)

where C and D represent convection and diffusion terms on the momentum equations and both are discretized with a second-order central-difference scheme. The face-velocities are subsequently evaluated from the cell-center velocities as

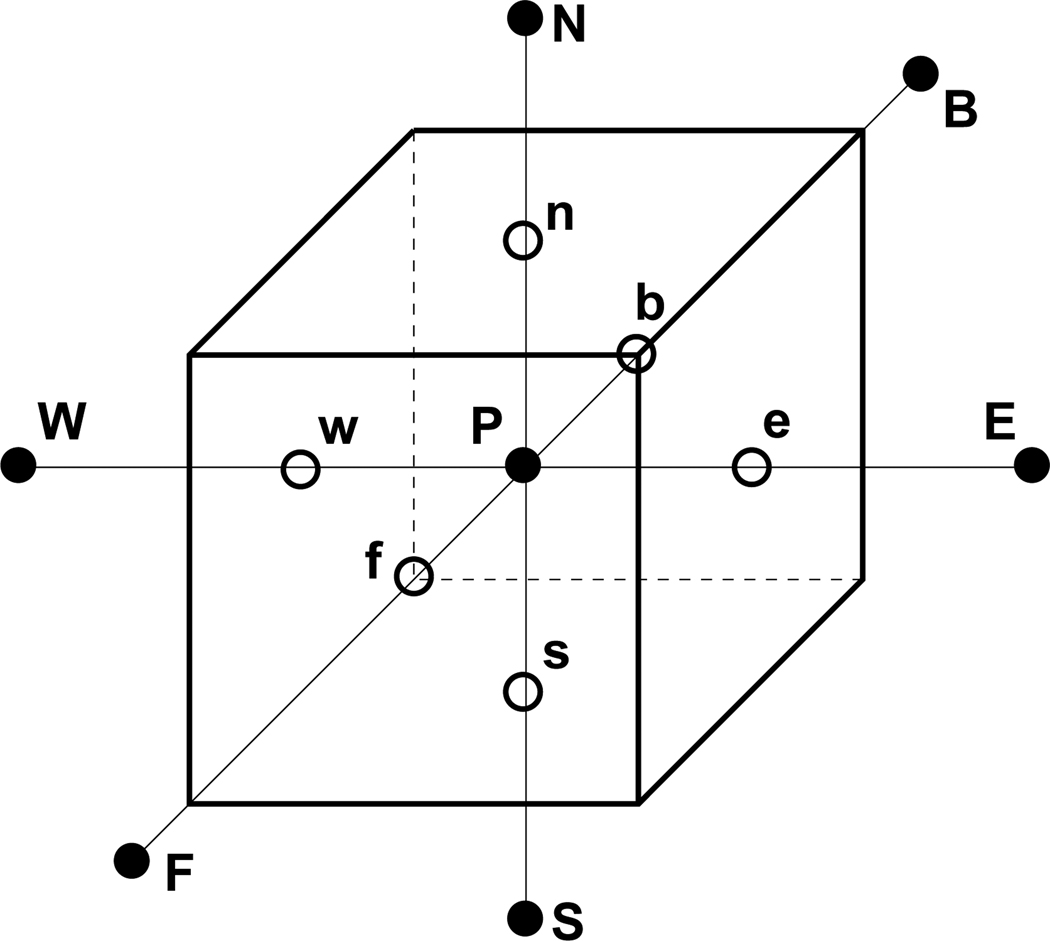
$$U_e^{*}=\frac{{\mathrm{\Delta }}_{\mathit{\text{eP}}}·u_E^{*}+{\mathrm{\Delta }}_{\mathit{\text{eE}}}·u_P^{*}}{{\mathrm{\Delta }}_{\mathit{\text{eE}}}+{\mathrm{\Delta }}_{\mathit{\text{eP}}}},$$ (17)

where Δ is the distance from the cell-face to the cell-center (see Fig.7). The pressure is computed by the Poisson equation:

$${\nabla }^2{p}^{n+1}=\frac{{\rho }_0}{\mathrm{\Delta }t}(\nabla ·{\overrightarrow{U}}^{*}).$$ (18)

Figure 7.

Notations of numerical stencils for the discretization of governing equations. Capital letters indicate neighboring cells (‘P’ denotes the current cell) and small letters represent cell faces.

Finally, the cell-center and cell-face velocities are corrected by

$${\overrightarrow{u}}^{n+1}={\overrightarrow{u}}^{*}-\frac{\mathrm{\Delta }t}{{\rho }_0}·{\nabla }_{\mathit{\text{cc}}}{p}^{n+1},$$ (19)

$$U_e^{n+1}=U_e^{*}-\frac{\mathrm{\Delta }t}{{\rho }_0}{\nabla }_{\mathit{\text{fc}}}{p}^{n+1},$$ (20)

where Δ_cc and Δ_fc denote the gradients at the cell-center and cell-face, respectively. The moving, immersed boundary is represented in terms of Lagrangian markers whose location and velocity is denoted by x⃗_b and U⃗_b, respectively. For fresh cells which have no time histories of the flow velocity, the intermediate velocities are estimated by a trilinear (3D) or bilinear (2D) interpolation[2] and this is followed by the pressure correction step.

Since we have determined that the major source of pressure oscillation associated with the boundary motion is spurious fluctuations in the fluid volume (and mass) as well as changes in the effective geometry of the immersed interface, the cut-cell approach is applied to Eq. (18) and (19) to achieve better volume and mass conservation. The momentum equation, Eq. (16) is solved as usual by a second-order central finite-difference discretization using the ghost-cell method[2] and one does not need to spend additional effort in computing momentum fluxes and stresses for the cut-cells. Furthermore, the stability restrictions (CFL and/or viscous stability depending on the temporal discretization of the method) caused by small cut-cells can be avoided.

The finite-volume integration of Eq. (18) and (19) are written as

$${\displaystyle \int }(\nabla p^{n+1}·\overrightarrow{n})\mathit{\text{dA}}=\frac{{\rho }_0}{\mathrm{\Delta }t}{\displaystyle \int }({\overrightarrow{U}}^{*}·\overrightarrow{n})\mathit{\text{dA}},$$ (21)

$${\displaystyle \int }{\overrightarrow{u}}^{n+1}\mathit{\text{dV}}={\displaystyle \int }{\overrightarrow{u}}^{*}\mathit{\text{dV}}-\frac{\mathrm{\Delta }t}{{\rho }_0}{\displaystyle \int }(p^{n+1}\overrightarrow{n})\mathit{\text{dA}}.$$ (22)

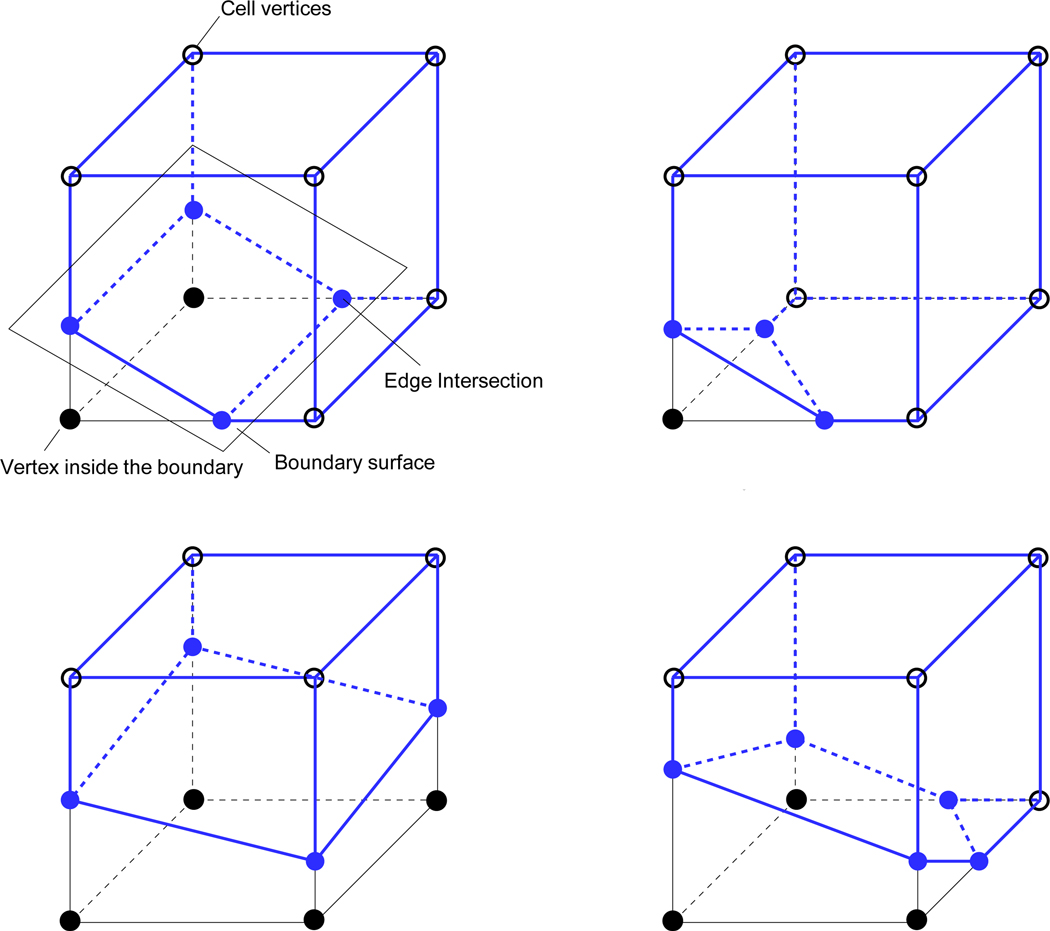
In order to apply the finite-volume discretization to Eq. (21) and (22), the volume-fraction (the ratio of fluid volume to the total cell volume) and face-fractions (the ratio of face area in fluid region to the total face area) should be determined for the cells cut by the boundary surface. The procedure for determining the cell cuts and the associated cell volumes and face areas is relatively straightforward and has been described in previous papers (Ye et al.[16], Udaykumar et al.[17]). In the present sharp-interface IBM, the arbitrary boundary surface is discretized with the triangular surface elements. For each cell near the immersed boundary we first determine if the vertex of a given cell is located inside or outside the boundary surface. If at least one vertex is determined to be inside the boundary surface, the cell is considered to be a cut-cell. For each boundary cell, we find the nearest surface element, and the cell-cut determination is based on the orientation of this surface element. This implies a local linearization of the boundary surface, if the grid resolution is coarser than the surface element resolution. Based on the vertex in/out test result, we also know which edge of the cell is cut by the boundary, and we find those ‘edge intersections’ (see Fig.8) through simple, three-dimensional coordinate geometry. The area of each cut-face and boundary surface segmented by the cell can then be computed by constructing polygons with the edge-intersections and cell vertices. Once all the areas are found, the cell volume is obtained using the divergence theorem:

$${\mathbf{V}}_{\mathit{\text{cell}}}=\frac{1}{3}{\displaystyle \int }{\overrightarrow{x}}_c·\overrightarrow{n}\mathit{\text{dA}}=\frac{1}{3}\left({\displaystyle \sum _j}{\overrightarrow{x}}_{c,j}·{\overrightarrow{n}}_j{A}_j+{\overrightarrow{x}}_{c,\mathrm{\Gamma }}·{\overrightarrow{n}}_{\mathrm{\Gamma }}\mathrm{\Gamma }\right),j=e,w,n,s,f,b,$$ (23)

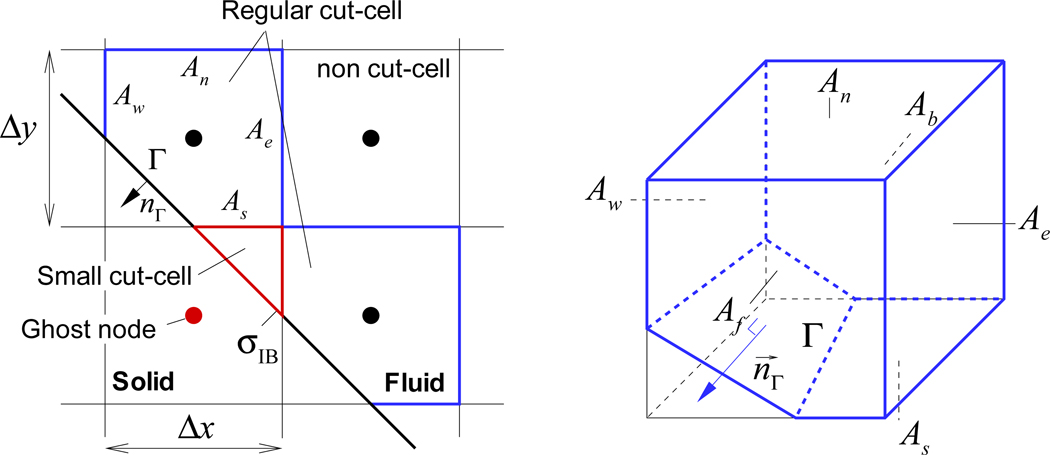
where x⃗_c is the position vector to the center of each surface, A_j and Γ are the areas of cut-face and boundary surface segmented by the cell, respectively (see also Fig.9). Figure 9 shows the typical cut-cell topology created by such a procedure and we note that there are two types of cut-cells created in the fluid; cells whose nodes are in the fluid region (called “regular” cut-cells) and cells whose nodes are in the solid (called “small” cut-cells). It should be noted that the volume-fraction, α = V_cell/ΔV, of regular cut cells is greater than 0.5 and those of the small cells is less than 0.5, and the discretization of the governing equations is done differently for these two types of cells.

Figure 8.

Schematic for determining cell cuts and some example of cut-cell topologies. Edge-intersection is the intersection between the boundary surface and the edges of the cell.

Figure 9.

Cut-cell notations in 2D (left) and 3D (right, only one regular cut-cell is shown). A: face area in the fluid region and Γ is the boundary surface area segmented by the cell. A cell of which volume fraction is smaller than 0.5 is determined to be a ‘small’ cut-cell and it is always a part of ghost cell.

For regular cut-cells, we proceed with a conventional discretization of the finite-volume equations (21) and (22) as described in Ye et al.[16]. With the given face and volume fractions, the discretization of Eqs. (21) and (22) leads to

$$\frac{p_E{a}_e-p_P(a_e+a_w)+p_W{a}_w}{\mathrm{\Delta }{x}^2}+\frac{p_N{a}_n-p_P(a_n+a_s)+p_S{a}_s}{\mathrm{\Delta }{y}^2}+\frac{p_F{a}_f-p_P(a_f+a_b)+p_B{a}_b}{\mathrm{\Delta }{z}^2}+\frac{\partial p}{\partial n}{|}_{\mathrm{\Gamma }}\frac{\mathrm{\Gamma }}{\mathrm{\Delta }V}=\frac{{\rho }_0}{\mathrm{\Delta }t}\left[\frac{U_e^{*}{a}_e-U_w^{*}{a}_w}{\mathrm{\Delta }x}+\frac{V_n^{*}{a}_n-V_s^{*}{a}_s}{\mathrm{\Delta }y}+\frac{W_f^{*}{a}_f-W_b^{*}{a}_b}{\mathrm{\Delta }z}+{\overrightarrow{U}}_{b,\mathrm{\Gamma }}·{\overrightarrow{n}}_{\mathrm{\Gamma }}\frac{\mathrm{\Gamma }}{\mathrm{\Delta }V}\right]$$ (24)

$${\overrightarrow{u}}^{n+1}={\overrightarrow{u}}^{*}-\frac{\mathrm{\Delta }t}{\alpha {\rho }_0}\left(\frac{p_e{a}_e-p_w{a}_w}{\mathrm{\Delta }x}\overrightarrow{i}+\frac{p_n{a}_n-p_s{a}_s}{\mathrm{\Delta }y}\overrightarrow{j}+\frac{p_f{a}_f-p_b{a}_b}{\mathrm{\Delta }z}\overrightarrow{k}+p_{\mathrm{\Gamma }}{\overrightarrow{n}}_{\mathrm{\Gamma }}\frac{\mathrm{\Gamma }}{\mathrm{\Delta }V}\right),$$ (25)

where a_j = A_j/ΔA are the face-fractions, α is the volume fraction, Γ is the area of boundary surface segmented by the cell, and subscript Γ indicates the value on the boundary surface (see Fig. 9). Note that Eq. (25) is only used to update cell-center velocities, while cell-face velocities are updated by:

$$U_e^{n+1}=U_e^{*}-\frac{\mathrm{\Delta }t}{{\rho }_0}\left(\frac{p_E-p_P}{\mathrm{\Delta }x}\right).$$ (26)

One can see that the above equations are very similar to the finite-difference discretization of Eqs. (18) and (19). For the cells located away from the boundary, all the face and volume fractions are equal to one and the above equations exactly coincide with the second-order, central finite-difference form of Eqs. (18) and (19). The Poisson equation, Eq. (24), retains a 7-point (5-point in 2D) stencil and can therefore still be solved efficiently with our existing line-SOR-based geometric multi-grid algorithm[2].

A different approach is adopted for the small cells. Given that a small cell can be arbitrarily small, discretization of the equations for these cells along the lines of that described for the regular cells can be highly problematic. While for convection-diffusion type of equations, these small cells can cause CFL or viscous stability problems, for elliptic equations such as the pressure Poisson equation, small cells produce ill-conditioned matrices that slow down the convergence of the iterative solution methods. Furthermore, disretization of these cells as separate finite-volumes changes the total number of unknowns that have to be solved for at any given time-step. One way to avoid such problems is to geometrically merge small cells with adjacent cut-cells as was done by Ye et al.[16] and Udaykumar et al.[17]. While this eliminates the small-cell problem, the merging process is highly complex, especially in 3D, and can also lead to additional dependencies in the computational stencil that can adversely impact convergence properties.

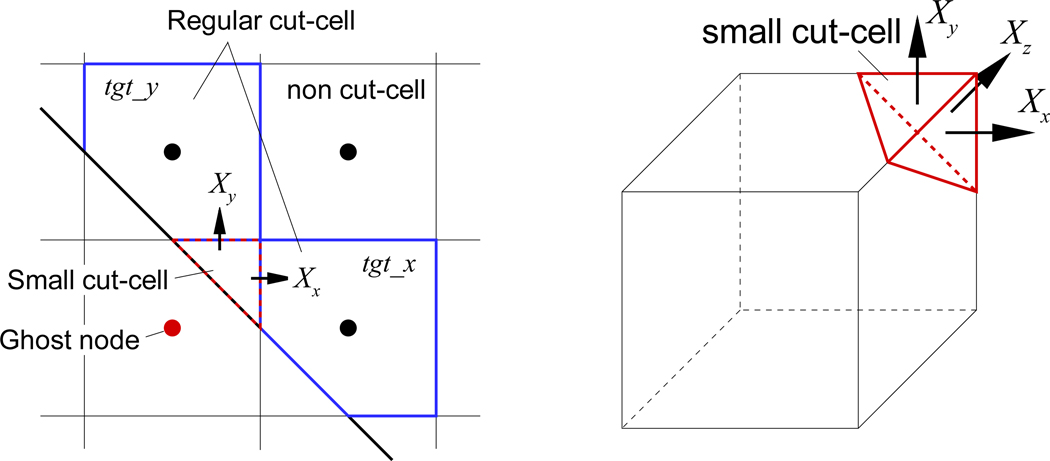
In the present method, the mass conservation associated with the small cell is accounted for through a “virtual” cell-merging technique. In this approach, merging is effected by transferring the source term of the Poisson equation for the small-cells to the adjacent cells (which may include regular cut-cells as well as non-cut, Cartesian cells). The approach is inspired by the ‘momentum exchange’ method proposed by Meyer et al.[19] to solve the momentum equations for small cells. However, instead of the momentum equation, we apply virtual merging to mass conservation via Eq. (24). The following discussion is based on the schematic shown in Fig. 10. First, the value of ∫(U⃗^* · n⃗)dA which is on the right-hand side of Eq. (24) is computed for all cells including the small-cells. For the small cells, the computed value is transferred to adjoining non-small cells (regular cut cells or normal, non-cut cells) which share a face with the small-cut cell using the following prescription:

$${[{\displaystyle \int }{\overrightarrow{U}}^{*}·\overrightarrow{n}\mathit{\text{dA}}]}_{\mathit{\text{ tgt}}-j}^{\prime }={[{\displaystyle \int }{\overrightarrow{U}}^{*}·\overrightarrow{n}\mathit{\text{dA}}]}_{\mathit{\text{ tgt}}-j}+X_j$$ (27)

$${[{\displaystyle \int }{\overrightarrow{U}}^{*}·\overrightarrow{n}\mathit{\text{dA}}]}_{\mathit{\text{ src}}}^{\prime }={[{\displaystyle \int }{\overrightarrow{U}}^{*}·\overrightarrow{n}\mathit{\text{dA}}]}_{\mathit{\text{ src}}}-{\displaystyle \sum _j}{X}_j=0,$$ (28)

where subscript ‘src’ indicates the source (small cell) and ‘tgt’, the face connected normal or regular cut-cell. In the above prescription, X_j is the amount of mass flux transferred to the j-th target cell and is evaluated by

$$X_j=\frac{{\beta }_j}{{\displaystyle \sum _j}{\beta }_j}{[{\displaystyle \int }{\overrightarrow{U}}^{*}·\overrightarrow{n}\mathit{\text{dA}}]}_{\mathit{\text{ src }}},j=x,y,z$$ (29)

$${\beta }_j=\{\begin{array}{cc}{n_j}^2{a}_j\hfill & ({\alpha }_{\mathit{\text{tgt}}-j}>0.5)\hfill \\ 0\hfill & ({\alpha }_{\mathit{\text{tgt}}-j}\le 0.5)\hfill \end{array},$$ (30)

where n_x,y,z are x, y, and z component of unit normal vector to the immersed surface which cuts the small cell, tgt_x, y, z indicate the target cells in the x, y, and z directions, and a_x,y,z is the face-fraction of a face connected to the target cell in each direction. Thus the amount transferred to each target cell is chosen based on the direction of surface normal vector as well as the face area shared with the target-cell. This is consistent with the general notion that mass-transport associated with boundary motion would primarily be aligned with the direction normal to the boundary and the amount of mass flux would be proportional to the area. Once the virtual merging is done, the source of Poisson equation for the small cell becomes identically zero. The pressure Poisson equation, Eq. (24) is then solved for the remaining cells which consist of regular cut-cell and non-cut Cartesian cells, and the pressure value on the ghost node associated with the small cell (see Fig. 10) is obtained explicitly by the ghost cell method[2] while satisfying the boundary condition.

Figure 10.

Schematic of virtual merging technique. The source of pressure Poisson equation on the small cut-cell is trasferred to adjoining non-small cut-cells. X denotes the transferred amount in each direction.

The above transfer procedure conserves the mass source regionally and ensures that the geometric conservation law is satisfied. We refer to this conservative property as “regional” conservation to distinguish it from strict local mass conservation which can only be achieved through a cut-cell based finite-volume method with full geometric cell merging. This property is also different from global mass conservation which conserves quantities only over the entire computational domain. Note however that as with local conservation, regional conservation also guarantees global conservation. Given our previous assessment of the source of pressure oscillations, the regionally conservative cut-cell approach should significantly diminish the local errors in mass conservation and in doing so, reduce the spurious pressure oscillations. The global conservation law applied in the present cut-cell method can be represented by

$$-\frac{{d\mathbf{V}}_{\mathit{\text{IB}}}}{\mathit{\text{dt}}}+{\displaystyle {\int }_{{\sigma }_{\mathit{\text{CV}}}}}\overrightarrow{U}·\overrightarrow{n}\mathit{\text{dA}}=\underset{S_V\prime }{\underbrace{\frac{{({\displaystyle \sum }{\mathbf{V}}_{\mathit{\text{cell}}})}^{n+1}-{({\displaystyle \sum }{\mathbf{V}}_{\mathit{\text{cell}}})}^n}{\mathrm{\Delta }t}}}+\underset{S_{\sigma }\prime }{\underbrace{[{\displaystyle {\int }_{{\sigma }_{\mathit{\text{IB}}}}}{\overrightarrow{U}}_b·\overrightarrow{n}\mathit{\text{dA}}-{\displaystyle \sum _j}{\overrightarrow{U}}_b·{\overrightarrow{n}}_{\mathrm{\Gamma },j}{\mathrm{\Gamma }}_j]}}$$ (31)

where V_cell is the discretized cell volume given by Eq.(23) and the summation (j) is for all the cut-cells (both small and regular). The error on the right-hand side is just caused by the local linearization of the immersed boundary surface when determining cell cuts based on the given grid resolution. The first term on the right hand side (S_V′) is the volume error caused by the linearization, while the second term (S_σ′) is the transpiration error due to the error in the surface area, and both terms are expected to be very small. The overall magnitude of each error term is estimated to be $S_V\prime \sim {\displaystyle \sum _j}\frac{1}{\mathrm{\Delta }t}O\left(\frac{{\mathrm{\Delta }}^{\gamma }}{{\mathbf{R}}_j}\right)\text{ and }{S}_{\sigma }\prime \sim {\displaystyle \sum _j}({\overrightarrow{U}}_b·{\overrightarrow{n}}_{\mathrm{\Gamma },j})O\left(\frac{{\mathrm{\Delta }}^{\gamma }}{{{\mathbf{R}}_j}^2}\right)$, where γ=3 or 4 for 2D or 3D problems, respectively, and R_j is the local radius of curvature of immersed boundary surface. In general, the order of magnitude of S_V′ and S_σ′ is smaller than the corresponding error terms in Eq.(8) by (Δ/R) and (Δ/R)², respectively. In the following sections we assess the efficacy and performance of this new approach by simulating a variety of carefully selected cases.

4. Result and Discussion

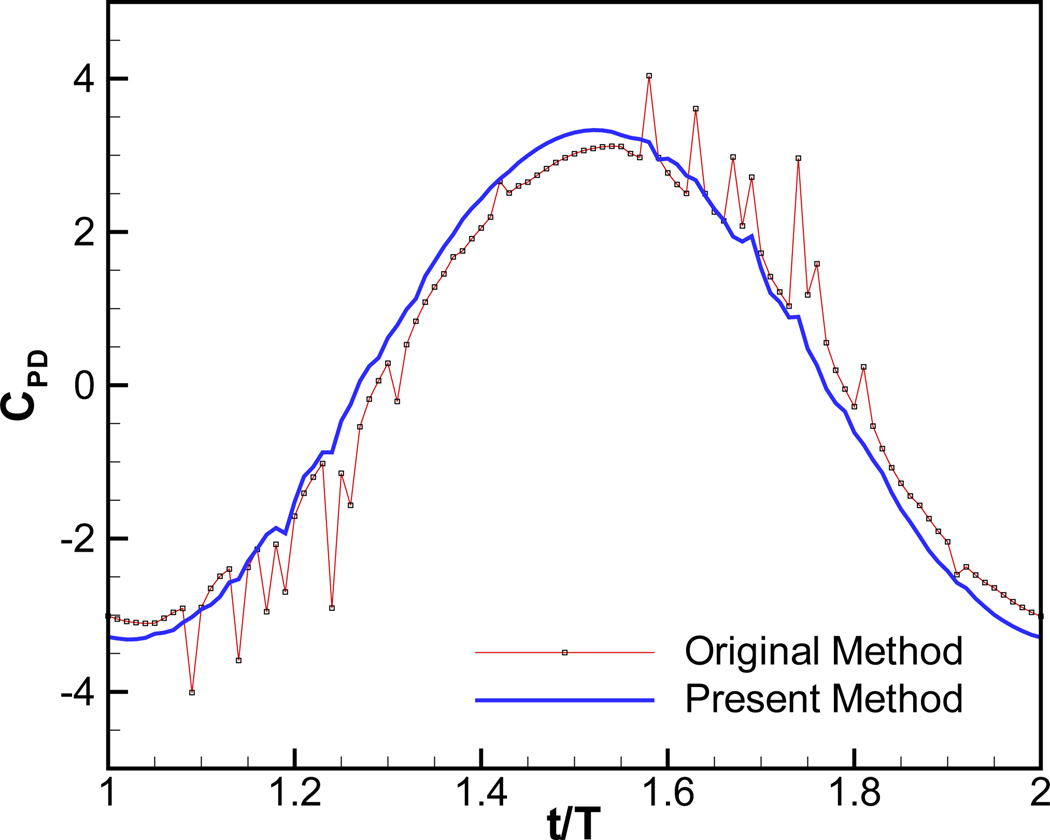
The oscillating cylinder problem considered in Sec. 2 is solved again with the current method. The time histories of the pressure drag coefficient, C_PD are plotted in Fig.11 for the original ghost cell method and the present regionally conservative cut cell approach. As one can see from this figure, the present method significantly reduces the pressure oscillations. While some small local extrema are still visible in the plot, the profile is smooth and sinusoidal. This improvement is achieved just by satisfying the fluid mass/volume conservation more accurately via the regionally conservative cut-cell method, and without any arbitrary boundary forcing or flow-field modification or ad-hoc adjustment of interpolation stencils. The results therefore confirm that the major source of spurious pressure oscillations is the violation of the geometric conservation law. It should be noted that in addition to the reduced amplitude of pressure oscillations, there is also a slight difference in the overall amplitude as well as phase of the drag between the two results. Thus, it seems that while the mass source errors are localized in time and space, these errors can in-fact have a global (in time as well as space) effect on the pressure field. This is likely due to a coupling between the pressure field, which is elliptic in nature, and the velocity field which is governed by convection as well as diffusion.

Figure 11.

Time histories of pressure drag coefficient for horizontally oscillating circular cylinder (total oscillation amplitude: 1Δx); comparison between the original sharp-interface IBM and the present regionally conservative cut-cell method

In order to further analyze the effect of grid spacing and time-step size on the pressure oscillation, we consider a horizontally oscillating cylinder but with a larger amplitude of oscillations. The circular cylinder in this case is placed at the center of a 4D × 4D square domain and the upper and lower boundaries of the domain are set to no-slip walls. Neumann type boundary conditions with zero gradient are applied for the pressure and velocities at the left and right outer boundaries. The oscillation parameter is set to X₀ = 0.125D(see Eq. (10)), and the Reynolds number, Re = U₀D/ν and Strouhal number, St = f₀D/U₀ are set to 78.5 and 1.27, respectively. This larger (25% of the diameter) amplitude of oscillations should lead to significant force generation and should serve as a more typical scenario for moving boundary problems.

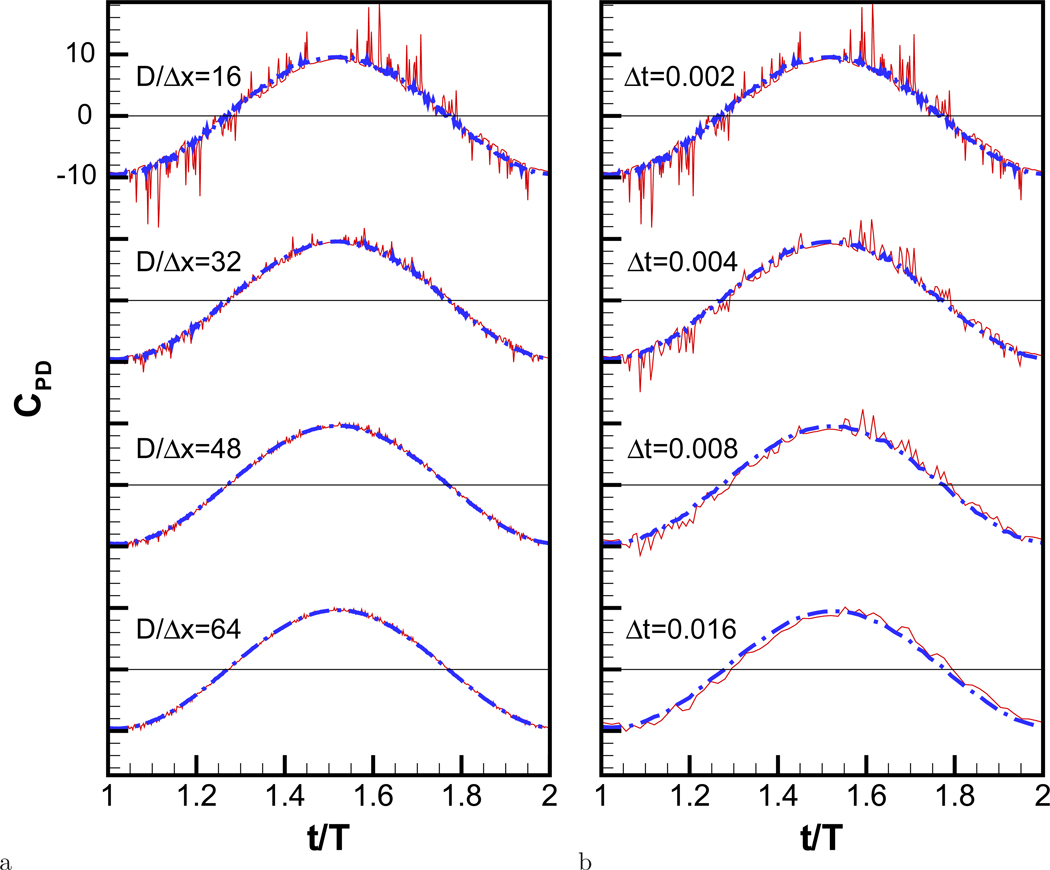
The problem is first solved on the following four uniform grids: 64², 128², 192², and 256² with a time-step is fixed to Δt = 0.002T (CFL =0.025, 0.05, 0.1, and 0.2). Thus on these four grids, the cylinder diameter D is spanned by 16, 32, 48 and 64 grid points, respectively. The computations are performed with the original IBM as well as the present cut-cell approach, and the time histories of the pressure drag coefficient are plotted in Fig. 12(a). As predicted by Eq. (9), the peak amplitude of pressure oscillation decreases as the grid is refined. An interesting observation is that the most severe pressure oscillation occurs when the body velocity is small (i.e. around the force is maximum and minimum) and this behavior is in line with Eq. (9) which indicates larger conservation errors when the instantaneous CFL number is small. It is notable that a much smoother solution is obtained with the present method for all grid resolutions. The temporal variation of drag force for the present method is acceptably smooth for D/Δx ≥ 32. Note, however, that the amplitude of pressure oscillations in the original results decreases rapidly with increasing grid resolution and only on the very coarse resolution (D/Δx ≤ 16), does the original method exhibit a noticeable phase shift in time and a different in peak force (see also Fig.11), compared to the present result. For the resolution of D/Δx = 64, the original result is almost the same with the present one in overall, except for some small oscillations. Thus, as shown in previous studies[3, 4, 5], one can in fact suppress the pressure oscillations in sharp-interface IBMs and obtain reliable results using fine enough grid resolution.

Figure 12.

Time histories of pressure drag coefficient for a oscillating circular cylinder, X₀ = 0.125D, Re = 78.5, St = 1.27. a) on different grid resolutions with fixed time step size, Δt = 0.002, b) for different time step size on the fixed resolution, D/Δx = 16. Solid lines: original finite difference method, Dash-dot lines: present.

The effect of time-step size is also investigated for this case and the results are shown in Fig. 12(b). For this study, we employ a 64 × 64 grid and the following time-steps are used: Δt=0.002, 0.004, 0.008, and 0.016 (CFL =0.025, 0.05, 0.1 and 0.2). For the original method, the oscillation amplitude decreases with increasing time-step size but remains un-smooth even for the largest time-step. In contrast, the present cut-cell method produces a much smoother temporal variation for all time-steps.

Figure 13 shows the time evolution of the pressure field around a cylinder on the 64 × 64 grid (D/Δx = 16) with Δt = 0.002 for both the present and original methods. A coarse grid is chosen here to accentuate the discretization errors. The plots clearly show the presence of massive and highly non-localized fluctuations in the pressure field for the original method. Thus, the elliptic nature of the pressure ensures that the pressure perturbations produced at the immersed boundary have an instantaneous and global effect on the pressure field. In contrast, the time evolution of the pressure field with the present method is much more continuous in time. It should be noted that the velocity field (not shown here) itself is not significantly different between the present and original method since the pressure correction to the velocity is scaled down by the multiplication with Δt during the velocity-update step of the fractional-step method.

Figure 13.

Time evolution of pressure field on 64² grid (D/Δx = 16) for t/T = 1.612 ~ 1.618. Upper half of each plot shows the contours for the present method whereas the lower half shows the corresponding contours for the original non-cut-cell method.

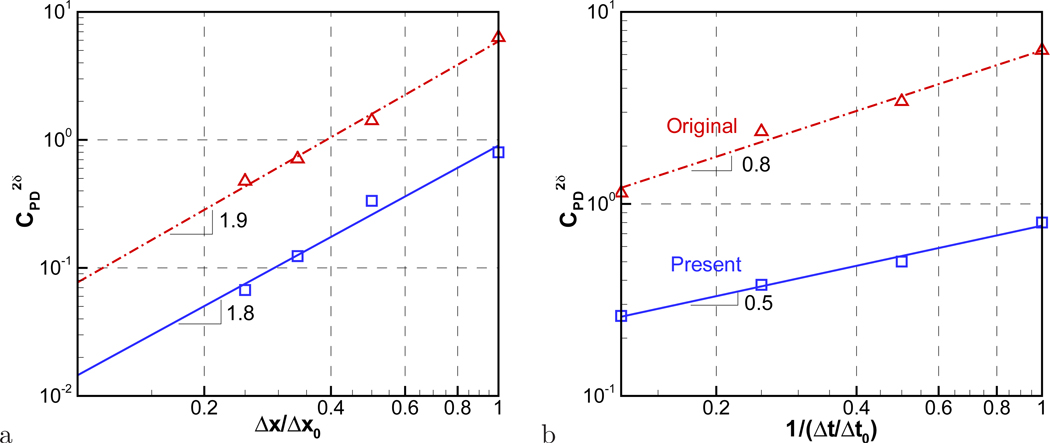
In order to quantify the pressure oscillations, we again compute the 2δ-discontinuity in the pressure drag as defined by Eq. (12). The RMS (root-mean-squared) values of this quantity are plotted in Fig. 14 both as a function of grid spacing as well as time-step size for both methods. Overall, the current method produces roughly a seven-fold reduction in the RMS values of the pressure oscillation. As seen for the previous case in Sec. 2, for the original method, the RMS values of $C_{\mathit{\text{PD}}}^{2\delta }$ can be fitted by a power-law (Eq. 13) with ξ = 1.9 and η = 0.8. On the other hand, a best-fit through the results of the new cut-cell method indicates a power-law with ξ = 1.8 and η = 0.5. The scaling with grid-size is effectively the same as the original method but the different scaling of the error with time-step suggests that the dominant source of pressure oscillation has been moved from the spurious volume source/sink associated with fresh/dead cells (expressed by Eq. (9)) to another mechanism. The candidates for these remaining mechanisms include:

• the inability to formulate a physically well-posed advection-diffusion equation for fresh cells. Past approaches to the discretization of fresh-cells have involved actual or effective merging of fresh-cells with neighboring cells[16], use of ghost-cells values to provide time-history for fresh-cell variables [21], and the use of Lagrangian interpolation along particle paths[13] to estimate the fresh-cell velocity;

• the abrupt change of velocity for boundary cells in the vicinity of fresh as well as dead-cells. Our simulations indicate that this is particularly important for cells in the neighborhood of dead-cells. This temporal discontinuity in velocities caused by the dead cell is also mentioned by Lee et al.[5]. One solution to this is the use of smooth stencils[3, 4] to alleviate the temporal discontinuity. However, this stencil modification process is ad-hoc and also reduces the sharpness of the immersed boundary;

• errors in momentum conservation around the immersed boundary. This could be remedied by a cut-cell method such as that of Ye et al.[16] or Günter et al.[20] or by application of the current regionally conservative cut-cell method to the momentum equation;

• geometric conservation errors associated with the local linearization of the surface employed in determining cell-cuts: right-hand side of Eq.(31). For the current case, these are O(10⁻⁵) but they could be larger in case where Δ/R is larger.

Figure 14.

2δ-discontinuity in pressure drag coefficient ($C_{\mathit{\text{PD}}}^{2\delta }$) for (a) different grid spacing and (b) time step size. Lines are power-law fitting, $C_{\mathit{\text{PD}}}^{2\delta }\sim {(\mathrm{\Delta }x)}^{\xi }\text{ and }{C}_{\mathit{\text{PD}}}^{2\delta }\sim {(1/\mathrm{\Delta }t)}^{\eta }$ (Δx₀ = 1/16, Δt₀ = 0.002)

Our current results however also indicate that, at least for the case simulated here, all these other mechanisms put together produce pressure oscillations which are about 6 times smaller than those produced by the mass-conservation errors which have been eliminated by the current cut-cell method. Furthermore, as shown by the above results, the residual oscillations can be further suppressed by refining the grid.

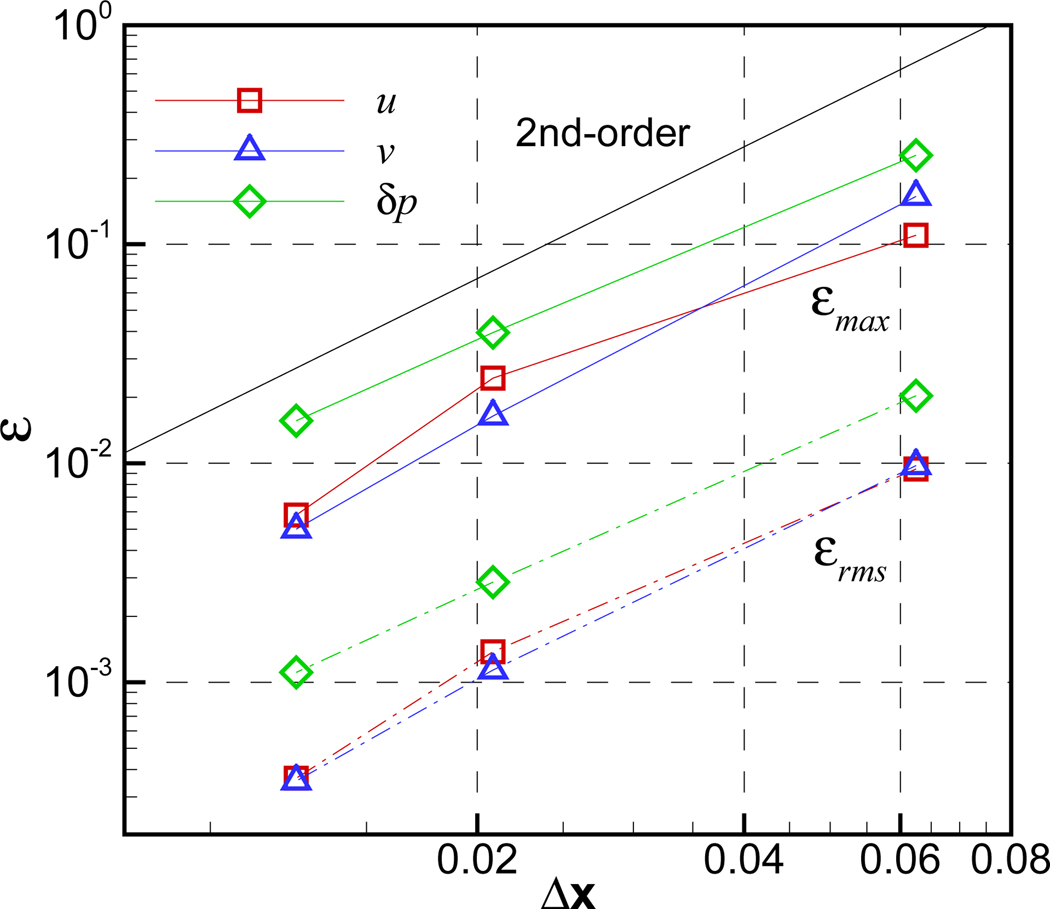
The original immersed-boundary method of Mittal et al.[2] is locally and globally second-order accurate. However, since the current, regionally conservative cut-cell modifies the discretization in the vicinity of the immersed boundary, it is useful to reassess the grid convergence and spatial accuracy of the present method. This is accomplished by solving the same oscillating circular cylinder problem described earlier in this section on three grids (64², 192², and 320² points) and assessing the behavior of the error on these grids. The time-step in these simulations is fixed to a small value of Δt = 5 × 10⁻⁴ and since the analytical or exact solution is not available, the reference solution for the estimation of the error is obtained from the computation with a fine 576² grid. For the flow field at t = 0.5T, the relative error, ε is computed for the velocity components u and v. The grid convergence of pressure is assessed by the relative error on the pressure gradient, δp = |▽p|, since the pressure value itself obtained with all Neumann boundary conditions is not unique. For the fair assessment of the error, the gradient is computed on the coarsest grid stencil. The variation of the RMS (ε_rms) and maximum-error (ε_max) norm plotted in Fig. 15 represent the global and local errors respectively, and it indicates that the local as well as the global accuracy of the original sharp-interface IBM[2] is preserved in the current method.

Figure 15.

Grid convergence of the present method for moving body problem. The relative error of u (square symbol) and v (triangle) velocities, and pressure gradient, δp (diamond) for the flow around oscillating circular cylinder at t = 0.5T.

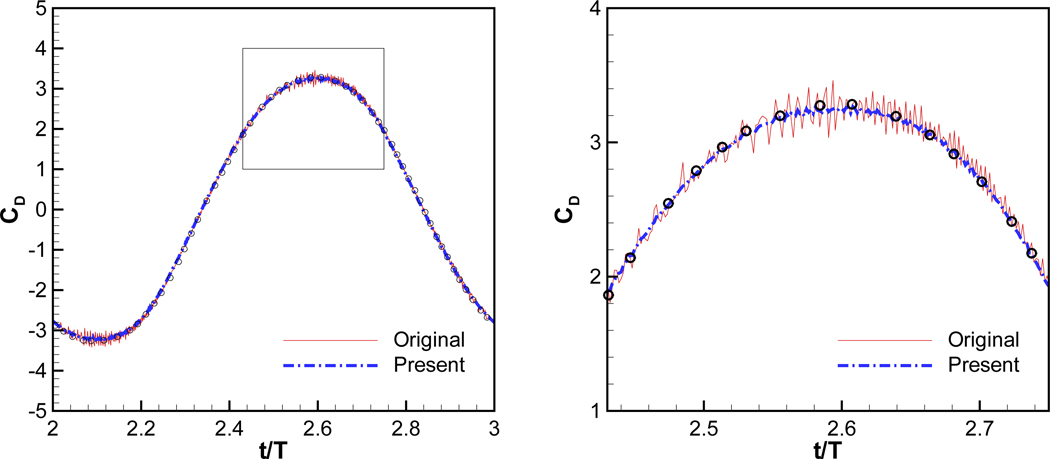
We now validate the present method by comparing the result with a well established case[6, 21, 22, 23] of a horizontally oscillating circular cylinder problem for which comparisons can be made with results from a body-fitted computational method[24]. The amplitude of vibration as defined by Eq. (10) is set to X₀ = 0.7957D and the Keulegan-Carpenter number is set to KC = U₀/f₀D = 5. The Reynolds number based on the maximum velocity is 100. This problem has been used as a validation case in many computational studies of moving boundary problems[6, 21, 22, 23]. In the present study, the overall computational domain of 100D × 100D is resolved by 512 × 256 grid points with a non-uniform grid spacing. The minimum grid spacing is Δx = Δy = 0.015D and the cylinder diameter is therefore resolved by about 60 grid points. The time step size, Δt, corresponds to the CFL number 0.533. At the outer boundaries, Neumann boundary conditions are applied for the pressure and velocities. The time histories of the total drag coefficient, $C_D=F_x/0.5{\rho }_0{U}_0^{2}D$ obtained with the present as well as the original method are plotted along with the data of Dütsch et al.[24] in Fig. 16. The present result is clearly smoother than the original result; the RMS value of 2δ-discontinuity is 0.23 for the original method, while the value decreased to 0.0322 with the present method. This degree of reduction of oscillation is consistent with the results of the previous test case. As predicted by Eq.(9), the largest pressure fluctuations for the original method are observed when the body velocity is small. Note however that, although the original result shows some small level of spurious oscillations, the phase and amplitude of the drag matches the reference value quite well. This reconfirms our earlier notion that with sufficient resolution, the original method provides good prediction of the forces.

Figure 16.

Time histories of drag coefficient for oscillating cylinder at Re = 100, KC = 5. Symbols are the result of Dütsch et al.[24]. Right: zoomed view of the region inside the box on the left figure

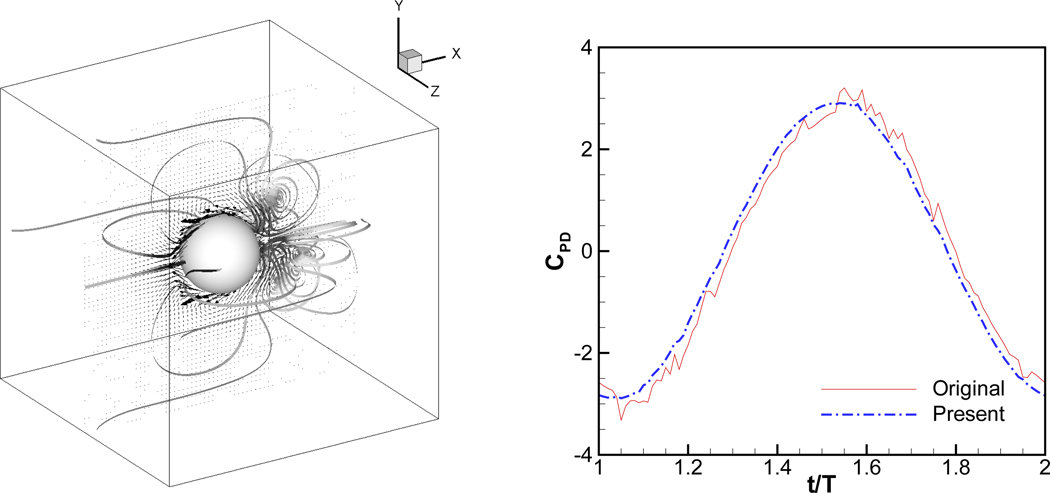
The current approach is easily applied to 3D geometries and we demonstrate this by simulating a canonical 3D problem. The problem tested is that corresponding to a sphere oscillating horizontally with X₀ = 0.125D, Re = 78.54 and St = 1.2732. The domain size is (4D)³ and is covered by a 64³ uniform Cartesian grids. Neumann velocity boundary conditions are applied for the velocities at the x-boundaries of the domain and all other boundaries are set to no-slip walls. The sphere diameter is resolved by 16 grid points (D/Δx = 16) and the time-step size is equal to 0.01T (CFL = 0.125). The time-histories of the pressure drag coefficient (in x-direction) are plotted in Fig. 17 for the original as well as the present method. Similar to the 2D case, the drag variation for the current method is significantly smoother than that for the original method. Thus the present method maintains its effectiveness for 3D moving boundary problems. It should be noted however that the pressure oscillations produced by the original method are somewhat smaller when compared to the corresponding 2D case (see Fig. 12). This is consistent with Eq. (9) which indicates that for 3D problems, the mass-error scales with the cube of the grid spacing whereas it scales with the square of the grid spacing for 2D problems.

Figure 17.

In-line oscillating sphere. Left: Instantaneous velocity vector and stream trace colored by pressure. Right: Time histories of pressure drag coefficient

We note that the moving sphere problem is particularly relevant to the direct numerical simulation of particulate flows[7, 25]. In such simulations, each particle might only be resolved by O(10) grid points per particle diameter. With such coarse particle resolution, diffuse-interface type method would result in significant numerical errors. However, if one solves this problem with a typical sharp-interface immersed boundary approach, the force on the particle (and therefore its motion) might be affected by spurious pressure oscillations. The new, regionally conservative cut-cell based method can alleviate this problem while retaining the accuracy of the sharp-interface approach and lead to acceptable results with a relatively coarse particle resolution.

5. Summary

We have presented an approach for reducing the spurious pressure oscillations that are observed in simulations of moving boundary problems with sharp-interface immersed boundary methods. The approach is grounded in analysis and numerical experiments that indicate that the primary source of these oscillations are the errors in the geometrical conservation law due to the appearance of fresh and dead cells, and local changes in the effective geometry of the immersed body, which together, lead to local mass conservation errors. In order to reduce these errors, we apply a Cartesian cut-cell method to the solution of the pressure Poisson equation. The cut-cell approach is coupled with a virtual merging technique to handle the small-cell problem. With this implementation of the cut-cell, we retain the simplicity, efficiency and accuracy of the original sharp-interface IBM while reducing the spurious pressure oscillations by a factor of about seven. Reduction of oscillations is demonstrated for 2D as well as 3D canonical moving boundary problems. While the current method is implemented for one particular ghost-cell based implementation of the sharp IBM[2], the ideas proposed here should be useful and effective for all methods in this category.

Spurious pressure oscillations for moving boundary problems have long been considered one of the primary deficiencies of sharp-interface immersed boundary methods. Although such oscillations can be suppressed by increasing grid resolution, this is very costly, especially for three-dimensional problems. The current method provides an effective and efficient approach for addressing this deficiency. The method proposed here would be particularly useful in flow problem such as fluid-structure interaction and flow-induced sound where smoothness and accuracy of the pressure field and the hydrodynamic force on the immersed body is essential.

Research Highlights.

• >The violation of geometric conservation law causes spurious pressure oscillations.
• >A cut-cell approach with a virtual cell-merging technique has been proposed.
• >The proposed method reduces pressure oscillations by roughly an order of magnitude.