A Theoretical Assessment of the Oligolysine Model for Ionic Interactions in Protein-DNA Complexes

Abstract

The observed salt dependence of charged ligand binding to polyelectrolytes, such as proteins to DNA or antithrombin to heparin, is often interpreted by means of the “oligolysine model.” We review this model as derived entirely within the framework of the counterion condensation theory of polyelectrolytes with no introduction of outside assumptions. We update its comparison with experimental data on the structurally simple systems for which it was originally intended. We then compute the salt-dependence of the binding free energy for a variety of protein-DNA complexes with nonlinear Poisson-Boltzmann (NLPB) simulation methods. The results of the NLPB calculations confirm the central prediction of the oligolysine model that the net charge density of DNA remains invariant to protein binding. Specifically, when a cationic protein residue penetrates the layer of counterions condensed on DNA, a counterion is released to bulk solution; and when an anionic protein residue penetrates the condensed counterion layer, an additional counterion is condensed from bulk solution. We also conclude, however, that the cumulative effect of charged protein residues distant from the binding interface makes a significant contribution to the salt dependence of binding, an observation not accommodated by the oligolysine model.

I. Introduction

Interactions between proteins and DNA are central in cellular biology.¹ Any given DNA-binding protein achieves its stability and specificity in the cognate binding complex through a mix of noncovalent intermolecular forces.^2,3 DNA-binding proteins often display a surface patch of positively charged ionized amino acids (lysines, arginines, and, depending on pH, histidines) that faces the DNA-binding site,^4,5 which itself is bordered by negatively charged ionized phosphate groups. These ionic interactions are mediated by the small univalent counterions and coions in the system, and therefore are expected and observed to be strongly dependent on the salt content of the solution.⁶ Indeed, the binding constants K_obs of cognate protein-DNA complexes typically decrease when the ionic strength of the solution is increased, thus weakening the ionic attractions.⁶ Less appreciated is the salt-independent part of the ion-ion interactions.⁷ Both salt-dependent and salt-independent components of the ionic interactions are central to this paper.

Plots of log K_obs vs. log[Salt] (1:1 salt molarity, frequently [NaCl] or [KCl]) are observed to be linear over a limited salt concentration range that includes physiological,⁶ and the typically negative slope of such a plot has formed the basis for a method,^8,9 which we will call the oligolysine model, of inferring the number of ionic interactions in the protein-binding interface. If structurally meaningful, this information would be useful in the absence of X-ray or NMR data. Additionally, the model is used to infer the “electrostatic” contribution to the total binding free energy, which is not available directly from experiment. Finally, the model then provides by subtraction the “non-electrostatic” contribution to the total binding free energy. Analyzing the total binding free energy into electrostatic and non-electrostatic parts, if accurate, would provide insight into the diverse interactions contributing to stabilization and specificity.

Privalov et al.⁶ have recently interpreted a large body of protein-DNA binding data as providing strong confirmation of the oligolysine model. We note that the oligolysine model has also found applications to systems other than DNA-binding proteins. Dubin¹⁰ has published a review in which he questions its use in the structural interpretation of the binding of the anionic polyelectrolyte/drug heparin to its antithrombin protein receptor.

The main point we shall make in this paper is that while the oligolysine model can provide useful insights, the formula that has customarily been used in practice is flawed and in principle can lead to misleading interpretations. We assess the oligolysine model from the standpoint of the counterion condensation theory of polyelectrolytes⁷ as supplemented by nonlinear Poisson-Boltzmann simulations. We provide a theoretically well-grounded version of it. Even this more rigorous model, however, is subject to uncertainties when applied to structurally complex systems, arising from a significant cumulative effect of ionic charges distant from the binding interface.

II. The Oligolysine Model and Counterion Condensation

The fundamental tenets of polyelectrolyte theory⁷ based on counterion condensation---the physical reality of a distinct layer of condensed counterions, the high degree of translational mobility of the condensed counterions, the onset of condensation at a critical linear charge density of the polyelectrolyte, and the exchange of lower-valent condensed counterions for higher-valent ones such that the net charge density of the polyelectrolyte remains constant---have been amply confirmed by experiments on synthetic polyelectrolytes, ^11,12 and on biopolyelectrolytes like DNA^13–16 and heparin.^17–19

A recent single-molecule measurement of the effective charge on DNA provides a good illustration.²⁰ The DNA charge as sensed by an applied electric field was found to coincide with the condensation-predicted net charge (bare phosphate charge less the charge on the condensed counterions). Moreover, the measured effective charge was invariant to KCl concentration over the range studied, 0.01 M—1.0 M, as predicted by condensation theory. No detectable difference was found when KCl was replaced with NaCl, again as predicted. Another, less direct, measurement concluded that the effective charge on a 25 bp DNA (50 bare phosphate charges) varied only slightly from 12 to 10 over a wide range of NaCl concentrations,²¹ an observation that can be compared with the predicted constant value 12. All-atom simulations of the counterion distribution around DNA²² have revealed to the eye a layer of condensed counterions that is spatially separate from the more diffusely held counterions, and that contains about the same number of counterions as predicted.

The success of counterion condensation theory led Record and coworkers to formulate what we will call the oligolysine model,⁸ and then to apply it to structurally complicated binding systems such as DNA-binding proteins.⁹ Assumptions outside the framework of condensation theory were introduced. In this section we present and discuss the formulas of the oligolysine model as they emerge directly from the counterion condensation theory with no outside assumptions.⁷ Our intent is to resolve some of the confusion that has become evident in the widespread use of this model to analyze the binding of proteins to polyelectrolytes like DNA and heparin. We make no claim in this section that the model is realistic for structurally complicated systems involving proteins, and subsequent sections are devoted to just that question. We see in this section that the model does give a realistic account of some of the simpler systems for which it was originally formulated.

Among the predictions of counterion condensation theory is a formula for the ionic component of the binding free energy of an oligolysine to DNA.⁷ We use oligolysine for the sake of concreteness, although the formula is equally applicable to any small Z-valent charged ligand, such as an ionized drug, trivalent cobalt hexamine, an oligoamine like spermine, or a multivalent metal ion like Ca²⁺, or for that matter to a univalent metal ion as well. It is also applicable not only to DNA but to any polyelectrolyte, such as heparin.

As it emerges from counterion condensation theory with no outside assumptions, the oligolysine model states that when Z charged lysine groups of the oligolysine molecule penetrate the layer of univalent cations M⁺ that are condensed but mobile on the free DNA, there is no effect other than the release of Z condensed counterions into bulk solution in order to maintain the DNA net charge at the critical value predicted by the theory. Just as the condensed counterions are hydrated and mobile, and do not form specific long-lived ion pairs with the phosphates,^7,22 the ε-NH₃⁺ ends of the lysine residues need not pair off with the phosphates, and in solution they probably do not.⁷ If, however, they (or cationic groups on some other ligand) do form such partially dehydrated specific complexes with the phosphates, then the additional free energy of formation of the “contact” from a starting state in which lysine ends have merely penetrated the condensation layer while remaining hydrated is not included explicitly in the counterion condensation model. Nor should it be, since such additional free energy reflects the molecular-level hydration changes and severe localization characteristic of specific cognate binding, and should be regarded as on the same level of interpretation as the “non-electrostatic” recognition components of binding like hydrogen bonding, dipole interactions, and van der Waals and hydrophobic contacts.

We begin a more precise presentation by defining the free energy of formation of a ligand-polyelectrolyte complex as the free energy difference ΔG between a final state in which one mole of complex LP is present in an infinite aqueous salt solution and an initial state in which there is one mole of free ligand L and one mole of free polyelectrolyte P. The counterion condensation formula for ΔG, for which detailed derivations may be found for Z=2 in Reference 23 and for any Z in Reference 7, may be written as,

$$\mathrm{\Delta }\mathrm{G}=\mathrm{\Delta }{\mathrm{G}}_0-(\mathrm{Z}-1)\text{RT}-\text{ZRTln}\{{[{\mathrm{M}}^{+}]}_{\text{cond}}/[{\mathrm{M}}^{+}]\}$$ (1)

where [M⁺] is the molarity of free counterions. It is assumed that the salt concentration, say MCl, is present in excess over the counterions originating from the polyelectrolyte, so that [M⁺]=[Salt]. Notice that the formula is valid if the “ligand” is a univalent counterion, Z=1, as well as for larger values of the ligand charge Z. All of the Z ligand charges are assumed to have penetrated the layer of counterions condensed on the polyelectrolyte. It may also be mentioned that if the ligand contains both cationic and anionic groups that penetrate the layer of condensed counterions, then Z is a net value (if the polyelectrolyte is DNA, Z is the number of ligand cationic groups minus the number of anionic groups, with the understanding that both penetrate the condensation layer).

The key to understanding this formula lies in the meaning of [M⁺]_cond, which is the local molarity of counterions condensed on the free polyelectrolyte. An important feature of counterion condensation theory is that it predicts with no adjustable parameters the numerical value of [M⁺]_cond . For example, [M⁺]_cond = 1.2 M for DNA, and [M⁺]_cond = 0.38 M for heparin. The general formula for [M⁺]_cond is given in the Appendix. The physical meaning of the logarithmic term in eq 1 is then transparent. It is the favorable entropic contribution of counterion release when the ligand binds. The counterions are released from a high local concentration [M⁺]_cond in the condensed layer to a lower bulk concentration [M⁺] of free counterions. Exactly Z univalent counterions M⁺ are released when a Z-valent ligand binds, because according to counterion condensation theory, the net charge density of the polyelectrolyte, including the charge of bound ligand and condensed counterions, is an invariant.⁷ The binding of ligand does not lower the net charge density, since an equivalent number of condensed counterions are released.

The physical meaning of the (Z−1)RT term is not transparent. It arises as a composite from several sources, including changes in the chemical potential of the aqueous solvent and a higher-order term in the change of chemical potential of the free counterions.^{7, 23} The Appendix provides more detail. This term is also a consequence of counterion release, as seen in the Appendix, and eq 1 makes clear that it contributes favorably to the entropy of release.

The two terms in eq 1, the RT(Z−1) term and the logarithmic term, together give the free energy of counterion release when the ligand binds. Notice that there is no other explicit electrostatic contribution. This is because the charge density of the polyelectrolyte is the same for both the initial state of free ligand and the final bound state. Obviously, these counterion release terms can account only for forces driving the ligand into a loose, non-specific, hydrated bound state. Any additional energetic effects that drive the ligand further from such a non-specific bound state to a tighter “lock-and-key” complex are not explicit in counterion condensation theory.

Finally, the implicit term ΔG₀ in eq 1 contains all physical contributions to the overall free energy of ligand binding other than counterion release. It includes the loss of translational and rotational degrees of freedom, additional vibrational degrees of freedom, loss of configurational entropy, hydrogen bonding, dipole interactions, van der Waal’s contacts, and solvation changes.⁵ The solvation changes include dehydration of tight ionic and dipolar contacts, hydrophobic caging, and release of structured water molecules (for example, from DNA grooves⁶). Following customary usage in the context of the oligolysine model, we refer to this term as the “non-electrostatic” component of the binding free energy, even though some items of the above list (dipole interactions, dehydration of ions) might be classified by others as “electrostatic.” The oligolysine model, then, classifies as “electrostatic” only the free energy of counterion release.

A caveat is in order about the invariant polyelectrolyte charge density. It is a rigorous result of counterion condensation theory for a system like NaDNA in aqueous NaCl; but in a mixture of charged ions with different valences, like monovalent sodium ions and Z-valent ligands, it is approximate, as shown by the “two-variable” theory.⁷ However, for low ligand binding levels, the situation of interest in this paper, it becomes exact. ⁷ Eq 1 is valid for low binding levels. It is also worth mentioning that at higher binding levels, the charged ligands exhibit an electrostatic anticooperative effect⁷ that is not needed in this paper but might be of interest in other contexts.

We now convert the formula for ΔG into a formula for the logarithm of the binding constant log K through the identities ΔG = −2.303 RT log K, and ΔG₀ = −2.303 RT log K₀, noticing the transfer from natural to common logarithms,

$$\text{log K}={\text{log K}}_0+0.434(\mathrm{Z}-1)+\text{Z log }\{{[{\mathrm{M}}^{+}]}_{\text{cond}}/[{\mathrm{M}}^{+}]\}$$ (2)

Note that all terms in this equation are dimensionless. The binding constant K is also dimensionless, since K=exp(−ΔG/RT), with an analogous equation holding for the dimensionless constant K₀.

It is customary to isolate the salt-dependent term log [M⁺] in eq 2, so we rewrite the equation while changing nothing,

$$\text{log K}={\text{log K}}_0+0.434(\mathrm{Z}-1)+\text{Z log }{[{\mathrm{M}}^{+}]}_{\text{cond}}-\text{Z log }[\text{Salt}]$$ (3)

since, as noted above, [M⁺]=[Salt]. Substituting [M⁺]_cond =1.2 M, the counterion condensation theoretical value for DNA, we get the numerical form for ligand-DNA binding,

$$\text{log K}={\text{log K}}_0+0.513\mathrm{Z}-0.434-\text{Z log }[\text{Salt}]$$ (4)

For ligand-heparin binding, the value 0.38 M should be use for [M⁺]_cond.

It is frequently but erroneously assumed that a salt-independent term in a formula for log K must not have its physical origins in ionic interactions. Equation 4, however, has been derived entirely from a theory of ions. Aside from log K₀, there are no terms in eq 4 from any other source. Again setting aside log K₀, we have assumed that the binding of the Z-valent ligand is driven entirely by an ionic process; namely, the release of condensed counterions into bulk solution, with no hydration changes or any other physical or chemical change. Yet the first two of the three explicit ion-derived terms in eq 4 are independent of salt concentration.

If now it is assumed that log K₀ also does not depend on salt concentration, the predicted dependence of log K on log [Salt] is linear with slope −Z, d log K /d log [Salt] = −Z. In their original paper,⁸ Record et al. analyzed previously published oligolysine data and found a linear dependence of log K on log [Salt] with slope − 0.9 Z, in reasonable agreement with the predicted value −Z. The slight discrepancy could be due to a number of factors. The flexibility of the oligolysine main and side chains could allow it not to bind with all of its Z charged lysines having entered the condensation volume. If the DNA or RNA is single-stranded, the same salt-dependence is predicted, and a greater deviation from measurement²⁴ could involve the flexibility of the polyelectrolyte as well as the ligand. An implied alternate interpretation would be that the measured slope indicates the actual number of charges on the ligand that enter the condensation volume, which, as an average number, could be fractional.

The linear dependence of log K on Z is also of interest. From eq 4, for ligand-DNA complexes,

$$\text{d log K }/\text{d Z}=0.513-\text{log}[\text{Salt}]$$ (5)

where we assumed that log K₀ does not depend on ligand charge Z. Lohman et al. ²⁵ measured the binding of a pentalysine to DNA over a range of pH that allowed the charge on the pentalysine to vary. From these data, Hallberg and Dubin²⁶ were able to extract the value dlogK/dZ = 1.1 at [Salt] = 0.19 M. The value predicted from the counterion condensation eq 5 is 1.23, in good agreement with the measured value 1.1 (no adjustable parameters).

It is also of interest to decompose the counterion release part of the oligolysine model free energy (i.e., with ΔG₀ excluded) into its enthalpic and entropic components. In eq 1 the Z−1 term and the −ZRTlog[M⁺] term are obviously entropic. The term ZRTlog[M⁺]_cond, however, depends on temperature not only through the factor RT. This can be seen from the explicit formula given for [M⁺]_cond in the Appendix. It contains the product εT, where ε is the dielectric constant of water (or whatever may be the solvent). Using the known temperature dependence of ε for water,²⁷ we calculate

$$\mathrm{\Delta }\mathrm{H}=\mathrm{\Delta }{\mathrm{H}}_0-0.4\text{RTZ}$$ (6)

and,

$$\mathrm{\Delta }\mathrm{S}=\mathrm{\Delta }{\mathrm{S}}_0+\mathrm{R}(0.8\mathrm{Z}-1-2.303\text{log}[\text{Salt}])$$ (7)

where the formula for the entropy pertains to a DNA-binding system (the general formula can be found in the Appendix). Both the enthalpy and entropy of counterion release (the terms other than ΔH₀ and ΔS₀) are favorable to binding, and both are significant. For example, if Z=5, ΔH − ΔH₀ = −5 kJ/mol, and the salt-independent part of T(ΔS − ΔS₀) equals 8 kJ/mol at room temperature.

As a final note for this section, we make the following practical comment. If an observed binding constant K_obs is defined for the reaction L + P → LP, where L is the ligand and P the host polyelectrolyte, that is, K_obs=[LP]/[L][P] at equilibrium, then it follows from a statistical mechanical analysis (G.S. Manning, unpublished lecture notes) that K_obs=VK, where V is the volume in liters of the reaction solution. Note that since K is dimensionless, both sides of this relation have liter units. The extra V factor arises when the natural dimensionless measure of volume in statistical mechanics is converted to the practical concentration units of molarity. From eq 4 we then have for DNA complexes,

$${\text{log K}}_{\text{obs}}={\text{log K}}_0+\text{log V}+0.513\mathrm{Z}-0.434-\text{Z log }[\text{Salt}]$$ (8)

In the use of this formula for practical data interpretation, it should be understood that the log V term does not represent an energetic or entropic effect; all of the non-electrostatic physical effects are contained in log K₀. For example, the entropically unfavorable lost degrees of translational freedom when L+P→LP are contained in log K₀.

Eq 8 contains DNA numerical parameters. For another polyelectrolyte, such as heparin, eq 3 should be used together with K_obs=VK and the appropriate numerical value for [M⁺]_cond, which equals 0.38 M for heparin. The general formula for [M⁺]_cond is in the Appendix.

III. Alternate Formulations of the Oligolysine Model

There are formulas for the oligolysine model that differ from eq 8, because they are only partially based on the counterion condensation theory. The one used most commonly in the literature is,^6,10

$${\text{log K}}_{\text{obs}}={\text{log K}}_0\prime -\mathrm{Z}\mathrm{\psi }\text{ log }[\text{Salt}]$$ (9)

where we use a prime to distinguish the K₀′ here from the non-electrostatic K₀ of the previous section. There are two aspects of this equation, one for each term, that require comment.

The “extra” factor ψ arises from the assumption that the Z charges on the ligand bind to a segment of the polyelectrolyte that itself carries Z charges, and that Z is sufficiently large such that the binding segment is itself long enough to be a polyelectrolyte. ^8,28 Strictly, the assumption would be valid for DNA binding only if the ligand were a polycation, and the complex were charge neutral. In the previous section, this assumption is not made, and ψ there is consequently equal to unity, signifying that binding of the charged ligand occurs while the net charge density of DNA is maintained at a critical non-zero value by one-for-one counterion release.⁷ Of course, it would be acceptable for a practical experimentalist to regard ψ as an empirical parameter that corrects the theory for end effects or some other poorly understood variable.

Possibly a more important comment is that the usual physical interpretation of the undetermined constant log K₀′ in eq 9 is fundamentally wrong. The interpretation is that, since the log[Salt] term represents the electrostatic contribution, log K₀′ must therefore be the non-electrostatic contribution to logK_obs, and hence to the binding free energy −2.314 RTlogK_obs, In the first place, a −RT log [Salt] term cannot by itself represent the complete electrostatic contribution to the free energy. If the units of [Salt] change from molarity to some other measure of concentration, the term changes its value. It does not have the units of energy RT and therefore cannot represent a free energy. This flaw does not appear in any of the counterion condensation equations in Section II. For example, in eq 3 the two last logarithmic terms combine to give a dimensionless argument to the combined logarithm, such that the combined term represents the entropy change of Z counterions when they are released to bulk solution from an initial condensed state. As in eqs 3 and 4, the electrostatic free energy must contain salt-independent terms in addition to the log[Salt] term. In eq 9, the log K₀′ term must contain an electrostatic contribution associated with the log[Salt] term, and therefore it cannot be interpreted as representing exclusively non-electrostatic interactions.

The difficulties that arise from the incorrect interpretation are exemplified by the analysis of Hallberg and Dubin,²⁶ who compared charge-variable pentalysine data to the slope d logK_obs / dZ = − ψ log [Salt] that is predicted from eq 9 on the assumption that log K₀′ is “non-electrostatic” and therefore cannot depend on ligand charge Z. The value 0.63 predicted on this basis at [Salt] = 0.19 M is in poor agreement with the value 1.1 from the data. Replacement of the extra ψ factor by unity, as is appropriate (Z varies from about 3.8 to 5, not enough to neutralize a polyelectrolyte-sized DNA segment), results in only a slightly improved value of 0.72 (since ψ_DNA = 0.88, not much different from unity). In contrast, from the full counterion condensation formula eq 8, where it can be seen that salt-independent terms of ionic origin are given explicitly, and in fact do depend on the oligolysine charge Z, the predicted value of the Z-slope of log K_obs is 1.23 (as detailed in the previous section), in good agreement with the data.

Our conclusion is that use of eq 9 should be discontinued. The counterion condensation formula eq 8 is more soundly grounded in theory. It lends itself just as easily to practical use. Perhaps most importantly, the log K₀ term in eq 8 really does represent the “non-electrostatic” component of free energy (i.e., the free energy from all effects other than counterion release).

In Sections II and III, we have emphasized small ligands with simple structure. It is reasonable to suppose that the entire charge of such ligands, or at least most of it, has penetrated the condensed layer of counterions on the host DNA, so that Z is actually equal to the ligand charge. However, if the ligand is a protein, then the cumulative effect of the many charged residues on the protein that are distant from the binding interface, and which therefore do not penetrate the condensed counterion layer, might contribute significantly to an effective value of Z. This effective value would not represent the number of cationic residues in the binding interface, nor would it be valid to use this value in the Z-containing terms of eq 8. In the next section we address this problem.

IV. The Effect of Near and Distant Charged Residues on Protein- DNA Binding

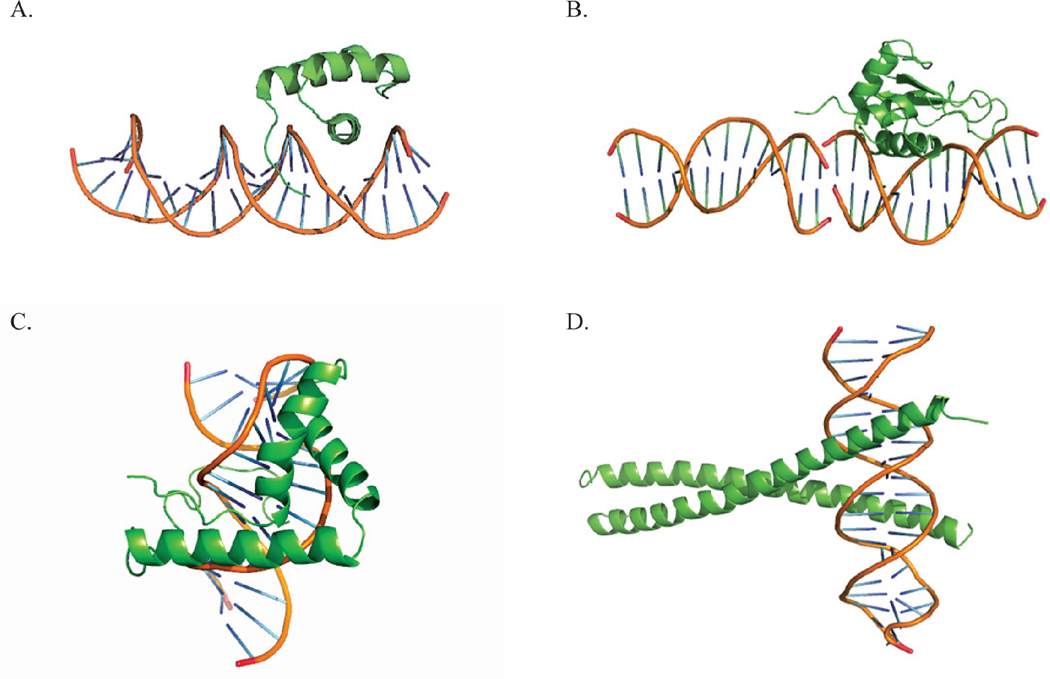
Although the interaction of individual ionized amino acids distant from the binding interface may be weak, proteins typically possess many charged residues, not all of them close to the DNA receptor sequence. Their concerted effect on binding free energy and its salt sensitivity may be significant. If it is significant, then it may not be feasible to separate the effects of ionized residues in the binding interface from the effects of more distant ionized residues by laboratory measurements alone. In this section we achieve the separation with the nonlinear Poisson-Boltzmann simulation techniques that have been described in detail elsewhere. ^29,30 We investigate representative complexes from four families of DNA-binding proteins: homeodomains, high-mobility groups, interferon regulatory factors, and basic leucine zippers. The complexes studied survey a variety of binding motifs, as illustrated in Fig. 1. Structures are obtained from the RCSB Protein Data Bank, and PDB identification codes are used in the figures and tables that report the results. The structures were treated as described previously.³¹

Figure 1.

Cartoon representation of DNA-binding proteins associated with its DNA binding partner. We show one representative of each family: a) Homeodomain Malt-α2 (PDBid, 1APL), b) high mobility group LEF-1 (PDBid, 2LEF), c) interferon regulatory factor IRF-1 (PDBid, 1IF1), d) leucine zipper GCN4 (PDBid, 1YSA).

We computed the nonlinear Poisson-Boltzmann free energy separately for the protein-DNA complex, and for the free protein and free DNA cognate sequence. In actuality, the free protein and free DNA can undergo conformational changes on binding, which may be difficult to take into account. Here we take the conformations of free DNA and free protein as possessing the same conformations as in the complex, since our focus is on exploration of some of the basic principles of ionic interactions, and not on an attempt at quantitative reproduction of the salt dependence of the observed binding constants. The free energy ΔG_PB for a binding reaction in which free protein combines with its free cognate DNA sequence to give the protein-DNA complex is then obtained by difference. The nonlinear Poisson-Boltzmann binding constant K_PB was obtained from ΔG_PB = −2.314 RT log K_PB. Only formal ionized charges were included in the computation: −1 for glutamate, aspartate, and phosphate, +1 for lysine and arginine. We assumed a pH such that histidine is not ionized. To maintain the focus on the effects of ionized charges, all fractional atomic charges that do not contribute to the formal ionic charges were set to zero, and the internal dielectric constant in the PB algorithm was set to 78. However, we verified that the results we report here are not significantly sensitive to changes in PB parameters. We performed computations at 1:1 salt concentrations [M⁺]=[Salt]= 0.1, 0.15, 0.2, 0.25, 0.3, 0.35, and 0.4 M, a typical range of ionic strengths in which experimental binding measurements are carried out.⁵ In this salt range plots of log K_PB vs. log[Salt] were found to be linear with negative slopes (binding is weakened by added salt). We denote by SK_PB the computed value of the slope, SK_PB=dlogK_PB/dlog[Salt].

To assess separately the effects of near and distant charged residues, we first computed values of SK_PB as described above, that is, with all amino acids possessing their formal charges, zero for neutral ones, ±1 for cationic or anionic residues. Then we selectively set the non-zero formal charges to zero, i.e, we selectively neutralized cationic or anionic groups, and recalculated the “mutated” SK_PB. We denote by ΔSK_PB the difference between the mutated SK_PB and the normal SK_PB,

$$\mathrm{\Delta }{\mathrm{SK}}_{\text{PB}}={\mathrm{SK}}_{\text{PB}}(\text{zero charge})-{\mathrm{SK}}_{\text{PB}}(\pm 1\text{charge})$$ (10)

From the definition of SK as the derivative of log K vs. log [Salt], we expect the values of ΔSK_PB to be positive when cationic residues are neutralized (the protein is bound more weakly with smaller salt dependence), negative when anionic residues are neutralized (the protein is bound more strongly with greater salt dependence). The data we obtained are organized into Figures 2 and 3 and Tables 1–4, and we proceed to a discussion of this presentation.

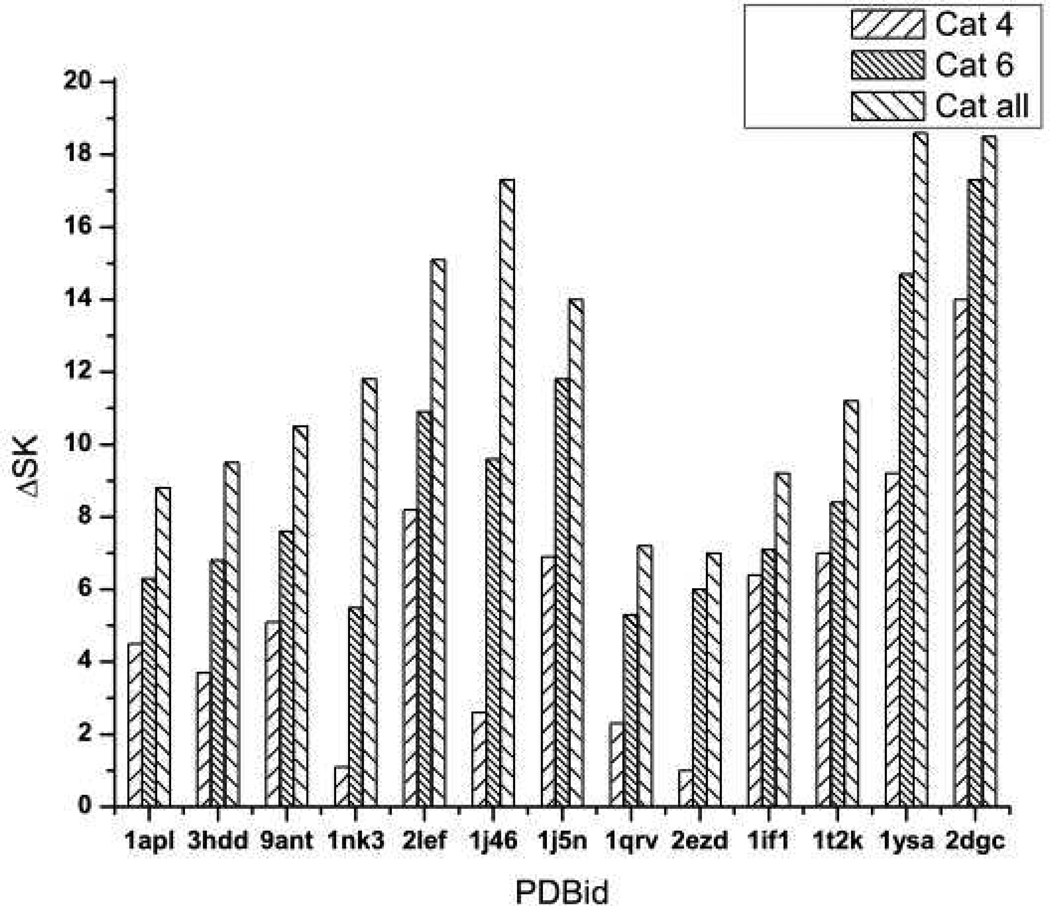
Figure 2.

A histogrammatic analysis of nonlinear PB results for the protein-DNA complexes listed on the abscissa. The vertical bars give values of ΔSK as calculated by PB computation. The left-most bar in each set of three is the result of switching off the charge on cationic residues within 4 Ǻ of a phosphate; the middle bar, of switching off cationic residues within 6 Ǻ; and the right-most bar, of switching off all cationic residues.

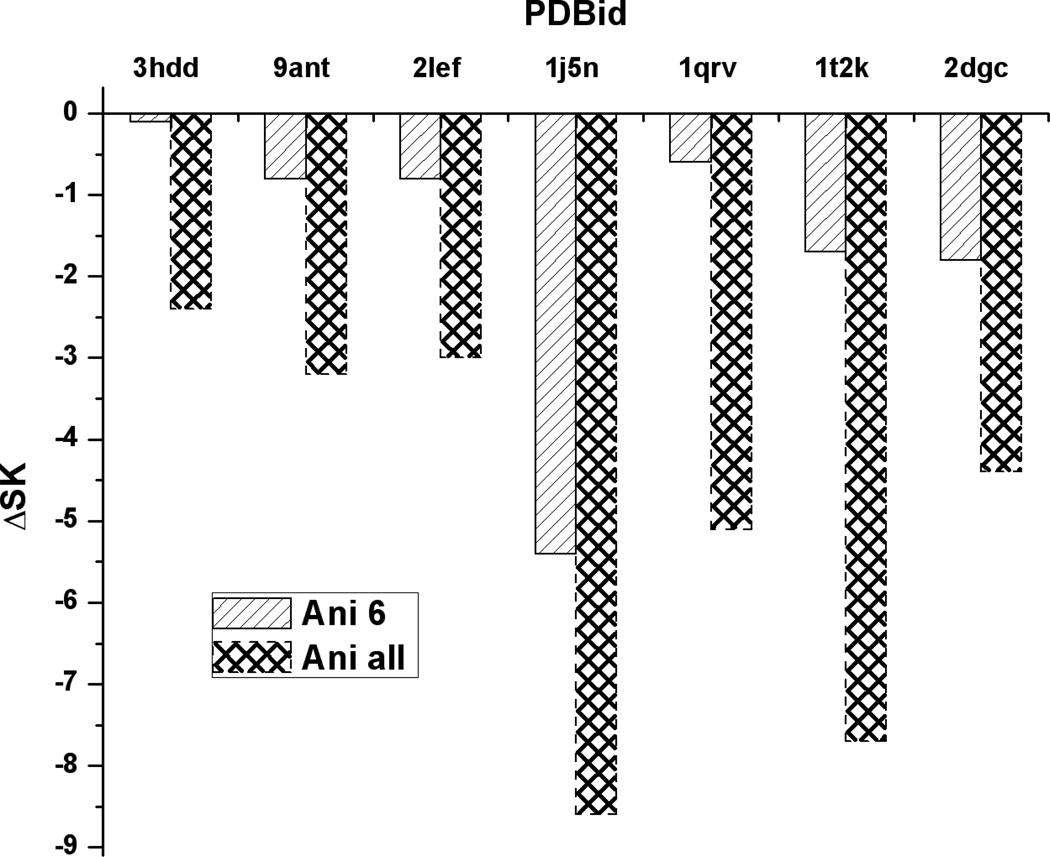
Figure 3.

A histogrammatic analysis of PB results for the effects of anionic residues. The left-hand bar in each set of two give values of ΔSK when anionic residues within 6 Ǻ are switched off. The right-hand bar in each set is the result when all anionic residues are switched off. There are no anionic residues within 4 Ǻ.

Table 1.

Effect of neutralizing 4 Å cationic contacts.

Protein Data Bank Identification	Nunber of 4 Å cationic contacts	ΔSK(CC)	ΔSK(PB)
1apl	5	5	5
3hdd	4	4	4
9ant	5	5	5
1nk3	1	1	1
2lef	8	8	8
1j46	3	3	3
1j5n	8	8	7
1qrv	3	3	2
2ezd	1	1	1
1if1	7	7	6
1t2k	7	7	7
1ysa	9	9	9
2dgc	14	14	14

Table 4.

Effect of neutralizing all distant ionized residues.

	9ant	3hdd	1nk3	1apl	1j46	1j5n	1qrv	2ezd	2lef	1t2k	1if1	1ysa	2dgc
ΔSKPB	0	2	5	1	3	1	−2	1	2	−1	−2	0	0
	1pvi	1bhm	1vkx	1esg	1p51	1kln	1j59	1ihf
ΔSKPB	1	3	1	4	0	1	1	6

The classes of ionized residues that we chose for neutralization are as follows: (1) with all anionic residues retaining their formal −1 charges, the charges on all cationic residues located within 4 Å of a phosphate oxygen were set to zero; (2) with all anionic residues at −1, the charges on all cationic residues located within 6 Å of a phosphate oxygen were set to zero; (3) with all anionic residues at −1, the charges on all cationic residues regardless of location were set to zero; (4) with all cationic residues at +1, the charges on anionic residues within 6 Å of a phosphate oxygen were set to zero; (5) with all cationic residues at +1, the charges on all anionic residues regardless of location were set to zero; (6) with all cationic and anionic residues within 6 Å at ±1, respectively, the charges on all cationic and anionic residues located further than 6 Å were set to zero.

The motivation for the 4 Å cut-off is that a frequently used criterion for an ion “contact” is that the charge on the cationic residue be located within 4 Å of a phosphate oxygen. The motivation for the 6 Å cut-off is two-fold. A 6 Å cut-off is another commonly used criterion for an ion “contact”. More fundamental in our view is the result of a Monte Carlo simulation reported by Young et al.¹⁴ on a protein-free DNA model related to ours insofar as water is treated as a dielectric continuum. Using an inflection point criterion and explicit Na⁺ ions, the authors exhibited a visually obvious layer of condensed Na⁺ ions located within 15 Å of the central DNA axis. The condensed counterions are mobile but adhere to the double-helical trajectory of the phosphate groups. Since the phosphates are at about 9 Å from the DNA central axis, a condensed counterion layer of width about 6 Å was therefore identified. Charged protein residues located within 6 Å of a phosphate oxygen in a protein-DNA complex can thus be said to have penetrated the layer of condensed counterions or to be on the periphery of the condensation layer. More distant charged protein residues are outside the condensation region.

Figure 2 shows the effect on SK_PB of neutralizing cationic residues within 4 Å, within 6 Å, and regardless of distance (classes 1–3 as enumerated above). Each vertical bar reports the change ΔSK_PB for the corresponding neutralization relative to the (negative) value of SK_PB when all residues are charged. For all protein-DNA complexes studied, the result is that an increase in the number of neutralized cationic residues weakens the binding and decreases the salt dependence of the binding constant K_PB. In particular, neutralization of even distant cationic residues strongly weakens the binding. The significance of this result for the interpretation of laboratory measurements is that the salt dependence of the binding constant contains the influence of long-range ion-ion interactions of cationic residues far from the binding interface, and thus is not a direct measure of the number of ionized residues in the binding interface.

Figure 3 shows the effect on SK_PB of neutralizing anionic residues within 6 Å, and all anionic residues regardless of distance (classes 4 and 5 as enumerated above). Not all of the proteins studied have anionic residues within 6 Å. For all complexes in Fig. 3, an increase in the number of neutralized anionic residues strengthens the binding and increases the salt dependence of the binding constant. In particular, neutralization of even distant anionic residues significantly strengthens the binding. The implication of this result for the interpretation of laboratory measurements is that the salt dependence of the binding constant contains the influence of long-range ion-ion interactions of anionic residues far from the binding interface (as well as of distant cationic residues), and thus is not a direct measure of the net number of ionized residues in the binding interface.

Tables 1–4 have a different emphasis. In Table 1, the number of 4 Å contacts (distance within 4 Å) as determined from the structure is listed for each protein-DNA complex. The third column lists the values of ΔSK_CC as predicted from the counterion condensation theory/oligolysine model when the cationic 4 Å residues are neutralized. According to eq 3, the prediction is that each ionic contact contributes one unit to ΔSK. Therefore, the entries for ΔSK_CC are identical to the number of 4 Å contacts (columns 2 and 3 are identical). Finally, the fourth column lists the values of the computed ΔSK_PB from Figure 1, rounded for clarity to the nearest integer.

The conclusion is clear: for 10 of the 13 entries, the agreement of the counterion condensation prediction and the Poisson-Boltzmann “experiment” is exact, while for the other 3 entries the agreement is off by only 1 unit. The 4 Å cationic residues have penetrated the layer of condensed counterions, releasing a number of counterions equal to the number of such residues. We refer to “Poisson-Boltzmann experiment” because the counterion release mechanism is buried so deeply in the mathematical structure of the nonlinear Poisson-Boltzmann equation itself that a PB numerical analysis such as is given here can at most confirm the numerical SK changes predicted by the counterion release (oligolysine model/counterion condensation) theory. In fact, however, the mathematical analysis of the PB equation,^32–38 as distinct from numerical PB computations, does show the existence of a condensed layer of counterions that compensates the bare polyelectrolyte charge up to a critical constant net charge density. Therefore, there must be a one-for-one replacement of condensed counterions for every cation that binds to DNA, and a one-for-one uptake of counterions for every anion that binds.

Table 2 is similar to Table 1 but extends the number of neutralized cationic residues to include 6 Å contacts. Again, the agreement between the counterion release/oligolysine model prediction, eq 1, is good, although not quite as good (5 exact matches, 5 off by one unit, 3 off by two or three units) as when only the 4 Å contacts are considered. Recalling the 6 Å width of the condensed layer of counterions, we may surmise that since some of the cationic residues within 6 Å are on the periphery of the condensation region, perhaps penetration is not sufficiently deep in some of the protein-DNA complexes to give sharp release of an equivalent number of condensed counterions.

Table 2.

Effect of neutralizing 6 Å cationic contacts.

Protein Data Bank Identification	Number of 6 Å cationic contacts	ΔSK(CC)	ΔSK(PB)
1apl	7	7	6
3hdd	7	7	7
9ant	9	9	8
1nk3	6	6	6
2lef	11	11	11
1j46	12	12	10
1j5n	15	15	12
1qrv	8	8	5
2ezd	6	6	6
1if1	8	8	7
1t2k	9	9	8
1ysa	15	15	15
2dgc	18	18	17

Table 3 gives analogous data for neutralization of anionic residues. In Table 3, anionic residues located within 6 Å of DNA phosphates are considered. Only those complexes that possess anionic residues so located are listed. The PB column is rounded to the nearest integer. The expectation from counterion condensation theory, eq 1, is that for each anionic residue that penetrates the condensation region, an additional counterion condenses. Five of the 7 entries in Table 3 confirm the expectation exactly, while the other two entries are off by one and two units, respectively.

Table 3.

Effect of neutralizing 6 Å anionic residues.

Protein Data Bank Identification	Number of 6 Å anionic residues	−ΔSK(CC)	−ΔSK(PB)
3hdd	1	1	0
9ant	1	1	1
2lef	1	1	1
1j5n	7	7	5
1qrv	1	1	1
1t2k	2	2	2
2dgc	2	2	2

Validation of the oligolysine/counterion condensation model for charged residues that penetrate the layer of condensed counterions does not have clear significance for the interpretation of measured salt dependencies of binding. The salt dependence measured in the laboratory is that of the overall binding, which as seen from Figures 1 and 2, appears to depend on the electrostatic interactions of distant charge residues, both cationic and anionic, as well as of the charged residues that “contact” the DNA phosphates. On the other hand, the effects of cationic and anionic residues are opposite in sign, so it is of interest to ascertain the extent of cancellation. If cancellation of the effects of distant cationic and anionic residues were exact, then the measured SK would indeed reflect only the charges in the binding interface. But since the number of distant cationic residues is different from the number of anionic residues, and the distances of the residues also are different, we do not expect exact cancellation. In Table 4, we list values of ΔSK_PB when the changes are caused by neutralization of all charged residues, cationic and anionic, at distances greater than 6 Å from the binding interface, while the ionized charges of closer residues remain at ±1. Values are rounded to the nearest integer.

Notice that we have included 8 additional protein-DNA complex structures, which have a very different distribution of positive and negative protein residues compared to the previous data set. We see that there are in fact several cases of exact cancellation, but they appear to be fortuitous. We conclude that according to our PB calculations, measured values of SK generally include the net effect of long-range electrostatic interactions from charged residues distant from the binding interface. On the other hand, the effects suggested by Table 4 can be construed in a number of cases not to be large. If a measured value of SK is interpreted as the number of ion contacts in the binding interface, then an uncertainty of 1 to 2 contacts may or may not be considered tolerable. An uncertainty of 3 to 6 presumably would be more serious.

V. Discussion and Summary

This paper has made several points in an effort to address a confused situation that exists in the field of the electrostatics of protein-DNA binding and, more generally, charged ligand-polyelectrolyte binding.¹⁰ We may summarize these points:

1. The oligolysine model for the ionic contribution to binding is embodied in the formulas of Section II, where all ions and ionized groups are taken as fully hydrated in both free and complexed forms. The negative of the slope of a log-log plot of K vs. [Salt] is equal to Z, the number of ionized protein groups that penetrate the layer of counterions that are condensed on free DNA. The formulas accurately predict the dependence on both ligand charge and salt concentration of experimentally observed binding constants for a series of oligolysines. The conclusion is that oligolysine binding to DNA is driven almost entirely by counterion release. Dehydration and other effects apparently play a negligible role.

2. The use of the customary but flawed eq 9 as a representation of the oligolysine model should be discontinued, as its identification of “electrostatic” and “non-electrostatic” components is incorrect.

3. To assess the performance of the oligolysine model as a description of cognate protein-DNA binding, we used a nonlinear Poisson-Boltzmann model together with structural information on the number of ion contacts for a set of protein-DNA structures. By selective neutralization of ionized residues, we found that the oligolysine model predicts with reasonable accuracy the effect of the charged residues that are in the protein-DNA binding interface, and that therefore have penetrated the layer of condensed counterions. For each such cationic residue, one condensed counterion is released into solution; for each such anionic residue, an additional counterion is condensed.

4. From the Poisson-Boltzmann simulation we also found that the cumulative effect of the many charged residues distant from the protein-DNA binding interface have a significant influence on the dependence of the binding constant on salt concentration. This means that the slopes of log-log plots of K_obs vs. [Salt] as measured in the laboratory may not be interpretable entirely in terms of the number of released counterions and hence the number of ion contacts made in the binding interface. It therefore also means that quantitatively accurate identification of a non-electrotrostatic −RTlnK₀ component of the binding free energy (which includes dehydration of ionic residues) by using the oligolysine model may not be possible, since Z is the number of released counterions. On the other hand, we found for several cases a considerable cancellation of the effects of distant cationic and anionic groups.

We mentioned also in the Introduction a review by Dubin¹⁰ covering the less well-characterized interactions of a group of biopolyelectrolytes called glucosaminoglycans (GAGs)---the most familiar of which are heparin and chondroitin sulfate---with their protein partners (antithrombin in the case of heparin). Dubin is critical of the use of the oligolysine model in analyzing GAG-protein binding, feeling that it has led to an oversimplified picture in which the actuality of a more nuanced, less specific, complex is seen unjustifiably through the same prism as lock-and-key cognate protein-DNA binding and protein-protein association. In our opinion, his criticism of the uses to which the oligolysine model has sometimes been put in his field overreaches too broadly into criticism of the model itself. As we have discussed, the oligolysine model does not imply lock-and-key charge complementarity, or structurally precise ion pairing. It merely asserts that the charged groups on the ligand (antithrombin in Dubin’s case) penetrate the layer of counterions condensed on the polyelectrolyte (heparin). Indeed, heparin, like DNA, is a highly charged linear polyanion that hosts a condensed layer of univalent counterions,^17–19 some of which would be released into solution if cationic protein groups penetrate it. A purely screening formulation of the electrostatics of heparin-antithrombin binding¹⁰ is incorrect. On the other hand, the limitations of the oligolysine model as discussed above would apply to antithrombin-heparin binding as well as protein-DNA binding. It should also be noted that if in experiments, the polyelectrolyte heparin is represented by an oligomer consisting only of five monomeric units,¹⁰ then the polyelectrolyte formulas of counterion condensation theory may not be fully accurate.

APPENDIX

We provide here some more detail for the derivation of the basic counterion condensation eqs 1 and 2.⁷ A detailed derivation for Z=2 and an outline for any Z have previously been published.^7,23 The derivation begins by noting that the free energy G of the solution is given by summing n_iμ_i over all solution species i, where n_i is the number of moles and μ_i the chemical potential of Species i. A complete list of the various species includes the free polyelectrolyte with its condensed counterions, the polyelectrolyte with low levels of ligand condensed on it, the free ligand, the free counterions and coions, and water. Additionally, the condensed ligands have a chemical potential, as do the condensed counterions. Some of these terms depend on the degree of ligand condensation θ_Z and/or the degree of condensation θ₁ of the univalent counterions M⁺. The free energy is then minimized with respect to these two variables. The problem is reduced to minimization with respect to a single variable by the relation

$${\mathrm{\theta }}_1+\mathrm{Z}{\mathrm{\theta }}_{\mathrm{Z}}=\text{constant}$$ (A1)

where the constant is the known net charge density of the polyelectrolyte after condensation of counterions. This constraint is relaxed by the “two-variable” theory,⁷ which shows its validity for low binding levels, the case of interest here. Among the terms that do not depend on the degrees of condensation of ligand and counterion are, of course, the term for the coion. Importantly, the combined terms for free polyelectrolyte and polyelectrolyte bearing low levels of ligand condensation do not depend on θ₁ or θ_Z. This is because the net charge density on the polyelectrolyte does not depend on these variables, so the long-range electrostatic free energy of the polyelectrolyte, which is all that concerns us in counterion condensation theory, is a constant.

When the free energy minimization is carried out, the equilibrium values of the binding fractions θ₁ and θ_Z are obtained, and eqs 1 and 2 of the text along with them. As observed in the text, the logarithmic term in eq 1 is of transparent physical meaning, but the Z − 1 term is not. This term in fact is a composite with components from several origins, of which we mention two here. The chemical potential of the solvent contains a contribution equal to minus the ratio of the number of solute molecules to the number of solvent molecules, so the contribution nμ for water contains a term proportional to θ₁ + θ_Z which figures into the free energy minimization. Furthermore, the concentration dependent term in the chemical potential of the free counterions is RTln[M⁺]_free, and [M⁺]_free equals the constant [Salt] plus a number of uncondensed counterions proportional to 1 − θ₁. Again, there is a binding fraction, θ₁, that figures into the free energy minimization and finds its way into the Z−1 term of eq 1 in the text, where [M⁺] is the zeroth-order term of [M⁺]_free, i.e., [M⁺]≡[Salt].

In the text, we noted that the local concentration [M⁺]_cond of condensed counterions is 1.2 M for DNA and 0.38 M for heparin. For any polyelectrolyte, the formula is,⁷

$${[{\mathrm{M}}^{+}]}_{\text{cond}}=(1-{\mathrm{\xi }}^{-1})/\mathrm{v}$$ (A2)

where ξ characterizes the charge density of the polyelectrolyte, and v is the local volume of the condensation region per mole charge site on the polyelectrolyte,

$$\mathrm{\xi }={\mathrm{\ell }}_{\mathrm{B}}/\mathrm{b}$$ (A3)

where b is the average charge spacing of the polyelectrolyte taken along the contour (0.17 nm for DNA), and ℓ_B is the Bjerrum length characteristic of the solvent, ℓ_B=e²/4πε₀DkT, where e is the elementary charge, ε₀ is the vacuum permittivity, k the Boltzmann constant, and D the dielectric constant of the pure solvent (ℓ_B=0.71 nm for water at room temperature), and, for 1:1 salt,

$$\mathrm{v}=8\mathrm{\pi }e{\mathrm{N}}_{\text{Av}}(\mathrm{\xi }-1){\mathrm{b}}^3$$ (A4)

where e=2.718… is the base of natural logarithms, and N_Av is Avogadro’s number.

In the text, we presented formulas for the enthalpy and entropy of counterion release. The latter was given for DNA parameters only. Here we give the general formulas. When the charge on a Z-valent ligand penetrates the layer of condensed counterions, releasing Z counterions to bulk solvent (water), and if dehydration effects are included only in the ΔH₀ and ΔS₀ non-electrostatic terms, then the enthalpy of this process is the same as stated in the text, while the entropy is given by,

$$\mathrm{\Delta }\mathrm{S}=\mathrm{\Delta }{\mathrm{S}}_0+\mathrm{R}\{0.6\mathrm{Z}-1+2.303\text{Zlog}\{{[\mathrm{M}]}_{\text{cond}}/[{\mathrm{M}}^{+}]\}$$ (A5)