Electrical Stimulation of the Rectus Femoris During Pre-Swing Diminishes Hip and Knee Flexion During the Swing Phase of Normal Gait

Abstract

Individuals who have suffered cerebral insults often exhibit stiff-knee gait, a condition characterized by reduced knee flexion during swing. We investigated the effect that an increment in normal rectus femoris (RF) activity can have on hip and knee joint angles during swing, as a first step to determining this muscle’s involvement in stiff-knee gait. For this, we developed a protocol that electrically stimulated the RF during pre-swing or after toe-off in randomly selected strides of treadmill walking, consistent with the timing of RF activity during normal gait. Seven healthy young adults participated in the study. Pre-swing stimulation induced a significant (p<0.05) reduction in peak knee flexion (avg 7.5deg) in all subjects, with an accompanying decrease in hip flexion in four of the subjects. RF stimulation after toe-off diminished peak knee flexion in three subjects and reduced hip flexion in four subjects. When compared to muscle-actuated gait simulations that were similarly perturbed, the induced motion measures were generally consistent in direction but exhibited greater variability across strides and subjects. We conclude that excess RF activity during pre-swing has the potential to contribute to stiff-knee gait, and that clinical treatment should consider the “counter-intuitive” function that the RF has in extending the hip.

I. INTRODUCTION

Stroke and cerebral palsy (CP) patients often exhibit a stiff-knee gait pattern. This walking abnormality is characterized by diminished knee flexion during swing, often accompanied by either vaulting or limb circumduction to achieve toe clearance. Excessive activity of the rectus femoris (RF) has been cited as a contributor to this reduced knee flexion [1–3]. As a result, the RF has been the target of medical treatments involving its distal tendon release or transfer [1–3] and of recent investigations using motor branch nerve blocks and botulinum toxin injections [4–5]. However, the outcomes of tendon surgeries have been inconsistent, with some subjects achieving substantial improvements in knee flexion during swing and others not [4, 6]. Inconsistent outcomes and the recognition that each patient normally presents a different set of deficits have made it clinically challenging to pinpoint the contribution of RF to stiff-knee gait patterns.

Simulation studies have provided some insights into the possible contribution of RF to knee flexion during swing [7–8] or to knee flexion velocity at toe-off [9], which affects knee flexion during swing [10–12]. For example, independent studies have concluded that the RF has both a large relative potential to influence toe-off knee flexion velocity when active during stance [9] and a small relative contribution (per unit force) to peak knee flexion when active during swing [7]. These conclusions suggest that activity of RF prior to toe off may be more important in restraining knee motion than its activity after toe off [8, 13]. Dynamic models further suggest that the RF may induce hip extension when active during early swing [12], which is opposite of what is traditionally assumed based on anatomy alone [1, 14]. Experimental in vivo validation of these predictions is essential for using models to investigate how gait impairments arise in pathology.

Recent studies have introduced electrical stimulation procedures to empirically measure the movement induced by activation of specific lower limb muscles [15–18]. Hernández et al. used a well controlled two-dimensional (2D) methodology to show that electrical stimulation of the RF can induce hip and knee extension acceleration at static postures representative of early swing [17], consistent with the predictions of a dynamic model. Hunter et al. followed with a three-dimensional (3D) experiment using a Lokomat™, which confirmed the sagittal-plane effects observed by Hernández et al. but also showed that RF stimulation can also induce hip abduction in the frontal plane [18]. These prior studies highlighted the posture-dependent nature of muscle function and confirmed some of the “counter-intuitive” behaviors of biarticular muscles previously predicted by dynamic musculoskeletal models [12, 19–22]. However, prior empirical investigations of RF function have not been conducted during actual walking, where the simultaneous activity of other muscles and foot-floor contact could affect induced movement patterns.

In this study, we directly measured dynamic rectus femoris function during walking by synchronizing electrical stimulation to specific points of the gait cycle. We hypothesized that RF stimulation would act to reduce hip and knee flexion during swing, with greater induced joint angle changes for stimulation delivered prior to toe-off. We also evaluated whether subject-specific gait simulations would properly predict the direction and variability of induced motion measured experimentally.

II. METHODS

A. Experimental Methodology Overview

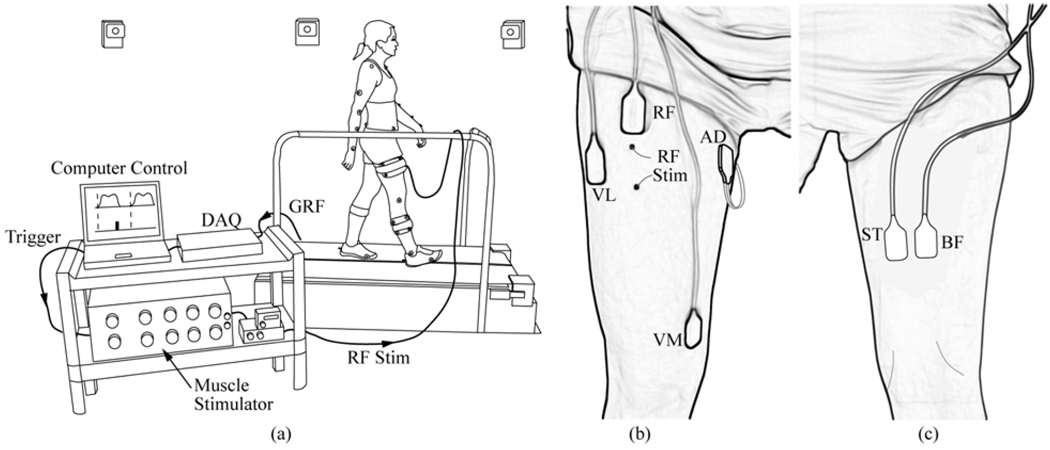
Seven healthy young adults (age = 30.7 ± 6.3 yr, mass = 71.2 ± 10.0 kg, height = 1.75 ± 0.06 m) participated in this study, approved by the University of Wisconsin’s Health Sciences Internal Review Board. The protocol involved subjects performing 90 s walking trials on a split-belt instrumented treadmill (Bertec Corp.; Columbus, OH) while their RF in the right limb was briefly stimulated during the pre- or early-swing phases of randomly-selected strides (Fig. 1).

Fig. 1.

Experimental Setup. (a) Subjects walked on a split-belt forceplate instrumented treadmill while a computer controller monitored the ground reaction forces (GRF) via a data acquisition unit (DAQ). Based on the frequency of heel strikes, the controller estimated the stride period in real time and then triggered a muscle stimulator to stimulate the rectus femoris (RF) at a prespecified percentage (50%, 60%) of the gait cycle using fine wire indwelling electrodes (RF Stim). An 8-camera motion capture system continuously recorded whole body kinematics. Surface EMG was recorded anteriorly (b) from the RF, vastus medialis (VM), vastus lateralis (BL) and hip adductors (AD) and posteriorly (c) from the semitendinosus (ST) and biceps femoris(BF).

B. Electrical Stimulation Synchronized to the Gait Cycle

A dual-channel, current-controlled stimulator (Grass S88, Astro-Med, Inc., West Warwick, RI) was used to stimulate the RF. We first located the motor point of the muscle by moving surface stimulating electrodes over the skin until a maximum twitch response was observed. Two indwelling stainless steel fine-wires (0.003” bare diameter, A–M Systems, Inc., Carlsborg, WA) were then inserted into the muscle where the motor point was located, approximately 3 inches apart (Fig. 1), using 25-gage hypodermic needles. The indwelling electrodes were used to deliver 90 ms current pulse trains (four 300 µs pulses at 33 Hz) to the RF upon the request of a trigger signal. Stimulation timing was controlled by using a custom LabView (National Instruments, Austin, TX) program to monitor vertical ground reactions, from which the stride duration was calculated based on the average of the last 3 strides. The controller triggered the stimulator starting at either 50% (pre-swing) or 60% (early swing) of the gait cycle. Each subsequent stimulus was introduced randomly between the fifth and tenth stride following the previous stimulation. The magnitude of the stimulus current was set to a level that would produce a visible alteration to the limb trajectory or reach a subjective value of 2 in the 1-to-10 pain scale, whichever was lowest and never exceeding 50 mA.

C. Kinematics

Three-dimensional whole body kinematics were recorded at 100 Hz using an 8-camera motion capture system (Motion Analysis, Santa Rosa, CA) to track 44 reflective markers (Fig. 1(a)). Twenty-five markers were placed over anatomical bony landmarks including the right and left anterior superior iliac spine, the posterior super iliac spine, the first and fifth metacarpals, the heel, and the lateral epicondyle and malleolus. Other tracking markers were attached to plates that were strapped tightly to the thigh and shank segments. All kinematic data was low-pass filtered at 6 Hz. Joint angles were computed using a whole body model that 21 lower extremity degrees of freedom (d.o.f.) to represent the low back, hip, knee and ankle joints [23], and 10 d.of. to represent the right and left upper extremity joints [24]. The pelvis was the base segment with 6 d.o.f. Each lower limb included a 3 d.o.f. ball-and-socket representation of the hip, a 2 d.o.f. ankle with non-intersecting talocrural and subtalar joints [25], and a 1 d.o.f. knee where translations and non-sagittal rotations were functions of knee flexion [26].

Segment lengths in the model were first scaled to each subject using anatomical marker positions measured in a standing upright trial. The hip joint center in the pelvic reference frame was then calibrated using a functional joint center identification routine [27]. At each frame of a motion trial, we then used a global optimization inverse kinematics routine to compute pelvic position and orientation, and lower extremity joint angles that minimized the discrepancy between measured marker positions and corresponding markers fixed to the body segments [28].

D. Muscle Activity

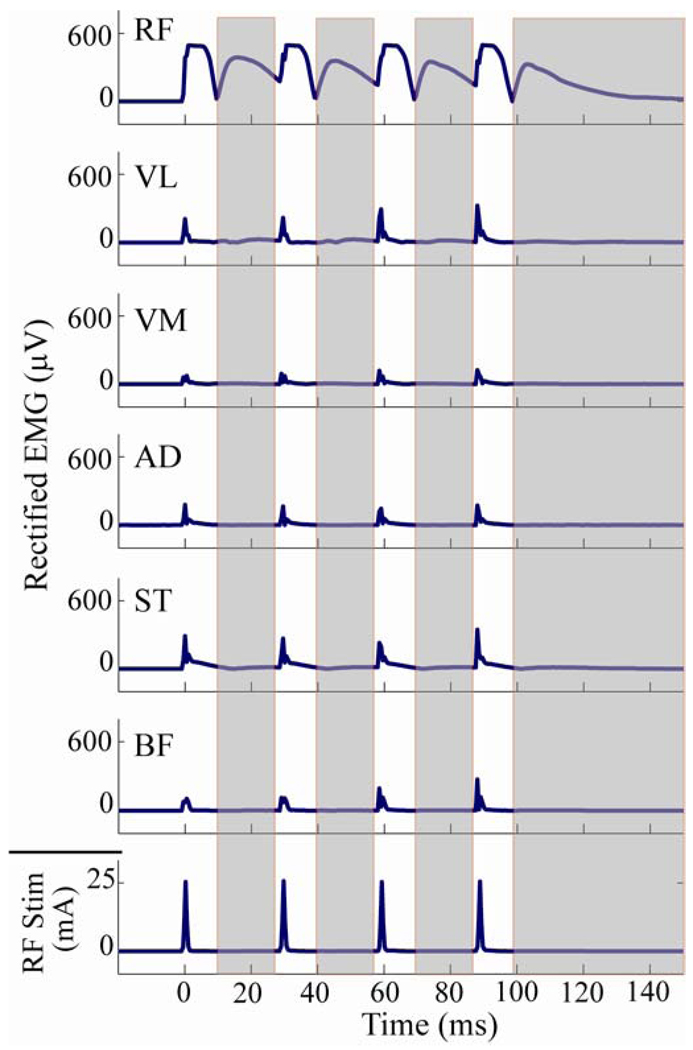
Pre-amplified, single differential electromyographic (EMG) electrodes (DE-2.1, DelSys Inc., Boston, MA) were placed on the rectus femoris, vastus lateralis, vastus medialis, semitendinosus, biceps femoris and adductor muscle group of the right limb (Fig. 1 (b) and (c)). These EMG activities, the ground reaction forces from the treadmill, and the stimulator’s trigger signal were sampled synchronously at 2000 Hz. The EMG recordings were full wave rectified and used to evaluate stimulus spill-over and potential reflex activity as a consequence of the electrical stimulation. To evaluate spill-over, we quantified induced activity between stimulus pulses, after a brief time period to allow for the direct stimulation pulse effects to dissipate on each electrode (Fig. 2). Reflex activity was then evaluated by comparing muscle activities in a post-stimulation window (150–300 ms after the stimulation onset) to baseline activity levels from non-stimulated strides (Fig. 2).

Fig. 2.

The current-controlled stimulation (RF Stim) induced activity in the surface EMG recordings of the RF, biceps femoris (BF), semitendinosus (ST), hip adductors (AD), vastus medialis (VM), and vastus lateralis (VL) muscles. The shaded regions correspond to the regions where the rectified EMG was measured to assess the induced activity in the RF and neighboring muscles. To do this, the central low point in the M-curve of the RF EMGwas first identified (typically occurred between 15–20ms after stimulation onset) after each stimulation pulse, and induced activity was then computed over a window between this point and a point 1 ms prior to the next pulse. The assessment window for the fourth (and last) stimulus pulse was ceased at 150 ms after the onset of stimulation.

E. Periodic Prediction Model

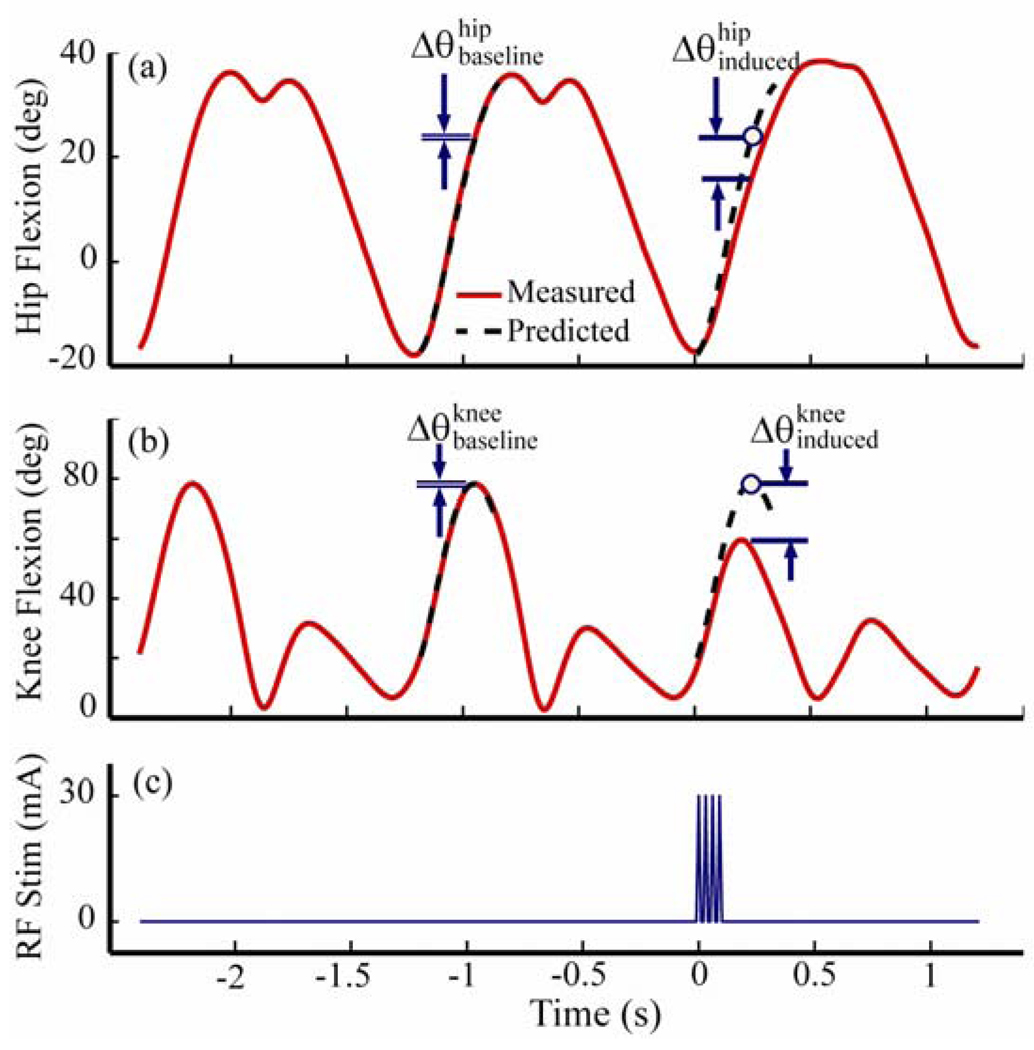
We employed a periodic prediction model [29] to estimate changes in hip and knee angles as a result of RF stimulation. This periodic prediction model represented the normal cyclic nature of movement kinematics and ground reactions during walking by a linear equation:

$$\theta (t-\tau )=\alpha +\beta \theta (t-2\tau )+\eta (t)$$ (1)

where θ was a joint angle of interest, α and β were slowly varying linear regression parameters, τ was the stride period, and η was a noise process. That is, a hip or knee joint angle could be approximated by its value one stride earlier after small offset and drift factors were accounted for. For each stimulation, we first identified the exact onset (t_o) of the pulse train and an expected stride period (τ_exp) based on the frequency of stepping. We then computed the cross-correlations of the joint angles between a window that was 0.9 τ_exp wide starting at t_o and corresponding windows of equal width whose starting points varied from 20 ms before to 20 ms after the point t_o−τ_exp. The current stride period (τ) was chosen as that which maximized the cross-correlations. We repeated the process using the two non-stimulated strides preceding the stimulated stride. We then used linear regression to estimate the parameters α and β relating these two strides. The model was then used to predict the hip and knee angles of both the current (stimulated) stride and the previous (non-stimulated) stride, each based on the stride that immediately preceded it (Fig. 3).

Fig. 3.

Periodic Prediction Model. A linear model is constructed based on the two strides preceding introduction of the stimulating current pulse train (c). This model then predicts expected joint angles for the stride preceding and following the stimulus. The difference in angles (Δ θθθ between the actual trajectory (solid curve) and the predicted trajectory (dashed curve) at the point of predicted peak knee flexion during swing are evaluated for both the hip (a) and the knee (b). Baseline differences, prior to the stimulation, represent normal variations in joint angle trajectories that are not captured by the periodic prediction model. Induced measures represent the joint angle differences observed during swing phase following stimulation.

The difference between the measured and predicted joint angle ($\mathrm{\Delta }{\theta }_{\mathit{\text{induced}}}^{\mathit{\text{hip}}}$ for the hip and $\mathrm{\Delta }{\theta }_{\mathit{\text{induced}}}^{\mathit{\text{knee}}}$ for the knee) was evaluated at the point of predicted peak knee flexion during swing in the stimulated stride. This point was always within 300 ms following the onset of the stimulus. Similarly, the difference between the measured and predicted joint angle ($\mathrm{\Delta }{\theta }_{\mathit{\text{baseline}}}^{\mathit{\text{hip}}}$ for the hip and $\mathrm{\Delta }{\theta }_{\mathit{\text{baseline}}}^{\mathit{\text{knee}}}$ for the knee) was evaluated for the previous, non-stimulated stride. The stimulated stride differences were compared to the non-stimulated stride differences for each trial using t-tests (p = 0.05). The difference between the baseline and induced angle measures was considered to be the effect of the stimulus.

F. Subject-specific forward dynamic simulations of gait

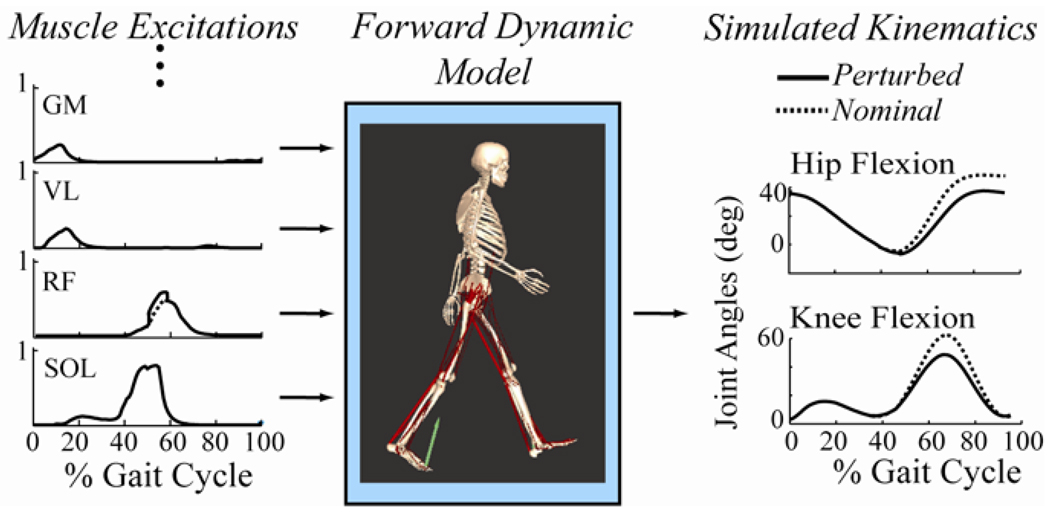
Simulations of subject-specific walking dynamics were used to generate predictions of rectus femoris muscle function that could be compared to the experiments. We included 92 musculotendon actuators in the gait simulation models, representing the major muscles acting about the low back, hip, knee and ankle joints [25]. The input to each muscle was an excitation that could vary between 0 and 1. Excitation-to-activation dynamics was represented by a bi-linear differential equation with activation and deactivation time constants of 10 and 40 ms, respectively [30]. A Hill-type musculotendon model was used to describe contraction dynamics [31]. For each subject, muscle fiber lengths, tendon slack lengths and the musculotendon origins, insertions and wrapping points were scaled by the ratio of the subject-specific musculotendon lengths in an upright posture normalized to the corresponding lengths in the generic musculoskeletal model [32]. This approach nominally maintains each muscle’s force generating characteristics and operating range, as is recommended [33].

For each subject, we generated multiple normal gait simulations of that emulated kinematic data collected in the strides that preceded a stimulation pulse train. To do this, we first used a least-squares forward dynamics algorithm to eliminate any inconsistencies between measured whole body kinematics and ground reactions [24]. We then used Computed Muscle Control was used to determine a set of muscle excitations that drove the model to closely track the lower extremity kinematic trajectories, while upper extremity motion was prescribed to track measured values [23]. In total, we generated simulations of 270 full gait cycles with simulated joint angles that were on average within 1 deg of measured values. Excitations were determined that minimized the weighted sum of squared muscle activations [34], which has been shown to provide reasonable estimates of coordination patterns seen in normal gait [35].

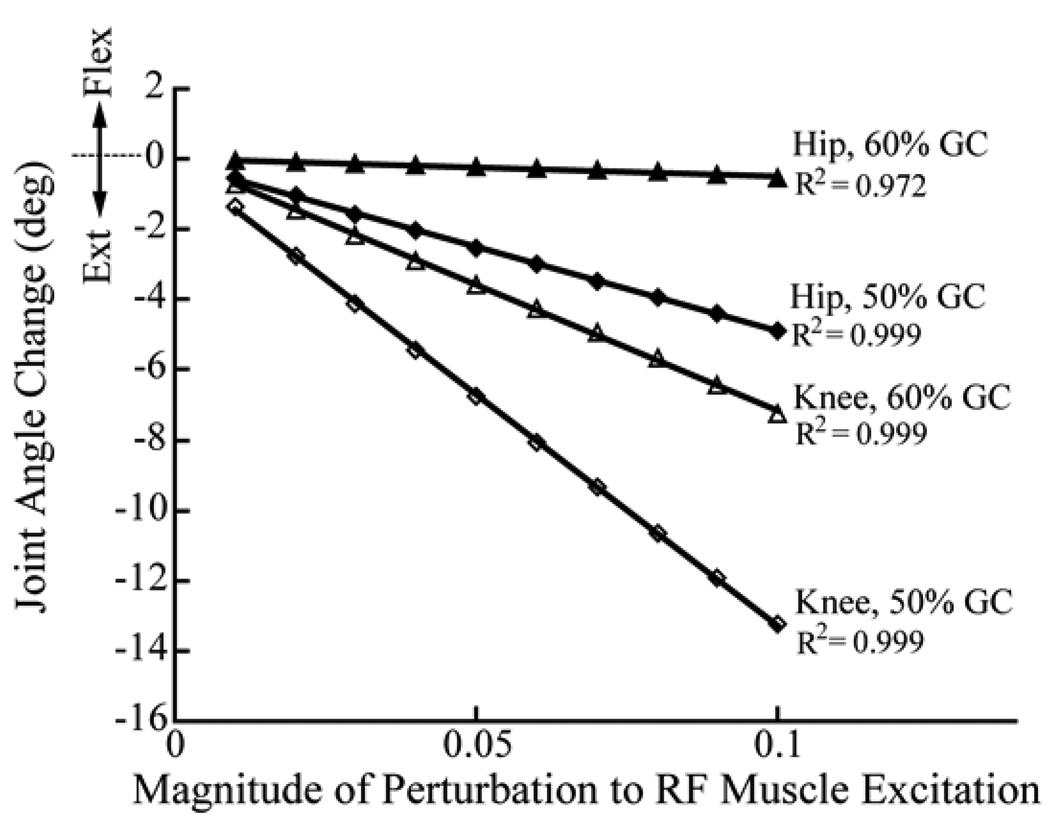
After generating the nominal simulations, we then perturbed the RF excitation patterns at either 50% (pre-swing) or 60% (early swing) of the gait cycle (Fig. 4). This was done by increasing the excitation level of the RF by magnitudes ranging from 0.01 to 0.1 units (1 corresponds to maximum excitation drive) for a 100 ms period. Changes in the interactions between the stance-limb foot and the ground were characterized by a set of rotational and translational spring-damper units [36]. Hence, the ground reaction forces and moments were allowed to change in response to the perturbations in force, and the effects of these changes were implicitly included in the actions attributed to the muscle. Simulations were continued for a minimum of 300 ms after the onset of the perturbation, so as to capture the time at which peak knee flexion occurred. As in the experimental case, the hip and knee angle changes caused by the perturbation at the point of peak knee flexion during swing were determined. The changes in hip and knee angles were found to vary linearly with perturbation magnitude (Fig. 5), such that a scaling procedure was used to determine the stimulation magnitude that would induce the average knee angle change in the experiment for the 50% GC stimulation condition. Thereafter, the simulation results for the hip perturbed at 50% GC, and for the hip and knee perturbed at 60% GC, were scaled using linear equations derived from a study of induced joint angle changes with perturbation size (Fig. 5). The F-ratio was used to compare the variability in induced motion measurements with the variability predicted by simulating multiple strides of gait for each subject.

Fig. 4.

We compared induced motion measures to perturbations of subject-specific gait simulations. To do this, we first computed nominal muscle excitation patterns that drove a forward dynamic musculoskeletal model to emulate measured gait kinematics. We then introduced small (0.01 to 0.1 units for 100 ms) increases in the rectus femoris’ nominal excitation at either 50% or 60% of the gait cycle, and re-simulated the gait cycle. The simulated changes in hip and knee flexion were compared to the same measures determined experimentally. Notation: GM-gluteus maximus, VL-Vastus Lateralis, RF-Rectus Femoris, SOL-Soleus.

Fig. 5.

Scaling procedure for determining the appropriate perturbation magnitude to use in the subject-specific gait simulations. A straight line through the origin (i.e., no joint angle change at 0 perturbation) was first used to relate the change in hip and knee angle to the perturbation magnitude. On a subject-specific basis, the knee angle change for perturbation at 50% GC was then matched to the experimental average for that condition. Then, the size of the perturbation that would have caused such a change was read off the x-axis. This value was subsequently used to scale the simulation average of the hip angle at 50%GC as well as the hip and knee angles at 60%GC.

The linked segment musculoskeletal models used in this study were generated in SIMM (Musculographics Inc., Chicago, IL), with dynamical equations of motion derived using Dynamics Pipeline (Musculographics Inc., Chicago, IL) and SDFast (Parametric Technology Corporation, Waltham, MA). Custom code was used to perform the global optimization inverse kinematics, residual elimination [24] and CMC analyses [23], with all numerical optimizations performed using a sequential quadratic programming routine (FSQP; AEM Design, Tucker, GA).

III. RESULTS

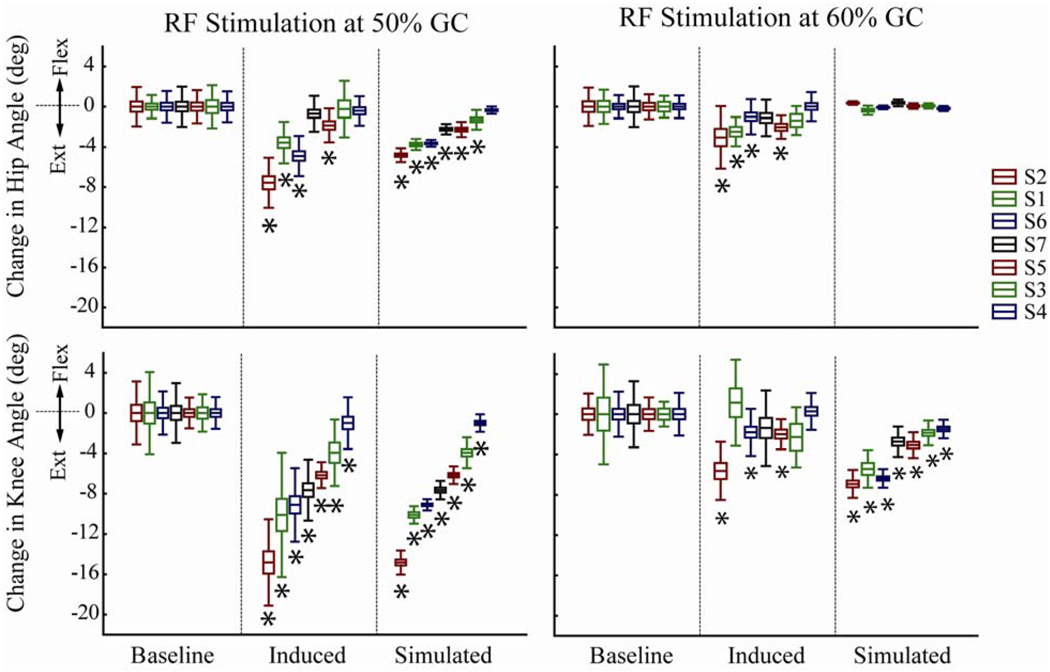
RF stimulation at 50% GC induced a significant (p<0.05) decrease (average decrease of 7.5deg) in peak knee flexion during swing in all seven subjects (Fig. 6). This same stimulus simultaneously acted to significantly (p<0.05) diminish hip flexion in four of the subjects tested. Simulations of these subjects’ gait patterns predicted a significant (p<0.05) reduction in knee flexion in all subjects, and a significant (p<0.05) reduction in hip flexion in 6 of the 7 subjects tested, with the scaled magnitude of hip angle changes comparable to that observed experimentally (Fig. 6).

Fig. 6.

Changes in Hip and Knee Angles. Joint angle changes for the experimentally induced and simulated results relative to baseline experimental values obtained via the periodic prediction model. Subjects have been ranked in all four plots by the order of decreasing absolute knee angle change in the 50% GC stimulation case. Simulated knee angle change averages for each subject have been matched to the experimental averages in the 50% GC stimulation condition. Thereafter, the simulation averages for the remaining conditions have been estimated on a subject-specific basis (Fig. 5). Central line = mean, box = standard error, whisker = standard deviation. * = significant differences when compared against the baseline values (p < 0.05).

RF stimulation at 60% GC induced a significant (p<0.05) decrease in peak knee flexion during swing in 3 of the 7 subjects tested, with the average change (1.7deg) being much lower than was observed with the 50% GC stimulus (Fig. 6). The 60% GC stimulus also significantly (p<0.05) diminished hip flexion in the same four subjects who showed a change in hip flexion in the 50% GC case. The perturbed gait simulations correctly predicted that the 60% GC stimulation would have a lesser effect on knee flexion in swing than the 50% GC case. However, the perturbed simulations incorrectly predicted no effect of the 60% GC stimulus on hip flexion.

Trial-to-trial variability in the model-predicted changes in hip and knee angles were significantly lower for all subjects than the variability measured experimentally in either the preceding baseline stride or the stimulated stride (Table 1).

Table 1.

F-ratios of the variances among baseline, experimental (Exp.) and simulated (Sim.) joint angle changes.

		Stimulation at 50%GC			Stimulation at 60%GC
	Subject	Induced vs Baseline	Simulation vs Baseline	Simulation vs Induced	Induced vs Baseline	Simulation vs Baseline	Simulation. vs Induced
Knee	2	1.9	6.9 *	12.8 *	1.9	2.2	4.3 *
Flexion	1	2.3	22.4 *	51.0 *	1.3	7.1 *	5.3
	6	2.8 *	14.9 *	42.2 *	1.1	5.9 *	6.4 *
	7	1.0	10.6 *	10.9 *	1.3	4.8 *	6.2 *
	5	1.5	3.1 *	2.1	1.3	1.7	1.4
	3	3.1	1.5	4.7 *	5.7	1.0	5.7 *
	4	2.6	3.3 *	8.7 *	1.3	5.3 *	3.9
Hip	2	1.7	8.0 *	13.1 *	2.7	>100 *	>100 *
Flexion	1	3.2 *	4.4 *	13.7 *	1.4	13.7 *	10.1 *
	6	1.7	21.3 *	35.2 *	2.3	36.8 *	84.1 *
	7	1.3	15.0 *	11.9 *	1.2	35.2 *	28.4 *
	5	1.1	4.7 *	5.0 *	1.1	21.7 *	19.2 *
	3	1.7	4.9 *	8.4 *	1.7	17.8 *	30.7 *
	4	1.1	18.3 *	16.5 *	1.6	19.6 *	31.7 *

F-ratio = $\frac{{\sigma }_1^2}{{\sigma }_2^2}$ where σ₁ > σ₂ are the standard deviations of the samples to be compared.

^*Significant at p < 0.05.

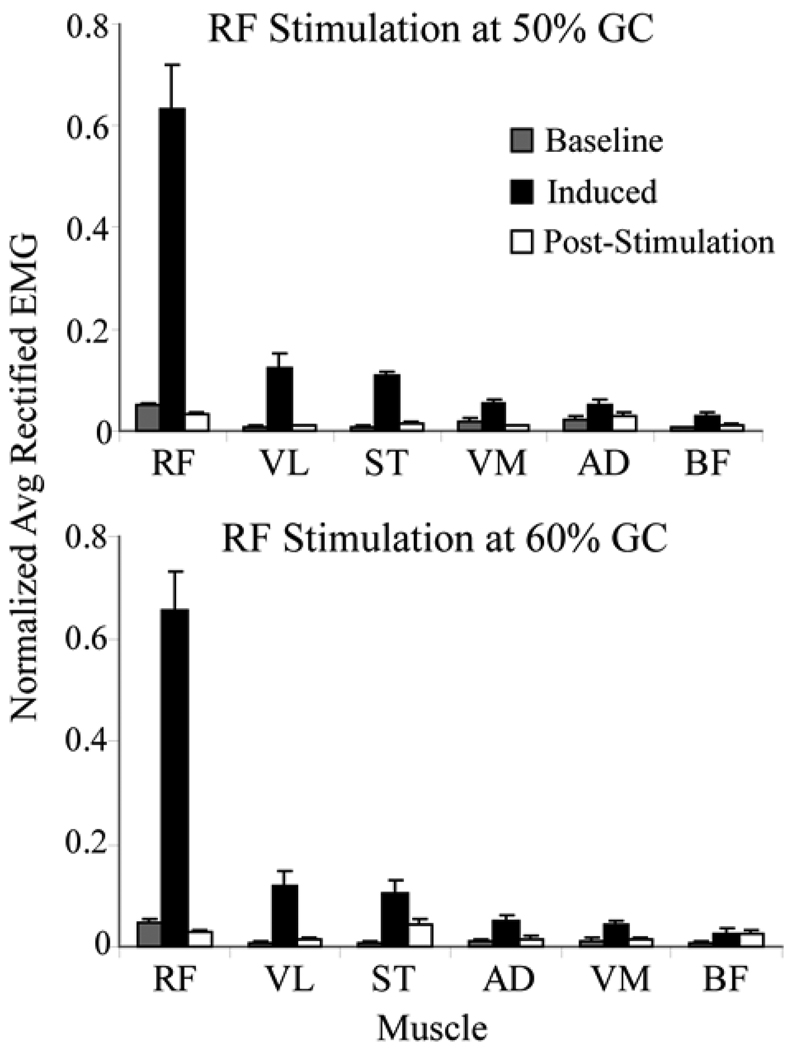
EMG measurements confirmed that the stimulus primarily induced activity in the RF, with a large majority of the net EMG activity being measured in that muscle during a 150 ms period following the stimulus (Fig. 7). The normal activity of any muscle during an equivalent 150 ms period in the non-stimulated strides was less than 10% of the EMG value measured from RF in the stimulated strides. The average activity of any muscle in the post-stimulation (150–300 ms) period, where we might expect reflexes to occur, was less than 8% of the RF EMG average during the stimulated stride.

Fig. 7.

Comparison of average (±1 s.d.) EMG activity in non-stimulated baseline strides with the induced EMG activity seen between stimulation pulses (Induced) and in a 150–300ms window (post-stimulation) following each stimulation pulse train. For each subject and category, the rectified EMG activity of each muscle was normalized by the total rectified EMG of all muscles such that the sum of the normalized values for all muscles was 1. The data for the baseline stride and post-stimulation categories were then normalized once more, this time by the ratio of the total induced EMG of the stimulated strides to the corresponding total for the category of interest. In this manner, the relative EMG magnitudes between the three categories were preserved. The results show that the greatest amount of stimulation-induced activity was seen in the RF, with relatively small residual effects after stimulation ceased.

IV. DISCUSSION

This study shows that activation of the RF prior to toe-off can substantially diminish knee flexion during swing. The result at the knee agrees with our hypothesis based on dynamic gait models, which have shown that knee flexion velocity at toe-off is a major determinant of knee flexion during swing [7, 9, 12], and that RF during double support likely reduces knee flexion velocity [8, 13]. Stimulation of the RF also induced hip extension in a majority of the subjects, which is opposite to the anatomical hip flexor moment generated by this muscle but consistent with prior dynamic model predictions [12, 17]. This effect reflects inter-segmental dynamics, in which biarticular muscles can induce non-intuitive motion at one joint via their action at a neighboring joint [19].

We found that forward dynamic simulations of subject-specific gait patterns were generally able to predict the direction of induced motions. In particular, the models correctly predicted that the RF can extend both the knee and hip, and that induced knee and hip extension motions are larger when the stimulus occurs prior to toe-off rather than after toe-off [7, 9]. The induced knee extension was roughly 2.7 times larger than the hip extension for the pre-swing stimulation, which is comparable to the average changes predicted by the gait simulations (Fig. 6). However, we found that the hip slightly extended for RF stimulation during early swing in four of the subjects, a result that was not predicted by the simulations. We previously showed that RF-induced motion predictions depend significantly on the hip-to-knee moment arm ratio, particularly in an early swing posture [17]. The generic musculoskeletal model [25] used in this study assumes a hip flexion-to-knee extension moment arm ratio that varies from ~0.8 in double support to ~1.1 after toe-off [17]. Individual variations in this moment arm ratio could contribute to differences between the simulation and experimental measures of induced motion that were observed. Given that pathological subjects can exhibit differences in muscle moment arms due to abnormal bone geometry [37], it would seem judicious to proceed with caution when using generic models to evaluate treatment in patients with stiff knee gait.

We note that induced motion measured in this study differ somewhat from induced acceleration analyses. In particular, induced motion reflects the changes in position that occur sometime after the stimulus, and thus is necessarily influenced by changing postures, contact conditions (e.g. toe-off) and other muscles, which can change length and exert forces on the systems over the evaluation period [7]. In contrast, induced acceleration analyses represent the instantaneous potential of a muscle to accelerate segments, a quantity which theoretically depends only on the current position of the segments [17]. While both analyses may be beneficial to understanding muscle function, induced motions may be closer to clinical gait analyses, which often focus on understanding how muscle actions give rise to abnormal movement patterns at the joint angle level.

The results of this study are relevant to consider in the context of treating stiff-knee gait. Justification for RF transfer surgery is that releasing the RF tendon from the patella and reattaching it to the knee flexors diminishes the potential for the muscle to extend the knee, while maintaining the capacity to induce hip flexion [1–2]. Our results would support the effect on knee motion, especially when the muscle is overactive in the pre-swing period. However, it is possible that RF transfer may actually also convert the muscle from a hip extensor into a hip flexor because the knee extensor moment, which induces hip extension acceleration via dynamic coupling, would be diminished [38–39] after surgery. Therefore, transferring the RF distal tendon could have two effects on the subject: one from eliminating the knee extensor moment (which should relieve the stiff-knee symptom) and another from allowing the RF to actually induce hip flexion. This latter effect may also contribute to enhanced limb flexion [7]. In a recent study of botulinum toxin injections to treat stiff knee gait in CP, the inactivity of the RF induced by the toxin caused the knee to flex more than when the RF was previously overactive. This effect was larger in patients whose RF overactivity was during pre-swing [40] rather than during swing. Similarly, we saw a greater effect of pre-swing RF activity on knee motion during swing. This result emphasizes the importance of considering neuromusculoskeletal dynamic processes, which give rise to substantial delays between abnormal excitation and movement at the joint level.

We took three steps to ensure that we were truly measuring movement induced by RF stimulation. First, we used fine wire electrodes inserted into the muscle belly to induce large RF contractions while reducing the potential for stimulation spillover to neighboring muscles. An analysis of the EMG activities suggests we succeeded, with induced RF EMG activity being both larger than the simultaneous EMG activity of other muscles, and greater than ten times the RF activity seen in non-stimulated strides (Fig. 7). Secondly, we limited our analysis window to 300 ms after the stimulus, which we previously found sufficient to measure stimulation induced motion in a static configuration [17]. Finally, we found that post-stimulation EMG activity (within a 150–300 ms window after stimulation onset) was much smaller than induced activities immediately after a stimulation pulse. We conclude that the RF stimulation was likely the major contributor to the induced motion since reflex activities were relatively small and the RF received most of the stimulus.

There was a fair amount of variability among subjects and between strides in the induced motion measures. Part of the inter-subject variability can be attributed to differences in the magnitudes of induced RF contraction forces, which depend substantially on electrode placement, the number of motor units recruited and the magnitude of stimulus that subjects could tolerate. We found that perturbed motions in the simulations varied substantially less than the induced motions in the experimental and baseline data (Fig. 6). This result suggests that differences in overall size or segment inertias among subjects, which are considered by the models, are only a small contribution to the stride-to-stride variance in the data. Rather, the inter-stride variance could arise from variability in individual subjects’ hip and knee joint angle trajectories [41]. Such inherent variability limits the ability of the periodic prediction model to accurately predict the behavior of future strides. This result highlights the need to consider many strides experimentally to determine the average induced motion.

V. CONCLUSION

A new methodology for the evaluation of dynamic muscle function has been introduced, whereby a muscle can be electrically stimulated at a precise time in a random gait cycle, and its effects on joint angles measured. We used this methodology to assess the effect of increasing the activation of the rectus femoris during pre-swing and early swing on the hip and knee flexion during swing. We showed that stimulating the RF diminishes hip and knee flexion, and that this effect is greater when the stimulus is delivered prior to toe-off. Perturbed forward dynamic simulations predicted these overall trends but did not represent stride-to-stride and subject-to-subject variability well. We conclude that early onset of RF activity has a greater potential than increased activity of this muscle during swing to contribute to stiff-knee gait, and that clinical treatments should consider the “counter-intuitive” function that the RF has in extending the hip.