The diffusional properties of dendrites depend on the density of dendritic spines

Abstract

We combined computational modeling and experimental measurements to determine the influence of dendritic structure on diffusion of intracellular chemical signals in mouse cerebellar Purkinje cells and hippocamal CA1 pyramidal cells. Modeling predicts that molecular trapping by dendritic spines causes diffusion along spiny dendrites to be anomalous and that the value of the anomalous exponent (d_w) is proportional to spine density in both cell types. To test these predictions we combined local photorelease of an inert dye, rhodamine-dextran, with two-photon fluorescence imaging to track diffusion along dendrites. Our results show that anomalous diffusion is present in spiny dendrites of both cell types. Further, the anomalous exponent is linearly related to the density of spines in pyramidal cells and d_w in Purkinje cells is consistent with such a relationship. We conclude that anomalous diffusion occurs in the dendrites of multiple types of neurons. Because spine density is dynamic and depends on neuronal activity, the degree of anomalous diffusion induced by spines can dynamically regulate the movement of molecules along dendrites.

INTRODUCTION

Transmission and processing of information within signal transduction pathways often relies on diffusion of chemical signals (Holcman et al., 2004; Cornelisse et al., 2007; Schmidt et al., 2007a; Schmidt et al., 2007b). However, aside from the case of simple, unbranched axons (Popov & Poo, 1992; Gabso et al., 1997), it is poorly understood how neuronal geometry affects the spatial and temporal spread of intracellular signals. This problem is particularly difficult in dendrites, because of their complex arborization patterns, large changes in diameter that might reduce diffusion rates, and the presence of local geometric features such as spines. Furthermore, it is not clear how much diffusional properties vary between different types of neurons.

Here we use a comparative approach to determine how a prominent dendritic structure - dendritic spines - affects molecular diffusion. We compared diffusion within two types of neurons with well-characterized and quite different dendritic structures: cerebellar Purkinje cells and hippocampal CA1 pyramidal cells. Despite these structural differences, our modeling work predicts that dendritic spines cause similar reductions in diffusion rates in both cell types. Specifically, the modeling predicts that trapping of molecules for random periods of time inside dendritic spines results in a non-linear process known as anomalous diffusion. We tested this prediction by combining two-photon fluorescence imaging with localized photorelease of a caged dye. As predicted, Purkinje cells showed a large degree of anomalous diffusion in spiny dendrites and much less in smooth dendrites. This is consistent with a previous report (Santamaria et al., 2006). We also detected anomalous diffusion in CA1 pyramidal cells. As predicted by our models, the amount of anomalous diffusion depends linearly upon spine density. Overall, our results show that spines cause anomalous diffusion in both Purkinje and pyramidal cells and therefore could be a general mechanism employed by neurons to regulate the spread of chemical signals in spiny dendrites.

MATERIALS AND METHODS

Electrophysiology and imaging

Sagittal slices from the vermis of the cerebellum and coronal slices from the hippocampus were prepared from 12-17 day old mice (Finch & Augustine, 1998), following procedures approved by the Animal Care and Use Committee of the Duke University Medical Center. The extracellular solution was composed of (in mM): NaCl, 125; KCl, 2.5; CaCl₂, 2; MgCl₂, 1.3; NaH₂PO₄, 1.25; NaHCO₃, 26; D-glucose, 20. The free radical scavenger trolox-C (0.1 mM) was added to the extracellular solution to reduce phototoxicity associated with fluorescence imaging.

Whole-cell patch clamp recordings were made from the somata of Purkinje cells and CA1 pyramidal cells. The intracellular recording solution was composed of (in mM): potassium gluconate, 130; NaCl, 2; Na₂ATP, 4; Na-GTP, 0.4; MgCl₂, 4; Hepes (pH 7.2), 30 mM; EGTA, 0.5. Caged rhodamine dextran (RD; 10 kD molecular mass; 5 mM) and cascade blue dextran (cBD, 5 kD, 5-10 mM) were added to these solutions as needed.

Fluorescence images were acquired using a two-photon microscope (Prairie Technologies, Madison, WI) at variable rates (5-27 frames per second). Caged compounds were photolyzed by brief flashes (5 ms duration) from a shuttered UV laser (Innova 305, Coherent). The total amount of UV energy was 3-10 μJ. Images were analyzed with routines written in Matlab (Natick, MA). All pseudocolor images representing changes in RD fluorescence were thresholded at 20% above the resting fluorescence level, which was approximately twice the background noise level. The diffusion coefficient of RD was calculated from photolysis experiments where caged RD was uncaged in the pipette and the fluorescence tracked with a line scan. The calculated diffusion coefficient was D_rd = 0.08 μm²/ms.

Measuring diffusion

The photoreleasing spot from our setup ranged from 3-8 μm in diameter, in most cases larger than the diameter of the monitored dendrites. Since the ratio of the dendritic diameter to dendritic length was small we assumed a one-dimensional diffusion process along the axis of the dendrite, originating at x = 0, described by

$$\langle x^2\rangle =2D(t)t$$ 1

where 〈x²〉 is the spatial variance at each time point, D(t) is the time varying diffusion coefficient and t time. The functional expression of D(t) is given by equation 2

$$D(t)=\frac{1}{2}\mathrm{\Gamma }{t}^{2/d_w-1}$$ 2

Where Γ is the constant generalized transport coefficient and d_w the anomalous exponent. Combining equation 1 and 2 results in the well known anomalous diffusion equation (Feder et al., 1996; Brown et al., 1999)

$$\langle x^2\rangle =\mathrm{\Gamma }{t}^{2/d_w}$$ 3

The anomalous exponent describes how the space where the molecule moves differs from a homogenous system (Gal & Weihs, 2010; Mika & Poolman, 2010). Diffusion within such a system cannot be characterized by a single diffusion coefficient; in this case, d_w indicates how close the volume where the molecule moves approximates a well-mixed and homogeneous solution. A value of d_w = 2 indicates free diffusion and D = Γ/2 is the constant diffusion coefficient. However, in the case when d_w <> 2 then diffusion is anomalous and D depends on time. In the particular case when d_w > 2 diffusion is slowed down with respect to normal diffusion. Thus, in order to characterize the diffusion of biochemical signals in dendrites we determined the anomalous exponent d_w. We determined D(t) via the relationship D(t) = (〈x²〉 − 〈x²〉₀)/2t where 〈x²〉₀ is the spatial variance of the initial condition.

The spatial variance was calculated as $\langle x^2\rangle =\mathrm{\sum }_x{(x-r_m(t))}^2{C}_n(x,t)$, where r_m(t) is the mean (or centroid) at each time point $(r_m={\int }_{x}x{C}_n(x,t)\mathit{dx}/{\int }_x{C}_n(x,t)\mathit{dx})$, C_n(x,t) the spatial concentration profile, proportional to the fluorescence, normalized to its area $(C_n(x,t)=\raisebox{1ex}{$\mathrm{\Delta }G(x,t)$}\!\left/ \!\raisebox{-1ex}{$G_0\left(x\right)$}\right./{\int }_x\raisebox{1ex}{$\mathrm{\Delta }G(x,t)$}\!\left/ \!\raisebox{-1ex}{$G_0\left(x\right)$}\right.\mathit{dx})$. Before calculating the variance, each frame was corrected for background fluorescence and the fluorescence along the entire width of the dendrite (F(x,t)) was integrated every 1 μm along the axis of the dendrite. We then convolved the resulting fluorescent profile with a Gaussian of 2 μm standard deviation (E(x), $G(x,t)={\int }_u\left(E\right(x,t\left)F\right(x-u,t\left)\right)du$). The background level of fluorescence (G_o) before photoactivating the RD was calculated using at least 10 frames of the RD fluorescence image.

In several cases we used the cBD images to determine the linear spine density (spines/μm) of pyramidal neurons. Due to limitations in spatial resolution, we could not rely on the presence of a spine neck to determine if a structure was a spine. Instead, we counted the numbers of putative spine heads up to 2 μm away from the axis of the dendrites; we projected the 3-D stacks in XY and XZ projections to distinguish spines directly above or below the dendrite. A spine head was defined as a high-intensity area in the image not larger than 1 μm in diameter. To calculate spine density we counted the number of spines (Ns), measured the length of the dendritic segment (Ls), and calculated the average dendritic diameter (ds), which influences spine density. Spine density was then determined calculating $\mathrm{Spine\; density}=\frac{\mathit{Ns}}{\mathrm{\pi }\cdot \mathit{ds}\cdot \mathit{Ls}}\mathrm{\pi }\cdot d=\frac{\mathit{Ns}}{\mathit{ds}\cdot \mathit{Ls}}$, where d = 1 μm was used to normalize all measurements of spine density to a standard dendrite of 1 μm diameter. Note that in other studies the linear density was not normalized (Harris & Stevens, 1988; Harvey & Napper, 1991; Vecellio et al., 2000).

Modeling diffusion in spiny dendrites

We used previously-developed software to model intracellular diffusion in dendrite-like structures (Santamaria et al., 2006). In brief, the model consisted of cylinders that could be concatenated (to simulate dendrites) or attached perpendicular to the surface of other cylinders (to simulate spines). The initial condition consisted of a section of a dendrite filled with a homogenous concentration of diffusible molecules. This initial distribution was subdivided in packets (walkers), with each packet equivalent to 100 molecules. We then applied a Green’s function Monte Carlo algorithm that allowed the walkers to move in a Cartesian set of co-ordinates at each time step. Boundary conditions consisted of reflecting walls and transitions between cylinders. The integration time step and D_rd were the only two parameters needed to fully characterize the simulation. Simulations were run on at the San Diego Super Computer Center and at UTSA’s Computational Biology Initiative (http://cbi.utsa.edu). Data analysis was performed using the same Matlab routines that were used to analyze the experimental results, as described above.

We modeled spines as two concatenated cylinders, one representing the spine head and the second representing the spine neck. We programmed an algorithm that generated a set of independent, normally distributed random numbers for the neck length and head length, constrained by reported anatomical measurements of the range, mean, and standard deviation for each structure (SI Table S1). Another normally distributed number was generated to assign spine head volume. We then calculated the head diameter of each spine from the assigned head volume and head length, $\mathrm{diameter}=2\sqrt{\mathit{volume}/\mathrm{\pi }\ast \mathit{length}}$. Finally, we generated a normally distributed random number between the minimum spine neck diameter, derived from literature values, and a maximum that was equal to a head/neck diameter ratio of 1.5.

RESULTS

The objective of this study was to determine whether neurons with quite different dendritic structures share similar mechanisms of intracellular diffusion. We started by modeling the effects of dendritic structure on intracellular diffusion in Purkinje and CA1 pyramidal cells. We then corroborated our experimental predictions by combining local photorelease of RD with two-photon fluorescence imaging to track diffusion along dendrites.

Predicting diffusion properties in neuronal dendrites

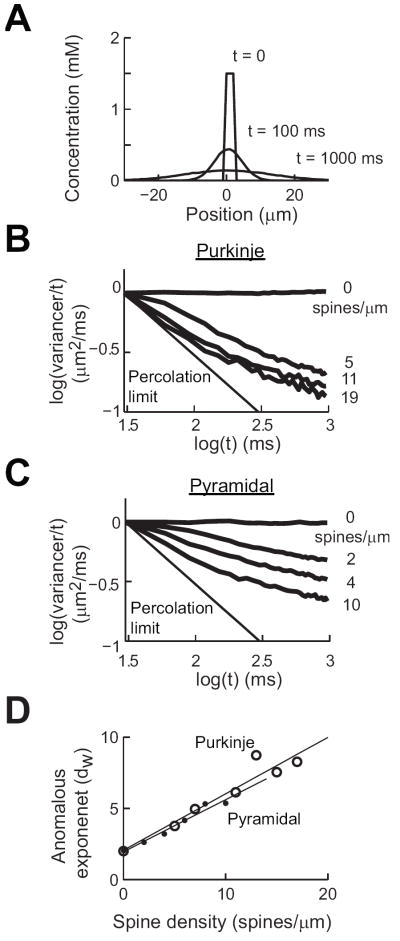
We built computer models of the dendritic spines of Purkinje and CA1 pyramidal cells based on published electron microscopy measurements (SI Table S1). Our models reproduced the statistical distribution of spine properties, such as the length and diameter of the spine head and neck, and total spine length (SI Fig. S1). We then used these models to simulate the diffusion of molecules within dendrites with different densities of spines. We tracked the spread of a focal release of molecules over a long dendrite by measuring the spatial variance of their distribution over time (Fig. 1A). We then calculated the value of the anomalous exponent, d_w, via the following rearrangement of Eqn. 3:

$$\mathit{Log}\frac{\langle x^2\rangle }{t}=\left(\frac{2}{d_w}-1\right)\mathit{Log}(t)+\mathit{Log}(\mathrm{\Gamma })$$ 4

With this transform, the slope of the linear region of the data in a log-log plot is equal to 2/d_w-1, where normal diffusion (d_w = 2) appears as a straight line with a slope of zero (Figs. 1B, C). The percolation limit indicates the limit that is reached when d_w approaches infinity.

Figure 1.

Modeling predictions of the properties of anomalous diffusion in Purkinje and CA1 hippocampal pyramidal cells. (A) Concentration profiles at three time points in a smooth dendrite. (B) Logarithmic transform of spatial variance values calculated in Purkinje cell dendrites at the indicated spine densities. (C) Similar analysis of diffusion in pyramidal cell dendrites. (D) Relationship between anomalous exponent (d_w) and spine density for both cell types.

Such an analysis was done for models of both cell types, while varying spine density. Pyramidal cell spine density was varied from 0-10 spines/μm and Purkinje cell spine density was varied from 0-19 spines/μm. For both types of neurons, increasing the density of spines resulted in higher values of d_w, as seen in the slopes for the plots shown in Figs. 1B and 1C. The major outcome of our simulations is that the relationship between spine density and calculated d_w is predicted to increase linearly with spine density for both types of neurons (Fig. 1D). Remarkably, even though spine structure differs between the two types of dendrites, the simulation predicts that the anomalous exponent for the two dendrites should be practically identical at a given spine density (Fig. 1D). In conclusion, the computational modeling predicts that molecular trapping by spines can cause anomalous diffusion in both types of neurons. Further, the model predicts that for both types of neurons the degree of anomalous diffusion, as defined by d_w, should vary as a linear function of spine density and the slope of this function should be similar for both neuron types.

Measuring diffusion in Purkinje cells

We next performed experimental measurements of diffusion in neuronal dendrites. For this purpose, we locally photoreleased caged RD and used a two-photon microscope to visualize the subsequent intracellular diffusion of photoreleased RD. We also filled each cell with a second, non-caged dye, cBD (5 mM), which served as a volume tracer to define dendritic structure. In all cases we insured that the image plane contained a large section of dendrite to allow measurement of diffusion for the longest possible time (SI Fig. S2).

We began by measuring diffusion in the dendrites of cerebellar Purkinje cells. Fig. 2A shows an image of cBD fluorescence within a Purkinje cell. RD was photoreleased at sites in the center of each of the two dendritic regions indicated by the colored rectangles in Fig. 2A. The photorelease of RD produced transient increases in RD fluorescence, which are indicated by the pseudocolor overlays of the relative changes in RD fluorescence (ΔF/F_o) in the enlarged images of the two regions shown on the right of Fig. 2A. The region within the green rectangle contains a smooth dendrite, while the region within the red rectangle includes a spiny dendrite. Photorelease of caged RD resulted in an increase of fluorescent molecules that slowly diffused along the dendrite. We tracked diffusion of these molecules by measuring fluorescence changes along the dendritic axes indicated with the colored lines shown in the Fig. 2A inset images and used these fluorescence profiles (Fig. 2B) to calculate the spatial variance of the signals as a function of time. Loss of fluorescence was small over long periods of time, indicating the relative absence of RD bleaching or loss of RD into other dendrites (Fig. 2C). Comparison of the spatial variance in the two dendrites revealed that diffusion was much slower in the spiny dendrite than in the smooth one (Fig. 2D). We analyzed the data in Fig. 2D using the log-log transform described in Eqn. 4 to obtain the anomalous exponent value (Fig. 2E). The log-log transformation of the data shows that diffusion in the smooth dendrite is essentially linear for a long period of time and has a low anomalous diffusion over the 3 second measurement period: d_w was 2.8 ± 0.2 (95% confidence interval) for the smooth dendrite, nearly the value of 2 associated with free diffusion. In contrast, anomalous diffusion was quite prominent in the spiny dendrite, with d_w being 6.4 ± 0.3. Thus, apparently diffusion was much slower in the spiny dendrite because the presence of spines increased d_w.

Figure 2.

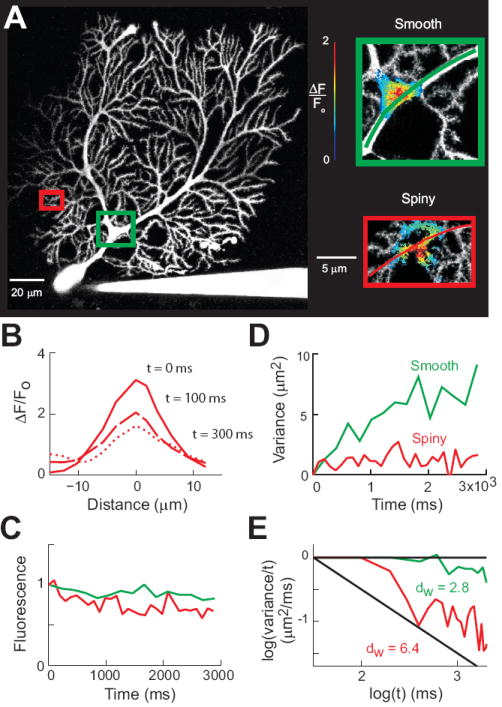
Measuring intracellular diffusion in Purkinje cells. (A) Left - Maximum intensity projection image of a Purkinje cell filled with cascade blue. Colored rectangles indicate areas enlarged at right. Inset - Photoreleasing of caged RD in smooth and spiny dendrites. Pseudocolor images indicate relative changes in RD fluorescence after a 5 ms long flash of UV light. The images were taken 203 ms (top) and 99 ms (bottom) after RD photorelease. (B) Spatial distribution of fluorescence changes after photorelease in the spiny dendrite. (C) Time course of RD fluorescence after photorelease for the diffusion paths in insets of (A). Values are normalized to the intensity of RD fluorescence at the first time point after photorelease. (D) Time course of changes in spatial variance for the two experiments shown in (A), measured along the pathways indicated by the colored lines in insets of (A). (E) Logarithmic transforms of the data shown in (D). Diffusion in the smooth dendrites (green) is close to normal (horizontal line), while in the spiny dendrite (red) the data have a steep slope, indicating anomalous diffusion.

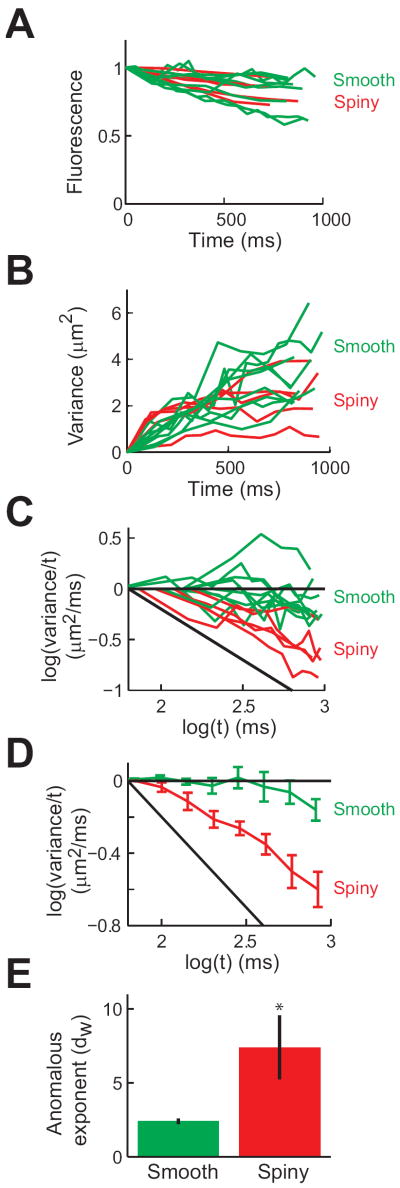
Such measurements were repeated in a total of 6 Purkinje cells and the collected results of these experiments are shown in Fig. 3. Plotting the fluorescence decay after photorelease of caged RD shows no difference between smooth and spiny dendrites (Fig. 3A). In each experiment, the spatial variance of fluorescence increased over time (Fig. 3B), indicating diffusion of photoreleased RD within the dendrites. A logarithmic transform of these plots emphasizes that diffusion was slower in spiny dendrites than in smooth dendrites (Fig. 3C). Linear fits to the data obtained for the two types of dendrite (Fig. 3D) produced an average value of d_w = 2.4 ± 0.2 (S.E.M.) for smooth dendrites (n = 9) and d_w = 7.3 ± 2.1 for spiny dendrites (n = 4), as shown in Fig. 3E. A t-test indicated that these two distributions differ significantly (p<0.001).

Figure 3.

Anomalous diffusion in Purkinje cell dendrites. (A) Time course of RD fluorescence after photorelease for all 6 experiments. Red lines indicate measurements from spiny dendrites (n = 4) and green lines indicate measurements from smooth dendrites (n = 9). Values are normalized to the intensity of RD fluorescence at the first time point after photorelease. (B) Time course of spatial variance changes measured in all experiments shown in (A). (C) Logarithmic transform of the data shown in (B). (D) Mean values of logarithmic transformed data from all experiments, showing normal diffusion in smooth dendrites and anomalous diffusion in spiny dendrites. Error bars indicate ± 1 S.E.M. (E) Mean values of anomalous exponent in smooth and spiny dendrites, extracted from all experiments. Error bars indicate ± 1 S.E.M.

Although these results suggest that the higher density of spines is responsible for the higher degree of anomalous diffusion in spiny dendrites, we considered alternative explanations. Previous work established that the branching pattern of the Purkinje cell dendrite cannot produce the anomalous diffusion observed in these cells (Santamaria et al., 2006). We additionally considered whether the calculated values of d_w were influenced by the shorter length of the spiny dendrites or by the smaller average diameter of these dendrites (or any other factor that scales with surface-to-volume ratio). However the values of d_w were correlated with neither the diameter of spiny dendrites (0.97 μm ± 0.17 S.E.M., with a range of 0.70 to 1.65 µm; r = -0.44, not significant) nor dendritic segment length (range of 8-18 μm; r = -0.09, not significant). Similarly, the final value of the total fluorescence along the dendrite did not correlate with the value of d_w (r = 0.30, not significant). Thus, the presence of spines seems to be the reason that anomalous diffusion is much more prominent in the spiny dendrites, as predicted by our computational simulations. This confirms and extends our previous conclusion that the presence of spines increases the degree of anomalous diffusion in Purkinje cell dendrites (Santamaria et al., 2006).

Anomalous diffusion in CA1 pyramidal cells is proportional to spine density

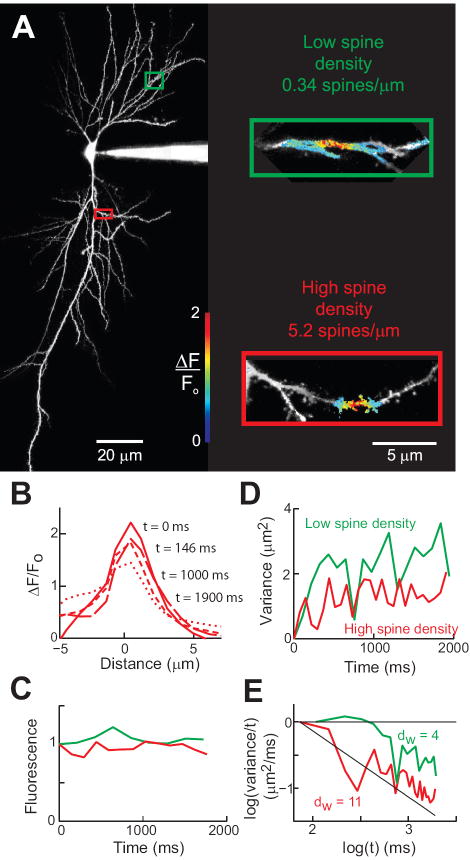
Using experimental techniques identical to those used to study diffusion in Purkinje cells, we next investigated the diffusional properties of hippocampal CA1 pyramidal cell dendrites. We specifically focused our efforts on testing the prediction of our modeling that the value of d_w in dendrites should depend linearly on the density of spines (Fig. 1D), taking advantage of the fact that spine density varies widely in pyramidal cell dendrites. As in the case of Purkinje cells, we insured that the image plane contained a large section of dendrite (SI Appendix Fig. S2). Figure 4 shows an example of such an experiment. After filling pyramidal cells with a mixture of caged RD and cBD (Fig. 4A), RD was photoreleased in two different dendrites of the same neuron (green and red rectangles in Fig. 4A). One of these dendrites had a low density of spines (0.34 spines/μm), while the other had a high density of spines (5.2 spines/μm). The photolysis of caged RD produced a Gaussian pattern of release that spread along the dendritic axis over time (Fig. 4B). Loss of molecules due to bleaching was not significant, as shown by the conservation of total amount of fluorescence along the scanned dendrite (Fig. 4C).

Figure 4.

Measuring intracellular diffusion in CA1 hippocampal pyramidal cells. (A) Maximum projection images of a pyramidal cell filled with cascade blue. Colored rectangles indicate areas enlarged at right. Inset - Photorelease of RD in dendrites with low (green) and high (red) densities of spines. Pseudocolor images indicate relative changes in RD fluorescence after a 5 ms long flash of UV light. The images were taken 108 ms (top) and 73 ms (bottom) after photorelease. (B) Spatial distribution of fluorescence along the high spine density dendrite in (A). (C) Normalized fluorescence after photorelease of RD (D) Time course of changes in spatial variance for the fluorescent profiles monitored along the dendrites shown in (A). (E) Logarithmic transform of the data shown in (B).

We tracked the fluorescent changes along the dendritic axes shown in Fig. 4A and used these fluorescence profiles to calculate the spatial variance of the signals at different times. Analysis of the spatial variance of the fluorescence of photoreleased RD shows that diffusion was faster in the dendrite containing few spines (Fig. 4A, green) than in the dendrite with high spine density (Fig. 4A, red). As a result, the spatial variance increased more slowly in the dendrite with the higher density of spines (Fig. 4D). The logarithmic transform analysis revealed that d_w was much smaller (3.9 ± 2.8, 95% confidence interval) in the dendrite with a low density of spines than in the dendrite with higher spine density (d_w = 11.8 ± 2.1; see Fig. 4E).

Analysis of comparable measurements from a total of 5 pyramidal cells indicated that spine density had a significant influence on d_w (Fig. 5). Spine density ranged from 0.3-6.1 spines/μm, with a mean of 2.74 ± 0.57 S.E.M. spines/μm. These measurements are in good agreement with previous reports based on electron microscopy (Megias et al., 2001; Fiala & Harris, 2007; Niu et al., 2008). The total fluorescence did not decrease significantly over time after photoreleasing RD (Fig. 5A), so that bleaching or loss of fluorescence outside the monitored volume did not influence the calculated spatial variance (for a detailed analysis of the influence of dendritic length on our measurements see SI Appendix Fig. S3). The spatial variance increased over time, with a more rapid spread of RD observed in dendrites with lower spine density (dark blue lines in Fig. 5B). From these measurements, d_w was calculated and had a mean value of 7.0 ± 1.1 S.E.M. However, d_w varied widely between dendrites and was correlated with the density of spines in the dendrites (Fig. 5C). This relationship was more evident when d_w was plotted as a function of spine density (Fig. 5D). As predicted by the simulations, the value of d_w was proportional to spine density and the relationship between the two parameters was well-fit (r = 0.74; p < 0.01) by a linear function (solid line in Fig. 5D; slope = 1.60 ± 0.03, 95% confidence interval), this correlation was also evident with the fraction of dendritic surface occupied by spines (SI Appendix Fig. S4). We found that the value of d_w measured in pyramidal cells was not significantly influenced by the average diameter of the dendrites (0.70 ± 0.10 S.E.M. μm, with a range of 0.38-1.42 μm; r = 0.08, not significant) or by dendritic length (range 11-19 μm; r = 34, not significant). As was the case for Purkinje cells, the final value of the total fluorescence along the dendrite did not correlate with the value of d_w (r = 0.16, not significant). Therefore, d_w only varied significantly with spine density. We therefore conclude that d_w depends on spine density, as predicted by the modeling.

Figure 5.

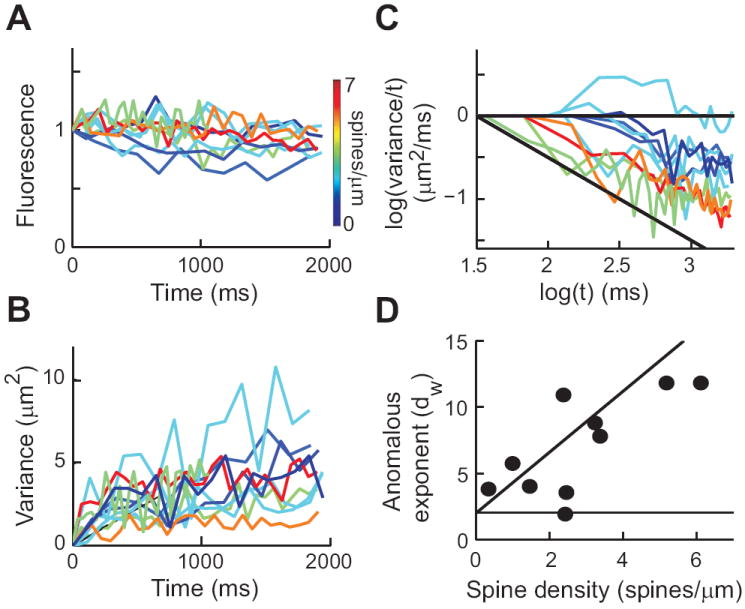
Anomalous diffusion in CA1 pyramidal cells. (A) Normalized fluorescence after photorelease of RD (n = 11 from 5 cells). Color scale indicates spine density measured for each pyramidal cell dendrite. (B) Plots of spatial variance against time for experiments shown in (A). (C) Logarithmic transform of data in (B). (D) Relationship between spine density and calculated d_w for each experiment.

COMPARING DIFFUSION IN PURKINJE AND CA1 PYRAMIDAL CELLS

Direct comparison of the results obtained in pyramidal and Purkinje cells is difficult because the small size of Purkinje cell spines makes it difficult to determine their density reliably. For Purkinje cell spine density, we used a value of 3.74 spines/μm obtained using confocal imaging of mouse Purkinje cells (Vecellio et al., 2000); this number could be an underestimate (Shigemoto et al. Society for Neuroscience Abstracts 551.17, 2010). The larger size of pyramidal cell spines allowed us to use our measured mean value of 2.74 ± 0.57 S.E.M. spines/μm, which is very similar to a previously published value (Konur et al., 2003). Thus, to compare measurements made in the two neuron types, we assumed that the average value of d_w of 7.3 measured in Purkinje cell spiny dendrites corresponds to an average density of 3.74 spines/μm in these dendrites (Vecellio et al., 2000). Interpolation of the linear fit of our pyramidal cell data (Fig. 5D) to a density of 3.74 spines/μm yields a value of 7.9 for d_w, which is practically identical to the value measured in Purkinje cell spiny dendrites. Therefore, we conclude that pyramidal and Purkinje cells have similar values of d_w at a given spine density as predicted by our simulations (Fig. 1D).

DISCUSSION

Using a combination of flash photolysis and two-photon imaging, we found that spines cause anomalous diffusion in dendrites of two very different neuron types. Specifically, we confirmed our modeling-based predictions that anomalous diffusion is linearly proportional to spine density and, surprisingly, that this dependence is very similar in Purkinje and hippocampal pyramidal cells. Our work therefore indicates that spines generate anomalous diffusion regardless of neuron type.

Anomalous diffusion in neurons

Our results show that anomalous diffusion occurs in both Purkinje and pyramidal cells and can last for at least several seconds. Our computational model of diffusion in dendrites indicates that such anomalous diffusion is caused by trapping of molecules in dendritic spines. We tested and confirmed three predictions of the computational model. First, measurements of d_w in Purkinje cells confirm that these cells have two dendritic compartments where diffusion of soluble molecules is very different: in smooth dendrites diffusion is almost normal, while in spiny dendrites it is highly anomalous. Thus, the degree of anomalous diffusion is correlated with the presence of spines. Second, in pyramidal cells, we considered dendrites with a wide range of spine densities and found that d_w was linearly correlated with spine density. Third, we found that the values of d_w were similar at a given density of spines, as predicted by the modeling. This result may be caused by the fact that the ratio of head volume to spine neck radius is practically identical in both pyramidal and Purkinje cells (SI Fig. S1I-J). Together, these results provide strong evidence that anomalous diffusion is caused, at least in part, by spines serving as molecular traps to retard diffusion.

With two-photon imaging, we had the advantage of minimizing the potential effects of photobleaching that would reduce the signal-to-noise ratio over long acquisition times, as well as being able to image diffusion in dendrites embedded deep with the slice. With this technical approach, we obtained values of d_w for Purkinje cells that are very similar to those determined using a different caged compound and a different (confocal) fluorescence microscope (Santamaria et al., 2006). Although the measured d_w was slightly lower in the current experiments, we suspect that this is due to the slower scanning rates (5-27 frames/sec) of the two-photon microscope that we used here, compared to the high-speed confocal (120 frames/sec) that we used previously; a discussion of the effect of acquisition rates on measurement of anomalous diffusion is provided by Saxton (1994); see also Ritchie et al. (2005). In our conditions it was difficult to monitor diffusion of uncaged fluorophores in dendritic segments over distances longer than a couple tens of microns. However, our models and experiments suggest that molecules could experience anomalous diffusion over longer distances and for longer periods of time.

Functional significance of anomalous diffusion

Our new results show that spines generate anomalous diffusion in dendritic arbors in at least two types of neurons. Because dendritic spine density varies between all types of neurons, it is likely that such differences will be translated into differences in dendritic diffusion. It is possible that, in combination with active sequestration/transport mechanisms (Schmidt et al., 2007b), molecular trapping by dendritic spines may regulate and target intracellular signaling processes in all neurons that possess spiny dendrites.

Our measurements reveal that different dendrites have different amounts of anomalous diffusion, depending on the density of spines. Because anomalous diffusion produces a time-dependent slowing of the diffusion coefficient of molecules, these differences will allow different types of dendrites to integrate intracellular signals to different extents. For example, the average value of 2.2 for d_w in smooth dendrites of Purkinje cells means that in 90 seconds a molecule with a diffusion coefficient equal to that of RD can spread $R_{\mathit{ct}}=\sqrt{2\cdot 0.08\cdot {90000}^{2/2.4}}=46\mu \mathrm{m}$, while such a molecule could diffuse only 1.9 μm in spiny dendrites of these cells. A similar calculation for the average value of d_w in pyramidal cells (7.0) indicate a diffusion range of 2.0 μm over this time. Thus, chemical signals can be integrated over a much larger range in smooth dendrites because of the reduced amount of anomalous diffusion.

Spine shape and density can change dynamically. For example, extension, retraction, and collapse of dendritic spines occurs during development (Segal, 2002) and such structural changes could help concentrate molecules through anomalous diffusion mechanisms. This would permit enrichment of molecules needed for the consolidation of dendritic structure and network function. In addition, dynamic changes in spine volume occur during induction of long-term synaptic plasticity (Lang et al., 2004; Matsuzaki et al., 2004; Zhou et al., 2004; Tanaka et al., 2008) and would be expected to change the trapping of signaling molecules by those spines. In summary, it is likely that neurons use structural changes at multiple levels - both acute and long-term - to employ anomalous diffusion as a mechanism for regulating the spread of chemical signals along dendrites and the subsequent sharing of these chemical signals among synapses.