Analysis of Biomarker Data: logs, odds ratios and ROC curves

Abstract

Purpose of review

We discuss two data analysis issues for studies that use binary clinical outcomes (whether or not an event occurred): the choice of an appropriate scale and transformation when biomarkers are evaluated as explanatory factors in logistic regression; and assessing the ability of biomarkers to improve prediction accuracy for event risk.

Recent findings

Biomarkers with skewed distributions should be transformed before they are included as continuous covariates in logistic regression models. The utility of new biomarkers may be assessed by measuring the improvement in predicting event risk after adding the biomarkers to an existing model. The area under the receiver operating characteristic (ROC) curve (C-statistic) is often cited; it was developed for a different purpose, however, and may not address the clinically relevant questions. Measures of risk reclassification and risk prediction accuracy may be more appropriate.

Summary

The appropriate analysis of biomarkers depends on the research question. Odds ratios obtained from logistic regression describe associations of biomarkers with clinical events; failure to accurately transform the markers, however, may result in misleading estimates. Whilst the C-statistic is often used to assess the ability of new biomarkers to improve the prediction of event risk, other measures may be more suitable.

Introduction

Biomarkers may be used to investigate potential biological mechanisms, to improve diagnosis or assessment of prognosis, or as surrogate endpoints in studies. We restrict this review to studies that use binary clinical outcomes (i.e., whether or not an event occurred), and biomarkers that are measured on a continuous scale (i.e., can take any value within a certain range). We consider two narrowly defined problems: (i) the choice of an appropriate transformation and scale when biomarkers are evaluated as explanatory factors in logistic regression; and (ii) assessing improvements in prediction accuracy when new biomarkers are added to an existing model. Our examples focus on biomarkers that are associated with increased risk of cardiovascular disease, an area of interest in HIV research.[1,2,3,4]

Biomarkers as explanatory factors in logistic regression

Logistic regression is widely used to evaluate associations of biomarkers with binary outcomes. Investigators must decide whether to include the biomarkers as continuous or categorical covariates. Biomarkers that have heavily skewed distributions should be “normalized” before they can be included as continuous covariates; often, this can be achieved by a log transformation. In this section, we give an example where highly sensitive C-reactive protein (hsCRP) needs to be log-transformed when included as a continuous covariate, and discuss scaling and categorizing covariates.

Transforming continuous biomarkers: the log scale

When biomarkers are included as continuously-valued covariates in logistic regression, the model makes the implicit assumption that the biomarker follows a Normal (Gaussian) distribution among individuals who experience the event (“cases”), and also among those without the event (“controls”).[5,6]. While many biomarkers have heavily skewed distributions, values on the log scale often approximate the Normal curve reasonably well; in these cases, the biomarker should be log-transformed in order to obtain reliable odds ratio (OR) estimates.

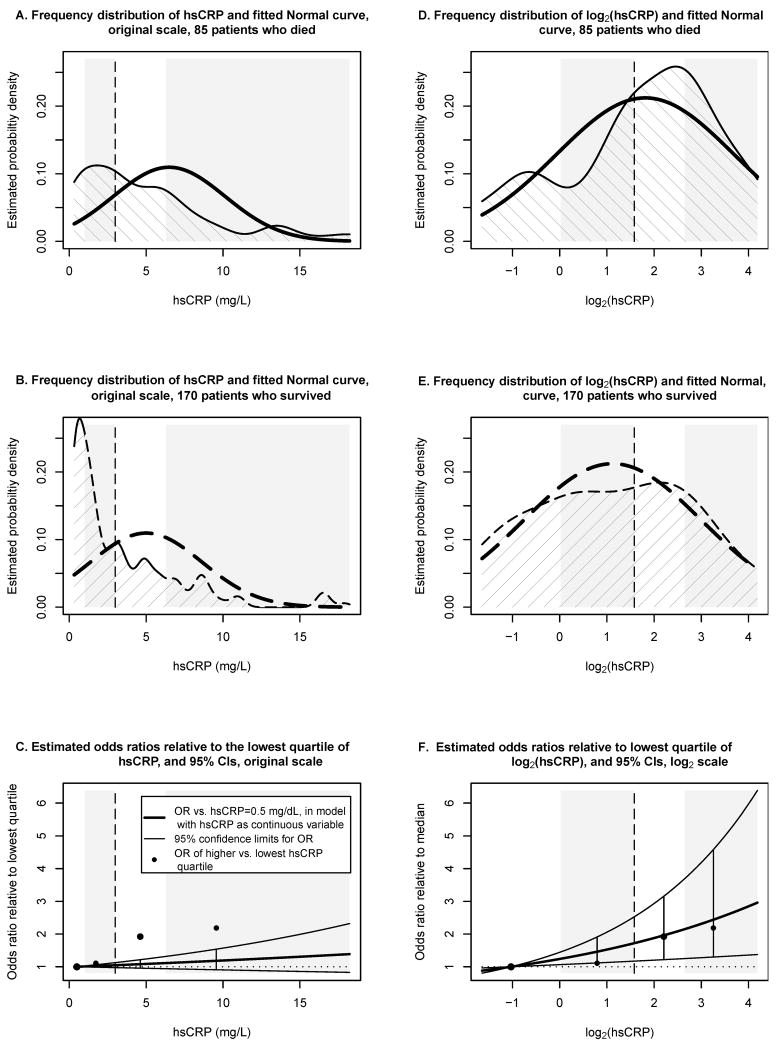
To illustrate the impact of skewed biomarker distributions, we re-analyzed the data of a case-control study with 255 participants that investigated associations of hsCRP and other biomarkers with all-cause mortality.[1] Figure 1 shows the frequency distribution of hsCRP for the 85 participants who died (cases, panel A) and 170 participants who survived (controls, panel B), along with the fitted Normal curves (bold lines). The distributions of hsCRP for cases and controls are both heavily skewed, and the Normal curves are a poor fit. As visual guides, the vertical line marks the median hsCRP for all 255 participants and the gray and white rectangles show the four quartiles.

Figure 1. Distributions of hsCRP and log₂(hsCRP), and estimated odds ratios in a case-control study.[1].

Panel A shows the frequency distribution of hsCRP for 85 participants who died, panel B the distribution of hsCRP for 170 participants who survived. Bold lines show the fitted Normal curves. The dashed vertical line marks the median hsCRP for all 255 participants, white and gray rectangles mark the four hsCRP quartiles. HsCRP ranged from 0.2 to 82.7 mg/L; the lowest and highest 5% were not displayed, but included in the analyses. Panel C shows odds ratios estimates (bold solid line) and 95% confidence limits (lighter lines above and below) obtained in a logistic regression model with continuous hsCRP; odds ratios are relative to hsCRP=0.5 mg/L, the median of the lowest hsCRP quartile. Circles mark direct odds ratio estimates comparing higher hsCRP quartiles to the lowest quartile. Confidence intervals do not contain the direct estimates, which indicates poor model fit for the logistic regression with continuous hsCRP. Panels D-F shows the corresponding analyses for log₂(hsCRP); distributions of log₂(hsCRP) are closer to Normal. The direct estimates are closer to the 95% confidence intervals by logistic regression, indicating better model fit and more reliable inference when analyzing hsCRP on the log₂ scale.

Abbreviations: hsCRP, highly sensitive C-reactive protein

Figure 1C demonstrates that OR estimates are incorrect when hsCRP is used on the original measurement scale. The bold solid line shows the estimated OR of death for patients with a given hsCRP value relative to patients with hsCRP=0.5 mg/L (the median of the lowest hsCRP quartile). For example, for patients with hsCRP=9.6 mg/L, the estimated OR is 1.18 (the odds of death are estimated to be 18% higher for these patients, than for patients with hsCRP=0.5). The lighter lines above and below show 95% confidence limits computed from the same model.

In contrast, the solid circles denote ORs estimated directly by considering the proportions of patients who did or did not die in each of the three higher hsCRP quartiles and comparing these to the proportions in the lowest quartile. The direct estimates differ substantially from those estimated by the model; none of the direct estimates are contained in the respective confidence intervals from the model. Using the logistic regression model, we would substantially underestimate the ORs for the two highest quartiles, and would overstate the precision of the OR estimates, since the computed confidence intervals are too narrow.

Note that the logistic regression model assumes a linear relationship between the covariate and the log-odds of death; in our example,

$$log\left(\frac{P_{\text{hsCRP}}}{1-P_{\text{hsCRP}}}\right)=a+b\times \text{hsCRP},$$

where p_hsCRP is the probability of death for a patient with a given hsCRP value, and (1-p_hsCRP) is the probability of survival. The linear relationship only holds, however, when the distributions of hsCRP are Normal for cases and controls.[5]

Figures 1D and 1E show the distributions of log₂(hsCRP) and the corresponding fitted Normal curves; the distributions of log₂(hsCRP) more closely approximate Normal curves than the untransformed hsCRP values. Consequently, the logistic model with log₂(hsCRP) more accurately describes the data (Figure 1F), and provides more reliable confidence intervals and p-values.

The authors of the original case-control study used log₁₀(hsCRP). We prefer logarithms to the base 2, as this allows for a more intuitive interpretation of the ORs: each one unit increase in log₂(hsCRP) corresponds to a doubling in hsCRP. The choice of the logarithmic base does not influence the model fit; Figure 1F would look exactly the same for log₁₀(hsCRP), except that the scale of the horizontal axis would be multiplied by a constant.

As translating results to the original scale when analyses were performed on a log or otherwise transformed scale is cumbersome, investigators may be tempted to avoid using transformations. However, failure to transform biomarkers when appropriate to do so may lead to incorrect answers.

Standardizing biomarkers

When incorporating biomarkers as continuous-valued covariates, associations are reported as OR per unit increase in the marker. If the aim of the analysis is to compare the potential value of several biomarkers measured on different scales, many investigators choose to report ORs that describe the increased odds of the event per 1 standard deviation (SD) of the biomarkers.[7*,8*] The distribution of biomarkers may vary across studies, however, particularly when study populations are different. Thus, in order to facilitate comparisons across different studies, it is essential that investigators also report the value of the SD in the manuscript. This will also permit readers to translate results into units that are relevant for clinical practice.

As an alternative, some authors report ORs per 1 inter-quartile range (IQR) increase.[1] In general, there is no clear preference for either approach. However, when outliers are present, the IQR tends to be less sensitive to outliers and is preferable.

Incorporating continuous biomarkers as categorical covariates

In some instances, investigators may prefer to categorize biomarker values and report ORs that compare the odds of the event in each category to those in some reference category. For example, hsCRP is often analyzed using clinically relevant thresholds (e.g., <1, 1-3, and >3 mg/L), or may be broken into quartiles (four equally sized groups), tertiles, or quintiles.[9*] Categories by equally sized groups are particularly useful when several biomarkers are being compared.

Categorizing biomarkers has advantages and disadvantages. Most importantly, when the relationship between the risk (log-odds) and the biomarker is nonlinear, then including the biomarker as a continuous covariate in the logistic regression model would give incorrect OR estimates, while estimation of ORs for categories would capture the relationship correctly. Categorization therefore provides an alternative approach for the analysis of highly skewed biomarkers for investigators who do not wish to use transformations. If the linear relationship is correct, however, analyzing the biomarker as a continuous covariate will have greater power.

Evaluation of biomarkers as prognostic markers

ORs and hazard ratios are useful for explaining the prevalence of clinical events in a given cohort; they are ill-suited, however, to provide guidance as to whether a new biomarker should be used in routine clinical practice. For example, treatment guidelines for high cholesterol consider three levels of 10-year risk of coronary heart disease (CHD), <10% (low risk), 10-20% (intermediate), and >20% (high), estimated by modified Framingham risk scores (Adult Treatment Panel III); [10,11,12]. Whilst there is strong evidence that increased hsCRP is independently associated with a higher risk of CHD [9*,13**,14], knowledge of the hsCRP level provides only limited improvements to our ability to correctly predict whether or not an individual will develop CHD.[13**,14,15] Popular measures of classification accuracy include the area under the curve (AUC) of the receiver operating characteristic (ROC) curve and reclassification measures.[9*,13**,8*,16**, 17*] Other measures assess improvement in the prediction of risk on a continuous scale.[18*,19]

ROC curves and C-statistics

ROC curves are a visual means to describe the ability of a model to correctly classify “cases” and “non-cases”. Assume that we have fitted a model for the risk of an event, and will predict that an individual will experience an event if his/her estimated risk is above a given threshold, c. Ideally, our prediction should have both high sensitivity (it should correctly identify a high proportion of true cases – those who will experience an event) and high specificity (it should correctly identify a high proportion of true non-cases). However, in practice, there is a trade-off between the two, depending on the threshold. The ROC curve plots the sensitivity of our prediction rule against one minus the specificity, for all possible values of the threshold.

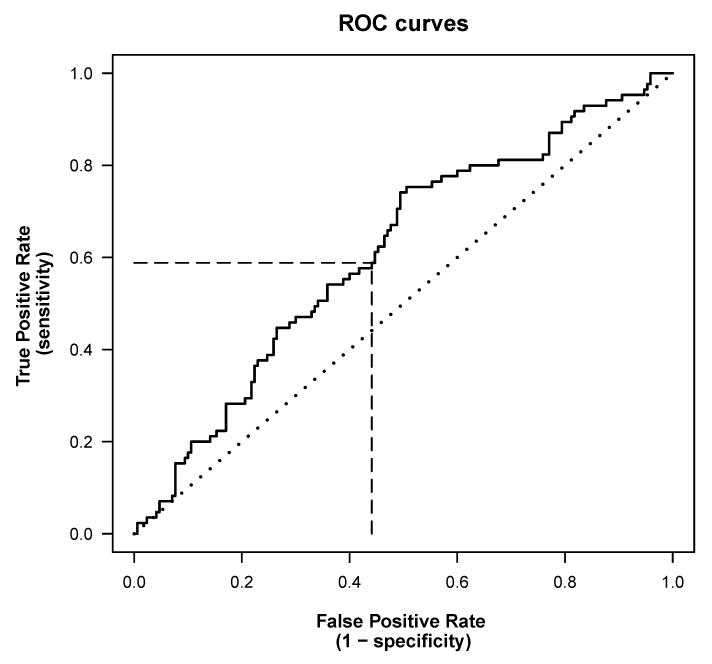
Figure 2 shows a ROC curve for predicting death based on hsCRP, using data from the case-control study described earlier.[1] The dotted diagonal line is the ROC curve for guessing the outcome at random; any sensible prediction model should have a ROC curve to the left of the diagonal line; better models will have curves closer to the upper left corner of the graph.

Figure 2. Receiver operating characteristic (ROC) curves.

The solid line shows an estimated ROC curve for the univariate prediction rule “predict death if baseline hsCRP > c”, calculated for data from a case-control study with 255 participants [1]; higher hsCRP was associated with a higher risk of death. The threshold c determines both the true prediction rate (TPR) and false prediction rate (FPR), and the estimated ROC curve plots the TPR versus the FPR for all possible values of c. When the threshold is at the median hsCRP, c=3.0 mg/L, the TPR is 0.59 and the FPR is 0.44 (dashed lines); this means, 59% of cases and 56% of controls are classified correctly. The C-statistic is the area under the ROC curve. The diagonal dotted line represents the ROC curve for random guessing.

Abbreviations: FPR, false prediction rate; hsCRP, highly sensitive C-reactive protein; ROC, receiver operating characteristic; TPR, true prediction rate

The C-statistic is the area under the ROC curve.[20,16**,21**] It summarizes the sensitivity/specificity trade-off of a risk prediction model over all possible thresholds, c, into one number. The C-statistic for random guessing (e.g., the diagonal line in Figure 2) would be 0.5; perfect discrimination corresponds to a C-statistic of 1. C-statistics have been used extensively to assess the utility of biomarkers for improving classification accuracy, by comparing C-statistics for risk prediction models fitted with and without the biomarker.[8*,9*,13**,15,22*] Reasons for the popularity of the C-statistic include:

1. The C-statistic has an intuitive interpretation: if two individuals are selected at random, one with the event and one without, then the C-statistic is the probability that the model predicts a higher risk for the individual with the event.[16**,23]

2. C-statistics don't depend on measurement units, and thus provide a common scale for comparing different markers.[23**]

3. Statistical tests for differences in C-statistics are available in commercial software.[24,25]

Recently, several authors have warned against indiscriminate use of the C-statistic to assess the predictive utility of biomarkers.[16**,21**,26*,27,28*] The C-statistic is relatively insensitive to the added contribution of a new marker when the two models, with and without biomarker, estimate risk on a continuous scale, because the C-statistic is based on the rank-order of the predicted risks for cases and non-cases, rather than the size of these predicted risks [16**,23] – if the threshold for predicting an event is set at 50%, and addition of the biomarker increases the estimated risk for an individual from 1% to 49%, the individual will still be classified as non-case. In fact, many new biomarkers provide only minimal increase in the C-statistic when added to the Framingham model for CHD risk.[9*,29] In clinical practice, however, the size of the predicted risk may be important.[16**] Also, the classical C-statistic assumes that high sensitivity and high specificity are equally desirable. This is not always the case – for example, when screening the general population for a low-prevalence outcome requiring invasive follow-up, high specificity is important, while cancer screening in a high-risk group would emphasize high sensitivity.[21**,26*]

To achieve a noticeable increase in the C-statistic, a biomarker must have a very strong independent association with the event risk (say ORs of 10 or higher per 1 SD increase). The reason is that the biomarker values for cases and non-cases will largely overlap for moderate ORs (see figure 2 in reference [21**]), indicating low power for discrimination.[21**,30*] In a recent study of 10 biomarkers in 3209 participants in the Framingham Heart Study, the biomarkers were summarized into a multimarker score; after adjustment for conventional risk factors, participants in the highest quintile of the score had a 4.08-fold risk of death compared with participants in the lowest two quintiles. Adding the biomarkers to the conventional risk factors, however, had minimal impact on the C-statistic, which increased from 0.80 to 0.82.[8*]

ROC curves do not provide the probability that a patient who is classified as high risk will develop the disease; this strongly depends on the disease prevalence in the investigated population. If improvement in predicting the actual risk is the goal, measures of reclassification accuracy [31**,28*,22*,17*] or model calibration [32**,23,33] are more appropriate.

Risk reclassification measures

Measures of reclassification accuracy are most useful when predefined, clinically meaningful risk categories are available (e.g., classification of 10-year risk of CHD as low [<10%], intermediate [10-20% ] or high [>20% ]). The U.S. Preventive Services Task Force assessed the utility of hsCRP and other biomarkers for predicting risk of CHD based on reclassification; they estimated that 11% of men in the intermediate-risk group would be reclassified as having high risk if information about hsCRP were added to the traditional Framingham risk factors, and predicted the number of CHD events that could be averted with intensive therapy for those men. [13**,14] The task force focused on the intermediate-risk group because reclassification from this group had the highest potential impact on therapy decisions.[14]

Several studies found that adding hsCRP to traditional risk factors had only minimal effect on the C-statistic, but resulted in improved classification when several risk categories were used. [9*,17* ] Summarizing reclassifications in a clinically meaningful way, however, is challenging, and depends on the question at hand. Ridker et al. (2007) used 4 categories for CHD risk; adding hsCRP and parental history to a standard model resulted in reclassification of 8% of individuals.[22*] Among those who were reclassified into the highest risk category (>20% risk), the estimated event rate was 31%, which was interpreted as evidence for improved risk prediction. Pencina et al. (2008) argued that the new model would improve risk classification only for 31 out of 100 persons, while 69 persons should have remained in the lower risk categories. They suggest measuring net reclassification improvement (NRI), rewarding correct reclassification and penalizing incorrect reclassification.[31**] Their integrated discrimination improvement (IDI) is an extension that does not depend on the cut-offs for risk categories. Gu and Pepe (2009) provide an extensive overview of measures for improved risk prediction; they also propose measures which consider the predicted risk on a continuum.[18*]

Melander et al. (2009) assessed 6 biomarkers for changes in C-statistics, NRI, IDI, and reclassification; improvements in risk prediction for the intermediate-risk group were mostly due to down-classification.[7*] The considered summary measures, however, don't distinguish between correct up-classification or down-classification, while clinical consequences may differ substantially; one solution may be to weigh reclassifications to reflect their clinical importance.[26*,32**] Table 1 summarizes several measures that have been used to assess improvements in risk prediction; see also [32**].

Table 1. Measures used to assess biomarkers for improvement in risk prediction.

Target and measure	Comments
Classification of subjects into risk categories
Proportion of subjects who are reclassified when adding the biomarker to an existing model [17]	Includes both correct and incorrect reclassifications
Net reclassification improvement (NCI) [31,32,26]	Rewards correct and penalizes incorrect reclassification; does not distinguish between up- and down-classification
Reclassification table: cross-tabulation of the proportion of subjects who are classified into each risk category by the models with and without biomarker, and comparison of the observed event rate with the assigned risk category. [28,19,32,17]	Straightforward, clinically relevant interpretation; no clear ordering of models; sensitive to choice of risk categories.
Discrimination accuracy
C-statistic (area under the ROC curve) [16,20,21]	Insensitive to moderate improvements in risk prediction; may not be clinically relevant
Integrated discrimination improvement (IDI) [31,26]	Extension of the NCI; does not depend on cut-points for risk categories
Graphical presentation
Plot of predicted risk against the risk percentile for models with and without the biomarker [19,18,15,16]	Intuitively, a stronger model should show a wider spread of predicted risks; does not measure the accuracy of the risk prediction [16]
Model calibration
Hosmer-Lemeshow statistic [32,33,23,17]	Compares estimated with observed proportions of subjects with events over several risk intervals; may be too sensitive in large samples. [32]
Global model fit
Akaike information criterion (AIC), and Bayesian information criterion (BIC) [32,23,17]	Widely used for variable selection; no direct clinical interpretation

Abbreviations: ROC, receiver operating characteristic, NCI, net reclassification index

Conclusion

The proper way to assess the utility of a biomarker depends on the research question. ORs obtained from logistic regression are useful for explaining associations of biomarkers with clinical events; failure to accurately transform the markers, however, may result in misleading estimates. Whilst the C-statistic is often used to assess the ability of new biomarkers to improve the prediction of event risk for individuals, other measures may be more appropriate.