Abstract
Purpose
Unique uptake and retention mechanisms of PET hypoxia tracers make in vivo comparison between them challenging. Differences in imaged uptake of two common hypoxia radiotracers, [61Cu]Cu-ATSM and [18F]FMISO, were characterized via computational modeling to address these challenges.
Materials and methods
An electrochemical formalism describing bioreductive retention mechanisms of these tracers under steady-state conditions was adopted to relate time-averaged activity concentration to tissue partial oxygen tension (PO2), a common metric of hypoxia. Chemical equilibrium constants of product concentration to reactant concentration ratios were determined from free energy changes and reduction potentials of pertinent reactions reported in the literature. Resulting transformation functions between tracer uptake and PO2 were compared against measured values in preclinical models. Additionally, calculated PO2 distributions from imaged Cu-ATSM tracer activity concentrations of 12 head and neck squamous cell carcinoma (HNSCC) patients were validated against microelectrode PO2 measurements in 69 HNSCC patients.
Results
Both Cu-ASTM and FMISO modeled PO2 transformation functions were in agreement with preclinical measured values within single deviation confidence intervals. High correlation (r2=0.94, p<0.05) was achieved between modeled PO2 distributions and measured distributions in the patient populations. On average, microelectrode hypoxia thresholds (2.5 mmHg and 5.0 mmHg) corresponded to higher Cu-ATSM uptake (2.5 and 2.0 SUV) and lower FMISO uptake (2.0 and 1.4 SUV). Uncertainties in the 1 models were dominated by variations in the estimated specific activity and intracellular acidity.
Conclusions
Results indicated that the high dynamic range of Cu-ATSM uptake was representative of a narrow range of low oxygen tension whose values were dependent on microenvironment acidity while FMISO uptake was representative of a wide range of PO2 values that were independent of acidity. The models shed light on possible causes for these discrepancies, particularly as it pertains to image contrast, and may prove to be a useful methodology in quantifying relationships between other hypoxia tracers. Comprehensive and robust assessment of tumor hypoxia prior to as well as in response to therapy may be best-provided by imaging of multiple hypoxia markers that provide complementary rather than interchangeable information.
Keywords: hypoxia, Cu-ATSM, FMISO, PET, PO2, Eppendorf, electrochemical model
Introduction
The definition of tumor hypoxia is multifaceted, ranging from a simple physiological absence of molecular oxygen in tumor cells [1] to a major factor in complex molecular pathways whose upregulation is associated with aggressive tumor phenotypes [2]. Hypoxia-induced malignant tumor phenotypes act as powerful prognosticators for treatment outcome, making hypoxia surrogates highly attractive targets for functional imaging and biologically-guided therapy.
Numerous surrogates exist which are used to assess tumor hypoxia [3]. The most direct measure is the Eppendorf polarographic microelectrode, which gained prognostic value within a multi-center clinical trial of head and neck cancer patients where outcome was successfully stratified by pre-treatment measurements of oxygen tensions below a fixed threshold of 2.5 mmHg [4]. Despite its clinical utility, this invasive technique does not provide spatial information on intra-patient variations in hypoxia, as measurements are not equally sampled in space but instead are sampled along linear tracks through the lesion. Histological staining of tissue biopsies allows visualization of the spatial distribution of hypoxia markers at the cellular scale [5]. Exogenous markers of hypoxia include pimonidazole, a nitroimidazole chemical compounds that is reduced and retained in hypoxic cells. Endogenous markers include hypoxia inducible factor 1 subunit alpha (HIF-1α, regulation of cell oxygenation status), carbonic anhydrase 9 (CA-9, maintenance of microenvironment acidity), glucose transporter 1 (GLUT-1, glycolytic metabolism) and osteopontin (OPN, plasma hypoxia marker). However, this method fails to provide information on the temporal evolution of these markers throughout the tumor volume as visualization is limited to a finite number of core samples.
Non-invasive volumetric imaging of hypoxia is becoming more prevalent for in vivo visualization and quantification over four space-time dimensions [6]. Imaging of specific radiotracer surrogates of tumor hypoxia with positron emission tomography (PET) include radiolabeled fluoromisonidazole ([18F]FMISO) and radiolabeled copper(II) diacetyl-di(N4-methylthiosemicarbazone) ([61,64Cu]Cu-ATSM). Shown in Figure 1, FMISO is taken up intracellularly due to its high lipophilicity, where it undergoes a reversible single electron reduction that is catalyzed by nitroreductase (NR) enzymes in the mitochondrial electron transport chain [7]. In the presence of molecular oxygen, the reduced tracer is oxidized back to a chemically inert state, while in its absence is trapped via binding to macromolecules [7–8]. Preclinical FMISO images have shown general agreement with pimonidazole and Eppendorf measurements [9], but this result is not well-preserved over time [10] and could not be translated to clinical measurements [11]. Slow washout of FMISO in normal tissues hampers the achievable image contrast [12]. Moderate correlation of pre-treatment FMISO uptake above standardized uptake values (SUV) of 1.1 or maximum tissue-to-blood ratio (T/Bmax) of 1.6 with outcome was demonstrated in head and neck patients and proved significantly more prognostic than pre-treatment FDG metrics [13–14].
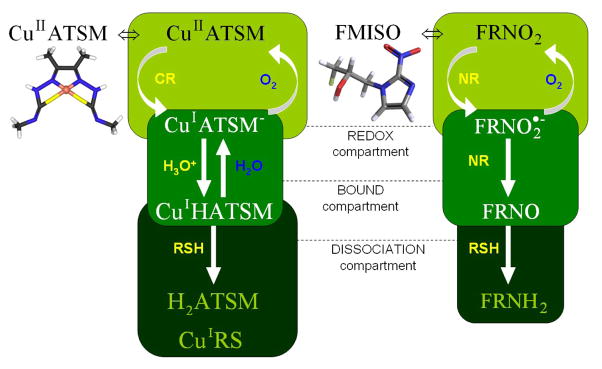
Figure 1. Chemical compartment schematic of the Cu-ATSM and FMISO retention mechanisms in hypoxic tumor cells.
The free tracer passively diffuses into cells and is reduced either by specific microsomal cytochrome reductases (CR) or more indiscriminate mitochondrial nitroreductases (NR) in the redox compartment. The reduced tracer is preferentially reoxidized by molecular oxygen in normoxic cells, while under hypoxic conditions it is protonated (Cu-ATSM) or further reduced (FMISO) in the bound compartment. Cu-ASTM is dissociated by reactive chemical species (RSH), while FMISO aliphatic and ring labels bind to intracellular macromolecules [15–16,26,30].
Cu-ATSM uptake and retention, shown in Figure 1, is dependent on a bioreductive mechanism that differs from nitroimidazoles. Its lipophilicity from planar molecular geometry allows for rapid passive uptake in tumor cells, where it is preferentially reduced by cytochrome reductase (CR) enzymes forming the microsomal electron transport chain [15]. The low reduction potential of this tracer resulting from methylation ensures selective retention in hypoxic cells [16]. Further entrapment is dependent on protonation of the unstable reduced state, followed by reactive thiol mediated dissociation [17]. High image contrast has been achieved between normal and hypoxic tissues, yielding mean Cu-ATSM SUV greater than 3, and was shown to be more sensitive to changes in oxygenation than FMISO in certain pre-clinical models [18]. Investigations implementing other pre-clinical models, however, have reported tumor cell line dependent-uptake along with a lack of co-localization with FMISO at early time points [9]. Nevertheless, its clinical relevance stems from observations that pre-treatment Cu-ATSM tumor-to-muscle ratio (T/M) was predictive of poor clinical outcome in cervical cancer patients and lack of clinical response to therapy in lung cancer patients [19–20]. The effectiveness of Cu-ATSM as an indicator of malignant tumor phenotypes may stem from its reliance on a particular reductive enzyme, NADP(H)-Cytochrome P-450 Reductase (CPR), which was discovered to play an integral role in the transcriptional activation of the HIF-1 pathway [21].
The aforementioned studies have concluded that molecular markers of hypoxia such as FMISO and Cu-ATSM are not identical surrogates. Challenges associated with the translation of well-controlled preclinical experiments to clinical settings repeatedly confound the quantitative interpretation of these surrogates. Without specific knowledge of underlying differences in uptake and retention mechanisms of tracers, direct comparisons continue to yield an inconsistent assessment of tumor hypoxia and therefore limit clinical utility. Modeling these mechanisms may provide a cost-effective means of comparing tracers quantitatively and serve as a guide in the design of future experiments seeking to characterize relationships between surrogate markers and clinical endpoints in patient populations.
Investigators have attempted to derive mechanisms of action from empirical studies that rely primarily on pharmacokinetic models. Although dynamic imaging data can decouple perfusion and permeability at early time points from specific retention at later time points, several assumptions and limitations still persist with these compartmental models. For instance, the number of compartments and reversibility of transfer between compartments must be decided based on a priori knowledge of each hypoxia tracer, which can contribute large uncertainties to any derived relationships between kinetic parameters and oxygenation status [22]. Segmentation errors in the image-derived input function from noisy early dynamic frames create large variability in kinetic parameter estimates at the voxel-scale, which can be mitigated by averaging over regions of interest whose mean values correlate to time-averaged uptake [23]. Acquisition of dynamic data sets is also rather cumbersome in a clinical setting, particularly for tracers with long biological half lives, which require serial imaging sessions that are subject to errors in patient setup.
An alternate and less conventional approach to deriving relationships between hypoxia tracers is founded on basic physical and chemical principles under steady-state conditions, which equate relative tracer concentrations through chemical equilibrium constants. Since the methodology does not rely on image-derived free parameters, it can be broadly applied to a set of tracers used in the acquisition of static image data. The aim of this study is to employ such a method to compare imaged Cu-ATSM and simulated FMISO uptake distributions relative to variations in tissue oxygenation. An electrochemical model quantifying their relationships is first described, followed by its validation against measured pre-clinical and clinical data, and lastly its application to time-averaged PET images of patients.
Electrochemical model of bioreductive retention mechanisms
The model is predicated on relating imaged Cu-ATSM and FMISO uptake to local tissue oxygenation under steady-state conditions, which requires imaging at time points when changes in bound tracer concentration over time due to washout or dissociation are insignificant. Under these assumptions, chemical kinetic and thermodynamic equations can be adopted that describe relative concentration ratios between products and reactants of a given chemical reaction. The model proceeds through three distinct steps: relating tracer activity concentration to tracer molar concentration, relating tracer concentration to oxygen concentration, and relating oxygen concentration to oxygen tension.
Relating activity concentration to molar concentration
Activity concentrations of a radionuclide can be converted to molar concentrations of a tracer of interest via the specific activity of the radiolabeled compound. Following physical decay, branching ratio, and scanner specific calibration corrections, reconstructed image voxels display a representation of the mean radiotracer activity concentration at each time point of a given acquisition frame. The relationship between this measured activity concentration and the molecular concentration is dependent on the manner in which the radiotracer is produced. End of bombardment radionuclide specific activities and consequent end of synthesis radiotracer specific activities can be determined from cyclotron machine parameters, target parameters, and chemical assay results. Once the specific activity and activity concentration have been time-corrected, the mean molar concentration of the tracer can be calculated by their quotient. The simple calculation is used to convert [61Cu]Cu-ATSM or [18F]FMISO activity concentration to Cu-ATSM or FMISO molar concentrations, respectively:
| (1) |
The molar concentration M in units of mol/L equates to the division of activity concentration [A] in units of MBq/L by the specific activity SA of the chemical compound in units of MBq/mol. This relationship holds true given that the radionuclide and tracer are in near perfect stoichiometric proportions following decay correction to a reference time [24]. From the reported specific activity of [64Cu]Cu-ATSM at the end of synthesis using high performance liquid chromatography, the relative yield of 61Cu compared to 64Cu at the end of bombardment, and the radiochemical purity, the specific activity of [61Cu]Cu-ATSM can be calculated [24]. Similar analysis can be applied to a specific activity calculation of [18F]FMISO from recent reported measurements [25].
Relating tracer concentration to oxygen concentration
Biochemical retention mechanisms of Cu-ATSM and FMISO, based on the schematic of Figure 1, can be used to relate bound tracer equilibrium molar concentrations to the mean local oxygen molar concentration in each image voxel. This assumption is maintained as long as PET images are acquired over times of pharmacokinetic stability, which for Cu-ATSM and FMISO was shown to begin by 60 minutes post injection [18,26] and was well established at 3 hours. Under these conditions, the predominantly retained and imaged chemical form of the tracer is its bound state prior to dissociation, which follows from the most probable retention mechanism in vivo based on quantum chemistry simulations [17]. The imaged tracer molar concentration M in steady state represents the compound in the bound compartment, or more aptly the reduction-oxidation pair of the oxygen-sensitive chemical state and the trapped chemical state. For Cu-ATSM, this refers to the CuIATSM−/CuIHATSM pair, while for FMISO, this refers to the FRNO2−/FRNO pair (see Figure 1 bound compartment). For each chemical reaction, chemical equilibrium constants K were calculated using the Nernst and Faraday equations (2) from measured or simulated thermodynamic quantities:
| (2) |
Model parameters include free energy changes ΔG0 and standard reduction potentials E0 for all reactions at a given temperature T and number of electrons transferred per mole ne. Table 1 lists all implemented parameters from reported values in the literature or calculated from model equations. The formalism was applied to each tracer, yielding a set of linear equations that was solved for the oxygen molar concentration as a function of tracer molar concentration in units of mol/L:
| (3) |
| (4) |
Table 1. List of model parameters relating Cu-ATSM and FMISO uptake to tissue oxygen partial pressure.
All reduction potentials have been converted relative to the standard hydrogen electrode potential. Parenthetical ranges represent single deviation confidence intervals.
| Symbol | Parameter | Value | Reference | |
|---|---|---|---|---|
| ÃCuATSM | [61Cu]Cu-ATSM Molar Specific Activity |
237 MBq-μmol−1 | [24] | |
| ÃFMISO | [18F]FMISO Molar Specific Activity |
75.0 (50.0–100.0) GBq-μmol−1 |
[25] | |
| R | Gas Constant | 8.31 J-mol−1-K−1 | [27] | |
| T | Cellular Temperature | 310 K | [31] | |
| F | Faraday Constant | 96.5 kJ-mol−1-V−1 | [27] | |
|
|
SRPa: NAD(P)H → NAD(P)+ + H+, ne = 2 | −0.320 V | [16] | |
|
|
SRP: Cytochrome Reductase FAD Cofactor, ne = 1 |
−0.168 V | [32] | |
|
|
SRP: Cytochrome Reductase FMN Cofactor, ne = 1 |
−0.333 V | [32] | |
|
|
SRP: CuIIATSM → CuIATSM−, ne = 1 | −0.328 V | [16] | |
|
|
SRP: RNO2 → RNO2−, ne = 1 | −0.389 V | [12] | |
|
|
SRP: Complex I Nitroreductase, ne = 1 | −0.250 V | [33] | |
|
|
SRP: O2 → O2−, ne = 1 | −0.330 V | [34] | |
|
|
Free Energy Change: CuIATSM− + O2 → CuII ATSM + O2− | −22.8 kJ-mol−1 | [17] | |
|
|
Free Energy Change: CuIATSM− + H3O+ → CuIHATSM + H2O | −17.1 kJ-mol−1 | [30] | |
| pH | Intracellular acidity in human squamous cell carcinomas | 7.20 (7.10–7.30) | [35] | |
| [H2O] | Cellular water molar concentration | 55.3 mol-L−1 | [31] | |
| KCR | LECb: Cu-ATSM reduction | −5.11 | Calculated | |
| pKpH | LEC: Cu-ATSM protonation | 2.88 | Calculated | |
| pKO2-Cu | LEC: Cu-ATSM reoxidation | 9.62 | Calculated | |
| pKNR | LEC: FMISO reduction | −1.12 | Calculated | |
| pKO2-F | LEC: FMISO reoxidation | 0.960 | Calculated | |
| KH | Henry Coefficient for O2 dissolved in H2O at 310 K | 959 L-atm-mol−1 | Calculated |
SRP – standard reduction potential
LEC – log equilibrium constant
These equations are approximations as the dissociated tracer concentration is assumed to be negligible compared to the reduced and bound tracer concentrations when imaging at appropriate time points. Parameter values reveal that Cu-ATSM reduction via interaction with the NAD(P)H-CR complex is more difficult than FMISO reduction via interaction with the NAD(P)H-NR complex (pKCR < pKNR), despite having similar single electron reduction potentials. On the other hand, Cu-ATSM is significantly easier to re-oxidize than FMISO (pKO2-Cu ≫ pKO2-F) in the presence of molecular oxygen. The inverse quartic relationship between oxygen concentration and Cu-ATSM concentration as opposed to the inverse linear relationship to FMISO concentration is due to differences in the number of electrons transferred per mol and consequent stoichiometry of their respective reactions. In the case of Cu-ATSM, there is a strong functional dependence on the cellular acidity, which makes it a less direct measure of oxygenation status than FMISO.
Relating oxygen concentration to oxygen tension
The average oxygen concentration in a given voxel provides a common metric by which comparison between hypoxia tracers can be carried out. However, it is not an easily measurable quantity and therefore few studies have investigated this measure as an indicator of clinical outcome. Instead, the local partial pressure of molecular oxygen has been measured in vivo through the use of polarographic microelectrodes. With this in mind, the model proceeds to relate the local oxygen concentration to the oxygen tension.
The ideal gas law is an invalid approximation for the behavior of molecular oxygen in human cells, since the microenvironment resides at lower temperatures where intermolecular forces come into play. These forces and other active modes of biological transport contribute to significant heterogeneity in oxygen concentration. To overcome this limitation, molecular oxygen is assumed to behave as a real gas dissolved in aqueous solution when averaging its concentration over the macroscopic image voxel. Employing Henry’s Law for real gases, the partial pressure of oxygen in units of mmHg can be deduced from its concentration in solution:
| (5) |
The constant KH, referred to as Henry’s coefficient, is solute and temperature dependent, which in this case was taken to be a water equivalent medium at 310 K:
| (6) |
The constants KH(298 K) and CO2 were taken to be 769 L-atm-mol−1 and 1700 K, respectively [27]. Combining (3) through (6), expressions are derived for the oxygen tension (mmHg) from Cu-ATSM and FMISO uptake values in each PET image voxel:
| (7) |
| (8) |
These relationships serve as the basis for subsequent validation of simulated oxygen tension against direct measurements, as well as cross-comparison of tracer uptake in a patient population.
Materials and methods
In order to validate the model, the resulting transformation functions of Cu-ATSM (7) and FMISO (8) uptake to tissue oxygen tension were compared against measured relationships in preclinical models [18,28]. In cases where measurements were reported relative to injected activity, these values were converted to SUV based on body mass. Furthermore, simulated PO2 values from Cu-ATSM uptake were tested for correlation to measured PO2 values from Eppendorf polarographic microelectrodes in 69 head and neck squamous cell carcinoma (HNSCC) patients at the Aarhus University Hospital [4]. Microelectrode measurements were taken at intervals of 0.7 mm along several linear tracks through each lesion. On average, each lesion of a microelectrode patient was represented by four tracks and 110 measurements, compared to thousands of voxel samples in each imaging patient. Independent two sample t-tests were performed along with calculations of Pearson correlation coefficients from regression analysis to compare the imaging and microelectrode patient population PO2 distributions at the 95 percent confidence level.
Once validated, the model was applied to data from 12 HNSCC patients with regional lymph node involvement at the University of Wisconsin Hospital. Each patient was injected with up to 5 mCi of [61Cu]Cu-ATSM (61Cu τ1/2 = 3.33 h) and underwent a PET/CT scan three hours post injection. Scans were acquired in 2D mode over three frames of either 10 minute or 15 minute duration. Images were reconstructed using an ordered subset expectation maximization algorithm (OSEM) on a 1.95 × 1.95 × 4.25 mm grid, which was run for two iterations over 28 subsets and subsequently filtered with a 3 mm full width half-maximum Gaussian. The uptake region of interest (ROI) was defined as the gross tumor volume on a diagnostic planning CT by a radiation oncologist. Time-averaged Cu-ATSM uptake values in this ROI were transformed to tissue oxygen tensions, 9 which were then converted back to equivalent [18F]FMISO (18F τ1/2 = 109.77 m) uptake values for comparison.
Results
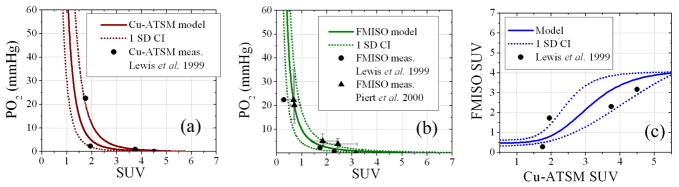
The transformation functions between tracer uptake and PO2 are shown in Figure 2, which indicate good agreement between modeled and measured values in preclinical models. Measured Cu-ATSM uptake values at fixed oxygenation fall within the single deviation confidence intervals of the Cu-ATSM model values in Figure 2a. FMISO model values follow measured values in Figure 2b, though some discrepancies are observed at low uptake values. Clinical hypoxia thresholds based on PO2 measurements (2.5 mmHg and 5.0 mmHg) correspond to lower FMISO SUV (2.0±0.6 and 1.4±0.5) and higher Cu-ATSM SUV (2.5±0.9 and 2.0±0.4). The Cu-ATSM and FMISO uptake relationship in Figure 2c appears linear at intermediate uptake values and sigmoidal over the entire uptake range.
Figure 2. Transformation functions between Cu-ATSM uptake, FMISO uptake, and tissue oxygen tension.
The modeled Cu-ATSM uptake to PO2 transformation (a) and FMISO uptake to PO2 transformation (b) are in good agreement with preclinical measurements [18,28] within single deviation confidence intervals. The resulting FMISO SUV relationship to Cu-ATSM SUV (c) is a non-linear sigmoid function. Uncertainties in some measurements are within displayed markers.
Validation against the clinical population data of Figure 3 shows that the modeled PO2 distribution within lymph nodes in Figure 3d is strongly correlated to the measured Eppendorf distribution within lymph nodes in Figure 3b (r2=0.94), while the modeled primary tumor distribution in Figure 3c is not (r2=0.66). The population mean modeled PO2 of 16.9 mmHg is not significantly different from the population mean measured PO2 of 17.3 mmHg (p=0.60), whereas the population mean primary tumor PO2 of 20.3 mmHg is significantly different (p<0.01). Stark contrasts between the primary and nodal volume oxygen tension distributions have been observed in prior investigations [29], which are reaffirmed in this study.
Figure 3.
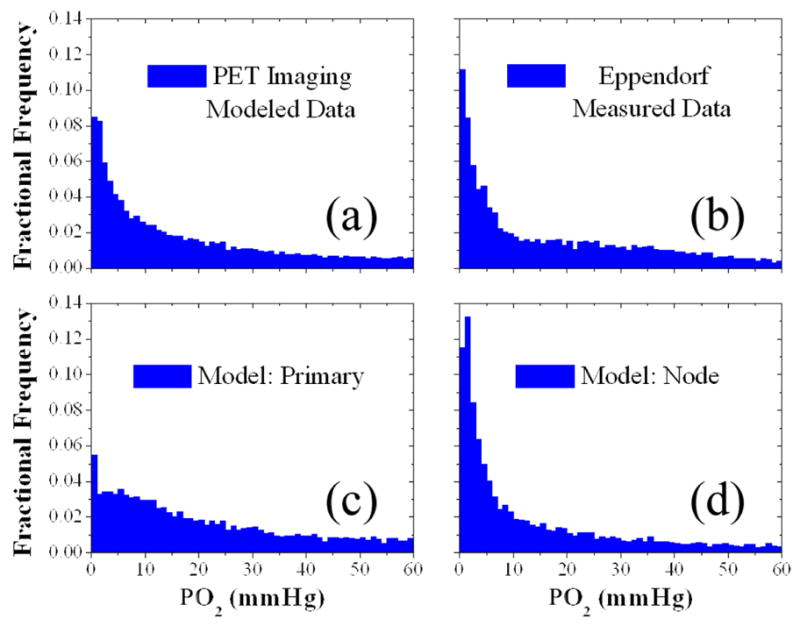
Tissue oxygen tension distributions of two head and neck cancer patient populations simulated from Cu-ATSM PET images or measured by Eppendorf microelectrodes. A simulated PO2 distribution within gross tumour volumes of 12 HNSCC patients imaged via Cu-ATSM PET/CT scans (a) was decomposed into a primary tumour volume distribution (c) and regional lymph nodal volume distribution (d). These simulated distributions were then tested for correlation with a distribution of direct PO2 measurements in 69 head and neck patient regional lymph nodal volumes using polarographic microelectrodes (b). High correlation (r2=0.94, p<0.05) exists between the distributions in (b) and (d).
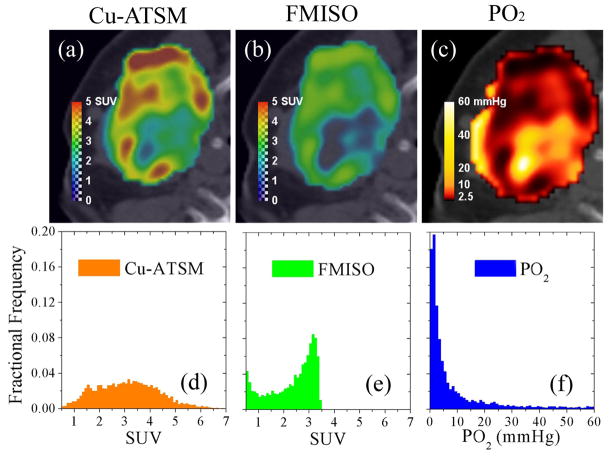
Application of the model to a representative patient is shown for the imaged Cu-ATSM uptake, simulated FMISO uptake and tissue oxygen partial pressure in Figure 4. The images show that higher contrast is achieved with Cu-ATSM than FMISO, particularly in regions of corresponding low oxygen tension. A Gaussian Cu-ATSM distribution characterized by a mean SUV of 3.1 and deviation of 1.2 corresponds to a skewed FMISO distribution with a mean SUV of 2.0 and deviation of 1.4, based on the same highly skewed PO2 distribution with a mean of 14 mmHg and deviation of 20 mmHg.
Figure 4. Comparison of measured Cu-ATSM uptake, modeled FMISO uptake, and modeled tissue oxygen tension in an example head-and-neck cancer patient.
High Cu-ATSM SUV regions (a) correspond to lower FMISO SUV (b) for a given PO2 level (c). The Gaussian Cu-ATSM uptake distribution (d) is equivalent to the skewed FMISO uptake distribution (e). The corresponding PO2 distribution (f) is highly skewed.
Discussion
The model provides a straightforward means of comparing hypoxia tracers, correlates well to clinical Eppendorf probe measurements, and allows for conversion of indirect measures of hypoxia to direct measures of tissue oxygen partial pressure. Comparisons made directly between Cu-ATSM and FMISO uptake values lead to inconsistent results, as it is clear that the same tracer uptake is representative of differing tissue oxygenation. Most notably, free model parameter values may shed light on causes for cell-line dependent uptake and inconsistent cross-validation between hypoxia tracers and tissue markers. Specifically, variations in enzymatic activity and intracellular acidity may have a profound impact on imaged Cu-ATSM uptake. Confidence intervals in the measured intracellular pH within a specific patient population propagate to uncertainties in tracer uptake at a given oxygen tension. Chemically, acidic microenvironments encourage protonation and entrapment of reduced Cu-ATSM, which may in turn produce images that are less sensitive to changes in oxygenation and therefore more correlated to intracellular pH than to PO2. Reported ranges of these parameter values across numerous site-specific histopathologies can eventually be incorporated into the model to improve the estimation of confidence intervals on the transformation functions.
Despite its promise, several limitations of the model require further elucidation. By simplifying the analysis to a subset of time-averaged PET scans under presumed steady-state conditions, the model only calculates differences in the magnitude of uptake between tracers. Without analysis from independent Cu-ATSM and FMISO image data of the same patient, the model does not convey any information on differences in spatial distribution, which would otherwise speak to the degree of co-localization. Definitive comparison of spatial distributions between Cu-ATSM and FMISO in vivo may require the use of dual tracer imaging that adequately separates the shorter lived 18F activity from the longer-lived 61Cu activity, provided that tracer retention is not competitive. From the modeled retention mechanisms, FMISO is reduced by a large family of nitroreductase enzymes that is inclusive of the smaller group of cytchrome reductases responsible for Cu-ATSM reduction. In other words, Cu-ATSM uptake does not inhibit FMISO uptake, but the converse can affect Cu-ATSM cellular entrapment. Dual tracer imaging at early time points would theoretically reflect a high proportion of bound FMISO compared to Cu-ATSM, while late time point imaging would reflect more equal proportions. Such a study would also need to account for inequalities between PET imaging system point spread functions when comparing activity concentrations from 18F and 61Cu radionuclides so as to properly assess the degree of spatial correlation between images.
Another limitation of the model is its inability to correct for perfusion or permeability in each image voxel of a given tumor, which would account for transient changes in hypoxia. As an interesting example, the calculated PO2 distribution of a patient was juxtaposed against a contrast-enhanced computed tomographic (CE-CT) image in Figure 5. The circle ROI indicates an area of low calculated PO2 from high tracer uptake, which corresponds to an area of average contrast distal to any major vessels. This ensures that the imaged tracer was indeed retained specifically and was neither the result of increased perfusion nor higher permeability. The triangle ROI, however, indicates high oxygen tension from low uptake proximal to the external jugular vein. The result in this region may be influenced by the negative blood flow from the interstitial space into the venous return supply. Lastly, the square ROI corresponds to a poorly perfused and possibly necrotic area in which low Cu-ATSM uptake may falsely lead to high calculated PO2. Delineating well-oxygenated regions from necrotic regions using time-averaged tracer uptake alone is difficult, since both regions yield low uptake values.
Figure 5. Calculated tissue oxygen tension from Cu-ATSM PET (PO2) versus contrast enhanced CT (CE-CT) in an example head-and-neck cancer patient.
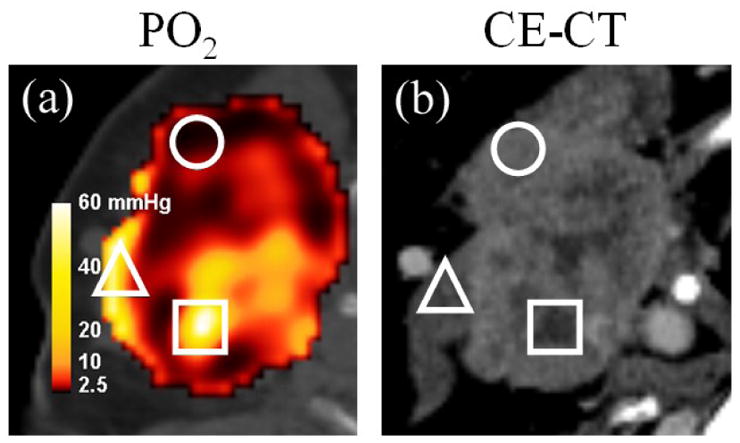
Regions of interest include an area of low calculated PO2 that is not perfusion-limited (circle), areas of high calculated PO2 under the possible influence of venous perfusion (triangle), and potentially poorly perfused necrotic tissue falsely yielding high calculated PO2 (square).
Comprehensive assessment of tumor hypoxia in vivo will require the use of multimodal imaging in visualizing numerous molecular markers. Whenever feasible, dynamic PET or dynamic contrast-enhanced imaging capable of quantifying perfusion and permeability should be used in the correction of SUV, especially at low values. Visualizing endogenous markers of the tumor microenvironment under hypoxic conditions, such as those marking glucose transport, lactate transport and acidity from tissue samples within avid tracer uptake regions may lead to more precise and accurate cross-validation. As the definition of the tumor hypoxia phenotype increases in complexity, so must its characterization encompass many specific measures, whose combination may be more prognostic of clinical outcome and predictive of treatment response than any single measure. Models of the biochemical relationships between hypoxia markers that have been benchmarked to clinical measurements may aid in the quantitative comparison of treatment response and perhaps help in the design of novel treatment protocols.
Conclusion
Direct comparison of hypoxia surrogate PET tracer uptake in vivo remains difficult due to differing retention mechanisms. Indirect measures of tumor hypoxia must instead be related to common metrics with well-defined clinical utility as prognosticators, such as tissue oxygen tension, which can be achieved non-invasively through computational modeling. Results of this electrochemical model relating tracer uptake to tissue partial oxygen pressure indicate that Cu-ATSM uptake is more sensitive to changes in low PO2 than FMISO, yet the latter is more discriminating over large ranges in oxygen tension. These findings may explain in part the lack of tracer correlation in certain small animal models. Further evidence of variations in reductive enzyme concentration and cellular acidity among tumor histologies in vivo is necessary to fully understand differences in tracer uptake at fixed tissue oxygenation. Comprehensive and robust assessment of tumor hypoxia prior to as well as in response to therapy may be best-provided by imaging of multiple hypoxia markers that provide complementary rather than interchangeable information.
Acknowledgments
This work was financially supported by NIH grant R01 CA136927. The authors greatly appreciate the efforts of Jerry Nickles and the Cyclotron Group who provided the [61Cu]Cu-ATSM radiotracer for PET imaging. The authors express their gratitude towards Scott Perlman and Chris Jaskowiak for overseeing the PET scans, as well as Paul Harari for the treatment plan contours in the head and neck patients from the University of Wisconsin Hospital.
Footnotes
Conflicts of Interest
The authors declare that they have no conflicts of interest.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Thomlinson R, Gray L. The histological structure of some human lung cancers and the possible implications for radiotherapy. The British Journal of Cancer. 1955;9:539–49. doi: 10.1038/bjc.1955.55. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Vaupel P, Mayer A, Hockel M. Tumor hypoxia and malignant progression. Methods Enzymol. 2004;381:335–54. doi: 10.1016/S0076-6879(04)81023-1. [DOI] [PubMed] [Google Scholar]
- 3.Le QT, Courter D. Clinical biomarkers for hypoxia targeting. Cancer Metastasis Rev. 2008;27:351–62. doi: 10.1007/s10555-008-9144-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Nordsmark M, Bentzen SM, Rudat V, Brizel D, Lartigau E, Stadler P, et al. Prognostic value of tumor oxygenation in 397 head and neck tumors after primary radiation therapy. An international multi-center study. Radiother Oncol. 2005;77:18–24. doi: 10.1016/j.radonc.2005.06.038. [DOI] [PubMed] [Google Scholar]
- 5.Arteel GE, Thurman RG, Raleigh JA. Reductive metabolism of the hypoxia marker pimonidazole is regulated by oxygen tension independent of the pyridine nucleotide redox state. Eur J Biochem. 1998;253:743–50. doi: 10.1046/j.1432-1327.1998.2530743.x. [DOI] [PubMed] [Google Scholar]
- 6.Mees G, Dierckx R, Vangestel C, Van de Wiele C. Molecular imaging of hypoxia with radiolabelled agents. Eur J Nucl Med Mol Imaging. 2009;36:1674–86. doi: 10.1007/s00259-009-1195-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Rasey JS, Koh WJ, Grierson JR, Grunbaum Z, Krohn KA. Radiolabelled fluoromisonidazole as an imaging agent for tumor hypoxia. Int J Radiat Oncol Biol Phys. 1989;17:985–91. doi: 10.1016/0360-3016(89)90146-6. [DOI] [PubMed] [Google Scholar]
- 8.Koh WJ, Rasey JS, Evans ML, Grierson JR, Lewellen TK, Graham MM, et al. Imaging of hypoxia in human tumors with [F-18]fluoromisonidazole. Int J Radiat Oncol Biol Phys. 1992;22:199–212. doi: 10.1016/0360-3016(92)91001-4. [DOI] [PubMed] [Google Scholar]
- 9.O’Donoghue JA, Zanzonico P, Pugachev A, Wen B, Smith-Jones P, Cai S, et al. Assessment of regional tumor hypoxia using 18F-fluoromisonidazole and 64Cu(II)-diacetyl-bis(N4-methylthiosemicarbazone) positron emission tomography: Comparative study featuring microPET imaging, Po2 probe measurement, autoradiography, and fluorescent microscopy in the R3327-AT and FaDu rat tumor models. Int J Radiat Oncol Biol Phys. 2005;61:1493–502. doi: 10.1016/j.ijrobp.2004.12.057. [DOI] [PubMed] [Google Scholar]
- 10.Troost EG, Laverman P, Philippens ME, Lok J, van der Kogel AJ, Oyen WJ, et al. Correlation of [18F]FMISO autoradiography and pimonidazole [corrected] immunohistochemistry in human head and neck carcinoma xenografts. Eur J Nucl Med Mol Imaging. 2008;35:1803–11. doi: 10.1007/s00259-008-0772-7. [DOI] [PubMed] [Google Scholar]
- 11.Mortensen LS, Buus S, Nordsmark M, Bentzen L, Munk OL, Keiding S, et al. Identifying hypoxia in human tumors: A correlation study between 18F-FMISO PET and the Eppendorf oxygen-sensitive electrode. Acta Oncol. 2010;49:934–40. doi: 10.3109/0284186X.2010.516274. [DOI] [PubMed] [Google Scholar]
- 12.Sorger D, Patt M, Kumar P, Wiebe LI, Barthel H, Seese A, et al. [18F]Fluoroazomycinarabinofuranoside (18FAZA) and [18F]Fluoromisonidazole (18FMISO): a comparative study of their selective uptake in hypoxic cells and PET imaging in experimental rat tumors. Nucl Med Biol. 2003;30:317–26. doi: 10.1016/s0969-8051(02)00442-0. [DOI] [PubMed] [Google Scholar]
- 13.Thorwarth D, Eschmann SM, Holzner F, Paulsen F, Alber M. Combined uptake of [18F]FDG and [18F]FMISO correlates with radiation therapy outcome in head-and-neck cancer patients. Radiother Oncol. 2006;80:151–6. doi: 10.1016/j.radonc.2006.07.033. [DOI] [PubMed] [Google Scholar]
- 14.Rajendran JG, Schwartz DL, O’Sullivan J, Peterson LM, Ng P, Scharnhorst J, et al. Tumor hypoxia imaging with [F-18] fluoromisonidazole positron emission tomography in head and neck cancer. Clin Cancer Res. 2006;12:5435–41. doi: 10.1158/1078-0432.CCR-05-1773. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Obata A, Yoshimi E, Waki A, Lewis JS, Oyama N, Welch MJ, et al. Retention mechanism of hypoxia selective nuclear imaging/radiotherapeutic agent cu-diacetyl-bis(N4-methylthiosemicarbazone) (Cu-ATSM) in tumor cells. Ann Nucl Med. 2001;15:499–504. doi: 10.1007/BF02988502. [DOI] [PubMed] [Google Scholar]
- 16.Fujibayashi Y, Taniuchi H, Yonekura Y, Ohtani H, Konishi J, Yokoyama A. Copper-62-ATSM: a new hypoxia imaging agent with high membrane permeability and low redox potential. J Nucl Med. 1997;38:1155–60. [PubMed] [Google Scholar]
- 17.Holland JP, Barnard PJ, Collison D, Dilworth JR, Edge R, Green JC, et al. Spectroelectrochemical and computational studies on the mechanism of hypoxia selectivity of copper radiopharmaceuticals. Chemistry. 2008;14:5890–907. doi: 10.1002/chem.200800539. [DOI] [PubMed] [Google Scholar]
- 18.Lewis JS, McCarthy DW, McCarthy TJ, Fujibayashi Y, Welch MJ. Evaluation of 64Cu-ATSM in vitro and in vivo in a hypoxic tumor model. J Nucl Med. 1999;40:177–83. [PubMed] [Google Scholar]
- 19.Dehdashti F, Mintun MA, Lewis JS, Bradley J, Govindan R, Laforest R, et al. In vivo assessment of tumor hypoxia in lung cancer with 60Cu-ATSM. Eur J Nucl Med Mol Imaging. 2003;30:844–50. doi: 10.1007/s00259-003-1130-4. [DOI] [PubMed] [Google Scholar]
- 20.Dehdashti F, Grigsby PW, Lewis JS, Laforest R, Siegel BA, Welch MJ. Assessing tumor hypoxia in cervical cancer by PET with 60Cu-labeled diacetyl-bis(N4-methylthiosemicarbazone) J Nucl Med. 2008;49:201–5. doi: 10.2967/jnumed.107.048520. [DOI] [PubMed] [Google Scholar]
- 21.Osada M, Imaoka S, Sugimoto T, Hiroi T, Funae Y. NADPH-cytochrome P-450 reductase in the plasma membrane modulates the activation of hypoxia-inducible factor 1. J Biol Chem. 2002;277:23367–73. doi: 10.1074/jbc.M112413200. [DOI] [PubMed] [Google Scholar]
- 22.Shi K, Souvatzoglou M, Astner ST, Vaupel P, Nusslin F, Wilkens JJ, et al. Quantitative assessment of hypoxia kinetic models by a cross-study of dynamic 18F-FAZA and 15O-H2O in patients with head and neck tumors. J Nucl Med. 2010;51:1386–94. doi: 10.2967/jnumed.109.074336. [DOI] [PubMed] [Google Scholar]
- 23.Wang W, Lee NY, Georgi JC, Narayanan M, Guillem J, Schoder H, et al. Pharmacokinetic analysis of hypoxia (18)F-fluoromisonidazole dynamic PET in head and neck cancer. J Nucl Med. 2010;51:37–45. doi: 10.2967/jnumed.109.067009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Avila-Rodriguez MA, Nye JA, Nickles RJ. Simultaneous production of high specific activity 64Cu and 61Co with 11.4 MeV protons on enriched 64Ni nuclei. Appl Radiat Isot. 2007;65:1115–20. doi: 10.1016/j.apradiso.2007.05.012. [DOI] [PubMed] [Google Scholar]
- 25.Reischl G, Dorow DS, Cullinane C, Katsifis A, Roselt P, Binns D, et al. Imaging of tumor hypoxia with [124I]IAZA in comparison with [18F]FMISO and [18F]FAZA--first small animal PET results. J Pharm Pharm Sci. 2007;10:203–11. [PubMed] [Google Scholar]
- 26.Thorwarth D, Eschmann SM, Paulsen F, Alber M. A kinetic model for dynamic [18F]-Fmiso PET data to analyse tumour hypoxia. Phys Med Biol. 2005;50:2209–24. doi: 10.1088/0031-9155/50/10/002. [DOI] [PubMed] [Google Scholar]
- 27.Oxtoby DW, Gillis HP, Nachtrieb NH. Principles of Modern Chemistry. 5. Thomson Learning, Inc; 2002. [Google Scholar]
- 28.Piert M, Machulla HJ, Becker G, Aldinger P, Winter E, Bares R. Dependency of the [18F]fluoromisonidazole uptake on oxygen delivery and tissue oxygenation in the porcine liver. Nucl Med Biol. 2000;27:693–700. doi: 10.1016/s0969-8051(00)00151-7. [DOI] [PubMed] [Google Scholar]
- 29.Nilsson J, Lind BK, Brahme A. Radiation response of hypoxic and generally heterogeneous tissues. Int J Radiat Biol. 2002;78:389–405. doi: 10.1080/09553000110113038. [DOI] [PubMed] [Google Scholar]
- 30.Holland JP, Green JC, Dilworth JR. Probing the mechanism of hypoxia selectivity of copper bis(thiosemicarbazonato) complexes: DFT calculation of redox potentials and absolute acidities in solution. Dalton Trans. 2006:783–94. doi: 10.1039/b512656h. [DOI] [PubMed] [Google Scholar]
- 31.Lodish H, Berk A, Matsudaira P, Kaiser CA, Krieger M, Scott MP, et al. Molecular Cell Biology. 5. W.H. Freeman and Company; New York: 2004. [Google Scholar]
- 32.Munro AW, Noble MA, Robledo L, Daff SN, Chapman SK. Determination of the redox properties of human NADPH-cytochrome P450 reductase. Biochemistry. 2001;40:1956–63. doi: 10.1021/bi001718u. [DOI] [PubMed] [Google Scholar]
- 33.Tuschen G, Sackmann U, Nehls U, Haiker H, Buse G, Weiss H. Assembly of NADH: ubiquinone reductase (complex I) in Neurospora mitochondria. Independent pathways of nuclear-encoded and mitochondrially encoded subunits. J Mol Biol. 1990;213:845–57. doi: 10.1016/S0022-2836(05)80268-2. [DOI] [PubMed] [Google Scholar]
- 34.Sawyer DT. International Series of Monographs on Chemistry. Vol. 26. Oxford University Press; New York: 1991. p. 21. [Google Scholar]
- 35.Gerweck LE. Tumor pH: implications for treatment and novel drug design. Semin Radiat Oncol. 1998;8:176–82. doi: 10.1016/s1053-4296(98)80043-x. [DOI] [PubMed] [Google Scholar]