Measures of central tendency: Median and mode

INTRODUCTION

Apart from the mean, median and mode are the two commonly used measures of central tendency. The median is sometimes referred to as a measure of location as it tells us where the data are.[1] This article describes about median, mode, and also the guidelines for selecting the appropriate measure of central tendency.

MEDIAN

Median is the value which occupies the middle position when all the observations are arranged in an ascending/descending order. It divides the frequency distribution exactly into two halves. Fifty percent of observations in a distribution have scores at or below the median. Hence median is the 50th percentile.[2] Median is also known as ‘positional average’.[3]

It is easy to calculate the median. If the number of observations are odd, then (n + 1)/2th observation (in the ordered set) is the median. When the total number of observations are even, it is given by the mean of n/2th and (n/2 + 1)th observation.[2]

Advantages

1. It is easy to compute and comprehend.

2. It is not distorted by outliers/skewed data.[4]

3. It can be determined for ratio, interval, and ordinal scale.

Disadvantages

1. It does not take into account the precise value of each observation and hence does not use all information available in the data.

2. Unlike mean, median is not amenable to further mathematical calculation and hence is not used in many statistical tests.

3. If we pool the observations of two groups, median of the pooled group cannot be expressed in terms of the individual medians of the pooled groups.

MODE

Mode is defined as the value that occurs most frequently in the data. Some data sets do not have a mode because each value occurs only once. On the other hand, some data sets can have more than one mode. This happens when the data set has two or more values of equal frequency which is greater than that of any other value. Mode is rarely used as a summary statistic except to describe a bimodal distribution. In a bimodal distribution, the taller peak is called the major mode and the shorter one is the minor mode.

Advantages

1. It is the only measure of central tendency that can be used for data measured in a nominal scale.[5]

2. It can be calculated easily.

Disadvantages

1. It is not used in statistical analysis as it is not algebraically defined and the fluctuation in the frequency of observation is more when the sample size is small.

POSITION OF MEASURES OF CENTRAL TENDENCY

The relative position of the three measures of central tendency (mean, median, and mode) depends on the shape of the distribution. All three measures are identical in a normal distribution [Figure 1a]. As mean is always pulled toward the extreme observations, the mean is shifted to the tail in a skewed distribution [Figure 1b and c]. Mode is the most frequently occurring score and hence it lies in the hump of the skewed distribution. Median lies in between the mean and the mode in a skewed distribution.[6,7]

Figure 1.

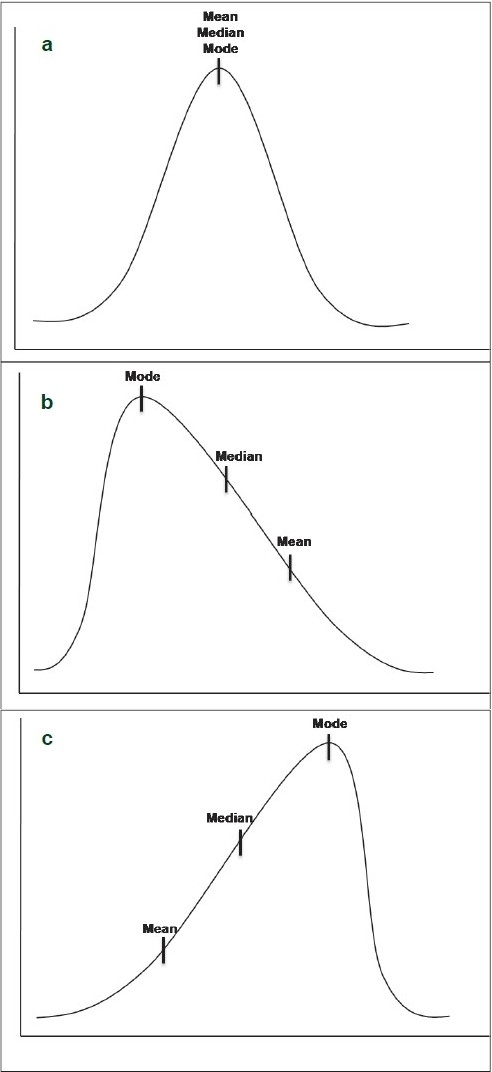
The relative position of the various measures of central tendency. (a) Normal distribution (b) Positively (right) skewed distribution (c) Negatively (left) skewed distribution

SELECTING THE APPROPRIATE MEASURE

Mean is generally considered the best measure of central tendency and the most frequently used one. However, there are some situations where the other measures of central tendency are preferred.

Median is preferred to mean[3] when

1. There are few extreme scores in the distribution.

2. Some scores have undetermined values.

3. There is an open ended distribution.

4. Data are measured in an ordinal scale.

5. Mode is the preferred measure when data are measured in a nominal scale. Geometric mean is the preferred measure of central tendency when data are measured in a logarithmic scale.[8]