COMPARISON OF PROPORTIONS FOR COMPOSITE ENDPOINTS WITH MISSING COMPONENTS

Abstract

Composite endpoints are commonly used in clinical trials. When there are missing values in their individual components, inappropriate handling of the missingness may create inefficient or even biased estimates of the proportions of successes in composite endpoints. Assuming missingness is completely at random or dependent on baseline covariates, we derived a maximum likelihood estimator of the proportion of successes in a three-component composite endpoint and closed-form variance for the proportion, and compared two groups in the difference in proportions and in the logarithm of a relative risk. Sample size and statistical power were studied. Simulation studies were used to evaluate the performance of the developed methods. With a moderate sample size the developed methods works satisfactorily.

1. INTRODUCTION

Composite endpoints are frequently used in medical diagnoses, epidemiologic research, and clinical trials. For example, the test-of-cure of Helicobacter pylori-associated duodenal ulcer disease could be based on culture, histology, and rapid urease test results. If the results from the three components are negative, the patient is classified as disease eradicated. A composite endpoint with more than three components is also used in practice.

If there are no missing data in individual components, the estimation of the proportion of successes in a composite endpoint and comparisons of proportions between two groups, such as an intervention or control group, can be performed using classical statistical methods for binomially distributed variables. However, the presence of missing values in one or more components will make the estimation of the proportion of the composite endpoint somewhat complicated. The approach most commonly used for addressing the missing data is the so-called complete-case analysis, an analysis using the data including subjects with complete data only and excluding these subjects whose components have missing values. However, such an approach may discard known composite endpoints and be less efficient, although it yields unbiased estimates when missingness is completely at random. In addition, multiple imputation has been used extensively in many applications with missing values. But the performance in composite endpoint settings is unknown.

A related missing value problem in contingency tables was studied in a partial cross-classification setting and with different modeling purposes as early as in the 1970s. In particular, maximum likelihood estimators (MLEs) of cell probabilities in two-dimensional contingency tables with both completely and partially cross-classified data were considered by Chen and Fienberg (1974) and Hocking and Oxspring (1974). Williamson and Haber (1994) extended this approach to three-dimensional contingency tables. In Chen and Fienberg (1974), MLEs for Poisson sampling were derived. The MLEs for the Poisson parameters in general had no closed form. Hence, an iterative procedure was used to obtain the MLEs. The authors also obtained the MLEs for multinomial sampling and the asymptotic variances and covariances of the estimated cell probabilities and developed the goodness-of-fit tests for the models. In Hocking and Oxspring (1974), a multinomial distribution was used. Assuming that completely classified data followed a multinomial distribution, the partially classified data also followed a multinomial distribution with appropriately combined parameters. With an assumption that the two sets of data were independent, the MLEs of the parameters from the combined data were obtained.

In order to estimate the proportion of success for composite endpoints with missing values, Li et al. (2007) proposed four estimators, including an MLE, when the missingness is completely at random. Similarly, Quan et al. (2007) considered comparison of treatment effects on composite endpoints comprised of two components with missing data. Instead of defining a composite endpoint for each individual, these methods focus on estimating the cell probabilities, thereby estimating the proportion of success in a composite endpoint, in order to avoid the difficulty of defining a composite endpoint for individuals with missing values.

In clinical trials or observational studies, often interest lies in the comparison of two proportions of successes for composite endpoints. The comparison could be the difference in the proportions of successes or the logarithm of a relative risk (i.e., proportion ratio). The methods for two-component composite endpoints do not easily apply to composite endpoints with three or more composite components, because the likelihood function and variance formulas are more complicated. Statistical methods for these very important multiple-component endpoints in comparative studies are needed. Therefore, in this paper, assuming that the values of individual components are missing completely at random or missing at random (dependent upon baseline covariates), we develop methods for estimation of the proportion of successes in a multiple-component composite endpoint and give an asymptotic variance for the estimate using a three-component composite endpoint as an example. Two-sample comparisons in terms of difference in proportions and in the logarithm of a relative risk in superiority clinical trials are also explored. We examine the performance of the developed methods, including the performance of confidence intervals, calculating statistical power and sample size, and type I error for the two measures for comparison.

This article is organized as follows. In section 2, we introduce a mathematical formalization of the problem and maximum likelihood estimator and asymptotic variance for proportion of success in a three-component composite endpoint. In section 3, we include the power and sample size formulas for superiority clinical trials. In sections 4 and 5, we highlight the results of simulation studies and the results of a hypothetical data analysis, respectively. The final section is devoted to a summary and discussion of directions for future research.

2. MATHEMATICAL FORMULATION AND MAXIMUM LIKELIHOOD ESTIMATOR

For ease of exposition, suppressing subscript t ε (0, 1) for group in notation, we consider K binary (yes/no) outcomes Y ⁽¹⁾, Y ⁽²⁾, … Y ^(K) and define their associated observed data 0/1 indicators as R⁽¹⁾ R⁽²⁾ R^(K) , where R^(k) = 1if Y ^(k) is observed; otherwise it is 0. The composite endpoint Y , defined from the K binary outcomes (individual components), is 1 if Y ⁽¹⁾ = 1 or Y ⁽²⁾ = 1,…, or Y ^K = 1; otherwise it is 0 (Table 1). Mathematically,

$$Y=1-(1-Y^{\left(1\right)})(1-Y^{\left(2\right)})\dots (1-Y^{\left(K\right)})$$

Table 1.

Cell probabilities and data availability probabilities for a three-component composite endpoint in one group

Component					Observed indicator
Y(2) = 0			Y(2) = 1		R(2) = 0			R(2) = 1
Y(1)	Y(3) = 0	Y(3) = 1	Y(3) = 0	Y(3) = 1	R(1)	R(3) = 0	R(3) = 1	R(3) = 0	R(3) = 1
0	π 000	π 001	π 010	π 011	0	γ 000	γ 001	γ 010	γ 011
1	π 100	π 101	π 110	π 111	1	γ 100	γ 101	γ 110	γ 111

Of course, our development trivially extends to the case where the K outcomes are combined via the Boolean “and” operator by considering the proportion of failures. Moreover, the composite endpoint could be defined easily in other ways, for example, Y = 1 if two out of three components are 1, depending on the clinical problems under study.

Let πl₁l₂…l_K be the probability that Y⁽¹⁾ = l₁, Y⁽²⁾ = l₂,…, Y^(K) = l_K and γ_m1m2…mK indicate the probability of R⁽¹⁾ = m₁, R⁽²⁾ = m₂,…, R^(K) = m_K where ${\Sigma }_{l_1=0}^1{\Sigma }_{l_2=0}^1\cdots {\Sigma }_{l_K=0}^1{\pi }_{l_1{l}_2\dots {ł}_K}$ = 1 and ${\Sigma }_{m_1=0}^1{\Sigma }_{m_2=0}^1\cdots {\Sigma }_{m_K=0}^1{\gamma }_{m_1{m}_2\dots m_K}$ = 1. We assume throughout that the components are missing completely at random, i.e., (Y ⁽¹⁾, Y⁽²⁾,…, Y ^(K)) ∐(R⁽¹⁾, R⁽²⁾,… R^(K)). However, the components can be dependent, as well as the observed data indicators.

Of scientific interest is the estimation of p₁ – p₀, the difference in proportions between the treatment and control groups, and log (p₁/p₀), the log relative risk, where p for each group is defined from group-specific cell probabilities as:

$$p=P(Y^{\left(1\right)}=1\mathrm{or}{Y}^{\left(2\right)}=1\dots \mathrm{or}{Y}^{\left(K\right)}=1)=1-{\pi }_{00\dots 0}$$

2.1. Likelihood Function

As (R⁽¹⁾, R⁽²⁾,…, R^(K)) are ancillary for π = (π_l1l2…_lk)′, the maximum likelihood estimate for π can be found by maximizing the conditional likelihood for the observed data given (R⁽¹⁾ R⁽²⁾,…, R^(K).

Suppressing i for individual, assuming observations are identically independently distributed, the contribution from an individual with observed data O to the conditional log-likelihood l (π; O) is one of the following terms (the plus sign in the subscript of π denotes the sum over the corresponding dimension(s), for example,π₊₀₀ = π₀₀₀ + π₁₀₀):

$$\underset{b\in \{1,\dots ,K\}\setminus a}{\overset{\sum }{a\in \{1,\dots ,K\}}}\left\{\prod _a{R}^{\left(a\right)}\prod _b(1-R^{\left(b\right)})\left[\underset{d\in \left\{a\right\}\setminus c}{\overset{\sum }{c\in \{\varnothing ,a\}}}\left(\prod _c{Y}^{\left(c\right)}\prod _d(1-Y^{\left(d\right)})\log \pi (\cdot )\right)\right]\right\},$$

where π(·) = π_{(Y^(b)=+, Y^(c)=1Y^(d)=0)}.

In the following part of this paper, we focus on a three-component composite endpoint, for which the likelihood function can be written as:

$$l(\pi ;O)=R^{\left(1\right)}{R}^{\left(2\right)}{R}^{\left(3\right)}[(1-Y^{\left(1\right)})(1-Y^{\left(2\right)})(1-Y^{\left(\mathrm{k}\right)})\log \left({\pi }_{000}\right)+(1-Y^{\left(1\right)})(1-Y^{\left(2\right)})Y^{\left(3\right)}\log \left({\pi }_{001}\right)+(1-Y^{\left(1\right)})Y^{\left(2\right)}(1-Y^{\left(3\right)})\log \left({\pi }_{010}\right)+(1-Y^{\left(1\right)})Y^{\left(2\right)}{Y}^{\left(3\right)}\log \left({\pi }_{011}\right)+Y^{\left(1\right)}(1-Y^{\left(2\right)})(1-Y^{\left(3\right)})\log \left({\pi }_{100}\right)+Y^{\left(1\right)}(1-Y^{\left(2\right)})Y^{\left(3\right)}\log \left({\pi }_{101}\right)+Y^{\left(1\right)}{Y}^{\left(2\right)}(1-Y^{\left(3\right)})\log \left({\pi }_{110}\right)+Y^{\left(1\right)}{Y}^{\left(2\right)}{Y}^{\left(3\right)}\log \left({\pi }_{111}\right)]+R^{\left(1\right)}(1-R^{\left(2\right)})R^{\left(3\right)}[(1-Y^{\left(1\right)})(1-Y^{\left(3\right)})\log \left({\pi }_{0+0}\right)+(1-Y^{\left(1\right)})Y^{\left(3\right)}\log \left({\pi }_{0+1}\right)+Y^{\left(1\right)}(1-Y^{\left(3\right)})\log \left({\pi }_{1+0}\right)+Y^{\left(1\right)}{Y}^{\left(3\right)}\log \left({\pi }_{1+1}\right)]+(1-R^{\left(1\right)})R^{\left(2\right)}{R}^{\left(3\right)}[(1-Y^{\left(2\right)})(1-Y^{\left(3\right)})\log \left({\pi }_{+00}\right)+(1-Y^{\left(2\right)})Y^{\left(3\right)}\log \left({\pi }_{+01}\right)+Y^{\left(2\right)}(1-Y^{\left(3\right)})\log \left({\pi }_{+10}\right)+Y^{\left(2\right)}{Y}^{\left(3\right)}\log \left({\pi }_{+11}\right)]+R^{\left(1\right)}{R}^{\left(2\right)}(1-R^{\left(3\right)})[(1-Y^{\left(1\right)})(1-Y^{\left(2\right)})\log \left({\pi }_{00+}\right)+(1-Y^{\left(1\right)})Y^{\left(2\right)}\log \left({\pi }_{01+}\right)+Y^{\left(1\right)}(1-Y^{\left(2\right)})\log \left({\pi }_{10+}\right)+Y^{\left(1\right)}{Y}^{\left(2\right)}\log \left({\pi }_{11+}\right)]+R^{\left(1\right)}(1-R^{\left(2\right)})(1-R^{\left(3\right)})[(1-Y^{\left(1\right)})\log \left({\pi }_{0++}\right)+Y^{\left(1\right)}\log \left({\pi }_{1++}\right)]+(1-R^{\left(1\right)})R^{\left(2\right)}(1-R^{\left(3\right)})[(1-Y^{\left(2\right)})\log \left({\pi }_{+0+}\right)+Y^{\left(2\right)}\log \left({\pi }_{+1+}\right)]+(1-R^{\left(1\right)})(1-R^{\left(2\right)})R^{\left(3\right)}[(1-Y^{\left(3\right)})\log \left({\pi }_{++0}\right)+Y^{\left(3\right)}\log \left({\pi }_{++1}\right)]$$

The conditional likelihood for the control or treatment group is ${\Sigma }_{i=1}^n{l}_i$(π; O). This likelihood function uses all observed data, regardless of missing patterns in the components. Therefore, the estimation is potentially more efficient. As mentioned in Li et al. (2007) in a two-component composite setting, there are no closed-form solutions for the estimates. The Newton-Raphson method was used to obtain estimates after re-parameterizing π to eliminate boundary constraints. In the re-parametrization, β = (log (π₀₀₁/π₀₀₀), log(π₀₁₀/π₀₀₀), log (π₀₁₁/π₀₀₀), log (π₁₀₀/π₀₀₀), log(π₁₀₁/π₀₀₀), log(π₁₁₀/π₀₀₀), log(π₁₁₁/π₀₀₀)). The cell probabilities and variances can be estimated for each group. The variance for the proportion of success in each group, var(${\widehat{p}}_0$) and var(${\widehat{p}}_1$) can be obtained from the delta method from the variance–covariance matrix for the estimated cell probabilities.

2.2. Asymptotic Variance of p₀ and p₁, p₁ – p₀, and log (p₁/p₀)

Although there is no closed-form solutions for the proportion, there is a closed-form solution for its variance. The closed-form asymptotic variance for $\widehat{p}$ each group was developed using the Fisher's information matrix derived from the conditional log-likelihood function. This derivation is not presented, but the R program is available from the first author upon request. Note that, due to missing values in outcomes, the variances of ${\widehat{p}}_1$ and ${\widehat{p}}_0$ are p_t(1 – p_t)/n_t, t = 0, 1, where n_t is the sample size for the treatment and control groups, standard binomial distribution. However, since the two groups are independent, the variance of ${\widehat{p}}_1-{\widehat{p}}_0$ is simply the sum of variances of the two estimated proportions. Similarly, using the delta method, the asymptotic variances of log$({\widehat{p}}_1∕{\widehat{p}}_0)$ can be easily obtained as follows: var$\left(\log ({\widehat{p}}_1∕{\widehat{p}}_0)\right)\approx \mathrm{var}\left({\widehat{p}}_0\right)∕{\widehat{p}}_0^2+\mathrm{var}\left({\widehat{p}}_1\right)∕{\widehat{p}}_1^2$.

Based on large-sample theory, the maximum likelihood estimators is approximately asymptotically unbiased and normally distributed. Therefore, hypothesis testing using a Wald test, confidence intervals, and statistical power for each measure can be constructed from the corresponding variances. As in the traditional two-sample proportion comparison, the pooled proportion and its variance used in power calculation can be simply estimated by the average of p₀ and p₁, and their variances, respectively.

2.3. Likelihood Function Under Missing-at-Random Missing Mechanism

When missingness is dependent on baseline variables (missing at random, MAR), but not on individual components, using the pseudo-likelihood function approach, the likelihood function can be decomposed into two parts: one being a function with cell probability parameters, the same as described earlier, and one with nuisance parameters associated MAR missingness. Therefore, the developed MLE applies directly to the data with MAR missing mechanisms.

3. SIMULATION STUDIES

We performed simulation studies to evaluate the performance of the proposed statistical methods for confidence interval, sample size, statistical power calculation, and type I error. We considered the following simulation scenarios.

3.1. Completely-at-Random Missingness

Scenario 1: This is the basic simulation scenario. For the control group, π₀₀₀ = 0.3 and all other seven cell probabilities are set to be 0.1. Therefore, p₀ = 0.70. For the treatment group, π₀₀₀ = 0.1 and π₁₁₁ = 0.3 and all other six cell probabilities are set to be 0.1. Therefore, p₁ = 0.90. All γ_m1m2m3 = 1/8 for the two groups; that is, each component has 50% missing values. Therefore, the distribution of subjects with missing values in components is a binomial distribution with (3, 0.5): 12.5% of subjects are with complete component data; 37.5% have missing values in one component; 37.5% have missing values in two components; and 12.5% have no component data. The sample size used in the simulations is 173 per group, which is designed to achieve an 80% statistical power for the given difference in proportions in composite endpoint with a two-sided type I error of .05. If there are no missing values, only 59 subjects per group are needed to achieve the same statistical power.

Scenario 2: The cell probabilities are same as in Scenario 1, but γ₁₁₁ = 9/16 and all other γ_m1m2m3 = 1/16. Therefore, 1/16 of subjects have no data; 3/16 have two components missing; 3/16 have one component missing; and 9/16 have complete data. With a large proportion of subjects with complete information, the sample size needed to have an 80% statistical power is reduced significantly.

Scenario 3: Compared with Scenario 1, for both groups π₀₀₁ = 0.05 π₀₁₀ = 0.15 π₀₁₁ = 0.05 π₁₀₀ = 0.15 π₁₀₁ = 0.05 π₁₁₀ = 0.15. For the control group, π₁₁₁ = 0.10. Therefore, p₀ = 0.7. For the treatment group, π₁₁₁ = 0.30. Therefore, p₁ = 0.9. This scenario is designed to have more unequal cell probabilities.

Scenario 4: For the control group, π₀₀₀ = 0.2 π₁₁₁ = 0.2, and all other cell probabilities are set to be 0.1. Therefore, p₀ = 0.80. For the treatment group, values are the same as in Scenario 1. Missing value probabilities are the same as in Scenario 1. This scenario is designed to have a smaller difference in proportions.

Scenario 5: Compared with Scenario 1, π₁₁₁ = 0.35 for the treatment group. All other parameters remain the same. Since the difference in proportions increases, the sample size to have a 80% statistical power decreases.

Scenario 6: Compared with Scenario 1, π₁₁₁ = 0.39 for the treatment group. All other parameters remain the same. Since the difference in proportions increases, the sample size to achieve an 80% statistical power decreases.

Scenario 7: Compared with Scenario 1, π₁₁₁ = 0.30 and 0.39 for control and treatment groups, respectively. Therefore, the difference in proportion is smaller and a larger sample size is needed.

3.2. Missing-at-Random Missingness

Under the missing-at-random mechanism, we assumed that missingness is dependent upon two baseline covariates X₁ and X₂, which were generated as independent binary variables with a success probability of 0.5. The cell probabilities for components are the same as in Scenario 1. The missing probability for each component was generated from a logistic regression model logit(P(R^(j) = 0) = β_j0 + β_j1X₁ + β_j2X₂. The sample size was 200 for both the treatment and control group. In the following scenarios, the intercept β_j0 were changed in different ways.

Scenario 8: Here, (β_j0, β_j1, β_j2) = (−2, 1, 1,) for all j components for two groups. The three components have same missing probability given a set of baseline covariates. The missing probability for each component for a subject with X₁ 1 and X₂ = 1 is 50%.

Scenario 9: Compared with Scenario 8, β₁₀ = −1, β₂₀ = −2, and β₃₀ = −3 for the two groups. The three components have different missing probabilities. However, the two groups have same missing probabilities.

Scenario 10: Compared with Scenario 8, β₁₀ = −1, β₂₀ = −2, and β₃₀ = −3 for the control group and β₁₀, = −2, β₂₀ = −1, and β₃₀ = 0 for the treatment group. The three components have different missing proportions and the two groups have different missing probabilities.

The number of iterations for each scenario was 1000 times.

If there are no missing values in components, given the proportion of 0.7 and 0.9 in the two groups, only 59 subjects per groups are needed to achieve the same statistical power and maintain the same level of a type I error. The severe missing value problem in this scenario makes the sample size almost tripled. In Scenario 1, if we used complete case analysis, to test the difference in proportions, the statistical power is only 40.8% and the coverage of the 95% confidence intervals (CIs) is 94.4%; to test log relative risk, the statistical power is only 33.0% and the coverage of 95% CIs is 94.3%. In this case, the calculated variance for the control and treatment groups is 0.0031 and 0.0019, close to the calculated 0.0032, 0.0019 based on the closed-form variance formula, respectively. The MLE performs very well in the first four scenarios (Table 2). The mean estimates are close to the true values, and the coverage of 95% CIs is close to 0.95 and the empirical statistical power is close to the designed power.

Table 2.

Calculated variances of proportions, estimated (SD), 95% confidence interval coverage (CIC), and designed power (P) and empirical power (EP) for estimated difference in proportions and log relative risk for a given sample size (n) per group

Missing scenario	n (effective)	1000Var(p1) True (mean)	1000Var(p0) True (mean)	${\widehat{p}}_1-{\widehat{p}}_0$				$\log ({\widehat{p}}_1∕{\widehat{p}}_0)$
				True	Mean (SD)	95% CIC	P (EP)	True	Mean (SD)	95% CIC	P (EP)
Missing completely at random
1	173 (87)	1.90 (1.93)	3.18 (3.13)	0.20	0.204 (0.072)	0.937	0.801 (0.806)	0.251	0.259 (0.096)	0.943	0.763 (0.788)
2	84 (63)	1.61 (1.61)	3.44 (3.41)	0.20	0.197 (0.069)	0.946	0.804 (0.793)	0.251	0.250 (0.093)	0.953	0.755 (0.780)
3	172 (86)	1.89 (1.95)	3.21 (3.20)	0.20	0.201 (0.074)	0.934	0.800 (0.795)	0.259	0.255 (0.098)	0.943	0.761 (0.778)
4	796 (397)	0.58 (0.58)	0.69 (0.69)	0.10	0.100 (0.034)	0.966	0.800 (0.811)	0.118	0.134 (0.046)	0.949	0.792 (0.808)
5	97 (49)	2.28 (3.49)	5.66 (5.62)	0.25	0.241 (0.089)	0.939	0.801 (0.735)	0.305	0.300 (0.121)	0.945	0.730 (0.708)
5	130 (65)	1.70 (2.05)	4.23 (4.18)	0.25	0.245 (0.072)	0.951	0.901 (0.869)	0.305	0.305 (0.098)	0.961	0.846 (0.856)
5	200 (100)	1.11 (1.18)	2.75 (2.75)	0.25	0.247 (0.062)	0.945	0.981 (0.970)	0.305	0.304 (0.083)	0.954	0.959 (0.964)
6	58 (29)	1.16 (4.51)	9.47 (10.88)	0.29	0.242 (0.105)	0.911	0.803 (0.591)	0.347	0.299 (0.144)	0.914	0.677 (0.515)
6	78 (39)	0.86 (3.54)	7.04 (7.14)	0.29	0.265 (0.105)	0.923	0.904 (0.770)	0.347	0.326 (0.131)	0.922	0.801 (0.735)
6	119 (60)	0.57 (1.54)	4.62 (4.70)	0.29	0.275 (0.073)	0.941	0.981 (0.937)	0.347	0.334 (0.102)	0.940	0.934 (0.927)
6	230 (115)	0.29 (0.93)	2.39 (2.38)	0.29	0.287 (0.051)	0.961	1.000 (0.998)	0.347	0.345 (0.072)	0.953	0.998 (0.998)
7	385 (193)	0.18 (0.26)	0.86 (0.87)	0.09	0.091 (0.031)	0.949	0.801 (0.817)	0.095	0.097 (0.035)	0.950	0.774 (0.804)
Missing at random
8	300 (213)	0.79 (0.78)	1.56 (1.57)	0.20	0.202 (0.048)	0.953	0.984 (0.988)	0.251	0.254 (0.064)	0.956	0.988 (0.988)
9	300 (207)	0.89 (0.88)	1.71 (1.73)	0.20	0.199 (0.051)	0.946	0.975 (0.969)	0.251	0.251 (0.068)	0.945	0.979 (0.968)
10	300 (179)	1.74 (2.04)	1.71 (1.73)	0.20	0.200 (0.059)	0.934	0.925 (0.909)	0.251	0.251 (0.076)	0.943	0.916 (0.910)

Scenario 5 shows that as sample size increases, the statistical power increases. However, since the sample size of 97 per group is too small given only about 12 patients having complete data, the empirical statistical power is only 74%, lower than the designed power. However, as sample size increases, the estimates, coverage of 95% CI, and statistical power are close to the true values.

Scenario 6 indicates that when a needed sample size is small due to a large difference in proportions between the two groups, even if it is calculated based on a 80% power by design, the estimation is not satisfactory. A larger sample size to achieve a greater than 90% or even a 95% statistical power is needed.

In general, the empirical statistical power using the logarithm of relative risk is slightly lower than that using the difference in proportions.

Under missing at random mechanism (Scenarios 8–10), the performance of the developed methods worked very well.

With different missing value proportions, it would be convenient in practice to decide whether or not to use the developed methods given a sample size. For this purpose, we use a measure of effective sample size. If we assign weights (1, 2/3, 1/3, 0) to subjects with complete data, two components available, one component available, and no components available, respectively, then the effective sample size is defined as the sum of weighted frequencies of each missing value pattern. For example, in Scenario 1 the effective sample size is 173(12.5% + 37.5% × 2/3 + 37.5% × 1/3 + 12.5% × 0) = 86.5. Generally speaking, the effective sample sizes should be greater than 60 in order to have a satisfactory performance. This is satisfied by the sample size to achieve an 80% power if the difference in proportions is small, say, less than 0.20. However, if the difference in proportions is greater than 0.25, the effective sample sizes should be greater than 100 even if a smaller sample size is indicated by an 80% statistical power.

In order to examine the performance of the sample size calculation, we calculated and simulated the statistical power given different sample size for Scenario 1. Figure 1 shows the calculated and simulated statistical power. The power curve from the developed methods given a sample size is lower than that from data without any missing values, but substantially higher than that from complete-case data. When a sample size is greater than 100 or an effective sample size is greater than 50, the simulated statistical power is very close to the calculated statistical power.

Figure 1.

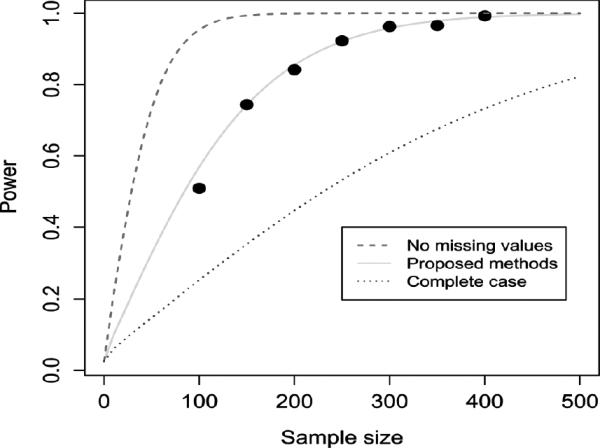
Sample size and statistical power for Scenario 1.

In order to investigate the type I error rate, the treatment group in Scenarios 1–4 had the same cell probabilities and missing value probabilities as the control group. The type I error rates are within [0.049, 0.062] with a mean of 0.055, consistent with the 95% confidence interval of [0.037, 0.064] given 1,000 simulation repetitions.

Finally, the developed methods work only if there are some observations with complete data (γ₁₁₁ ≠ 0) and all cell probabilities, except for π₀₀₀, not equal to 0 (boundary of parameter space) for both groups. Otherwise, the closed-form variance may not work because some terms have a zero denominators and identifiability problem may occurs in estimating cell probabilities. Therefore, if any parameter is believed to be 0, the parameter should not be estimated and the variance formula and likelihood function need to be modified accordingly.

4. DATA ANALYSIS EXAMPLE

For illustration, we used a hypothetical data set generated based on the results from randomized placebo-controlled, double-blind clinical trials, which were designed to test the efficacy of triple therapy (PRILOSEC/clarithromycin/amoxillin) in H. pylori eradication in patients with duodenal ulcer disease compared with clarithromycin plus amoxicillin (FDA, 2009). In the studies, H. pylori was considered eradicated if at least two of three tests (CLOtest, histology, and culture) were negative, and none was positive. It is the same as the definition that H. pylori was positive if any test was positive. Missing values were possibly encountered in such trials, because the sample sizes from three trials in intent-to-treat population were different from those in per-protocol population. There were no individual records available. To illustrate the developed methods, the sample size was set to be 300 per group, and the values of each component were changed to missing values with a probability of 0.2. Therefore, only 51.2% of subjects had complete data.

Figure 2 shows the estimated differences in eradication rates between the two groups and 95% confidence intervals from the original data, data with complete case only, and all available data using the developed methods. The point estimates were very close. However, the confidence interval derived using the developed methods with all available data was much (22%) narrower than that from the complete-case analysis. However, given the large sample size, the differences were statistically significant (p value < 001) from the three methods.

Figure 2.

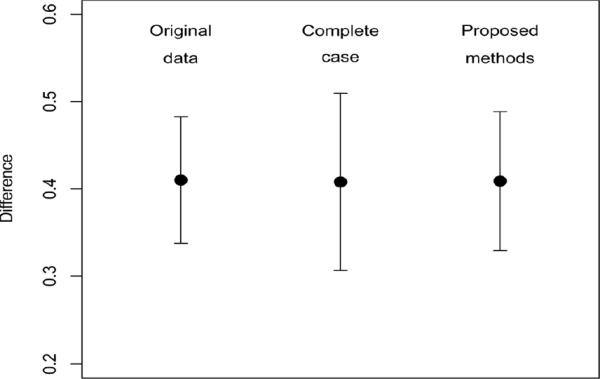
Estimated difference in proportions and 95% confidence interval from three data sets.

5. DISCUSSION AND CONCLUSION

Binary composite endpoints are widely used in clinical trials. A binary composite endpoint is usually defined from its components for each subject in a study. However, when there are missing values in the components, coding the composite endpoint in different ways may yield different and, very often, biased estimates of the prevalence rate in the composite endpoint.

In order to avoid this problem, instead of defining the composite endpoint for each subject, new methods using different parametrization approaches have been developed for estimating each probability of different combinations of the its components (cell probability) using the maximum likelihood methods (Li et al., 2007; Quan et al., 2007). Then the prevalence of success in the composite endpoint is derived from the cell probabilities. In this way, even if one or more components are missing for a subject, the remaining components can still contribute to the likelihood function through including a function of the cell probabilities. The comparison of prevalence rates in a two-component composite endpoint was also investigated (Quan et al., 2007).

In this paper, assuming the missingness is completely at random, we extended the maximum likelihood estimation methods to a three-component composite endpoint setting. We estimated the proportion in the composite endpoint and its variance using maximum likelihood estimation methods. A formula for the variance of proportion was also developed, which makes possible the use of traditional methods for sample size and statistical power calculation in two-sample proportion comparison. Furthermore, under the missing at random mechanism, the likelihood function also applies because the pseudo-likelihood function can be decomposed into two parts: one being the same as the conditional likelihood function under completely-at-random missingness, and one being related to baseline-covariate dependent missingness.

We recommend the maximum likelihood estimation be used in these problems. Simulation studies indicated that the developed methods performed satisfactorily. A hypothetical clinical data analysis showed its practical use in real data. Depending on the magnitude of missing value probabilities, statistical efficiency could be significantly improved compared with the analysis using subjects with complete data. The likelihood function was straightforward and easy to use and program.

There are some limitations in the developed methods. Most notably, we only considered completely at random missingness and missing at random mechanism. We relegate the study of different missing mechanisms to future research. In addition, the methods are based on large-sample theory. Therefore, the methods may not be applicable for small sample size, where both the asymptotics are not necessarily applicable and computational convergence issues may arise. Exact small sample procedures are another area for future research. Furthermore, though two- and three-component composite endpoints are the norm, extension to settings with more components is straightforward and potentially useful in practice.