A Comparison of Methods for Estimating Change in Drinking following Alcohol Treatment

Abstract

Background

The ultimate goal of alcohol treatment research is to develop interventions that help individuals reduce their alcohol use. To determine whether a treatment is effective researchers must then evaluate whether a particular treatment affects changes in drinking behavior after treatment. Importantly, drinking following treatment tends to be highly variable between individuals and within individuals across time.

Method

Using data from the COMBINE study (COMBINE Study Research Group, 2003) the current study compared three commonly used and novel methods for analyzing changes in drinking over time: latent growth curve analysis, growth mixture models, and latent Markov models. Specifically, using self-reported drinking data from all participants (n = 1,383, 69% male) we were interested in examining how well the three estimated models were able to explain observed changes in percent heavy drinking days during the 52 weeks following treatment.

Results

The results from all three models indicated that the majority of individuals were either abstinent or reported few heavy drinking days during the 52 week follow-up and only a minority of individuals (10% or fewer) reported consistently frequent heavy drinking following treatment. All three models provided a reasonably good fit to the observed data with the latent Markov models providing the closest fit. The observed drinking trajectories evinced discontinuity, whereby individuals seem to transition between drinking and non-drinking across adjacent follow-up assessment points. The latent growth curve and growth mixture models both assumed continuous change and could not explain this discontinuity in the observed drinking trajectories, whereas the latent Markov approach explicitly modeled transitions between drinking states.

Conclusions

The three models tested in the current study provided a unique look at the observed drinking among individuals who received treatment for alcohol dependence. Latent Markov modeling may be a highly desirable methodology for gaining a better sense of transitions between positive and negative drinking outcomes.

Introduction

Between 2005 and 2007 more than 2.2 million individuals were admitted for alcohol treatment in the United States (Substance Abuse and Mental Health Services Administration, 2009). Once admitted for treatment, continuing to drink during treatment or returning to drinking after a period of abstinence has been the modal outcome across numerous treatment studies (see McKay and Weiss, 2001 for a review). The high rates of lapses, defined as the return to problem drinking following a period of abstention or non-problem drinking, following treatment has led many to propose that alcohol use disorders are chronic, relapsing conditions (McLellan, 2007).

Over the past twenty years, alcohol researchers have recognized the existence of multiple pathways in the relapse process, defined as the process of returning to problematic alcohol use, as well as the risk factors that are often related to relapse. Oftentimes researchers and clinicians are interested in what predicts a good outcome following alcohol treatment, without forcing the definition of outcome to be drinking or not-drinking (Maisto et al., 2003). Thus, researchers and clinicians are often interested in understanding how drinking behavior changes over time. Notably the observed changes in drinking behavior following treatment do not follow a linear, continuous trend and it has been observed that there is significant variation in the observed drinking trajectories both between individuals and within individuals over time (Gueorguieva et al., 2010; Witkiewitz and Masyn, 2008; Witkiewitz et al., 2007). Given the considerable heterogeneity of posttreatment drinking it has been suggested (Hser et al., 2001; McKay et al., 2006; Stout, 2007) and demonstrated (Witkiewitz et al., 2007) that the statistical methods used to analyze treatment outcome data need to accommodate this variability.

Statistical Methods for Analyzing Change across Time

The simplest approach to analyzing treatment outcome data is to calculate a change score, which is the mean difference between post-treatment and pre-treatment alcohol use. Analysis of covariance (ANCOVA) can also be used to test mean differences on posttreatment alcohol use between groups, while controlling for pretreatment alcohol use. Note that both of these methods characterize average change and do not provide information about within person change across time. Repeated measures analysis of variance (ANOVA) and multivariate ANOVA provide estimates of both the average change over time (i.e., fixed effect), as well as variability around the average change (i.e., random effects). ANOVA and MANOVA approaches are widely used however they are also very limited. The ANOVA model assumes the variances for each pair of difference scores are equal (i.e., sphericity), which is often violated with repeated measures data. The MANOVA model has a more general variance-covariance structure, but requires equally spaced measurement occasions and does not allow for missing data. These limitations are particularly relevant when examining the clinical course of alcohol use following treatment, given measurement occasions are often not equally spaced and there are often missing data.

Two alternatives to the ANOVA and MANOVA approach are the latent growth curve model and longitudinal mixture models (including both latent growth mixture models and latent Markov models), which will be the focus of the current study due to their increasing popularity in the literature. Latent growth curve models and longitudinal mixture models are particularly valuable because they can allow for missing data, can accommodate violations of sphericity, and do not require equal measurement occasions. Most importantly, both latent growth curve models and longitudinal mixture models take advantage of individual variability in drinking trajectories across time.

Motivation for Current Study

The goal of the current study was to review three separate methods that could be used to examine posttreatment drinking changes and when each of the methods might be most useful. In doing so we were specifically interested in reviewing and examining the following substantive questions. What statistical methods are useful when trying to evaluate continuous population-based changes in drinking behavior? What methods can be used when there are differences in the ways that individuals change over time? In other words, what methods can accommodate heterogeneity in drinking changes across time? What statistical methods are most appropriate when drinking changes are discontinuous and individuals tend to transition in and out of abstinence?

In addition, we were interested in how the models compared with one another and how each model could be used to evaluate treatment outcomes. As described in more detail below, longitudinal mixture models (including latent growth mixture models and latent Markov models) provide the opportunity to examine subpopulations (i.e., classifications) of individuals who have similar patterns of drinking outcomes. Thus we were interested in whether the latent growth mixture and latent Markov models resulted in similar subpopulations. Finally, we were interested in whether drinking outcomes derived from the methods used in the current study corresponded with the conclusions derived from previous analyses of drinking outcomes using the same data (Anton et al., 2006; Donovan et al., 2008).

Materials and Methods

Design Overview

The data for this study are from the COMBINE study (“Combined Pharmacotherapies and Behavioral Interventions for Alcohol Dependence;” COMBINE Study Research Group, 2003), a multi-site randomized trial. A total of 1383 subjects across 11 research sites were randomized into 9 treatment groups, described below. Treatment was provided for 16 weeks and participants were followed for one year following treatment.

Participants

The sample was recruited from inpatient and outpatient referrals at the study sites and throughout the community. Prior to baseline, 4965 volunteers were screened by telephone to determine whether the individual met eligibility criteria. Participants were excluded if they were dependent on another drug besides alcohol, nicotine, or cannabis, recently used opioids, had a serious mental illness, had any other medical condition that could disrupt study participation, had taken one of the study medications 30 days prior to baseline, or took medication that could raise the potential risks of the study. To be included in the study, subjects needed to have a minimum of 14 drinks (females) or 21 drinks (males) average per week over a successive 30-days in the 90-day period prior to beginning abstinence. Additionally, participants needed to have two or more days of heavy drinking in the 90-day period with the last drink being within 21 days of enrollment. Heavy drinking days was defined as 4 drinks for females and 5 drinks for males. Following meeting eligibility criteria, subjects were required to produce a breath alcohol level of zero before completing consent and baseline assessments.

The final sample included 1,383 participants from 11 sites throughout the United States. Within the study group, 31% were female and 69% were male with alcohol-use disorders that had been drinking 90 days prior, but were abstinent for at least 4 days at the time of randomization. Ethnic minorities constituted 23% of the study population. Ethnic composition was as follows: 76.3% Non-Hispanic White, 11.6% Hispanic American, 7.8% African American, and 4.1% Other. The subjects’ median age was 44 years, 71% had at least 12 years of education, and 42% were married. Research retention rates did not differ significantly between groups even though a number of people did not complete portions of treatment. Within treatment, 94% completed all drinking data, while one year post treatment 82.3% completed the drinking data.

Procedures

Upon meeting inclusion and exclusion criteria, subjects completed a baseline measures assessment and were randomly assigned to one of nine treatment groups. The Medical Management groups (n=607) included: Naltrexone, Acamprosate, Naltrexone + Acamprosate, and Placebo. The Medical Management with CBI groups (n=619) consisted of: Naltrexone + CBI, Acamprosate + CBI, Naltrexone + Acamprosate + CBI, Placebo + CBI. The final group, CBI only (n=157), was included to examine the effects of pill taking on outcomes with only CBI (COMBINE Study Research Group, 2003).

Subjects received treatment for a total of 16 weeks; participants receiving study medication were offered 9 Medical Management visits during weeks 0, 1, 2, 4, 6, 8, 10, 12, and 16. Those who received CBI had a maximum of 20 sessions available to them over the 16 weeks. Participants were subsequently followed for 52 weeks post-treatment and seen at the site on weeks 26, 52, and 68 for assessments. Both study participants and researchers were blinded to treatment group assignments during treatment and through-out the 1-year post treatment assessment period.

Measures

The drinking outcome percent heavy drinking days was used as the primary outcome variable in the current study because it combines both frequency and intensity of drinking. The Form-90 interview (Miller and Del Boca, 1994) was used to calculate Percent Heavy Drinking Days (PHD). At all assessment time-points percentage of heavy drinking days was computed for each consecutive one month period following treatment. A heavy drinking day was defined as 4 or more drinks per day for women and 5 or more drinks per day for men. The primary outcome in the current study, percent heavy drinking days was calculated by dividing the number of heavy drinking days during a one month period by 30. In the COMBINE study, drinking measures were derived in the 30 days prior to baseline and during the 30 days prior to each of the post treatment assessment visits, which occurred immediately post treatment (16 weeks post-baseline), 10 weeks following treatment (26 weeks post-baseline), 36 weeks following treatment (52 weeks post-baseline) and 52 weeks following treatment (68 weeks post-baseline).

Statistical Analyses

All models were estimated using Mplus version 5.21 (Muthen and Muthen, 2007). Considering the complex sampling design in the COMBINE study (participants recruited from 11 academic sites), all parameters were estimated using a weighted maximum likelihood function and all standard errors were computed using a sandwich estimator¹ (the MLR estimator in Mplus). MLR provides the estimated variance-covariance matrix for the available data and therefore all available data were included in the models. Maximum likelihood is a preferred method for estimation when some data are missing, assuming the data are missing at random (Schafer, 1997). Attrition analyses revealed no significant differences on any study variables between those with missing data and those with complete data.

Latent Growth Curve Models

Latent growth curve (LGC) models have been increasingly used to model inter- and intraindividual change across time.² The basic latent growth curve model, for person i with repeated measures variable y measured over time points t is defined by

$$y_{ti}={\lambda }_{0t}{\eta }_{0i}+{\lambda }_{1t}{\eta }_{1i}+{\epsilon }_{ti}$$ (1)

with λ_1t denoting the factor loadings that indicate time of measurement for repeatedly measured y_ti and λ_0t is a constant equal to the value of 1. The latent variables (η_0i, η_1i) are identified by

$${\eta }_{0i}={\nu }_0+{\zeta }_0$$ (2)

$${\eta }_{1i}={\nu }_1+{\zeta }_1,$$ (3)

denoting the individual intercept (η_0i ; i.e., starting value or initial level) and slope (η_1i ; i.e., change over time) and random variance around the individual intercept and slope (ζ₀ and ζ₁, respectively). The means of the growth factors are defined by ψ₀ and ψ₁ for the intercept and slope, respectively. Time-specific deviations are represented by the independent and identically standard normally distributed ε_ti with variance σ²_ε . The residuals ε_ti , ζ₀, ζ₁ are assumed normally distributed with zero means.

In the current study, LGC models were defined by linear and quadratic slope effects with the intercept centered at the first assessment following treatment (26 weeks). Model fit of the LGC models were evaluated by χ² values, the Root Mean Square Error of Approximation (RMSEA; Browne and Cudeck, 1993), and the Comparative Fit Index (CFI; Bentler, 1990). Models with non-significant χ², RMSEA less than 0.06 and CFI greater than 0.95 were considered a good fit to the observed data (Hu and Bentler, 1999).

Longitudinal Mixture Models

In the specification of the latent growth model it is assumed that the latent variables represent an underlying continuous growth pattern, in other words the latent variables are assumed to be continuous and normally distributed. The growth pattern can be linear, quadratic, polynomial, or any other functional form that provides a measure of change over time, but the growth must follow a continuous distribution. This assumption might not always be appropriate, particularly when change over time differs across individuals or is discontinuous. Latent class models incorporate a categorical latent variable, which represents an unobserved variable that is assumed to be a mixture of subpopulations (Clogg, 1995). In other words, a categorical latent variable is an unobserved measure that is assumed to be categorical in nature, such that the underlying distribution of the latent measure is assumed to be discrete.

The basic latent class model is a measurement model where the classes are defined by an individual’s pattern of responses to each item and individuals with similar patterns of responding are considered part of the same subpopulation. The parameters of the latent class model help to define the latent classes: (1) latent class proportions indicate how many people are expected to be in each class; (2) response probabilities are the probabilities of responding to an item, given one is expected to be in each latent class (probabilities closer to 1.0 indicate a strong correspondence between latent class membership and endorsement of the item). It is assumed that the latent class variable explains all of the variation between variables within each class (i.e., within each class the variables are uncorrelated) an assumption called conditional independence. The current study highlights two types of longitudinal mixture models (growth mixture and latent Markov models), described below, however several extensions of the latent class model exist and the interested reader is referred to Hagenaars and McCutcheon (2002) for more information.

Latent growth mixture models (LGMM) combine the latent growth curve with a categorical latent variable (Muthen and Shedden, 1999). The latent categorical variable is used to identify discrete subgroups of individuals who follow a similar pattern of change over time. Each individual has their own unique growth curve and the heterogeneity in growth curves across individuals is summarized by a finite number of growth trajectory classes. The latent class growth model specifies continuous latent growth factors (intercept and slope), as described in the prior section, and the continuous growth factors are indicators of a categorical latent variable, k. LGMM is an extension of equations 2 and 3, where equations 2 and 3, can be described for class k (k = 1, 2, 3, …, K),

$${\eta }_{0i}={\nu }_{0k}+{\zeta }_0$$ (4)

$${\eta }_{1i}={\nu }_{1k}+{\zeta }_1.$$ (5)

The residuals ζ_i in LGMM have a 3×3 covariance matrix Ψ_k, which can be specified to vary across k classes. In addition, the residuals of equation 1 ε_ti can vary across trajectory classes. Variances and covariances can be estimated within each class, thus individual differences in change over time are decomposed into a between-class component and a within-class component.

In the current study, LGMM were estimated by including a categorical latent variable as a predictor of the LGC intercept, linear slope and quadratic slope factors. The variance of the quadratic growth effect was constrained to zero (for model convergence) and the variances and covariances of the intercept and linear slope were estimated. In the current analyses we estimated class-invariant growth factor variances and covariances (i.e., the variances and covariance were constrained to be equal across classes), although this restriction can be relaxed. The number of classes was determined by multiple indices of model fit and classification precision: Bayesian Information Criteria (BIC; Schwartz, 1978), the Lo Mendell Rubin Likelihood Ratio Test p-value (LRT; Lo et al., 2001), classification precision (defined by entropy, a summary measure of the estimated posterior class probabilities), and interpretability of latent classes. Nylund and colleagues (2007) showed superior performance of the BIC in correctly identifying the correct number of classes most of the time, with a lower BIC indicating a better fitting model. The LRT provides a test of the improvement in fit for each additional estimated class (k), thus testing whether a k class model fits significantly better than a k-1 class model. The Bootstrapped Likelihood Ratio Test (BLRT), which has been shown to be a superior method for determining class enumeration compared to the LRT in simulation studies (Nylund et al., 2007), is not available for complex survey analyses, in which standard errors are adjusted for the potential correlation between observations within treatment site.

Latent Markov modeling (LMM) is also a mixture model, in which change over time is modeled by estimating the probabilities of transitioning between discrete states (or classes) across time (Vermunt et al., 1999). Random effects at each point in time include the variation around the outcome variable, the probability of belonging to a particular state, the probability of belonging to that state given the previous state, and the amount of time spent in a particular state. Using the terminology of Böckenholt (2005) and the example of drinking states, the transition rate is defined ω_s1s2 as the probability of transitioning from state s₁ to s₂ at the current point in time, t, given that the state s₁ was observed at time t - Δt:

$${\omega }_{s_1{s}_2}=\underset{\Delta t\to 0}{\lim }\frac{\mathrm{Pr}\left[{\text{transition}}_{S1\to S2}\mathit{in}\right(t,t+\Delta t\left)\right]}{\Delta t}$$ (6)

The sequence of states follow a first-order Markov chain with:

$${\tau }_{s_1{s}_2}={\omega }_{s_1{s}_2}∕{{\omega }_{s_1}}^{•}$$ (7)

Thus, τ_s1s2 represents the probability of transitioning to heavy drinking (s₁), given an individual is currently classified in the light drinking (s₂) state.

In the current study, latent Markov models were conducted using two steps. First, latent profile measurement models (i.e., latent class models in which the observed indicators are continuous, rather than categorical) of percent heavy drinking days were estimated at each time-point and the BIC, LRT, and classification precision were used to determine the ideal number of classes for each point in time. The latent profile models at each time point were then combined into a single model that included the estimation of the transition probabilities, which are the estimates of the probability of transitioning between adjoining latent classes across time.

Results

At baseline the average percentage of heavy drinking days (PHD) was 65.52% (SD = 28.57%), all participants drank on at least one day in the 30 days prior to baseline and only 0.9% of the sample (n = 12) did not engage in a heavy drinking day during the pre-baseline period. In the 30 days prior to the end of treatment 53.1% of the sample did not engage in a heavy drinking day and the average PHD was 16.78% (SD = 28.61%). The average PHD increased to 21.98% (SD = 31.43%) during the 30 days prior to the 2.5 month follow-up and by the 9- and 12-month follow-ups the average PHD was approximately 26% (26.40% (SD = 33.40%) at 9-months and 26.20% (SD = 34.27%) at 12-months). More than 1/3 of the sample did not engage in any heavy drinking days across the first year following treatment (32% and 38% at 9- and 12-months, respectively).

Latent Growth Curve Models

First, a latent growth curve model with linear and quadratic effects was estimated. The model provided a good fit to the data based on CFI (CFI = 0.997), but did not fit well based on χ² (χ² (1) = 14.78, p < 0.001) or RMSEA (RMSEA = 0.10 (90% C.I. 0.06 – 0.15)). As seen in Table 2 the average intercept was 21.21 with a significantly positive linear slope (B = 3.67 (SE = 0.31), p < 0.001) and negative quadratic slope (B = −0.62 (SE = 0.06), p < 0.001), indicating an increase in PHD initially with a deceleration of PHD over time. The variances around the growth factors (also in Table 2) indicate significant variability around the mean growth curve.

Table 2.

Class proportions, means and variances of growth factors, based on estimated model.

	Means (Variances)
	Intercept	Linear slope	Quadratic slope
LGC (100%)	21.21* (725.08*)	3.67* (91.28*)	−0.62* (3.56*)
LGMM
Infrequent (78 %)	9.61* (86.39*)	5.37* (26.45*)	−0.83* (0.00 a)
Increasing (12%)	46.14* (86.39*)	3.53* (26.45*)	−0.72* (0.00 a)
Frequent (10%)	82.36* (86.39*)	−7.60* (26.45*)	0.83* (0.00 a)

^*Note. p < 0.05;

^aquadratic slope variance constrained to zero in LGMM.

Latent Growth Mixture Models

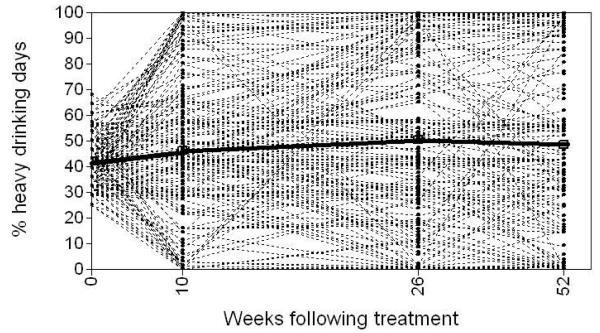
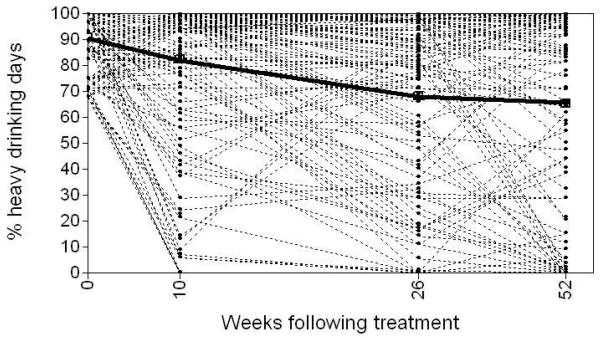
A series of analyses were conducted to examine the optimal class solution for the LGMM based on the BIC, LRT p-value, classification precision, and interpretability of latent classes. The 3-class model provided the best balance of parsimony and model fit, with a significant improvement in fit over the 2-class model (LRT = 666.21, p = 0.0006). The 4-class models did not significantly improve model fit (LRT = 367.36, p = 0.10) and the addition of the 4^th class did not add significantly to the substantive interpretation of the models. The classification quality was excellent (entropy = 0.98) and there was clear distinction between classes (average latent class probabilities for most likely class ranged from 0.96 to 1.00). The three classes could be described as: non- or infrequent heavy drinking (mean intercept = 9.61, linear slope = 5.37, quadratic slope = −0.83), occasional heavy drinking with a non-significant increase in heavy drinking over time (mean intercept = 46.14, linear slope = 3.53, quadratic slope = −0.72), and frequent heavy drinking (mean intercept = 82.36, linear slope = −7.60, quadratic slope = 0.83). It is important to note that the estimated classes do not explain all of the heterogeneity in PHD over time. As seen in Figures 1a-1c the estimated classes (thick lines) only explain a general trend in the observed data (thin lines) and there are many individuals who are most likely classified as “infrequent heavy drinkers” who are engaging in heavy drinking 100% of days in a given month.

Figure 1.

(A) Estimated means and observed individual values based on most likely class membership for the infrequent heavy drinking class in the latent growth mixture model (n = 1,011). (B) Estimated means and observed individual values based on most likely class membership for the occasional heavy drinking class in the latent growth mixture model (n = 156). (C) Estimated means and observed individual values based on most likely class membership for the frequent drinking class in the latent growth mixture model (n = 129).

Latent Markov Models

First we conducted a latent profile analysis at each time-point. At all time-points the LRT identified the 7-class models as the best fitting models; however across all time-points four of the seven classes had class proportions less than 5%. Given prior research supporting 3-class solutions for both growth mixture models (Witkiewitz and Masyn, 2008; Witkiewitz et al., 2007) and latent transition analyses (Witkiewitz, 2008), as well as considerations of the size of the model when incorporating multiple classes across 4 time-points, we opted for a 3-class model for each time-point. For example, with 3-classes per time-point and 4 time-points there are 3⁴ = 81 latent class patterns. With 7-classes per time-point and 4 time-points there would be 7⁴ = 2401 latent class patterns, which would be more class patterns than participants. Across all time points the 3-class models yielded significant improvements in fit over the 2-class models (16 weeks: LRT = 638.40, p < 0.005; 26 weeks: LRT = 562.65, p < 0.005; 52 weeks: LRT = 492.75, p < 0.005; 68 weeks: LRT 462.86, p < 0.005). For all time points the three classes could be described as infrequent heavy drinking (approximately 64.1% of the sample), frequent heavy drinking (approximately 17.0% of the sample), and occasional heavy drinking (approximately 18.9% of the sample).

The latent Markov model was then estimated to examine the transitions between latent classes across time points. First order autoregressive paths were estimated. The model had good classification precision based on entropy = 0.95. Latent transition probabilities (P), shown in Table 3, indicate the most likely transitions were from occasional to frequent heavy drinking (week 16 to 26: P = 0.24; week 26 to 52: P = 0.24; week 52 to 68: P = 0.16) and from occasional to infrequent heavy drinking (week 16 to 26: P = 0.18; week 26 to 52: P = 0.17; week 52 to 68: P = 0.30). The joint probabilities (a summation of conditional probabilities for each latent class pattern) of remaining in the same class across every time-point (not shown in the Table) was highest for infrequent heavy drinkers (P = 0.51), then frequent heavy drinkers (P = 0.05), and occasional heavy drinkers (P = 0.03). The joint probability of transitioning from frequent heavy drinking or occasional heavy drinking to infrequent heavy drinking was 0.14, whereas the joint probability of transitioning from infrequent or occasional heavy drinking to frequent heavy drinking was 0.17. Figures 5a-5c provide the estimated profiles (thick lines) and the observed individual trajectories (thin lines) for the three most common latent class patterns, which can be described as an infrequent heavy drinking pattern, a frequent heavy drinking pattern, and an infrequent-to-occasional heavy drinking pattern. As seen in these figures the estimated patterns provided an excellent fit to the observed drinking trajectories.

Table 3.

Class proportions and latent transition probabilities, based on latent Markov model.

	Week 16				Week 26				Week 52
	Infreq.	Occas.	Freq.		Infreq.	Occas.	Freq.		Infreq. (n≈831)	Occas. (n≈239)	Freq. (n≈226)
Week 0				Week 10				Week 26
Infreq. (n≈1006)	0.84	0.13	0.03	Infreq. (n≈887)	0.85	0.11	0.04	Infreq. (n≈822)	0.90	0.09	0.01
Occas. (n≈162)	0.18	0.58	0.24	Occas. (n≈238)	0.17	0.59	0.24	Occas. (n≈256)	0.30	0.54	0.16
Freq. (n≈128)	0.08	0.13	0.79	Freq. (n≈171)	0.11	0.13	0.76	Freq. (n≈218)	0.08	0.15	0.77

Note. Infreq.=infrequent heavy drinking class; Occas.=occasional heavy drinking class; Freq.=Frequent heavy drinking class

Correspondence between Models and Previous COMBINE Analyses

The similarities between the latent growth curve model and the longitudinal mixture model can be evaluated by considering the average intercept and slope in the latent growth curve model and the most common trajectories/patterns in the longitudinal mixture models. The average percent heavy drinking days for the growth curve models was around 20%. In the latent growth mixture model the infrequent heavy drinking class was the largest class (approximately 64% of the sample most likely classified), which had an average trajectory of less than 20% heavy drinking days. The latent Markov model indicated that the largest response pattern (n ≈ 675) was an infrequent heavy drinking pattern, where no individual’s percent heavy drinking days exceeded 30% and the average percent heavy drinking days for that response patterns was around 5%.

The correspondence between the latent growth mixture and latent Markov models was estimated by examining the overlap among individuals who were most likely classified as infrequent, occasional and frequent drinkers across both models. In general, cross-classification tests indicated significant overlap between growth mixture classes and Markov class patterns (χ² (4) = 787.25, p < 0.001). Sixty-seven percent of those who were likely classified as infrequent heavy drinkers by the latent growth mixture model had an infrequent drinking pattern based on the latent Markov models, whereas 100% of individuals who were expected to follow an infrequent drinking pattern based on the latent Markov model were also likely to be classified as an infrequent heavy drinker by the latent growth mixture model. All individuals who were classified as frequent heavy drinkers by the latent growth mixture models were not expected to follow an infrequent drinking pattern.

Finally, results from the mixture models tested in the current study were compared to the conclusions derived from prior analyses of treatment effects on drinking outcomes in the COMBINE study (Anton et al., 2006; Donovan et al., 2008). These previous studies of the COMBINE outcomes utilized mixed effects general linear models to assess time-by-treatment effects, with planned comparisons of treatment interactions. Results from these analyses indicated that individuals who received naltrexone and those who received the combined behavioral intervention in combination with active treatment or placebo had the best clinical outcomes, defined by more abstinent days and lower rates of relapse, and were less likely to return to heavy drinking. The percentage of individuals with a good clinical outcome, defined as abstinence or moderate drinking without alcohol-related problems (with moderate drinking defined as a maximum of 11 (women) or 14 (men) drinks per week, with no more than 2 days on which more than 3 drinks (women) or 4 drinks (men) were consumed; and alcohol-related problems defined as endorsing 3 or more consequences on the Drinker Inventory of Consequences), were estimated for each treatment group (Anton et al., 2006) and are presented in Table 4 alongside the percentages of individuals most likely classified as infrequent heavy drinking based on the latent growth mixture and Markov models in the current study. As seen in Table 4, the overall conclusions across definitions of outcomes are consistent: individuals who received naltrexone or combined behavioral intervention in combination with active treatment or placebo had the best outcomes. The expected pattern of infrequent heavy drinking, as defined by the latent Markov models, was the strictest criterion of good outcomes (i.e., lower percentage of individuals across treatment groups were expected to be classified in the infrequent heavy drinking pattern) and the infrequent heavy drinking class, as defined by the latent growth mixture model, was the least strict criterion of good outcomes.

Table 4.

Percentage of individuals with good clinical outcomes, as defined by Anton et al., (2006) and the results from the current study.

Treatment group	Good clinical outcome based on Anton et al.	Infrequent drinking class based on GMM	Infrequent drinking pattern based on LMM
Placebo + MM	58.2	68.3	38.0
Naltrexone + MM	73.7	83.9	55.9
Acamprosate + MM	60.8	68.1	47.9
Naltrexone + Acamprosate + MM	78.4	85.8	54.6
Placebo + CBI	71.3	82.1	57.2
Naltrexone + CBI	74.4	80.3	57.1
Acamprosate + CBI	74.4	78.5	55.6
Naltrexone + Acamprosate + CBI	73.5	82.5	57.3
CBI only	60.6	72.8	44.9

Note. CBI = Combined Behavioral Intervention; MM = Medication Management

Discussion

The current study examined three different methods for examining drinking trajectories following treatment using a latent variable modeling approach. The latent growth curve (LGC) model was the most parsimonious and provided a reasonable fit to the observed data. The latent growth mixture model (LGMM) indicated a three class model provided the best fit to the observed data however there was generally a trend for some misclassification as seen in Figures 1a-1c. The latent Markov (LMM) model provided an excellent fit to the observed data.

The results from all three models were relatively consistent. The majority of individuals did not engage in frequent heavy drinking in the first year following treatment. These results contradict the notion that a single episode of heavy drinking (i.e., a “lapse”) following treatment is a treatment failure. Rather, individuals who engage in some heavy drinking can return to abstinence or non-heavy drinking. That being said, the consequences that occur during a single episode of heavy drinking can be severe and treatment researchers should continually seek to develop interventions that target the prevention of any heavy drinking episodes.

Strengths and Limitations of Each Model

LGC modeling would be particularly useful in situations where the data are continuously normally distributed and the researcher is interested in making population based inferences. In other words, the researcher is interested in describing the average changes in drinking for an entire group of individuals. The latent growth curve model also naturally extends to a multiple group situation, where the researcher might be interested in describing the average drinking for a particular treatment group or across treatment groups. Covariates (e.g., individual characteristics, within treatment characteristics) can easily be incorporated into LGC models, which is a major advantage of the approach. The primary limitation of traditional LGC models is that they cannot accommodate discontinuity in individual drinking, and thus are not useful for making specific statements about discrete changes in individual drinking states over time. Therefore, LGC modeling may be much less useful for evaluating individual clinical course. Piecewise LGC models may be able to accommodate some discontinuity by estimating trajectories across discrete time periods (e.g., during treatment vs. posttreatment), however the “jumping” between drinking and non-drinking across time could not be accommodated by a piecewise model because at least three time points are needed to estimate a LGC model.

LGMM can be useful when the researcher suspects that the individuals in a particular sample might be changing in qualitatively distinct ways. For example, if the researcher suspects that there is a group of treatment responders who all experience reductions in drinking over time and a group of treatment non-responders who experience no change or increases in drinking over time. By assuming the responders and non-responders come from the same population of drinkers could lead to the erroneous conclusion that, on average, there were no changes in drinking behavior following treatment. Whereas estimating a categorical latent variable that represents two classes of individuals (e.g., responders and non-responders) provides an opportunity to model these two trajectories separately. Covariates can also be incorporated as predictors of within class trajectories (i.e., predicting intercept and slope within each class) or can be incorporated as predictors of class membership (e.g., odds of being classified as a heavy vs. light drinker). There are numerous problems with the application of latent growth mixture models in the field and researchers are encouraged to proceed with caution in using these models. Several methodological papers have addressed these problems and all users of LGMM are encouraged to read these papers prior to estimating a model (Bauer and Curran, 2003; Bauer, 2007; Hipp and Bauer, 2004; Sampson and Laub, 2005). In brief, the primary concerns are the tendency for over-extraction of latent classes (Bauer and Curran, 2003), reification of groups that do not exist (Raudenbush, 2005), loss of power due to artificially dividing growth trajectories into classes and detecting spurious covariate by class interactions that do not exist (Bauer and Curran, 2003). In the current study we observed the LGMM classified (incorrectly) a number of individuals as infrequent heavy drinkers who engaged in frequent heavy drinking at some occasions. Thus, latent growth mixture modeling could be a very dangerous tool if being used to make decisions about whether a particular treatment is effective in producing good outcomes, when it is important for “good drinking outcomes” to mean few episodes of frequent heavy drinking.

LMM, and variants of LMM (e.g., latent transition analysis for categorical indicators, see Witkiewitz, 2008), can be useful when there are discontinuous changes in drinking across time. There were many instances where individuals transitioned from 0% to 100% abstinent between each measurement occasion. Using a continuous LGC or a LGMM (in which the growth functions are estimated as continuous within class) we would be unable to capture this discontinuity, whereas LMM provided an excellent representation of the observed transitions across measurement occasions. Unlike the LGMM, the LMM provided a more accurate classification of individuals who followed an infrequent heavy drinking pattern and could be very useful for individuals needing a high degree of specificity in identifying whether individuals respond well to a particular treatment. It is important to note that while the current study focused on frequency of heavy drinking, LMM could also be used to identified patterns of moderate drinking, drinking-related problems, or other types of outcomes (e.g., quality of life) Unfortunately, LMM is a much more idiographic technique, which requires the estimation of large contingency tables. Thus, the estimation of LMM often requires extensive computational power, particularly when covariates are included in the model.

Similarities and Differences between Mixture Models in Prediction of COMBINE Outcomes

Cross-classification tests indicated significant overlap in the likelihood of individuals being classified as most likely to be infrequent heavy drinkers and frequent heavy drinkers. The latent growth mixture models classified more individuals as infrequent heavy drinkers than the latent Markov models, and based on the observed trajectories seen in Figure 1a some of the individuals classified as infrequent heavy drinkers by the growth mixture models reported 100% frequent heavy drinking days at some assessment points.

With respect to the COMBINE treatment outcomes, the results from the latent growth mixture and Markov models were entirely consistent with the findings of previous COMBINE analyses (Anton et al., 2006; Donovan et al., 2008) in suggesting that individuals who received naltrexone with or without the combined behavioral intervention and those who received the combined behavioral intervention with active treatment or placebo were more likely to be classified as infrequent heavy drinkers who followed an infrequent drinking pattern. These analyses were based on post-hoc classification of individuals into their most likely latent class or latent class pattern and future research could be conducted to evaluate whether treatment group predicts different likelihood of class membership or most likely class pattern. For example, recent analyses of the COMBINE data by Gueorguieva and colleagues (2010) examined whether treatment condition predicted likelihood of membership in distinct drinking trajectories that were derived using latent class growth analysis. Latent class growth analysis is a special case of latent growth mixture modeling in which the variances of the growth trajectories are constrained to zero. Results from the study indicated that individuals who received naltrexone had a lower probability of following a “nearly daily” drinking trajectory and receiving the combined behavioral intervention predicted a lower probability of following an “increasing to nearly daily” trajectory of any drinking (Gueorguieva et al., 2010).

Limitations

There are several notable limitations of the current study. The most important limitation is that all of the models were wrong and there is unlikely to ever be a “right” model. Rather, the goal of this study was to determine which model provided the closest representation of reality. Using simulated data could have provided more insight into what model was most appropriate for the underlying distribution in the population, but our goal was to generalize the findings from previous mixture model simulation studies (Bauer, 2007; Bauer and Curran, 2003) to the estimation of real data. One primary problem with all of the models tested in the current study was the use of arbitrarily selected time points for the assessment of drinking outcomes. Significant within-individual variability could be observed between these discrete time points and it is unclear to what extent the current results would change if different assessment points were selected.

Second, the models did not include covariates that might have influenced drinking patterns over time. For example, previous work has indicated the importance of alcohol dependence in the prediction of drinking classes (Witkiewitz & Masyn, 2008) and drinking patterns (Witkiewitz et al., 2007). Including covariates in growth curve and mixture models provides an added level of complexity that was beyond the scope of the current study. In addition, the methodological research on these methods has provided little guidance on how to incorporate covariate predictors within growth mixture and latent Markov models (with the exception of Vermunt et al., 1999). Finally, we did not examine other potential problems with mixture models that have been described. Notably it is impossible to test the assumption that data were missing at random. And although we established that missing data did not influence the study variables, future research should examine the extent to which non-ignorable missing data could impact the model results.

Conclusions

The current study sought to examine the differences in model fit and utility using different modeling specifications with real data. In particular, our goal was to determine whether disaggregating the continuous growth curves estimated using a latent growth curve model, by estimating mixtures, provides any additional information or utility. In our prior work (Witkiewitz, 2008; Witkiewitz and Masyn, 2008; Witkiewitz et al., 2007) we have argued that mixture models have been useful to disaggregate the heterogeneity in drinking trajectories following treatment. And, in the words of Bauer (2007): “there are some situations in which groups exist, or at least putatively exist, for which mixture analyses may be appropriate and valuable.”

Based on the current results it is suggested that latent Markov modeling (including latent transition analyses for categorical data) may be a highly desirable methodology for gaining a better sense of transitions between positive and negative drinking outcomes, however more research on the use of latent Markov models with alcohol use data is necessary. In general, methodological research examining different mixture modeling assumptions and problems with the violations of assumptions has yet to be conducted. Future research may also benefit from a systematic approach to examining drinking trajectories. For example, one could start with a latent Markov model to determine the most common drinking patterns and then examine whether certain covariates predict those patterns. Once patterns are identified a latent growth model of individuals within each pattern could be estimated with covariates predicting variation in intercept and slope among those who follow a particular drinking pattern.

Figure 2.

(A) Estimated means and observed individual values based on most likely class membership for the frequent drinking pattern in the latent Markov model (n = 70). (B) Estimated means and observed individual values based on most likely class membership for the infrequent-to-occasional heavy drinking pattern in the latent Markov model (n = 54). (C) Estimated means and observed individual values based on most likely class membership for the infrequent heavy drinking pattern in the latent Markov model (n = 675)

Table 1.

Fit statistics and classification precision across models.

Model	# parameters	LL	BIC	Entropy
LGC	13	−22700.5	45494.3	1.00
LGMM (2-class)	14	−22251.8	44603.9	0.97
LGMM (3-class)	18	−21907.1	43943.2	0.98
LGMM (4-class)	22	−21717.0	43591.7	0.95
LGMM (5-class)	26	−21599.0	43384.4	0.95
LMM (3-classes each time)	27	−20468.7	41130.9	0.95

Note. LGC = latent growth curve model; LGMM = latent growth mixture model; LMM = latent Markov model; LL = log likelihood; BIC = Bayes Information Criteria.