Computer Simulations of Atherosclerotic Plaque Growth in Coronary Arteries

Abstract

A three dimensional mathematical model with a linear plaque growth function was developed to investigate the geometrical adaptation of atherosclerotic plaques in coronary arteries and study the influences of flow wall shear stress (WSS), blood viscosity and the inlet flow rate on the growth of atherosclerotic plaques using computational plaque growth simulations. The simulation results indicated that the plaque wall thickness at the neck of the stenosis increased at a decreasing rate in the atherosclerosis progression. The simulation results also showed a strong dependence of the plaque wall thickness increase on the blood viscosity and the inlet flow rate. The progression rate in a coronary artery was lower with a higher inlet velocity flow rate and higher with a smaller value of the blood viscosity.

1 Introduction

Atherosclerosis is a leading cause of mortality in the western countries. Atherosclerosis is the hardening and narrowing of the arteries, caused by the slow buildup of plaque on the inside of walls of the arteries. It has been observed that human atherosclerotic lesions preferentially form in relation to branch, bifurcation and bends of the major arteries, where the flow is highly disturbed with complex secondary flow pattern, flow separation and reversal with low and oscillating flow shear stress. The initiation and progression of atherosclerotic plaques involve complex interactions between the blood flow and the vessel wall. An important haemodynamic parameter in this interaction is the wall shear stress (WSS), which is the mechanical force imposed on the endothelium by the flowing blood.

The role of the WSS in the genesis and the development of atherosclerotic diseases has been intensively investigated by many researches, examining the relationship between shear stress and the presence of lesions and the intima-media thickness [1–9]. Caro et al [1] suggested that the distribution of fatty streaking in human aorta might be coincident with the regions in which the shear rate at the arterial wall is locally reduced. The low shear stress contributes to an increased fluid residence time, which may result in modification of the mass transport of atherogenic substances between lumen and the wall or in interference with endothelial metabolism [1, 2]. Ku et al [2] and Zarins et al [3] have estimated shear stress with laser-Doppler anemometry and found that intimal thickening bears an inverse relationship to both maximum shear stress and minimum shear stress. Krams and Van Langenhove et al used angiographically-guided intravascular ultrasound and computational fluid dynamics to reconstruct the local haemodynamics in a coronary artery. An inverse relationship between shear stress and wall thickness was demonstrated [4, 5]. Gnasso et al [6] and Jiang et al [7] investigated the WSS in the carotid arteries in normal healthy subjects and in hypertensive patients, respectively. They found that the WSS at both mean and peak velocity is significantly and negatively related to the intima-media thickness.

During the last two decades, numerous in vivo and in vitro studies have also been conducted on determining, by means of quantitative angiography, the correlation between the WSS and the change in luminal diameter over time [6, 7, 10–12]. Gibson et al [10] conducted a study to assess the rate of change in coronary arterial diameter in patients over three years. They found a significant correlation between the low shear stress and an increased rate of atherosclerosis progression. Pedersen et al [11] studied the relationship between WSS measured in vivo and early atherosclerotic lesions in the abdominal aorta. They presented three scatter plots of relative intimal thickness as functions of mean WSS, maximum WSS and oscillating shear index showing that relative intimal thickness has a significant linear decreasing with mean WSS and with maximum WSS. Tang et al [12] investigated the correlation between human carotid atherosclerotic plaque progression with plaque wall stress and fluid shear stress based on in vivo patient tracking MRI data. They found that the wall thickness increase correlates negatively with flow wall shear stress calculated from previous observation time and positively with flow wall shear stress calculated from current observation time (time interval: 18 months). A linear approximation formula was given by the least squares method. However, not much work has been reported on the computational models that simulate plaque progression and predict the future plaque rupture risk. Yang and Tang et al [13] introduced a computational procedure based on a meshless generalized finite difference method and serial MRI data to simulate carotid atherosclerotic plaque progression. The numerically simulated plaque progression agreed well with the actual plaque geometry. In a previous paper [14] we carried out computations to simulate the plaque growth in a curved artery using a growth function obtained by Tang and Yang et al in [12].

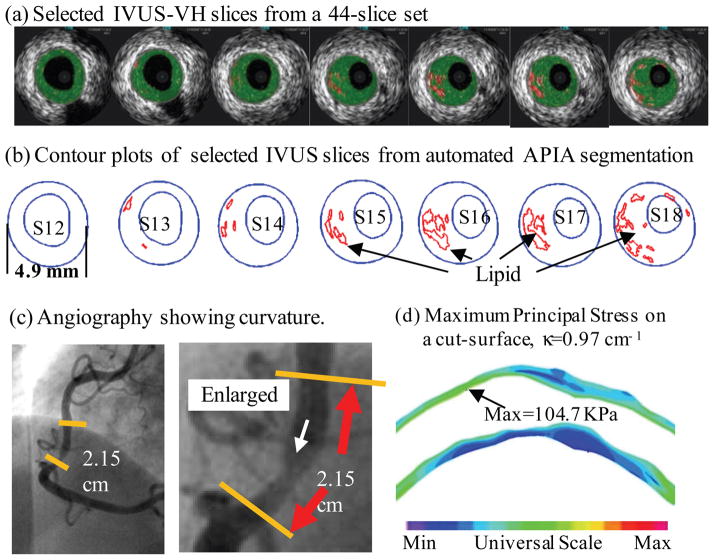
The aims of the present work are to investigate how the geometrical adaptation of atherosclerotic plaques in coronary arteries is related to the WSS and to study the influences of flow parameters, such as blood viscosity, inlet flow rate and flow velocity profile, on the plaque wall thickness increase by computer simulations. Numerical computations are carried out under a variety of physiological flow conditions to study the local flows in curved arteries with progressing stenosis. The initial domain of computation is simplified from the geometry of a human coronary atherosclerotic plaque re-constructed from in vivo intravascular ultrasound image of a patient with informed consent obtained [15].

2 Mathematical model and computational approach

The blood flow is assumed to be incompressible, laminar and Newtonian. The validity of the assumption of laminar flow in the calculation of blood flow in stenotic arteries with bend had been confirmed by Nosovitsky et al [16]. They presented figures comparing the shear stress profiles on the inner wall of laminar with κ-ε turbulent models (The results for the velocity vectors were similar and were not presented). The figures show that within the stenotic curved section of interest the two results are essentially the same, leading to the conclusion that the effects of the turbulence are small and can be safely neglected. To treat blood as a Newtonian fluid is a common assumption used in simulating flow in large arteries. Johnston et al [17] compared the effects of different blood viscosity models on the WSS distributions in right coronary arteries during the cardiac cycle. Their study showed that the use of a Newtonian blood model is a reasonably good approximation when studying the WSS distribution for transient blood flow in large arteries. As an initial modeling effort, a rigid wall model was used in this paper for our simulation. Differences of WSS predictions between a compliant model and a rigid wall model depend on vessel compliance, dimensions, geometry, curvature, stenosis severity and other factors. WSS difference is mainly caused by vessel deformation under pulsating pressure. For stiff coronary arteries with mild stenosis under consideration of this paper, vessel diameter variation would be less than 2% in a cardiac cycle. Peak WSS differences between compliant and rigid wall models would be less than 10%. For arteries with severe stenosis, Yang et al reported that peak WSS differences from compliant and rigid models can differ by 30–40% [18]. The rigid wall model should be a good approximation for the case studied in this paper. The following time dependent three dimensional Navier Stokes equations are used as the governing equations:

$$\rho (\partial \mathbf{u})/(\partial t)-\nabla ·[-p\mathbf{I}+\eta (\nabla \mathbf{u}+{(\nabla \mathbf{u})}^T)]+\rho (\mathbf{u}·\nabla )\mathbf{u}=\mathbf{0},\text{in}\hspace{0.17em}\mathrm{\Omega },$$ (1)

$$\nabla ·\mathbf{u}=0,\text{in}\mathrm{\Omega },$$ (2)

where η is the viscosity of the fluid, u = (u_1, u_2, u₃) is the flow velocity, p is the internal pressure and ρ is the density of the fluid. The initial computational domain Ω is a simplified geometry re-constructed from in vivo intravascular ultrasound (IVUS) image of a patient [15] shown in Fig. 1. The initial conditions u₀ and p₀ are obtained by solving the system of steady state Navier Stokes equations. The boundary conditions are as follows: at the inlet boundary, a blunt inlet velocity profile with a time varying wave-form is assumed for the axial velocity,

Figure 1.

A human coronary plaque sample re-constructed from in vivo IVUS images [15].

$$u=Qf(\mathbf{x})w(t),$$ (3)

where f is the velocity profile in spatial variable; Q is a scale chosen as different values in the computation such that Qf (x)w(t) yields different mean flow; w is the velocity pulse waveform, shown in Fig. 2, reproduced based on a physiological pulsatile coronary velocity wave-form [17, 19], which was recorded in the right coronary artery of a human and contains a period of reverse flow in systole and a rapid acceleration and deceleration in diastole. The outlet boundary is treated as an open boundary, imposed with zero normal stress:

$$(-p\mathbf{I}+\eta (\nabla \mathbf{u}+{(\nabla \mathbf{u})}^T))\mathbf{n}=\mathbf{0},$$ (4)

where n = (n_1, n_2, n₃) is the outward normal unit vector at the outlet boundary. A no-slip condition is applied to the velocities at the wall boundary.

Figure 2.

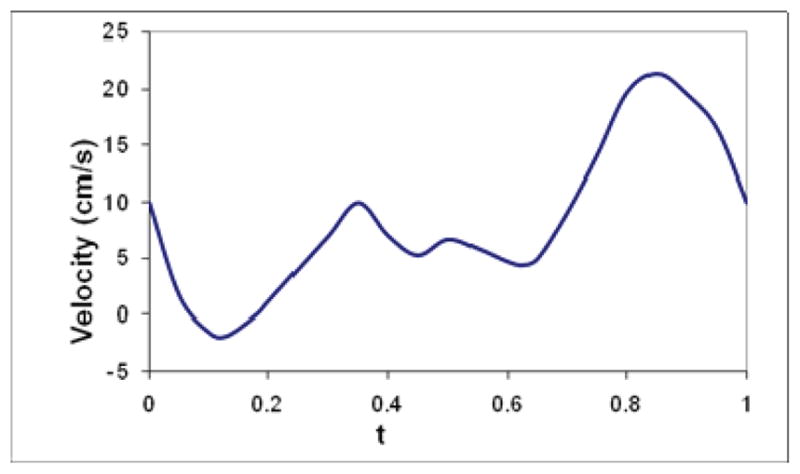
Pulsatile coronary inlet velocity waveform.

Based on a well accepted hypothesis that the low shear stress promotes a luminal narrowing in human coronary arteries, we propose the following plaque progression function which calculates plaque wall thickness increase (WTI) using the mean flow WSS:

$$\mathit{WTI}=K_1-K_2\tau ,$$ (5)

where K₁ and K₂ are constants determined by the best linear fitting function based on data given by the scatter plot showing the relation between the WSS and the change in coronary arterial diameter in an arterial segment of a patient following a 3-year period [10], τ is the time-averaged WSS at the wall boundary. With an equivalent conversion of one 3-year period into twelve 3-month periods, we have K₁ = 0.00199833 and K₂ = 0.00005167 for wall thickness increase for every 3 months.

In the computations, the density of the fluid ρ is chosen as 1.05g/cm³. When examining the effect of the blood viscosity, η is chosen as 0.0245, 0.0295, and 0.0345 dyne·s/cm², respectively, while the scale Q for the inlet flow rate is fixed as 1.50. With a diameter of D=0.29cm at the inlet, it results in Reynolds numbers of R_e = 337, 280 and 239, respectively. Here the Reynolds number is calculated by R_e = Ū Dρ/η, where Ū is the mean inlet velocity at the peak time. On the other hand, when examining the effect of the inlet flow rate, the scale Q is chosen as 1.30, 1.50 and 1.80, while η is fixed as 0.0245 dyne·s/cm². It results in Reynolds numbers of R_e = 292, 337 and 404, respectively. Navier-Stokes equations are solved using the finite element method with piece-wise quadratic functions for velocity and piece-wise linear functions for pressure over a tetrahedral mesh. GMRES method is used to solve the linear system of equations iteratively. Computations are repeated over different meshes to ensure that the numerical solutions are mesh-independent. Numerical computations are performed using Comsol Multiphysics.

Simulation of plaque progression was performed by the following steps: a) Start from the initial domain Ω (see Fig. 3) which is a curved human coronary artery with no stenosis, solve the Navier-Stokes equations to obtain flow velocity and WSS data; b) Initiate the stenosis at the location of the wall where the minimum mean WSS occurs. c) Use (5) to calculate the plaque wall thickness increase (WTI) at the stenosis; d) Adjust the wall boundary by reducing the diameter of the vessel stenosis corresponding to the WTI; e) with the newly adjusted boundary and fluid domain, solve the Navier-Stokes equations again; e) repeat c)-e) until final time is reached (Each boundary update is 3 months). The initial wall thickness of the artery was assumed to be 0.5mm. The reduction in luminal diameter was made equivalent to corresponding wall thickness increase.

Figure 3.

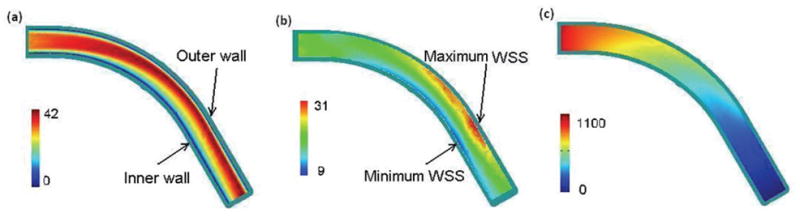
Band plot of (a) the velocity magnitude (cm/s); (b) WSS along the wall (dyne/cm²), and (c) blood pressure in the curvature plane of an initially healthy coronary artery (dyne/cm²), t = 0.85s, η = 0.0245 dyne·s/cm², Q=1.30.

3 Numerical results and observations

3.1 Overall solution behaviors

Computations were carried out with various values of physiological parameters to reveal the detailed characteristics of the blood flow in a segment of normal coronary artery. The pattern of a disturbed flow with a complex secondary flow, maximum flow shifting, blood pressure drop and distribution of WSS were observed, similar to those previously reported on curved coronary arteries [20–22]. Fig. 3 shows band plots of (a) the velocity magnitude, (b) WSS along the wall, and (c) blood pressure in the curvature plane of the artery. From Fig. 3(a) we could see that the maximum axial flow shifted to the outer wall and a region with low velocity occurred near the inner wall. Since the WSS is related to the velocity gradient at the wall, the shift in maximum velocity indicates that the shear stress is higher along the outer wall than that at the inner wall. Fig. 3(b) shows that maximum WSS occurred at a point near the outer wall and the minimum WSS occurred at the inner wall in a curved artery without stenosis.

3.2 Effects of flow rate and fluid viscosity on WSS

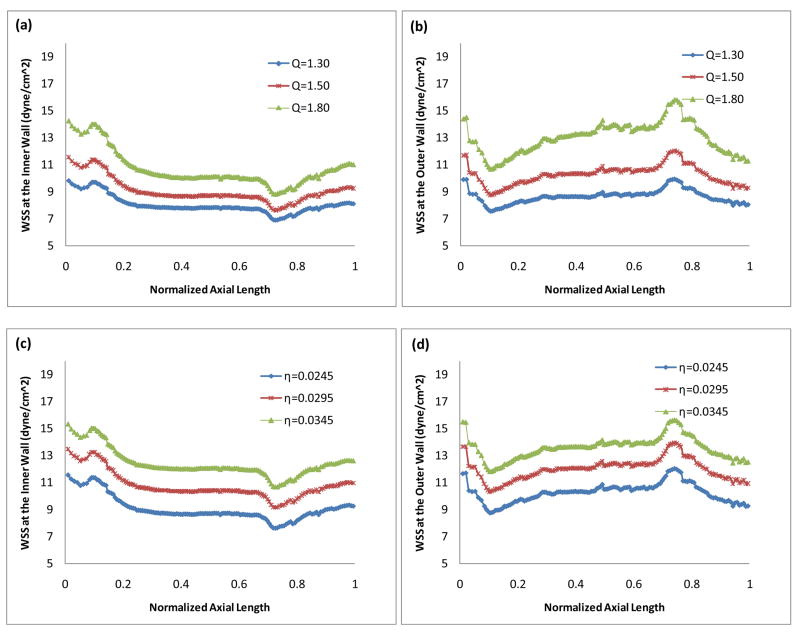
Fig. 4 demonstrates the effects of the inlet flow rate (Fig. 4(a) and Fig. 4(b)) and the blood viscosity (Fig. 4(c) and Fig. 4(d)) on the WSS at the systolic peak (t = 0.35s) during the cardiac cycle. The horizontal axis is the normalized axial length of the artery. x = 0 and x = 1 correspond to the inlet and outlet boundary, respectively. Fig. 4 shows that at a higher Reynolds number corresponding to a larger inlet flow rate, the WSS along both the inner wall and the outer wall is higher. Contrarily, at a higher Reynolds number corresponding to a smaller viscosity, the overall WSS along both the inner wall and the outer wall is lower.

Figure 4.

WSS (a) (c) along the inner wall and (b) (d) along the outer wall, t = 0.35s. (a)(b): Effect of the inlet flow rate, η = 0.0245 dyne·s/cm²; (c) (d): Effect of the blood viscosity, Q = 1.5.

3.3 Atherosclerosis progression

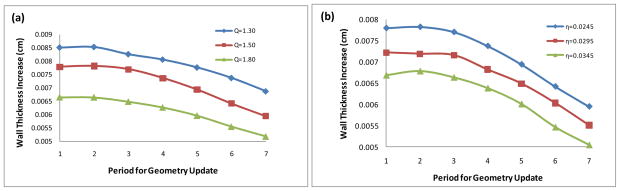
Fig. 5 is a plot of the WTI at the neck of stenosis for 10.5 years of consecutive updates of the geometry of the coronary artery simulating the initiation and the growth of the atherosclerotic plaque. The horizontal axis represents the time with each unit as a period of 18 months. Let T=0 be the time when the plaque starts to initiate at the healthy coronary artery. WTI=0.007789 cm when T=1 in the top curve of the plot in Fig. 5(b) represents that the wall thickness increase from the initial time to 18 months was 0.007789cm. WTI=0.007818 when T=2 means that an additional wall thickness increase of 0.007818cm occurred during the period of 18 months to 36 months, etc. Fig. 5(a) plots the plaque WTI in arteries having the same blood viscosity η = 0.0245 dyne·s/cm² but different inlet flow rates associated with the scales Q = 1.3, 1.5 and 1.8. After 7x18 months (=10.5 years), the stenosis size becomes 30.7 %, 27.9%, and 24.2%, respectively, corresponding to the different flow rate. Here the percent stenosis is defined as the percentage of the cross-section reduction at the neck of the stenosis compared to its normal cross-section area of the artery. Fig. 5(a) also shows the effect of the flow rate on the plaque WTI of the coronary arteries with mild stenoses. We can see that the plaque grows at a slower rate corresponding to a higher inlet velocity flow rate. This is consistent with the fact that rapid laminar flow tends to prevent the deposition of particles on the wall and may inhibit lesion formation. Fig. 5(b) plots the plaque WTI in arteries having the same inlet flow rate with the scale Q = 1.5 but different blood viscosities η = 0.0245, 0.0295 and 0.0345 dyne·s/cm². After 7x18 months (=10.5 years), the stenosis size becomes 27.9%, 26.3%, and 24.8%, respectively, corresponding to the different blood viscosity. Fig. 5(b) also shows the effect of the blood viscosity on the plaque WTI of the coronary arteries with mild stenoses. It shows that the plaque grows at a faster rate corresponding to a smaller value of blood viscosity.

Figure 5.

10.5 years of wall thickness increases at the neck of stenosis. (a): Effect of the inlet flow rate, η = 0.0245 dyne·s/cm²; (b): Effect of the blood viscosity, Q = 1.5.

Fig. 5 also shows that the plaque grows at a decreasing rate in the progression process. This is consistent with the results obtained by Stone et al [23]. Using quantitative angiographic techniques, they observed that the least severely obstructed segments are most likely to progress. Biological explanations for the more rapid progression of obstructed arteries with the least initial obstruction are that lesions of more minor severity may progress in a different manner than severe ones do. The progression of mild to moderate obstructions may be due to gradual and progressive smooth muscle proliferation and macrophage infiltration, as well as the progressive accumulation of an extracellular lipid pool. The severe and advanced lesions are characterized more by destruction of the cell necrosis and collagen deposition with fibrosis [23–25].

3.4 Effects of stenosis severity on WSS

Fig. 6 is a band plot of (a) the velocity magnitude, (b) WSS along the wall, and (c) blood pressure in the curvature plane of the coronary artery with a 41% stenosis after 13.5 years’ atherosclerotic plaque growth. The reduction of the cross section area at the neck at this stage is approximately the same to the status showing by the last selected IVUS slice in Fig. 1 corresponding to the cross section of the diseased artery with the minimum diameter. Comparing Fig. 6 with Fig. 3 we can see that the region with low velocity and low WSS near the inner wall is larger in a stenosed curved artery. The maximum WSS occurs at a point near the inner wall upstream of the neck in the stenosed artery while the maximum WSS occurs near the outer wall in the curved artery with no stenosis.

Figure 6.

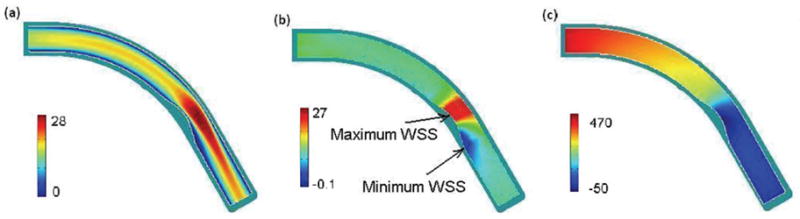
Band plot of (a) the velocity magnitude (cm/s); (b) WSS along the wall (dyne/cm²), and (c) blood pressure in the curvature plane of the artery with a 41% stenosis after 13.5 years (dyne/cm²), t = 0.35s, η = 0.0245 dyne·s/cm², Q=1.30.

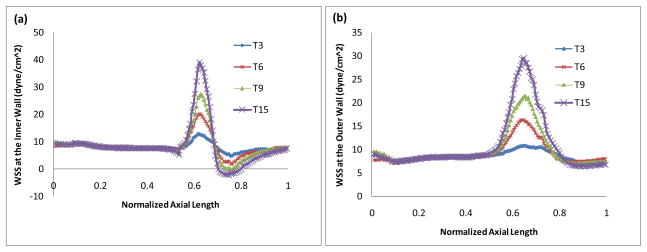
Fig. 7 is a plot of the WSS along the inner wall (a) and along the outer wall (b) in arteries at different stages in the progression process (after 4.5 years, 9 years, 13.5 years and 22.5 years respectively). T_n represents the artery after n 18-month periods of updates of the geometry. Corresponding to T₃, T₆, T₉ and T₁₅, the stenosis sizes are 17%, 31%, 41% and 51%, respectively. Fig. 7 shows how WSS changes in the plaque progress. We can see that WSS at the inner wall peaks at the neck of the stenosis and reaches the minimum in the post-stenosis region, and then recovers gradually in downstream. The more severe the stenosis, the higher the maximum WSS and the lower the minimum WSS. The WSS is significantly affected by the presence and the size of the stenosis. The low and negative WSS in the post-stenosis region may promote further development of the atherosclerotic plaque and thus may result in an expansion of the stenosis downwards. Smedby [26] did an angiographic study in a femoral artery on the direction of growth of plaques, participated by 237 patients with slight or moderate atherosclerosis. The results suggested that the growth in the downstream direction is significantly more frequent than the growth in the upstream direction.

Figure 7.

WSS (a) along the inner wall and (b) along the outer wall in arteries at different stages in the progression process (4.5 years, 9 years, 13.5 years and 22.5 years respectively), t = 0.35s, η = 0.0245 dyne·s/cm², Q=1.30.

4 Discussion and model limitations

The current model is very limited. It is a good starting point for the investigation of the initiation and the progression of mild to moderate stenoses in coronary arteries. Our initial results suggest that for a more realistic model, the growth function might include the factors depending on flow parameters, such as the blood viscosity, the inlet flow rate and the normal diameter of the artery. The choices of these constants would be justified by comparing the geometry adaptations of the computer simulations with lots of angiographic data from patients over a certain period of time [12, 13]. The hypothesis that low shear stress favors atherosclerosis progression does not explain the rapid progression of some moderate and advanced lesions under high shear stress condition, thus should be restricted to mild to moderately diseased vessels [10]. Progression of more severe and complicated obstructions may not be due to a gradual enlargement of the plaque by mitotic activity, but to relatively infrequent, intermittent plaque rupture and a more stepwise encroachment into the arterial lumen [23, 24]. A more sophisticated model may be constructed in such a way that our model with a linear growth function is used to simulate the initiation and the progression of the mild to moderate stenoses and then another growth function is used for the simulation of the moderate to severe stenoses. Such model will be developed to better simulate plaque progression and to predict future plaque morphology in our future work.

5 Conclusions

A mathematical model with a linear plaque growth function is constructed to simulate the geometrical adaption of atherosclerotic coronary arteries under the effect of the WSS. The computer simulation results indicate that the plaque grows at a decreasing rate in the progression process. The simulation also demonstrates the effects of the flow rate and the blood viscosity on the plaque WTI, showing that the plaque grows at a slower rate corresponding to a higher inlet velocity flow rate and that the plaque grows at a faster rate corresponding to a smaller value of blood viscosity.