Social conflict drives the evolutionary divergence of quorum sensing

Abstract

In microbial “quorum sensing” (QS) communication systems, microbes produce and respond to a signaling molecule, enabling a cooperative response at high cell densities. Many species of bacteria show fast, intraspecific, evolutionary divergence of their QS pathway specificity—signaling molecules activate cognate receptors in the same strain but fail to activate, and sometimes inhibit, those of other strains. Despite many molecular studies, it has remained unclear how a signaling molecule and receptor can coevolve, what maintains diversity, and what drives the evolution of cross-inhibition. Here I use mathematical analysis to show that when QS controls the production of extracellular enzymes —“public goods”—diversification can readily evolve. Coevolution is positively selected by cycles of alternating “cheating” receptor mutations and “cheating immunity” signaling mutations. The maintenance of diversity and the evolution of cross-inhibition between strains are facilitated by facultative cheating between the competing strains. My results suggest a role for complex social strategies in the long-term evolution of QS systems. More generally, my model of QS divergence suggests a form of kin recognition where different kin types coexist in unstructured populations.

Cooperative behavior in bacteria is guided in many cases by quorum sensing (QS) signaling where a response is produced only once a secreted signal’s level is sufficient to activate its cognate receptor (1). Multiple bacterial species show intraspecific divergence of their QS systems, where signals from one strain can activate their own receptor but fail to activate and sometimes inhibit a receptor from a different strain (2–7). This divergence seems to be under strong selection, as implied by the functional divergence and is also corroborated by rapid sequence divergence (8–9), the signatures of diversifying selection (10–11), and the spread of divergent QS systems through horizontal gene transfer (3, 12). These observations provoke two related questions: How does this divergence evolve in the first place, and what are the selective advantages that maintain it? Moreover, in some of the systems, a signaling molecule from one strain inhibits a diverged receptor from receiving its own signal (2, 7, 12). It is unclear whether the same evolutionary forces that drive divergence can drive the evolution of cross-inhibition.

The cross-inhibition between diverging strains in some of these species and the ecological coexistence of divergent strains in others (13) imply a possible intraspecific social role for this divergence. Therefore, to understand QS diversification, one has to consider it in a social context. It has been shown in numerous species that QS controls the production of secreted substances (e.g., exoproteases, surfactants, and antibiotics; see SI Text, section 1 for further discussion). From a social perspective these can be characterized as “public goods”—costly actions to the individual that benefit the whole population (SI Text, section 1). As such, QS was shown both theoretically (14–16) and experimentally (17–20) to be susceptible to invasion by QS mutants that act as “cheaters” and exploit the public goods produced by a functioning QS strain. Such cheating can be repressed by mechanisms that increase relatedness and lead to preferential assortment of cooperators and cheaters through structured populations (21–24). Recent experimental work in fruiting body and biofilm formation has suggested that cheating can also be evolutionarily counteracted by mechanism-specific strategies (25–34). Nevertheless, there is little mechanistic understanding of these types of interactions and their long-term evolutionary impact remains unclear.

Model

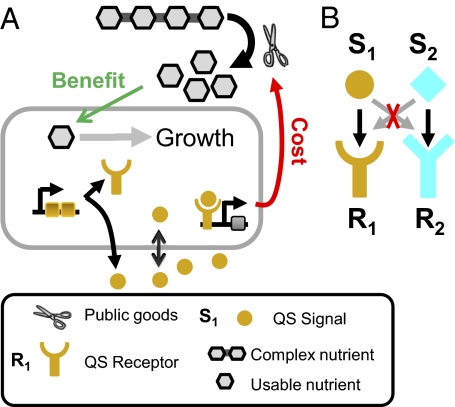
I sought to understand whether social evolution can explain the divergence of quorum sensing systems. To this end, I constructed a general model of a quorum sensing system guiding public goods production (Fig. 1A and SI Text, sections 2 and 3 for mathematical details). I assumed that a QS system is composed of three genes encoding a signaling molecule (or the synthase producing it) denoted as S, a receptor (denoted as R), and a public good product whose expression is regulated by the signal–receptor complex. I assume that the public good is a secreted enzyme whose product is a usable nutrient (generalizations to other public goods are discussed in SI Text, section 1). I assume that the growth rate of the bacteria is dependent on the usable nutrient and that enzyme production carries a cost that reduces the growth rate. In addition I assume a density-dependent cell death that leads to a logistic form of growth equation. In such a model, enzyme production by the wild type benefits a nonproducing mutant strain. The mutant strain does not pay the production cost and therefore has a higher growth rate than the wild type and will act as a cheater. As expected from this model, a strain with no QS system can cheat the wild type (SI Text, section 2).

Fig. 1.

A model for the divergence of QS systems. (A) I assume QS to control the production of public goods. A signaling molecule is secreted out of the cell and accumulates in the environment. A cellular receptor is activated by the signaling molecule at high cell densities and leads to the production of public goods: an exo-enzyme that metabolizes a complex nutrient into a usable form. Enzyme production carries a growth cost to the producing cell, but usable nutrient brings benefit to the whole community. See Materials and Methods and SI Text, section 2 for further discussion and model equations. (B) For simplicity, I assume that both receptor and signal have two alleles with specific and orthogonal interaction (i.e., each receptor is completely specific to its cognate signal) and that a single mutation allows transition between corresponding alleles. In SI Text, section 7 I show how diversification can evolve in the presence of null alleles of receptor, signal, and public goods enzyme or if receptor and signal alleles are not fully orthogonal.

To understand the evolution of divergent specificities in QS pathways, I extended the model to include two divergent alleles of receptor (R₁, R₂) and signal (S₁, S₂). I assume that a single mutation allows the transition between the two alleles of a given gene. I also assume that R₁ interacts only with S₁ and R₂ only with S₂ (Fig. 1B; this assumption can be relaxed, see below). I start with a population composed of bacteria expressing the S₁ signal and the R₁ receptor and examine the evolution of a population of diverged individuals expressing the R₂–S₂ pair.

Cooperation through public goods can be maintained only in a structured population, where the population is divided into multiple subpopulations with higher relatedness than total population average (21, 24) (e.g., bacterial growth on surface is more structured than in liquid). I therefore analyzed the competition between various strains in a population evolving through bottlenecks—a simple type of structured population that has been experimentally demonstrated to maintain cooperation (17, 21, 22, 35). I assume multiple subpopulations (demes) where in each round N lineages seed each subpopulation and then grow together for a given time. After the growth phase, bacteria are resampled, either from the same subpopulation (local competition) or from the whole population (global competition), to seed the next growth cycle of new subpopulations. The asymptotic distribution of the various genotypes involved in the competition can be either simulated or analytically derived (see SI Text, section 6 for mathematical analysis).

Results

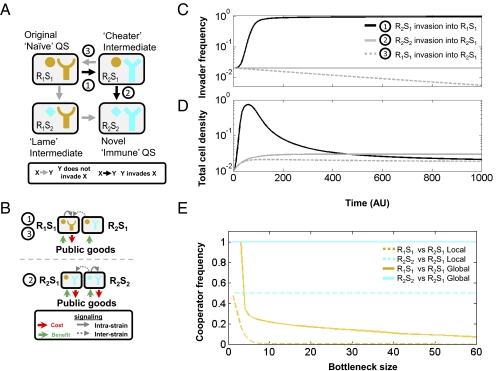
Two problems confine the selection of the divergent QS system R₂S₂. First, the receptor and signal alleles have to evolve sequentially, so their coevolution has to occur through an intermediate strain with a mutation in either the receptor (R₂S₁) or the signal (R₁S₂), but not both (Fig. 2A). These two intermediate strains will have a nonfunctional QS system. Second, once formed, the divergent QS strain (R₂S₂) has to compete with the more prevalent original strain (R₁S₁).

Fig. 2.

Coevolution of receptor and signaling molecule during divergence is positively selected. (A) The original QS system R₁S₁ (‘Naive’) can evolve into the novel QS system R₂S₂ (‘Immune’) through one of two intermediates. I find that the evolutionary trajectory through the receptor-modified intermediate (R₂S₁, ‘cheater’) is positively selected at both steps but the one through the signal-modified intermediate (R₁S₂, ‘lame’) is not (SI Text, section 5). (B) Scheme of contribution to public goods and communication during the two evolutionary steps (compare circled numbers to those in A). Shown are the two competing strains, the signaling relations between them, and the contribution to public goods production (red) and benefit (green). (Upper) Competition between the original QS system (R₁S₁) and the intermediate cheater strain (R₂S₁). Only R₁S₁ produces public goods. (Lower) Competition between the intermediate cheater strain (R₂S₁) and the novel QS system (R₂S₂). R₂S₂ signal induces public goods production by both itself and the intermediate strain R₂S₁ and is therefore immune to cheating by R₂S₁. (C and D) Results of invasion simulations of R₂S₁ into R₁S₁ (black line), R₂S₂ into R₂S₁ (gray solid line), and R₁S₁ into R₂S₁ (gray dashed line) in well-mixed conditions. Invading strain initial frequency is 2%. (C) Frequency of invading strain as a function of time. (D) Total cell density as a function of time. I note that the immune cooperator (R₂S₂) frequency remains constant but the production of public goods leads to a higher total cell density compared with a pure cheater (R₂S₁) population. Inset in D is as in C. (E) The immune cooperator outcompetes its ancestor in a structured population. Shown are the asymptotic frequencies as a function of bottleneck size of naive (R₁S₁, orange) and diverged immune (R₂S₂, cyan) QS strains when separately competed with the intermediate cheater strain (R₂S₁). Each pair of strains undergoes cycles of growth and population bottlenecks, as explained in Materials and Methods and SI Text, section 6. Whereas the naive cooperator frequency is quickly reduced when bottleneck size increases, the immune cooperator’s level remains maximal for any bottleneck size.

The relative fitness of a mutant in a social trait such as QS has to be judged by its interaction with its parental strain. I therefore simulated the invasion of all possible mutations of receptor and signaling molecule during coevolution into their respective parental strain. The results are striking: Divergence is positively selected through a nonfunctional intermediate. This process occurs through the evolutionary trajectory where the receptor mutates first and then the signaling molecule coevolves (Fig. 2).

Divergence Is Positively Selected by Rounds of Cheating and Immunity to Cheating.

To understand why the pathway in which the receptor mutates first and the signaling molecule follows is selected I first analyzed the two steps of this process in an unstructured, well-mixed, environment (Fig. 2 B–D). The receptor-mutated intermediate strain (R₂S₁) is insensitive to neither its own signal nor its parental strain’s (R₁S₁) signal (Fig. 2B, Upper) and will therefore invade into its parental strain by cheating (Fig. 2C, solid black line). Furthermore, the signal produced by the intermediate strain (R₂S₁) induces the quorum response of the parental cooperator strain, which may lead to increased exploitation (SI Text, section 4). Like other obligate cheaters in well-mixed environments, R₂S₁ rise in frequency will eventually lead to a population collapse (Fig. 2D, solid black line). Its success is therefore transient, but provides a window of opportunity for the occurrence of a second mutation that will restore the QS system.

Restoration of QS cooperativity to strain R₂S₁ can occur by either reversion of the receptor to the original QS system, R₁S₁ (Fig. 2A, step 3), or divergence of the signal to the novel QS system, R₂S₂ (Fig. 2A, step 2). Reversion is unfavorable, however, because the revertant strain remains sensitive to cheating by strain R₂S₁ and will therefore decrease in frequency when mixed with it (Fig. 2 C and D, gray dashed lines). In a sharp contrast, the novel cooperator (R₂S₂) retains its initial frequency when mixed with strain R₂S₁ (Fig. 2C, solid gray line). The novel cooperator is therefore immune to the cheating of R₂S₁. Immunity arises because the signal of strain R₂S₂ induces the quorum response of itself and of its ancestor R₂S₁, as both have the novel receptor R₂ (Fig. 2B, Lower). Therefore, both strains will produce the enzyme to the same extent, sharing both its benefit and production cost. As the signal of the “immune” cooperator (R₂S₂) leads to public goods production by both strains, the total cell density of the mixed population increases monotonically with the frequency of R₂S₂ in the population (Fig. 2D, solid gray line and SI Text, section 5).

I reasoned that due to its immunity to cheating and its global benefit to the population, the diverged QS strain (R₂S₂) would perform better than the original QS strain (R₁S₁) when each strain competes with the intermediate strain R₂S₁ in a structured population (18–20). I analyzed the two competitions in the bottlenecked growth model for various bottleneck sizes (Fig. 2E and SI Text, section 6). I find that the frequency of the original cooperator (R₁S₁) diminishes with increasing bottleneck size. In sharp contrast, the immune cooperator (R₂S₂) frequency is independent of bottleneck size and under conditions of global competition will asymptotically outcompete the cheater intermediate strain for any bottleneck size.

Immunity to cheating also explains why the evolutionary pathway where the signaling molecule changes first (“lame” intermediate) is not selected. The original quorum sensing strain, R₁S₁ is immune to the cheating of the mutant R₁S₂ in the same way R₂S₂ is immune to R₂S₁. Therefore, R₁S₂ is nonbeneficial in a well-mixed population and counterselected in a structured population by R₁S₁.

Facultative Cheating Underlies the Maintenance of Divergence and the Evolution of Cross-Inhibition.

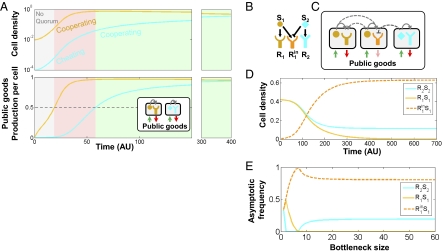
My model suggests that diversification of QS systems can occur by sequential evolution of an obligate cheater and immune cooperator. The long-term maintenance of diversity also depends on the interaction between the novel cooperator R₂S₂ and the still-prevalent original QS system, R₁S₁. I find that both R₂S₂ and R₁S₁ can invade a territory dominated by the other strain to reach an equal abundance (Fig. 3A). This dynamic can be understood as follows: At low initial cell densities, before any quorum response is activated, the strains are equivalent and grow at the same rate (Fig. 3A, gray area). Once the predominant strain (R₁S₁ in Fig. 3A) reaches a high density, it will activate its quorum response and produce the public goods. The invading strain’s density is still low and because it is insensitive to the signal of the dominant strain, it will not participate in public goods production and therefore increases its relative frequency (Fig. 3A, pink area). Finally, when the cell density of the invading strain becomes high enough to activate its own quorum response, it will participate in enzyme production (Fig. 3A, green area). The invading strain therefore performs a facultative cheating strategy (36), exploiting the invaded strain at low frequencies and cooperating in public goods production at high frequencies. This strategy leads to a negative frequency-dependent selection and coexistence of both cooperators with a high steady-state yield of public goods.

Fig. 3.

Maintenance of diversity and evolution of cross-inhibition. (A) Divergent QS systems act as facultative cheaters. A minority strain (cyan) activates its quorum response later than a majority strain and therefore facultatively exploits the majority strain. Shown are cell densities of each strain (Upper) and the level of public goods produced by single cells from each strain (Lower). The facultative cheating domain is colored pink and cooperation (arbitrarily defined at half-maximum production rate) is green. (Right) Graphs show convergence of strain frequencies to 50% at later times. (Inset) A scheme of public goods production and communication in the competition between divergent strains. (B–E) The evolution of cross-inhibition. (B) The QS diversification model can be extended by assuming that one of the receptors (R₁ⁱⁿ, orange) can mutate to a novel form (R₁ⁱⁿ, deep orange) that is inhibited by a divergent signal (cyan). (C) A scheme of signaling and public goods contribution in the three-way competition between the two divergent strains and the one with cross-inhibited receptor. (D) Cross-inhibition is beneficial for the inhibited strain. A strain with a receptor that is inhibited by a divergent strain can invade into its parental population that is fully orthogonal to the divergent strain. Initial conditions of the divergent strains are their steady-state level when mixed without the cross-inhibited strain. The cross-inhibited strain’s initial density is 1% of the other strains. (E) Cross-inhibition is selected in structured populations. Shown are the frequencies of the three strains described in C as a function of bottleneck size for a three-way competition analysis in a population going through cycles of growth and bottleneck phases, similar to Fig. 2E. The strain with the cross-inhibited receptor (dashed deep orange line) is selected over its ancestral orthogonal strain (solid orange line). The nonmonotonicity of the frequencies at low bottleneck sizes is discussed in SI Text, section 8.

Many of the diverging QS systems display patterns of cross-inhibition of a receptor by a noncognate signal (2, 7, 10) (Fig. 3B). The evolution of cross-inhibition can be explained by my model as an eavesdropping strategy of the inhibited strain that is used for cheating the inhibiting strain. In the presence of the competing inhibiting strain, the inhibited strain will contribute less to public goods production than either its ancestral (noninhibited) strain or the inhibiting strain and will therefore invade into the population (Fig. 3 B and C). This facultative cheating strategy cannot be eliminated by structured population models that eliminate obligate cheaters (Fig. 3E and SI Text, section 8), as all of the strains perform equally when alone. Cross-inhibition can easily evolve into mutual cross-inhibition of the QS pathways. This evolutionary path may eventually lead to complete mutual exclusion between strains and, under a low level of recombination, to speciation, as was proposed for Staphylococci (37).

Divergence of QS Can Occur Under More Complex Scenarios.

I have so far neglected the effects of other types of cheaters on the evolutionary divergence of QS. In fact, I expect most mutations in receptor or signaling genes to yield effective null mutations. The receptor null mutants (and also the public goods enzyme null mutant) will act as obligate cheaters in public goods production. The signal null mutant will act as a cheater by saving the cost of signal production (which is most likely smaller than that of public goods production) (17, 19, 20). To examine the effect of such mutants on the evolution of a novel receptor–signal pair, I simulated the effect of these null mutants on the evolution of the novel receptor (SI Text, section 7). I find that both types of mutants reduce the total level of public goods in the population, but do not prevent the positive selection of a divergent pair. I emphasize that the cost of signaling is not directly affecting the evolutionary pathway leading to QS divergence, as all strains on this pathway produce a signal (either S₁ or S₂) and therefore pay the cost of signaling. Only the relevance of the signal changes under various social contexts.

The situation where a single mutation in the receptor and signaling genes will lead to complete orthogonality (full interaction with the mutated partner and no interaction with the nonmutated partner) is an extreme case. I find that divergence can occur by smaller mutational steps where the receptor mutation reduces its affinity to the original signal (but does not eliminate it) and the novel signal mutant increases the signal’s affinity to the mutated receptor. Such small steps still lead to cheating and immunity (SI Text, section 7) and are most likely more realistic than large mutational jumps (8).

Finally, a secreted substance can lead to a higher benefit to the secreting cell than to a nonsecreting, cheater, cell. This relation can lead to a snowdrift type of social interaction, where cheaters invade to coexistence with the cooperators but do not eliminate them. Such a scenario was recently demonstrated for the degradation of sucrose by the yeast’s invertase (38). In SI Text, section 7 I demonstrate that QS diversification can also occur if the QS-regulated enzyme leads to snowdrift dynamics.

Discussion

QS Evolution as an Intraspecific Diversification Mechanism.

Treated at the level of the single genotype, the fitness landscape of divergent QS is that of equally fit peaks separated by unfit valleys, where at least two mutations are needed to shift from one peak to the other. Here I demonstrated how social interaction can turn this rugged landscape into an “evolutionary ratchet” process that strongly selects for divergence without any form of an arms race with other species or strains—the usual mechanism invoked to explain diversification. In contrast to the common view of cheating (36), here a cheater is a necessary evolutionary intermediate in the evolution of social interactions.

QS Diversity Is a Unique Form of Kin Recognition.

The mode of action of the divergent QS systems in bacteria bears resemblance to the phenomenon of kin recognition as characterized in other species (39–40). Whereas kin recognition may help raise the level of cooperation in a population, the maintenance of kin diversity by selection for cooperation alone is highly debated (41–45). Two characteristics distinguish my model for QS divergence from other such models. First, most of the previous models are inspired by a “matching” kin-recognition mechanism (“the armpit effect”) and assume the existence of a single locus for kin recognition, coding for a displayed tag. My model dissects another plausible kin-recognition type where two separate loci code for tag display (signal) and tag recognition (receptor). I show how in the context of a public-goods cooperation, rapid transition between tag types is selected without reducing the level of cooperation in the population. The evolutionary dynamics of cheating and immunity may explain the switch from one tag to another also in cooperative systems with direct cooperation.

Second, the underlying population dynamics in all of the previously described kin-recognition models are those of positive frequency-dependent selection—the majority kin (as long as it is cooperative) will be selected for in a well-mixed population, as it has a higher chance of obtaining cooperation than the minority kin (41). The divergent QS systems, on the other hand, display a negative frequency-dependent selection in a well-mixed population. This dependence is a consequence of the public goods nature of cooperation—kin recognition establishes the decision to cooperate, but all neighboring bacteria are beneficiaries of cooperation. Negative frequency-dependent selection, however, comes with a price; the diversity of alternative QS systems does not increase the level of cooperativity in the population. This result is true because an obligate cheater will always benefit from the cooperation of others, irrespective of its tag, which is unlike the case of kin discrimination by reciprocal cooperation (see SI Text, section 9 for further discussion).

Limits of Diversification.

If QS diversification is so strongly selected, why is it not found in all species? Multiple factors may confine this divergence. One limit is the availability of divergent signaling molecules. Perhaps this limit is the main reason why QS divergence has been mostly (but not exclusively) (6, 7) observed in Gram-positive bacteria. The peptide signaling molecule family used by Gram-positive bacteria for signaling probably encompasses greater potential molecular variability than that of acyl homoserine lactones (AHL) often used by Gram-negative bacteria (14). Other constraints on QS divergence include the duration of intermediate obligate cheater (R₂S₁) survival and the population size it reaches. Finally, this evolutionary mechanism requires that the principal use of QS is for social regulation of public goods. It is known that QS may serve other functions (46) or impact the behavior of single cells in a nonsocial manner (14, 47) (SI Text, section 1).

My results may help to explain some of the social strategies observed during fruiting body development in bacteria and amoebas (25–31, 34). Specifically, immunity by signaling induction can explain the emergence of a novel immune cooperator from a cheater strain in Myxococcus xanthus (29) (SI Text, section 1). Immunity by induction can also help explain the restoration of QS-dependent growth to a lasR cheater mutant by a secondary rhlI overexpression mutation (48). Further understanding of the evolution of QS systems may help predict the evolution of resistance to QS inhibitory drugs (49) and enable synthetic biologists (50) to rationally design strains with superior cheating strategies to interfere with pathogenic bacterial cooperation (51, 52).

Materials and Methods

Basic Model for Quorum Sensing.

I used the following equations to describe the time-dependent density of M strains (n₁, n₂, … , n_M), the signaling molecules they produce (S₁, S₂,…, S_M), the exo-enzyme (E), and the usable nutrient (P_d):

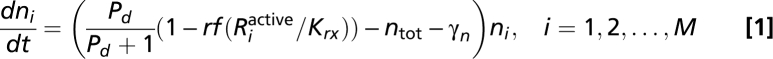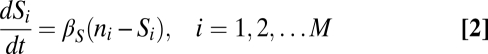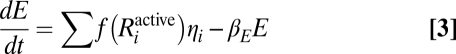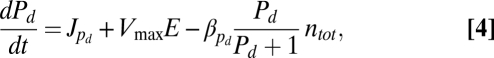where the enzyme activation function 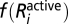(which is also reflected in the growth cost term) is of the form f(x) = x^m and the level of active receptor is calculated from the equation

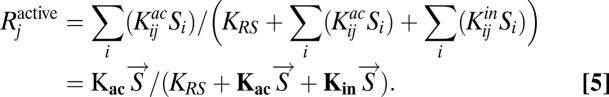The values used in all figures for the above equations are, r = 0.1, γ_n = 0.01, β_S = 0.1, β_E = 0.2, 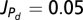, V_max = 20, 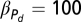, m = 1, and K_RS = 0.025. Initial conditions of all variables but the cell densities are set to 0 (except for Fig. 3D, where they are set as described in the legend). Initial cell densities depend on the specific simulation. The competition matrices are

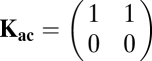for “naive” cooperator vs. the intermediate cheater and

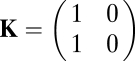for immune cooperator vs. the intermediate cheater (Fig. 2 C–E), and

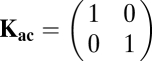for two strains with divergent QS systems (Fig. 3A). For the case of cross-inhibition I use three species with

(Fig. 3 D and E). All simulations were done using the MATLAB (Mathworks) ordinary differential equation solver and self-written routines.

Selection for Cooperation Through Population Bottlenecks.

I mathematically generalized the experimental selection scheme used by refs. 17 and 21 to a general bottleneck size. I used a semianalytical approach to solve the change in cooperator fraction under different types of selection when the intermediate cheater strain (R₂S₁) competes with one of the cooperators(naive R₁S₁ or immune R₂S₂). A full description and analysis of this computation is given in SI Text, section 6. Briefly, I assume an infinite number of subpopulations where bacteria grow separately. I simulate a growth cycle of time τ that is initiated by N bacterial lineages (N being the bottleneck size), where each lineage can be either a cooperator or a cheater. After growth, new N lineages are reselected for growth from a Poisson distribution on the basis of the relative frequency of cooperators and cheaters in a single subpopulation (local competition) or in the general population (global competition). Analytical methods were used to demonstrate that the immune cooperator will outcompete the intermediate cheater strain in all bottleneck sizes. Numerical values for global competition are obtained after 500 cycles of growth. For the three-way competition shown in Fig. 3E, I repeated the same simulations but now analyzed all 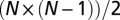possible states and mixed them according to their Poisson distribution in every cycle.