Satellite methods underestimate indirect climate forcing by aerosols

Abstract

Satellite-based estimates of the aerosol indirect effect (AIE) are consistently smaller than the estimates from global aerosol models, and, partly as a result of these differences, the assessment of this climate forcing includes large uncertainties. Satellite estimates typically use the present-day (PD) relationship between observed cloud drop number concentrations (N_c) and aerosol optical depths (AODs) to determine the preindustrial (PI) values of N_c. These values are then used to determine the PD and PI cloud albedos and, thus, the effect of anthropogenic aerosols on top of the atmosphere radiative fluxes. Here, we use a model with realistic aerosol and cloud processes to show that empirical relationships for ln(N_c) versus ln(AOD) derived from PD results do not represent the atmospheric perturbation caused by the addition of anthropogenic aerosols to the preindustrial atmosphere. As a result, the model estimates based on satellite methods of the AIE are between a factor of 3 to more than a factor of 6 smaller than model estimates based on actual PD and PI values for N_c. Using ln(N_c) versus ln(AI) (Aerosol Index, or the optical depth times angstrom exponent) to estimate preindustrial values for N_c provides estimates for N_c and forcing that are closer to the values predicted by the model. Nevertheless, the AIE using ln(N_c) versus ln(AI) may be substantially incorrect on a regional basis and may underestimate or overestimate the global average forcing by 25 to 35%.

An increase in aerosol concentrations leads to an increase in cloud droplet number concentration (N_c) for a cloud with a constant cloud liquid water content. The increase in N_c implies a decrease in the cloud droplet effective radius, which leads to an increase in cloud optical depth and an increase in cloud reflectivity (1); this climate forcing is known as the first aerosol indirect effect (AIE).

Satellite measurements of N_c versus aerosol optical depth (AOD) have been used to estimate the effect of changes in clouds due to anthropogenic aerosols. The estimated changes to clouds from preindustrial (PI) to present-day (PD) conditions gives an AIE that ranges from -0.2 Wm^-2 to -0.5 Wm^-2 at the top of the atmosphere (TOA) (2, 3). In contrast, model results that rely on mechanistic descriptions of the relationship between aerosols and cloud drop number concentrations give an AIE that ranges from -0.5 to -2.03 Wm^-2 (4, 5).

Satellite-based estimates rely on a linear fit to the spatial variation of ln(N_c) versus ln(AOD) in the PD to determine PI values for N_c, rather than temporal variations induced by actual changes between PD and PI aerosol concentrations. Improved estimates from satellites are expected if measurements of N_c versus AI (where AI is the Aerosol Index, or the angstrom exponent times AOD) are used rather than N_c versus AOD, because AI is a better measure of aerosol number concentration (6), but can still give values smaller than process-based models. Previous studies have attempted to combine satellite data with models by adjusting the parameterizations used in the models to fit the present-day satellite relationships together with model-calculated preindustrial AOD or AI (2, 7). Most such model results also find lower values of forcing than those based on mechanistic treatments of N_c alone.

Here we use model simulations to analyze whether the methods used in satellite estimates provide the same AIE as those from the full (or true) model calculation. Thus, we analyze the results of model simulations in the same manner as that used by the satellite-based estimates to understand why the estimates from satellites and models differ. Our goal is to test the accuracy of using fits to present-day ln(N_c) versus ln(AOD) [hereafter R(AOD)] or fits to ln(N_c) versus ln(AI) [hereafter R(AI)] for determining the aerosol indirect effect. We find significant regional and global average differences in forcing between results based on the true model PD and PI values of N_c and those based on satellite methods because the slope of the regressions using present-day values does not accurately capture the PI to PD change in N_c.

Some of the differences in satellite and model estimates of the AIE are due to limitations in satellite measurements, but these are not explored here. Thus, we assume that the satellite estimates for AOD, which are spatially near, but not coincident with observed clouds, are reasonably accurate estimates of the cloud-coincident AOD. In addition, although the use of large spatial averages of aerosol and cloud properties in satellite estimates of the AIE can result in a low bias (8, 9), this is not explored because we use the same spatial resolution for both the true model estimate and for the satellite-based model estimate for the AIE. We note that model estimates of the AIE are also highly uncertain, because they vary significantly between different models due, in part, to differences in modeled aerosol properties and amounts and to differences between the modeled droplet concentrations for a given aerosol amount (10, 11), but this, too, is not explored.

Results

The Use of PD Regressions.

Here, we use an off-line model to quantify whether the fit of PD values of N_c with AOD or AI can be used to accurately calculate the decrease in N_c for preindustrial conditions. Forcing Estimates discusses the forcing or AIE calculated using these regressions and the AIE using the true model results for PI N_c.

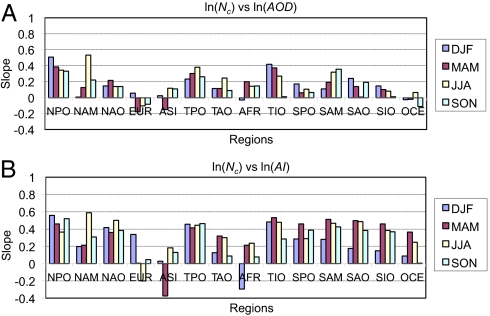
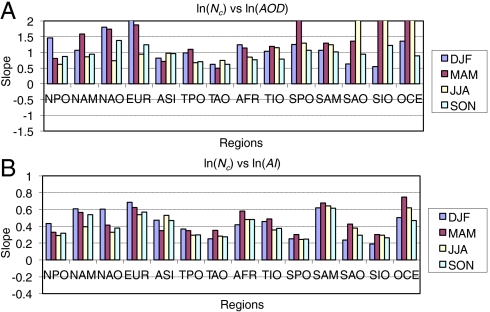
Fig. 1 shows the slopes computed from regressions to scatter plots for present-day simulations for 14 different regions and seasons for (i) R(AOD) and for (ii) R(AI), whereas Fig. 2 shows similar slopes computed using the true average values for the present-day and preindustrial N_c and AOD or AI for each region from the model. Examples of R(AOD) and R(AI) in Fig. 1 are shown by the red lines in Fig. 3, whereas examples of the slopes in Fig. 2 are given by the black lines. Note that the range shown in Fig. 2A goes from −1.5 to 2.0, whereas that in Fig. 1A is only from −0.4 to 1.0. The slope R(AOD) using the actual modeled PD and PI values (Fig. 2A) are, for the most part, larger than those using only the spatial variation in PD values (Fig. 1A). Larger slopes lead to larger differences between PD and PI N_c and therefore would be expected to lead to larger estimates for the (negative) forcing (Forcing Estimates).

Fig. 1.

Slope of the regression between ln(N_c) and ln(AOD) (Top) and ln(AI) (Bottom) for the PD simulation for all seasons for the 14 regions used in the analysis in ref. 3. (See Table S1.)

Fig. 2.

Slope computed from the difference in the average values of ln(N_c) and ln(AOD) (Top) and ln(AI) (Bottom) for the PD and PI simulations for all seasons for the regions in ref. 3.

Fig. 3.

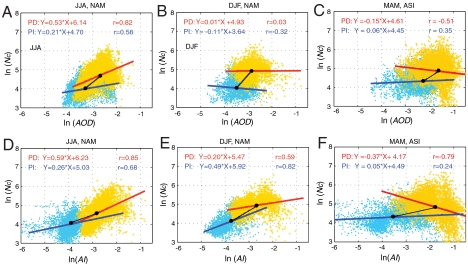
Scatter plot of ln(N_c) versus ln(AOD) and versus ln(AI) for North America in JJA and DJF and for Asia in MAM. The red line shows the best-fit linear regression from PD values, whereas the blue line shows the best fit linear regression for the PI values. The black line shows the fit computed using the difference in the average of the PD and PI values.

The slope R(AI) computed for the actual modeled PD and PI values (Fig. 2B) are, for the most part, only slightly larger than those using only the PD values (Fig. 1B), but can also be smaller, especially in oceanic regions [compare regions North Pacific Ocean (NPO), Tropical Pacific Ocean (TPO), and Southern Pacific Ocean (SPO) in all seasons, North Atlantic Ocean (NAO) in June, July, and August (JJA), and Southern Atlantic Ocean (SAO) and Southern Indian Ocean (SIO) in all seasons except December, January, and February (DJF)]. The ocean regions with smaller slopes might be expected to have a smaller negative forcing when the actual modeled N_c values for PD and PI conditions are used rather than values extrapolated using the fits to PD values. This statement is only approximate, however, because the slope of the average values for each region plotted in Fig. 2B will not exactly match the changes in N_c when the true variations between PD and PI values of N_c, which are paired in time and space, are used. We also note that the slopes using only the PD data for R(AI) are typically larger over ocean areas than over land (Fig. 1B), whereas the slopes using the PD and PI data are usually larger over land than over oceans (Fig. 2B). These larger slopes over land are associated with a larger increase in N_c, which is likely due to the larger increase in sulfate over land than over ocean in going from PI to PD conditions.

Fig. 3 shows examples of scatter plots for two different regions to examine these results in more detail. Fig. 3 A and B shows ln(N_c) versus ln(AOD) in JJA and DJF over North America (NAM), whereas Fig. 3 D and E shows a similar set of scatter plots for ln(N_c) versus ln(AI). PD values are in maize and PI values are blue. It is clear from these plots that the slopes computed from the PD simulation in Fig. 3 A and B are not as steep as they would be if values from the PI simulation were included because the spatial variation for the PD simulation does not include values for AOD and N_c as small as those from the PI simulation. Moreover, the black line demonstrates that the slope can be much larger if the average of the actual PI values is used in place of the extrapolation based on the red line. The AI scatter plots in Fig. 3 D and E shows that the values for AI between the PD and PI simulations are better differentiated than are the values for AOD, but the values for PI N_c can be both underestimated (Fig. 3D) or overestimated (Fig. 3E) if extrapolated from the PD slopes.

Fig. 3 C and F shows a similar set of scatter plots for the region associated with Asia (ASI) in March, April, and May (MAM). This region illustrates what occurs with the slopes when dust is present in the region. Both the slope for R(AOD) and the slope R(AI) for the PD values are negative in this season because dust has a significant influence on AOD, but it does not strongly contribute to increases in droplet concentration. Dust must become mixed with hygroscopic (sulfate) aerosols in the model before it can act effectively as a good cloud condensation nucleus. Similar considerations apply when black carbon/organic matter (BC/OM) aerosols dominate the aerosol optical depth, but not the calculation of N_c. This mechanism also explains the negative slopes for Europe (EUR) in MAM, JJA, and September, October, November (SON) and for Oceania (OCE) during SON in Fig. 1A.

We note that the slopes computed using the average of the PD and PI values of N_c and AOD (Fig. 2A) are in general greater than zero, but examination of individual PD and PI points that are paired in space and time shows that slopes can also be less than zero. Negative slopes can in general be caused when the number concentrations from dust and/or fossil fuel BC/OM decrease for the PD conditions due to the increase in sulfate deposition on these aerosol types and thus their stronger precipitation scavenging rate. This decrease can then lead to a slight decrease in the PD AOD so that even though the overall droplet number concentration increases, the slope computed for individual paired PD and PI values of N_c versus AOD is negative. The number of such occurrences, however, is small enough that the overall forcing using PD and true PI values of N_c is usually larger than that using the satellite method (see Forcing Estimates).

Fig. 1 may be compared to the satellite analysis shown in figure 3 of ref. 3 and to the variability shown by different models (12). Clearly there is no one model that is able to capture the variability in N_c with AOD estimated by satellite. Nevertheless, by comparing the estimated slopes shown in Fig. 1 with those based on the true model-generated present-day and preindustrial conditions (Fig. 2), we have established the fact that estimates of the change in N_c based on present-day results are not likely to be accurate.

Forcing Estimates.

Here, we evaluate the method used in satellite-based estimates to calculate the indirect forcing using the PI value of N_c from PD fits to the slopes in each region and compare this to the forcing calculated by the model using the actual (true) PD and PI values of N_c from the model. The Intergovernmental Panel on Climate Change (IPCC) has defined the aerosol indirect radiative forcing as the forcing obtained by holding all values constant except the estimated change in N_c (13, 14), thereby requiring that the feedbacks associated with droplet coalescence and precipitation not be included. This is the definition used here, but we include the effect of some of the feedbacks in Table 1.

Table 1.

Global annual average aerosol first indirect forcing (W/m²)

	PD − PI*	PD − PI based on fit to AOD*	PD − PI based on fit to AI*
Inline Nc†	−1.29	−0.43	−1.59
Off-line Nc	−1.69	−0.27	−1.09

^*PD − PI forcing is based on the true modeled PD and PI results for droplet number concentrations. The PI values based on fits to AOD or AI are from the regression between the PD ln(N_c) versus ln(AOD) or between the PD ln(N_c) versus ln(AI).

^†Inline model results for PD and PI droplet number concentrations include changes from the initial concentration due to sedimentation, coagulation, and precipitation.

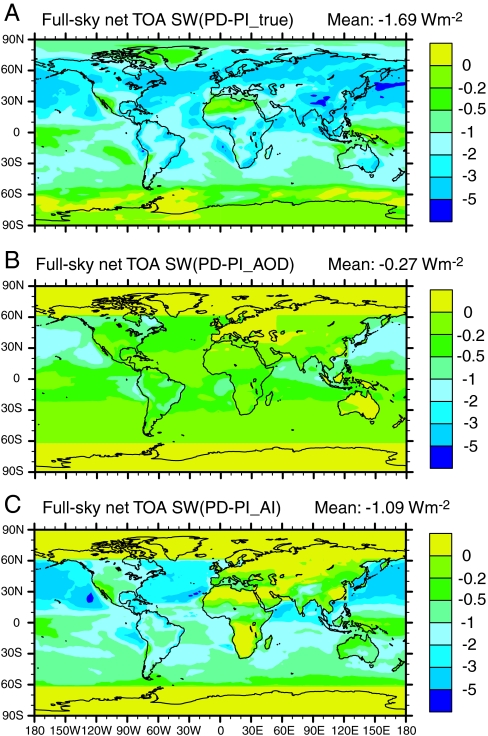
Fig. 4A shows the TOA shortwave forcing using the true modeled PI N_c. The forcing based on the estimated PI N_c from R(AOD ) is shown in Fig. 4B, whereas that based on R(AI) is shown in Fig. 4C. The global average indirect forcing using the true PD and PI values for N_c is -1.69 Wm^-2 but that using the satellite method based on R(AOD) is only -0.27 Wm^-2. The forcing in every region is smaller using the satellite-based regression (see Fig. S1). If R(AI) is used rather than R(AOD), the forcing is significantly larger, -1.09 Wm^-2, but is still smaller than the value based on the true model estimate of preindustrial N_c, even if we restrict the true model estimate to the satellite region that spans only the latitudes from 60 °N to 60 °S. As noted above from the discussion of slopes, there are some regions where the estimated forcing is actually more negative using the satellite method based on AI, most notably in the NPO, TPO, and SPO regions. However, the satellite method underestimates the negative forcing over all continental regions (see Fig. S1).

Fig. 4.

Shortwave indirect forcing from the true modeled PD and PI values of N_c (Top), from the PI N_c based on the regression between N_c and AOD (Middle), and from the PI N_c based on the regression between N_c and AI (Bottom). The satellite estimates of forcing include only the region from 60 °N to 60 °S. If the true model forcing is restricted to this region, the total forcing is -1.56 Wm^-2.

The values for the PD slopes based on R(AOD) shown in ref. 12 as well as those from satellite observations include the effects of changes to N_c that result from feedbacks between aerosols and N_c. In the above, we emphasized the use of an off-line model to calculate N_c in order to report results that are consistent with the IPCC definition of the first aerosol indirect forcing. Table 1 summarizes these off-line model results for forcing as well as results using the inline values for N_c, AOD, and AI from the coupled Community Atmospheric Model/Integrated Massively Parallel Atmospheric Chemical Transport (CAM/IMPACT) model, but holding cloud liquid water path and cloud fraction constant at PD values.

The forcing based on inline-calculated values for N_c from PD and PI simulations (-1.29 W/m²) is slightly smaller (in absolute value) than that deduced from the method based on the IPCC definition of forcing (-1.69 W/m²). This might be expected because the effect of coagulation and coalescence will be to decrease values of N_c more at larger values of N_c thereby making the difference in N_c between PD and PI conditions smaller, which then causes smaller forcing.

The forcing based on R(AOD ) and that based on R(AI) using the inline calculations is larger than that of the off-line calculations using R(AOD ) or R(AI). Values for the slope based on R(AI) or R(AOD) from the inline model results are, in general, larger than those based on R(AI) or R(AOD) from the off-line model, and this causes the estimated PI droplet concentrations to be smaller and the forcings larger (in absolute value) than those from the off-line method. The increased slope in the inline model is caused by the decreased loss of cloud droplets when aerosols increase within a region. More aerosols lead to less droplet sedimentation and precipitation, which then reduces the sink of cloud droplets and leads to relatively higher droplet number concentrations for a given aerosol concentration, which in turn increases the slope based on R(AI) or R(AOD). The PD slopes from satellite data include the effects of these feedbacks between aerosols and clouds, so this example also shows that the use of satellite slopes should not be expected to fit the IPCC definition of forcing.

We also note that the increase in slope using inline values causes the forcing based on estimating PI N_c from R(AI) in the inline model to be larger than the forcing using the true PI values, whereas the forcing based on the off-line model is smaller. This larger forcing is mainly caused by differences in slopes over ocean regions, because land areas still have smaller forcing than that based on the true PI values (see Fig. S2). The larger forcing is again caused by the feedbacks between aerosols and cloud drop number concentrations, which increase the slopes. This feedback is larger over ocean areas because the role of insoluble aerosols (which do not form drops as easily as soluble aerosols, and thus do not enhance the effects of feedbacks as much as soluble aerosols) is smaller in general over ocean areas in comparison with land areas. Nevertheless, as was true for the off-line model, the forcing calculated based on estimating the PI concentrations of N_c from the inline PD R(AOD) is still smaller (in absolute value) than that using the true PI value. This is because the neglect of temporal variations causes this method to underestimate the forcing.

Discussion

Satellite estimates of forcing can be improved if models are used in conjunction with the satellite estimates to examine the sources of possible errors. Here we demonstrate that the use of PD values of N_c and AOD or AI to estimate preindustrial values of N_c is likely flawed. This is because the use of regression techniques hides the true relationship between PD and PI values based on fundamental physics. This result is in keeping with previous analyses based on box-model results (15), but here we demonstrate that the associated error in forcing can be between a factor of 3 to more than a factor of 6 too small on a global average basis if one uses AOD to estimate preindustrial N_c or of order ± 25–35% if one uses AI.

Previous model studies have attempted to use satellite data to tune the model droplet number parameterization to reproduce the slope of the relationship between values for N_c and AOD or AI (2, 7). We suspect that this type of procedure is also flawed, because there is no guarantee that the relationship between AOD and N_c would be the same for preindustrial conditions as it is for present-day conditions (compare, for example, the slopes of the lines for PD and PI conditions shown in Fig. 3). Unfortunately, pure model estimates of indirect forcing are also suspect, because they are not able to reproduce the PD slopes between N_c and AOD in different regions (12). In addition, because other models get different values for these slopes, their estimates of forcing using the methods described here might differ. We can hope that improvements in both satellite data and models may eventually bring these differing results closer together and thus help to improve both model-based and satellite-based estimates.

Methods

We used the same 14 regions defined in ref. 3 (see Table S1) as well as data from all four seasons to estimate the slope of the relationship between the ln(N_c) and ln(AOD) or ln(AI) from PD simulations.

We used the aerosol model described in Wang et al. (16) and the off-line analysis described by Chen and Penner (11) for the calculation of cloud droplet number concentrations and radiative forcing. Here we used monthly average aerosol concentrations together with four-hourly meteorological fields at a 2° × 2.5° resolution to estimate the instantaneous aerosol optical depths, angstrom exponents, and cloud droplet concentrations as seen each day at the satellite overpass time of 1:30 pm (using methods described in 12). This off-line method differs from that based on satellite-derived quantities, because the observations include feedbacks, but was used here to avoid these feedbacks in order to calculate the IPCC-defined forcing. We also reported results for instantaneous values of N_c, AOD, and AI from our inline model that partially includes these feedbacks (i.e., we specified the cloud liquid water path and cloud fraction using our PD meteorological fields, but allowed the droplet number concentrations to change according to the inline calculations as a result of changes in aerosol concentrations, sedimentation, precipitation, and coagulation).

The aerosol model described in ref. 16 includes the prediction of the aerosol size distribution for pure sulfate aerosols in three modes using the aerosol module described by Herzog et al. (17) together with an empirical boundary layer aerosol nucleation scheme (18). Also, 2% of the anthropogenic sulfur emissions are emitted as primary aerosols to mimic the effects of subgrid scale processes leading to aerosol nucleation (16). The condensation of gas phase sulfate onto other aerosol types as well as the coagulation of pure sulfate aerosols with other aerosol types is included. Aerosol number concentrations for other aerosol types were calculated based on prescribed aerosol size distributions (16). Both PD and PI (for the year 1850) aerosol emissions were used (5).

The aerosol optical depth was calculated using a three-dimensional table lookup that included the optical properties from a Mie scattering calculation, i.e., the real and imaginary refractive indices and the size parameter (x = 2πr/λ, where r and λ are the aerosol radius and wavelength, respectively), so that arbitrary internal mixtures and sizes could be included. The optical depths at 495 and 670 nm were used to estimate the angstrom exponent. Fossil and biofuel OM and BC were treated as an internal mixture together with the amount of sulfate coated on these aerosol types, as was open biomass burning OM/BC aerosol and its sulfate coating. The internal mixing of sulfate with dust, sea salt, and natural organics was also treated in the radiation scheme, but each of the sulfate-coated aerosol types was externally mixed. The value for the hygroscopicity of organic matter and sulfates, which determines the growth of the particles under different humidity conditions as well as the formation of cloud droplets, followed the choices made in ref. 19. For dust and sea salt, the optical properties are calculated separately for the four size bins carried in the model (0.05–0.63 μm, 0.63–1.26 μm, 1.26–2.5 μm, and 2.5–10 μm).

The PD and PI aerosol fields calculated in the coupled model were used to calculate the cloud droplet number concentration using an activation parameterization (20, 21). This parameterization combines the treatment of multiple aerosol types and a sectional representation of size to deal with arbitrary aerosol mixing states and arbitrary aerosol size distributions. The effective radius of the nucleated droplet population accounted for the effects of droplet dispersion (22). The cloud droplet effective radius was used to calculate the cloud optical depth and the first aerosol indirect forcing in an off-line radiative transfer model as in ref. 5. (This method differs from that used in ref. 3, because these authors fitted the measured planetary albedos to measured aerosol optical depths, cloud fractions, and liquid water paths to obtain the forcing.) Alternatively, the off-line model was used with an estimate of the PI droplet concentrations, based on a linear regression of the PD ln(N_c) versus ln(AOD) or PD ln(N_c) versus ln(AI) together with the change in AOD or AI between the PD and PI aerosols. The use of the calculated N_c from a parameterization based on the calculated aerosol concentrations is used in global models of the aerosol indirect effect, whereas satellite methods use a linear regression inferred from present-day measurements to estimate the change in radiative fluxes based on anthropogenic aerosol optical depths (3). Present-day measurements can also be used to adjust estimates of droplet number concentration in global models to be consistent with those based on satellite measurements (2, 7). Both estimates of forcing presented here use model-estimated PI values of AOD or AI.