Dichroic coherent diffractive imaging

Abstract

Understanding electronic structure at the nanoscale is crucial to untangling fundamental physics puzzles such as phase separation and emergent behavior in complex magnetic oxides. Probes with the ability to see beyond surfaces on nanometer length and subpicosecond time scales can greatly enhance our understanding of these systems and will undoubtedly impact development of future information technologies. Polarized X-rays are an appealing choice of probe due to their penetrating power, elemental and magnetic specificity, and high spatial resolution. The resolution of traditional X-ray microscopes is limited by the nanometer precision required to fabricate X-ray optics. Here we present a novel approach to lensless imaging of an extended magnetic nanostructure, in which a scanned series of dichroic coherent diffraction patterns is recorded and numerically inverted to map its magnetic domain configuration. Unlike holographic methods, it does not require a reference wave or precision optics. In addition, it enables the imaging of samples with arbitrarily large spatial dimensions, at a spatial resolution limited solely by the coherent X-ray flux, wavelength, and stability of the sample with respect to the beam. It can readily be extended to nonmagnetic systems that exhibit circular or linear dichroism. We demonstrate this approach by imaging ferrimagnetic labyrinthine domains in a Gd/Fe multilayer with perpendicular anisotropy and follow the evolution of the domain structure through part of its magnetization hysteresis loop. This approach is scalable to imaging with diffraction-limited resolution, a prospect rapidly becoming a reality in view of the new generation of phenomenally brilliant X-ray sources.

Materials such as magnetic multilayers and alloys, polymers, liquid crystals, biofibers, and biominerals all exhibit self-organizing, reaction-diffusion, and pattern-forming behavior not fully understood. New schemes for directed domain formation in magnetic multilayers and alloys are integral parts of next-generation magnetic data storage and spintronic technologies (1, 2). Controlled phase transitions and ordering dynamics in polymers and liquid crystals under applied electric fields, with consequent photonic bandgap shifts, play a major role in organic laser technology (3). In the biological sciences, certain biofibers display tensile properties similar to that of steel yet are far more lightweight, properties thought to be the result of self-organized phase separation of molecular crystalline and amorphous regions within the fibers (4, 5). Deeper understanding of biomineral growth and the interaction between inorganic material and organic macromolecule phases could enable use of similar techniques to fabricate novel synthetic materials.

Microscopy using dichroism as a contrast mechanism can reveal much about phase ordering, separation, and coexistence in these kinds of systems. All of these materials have an order parameter that scatters light differently depending on the direction or helicity of the photon polarization. Polarized X-rays are an ideal choice of probe for imaging buried magnetic structure due to strong resonant enhancement of the scattering at electronic transitions split by the spin-orbit effect. Because X-ray beams are unaffected by magnetic or electric fields, they are also well suited to studying phase transitions as a function of applied fields. Established techniques such as transmission X-ray microscopy and X-ray photoemission electron microscopy as well as novel holographic methods have dramatically improved our understanding of dichroic materials at the nanoscale (6–9). However, these approaches require focusing optics or apertures that must be made to a precision comparable to the desired spatial resolution. On the other hand, techniques such as magnetic force and electron microscopy offer nanoscale imaging but only near surfaces and generally with weak external fields (10).

An alternative approach to nanoscale dichroic microscopy is resonant X-ray coherent diffractive imaging (CDI), whereby the diffraction pattern formed by scattering a coherent X-ray beam from a sample is inverted numerically to form an image of the sample (11). In CDI, the spatial resolution is not limited by the quality of the optical elements but by the highest spatial frequencies measured in the X-ray diffraction pattern. CDI can provide three-dimensional information by sufficiently mapping the Ewald sphere (12–14) and offers elemental selectivity near electronic resonances (15). When combined with “ptychographic” methods, regions of arbitrary large lateral dimensions can be imaged quantitatively with a spatial resolution defined solely by the wavelength, coherent X-ray flux, and scan precision and stability (16–20). In CDI the phases of the scattered amplitudes lost by recording the diffraction intensity are recovered computationally by an iterative algorithm. For the algorithm to converge to a unique solution, there must be sufficient constraints on the problem, and the diffraction pattern must be adequately sampled with respect to the spatial Nyquist frequency (21). This requirement, known as “oversampling” (22), is necessary to regain phase information in the complex-valued diffraction signal. The algorithm starts with a random guess for the phase of the measured diffraction, then iterates between the sample (real space) and the diffraction measurement (reciprocal space) using fast Fourier transforms, refining the initial guess by enforcing constraints in both real and reciprocal space at each step (23). A solution is found when the initial guess is refined to a degree such that it satisfies all the constraints.

Here we demonstrate that lensless resonant scanning CDI can be used to image nanometer-scale ferrimagnetic domains in a multilayer Gd/Fe film. In such multilayer systems, alternating layers of a transition metal and a rare-earth metal are deposited to create an artificial ferrimagnet with perpendicular magnetic anisotropy. The balance between exchange, anisotropy, and dipolar energies results in stripe domain patterns as first described by Kittel (24) and further developed and studied experimentally by Kooy and Enz (25). A schematic of this system is shown in Fig. 1A. Perpendicular anisotropy magnetic films are extensively studied to probe the physics of stripe-forming systems (26, 27), where local pinning sites, external magnetic fields, and temperature can strongly affect the domain structure. Interest in Gd/Fe and related multilayer structures has grown recently with demonstrations of laser-induced femtosecond switching, leading to the possibility of dramatically faster magnetic recording (28).

Fig. 1.

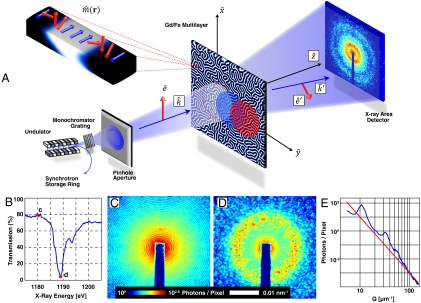
(A) Schematic of an X-ray scanning CDI measurement with a dichroic sample. For the sample under investigation, the magnetization direction 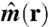is primarily parallel/antiparallel to the propagation vector 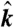. When linearly polarized synchrotron radiation with a polarization direction defined by 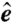is used to illuminate the sample, contrast arises primarily from the X-ray magnetic circular dichroism (XMCD) effect. Diffraction patterns are recorded in the far-field by an X-ray area detector by scanning the sample, depicted as the overlapping white, blue and red circles. (B) X-ray energy transmission scan across the Gd M₅ edge, with red circles marking the X-ray energy values for which diffraction patterns C and D were collected. (C) Off-resonance diffraction pattern taken at an X-ray photon energy of 1,180 eV has no discernible magnetic scattering and contains only Airy diffraction fringes from the circular pinhole. (D) On-resonance diffraction pattern taken at 1,189 eV exhibits a magnetic scattering ring arising from magnetic stripe domains, in addition to the pinhole scattering. (E) Azimuthal average of diffraction intensity showing higher-order magnetic diffraction rings. The red line illustrates a Q^-4 power-law decay of the signal.

The present experiments take advantage of the brilliance, polarization, and tunability of X-ray undulator radiation. The scattering resulting from polarized photons interacting with the magnetic ordering is strongly enhanced at resonances (29, 30); Fig. 1B shows a transmission spectrum for the sample in the vicinity of the Gd M₅ edge. This spectrum is highly sensitive to the photon polarization state and magnetic spin state of the Gd. For the Gd/Fe multilayer studied here in the small angle scattering geometry, as shown in Fig. 1A, the scattered signal is maximal when the incident photon propagation 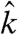is perpendicular to the sample surface. Off resonance, at 1180 eV, the diffraction pattern is dominated by charge scattering as well as the unscattered direct beam from the pinhole (see Fig. 1C). The rectangular shadow in Fig. 1 C and D is due to the beam stop used to protect the CCD from the bright, unscattered beam. Because this sample appears electronically homogeneous in projection, a diffraction pattern taken with the sample out of the X-ray beam, arising solely from the pinhole aperture, is identical to Fig. 1C up to a known absorption scale factor. The same diffraction pattern was obtained by saturating the magnetization by applying an out-of-plane magnetic field and coercing the sample into a single domain state.

A coherent diffraction pattern taken on resonance at 1189 eV is shown in Fig. 1D. The speckle ring at a wavevector of ≃0.01 nm^-1 corresponds to spatial features of π/0.01 nm^-1 ≃ 300 nm. There are several additional higher-order (odd) diffraction rings at wavevectors of ≃0.03 nm^-1 and ≃0.05 nm^-1, which can be seen in the azimuthally averaged diffraction pattern shown in Fig. 1E. This suggests that the magnetic domains are monodisperse with a characteristic domain width of ≃300 nm. Beyond ≃0.06 nm^-1, the diffraction signal is difficult to distinguish from the noise background of the measurement. This maximum value of the momentum transfer over which the diffraction pattern can be sampled roughly defines the spatial resolution in our experiments and corresponds to spatial information down to π/0.06 nm^-1 ≃ 50 nm. When using linearly polarized X-rays, the charge scattering does not interfere with the magnetic scattering (31). As a result we can isolate the resonant magnetic scattering by straightforward subtraction of the magnetically saturated diffraction intensities from those of the nonsaturated measurement, both taken on-resonance. This difference results in a diffraction pattern that arises solely from magnetic contrast. The resulting magnetic diffraction is used to reconstruct maps of the magnetic domain configuration; further details are provided in the Materials and Methods section.

Results and Discussion

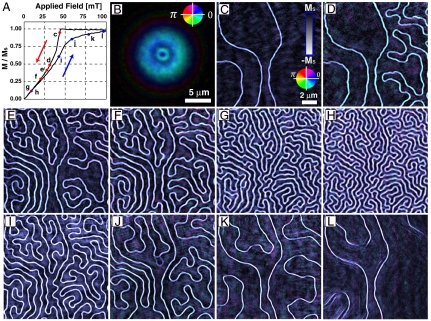
Starting from a magnetically saturated state (i.e., the entire sample is in a single-domain ferrimagnetic state with the net magnetization parallel to the applied field), the external field was reduced until magnetic diffraction becomes visible; this occurs at about 44 mT as shown on the hysteresis curve in Fig. 2A. A reconstruction of the ptychographic diffraction data at this point is shown in Fig. 2C, while Fig. 2B shows the reconstructed X-ray wave incident on the sample. We then recorded a series of ptychographic measurements while reducing the field near to zero, with representative reconstructions at selected points on the hysteresis curve (Fig. 2A) shown in Fig. 2 D–G. Fig. 2H–L shows the reconstructions of the Gd spin density at the same sample region as the field is increased toward saturation (corresponding to points h through l in Fig. 2A). As the magnetic field is decreased, the magnetic domain pattern undergoes classic evolution toward a labyrinthine stripe pattern. This type of pattern is commonly found in a wide class of uniaxially modulated condensed matter systems, including diblock copolymers, liquid crystals, Langmuir monolayers, adsorbates at metallic surfaces, incommensurate structures, membranes, vesicles, and ferrofluids, as well as dewetting, phase separation, dealloying, and convection patterns (27, 33, 34). The characteristic length scale corresponding to the width of the stripe is generally defined by the energetic balance between short- and long-range interactions. The ability to tune the relative strength of these interactions and to control the degree of orientational or translational order in many of these systems represents a pathway for driven or guided self-assembly at nanoscale, a concept especially appealing in areas of soft matter and magnetism.

Fig. 2.

(A) Hysteresis loop of the sample magnetization as a function of magnetic field applied perpendicular to the film surface. (B) Reconstruction of the X-ray beam that illuminated the sample. The phase of the reconstruction is encoded as hue of the image, while the magnitude is encoded as brightness. The X-ray flux incident on the sample is estimated to be 2.5 × 10⁵ photons/s·μm². (C–G) Gd spin density reconstructions at indicated points on the magnetic hysteresis curve shown in A while decreasing the external field. Bright domains are antiparallel to the applied magnetic field. Phase is encoded as hue and magnitude is encoded as brightness, as for the probe reconstruction. The color bar shows the areal magnetization in terms of the saturation value, M_s = 0.011 emu/cm². Because only the Gd is resonantly scattering, the reconstructions only show the evolution of the Gd magnetic configuration. (H–L) Gd spin density reconstructions at indicated points on the magnetic hysteresis curve shown in A while increasing the external field. Note that near the top in E and toward the middle in J we observe that part of the bright domain appears to move, suggesting the domain configuration had not quite settled when the measurements began. Each reconstruction presented is the average of 10 reconstructions using random initial phase guesses. The small variations visible in the images are artifacts caused by statistical noise due to the low photon count at large Q and by unconstrained modes in the reconstruction (32).

The magnetization behavior with field of the Gd/Fe multilayer studied here follows closely the classic theory of Kooy and Enz first developed in context of BaFe₁₂O₉ (25) and subsequent modeling of periodic stripe domains in an infinite plate. The sharp downturn in the magnetization with decreasing field (point c in Fig. 2A) occurs when isolated domains become unstable. These domains seed an avalanche of stripe domains that quickly fill the sample and a characteristic domain periodicity rapidly develops across the sample (as reflected by the ring in the magnetic scattering in Fig. 1D). The resulting morphology and ratio of “up” domains to “down” domains depends on the dipolar interactions that drive the domain formation, the field history, the density of nucleation sites, and the interaction of the domain walls with quenched disorder (e.g., pinning centers arising from local variations in the magnetic properties) in the sample. With decreasing field, the average domain period decreases as domains fill the space while the domain width remains relatively constant. This indicates that domain evolution in Gd/Fe films is qualitatively different from that in Co/Pd multilayer films where the domain period is relatively insensitive to field and only the relative ratio of up and down domain widths changes with field (35, 36). The current results more closely follow the expectations of models (25) and suggest a relatively low defect density. However, the two early forming vertical domains seen in Fig. 2C appear more heavily pinned than other domains, retaining their position and shape down to the lowest magnetic field. These early forming domains define a boundary, dividing the imaged field of view into three distinct regions. Each region contains self-connected domains, which remain separated during their evolution (37). Close comparison of Fig. 2 E and F as well as Fig. 2 G and H shows that the final and initial stages of labyrinthine growth are dominated by the unbinding of the disclination dipoles (26), resulting in formation of split-off Y-shaped branches and “cul-de-sac” domain lines that are not present in domain patterns shown in Fig. 2 C and D and Fig. 2 I–K. The behavior for increasing and decreasing field in this region, where the divergence of the periodicity is the fundamental saturation mechanism, is nearly reversible.

Spatial Resolution.

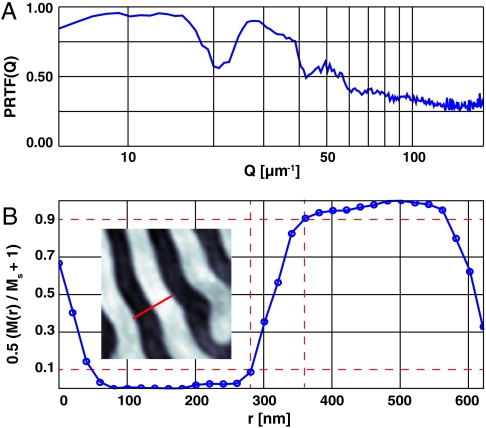
To characterize the quality of the reconstructions in Fig. 2, we use the concept of the phase retrieval transfer function (PRTF) (13). The PRTF is defined as the ratio of the reconstructed diffraction magnitude (the absolute value of the Fourier transform of the reconstruction) to the measured diffraction magnitude as a function of momentum transfer (see Materials and Methods). The PRTF provides a quantitative estimate of the range of spatial frequencies over which the domain reconstructions can be trusted. Imperfections of the diffraction measurements due to photon shot noise and missing diffraction behind the beamstop, as well as imperfect real-space constraints, such as mechanical stage errors when scanning the sample, contribute to numerical artifacts and degradation of the reconstruction. A typical PRTF of the domain reconstructions is shown in Fig. 3A. The dips in the PRTF arise because of low signal to noise at spatial frequencies between the highly ordered magnetic scattering rings seen in Fig. 1 D and E. Using a PRTF cutoff value of 0.5 as described previously (13) indicates that reconstruction is robust up to spatial frequencies of about 57 μm^-1. This corresponds to a spatial resolution ofπ/57 μm^-1 ≃ 55 nm, in good agreement with the estimate above based on the largest wavevector at which speckles are still visible among the noise.

Fig. 3.

(A) The phase retrieval transfer function (PRTF) of a reconstruction. Defining a cutoff of 0.5 predicts a spatial resolution of π/57 μm^-1 ≃ 55 nm. (B) Line cut (r) through two domains shown in inset. The 10% to 90% edge response gives a resolution of ≃80 nm. The point spread function of the imaging process blurs the Bloch wall width of ≃30 nm, which accounts for the discrepancy.

We can arrive at another estimate of the spatial resolution by taking a line scan across a reconstructed domain wall. As seen in Fig. 3B, the 10% to 90% edge response provides a width of 77 nm (corresponding to a standard deviation of 60 nm). The Bloch wall width for this system is ≃30 nm (38–41). Convolution of this domain wall width and a Gaussian point spread function with standard deviation 0.5 × 55 nm would result in a blurred Bloch wall with a width of 62 nm and 10% to 90% edge response of 80 nm, which accounts for the results obtained here.

During data acquisition the positions of the magnetic speckles comprising the diffraction patterns did not move detectably even at the largest wavevector values, indicating that sample vibration within the illuminated region was negligible in our experiments. However, sample vibration and positioning errors in scanning could become practical limitations of the CDI approach at higher resolution.

Conclusions.

We have demonstrated X-ray microscopy of an extended disordered magnetic nanostructure using numerical inversion of a scanned series of resonant dichroic coherent diffraction patterns. Like X-ray holography and transmission X-ray microscopy, this approach can be used to image magnetic domains at nanometer resolution. In contrast to these techniques, the approach described here does not require circularly polarized light for magnetic contrast nor nano-fabricated optics or apertures to reach high spatial resolution. Indeed, it works equally well using circularly or linearly polarized light, allowing this approach to be expanded to image both magnetic and structural heterogeneity. As it replaces optical elements with a “numerical” lens, in addition to greatly simplifying the experiment, the spatial resolution is solely determined by the signal to noise at high spatial frequencies recorded in the coherent diffraction measurements and by the precision and stability with which the sample is scanned in the X-ray beam. It can be used to image an arbitrarily large area of interest, and the sample under investigation can be easily interchanged without the need for additional off-resonance calibration measurements. The technique can be adapted for imaging a wide range of dichroic materials. Study of order parameters on ultrafast time scales by this technique would require working below radiation damage thresholds due to the probe overlap requirement of the reconstruction algorithm used here. Use of additional real-space constraints such as known material indices of refraction (42), compressed sensing (43), and probes with phase curvature (44) may enable extension of this approach to single-view dichroic imaging. While the measurements presented here were performed at a third-generation synchrotron, this experimental technique will benefit tremendously as the new generation of high brilliance X-ray sources that produce beams with nearly full transverse coherence, including ultra low-emittance synchrotrons (45), energy recovery linacs (46), and free electron lasers (47) become available.

Materials and Methods

Sample Preparation.

The sample investigated here consisted of 116 layers of 0.41 nm of Fe and 0.45 nm of Gd, capped with 2 nm of Ta to prevent oxidation. The multilayer was deposited on a 100 nm thick Si₃N₄ membrane at room temperature at an Ar pressure of 3 mTorr with a deposition rate of 0.04 nm/s for Fe and 0.18 nm/s for Gd.

X-ray Diffraction Intensity.

The resonant elastic scattering amplitude for polarized photons interacting with this dichroic sample is

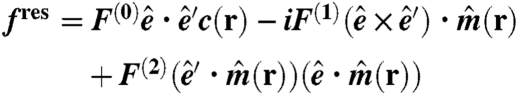[1]

where 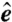and are Jones vectors of the incident and scattered radiation, respectively, 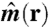is the unit vector magnetization structure factor, as shown in Fig. 1A, and c(r) is the resonant charge structure factor (29, 30). The F^(0,1,2) are complex (dispersive and absorptive) resonant scattering strengths, with F⁽⁰⁾ describing any nonmagnetic scattering, F⁽¹⁾ describing circular dichroic scattering, and F⁽²⁾ describing linear dichroic scattering. In our experiment (see Fig. 1A), the incident radiation was linearly polarized and the resonant Fraunhofer diffraction intensity is given by

[2]

where 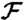denotes the spatial Fourier transform, p(r) is the X-ray probe (see Fig. 2B), and m_z(r) describes magnetization direction parallel/antiparallel to the propagation vector 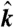. The scattering mechanism from the m_x(r) and m_y(r) components within Bloch walls arises from X-ray magnetic linear dichroism (XMLD), which is many times weaker than the XMCD signal (48). Also, the Bloch wall width is a small fraction of the size of the ferrimagnetic domains, and so the scattering contribution from this in-plane magnetization is negligible.

Data Collection.

The experiments were conducted at the 2-ID-B coherent imaging beamline at the Advanced Photon Source. The pinhole aperture used in Fig. 1A was 10 μm in diameter and positioned 6.5 mm away from the sample. We scanned a 4-by-4 grid with 3-μm step sizes to give a total illuminated field of view of 19 μm by 19 μm. A CCD camera with 2,048 × 2,048 pixels (pixel dimension a² = 13.5 μm by 13.5 μm) was placed z = 455 mm downstream from the sample. This gave a reconstructed square field of view of width L = λz/a = 35 μm for the array sizes in the reconstructions and a pixel size of 35 μm/2,048 = 17.1 nm, where the wavelength λ = 1.04 nm at 1,189 eV. Because the illuminated region on the sample has an area of A = π(5 μm)², the sampling ratio is about L²/A ≃ 15.6. We collected 40 exposures at each of the 16 illuminated regions on the sample, each with an exposure time of 0.5 s, resulting in estimated flux per exposure of 2.5 × 10⁵ photons/s·μm². The 40 exposures were summed at each scan position to form a single diffraction pattern with improved counting statistics. Approximately 95% of the radiation is absorbed on resonance (see Fig. 1B), resulting in an estimated radiation dose per exposure of 5.6 × 10⁴ Gy.

Numerical Inversion.

We used the difference map algorithm (17–19) combined with the ptychographic steepest descent method (16) to reconstruct the Gd spin density and X-ray probe. The square-root values of the integrated diffraction intensities at each scan position were used as constraints in reciprocal space. Unmeasured pixels behind the beam stop were left unconstrained. The known scan positions (with 70% probe overlap between adjacent positions) were used as constraints in real space. In addition, because the dispersive part of the refractive index ideally vanishes on-resonance (48), the imaginary part of the reconstructed map (arising from the real component of the refractive index) can be constrained to be small. We therefore constrained the imaginary part of reconstructed density map between ± 0.05i for the first few hundred iterations and then gradually relaxed it to ± 0.5i for subsequent iterations. We solved the Gd spin density and probe simultaneously as in ref. 19 using a random set of initial phases for the sample and a set of uniform amplitudes and phases over a circle of diameter 10 μm as the initial guess for the probe. The diffracted intensity was highest when the average sample magnetization was close to zero and the number of magnetic domains was greatest. At low applied fields the reconstruction of the Gd spin density and X-ray probe converged in about 500 iterations of the difference map followed by 100 iterations of the steepest descent method. When the sample was close to magnetic saturation, using a previously reconstructed probe, about 800 iterations of the difference map followed by 100 iterations of steepest descent were necessary to obtain a high quality reconstruction.

Quantitative Gd Spin Density Maps.

Quantitative maps of the Gd magnetization M(r) were obtained by scaling the reconstructions by the calculated XMCD contrast—the dependence of f^res on the relative direction of the Gd spin magnetization and photon helicity—based on the measured X-ray transmission. The X-ray intensity just exiting the sample can be written as

[3]

where I₀ is the the X-ray intensity incident on the sample times attenuation contribution of Fe layers, D is the net thickness of the Gd layers, ± represents the photon polarization helicity, and μ_± is the polarization dependent extinction coefficient for a given out-of-plane magnetization. The reconstructed exit wave amplitudes Φ(r) for the on-resonance diffraction patterns vary from Φ_C - Φ_M to Φ_C + Φ_M, where Φ_C and Φ_M represent charge and magnetic scattering component amplitudes, respectively. The XMCD spectrum is defined as the difference between μ₊ and μ_-, the difference in extinction coefficients between the two out-of-plane magnetization directions for a given circular polarization:

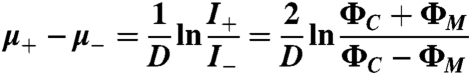[4]

The absolute value of the magnetization is directly related to this XMCD contrast through the known magneto-optical constants of Gd (48). From the reconstructions, Φ_M/Φ_C = 0.49, giving an XMCD atomic photoabsorption cross-section of 0.24 Å², in good agreement with XMCD spectra measured with a fully saturated Gd moment (48), corresponding to an areal magnetization of M_s = 0.011 emu/cm².

Note that due to the use of linearly polarized light, a negative of any reconstructed map of M(r) [i.e., -M(r)] would also satisfy the constraints. This twofold degeneracy in the solution is lifted upon application of a magnetic field, because the Gd magnetization aligns in the direction of applied field. Measurements at the Gd M edges provide us with an elemental distribution of the Gd magnetization. The measurements would have to be repeated at the Fe L edges to obtain similar maps of the Fe magnetization. However, because Gd and Fe are known to be antiferromagnetically coupled, the Fe magnetization map is expected to be the negative of the Gd magnetization map, rescaled by the ratio of the magnetic moments and total layer thicknesses for the two elements.

Phase Retrieval Transfer Function.

The PRTF can be expressed as (13)

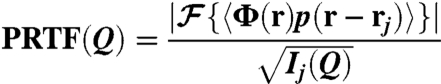[5]

where I_j(Q) is the measured diffraction intensity at scan position r_j, and denotes averaging over many independent reconstructions of Φ(r). For the PRTF shown in Fig. 3A, the Q axis pixel size is πa/λz ≃ 0.089 μm^-1, and annuli 3 pixels wide in both the numerator and denominator of Eq. 5 were integrated from Q = 0 μm^-1 to Q = 178 μm^-1. The ratio of these two results is shown in Fig. 3A.