Abstract
We have explored suitability of fixed-charges and polarizable force fields for modeling interactions of the monovalent Cu(I) ion. Parameters for this ion have been tested and refitted within the fixed-charges OPLS-AA and polarizable force field (PFF) frameworks. While this ion plays an important role in many protein interactions, the attention to it in developing empirical force fields is limited. Our PFF parameters for the copper ion worked very well for the Cu(I) interactions with water, while both the original OPLS2005 and our refitted OPLS versions moderately underestimated the copper-water interaction energy. However, the greatest problem in using the non-polarizable fixed-charges OPLS force field was observed while calculating interaction energies and distances for Cu(I) – benzene complexes. The OPLS2005 model underestimates the interaction energy by a factor of four. Refitting the OPLS parameters reduced this underestimation to a factor of 2.2 to 2.4, but only at a cost of distorting the complex geometry. At the same time, the polarizable calculations had an error of about 4%. Moreover, we then used the PFF and non-polarizable refitted OPLS models for finding free energy of hydration for copper ion via molecular dynamics simulations. While the OPLS calculations lead to a 22% error in the solvation energy, the PFF result was off by only 1.8%. This was achieved with no refitting of the parameters but simply by employing the model developed for the Cu(I) interaction with a single water molecule. We believe that the presented results not only lead to a conclusion about a qualitatively greater suitability of polarizable force fields for simulating molecular interactions with ions but also attest to the excellent level of transferability of PFF parameters.
Keywords: copper(I) ion, polarizable force fields, cation interactions, gas-phase dimers, free energy of hydration
I. Introduction
Cu(I) ion plays an important role in many biological processes. Copper-protein binding is essential in phenomena ranging from respiration and photosynthesis to countering toxicity.1 At the same time, carefully developed potential energy parameters for this ion to be used in empirical force field calculations are not easily found. In some cases, metal ions interacting with proteins are represented by mere point electrostatic charges.2a This obviously limits the realism of the molecular mechanics, molecular dynamics and Monte Carlo simulations which can be carried out. One possible alternative to developing copper parameters for empirical force fields is to employ quantum mechanical or combined quantum mechanical/molecular mechanical techniques,2b,c but they have their limitations. Yet another way of treating these ions is to include a number of additional parameters, such as constraints prohibiting the ion from leaving the prescribed coordinated place.2d
On the other hand, an additional problem is presented by the lack of explicit treatment of electrostatic polarization in many commonly used force fields. At the same time, it has been shown that the explicit polarization is critical in reproducing energetic properties of systems with strong electrostatic influences (for example, we have previously demonstrated the importance of including polarization when calculating acidity constants of protein residues and small molecules3). It has long since been shown that cation-benzene interaction energies can be underestimated by a factor of two without explicitly present polarization.4 However, the attention is usually focused on relatively light metal ions.
Our goal was to design parameters for the monovalent copper ion in the framework of our previously developed polarizable force field (PFF)5 and to benchmark them against the fixed-charges OPLS model. We have also refitted and tested two new sets of OPLS-like parameters in order to have a fair comparison. First, we calculated energies and geometries of the Cu(I) complexes with water and benzene molecules. The former one is related to the aqueous solution as the most common environment for biochemical and other chemical processes. The latter represented a simple model of the cation interaction with a polarizable system (which could range from a simple aromatics to proteins and nucleic acids). Then we used the OPLS and PFF copper(I) ion models to obtain free energies of hydration in infinitely dilute aqueous solution. Both this last step and the Cu(I) – benzene interaction calculations were carried out without any refitting of the parameters. Therefore, this represented a true benchmarking of the polarizable and fixed-charges formalisms and the resulting parameter values.
The rest of the paper is organized as follows. The Methods section presents the techniques utilized in this project. The third section contains results and discussion. They are followed by conclusions in Section IV.
II. Methods
Force Fields
Detailed descriptions of the OPLS and PFF force fields are available elsewhere.5,6 Briefly, the total energy Etotal is computed as a sum of the electrostatic term Eelectrostatics, the non-electrostatic van-der-Waals part EvdW, bond stretching and angle bending energies Ebond and Eangles, and the torsional term Etorsion:
| (1) |
In the case of the polarizable force field, the total electrostatic energy of the model results from interactions of fixed-magnitudes atomic charges, fixed point dipoles, and inducible dipoles:
| (2) |
Here Jij,kl is a scalar coupling between bond-charge increments on sites i,j and k,l qij and qkl; Sij,k is a vector coupling between a bond-charge increment on sites i,j and a dipole on site k μk; a rank-two tensor coupling Ti,j describes interactions between dipoles on sites i and j. αi is the polarizability of site i. Parameters χi describe “dipole affinity” of site i.
According to the Coulomb formalism,
| (3) |
| (4) |
| (5) |
Inducible dipoles are placed on all the heavy atoms and on some polar hydrogens (such as the water hydrogens), as described in References 3a and 5. Fixed charges q and permanent dipoles defined by the “dipole affinities” χ are present on all the atoms. “Virtual sites” representing electron lone pairs were placed on the water oxygen atoms with the virtual site – oxygen distances set to 0.47Å. Dipole-dipole and charge-dipole screening is used to damp the polarization response when the perturbing site is at short distances. Each dipole and each charge has an individually set screening length. The corresponding length parameters for two atoms are added together to obtain the effective screening length for the pair interaction.
The overall non-electrostatic pair potential form is:
| (6) |
The A parameter is set so that the 1/r12 term is close to zero in the hydrogen bonding region, but is large enough to prevent atoms from being positioned too close and thus penetrating the nonphysical region of the phase space.
Finally the bond stretching and angle bending terms have the standard harmonic functional form, and the torsional energy of benzene molecules is described by a sum of Fourier series:
| (7) |
| (8) |
| (9) |
Here Kr and KΘ represent the force constants; r, req, Θ, and Θeq are actual and equilibrium values of bond lengths and angles; ϕ are the dihedral angles.
We utilized the values of the parameters from previously developed PFF models for water3a and benzene.5
The non-polarized OPLS-AA force field differs in its non-bonded component, with the Eelectrostatics and EvdW terms in Equation 1 replaced by the sum of the Coulomb and Lennard-Jones contributions for pairwise intra- and intermolecular interactions:
| (10) |
Geometric combining rules for the Lennard-Jones coefficients were employed. The summation runs over all the pairs of atoms i < j on molecules A and B or A and A for the intramolecular interactions. Moreover, in the latter case, the coefficient fij is equal to 0.0 for any i−j pairs connected by a valence bond (1–2 pairs) or a valence bond angle (1–3 pairs). fij = 0.5 for 1,4-interactions (atoms separated by exactly 3 bonds) and fij = 1.0 for all the other cases. The water and benzene models were adopted directly from the standard OPLS-AA,6 while various copper(I) parameters were taken from either the OPLS20057 or refitted in this work, depending on the particular copper model (as presented in the Results and Discussion section).
Gas-Phase Geometry Optimizations
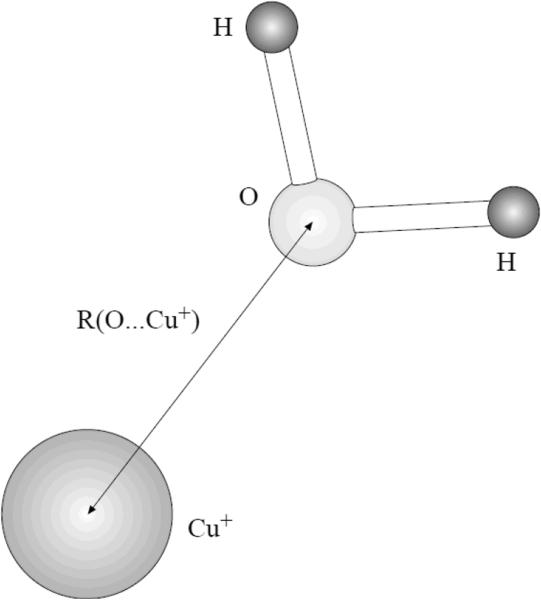
The first step of the Cu(I) parameter fitting and benchmarking proceeded as follows. We considered a symmetric complex of the ion with a water molecule, as shown on Figure 1. Parameters for the copper ion were adjusted to reproduce the reference distance between the centers of the Cu(I) and O atom and the interaction energy (calculated as the difference between the complex energy and energies of the water molecule and Cu(I) separately) as close as possible. The reference values are 1.93Å and −41.8 kcal/mol, respectively8a. The quality of these data which we used as the reference can be further justified by their close correspondence to the CCSD(T) results with the aug-cc-pVQZ basis set yielding a complex formation energy of −39.8 kcal/mol and Cu(I)…O distance of 1.933Å and the experimental binding energy of −41.0 kcal/mol.8b
Figure 1.
The symmetric Cu(I) complex with water.
We are reporting results for four versions of the simulated system: the original fixed-charges OPLS2005, two refitted versions of the OPLS (one with the water molecule simulated with the TIP3P model and the other with TIP4P) and the polarizable PFF. It should be emphasized that the refitted OPLS parameters for Cu(I) are produced by us and by no means belong to the official OPLS parameter set, thus we retain their designation only because of the truly OPLS-AA water parameters and the overall OPLS formalism.
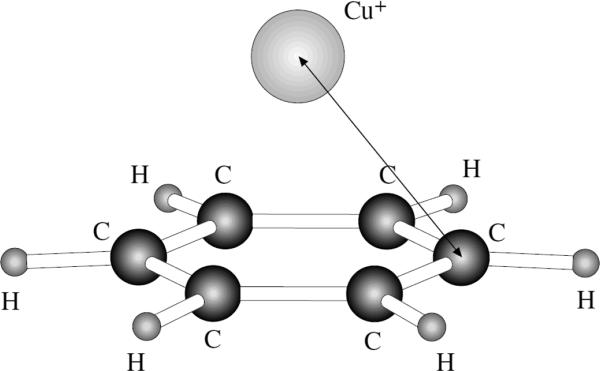
The symmetric Cu(I)…benzene complex studied in this work is shown on Figure 2. The quantum mechanical reference energy for this complex is known to be between −56.9 and −61.3 kcal/mol.9 As described in detail in Reference 9, the basis sets used in computing these numbers ranged from a combination of 6-31G** to TZ2P (triple-zeta plus two sets of polarization functions) for the carbon and hydrogen atoms and from the RECP potential in conjunction with the recommended basis set for the metal valence electrons to the same set augmented by three s, one p, three d and one f uncontracted functions for Cu+. BLYP and CCSD(T) levels of theory were employed.
Figure 2.
The C6V symmetric Cu(I) complex with benzene.
We have simulated this complex with the PFF formalism and with all the Cu(I) ion parameters noted above (OPLS2005 and the parameters fitted to work with the TIP3P and TIP4P water models for the complex shown on Figure 1).
All the polarizable geometry optimizations were carried out with the PFF software10 and all the fixed-charges OPLS ones were done with the BOSS program.11
Free Energy of Hydration of Cu(I)
The only case when the Cu(I) parameters were adjusted was for the Cu(I) complex with one water molecule. Both copper – benzene complex and solvated Cu(I) ion were studied without any parameter adjustment. The goal of the liquid simulations was to “shrink” the Cu+ particle into a dummy atom in molecular dynamics simulations and thus to calculate the free energy of hydration via the statistical perturbation theory. These simulations were carried out with the SIM software.10 The solvent water molecules were completely flexible, with no geometric constraints. All the molecular dynamics simulations were carried out with the target temperature of 298.15 K and at 1 atm. constant pressure. Time steps of 8 × 10−1 fs were used, with 105 steps of equilibration followed by 105 steps of the actual perturbation. A cubic cell of 215 water molecules was included in each of the solvated simulations, with the periodic boundary conditions applied and the Ewald summation technique used to account for the interactions beyond the cell boundaries.12
For the fixed charges calculations, the non-bonded parameters for water were taken from the OPLS TIP3P parameter set.6a We have carried out calculations of the pure water heat of vaporization and density at 298.15K in order to make sure adding the internal flexibility to the TIP3P molecules does not invalidate the model. The resulting calculated ΔHvap was equal to 10.68 kcal/mol and the density was found to be 0.968 g/cm3, in good agreement with the experimental values of 10.51 kcal/mol and 0.997 g/cm3 for the heat of vaporization and density, respectively.
We used the previously developed PFF model for water3a in the polarizable calculations. This model was parameterized to reproduce gas-phase dimerization energies and geometries and liquid state heat of vaporization and density.3a
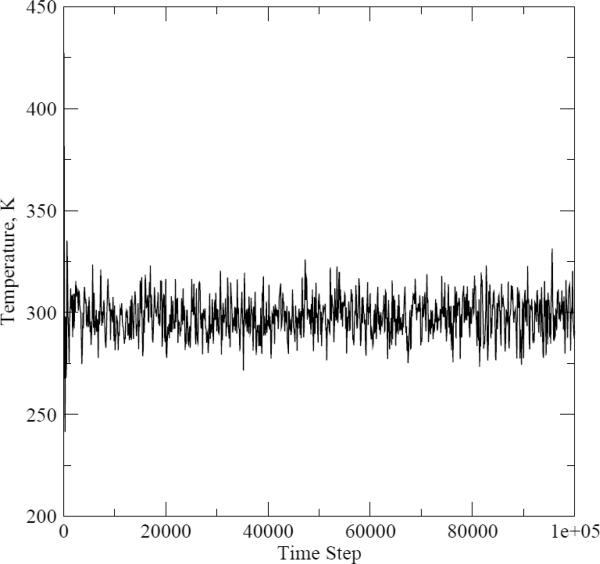
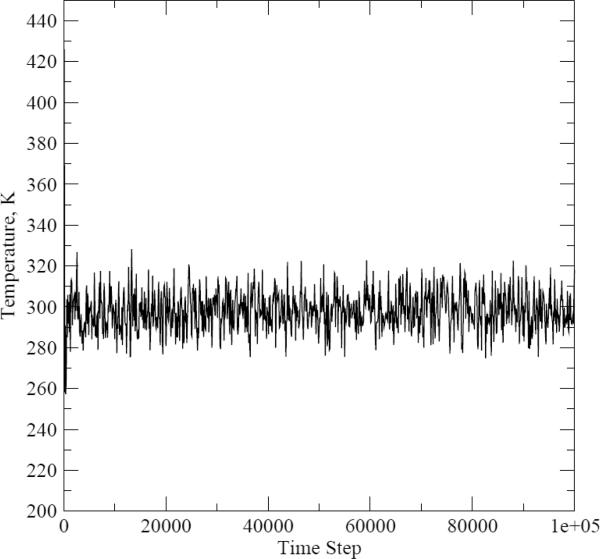
To make sure that the chosen time step value was short enough to ensure that the energy is conserved, we ran pure water simulations with both OPLS and PFF while monitoring the temperature of the system. The dependence of the temperature on the time step number is shown on Figures 3 and 4. The average temperature for the fixed-charges and polarizable simulations were equal to 298.16K and 298.06K, respectively. We concluded from these data that our choice of the time step parameter was adequate.
Figure 3.
Temperature as a function of the molecular dynamics time step number for the pure water simulations with the fixed-charges model.
Figure 4.
Temperature as a function of the molecular dynamics time step number for the pure water simulations with the polarizable model.
The actual simulations for calculating free energies of hydration proceeded in two steps. In the first step, the charge on the copper(I) ion was gradually switched to zero. During the second step, the van-der-Waals part of the parameters was removed.
An important issue is in choosing the correct value of the reference Cu(I) solvation energy. Fawcett13 and subsequently Kelly, Kramer and Truhlar14 demonstrated that hydration energy for ions should be determined in accordance with Equation 11:
| (11) |
The values of the free energies in the right-hand-side of the equation can be determined from the free energies of formation and the copper ionization energy listed in Table 1. The resulting reference value of the Cu+ free energy of hydration is −152.58 kcal/mol. We used this number for comparison with the results of the statistical perturbation theory calculations of free energy of eliminating the ion in the aqueous solution.
Table 1.
Free energies for Cu, Cu(I) and water.
III. Results and Discussion
Copper(I) Complex with Water Molecule
The results are presented in Table 2. It can be easily seen that the OPLS2005 Cu(I) parameters produce the worst results with both TIP3P and TIP4P water molecules. The magnitude of the binding energy is underestimated by almost a factor of two and the distance between the heavy atoms in the copper-water complex is too large by about 0.3 – 0.4 Å. Therefore, refitting of the parameters for the copper ion in the OPLS framework is completely justified. Thus, we produced two more sets of OPLS-type parameters, one optimized for the complex formation with a TIP3P water molecule, and the other one for the TIP4P formalism.
Table 2.
Energies in kcal/mol and Cu+…O distances in Å for complexes of Cu(I) ion and a water molecule.
| Model | Energy | Cu+…O(H2O) distance |
|---|---|---|
| OPLS2005with TIP3P water | −23.6 | 2.29 |
| OPLS2005with TIP4P water | −21.3 | 2.32 |
|
| ||
| OPLS, refitted for TIP3P | −37.6 | 1.78 |
| OPLS, refitted for TIP4P | −34.4 | 1.78 |
|
| ||
| PFF | −41.8 | 1.84 |
|
| ||
| Referencea | −41.8 | 1.93 |
Reference 8a. .
Since the charge on the ion has to be +1 electron, the only flexibility we had was that of producing new Lennard-Jones parameters for this atom. In the essence, we could control the distance between the molecules in the complex shown on Figure 1. The magnitude of the binding energy was still moderately underestimated, even at a distance of 1.78 Å. This meant underestimating the distance by 0.15 Å and we did not want to permit a greater error in the geometry. The smallest error for the fixed-charges formalism being 4.2 kcal/mol (or about 10%) for the model produced to be compatible with the TIP3P parameters for water. The difficulties in fitting such parameters in a non-polarizable formalism have been reported previously by other authors.2b
At the same time, the PFF parameters for Cu(I) which were fitted in this work, combined with the previously created PFF water model,3a gave an exact match in the binding energy (−41.8 kcal/mol) with a distance deviation of only 0.09 Å). Therefore, the polarizable model was clearly capable of reproducing the properties of this Cu(I) – water complex.
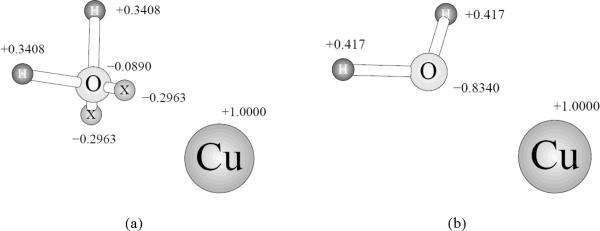
It is interesting to compare not only the total energies obtained with the different models but also their breakdown into components. For the copper complex with water, this is done in Table 3. Surprisingly, the polarization contribution is not the main reason for the PFF energy being lower (and thus closer to the reference value) than the OPLS ones. In fact, the polarization energy for the Cu(I) – water dimer is −5.2 kcal/mol, and thus it is actually higher than that for an isolated PFF water molecule (−9.3 kcal/mol). Therefore, the polarization contribution is negative. The leading term in creating the correct interaction energy for the complex is the −48.4 kcal/mol fixed-charges part of the PFF energy, which is the greatest one among all the models tested in this study. This greater magnitude of the non-polar part of the electrostatic energy is probably due to the fact that the water oxygen negative charge is concentrated mostly on the virtual sites, which are protruding from the center of the oxygen position toward the copper(I) ion. Thus, the effective distance for this charge-charge interaction is smaller than for the OPLS models, and the interaction energy is greater. This effect is illustrated on Figure 5.
Table 3.
Breakdown of interaction energies of Cu(I) ion and water molecule, in kcal/mol.
| Model | Non-Polar Electrostatics | Polar Electrostatics |
||
|---|---|---|---|---|
| Cu(I)…H2O | H2O monomer | van-der-Waals | ||
| OPLS2005with TIP3P water | −27.5 | − | − | 3.9 |
| OPLS2005with TIP4P water | −24.7 | − | − | 3.4 |
|
| ||||
| OPLS, refitted for TIP3P | −43.9 | − | − | 6.3 |
| OPLS, refitted for TIP4P | −39.9 | − | − | 5.6 |
|
| ||||
| PFF | −48.4 | −5.2 | −9.3 | 3.2 |
Figure 5.
Water-copper complex as simulated with different force fields with partial charges on the atomic centers shown (in electrons). The distance between the negative charge and the cation is smaller in the PFF case (a) than in either TIP3P (b) or TIP4P (c) OPLS models.
It might appear that the polarization as such is therefore not so greatly important in fitting the copper cation interaction energies, but the data discussed in the following two subsections point to the conclusion that the explicit polarization is actually crucial for such systems.
Copper(I) Complex with Benzene Molecule
The truly significant failure of the fixed-charges formalism and the superiority of PFF became apparent after we obtained results of the next experiment. We took all the OPLS and PFF parameters obtained at the previous step without any change or refitting and combined them with the benzene parameters from the respective force fields. Then we simulated the C6V symmetric complex of Cu(I) and benzene shown on Figure 2. The benzene molecule was used not only as such but also as a generalized model for polarizable media (such as, for example, can be found in proteins). The results are presented in Table 4. It has been known for a long time that energy of interaction of cations with benzene is underestimated.4 However, the case of the copper(I) ion shows an even greater deviation than that which could be observed for lighter ions. And we believe that this fact has significant implications for studies of copper ion interactions with various systems, including biological ones. The quantum mechanical reference energy for this complex is known to be between – 56.9 and −61.3 kcal/mol.9 The original OPLS2005 result is −14.0 kcal/mol, which underestimates the magnitude of this energy by about a factor of four. The refitted OPLS does a bit better, with the −25.2 and −26.0 kcal/mol energies for the TIP3P- and TIP4P-compatible parameters, respectively. At the same time, the PFF result is −54.4, which is essentially correct given the range of the reference energy values. Moreover, the distance from the ion to the carbon atoms of the benzene molecule is found to be 2.30 Å with the PFF, in an outstanding agreement with the reference 2.31 Å value. We should keep in mind that these results were achieved without any refitting for the complex of the copper(I) ion with benzene but rather by adopting the parameters obtained at the previous step directly. The OPLS2005 distance is 2.77 Å, and the refitted OPLS ones are 2.14 and 2.11 Å, which means that the errors in the distance are 0.46, 0.17 and 0.20 Å, respectively. Therefore, the improvement over the OPLS2005 result requires either an explicit treatment of the electrostatic polarization or, as in the case of the refitted OPLS, shortening the distance between the ion and the benzene molecule. We believe that the latter is physically incorrect and is no more than compensating for the insufficient flexibility of the distribution of the electron density in fixed-charges force fields by distorting the geometry of the Cu(I)…benzene complex.
Table 4.
Energies in kcal/mol and distances from Cu+ to the carbon atoms of the C6H6 molecule in Å for complexes of Cu(I) ion and a benzene molecule.
| Model | Energy | Cu+…C(C6H6) distance |
|---|---|---|
| OPLS2005 | −14.0 | 2.77 |
|
| ||
| OPLS, refitted for TIP3P | −25.2 | 2.14 |
| OPLS, refitted for TIP4P | −26.0 | 2.11 |
|
| ||
| PFF | −54.4 | 2.30 |
|
| ||
| Referencea | −56.9–−61.3 | 2.31 |
In order to confirm the importance of the explicit electrostatic polarization for this system, let us take a look at the breakdown of the interaction energies presented in Table 5. In this case, it is absolutely clear that the polarization is responsible for most of the interaction energy as computed with the polarizable force field. The dimer polarization energy is −47.1 kcal/mol, as opposed to the −7.1 kcal/mol for the benzene monomer. Interestingly, the van-der-Waals energy as obtained with PFF for this complex is actually negative at −6.6 kcal/mol. This is due to a relatively large contribution of the – 1/R6 term in Equation 6. The overall van-der-Waals gradient of energy as a function of distance between the copper ion and the benzene molecule plane is still negative due to the exponential repulsion term.
Table 5.
Breakdown of interaction energies of Cu(I) ion and benzene molecule, in kcal/mol.
| Model | Non-Polar Electrostatics | Polar Electrostatics |
||
|---|---|---|---|---|
| Cu(I)…C6H6 | C6H6 monomer | van-der-Waals | ||
| OPLS2005 | −17.0 | − | − | 2.6 |
|
| ||||
| OPLS, refitted for TIP3P | −30.5 | − | − | 5.0 |
| OPLS, refitted for TIP4P | −31.5 | − | − | 5.1 |
|
| ||||
| PFF | −7.8 | −47.1 | −7.1 | −6.6 |
We can thus conclude that the lack of explicit electrostatic polarizability is in fact responsible for the failure of the OPLS parameters to reproduce the energy of the copper-benzene complex.
Copper(I) Free Energy of Hydration in Bulk Water
The molecular dynamics simulations with the statistical perturbation theory were carried out to find the free energy of “disappearance” of the monovalent copper ion in a box of water and thus the free energy of hydration. We chose the TIP3P-compatible version of the OPLS Cu(I) ion as the counterpart for the PFF case, since it is for the TIP3P-compatible model that the energy of the Cu(I) interaction with one water molecule shown in Table 2 was the most accurate of all the OPLS models. TIP3P water molecules were used to hydrate this OPLS copper(I) ion, while our previously developed PFF model of water3a was employed with the PFF-compatible Cu+ particle. The statistical perturbation theory was applied via two steps. First, the copper particle was stripped of its electrostatic charge. Then the van-der-Waals part of the copper potential was removed in the second step. This course of action was chosen in order to reduce the noise in the calculated free energy changes.
The resulting values of the free energy of hydration are shown in Table 6. It can be seen immediately that the polarizable result of −149.90 kcal/mol is only 1.76% off the reference value of −152.58 kcal/mol. This result is quite amazing. It should be emphasized again that the only fitting in producing the PFF parameters for Cu+ was carried out to reproduce the copper(I) interaction energy and geometry in complex with one water molecule. No further refitting was done, and the energies of interaction of the monovalent copper ion with benzene and bulk water are in a remarkable agreement with the reference data not because of any additional parameterization but by virtue of the polarizable force field being based on a more physically correct model than the fixed-charges one.
Table 6.
Free energies of hydration for Cu+ ion in bulk water, in kcal/mol.
| Model | ΔG(hyd) | Error, kcal/mol | Error, % |
|---|---|---|---|
| OPLS (TIP3P-compatible) | −119.05±1.00 | 33.53 | 22.0 |
| PFF | −149.90±0.36 | 2.68 | 1.76 |
|
| |||
| Reference | −152.58 | − | − |
The fixed-charges Cu+ hydration energy in bulk water of −119.05 kcal/mol is 22.0% lower in magnitude than the reference value. This result is not so catastrophically incorrect as in the case of copper(I)…benzene interaction, just as could be expected from the moderately underestimated strength of the Cu(I)…H2O complex for the TIP3P-compatible ion model presented in Table 2. But it is clear that the fixed-charges model is qualitatively inferior to the PFF one.
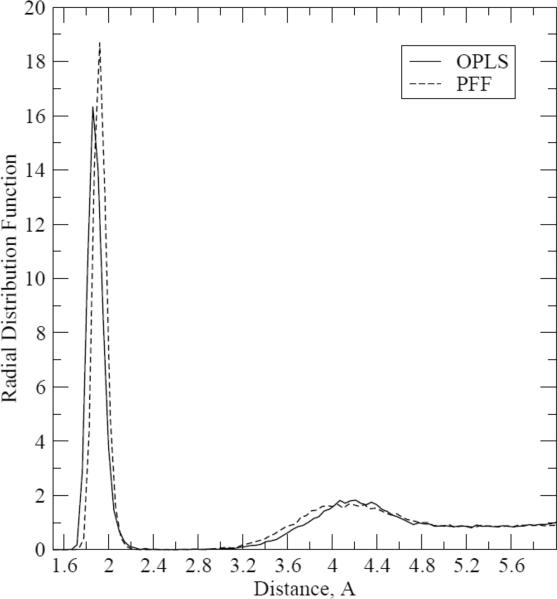
In order to understand the specific physical reason for the difference, we have analyzed the Cu-O(water) radial distribution functions (rdf) obtained with the PFF and fixed-charges molecular dynamics simulations for the ion in bulk water. The rdfs are plotted on Figure 6.
Figure 6.
g(Cu-O), Cu+ − O(water) radial distribution functions.
It should be noted that the radial distribution functions are going to zero after this first peak. While such a behavior is not common for pure liquids or solutions of electrostatically neutral molecules, it can occur in simulations of solvated ions due to very strong interactions between the ion and its first hydration sphere.17
It can be seen that the distributions are essentially identical except for the location and height of the first peak. The OPLS-TIP3P fixed-charges first peak maximum is at R = 1.86Å, and the PFF one is at 1.92Å. If the distance for the PFF peak were shorter than that for the OPLS one, one could suggest that the reason for a better solvation of the Cu(I) ion in the polarizable formalism lies in stronger interactions between water molecules and the ions due to the shorter distance. But this is not the case, given that the OPLS peak distance is even a bit shorter. Integrating the distributions, one can obtain values of equal to 123.94 and 127.26 for the OPLS and PFF simulations, respectively. If the PFF number were significantly higher than the OPLS one, it could mean that the more negative hydration energy in the PFF system results from more water molecules interacting with the copper(I) ion in the first solvation sphere. However, while the PFF value is about 2.6% higher, this is not enough to explain the 30 kcal/mol difference in the solvation energy. Therefore, we conclude that the physical reason for the greater magnitude of the PFF hydration energy is not a shorter distance between the water molecules and the copper ion and not a greater number of water molecules interacting with the ion but rather a more negative interaction energy at similar distances which is produced by the polarizable calculations.
IV. Conclusions
We believe that the implications of our findings are two-fold. First, explicit treatment of electrostatic polarization is necessary if interactions with Cu(I) ions are to be modeled with an empirical force field and the ion is represented in a more detailed way than just a simple point charge. At the same time, our polarizable force field is clearly capable of a robust representation of the system. Naturally, the problem is most likely not in the ion itself, but rather in the explicit polarizability of the environment of the ion. Still, the degree of the energy error produced by the non-polarizable treatment of the system is likely to be very detrimental if a realistic simulation of copper-containing systems with empirical force fields is to be undertaken.
The second conclusion is by no means less important. The PFF parameters produced by fitting to the copper – water complex energy and geometry worked well in simulating both the copper…benzene complex and the hydration of the Cu+ ion in bulk water, and no adjustment was necessary. This, once again, confirms that polarizable force fields display a great degree of transferability because of their superior (as compared with fixed-charges) physical accuracy. This means not only a greater degree of reliability of polarizable force fields but also a high degree of flexibility in techniques for fitting potential energy parameters. If a set of polarizable parameters can reproduce electrostatic response of the system in one environment, it is very likely to work in any reasonable environment, as is once again proved by this transferability.
It is also interesting to note that it has been shown previously that polarization plays a relatively small role in Cu(I) interaction with water.6 Our results confirm this, and the OPLS interaction energies for this system are only moderately underestimated. At the same time, the fixed-charges approach obviously fails when working with more polarizable systems, such as the benzene molecule. Moreover, while the fixed-charges model leads to a relatively small error in the gas-phase interaction between Cu(I) and water, the solvation free energy in bulk water is underestimated by about 22%. Therefore, a small problem in the case of dimerization can lead to a large compounded error in a significantly many-body environment. At the same time, the performance of the polarizable model is uniformly adequate.
We hope that the reported results will contribute positively into the still developing area of explicit inclusion of metal ions into simulations of organic, physical and biological systems with empirical force fields. We also hope that it will help to further clarify in which areas explicit treatment of the electrostatic polarization is truly crucial.
Supplementary Material
Acknowledgments
This project was supported by Grant Number R01GM074624 from the National Institutes of Health. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institute of General Medical Sciences or the National Institutes of Health. The authors express gratitude to Schrödinger, LLC for the PFF and SIM programs and to Professor William L. Jorgensen for the BOSS software.
Footnotes
Supporting Information Available: All the parameters developed in the course of this project and the OPLS2005 copper(I) parameters. This material is available free of charge via the Internet at http://pubs.acs.org.
References
- (1).See for example: Chintalapati S, Kurdi RA, van Scheltinga ACT, Kuhlbrandt W. J. Mol. Biol. 2008;378:581–595. doi: 10.1016/j.jmb.2008.01.094.; Dudev T, Lim C. Annu. Rev. Biophys. 2008;37:97–116. doi: 10.1146/annurev.biophys.37.032807.125811.; Gonzalez-Guerrero M, Eren E, Rawat S, Stemmler TL, Agruello JM. J. Biol. Chem. 2008;283:29753–29759. doi: 10.1074/jbc.M803248200.; Zhou L, Singleton C, Le Brun NE. Biochem. J. 2008;413:459–465. doi: 10.1042/BJ20080467..
- (2).(a) Banci L. Curr. Opinion Chem. Biology. 2003;7:143–149. doi: 10.1016/s1367-5931(02)00014-5. [DOI] [PubMed] [Google Scholar]; (b) Fuchs J-F, Nedev H, Poger D, Ferrand M, Brenner V, Dognon J-P, Crouzy S. J. Comput Chem. B. 2006;27:837–856. doi: 10.1002/jcc.20392. [DOI] [PubMed] [Google Scholar]; (c) Venkateswarlu D. BMS Struct. Biology. 2010;10 doi: 10.1186/1472-6807-10-7. doi:10.1186/1472-6807-10-7. [DOI] [PMC free article] [PubMed] [Google Scholar]; (d) Rodriguez-Granillo A, Crespo A, Estrin DA, Wittung-Stafshede P. J. Phys. Chem. B. 2010;114:3698–3706. doi: 10.1021/jp911208z. [DOI] [PubMed] [Google Scholar]
- (3).(a) Kaminski GA. J. Phys. Chem. B. 2005;109:5884–5890. doi: 10.1021/jp050156r. [DOI] [PubMed] [Google Scholar]; (b) MacDermaid CM, Kaminski GA. J. Phys. Chem. B. 2007;111:9036–9044. doi: 10.1021/jp071284d. [DOI] [PubMed] [Google Scholar]; (c) Click TH, Kaminski GA. J. Chem. Theory Comput. 2009;5:2935–2943. doi: 10.1021/ct900409p. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (4).Caldwell JW, Kollman PA. J. Am. Chem. Soc. 1995;117:4177–4178. [Google Scholar]
- (5).Kaminski GA, Stern HA, Berne BJ, Friesner RA. J. Phys. Chem. A. 2004;108:621–627. [Google Scholar]
- (6).(a) Jorgensen WL, Chandrasekhar J, Madura JD, Impey RW, Klein ML. J. Chem. Phys. 1983;79:926–935. [Google Scholar]; (b) Jorgensen WL, Severance DL. J. Am. Chem. Soc. 1990;112:4768–4774. [Google Scholar]; (c) Jorgensen WL, Maxwell DS, Tirado-Rives J. J. Am. Chem. Soc. 1996;118:11225–11236. [Google Scholar]
- (7).As implemented in Impact, version 5.5. Schrödinger, LLC; New York, NY: 2009. [Google Scholar]
- (8).(a) Burda JV, Pavelka M, Simanek M. Theochem. 2004;683:183–193. [Google Scholar]; (b) Feller D, Glendening ED, deJong WA. J. Chem. Phys. 1999;110:1475–1491. [Google Scholar]
- (9).Dargel TK, Hertwig RH, Koch W. Mol. Phys. 1999;98:583–591. [Google Scholar]
- (10).SIM/PFF. Schrödinger, Inc.; Portland, OR: 2002. [Google Scholar]
- (11).Jorgensen WL, Tirado-Rives J. J. Comput. Chem. 2005;26:1689–1700. doi: 10.1002/jcc.20297. [DOI] [PubMed] [Google Scholar]
- (12).Smith W. CCP5 Newsletter. 1998;46:18. [Google Scholar]
- (13).Fawcett WR. J Phys Chem B. 1999;103:11181–11185. [Google Scholar]
- (14).Kelly CP, Cramer CJ, Truhlar DG. J Phys Chem B. 2006;110:16066–16081. doi: 10.1021/jp063552y. [DOI] [PubMed] [Google Scholar]
- (15).Lide DR. CRC handbook of chemistry and physics : a ready-reference book of chemical and physical data. 87th ed. CRC Press; Boca Raton, Fla.: 2006. [Google Scholar]
- (16).Curtiss LA, Jurgens R. J. Phys. Chem. 1990;94:5509–5513. [Google Scholar]
- (17).See, for example J. Phys. Chem. 1996;100:1420–1425..
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.