Abstract
Twins have been extensively used in economics, sociology and behavioral genetics to investigate the role of genetic endowments on a broad range of social, demographic and economic outcomes. However, the focus in these literatures has been distinct: the economic literature has been primarily concerned with the need to control for unobserved endowments—including as an important subset, genetic endowments—in analyses that attempt to establish the impact of one variable, often schooling, on a variety of economic, demographic and health outcomes. Behavioral genetic analyses have mostly been concerned with decomposing the variation in the outcomes of interest into genetic, shared environmental and non-shared environmental components, with recent multivariate analyses investigating the contributions of genes and the environment to the correlation and causation between variables. Despite the fact that twins studies and the recognition of the role of endowments are central to both of these literatures, they have mostly evolved independently. In this paper we develop formally the relationship between the economic and behavioral genetic approaches to the analyses of twins, and we develop an integrative approach that combines the identification of causal effects, which dominates the economic literature, with the decomposition of variances and covariances into genetic and environmental factors that is the primary goal of behavioral genetic approaches. We apply this integrative ACE-β approach to an illustrative investigation of the impact of schooling on several demographic outcomes such as fertility and nuptiality and health.
1 Introduction
Twins studies have been extensively undertaken in economics, sociology and behavioral genetics to incorporate the role of genetic endowments in relations for a broad range of social, demographic and economic outcomes. However, the focus in these literatures has been distinct: on the one hand, the economic literature has been primarily concerned with the need to control for unobserved endowments—including as a possibly important subset, genetic endowments—in analyses that attempt to establish the impact of one variable, often schooling, on a variety of economic, demographic and health outcomes (Behrman et al. 1994, 1996). On the other hand, behavioral genetics analyses have mostly been concerned with decomposing the variation in the outcomes of interest into genetic, shared environmental and non-shared environmental components, with recent multivariate analyses investigating the contributions of genes and the environment to the correlation and causation between variables (Plomin et al. 2005). Sociological research using twins has mostly build on either the economic or the behavioral genetics approach (Conley and Bennett 2000; Freese 2008). Despite the fact that data on twins and the recognition of the role of endowments are central to both the economic and behavioral genetics literatures, the methodological developments in these two areas have mostly evolved independently. And while both of these approaches are increasingly valued within sociology and related social science fields as important tools to investigate the interaction of social processes and social structures with genetic and related biological processes (e.g., Bearman 2008; Conley et al. 2003; Freese 2008; Guo et al. 2008; Schnittker 2008), a detailed comparison and potential integration of these two approaches to the study of twins data has been lacking so far.
This paper formally develops the relationship between the economic and behavioral genetics approaches to the analyses of twins, and discusses both the economic within-MZ and the behavioral genetics ACE model within a unified conceptual framework that highlights the similarities and differences between these models.1 It also reviews some of the approaches that are available to test and/or relax some of the key assumptions underlying these methods. Most importantly, this paper also develops an extension of the conventional ACE model, denoted ACE-β, that bridges between the economic within-MZ approach and the behavioral genetics approach. The new features of this model include that it allows the joint estimation of the causal relationship—denoted by β—between, say, schooling and fertility or health, and the contributions of genetic and social endowments to the variation and covariation of outcomes within and across individuals. This model also provides a definition of heritability h2 that appropriately captures the different pathways through which genetic endowments affect both schooling x and outcomes y such as fertility or health in an ACE-β framework where schooling has a direct effect on fertility (health). In addition, extensions of our ACE-β model can identify the extent to which social interactions between twins affect schooling or fertility/health, or the extent to which schooling is affected by measurement error. In the instrumental variable version, the ACE-β model can also provide estimates of all model parameters—including the casual effect of schooling on fertility and the extent of heritability of the different outcomes—even if unique environmental factors affecting schooling affect fertility (health) not only through schooling but also directly. The ACE-β model therefore enriches both the economic within-MZ approach by providing a more finely grained picture about the influence of unobserved endowments on schooling and fertility (health), and it extends the ACE model, which has been one of the cornerstones of research in behavioral genetics, by integrating causal pathways between schooling and fertility (health).
The “cost” of the additional analytic leverage of the ACE-β model, which extends both beyond the within-MZ model in economics and the ACE model in behavioral genetics, is that the model is subject to more restrictive assumptions than the within-MZ approach in economics. In particular, the model is subject to the same assumptions as the behavioral genetics ACE model. The most relevant restrictions of the ACE model, beyond what is already required in the within-MZ model, pertain to the underlying genetic model and other assumptions required for decomposing the sources of variation into social and genetic endowments and individual-specific factors. Specifically, the ACE-β model—just like the ACE model in behavioral genetics assumes: (i) an additive genetic model with no assortative mating (albeit both can be relaxed with suitable data), which establishes the correlation of genetic endowments between DZ twins, and (ii) the absence of gene-environment interactions, which implies that the latent endowments (genetic factors A, shared environments C, and individual-specific factors E) are independent of each other and additively affect the outcomes.2
2 Twins and Twinning: Setting the Stage
To help set the stage for what follows, there are two kinds of twins: monozygotic (MZ) or “identical” twins and dizygotic (DZ) or “fraternal” twins. Except for being born at the same time, DZ twins are ordinary siblings in the sense that they are the product of two different eggs and two different sperm. MZ twins are genetically identical at conception, emerging from a single sperm and egg, from which two separate eggs later emerge. Whereas the rate of DZ twinning is affected by several factors, including maternal age and fertility drugs, and is therefore subject to change over time, across women, and among countries, MZ twinning occurs at a relatively constant rate among contexts (Kiely and Kiely 2001). Irrespective of context, MZ twins are rarer than DZ twins. In most pre-fertility drug populations, about 1 in 85 births are twins (Plomin et al. 2005), of which about a third are MZ, a third same-sex DZ, and a third opposite-sex DZ (Keith et al. 1995). While some prominent datasets of twins raised apart exist (e.g., the Minnesota Study of Twins Raised Apart (Bouchard et al. 1990) or the Swedish Adoption/Twin Study on Aging (SATSA) (Björklund et al. 2005)), most twins data include twins that were raised together. Important U.S. twins datasets, for example, include the National Longitudinal Study of Adolescent Health (Add Health) Twin Data (Harris et al. 2006), the Midlife Development in the United States (MIDUS) Study (Brim et al. 1996) and the National Academy of Science-National Research Council (NAS-NRC) Twin Registry of World War II Veterans (Page 2002). Extensive register-based twins data exist in Denmark, Sweden, Norway and Australia (Harris et al. 2002; Lichtenstein et al. 2002; Miller et al. 1997; Skytthe et al. 2002).
Because twins raised together share both genetic factors and important social and economic contexts during childhood and adolescence, they provide a unique opportunity to better understand how genetic and social endowments affect a variety of behaviors and outcomes that are of key interest to social scientists. For example, in the economic “fixed-effects” approach to twins data, twins have been extensively used to control for genetic and other background unobserved confounding factors. Social scientists long have used sibling comparisons for this purpose, reasoning that if brothers/sisters are similar with respect to family background and other characteristics, using differences between them in levels of schooling controls a great many relevant confounding factors.3 However, twins are more attractive than other siblings data insofar as they share a birth. Differences between twins are therefore not confounded by parental family life-cycle differences and, in the case of MZ twins, genes at conception, both of which can have substantial confounding effects on both the outcome and explanatory variables in a particular study.4 To overcome these concerns, twins fixed-effects studies have been interested in estimating the causal effect of one (or more) variable (e.g., schooling, birth weight) that may be partly determined directly by unobserved endowments on other variables (e.g., fertility, marital status, health-related behaviors and outcomes, social interactions, wages and well-being) that are themselves partly determined directly by endowments (e.g., Behrman and Rosenzweig 2004; Behrman et al. 1994, 1996; Kohler et al. 2005). These analyses explicitly acknowledge that both schooling and outcomes such as fertility, nuptiality or health are possibly determined by unobserved genetic or social endowments, where examples of the latter include as an important dimension socioeconomic and psychological characteristics of the twins’ parents, and these studies argue that twin designs can be used to obtain correct estimates of the relevant relations even in the presence of such unobserved endowments.
3 Use of Twins in Economics: The Fixed-Effects Approach
The general framework of our discussion in this paper is a context where a researcher would like to infer the causal effect of some variable x, which in our running example will be schooling, on a second variable y. For our methodological discussions in Sections 3–7, we will use (completed) fertility as the running example for y, and in the empirical examples (Section 8) we will obtain estimates for the effect of schooling on health, spouse’s schooling (which is an important indicator of marriage market outcomes) and fertility. The notion of causality that underlies our discussions in this paper of the relationship of schooling with outcomes such as health and fertility is thereby closely related to the recent discussion of causality in the social sciences (Heckman 2008; Moffitt 2005, 2009; Rosenzweig and Wolpin 2000; Winship and Sobel 2000). A basic point in this literature, emphasized by Moffitt (2005) among others, is that the causal effect of, say, schooling x on fertility y, cannot be estimated without some type of assumption or restriction, even in principle, because of the inherent unobservability of the counterfactual.5 A cross-sectional regression coefficient on x is necessarily estimated by comparing the values of y for different individuals who have different values of x, not by comparing different values of y for a single person observed at different levels of schooling x. Because individuals with different values of schooling x are likely to differ in unobservable ways, the differences in their fertility y may not accurately reflect the extent to which a specific person’s fertility would vary if this individual could be observed at different levels of schooling. In light of this inherent identification problem of the causal influence of, say, schooling x on fertility y, the literature on causal modeling emphasizes that the estimation of a causal effect always requires a minimal set of identifying assumptions, and moreover, that social science theory needs to guide these assumptions because the minimal set of identifying assumptions for causal inference cannot be empirically tested. Outside evidence, intuition, theory, or some other means outside the specific empirical model and the specific data, are required to justify any empirical approach to causal modeling. Using the words of Moffitt (2005), “while the necessity to make these types of arguments may at first seem dismaying, it can also be argued that they are what social science is all about: using one’s comprehensive knowledge of society to formulate theories of how social forces work, making informed judgments about these theories, and debating with other social scientists what the most supportable assumptions are.”
We will argue in this paper that social science methods for twins data provide one promising approach to the identification of causal effects that relies on transparent assumptions that are consistent with the contemporary understanding about the underlying social and biological processes that determine social, demographic and economic outcomes such as schooling, nuptiality, fertility, wages and related aspects. By integrating the economic and behavioral genetics approaches to the analyses of twins, we develop an approach that combines the identification of causal effects, which dominates the economic literature, with the decomposition of variances and covariances into genetic and environmental factors, which is the primary goal of behavioral genetics approaches.
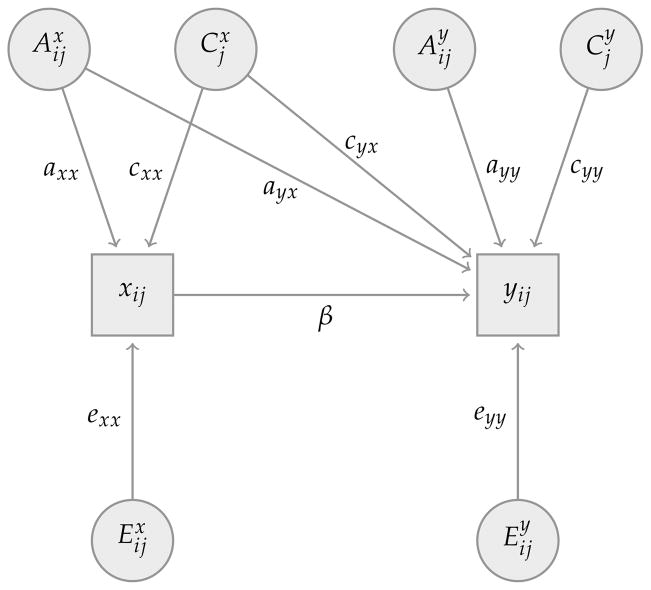
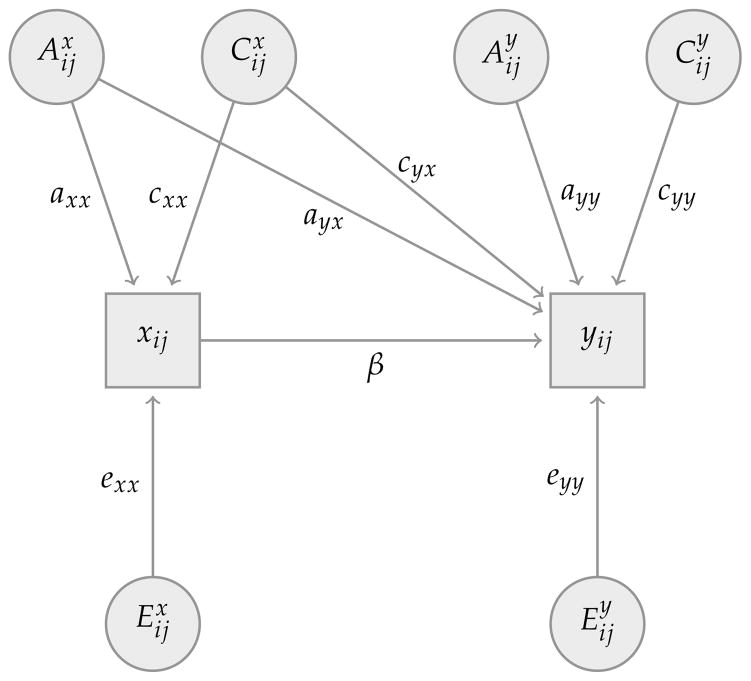
Figure 1 illustrates one possible conceptual framework about how unobserved genetic and social endowments affect both schooling x and fertility y. While the economic fixed-effects approach is usually presented somewhat differently, the representation in Figure 1 is observationally equivalent and facilitates our subsequent comparison with the behavioral genetics models and the integration of both approaches.6 Specifically, the conceptual framework in Figure 1 assumes that schooling xij of twin i in pair j has a direct and causal influence on the fertility yij of twin i in pair j that is represented by the coefficient β. In addition, each of the phenotypic variables, xij and yij, is potentially subject to influences from the three latent sources: genetic endowments ( and ), common environmental influences ( and ), which we refer to as social endowments, that are shared by twins reared together in the same family j, and unique or individual-specific environmental influences and that in the economic literature are sometimes referred to as shocks to either schooling xij or fertility yij. In this path diagram in Figure 1, the paths axx and cxx indicate, respectively, the effects of the latent genetic component and shared environmental component on schooling xij, while the paths ayx and cyx reflect the effect of these latent genetic and shared environmental factors on fertility yij. The path exx measures the effect of the unique environmental factors on schooling xij, and eyy measures the effect of the unique environmental component on fertility yij.
Figure 1. Path-diagram for the economics fixed-effects model for twins.
As we will argue in more detail below, a required assumption of the standard economic fixed-effects approach to twins data is that the unique environmental influences affecting schooling xij and the outcome yij, say fertility, are independent.7 It is therefore important to observe that, consistent with this assumption, we have drawn the path-diagram in Figure 1 without a path eyx that would connect the unique environmental factor to fertility yij.
The economic “fixed-effects” approach to twins data rests on the insight that, if unobserved genetic and social endowments affect the variables x and y together with individual-specific environmental factors as outlined in Figure 1, MZ twins data—but not other siblings data—can be used to estimate the causal effect of schooling x on fertility y. This causal effect, which we have denoted with β in Figure 1, is often a primary focus of analyses in the social sciences. In the presence of unobserved endowments, however, cross-sectional estimates or inferences based on sibling data (within-siblings analyses) are generally not able to correctly infer these causal pathways.
To illustrate this within-MZ twins approach and its underlying assumption in more detail, consider the following formal statement of the model in Figure 1 that is based on a linear representation of a reduced-form equation relating fertility yij of twin i in pair j to his or her schooling xij and to three sets of unobserved variables representing (i) social endowments and affecting schooling xij and fertility yij that are common among both members of twins pair j (e.g., exogenous features of the parental family environment in childhood, including family income, parents’ human capital, average genetic endowments among siblings, local schooling and health-related options), (ii) genetic endowments and that additively affect both xij and yij and that are correlated among the members of each twins pair, and (iii) unique individual environmental influences and that capture random “shocks” to the schooling attainment and fertility outcomes of twin i in pair j. For schooling, the path diagram in Figure 1 then implies the specification
| (1) |
where and are independently distributed and standardized to mean of zero and a variance of one.
Schooling xij is assumed to have a direct causal effect, denoted by β, on fertility yij for twin i in pair j. In addition, we assume that yij is also influenced by unobserved endowments. On the one hand, yij is assumed to possibly depend on the shared environmental factors and the genetic endowments that also affect schooling of the twin i in pair j. In addition, fertility yij is potentially affected by unobserved endowments and shocks that are specific to fertility y: (i) social endowments that are common for both twins in pair j, (ii) genetic endowments , which are correlated within a twins pair, and (iii) a random individual-specific shock that also includes measurement error. Assuming a linear relationship, we thus obtain:
| (2) |
where and are independently distributed and standardized to mean of zero and a variance of one. In addition, the model in Eqs. (1–2) and Figure 1 also assumes, as we have mentioned earlier, that the random shocks affecting schooling xij of twin i in pair j have no direct effect on the fertility yij, and that these random shocks affect the fertility yij of twin i in pair j only through their effect on schooling (in the path diagram in Figure 1 this assumption is equivalent to specifying eyx = 0.). The coefficients ayx and cyx in Eq. (2), which reflect the importance of the “cross-paths” in Figure 1 from the endowments and to the fertility yij, indicate the extent to which the endowments affecting schooling xij and fertility yij are interrelated. For example, when studying the effect of schooling attainment on labor market outcomes or fertility, this interrelation is conceivably strong—and the path coefficients ayx and cyx are correspondingly large—because unobserved differences in abilities and preferences tend to affect both decisions about schooling and fertility and other outcomes of interest such as wage rates.
As is well known, the parameter β in Eq. (2) is not identified in standard cross-sectional regression analyses if at least one of the coefficients ayx or cyx is not zero, that is, if the unobserved endowments and affecting schooling xij have also a direct effect on fertility yij. In this case, β is estimated with bias if equation (2) is estimated across individuals with different values of and . The extent of bias in these cross-sectional analyses depends on the covariance between the unobserved determinants of xij and yij in Eqs. (1–2). It can be shown that the cross-sectional OLS regression coefficient β̂ for schooling is equal to
where β is the “true” effect of schooling x on fertility y from Eq. (2). The cross-sectional OLS estimate of β is therefore biased unless both ayx and cyx equal zero, that is, unless the genetic and social endowments affecting schooling have no effect on yij except through their effect on xij. This assumption, however, is not plausible in many empirical applications. Thus, generally, the cross-sectional estimate of the association between schooling and fertility is a biased estimate of the causal impact of schooling on fertility because schooling is partially proxying for genetic, family background, and other endowments.
It is important to emphasize that, in situations where the paths ayx and cyx in Figure 1 cannot be assumed to be both equal to zero, using sibling rather than standard cross-sectional data for the estimation does not provide a remedy. While siblings from the same family j have the same shared environments in common, siblings (other than MZ twins) do not share all genetic endowments and therefore .8 Sibling data thus do not (fully) control for unobserved genetic endowments, and if ayx ≠ 0 in Eq. (2), the estimate of β is biased also in sibling analyses. With no further assumptions, it is therefore clear that β is not identified even if sibling-pair data are used in the estimation of β. This is because of the individual-specific genetic endowments that are not equal for siblings, expect for MZ twins. As long as families or individuals respond to individual-specific differences in endowments, and such differences are important, then sibling estimators do not provide unbiased estimates (Behrman et al. 1994, 1996). In recognition of this problem, researchers have employed samples of monozygotic (MZ) twins, between whom there are as minimal as possible endowment differences at conception, to identify β in estimates of relations (1–2).
One potential solution to the dilemma of identifying the effect β of schooling x on fertility y is provided by using MZ twins because Eqs. (1–2) can be rewritten for MZ twins as:
| (3) |
| (4) |
where for MZ twins we can assume that (and, by definition, for shared environments, ). Relations parallel to Eqs. (3) and (4) can be written for the other member k of twins pair j.
The fixed-effects MZ twins estimation, or a within-MZ twins estimation, of Eqs. (3) and (4) then controls for all right-side variables in these relations that are common to both members of a MZ twinship: the genetic endowments and , and the social endowments and . In particular, the within-MZ-twins estimator for the effect β of schooling x on fertility y is obtained by subtracting relations (3) and (4) for twin 1 and 2 in each twins pair j. With such a within-MZ-twins estimator, all of the unobserved endowment components in (3) and (4) are swept out so that consistent estimates of β can be obtained from within-MZ estimation under the maintained assumption that eyx = 0 (i.e., the assumption that the individual-specific shocks to schooling of twin i in pair j are not correlated with the unobserved shocks to fertility yij):
In summary, under the assumption noted above, MZ fixed-effects estimators can be used to identify the true reduced-form impact β of schooling x on fertility y. In addition, comparisons can be made with estimates of relation (2) for the same fertility outcomes to learn to what extent the estimates of the impact of schooling on fertility β are biased in cross-sectional estimates that fail to control for unobserved endowments and . Comparisons can also be made between the within-MZ estimates for females and males, between racial and ethnic groups, across birth cohorts, across levels of SES, over time, and across countries. Comparisons can also be made between MZ fixed-effects and DZ fixed-effects estimators to see if the unobserved individual specific genetic endowments are important so that within-sibling estimates that control only for common family endowments are misleading. Finally, comparisons can be made between DZ fixed-effects and ordinary sibling fixed-effects estimators controlling for birth spacing to investigate the impact of changes in the timing of births and birth order on the estimated impacts.
Although the MZ fixed-effects literature emphasizes the value of controlling for endowments in the context of twins, there are other potential estimation strategies to break the correlation between the disturbance term and the right-side schooling variable in relation (2). Although these approaches are popular, data on twins may be preferable. Continuing with the schooling example, the dominant alternative has been to use instrumental variables (IV) or two-stage least squares (2SLS) in which actual schooling in relation (2) is replaced by the estimated value of schooling based on first-stage instruments that predict schooling but are not correlated with the disturbance term in relation (2). These approaches are discussed in more detail in Section 4 below. Perhaps the most widespread example is the use of changes in compulsory schooling regulations as a first-stage instrument to predict schooling (Angrist and Krueger 1991; Lleras-Muney 2005). However, as noted by several scholars (Amin et al. 2010; Behrman et al. forthcoming; Lundborg 2008), these IV estimates tend to be local average treatment effects (LATE) that are relevant for individuals who are at the margin to be affected by the instruments used (e.g., at the margin of completing only compulsory schooling levels); however, IV estimates are not average treatment effects (ATE) for the broader population beyond this margin (Angrist and Krueger 1991; Moffitt 2009). Because within-MZ schooling differences exist over most schooling levels, the MZ fixed-effects estimate are likely to be closer to average treatment effects (ATE) rather than local average treatment effects (LATE).
4 Extensions of the Fixed-Effects Approach
Several extensions of the fixed-effects approach to twins data have been developed to address the concern that, at least in some applications, the assumptions required for the within-MZ estimator to identify the causal effect β of schooling on, say, fertility may not hold. In our discussion below we address some of the concerns that have received the most emphasis in the literature, and we present some of the approaches that have been developed to address or remedy these concerns.
4.1 Gene-Environment Correlations
The model in Eqs. (1–2) and Figure 1 has been presented under an assumption that there are no gene-environment correlations. One aspect of this assumption is that the genetic endowments (Ax and Ay) are independent of the social endowments (Cx and Cy) and the unique environmental effects (Ex and Ey). While this is a necessary assumption for the behavioral genetics models discussed below, this assumption is overly restrictive for the economic fixed-effects models. In order for the within-MZ estimator in Eqs. (3–4) to give an unbiased estimator of β it is sufficient that, within monozygotic twins, the individual-specific influences (“shocks”) and that affect schooling xij and fertility yij are independent of the endowments and that are common to both members of a MZ twins pair. It is not necessary that the genetic and social endowments ( and ) and ( and ) are independent of each other, as will be assumed later on when we discuss the behavioral genetics analyses of twins data. Moreover, the independence of the individual-specific influences of the social and genetic endowments in the within-MZ analyses, is a relatively innocuous assumption because the variance of the variables xij and yij in MZ twins can always be decomposed into within-MZ twins pair variation resulting from the individual-specific influences and between-twins pair variation that results from social and genetic endowments. It is therefore important to point out that the ability of the within-MZ model to correctly estimate β is not affected if there is a gene-environment correlation between the genetic endowments (Ax or Ay) and the corresponding social endowments (Cx and Cy). For example, if children with a higher-than-average genetic ability, which is reflected in the genetic endowments Ax, also grow up in families that foster intellectual development more than the average family, then the genetic endowment Ax is positively correlated with the social endowment Cx. While a gene-environment correlation of this sort is potentially problematic for a behavioral genetics model and can result in biased estimates of heritability and related parameters, the within-MZ model provides an unbiased estimate of β in the presence of gene-environment endowment correlations.
There is an another form of gene-environment interaction that merits consideration if “environment” is interpreted to include observed right-side variables such as schooling xij. Eq. (2) is written in a linear form, which means that the marginal impact of schooling xij on fertility yij of twin i in pair j is assumed to be a constant β independent of the genetic—and social, for that matter—endowments. While this linear form is widely used, the approach above can be modified to accommodate some alternative functional forms with different implications. For example, if log-linear functions are used by defining the variables to be all in logarithmic form, the marginal impact of schooling xij on fertility yij no longer is, by assumption, the constant β independent of the genetic and social endowments. Instead this marginal effect is β multiplied by yij/xij. In this specification, thus, this marginal effect depends on both genetic and social endowments because yij/xij depends on both genetic and social endowments. This particular specification is restrictive to be sure regarding the possible interactions between endowments and schooling. And given that the endowments are unobserved latent variables, more flexible specifications are not easily tractable. But it does permit at least some exploration of schooling–endowment interactions.
4.2 Correlated cross-equation shocks
Perhaps the most emphasized criticism of the economic fixed-effects approach to the analyses of twins data (as opposed to more general criticisms that also apply to other uses, such as that twins are basically different from singletons), pertains to the assumption noted above that the path eyx in Figure 1 and Eq. 2 is assumed to be zero. As mentioned earlier, this assumption implies that the individual-specific shock to schooling x does not have a direct effect on the fertility yij. If this assumption holds, the individual-specific factors affecting schooling are not correlated with the individual-specific factors affecting fertility y. On the other hand, if between-twins differences in schooling reflect unobserved factors that also directly determine fertility (or whatever is the dependent variable in Eq. 2), the estimated schooling-fertility association is still biased in the within-twins estimator (Bound and Solon 1999; Griliches 1979). Somewhat more formally, suppose that there exists a path eyx in Eq. (4) such that the unobserved individual shocks have a direct effect on fertility y as in
| (5) |
In this case, the individual-specific influences affecting schooling xij and fertility yij are correlated because some of the unobserved individual twin-specific factors contained in affect directly both the schooling and fertility of twin i in pair j. Hence, if eyx ≠ 0, some of the shocks affecting schooling are “persistent” and also affect later-life outcomes such as fertility; if eyx > 0, then the impact of the persistent shock on schooling is in the same direction as the impact on fertility, and schooling and fertility are affected in opposite directions if eyx is negative. An example for the latter case, for instance, is an unintended teenage pregnancy that disrupts schooling and increases completed fertility.
Within-MZ-twins estimators are obtained by subtracting relations (1) and (5) within twins pairs. While the unobserved endowment components and are, again, swept out when using this within-MZ estimator, there remains the difference in the unobserved twin-specific persistent shocks:
| (6) |
| (7) |
Because of the presence of eyx in Eq. (7), therefore, the unobserved determinants of schooling differences within twins pairs are correlated with the unobserved residuals affecting differences in fertility within twins pairs. The within-MZ estimator in equation (7) thus no longer gives an unbiased estimate of the effect β of schooling on fertility. The sign of the bias is determined by the sign of the correlation of the unobserved factors in Eqs. (6–7), which is equal to the sign of eyx. This sign is positive (negative) if the impact of the shock on schooling is in the same (opposite) direction as the impact of the shock on fertility. The estimate of β from equation (7), then, is an overestimate (underestimate) or upper (lower) bound of the true value of β. For example, if more favorable in utero environments due to proximity to the placenta increase both schooling and fertility beyond any effect through schooling, as might be suggested by the results in Behrman and Rosenzweig (2004), then the estimate of β from equation (7) is an overestimate of the true value of β. Although in utero influences receive considerable attention, this overestimate due to positively correlated shocks is not limited to the early life course: the same holds if an accident or illness limits schooling and has persistent effects on later fertility.
Empirical studies have examined some of the implications of these concerns. Some studies, for example, have explored how sensitive the estimates of interest are to the exclusion of outliers regarding schooling differences between twins based on the argument that large differences are more likely to be based on persistent factors that directly affect both schooling and fertility in relation (2). In some cases, excluding such outliers does not change the estimates substantially (Amin and Behrman 2010a,b; Amin et al. 2010), but in at least one case it does. Amin (2010) reports that the Bonjour et al. (2003) estimates change a great deal if a single outlier is eliminated. Another possible approach is to include additional variables that might have persistent effects on both schooling and the outcome of interest, such as measures of cognitive ability (Behrman et al. 1980) or birth weight (Amin et al. 2010). In these two cases, the estimates of interest are not changed much by including these additional controls, but other applications could reveal different results.
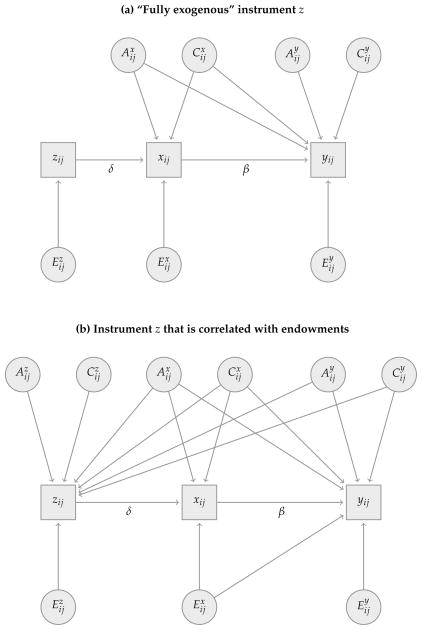
In certain contexts, when the data include variables that satisfy the conditions for an instrumental variable in the within-MZ model, a instrumental variable estimation of the within-MZ model—to which we refer as within-MZ IV approach—can provide a direct test of the assumption that eyx = 0. And if this assumption is rejected, the within-MZ IV model can provide an estimate for the effect of schooling on fertility under the condition that eyx ≠ 0. Finding a valid instrument that can be used in combination with within-MZ analyses can sometimes be challenging, as these instruments need to predict differences in schooling x within identical twins, but affect fertility y only through the effect on schooling. Two broad category of instruments exit. On the one hand, one can envision for the estimation of the within-MZ IV model an instrument z that is completely exogenous in the sense that it predicts x but is not correlated with any of the unobserved endowments that affect the schooling x and fertility y. In the context of twins reared together, instruments meeting these criteria are likely to be rare, though random assignment to different teachers who inspire different degrees of schooling might provide good instruments. On the other hand, within the within-MZ framework, an acceptable instrument can be found under much weaker conditions. In particular, in observational studies, it is more likely that there exists a variable z that is correlated with the genetic and social endowments that affect x and y, but is not correlated with the individual-specific environmental effects that affect schooling x and/or fertility y. An example that has been used in the context of the economic twins model is birth weight, where the birth weight of each twin in a pair is likely to be affected by common endowments. But in the case of the effect of studying the effect of schooling x on fertility y it might be reasonable to assume that the effect—net of endowments—of birth weight on fertility works only through the effect of birth weight on schooling. More formally, a suitable instrument z for the within-MZ IV approach is provided by a variable z that depends on the social and genetic endowments that affect schooling x and/or fertility y, and is additionally determined by its own set of social and genetic endowments and individual-specific influences in the form:
with schooling xij being determined by both zij and the endowments and as
and fertility yij depending, as is given in Eq. (5), on the endowments ( and ), the individual-specific shocks to fertility , and additionally, also on the individual-specific shocks to twin i’s schooling.
In this case, a valid instrument for the within-MZ IV approach can therefore depend on the social and genetic endowments, as long as it affects schooling zij and is not correlated with the individual-specific shocks and that affect schooling xij and fertility yij respectively. If such an instrument exists, an unbiased estimate of the effect β of schooling on fertility can be obtained—even if eyz ≠ 0 in Eq. (5)—by regressing the within-MZ difference in fertility y,
| (8) |
on the within-MZ difference in schooling x,
| (9) |
using the within-MZ difference in z, , as an instrument for the within-MZ difference in schooling . Because these within-MZ IV analyses difference out all endowments that are shared by twins within a twins pair, and only because this is the case, the difference is a valid instrument in that it is not correlated with the unobserved residuals for the within-MZ schooling and fertility differences in Eqs. (8) and (9).
4.3 Cross-twins endowment effects
In some applications of the within-MZ model in Figure 1 it might seem plausible that the value of xij of twin i in pair j is affected by the endowments of i’s co-twin k. For example, in contexts where x measures schooling attainment, it might be reasonable to assume that a particularly high genetically-determined “ability” of i’s co-twin k has a positive spill-over effect on i, and that as a result of k’s endowments and high ability, twin i attains a higher level of schooling than would otherwise be the case. To capture this possibility, Eq. (1) can be modified as
| (10) |
where is the effect of a twin’s own genetic endowments on twin i’s schooling attainment xij, and is the effect of the co-twin’s genetic endowment on i’s schooling.9 Obtaining the within-MZ estimator by differencing within monozygotic twins pairs the relations (10) and (2) then shows that the cross-endowment effects as specified in Eq. (10) do not bias the within-MZ estimator. Hence, conditional on the other assumptions of the within-MZ approach being satisfied, analyses that focus on the differences in schooling x and fertility y within MZ twins continue to provide an unbiased estimate of the causal effect β of schooling on fertility.
4.4 Social interactions: Twins reacting to each other
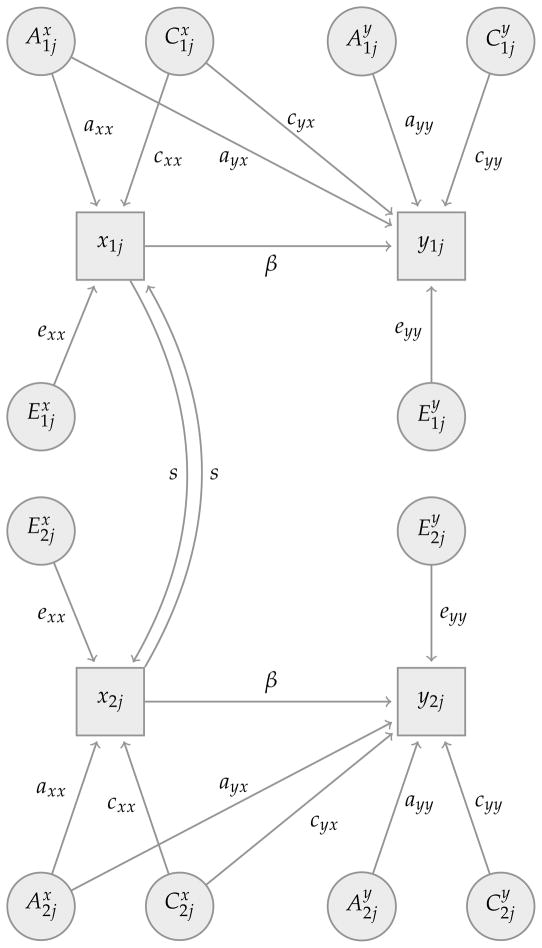
A somewhat related concern in twins studies pertains to the empirical implications of one twin’s behavior occurring in reaction to the other. For example, twin i’s schooling attainment could be affected—positively in the case of imitation, or negatively in the case of competition for scarce resources such as money or parental time or by efforts of one twin to distinguish herself/himself from her/his co-twin—by the co-twin k’s schooling attainment. The implications of such social interactions for the fixed-effects approach, which are somewhat distinct from the case of cross-twins endowments explored in Section 4.3 above—can be investigated by introducing a social interaction parameter s into the framework in Figure 1. In particular, in the context of social interactions, a shock to co-twin k’s schooling will have implications for i’s schooling attainment because of the social interaction among twins, while in the case of cross-twins endowment effects discussed in the previous section, twin i’s schooling responds only to the co-twin k’s endowment but not to k’s specific schooling attainment that is a function of both k’s endowments and individual specific shocks.
The implications of social interactions with respect to schooling can be investigated by augmenting our earlier framework in relations (1) and (2) with a cross-twins effects on schooling x, where the cross effects are assumed to be less than the own effects (|s| < 1). Specifically, social interactions on x among twins can be incorporated as
where sxkj is the effect of co-twin k’s schooling, denoted xkj, on twin i’s schooling attainment xij. The corresponding within-MZ expression can then be obtained as:
This relation suggests that: (i) the usual MZ fixed-effects estimator is unbiased even though the disturbance term includes in addition to under the assumption that the maintained assumption that does not enter the disturbance term in Eq. (2), which means that, as is intuitively appealing, the schooling difference is less (more) than the difference in the random shocks that affect schooling if there is imitation (reaction).
Instead of a social interaction processes that affects schooling x, we can assume a cross-twins effect that affects y, say, because twins imitate each others’ fertility behavior, with the social interaction effect less than the own effect so that |s| < 1:
The manipulation of this relationship parallel to that for Eq. (11) leads to
In the case of social interactions regarding fertility y, and in contrast to our earlier discussion in this section of social interactions on schooling x, this relation suggests that the usual twins estimator of β is biased downwards (if s > 0) or upwards (if s < 0) even if eyx = 0 because of the imitation/reaction effects with respect to the fertility y.
In summary, if there are social interactions—either in the form of imitation or reaction—with respect to the right-side determinant, such as schooling in relation (2), there is no bias in either direction for the MZ fixed-effects twins estimator. But if there are social interactions with regard to the dependent variable, such as fertility in relation (2), the estimated β is a lower bound if there is positive imitation (if s > 0) and an upper bound if there is negative imitation (reaction) with s < 0. If there is positive imitation on the outcome y, the maximum downward bias is 50%, but the actual bias is likely to be considerably less because the maximum is for the unlikely situation in which the twin’s fertility is weighted as much as the own direct determinants of one’s own fertility
4.5 Classical Measurement Error
Another critique of twins fixed-effects estimates—or, for that matter, of any fixed-effects estimates—pertains to the consequences of classical random measurement error. Because much more of the variation in schooling is across twins pairs rather than within twins pairs, the fixed-effects estimator filters out much of the true signal of schooling without also reducing measurement error (Bishop 1977; Griliches 1979). Because of this larger noise-to-signal ratio, the fixed-effects twins estimator is subject to more of the measurement error bias towards zero than is the cross-twins pairs or simple cross-sectional estimator. If the coefficient estimate from the fixed-effects twins estimator is smaller, it may be because it controls for the endogenously determined part of schooling or because of the larger bias due to measurement error or due to some combination of these two factors.
To see the impact of measurement error, assume that measured schooling xij is linearly related to true schooling but is measured with random measurement error εij:
Bishop (1977) and Griliches (1979) show that if measurement error is not correlated across siblings,10 the bias towards zero in β̂w, the estimated within-sibling coefficient β, is:
| (11) |
where ρx is the correlation in schooling between siblings (which is zero in standard individual estimates) and σ2(εij) and denote the variance of εij and xij respectively. This bias towards zero due to measurement error is likely to be greater for within-DZ estimates than for individual estimates and for within-MZ estimates than for within-DZ estimates because ρx is likely to be positive and greater for MZ than DZ twins.
Table 1 gives some illustrations, with each row representing different noise-to-signal ratios as given in column 1; the percentage biases in individual, within-DZ and within-MZ estimates due to measurement error in columns 2–4, and the ratios of the coefficients from DZ estimates and MZ estimates to individual estimates due to measurement error in columns 5 and 6.
Table 1.
Implications of Random Measurement Error for Individual, Within-DZ, and Within-MZ estimates
| Noise-to-signal ratio | Biases towards zero in estimated βs (percentages)
|
Ratio of estimated βs due to measurement error biases alone
|
|||
|---|---|---|---|---|---|
| Individual | Within DZ | Within MZ | Within DZ/Individual | Within MZ/Individual | |
| (1) | (2) | (3) | (4) | (5) | (6) |
| 0.02 | 2% | 4% | 8% | 0.98 | 0.94 |
| 0.04 | 4% | 8% | 16% | 0.96 | 0.88 |
| 0.06 | 6% | 12% | 24% | 0.94 | 0.81 |
| 0.08 | 8% | 16% | 32% | 0.91 | 0.74 |
| 0.10 | 10% | 20% | 40% | 0.89 | 0.67 |
| 0.12 | 12% | 24% | 48% | 0.86 | 0.59 |
| 0.14 | 14% | 28% | 56% | 0.84 | 0.51 |
| 0.16 | 16% | 32% | 64% | 0.81 | 0.43 |
| 0.18 | 18% | 36% | 72% | 0.78 | 0.34 |
| 0.20 | 20% | 40% | 80% | 0.75 | 0.25 |
Note: Based on equation (11) in text with ρx = 0 for individuals, 0.50 for DZ twins and 0.75 for MZ twins.
Twins studies that have reports from other respondents (i.e., the other member of a twins pair, the twins’ adult children), so that they can estimate measurement error models, report estimated noise-to-signal ratios of 0.04–0.12 (Amin et al. 2010; Ashenfelter and Krueger 1994; Ashenfelter and Rouse 1998; Behrman et al. 1994). Therefore a noise-to-signal ratio of about 0.08 is suggestive of the extent of bias due to measurement error near the midpoint of the range of noise-to-signal estimates from these studies and how these biases differ across the three types of estimates: 8% for individual estimates, 16% for within-DZ estimates, and 32% for within-MZ estimates. Thus fairly substantial drops in the coefficient estimates for the within-DZ and within-MZ estimates occur due to measurement errors of this magnitude, even if in reality there are no biases due to unobserved endowments. These measurement error biases result in the coefficient estimates for the within-DZ estimates being 9% smaller and those for the within-MZ estimates 26% smaller in absolute magnitude than those for the individual estimates. Behrman et al. (1980) observed that estimates of noise-to-signal ratios from other studies could account for up to half of the difference between their fixed-effects estimates and OLS estimates. Ashenfelter and Krueger (1994) and Behrman et al. (1994) introduced the use of another report on the twin’s schooling to instrument schooling and therefore eliminate the bias due to measurement error under the assumption that the measurement error in the other report is independent of the measurement error of one’s own. Both studies find that this method for controlling for measurement error increases the estimated returns to schooling in comparison with estimates that do not correct for measurement error.11
5 Behavioral Genetics Structural Equation Models for Twins Resemblance
In contrast to the economic approach that has been outlined above, the behavioral genetics approach to twins data has traditionally been concerned with identifying the contributions of genetic and social endowments to variation in phenotypes, and to use this approach to measure aspects such as the “heritability” of phenotypes that reflect the proportion of variance of a phenotype in a given population that is attributable to genetic factors. We briefly discuss in this section the univariate behavioral genetics model, but then focus on the bivariate behavioral genetics (ACE) model that is more closely related to the economic approach discussed in the previous sections. The emphasis in interpreting the results, and the assumptions underlying the analyses, however differ in important ways between the economic and behavioral genetics approaches to twins data, and these differences will be highlighted in our discussion below.
5.1 Univariate ACE model
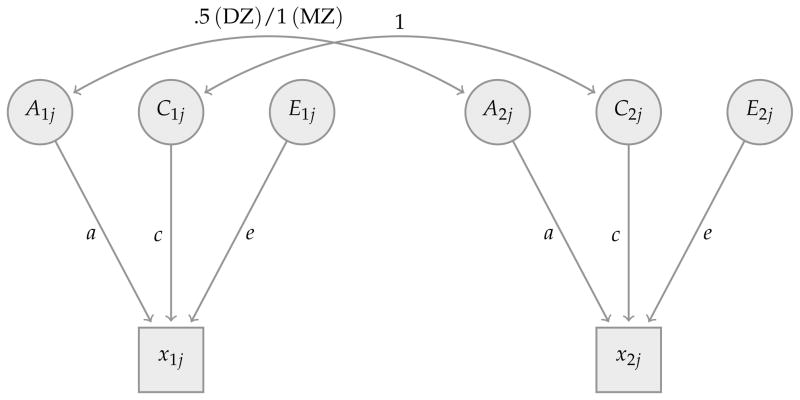
Resemblance between twins can be modeled using a two-group structural equation model fit to variance-covariance matrices. Figure 2 presents the basic ACE model for a single phenotype xij (say, schooling). Parallel to the discussion of the MZ fixed-effects twins model above, the three latent components in the model refer to additive genetic influences (Aij), common environmental influences (Cij), and unique environmental influences (Eij). These unobserved latent factors are independently distributed and standardized to a mean of zero and a variance of one.12 The ACE model is usually identified (as for heritability), by assuming different correlations between different types of twins. The ACE model is often limited to MZ and same-sex DZ twins, although other models, such as the sex-limitation model, consider cross-sex DZ pairs. The C factors are correlated at 1, as they denote environments shared by twins, and therefore C1j = C2j = Cj. The Aij factors are correlated at different levels depending on the type of twins. Because they represent unique influences (including measurement error) affecting only twin i in pair j, the Eij factors are not correlated within twins pairs.13,14
Figure 2. ACE model for the analyses of genetic, shared environmental and unique environmental components to variation in phenotype x.
Formally, the univariate behavioral genetics approach usually assumes an additive genetic model with no assortative mating and with equal environmental influences across kinship categories.15,16 In this additive genetic models, multiple genes each have small effects on a particular phenotype xij (e.g., schooling), and the overall influence of genetic factors on the phenotype xij can then be represented as aAij, where Aij is the relevant genetic endowment that affects the phenotype xij, and a measures the extent to which xij is affected by this genetic endowment. In order to establish the degree of genetic relatedness among DZ twins, an additional assumption about assortative mating is required. Since traditional twins data often do not provide information that would allow the identification of assortative mating, traditional behavioral genetics analyses assume that there is no assortative mating.17 In this case, an immediate corollary of the additive genetic model is that the correlation in genetic endowments between DZ (fraternal) twins is . This correlation of .5 in DZ twins occurs because in the additive genetic model, DZ twins (like ordinary siblings) share 50% of their genes on average. For MZ twins, who share all of their genes at conception, this correlation is equal to one at conception. In the path diagram in Figure 2 the paths linking the genetic endowments of twins 1 and 2 therefore have a value of 1 for MZ and .5 for DZ twins.
Similar to the structure of the economic model that we outlined above, the behavioral genetics model can then be presented (again, as deviations from the means) as
| (12) |
where Aij, Cij and Eij are independently distributed latent factors, standardized to a variance of one, that represent respectively the additive genetic, shared environmental and unique environmental influences on the observed phenotype xij of twin i in pair j. This specification for the determinants of the phenotype xij is analogous to the relation (1) that we specified for schooling in our earlier discussion of the within-MZ model in Section 3.
Assuming an additive genetic model with no assortative mating, the correlations of the genetic endowments within twins pairs is for DZ twins and for MZ twins. Shared environmental factors, or social endowments, are assumed to be identical for both members of a twins pair (Cor(C1j, C2j) = 1, independent of zygosity), and the individual-specific influences are independent within twins pairs. Stacking the observed phenotype for both twin 1 and twin 2 in a twins pair into a vector P, which in the case of the univariate ACE model means that Pj = (xij, x2j)′, then allows us to then obtain the variance and covariances of the observed phenotypes for MZ twins (denoted ) and DZ twins (denoted ) as
where the subscript j for twins pairs has been omitted for simplicity and εMZ and εDZ denote the expectation operators taken for MZ and DZ twins respectively.
Heritability (usually denoted h2) in the behavioral genetics literature is defined as the ratio of the variance of the genetic contributions to x, which are given by of aAij in Eq. (12), to the variance in the phenotype x for a given population. In the univariate ACE model, heritability h2 is obtained as , where a2 is the total genetic variance in the phenotype x, and is the overall variance of x. In a similar fashion, the proportion of the variance that can be attributed to social endowments (or shared environmental factors) in this model can be obtained as .
An important advantage of the ACE model for obtaining estimates of the heritability and the underlying parameter a, c and e, is the transparency of the approach and the flexibility of its assumptions. As with other structural equation models, the assumptions of the ACE model can be relaxed directly based on theory, prior perceptions and relative fit of different models. For example, if one assumes no genetic influence on a phenotype, a model that freely estimates a can be compared with a model that constrains a to zero. Likewise, if one knows that DZ twins share more than 50% of their genes owing to assortative mating, the correlation between the A components can be increased (e.g., Neale and Maes 2004). More complicated explorations are possible, but require additional information for identification.18
5.2 Bivariate ACE model
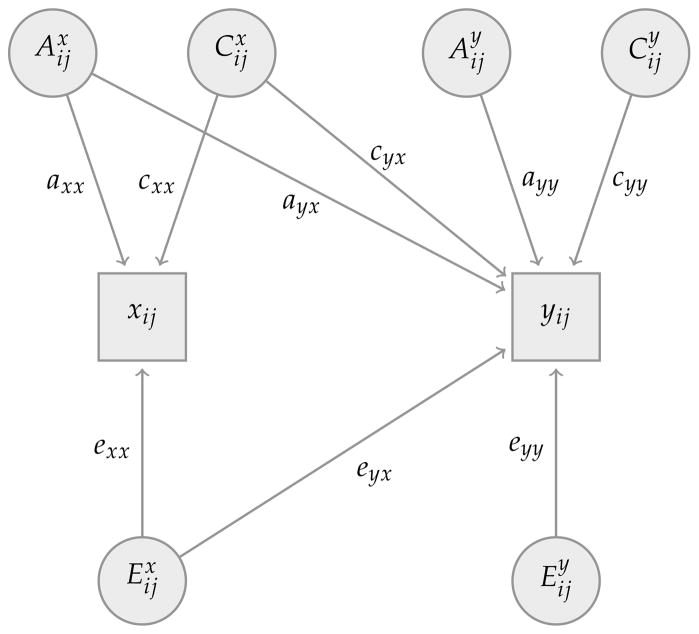
Of particular relevance to our previous discussion about the use of twins data in economics is the extension of the ACE model to multivariate contexts. We focus here particularly on the bivariate case where the observed phenotypes include xij (say schooling) and yij (say fertility) of twin i in pair j. While several observationally-equivalent specifications for the bivariate behavioral genetics model are possible, Figure 3 shows the most common specification that includes two latent additive genetic components ( and ), two additive latent shared environmental components ( and ), and two latent unique environmental components and .19 As in the univariate model, within a twins pair, the genetic and shared environmental components are correlated within twins pairs. Assuming an additive genetic model with no assortative mating, as is done in most applications, the correlation for the genetic endowments and within-pairs is .5 for DZ and 1 for MZ twins, the correlation for shared environmental factors is 1, and hence and independent of zygosity. The unique environmental factors and are not correlated within twins pairs.
Figure 3. Bivariate ACE model for schooling and fertility.
This graph shows the path-diagram for one twin, twin i in pair j only; an analogous diagram exists for twin k in pair j, and the genetic and shared environmental components are correlated across twins within the same pairs as for MZ twins, for DZ twins, independent of zygosity, and also independent of zygosity.
The bivariate ACE model is attractive because it allows for the possibility that schooling and fertility are affected by common genetic factors, or are similarly affected by the same shared environmental influences. For example, the paths axx and cxx indicate, respectively, the effects of the latent genetic component Ax and shared environmental component on schooling xij, while the paths ayx and cyx reflect the effect of these latent genetic and shared environmental factors on fertility yij.20 The path exx measures the possibly effect of the unique environmental factors Ex on schooling x, and the path eyx measures the effect of the unique environmental component Ex on fertility y. In addition, fertility y is affected by additional genetic, shared environmental and unique environmental components Ay, Cy and Ey that contribute to variation in fertility, but not to variation in schooling.
In a close resemblance to the economic twins model outlined earlier in this paper, the relationship between the observed phenotypes, xij and yij, and the latent genetic, share environmental and unique environmental factors are specified as
| (13) |
| (14) |
where in contrast to the economic model in Section 3 there is no direct effect β of schooling x on fertility y and the model allows for a direct influence of the individual-specific factors affecting schooling, Eij, on fertility y (i.e., the path eyx in relation 14 can be non-zero).
To derive the variance-covariance matrix in the bivariate ACE model of the observed phenotypes, stacked again in a vector P = (x1j, y1j, x2j, y2j)′, it is useful to arrange the coefficients of the path diagram in Figure 3 (see also Eqs. 13–14) into lower triangular matrices as
with their corresponding products being given by A = LaLa′, C = LcLc′, and E = LeLe′. Maintaining the assumption of an additive genetic model with no assortative mating, we then can obtain the variance and covariances of the observed phenotypes P = (x1j, y1j, x2j, y2j)′ for MZ twins (denoted ) and DZ twins (denoted ) as
| (15) |
| (16) |
where εMZ and εDZ denote again the expectation operator taken for MZ and DZ twins respectively.
The expected variance of the phenotypes, for x and for y in the bivariate ACE model is equal for MZ and DZ twins and can be obtained from Eqs. (15–16) as and . In addition, Table 2 provides co-variances that are implied by the bivariate ACE model in Eqs. (15–16) as a function of the path values in Figure 3. While there are a total of 20 variances and covariances in the data they correspond to only nine unique moment conditions when stated as functions of the coefficients axx, ayx, ayy, cxx, cyx, cyy exx, eyx and eyy. The nine parameters of the bivariate ACE model in Figure 3 are therefore exactly identified with data on twins reared together.
Table 2.
|
MZ Twins: | ||||||
|---|---|---|---|---|---|---|
| Observed outcome (phenotype)
|
||||||
| x1j | y1j | x2j | y2j | |||
| x1j |
|
|||||
| y1j | axxayx + cxxcyx + exxeyx |
|
||||
| x2j |
|
axxayx + cxxcyx |
|
|||
| y2j | axxayx + cxxcyx |
|
axxayx + cxxcyx + exxeyx |
|
||
|
| ||||||
|
DZ Twins:
| ||||||
| Observed outcome (phenotype)
|
||||||
| x1j | y1j | x2j | y2j | |||
|
| ||||||
| x1j |
|
|||||
| y1j | axxayx + cxxcyx + exxeyx |
|
||||
| x2j |
|
.5axxayx + cxxcyx |
|
|||
| y2j | .5axxayx + cxxcyx |
|
axxayx + cxxcyx + exxeyx |
|
||
Note: All unique moment conditions that identify the parameters of the ACE model are given in black, while duplicate moment conditions are given in gray. The expected variance of the phenotypes, for x and for y is equal for MZ and DZ twins and can be obtained from the above table as and .
In most empirical applications, similar to the univariate behavioral genetics model, the bivariate ACE model in Figure 3 and Eqs. (13–14) has primarily been used to decompose the variance in the observed phenotypes x and y, say schooling and fertility, into the latent genetic, shared environmental and unique environmental components (Coolidge et al. 2004; Willcutt et al. 2007). In addition, the bivariate ACE model in Figure 3 can reveal that a certain fraction of the variance in fertility y is due to genetic factors that also contribute to variation in schooling x (path ayx), and that another part of the variation in fertility is due to genetic factors that contribute to fertility but not schooling (path ayy). For example, Table 3 shows the contributions of genetic endowments to the variance and co-variance matrices implied by ACE model in Eqs. (15–16). The heritability of schooling x, using the genetic contributions given in Table 3, is then obtained from the top panel ( for monozygotic twins) as , where the numerator is the genetic variance and the denominator is the overall variance of x. Analogously, the heritability of fertility y is given by , where in the numerator and denominator reflects the contribution to the genetic variance in fertility y that stems from genetic factors that also affect schooling. In a similar vein, the ratio axxayx/(axxayx + cxxcyx + exxeyx) is the fraction of the covariance between schooling x and fertility y within each individual that can be attributed to genetic factors that affect both schooling and fertility, and is the correlation between the genetic endowments that affect schooling x and the genetic endowments that affect fertility y. Similar calculations can be conducted for social endowments (shared environments) and individual-specific factors.
Table 3.
Contribution of genetic endowments to the variance and co-variance matrices implied by the ACE model in Eqs. (15–16)
|
MZ Twins: | ||||||
|---|---|---|---|---|---|---|
| Observed outcome (phenotype)
|
||||||
| x1j | y1j | x2j | y2j | |||
| x1j |
|
|||||
| y1j | axx ayx |
|
||||
| x2j |
|
axx ayx |
|
|||
| y2j | axx ayx |
|
axx ayx |
|
||
|
| ||||||
|
DZ Twins:
| ||||||
| Observed outcome (phenotype)
|
||||||
| x1j | y1j | x2j | y2j | |||
|
| ||||||
| x1j |
|
|||||
| y1j | axx ayx |
|
||||
| x2j |
|
.5axx ayx |
|
|||
| y2j | .5axx ayx |
|
axx ayx |
|
||
Note: One set of unique elements of the table are given in black, while duplicate elements given in gray.
For example, using data on Danish twins born between 1953 and 1970 and who participated in a survey in 1994, Kohler and Rodgers (2003) conclude that a bivariate behavioral genetics analysis confirms earlier findings that fertility in low-fertility settings, such as contemporary Denmark, is subject to important genetic influences, while at the same time, the bivariate model shows the new and somewhat unexpected result that genetic variance in fertility is not necessarily shared with genetic variance in completed schooling (measured in years of tertiary schooling). Instead, Kohler and Rodgers’ results show that for both males and females most genetic variance in fertility is residual variance that affects the number of children but not schooling attainment. Overlapping influences mainly exist for shared environmental factors analyses of females, where all shared environmental factors affecting fertility also affect schooling.
6 Introducing causal pathways between phenotypes: Extending the ACE framework
While univariate, bi- and multivariate behavioral genetics models have been widely used in the behavioral genetics literature, and have received some interest from social scientists, their use within the social sciences remains limited. One possible reason for this is that, from a social science perspective and in light of our earlier discussion of the economic approach to twins data, the behavioral genetics model in Figure 3 is not fully satisfactory because it attributes the association between schooling x and fertility y exclusively to the latent components in this model that reflect genetic, shared environmental or unique environmental factors. Specifically, schooling and fertility within each individual in this ACE model are correlated because at least one of the paths ayx, cyx or eyx is non-zero. In addition, a non-zero pathway ayx or cyx implies that fertility and schooling are correlated between twins within the same twins pair. The ACE model, however, does not allow for the possibility that there is a direct effect of schooling x on fertility y, i.e., it explicitly ignores a direct pathway from schooling and fertility, a pathway that has been subject of an extensive literature in the social sciences and the identification of which is the primary goal of the economic model for twins data discussed earlier.
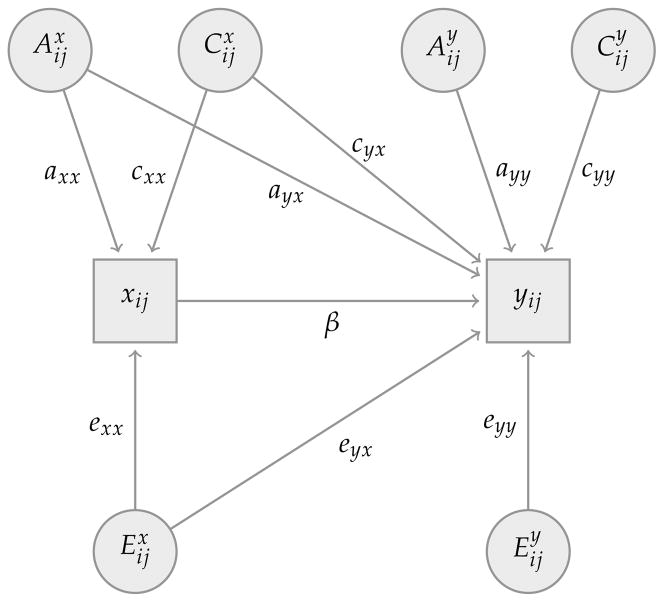
Therefore, in order to allow for a direct effect of schooling on fertility, as is shown in Figure 4, it is desirable to introduce causal pathways between the variables x and y in the bivariate ACE model. We denote the ACE model that includes such a direct effect of x (schooling) on the outcome y (fertility) as an ACE-β model, where β refers to the causal effect of x on y that is present in the ACE-β but absent in the conventional ACE model. While conceptually appealing, however, the ACE-β model in Figure 4 is not empirically identified in twins or other family data. If one allows for the direct pathway from schooling to fertility, the data do not contain enough moment conditions to identify all pathways included in the model.21 Moreover, this lack of identification cannot be overcome by using an extended twins design that would include other siblings that have a different degree of genetic relatedness or that include twins reared apart because identification of all pathways in Figure 4 would require more moments between the observed variables for each twin within a twins pair (see also Table 4).
Figure 4. ACE-β model with direct effect of schooling on fertility.
Table 4.
| MZ and DZ Twins: and | ||||
|---|---|---|---|---|
| Observed outcome (phenotype)
|
||||
| x1j | y1j | x2j | y2j | |
| x1j | V[1, 1] | |||
| y1j | βV[1, 1] + V[2, 1] | β2V[1, 1] + 2βV[2, 1] + V[2, 2] | ||
| x2j | V[3, 1] | βV[3, 1] + V[4, 1] | V[1, 1] | |
| y2j | βV[3, 1] + V[4, 1] | β2V[3, 1] + 2βV[4, 1] + V[4, 2] | βV[1, 1] + V[2, 1] | β2V[1, 1] + 2βV[2, 1] + V[2, 2] |
While there have been some models in the behavioral genetics tradition that include causal pathways, such as for example directed causality models (e.g., Gillespie and Martin 2005; Gillespie et al. 2003; Heath et al. 1993) and the children of twins design (D’Onofrio et al. 2009, 2003; Eaves et al. 2005), these approaches are targeted for research questions that are different from the ones emphasized in this paper. The directed causality models are aimed at identifying the direction of causality between two variables in cases where the genetic and social endowments for these variables are distinct. These models therefore attempt to identify whether x has a causal effect on y, or vice versa with y having a causal effect on x, in contexts where each of these variables is affected by its own distinct set of latent influences (endowments and individual specific factors).22 The children of twins (COT) design has been proposed as an alternative to the adoption study to resolve the direct effects of parental treatment from secondary parent-child association due to genetic factors. In particular, because parents provide the environmental context for the family and transmit genetic makeup to their offspring, the genetic and environmental processes responsible for associations between family risk factors and offspring adjustment are confounded. The children of twins design therefore uses a twins design to delineate intergenerational associations into (i) environmental processes specifically related to the risk factor, (ii) genetic factors that influence the risk factor and offspring characteristic, and (iii) common environmental factors that vary between families. Neither the directed causality model nor the children of twins design provide a substitute for the framework developed here. In particular, in the contexts that are of primary interest for our discussion in this paper, the direction of causality is usually given from the context or the sequencing during the life-course—e.g., as in studying the causal effect of schooling attainment on completed fertility later in life—and it is the potential presence of correlated unobserved endowments between schooling x and fertility y that is of primary concern. In addition, the primary concern in this paper is about the interrelations of behaviors/outcomes that occur over the life-course of an individual, such as the effect of schooling on fertility, rather than on the intergenerational aspects that link parental behaviors (or risk factors) to child outcome as studied in the children of twins design.
Given our previous discussion, one might conclude that there is an inherent empirical incompatibility between, on the one hand, the behavioral genetics analyses of schooling x and fertility y within a multivariate ACE model that focuses on identifying the contributions of genetic and social endowments on the variation and covariation of the phenotypes x and y (Figure 3), and on the other hand, the conventional social science approaches that would generally emphasize the direct effect of schooling x on fertility y as one of the primary parameters that need to be inferred from data (Figure 1).
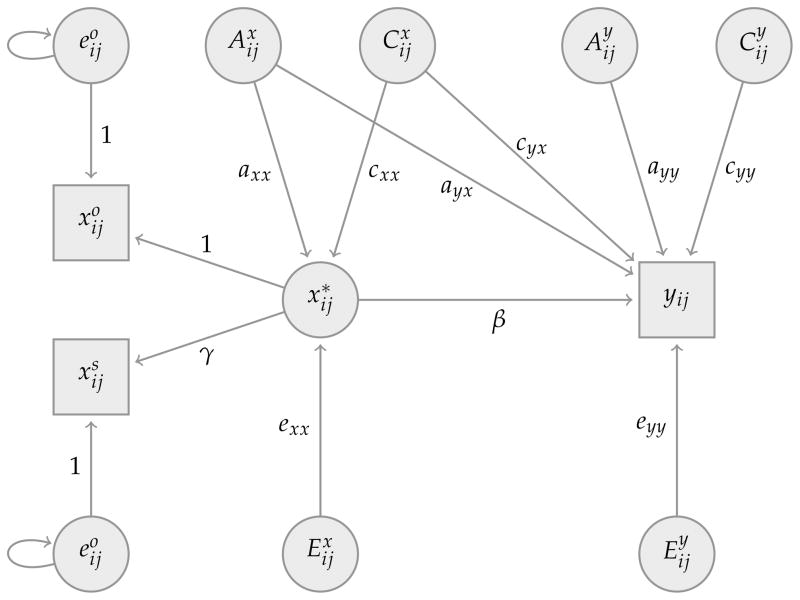
This incompatibility, however, can be resolved if one is willing to make identifying assumptions that one of the diagonal paths within the ACE-β model in Figure 4 is known a priori. Of particular interest in this context is the ACE-β model in Figure 5 that constrains the path eyx to zero.
Figure 5. ACE-β model with direct effect of schooling on fertility, including identifying assumption e12 = 0.
It is important to emphasize that the restriction eyx = 0 is a plausible—and probably the most plausible—identifying assumption in the ACE-β model in Figure 5. This assumption is equivalent to the assumption that underlies the identification of the parameter β in the economic fixed-effects model for twins analyses, and similar to our earlier discussion, this assumption implies that the unique environmental factors that affect schooling x are assumed to affect fertility y only through its effect on schooling, but not directly.23,24
The ACE-β model in Figure 5 therefore blends the economic fixed-effects approach and the behavioral genetics bivariate ACE model. As in the twins fixed-effects model, this model includes a direct effect β of schooling x on fertility y. In addition, the diagonal paths ayx and cyx in the extended ACE-β model in Figure 5 also reflect the contributions of unobserved endowments—either genetic or shared environmental factors—to both fertility and schooling. As our earlier analyses has shown, if one of these paths is non-zero, standard estimates of the effect β of schooling on fertility are biased. To avoid this bias, both the economic fixed-effects model in Eqs. (1–2) as well as the ACE-β model in Figure 5 explicitly allow for the possibility that genetic and/or social endowments jointly affect schooling x and fertility y.25,26
The ACE-β model in Figure 5 has an important advantage over the within-MZ approach discussed earlier in this paper in that it not only provides a consistent estimate of the direct effect β of schooling x on fertility y, like the economic model in Eqs. (1–2), but it also differentiates between the genetic and shared environmental components contributing to the (co-)variation in schooling x and fertility y within a population. The model therefore integrates the economic approach that has focused on identifying the causal effects of schooling on fertility and the behavioral genetics approach that has focused on identifying the sources of variation and covariation in schooling and schooling in term of genetic, shared environmental and unique environmental factors. The ACE-β model in Figure 5 achieves both of these aims.
The ability of the ACE-β model to not only infer the causal effect β of schooling x on fertility y, but also to distinguish between the genetic and social endowments that contribute to the variation and covariation of x and y within individuals and within twins pairs, is attained at the cost of somewhat more restrictive assumptions. In particular, for the ACE-β model to accurately identify the model parameters (see Figure 5), one needs to accept the assumptions of the bivariate behavioral genetics model that are more restrictive than those required for the economic fixed-effects model to provide an unbiased estimate of β. In addition to the assumption that the path eyx = 0 in Figure 5, which is common to both the economic fixed-effects model and the ACE-β model proposed in this section, the ACE-β model requires two assumptions underlying the bivariate ACE model in order to provide accurate estimates of the model parameters: (i) an additive genetic model with no assortative mating, which establishes the correlation of genetic endowments between DZ twins as , and (ii) the absence of gene-environment interactions, which implies that and are independent of and .27 In comparison, the within-MZ approach only requires the assumption that MZ twins share their genetic endowments, but not a specific genetic model, and in the economic model, gene-environment latent variable interactions do not affect the unbiasedness of the within-MZ estimator of β.
More formally, the ACE-β model in Figure 5 is obtained by introducing a direct effect of x on y into the earlier relation (14) for the ACE model that specified fertility y in terms of the latent genetic, shared environmental and unique environmental factors. The resulting specification then is
| (17) |
which is merely a restatement of the corresponding equation (2) of the economic twins model. The relation for schooling xij is as in the standard bivariate ACE model (13), which is equivalent to the corresponding relation of the economic twins model (1).
Stacking the observed phenotype for each twins pair as Pj = (x1j, y1j, x2j, y2j)′, we can restate the ACE-β model in Eqs. (13) and (17) as , or equivalently, as
where , Im is the m × m identity matrix, and , and are the stacked latent genetic, shared environmental and unique environmental factors that for twins pair j are given by and .
Similar to the bivariate behavioral genetics model discussed in the previous section, the variance and covariances of the observed phenotypes P = (x1j, y1j, x2j, y2j)′ for MZ twins (denoted ) and DZ twins (denoted ) can then be obtained as
| (18) |
| (19) |
where the inverse , εMZ and εDZ denote again the expectation operator taken for MZ and DZ twins respectively. The matrices and denote respectively the variance/covariance matrix of the combined latent genetic, shared environmental and unique environmental model that are given by
| (20) |
| (21) |
To illustrate the moment conditions that are used in the estimation of the model parameters, Table 4 gives the variance and covariances of xij and yij that implied by the ACE-β model in Eqs. (18–19) as a function of the coefficient β and V[l, k], which refers to rowl and column k of the variance/covariance matrix for MZ or DZ twins in Eqs. (15–16) under the maintained assumption that eyx = 0 (see also Table 2). Specifically, the expected variances of the phenotypes, for x and for y, that are implied by Eqs. (18–19) are equal for MZ and DZ twins and are given by and . While for schooling x, the components of the variance merely reflect the influence of the three latent factors Ax, Cx and Ex, the terms in the relation for the variance of fertility y reflect respectively the different pathways that determine variation in y: (i) variation in schooling x that results in variation in y because of the direct effect β of schooling x on fertility y; (ii) variation in y that results from the fact x has a direct effect on y and the genetic and social endowments affecting schooling x and fertility y are correlated; and (iii) the direct influences on fertility y of the genetic and social endowments (Ax, Ay, Cx and Cy) and the unique environmental factor Ey.
In addition, Table 4 shows that the observed covariance between schooling x and fertility y for individuals, which is given in row2 and column 1 of the table, is the result of a direct effect of schooling on fertility, which is measured by β, and the fact that a part of the genetic and social endowments affecting schooling also affect fertility, which is measured by V[2, 1]. Schooling is correlated among members of the same twins pair because the genetic and social endowments are correlated within twins pairs, which is reflected in row3 and column 1 of Table 4 by V[3, 1]. And schooling of twin 1 will be correlated with the fertility of twin 2 (see row4 and column 1) because (i) twin 1’s schooling is correlated with twin 2’s schooling, and twin 2’s schooling has a direct effect on 2’s fertility through β, and (ii) because the genetic and social endowments that jointly affect schooling and fertility are correlated within twins pairs.
The variances/covariances in Table 4 are also informative because they illustrate how the effect β of schooling x on fertility y can be obtained from MZ twins, and only from MZ twins, as
which represents—in terms of the parameters of the ACE-β model—the moment condition that is used by the economic within-MZ model for the estimation of the causal effect β of schooling x on fertility y.28
Within the two-fold goals of the ACE-β model to identify both the effect β of schooling x on fertility y, as well as the contribution of genetic and social endowments to the variation/covariation of schooling and fertility within and across individuals, the definition of heritability deserves some discussion. For schooling x, the definition is analogous to the bivariate ACE model and can be obtained from the model parameters as . For fertility however, one needs to consider the fact that the genetic variation in schooling is through three distinct pathways: first, direct influences of the genetic factors Ay on fertility y (path ayy in Figure 5); second, direct influences of the genetic factors Ax, which also affect schooling (path ayx); and third, indirect influences of the genetic factors Ax that directly affect schooling x (via path axx) and subsequently affect schooling y through the causal effect of schooling on fertility (path β in Figure 5).
One could think of heritability as the contribution of the first two pathways to the total variation y. In this case, heritability would be defined, like in the bivariate ACE model, as .29 This definition of heritability, however, would ignore the third indirect pathway through which genetics affect fertility, i.e., the extent to which the genetic factors Ax affect fertility y through their effect on schooling x.
To avoid this limitation, we therefore propose as a measure of heritability of y, say fertility, in the ACE-β model that is based on the expressions in Table 4. In particular, the genetic contributions to all the variances and covariances in the ACE-β model can be obtained in Table 4 by replacing V[l, k] with , where refers to rowl and column k of the top panel of Table 3 (for monozygotic twins). An appropriate definition of heritability in the ACE-β model then is obtained from Table 4 as
| (22) |
which expresses heritability of y, say fertility, as the overall contribution of genetic endowments—including genetic factors that affect fertility y directly and genetic factors that affect y indirectly through schooling x—to the variance of y. In particular, the three components in the numerator of the heritability h2 in Eq. (22) reflect, respectively, the contributions to the variation in y of (i) genetic factors that affect schooling x, and then fertility y through x; (ii) the genetic factors that are common to both schooling x and fertility y and affect fertility y through x; (iii) the direct influences of the genetic endowments Ax and Ay on fertility y.
7 Variations of the ACE-β model
An attractive feature of the ACE-β model introduced in the previous section is that several of the extensions of the economic within-MZ approach can be applied also to the ACE-β model to investigate and/or ameliorate concerns about the validity of the estimates. We discuss some of the most important issues in this context below, and the formal presentation of the corresponding models is provided in the Appendix.
7.1 Measurement error in x
Earlier in this paper (Section 4.5) we discussed the potential relevance of measurement error in xij (schooling) for obtaining a correct estimate of the causal effect β of schooling x on fertility y. These concerns about measurement error in x carry over analogously to the ACE-β framework, and in particular, measurement error in schooling has received extensive attention in the economic literature on twins. Measurement error in x (e.g., schooling) is known to bias the inferences of β and other parameters of the ACE model. In contrast, random measurement error in y is usually subsumed in the unique environmental influences Ey affecting y and it causes no biases in the estimated impact β̂ of schooling x on fertility y.
To control for the measurement error in x, some twins datasets contain multiple measures of x. For example, to control for measurement error in schooling, some twins data contain a twin’s own report of schooling, denoted and a co-twin’s report of the twin’s schooling, denoted . Figure 6 presents the corresponding path diagram where both a twin’s own and co-twin’s report on schooling x are available, under the maintained assumption that the measurement error between a twin’s own and co-twin’s report on schooling x are independent. Appendix A.1 provides the corresponding formal representation. Using these dual reports about the schooling of each twin, the ACE-β model can control for measurement error in both the estimation of the causal effect β of schooling x on fertility y and the inference of heritabilities and the contributions of the genetic and social endowments to the variation in schooling and fertility.
Figure 6.
ACE-β model with measurement error in x: own and co-twin report of schooling are indicators of the unobserved true schooling level
7.2 Social interactions: twins react to each other
Social interactions among twins is a second frequently-raised criticism leveled against the use of twins data in the social sciences. We have already discussed earlier that, within the economic twins model, social interaction between twins with respect to x does not affect the estimate of β, while social interactions with respect to y will bias the estimates.
The corresponding key questions in the ACE-β model are twofold: On the one hand, does the fact that social interaction with respect to x does not bias the inferences, which was the case in the within-MZ model (Section 4.4), also apply to the ACE-β model? And on the other hand, given that additional data—DZ and MZ twins—are used for the analyses, is it possible to empirically infer the extent of social interactions?
Social interaction with respect to schooling x can be included in the path-diagram for the ACE-β model by introducing paths s (with |s| < 1) from schooling of twin i, xij to the schooling of i’s co-twin k, xkj (see Figure 7). There will be positive (s > 0) social interaction if schooling of twin i benefits from the schooling attainment of twin k, and there will be negative (s < 0) or competitive social interaction if the twins compete for limited resources—such as money or parental time—in order to increase their schooling attainment, or if twins attempt to distinguish themselves from their co-twins through different behaviors.
Figure 7. ACE-β model with social interaction on schooling x.
The paths connecting the endowments and between twin 1 and twin 2 in pair j have been omitted for clarity of the diagram
It turns out that an attractive feature of the ACE-β model is the fact that not only can β be estimated in the presence of social interactions on x, but the degrees of social interaction can be estimated. In particular, solving for the variance/covariance matrix of the observed phenotypes x and y (Appendix A.2) reveals that social interaction results in a different variance for x for DZ and MZ twins. Table 5 shows that the variance of x depends on the social interaction parameter s as well as V[3, 1], which is equal to for MZ and for DZ twins (Table 4). Using this differential variance in x, the coefficient of social interaction can be identified in addition to the other parameters of the ACE-β model (Plomin et al. 1997). An important advantage of the ACE-β model therefore is that, subject to the model assumptions, the analyses can jointly estimates (i) the causal effect β of schooling x on fertility y, (ii) the extent s to which social interactions affect schooling within twins pairs, and (iii) the contributions of genetic and social endowments to the variation and covariation of schooling x and fertility y within and across individuals.
Table 5.
| Variance xij | w((1 + s2)V[1, 1] + 2sV[[3, 1]) |
| Variance yij | w(β2(1 + s2)V[1, 1] + 2β(1 − s2)V[2, 1] + (1 − 2s2)2V[2, 2]+ 2β2sV[3, 1] − 2βs(1 − s2)V[4, 1]) |
In addition, despite the presence of social interaction on x, the coefficient β can be inferred from the observed variances/covariances of MZ twins (and only those of MZ twins) as
as long as the assumption eyx = 0 remains valid,30 which is congruent with the fact that the within-MZ model continues to give an accurate estimate of β in the presence of social interactions on x.
Social interaction with respect to fertility y can also be incorporated in the ACE-β model, and in contrast to the within-MZ approach, all parameters can be estimated because social interactions with respect to fertility y imply a different variance of y for MZ and DZ twin, while the variance of x remains equal for MZ and DZ twins.
Because of the effect of social interactions on the variance of schooling x and/or fertility y, and the fact that in the presence of social interactions the variance of these outcomes will differ between MZ and DZ twins, the possible presence of social interactions can be inferred from the pattern of variances of x and y by zygosity (Table 6). For example, in a situation in which one expects β > 0, a pattern where VarMZ(x) > VarDZ(x) and VarMZ(y) > VarDZ(y) is indicative of positive (s > 0) or reinforcing social interaction with respect to schooling x; a pattern where VarMZ(x) = VarDZ(x) and VarMZ(y) > VarDZ(y) possibly indicates positive (s > 0) or reinforcing social interaction with respect to fertility y.
Table 6.
Indications of social interactions in the ACE-β model with twins data (under assumption that β > 0)
| Variance | Social Interaction |
|---|---|
| VarMZ(x) > VarDZ(x) and VarMZ(y) > VarDZ(y) | possible reinforcement interaction on x: s > 0 |
| VarMZ(x) < VarDZ(x) and VarMZ(y) < VarDZ(y) | possible competition on x: s < 0 |
| VarMZ(x) = VarDZ(x) and VarMZ(y) > VarDZ(y) | possible reinforcement interaction on y |
| VarMZ(x) = VarDZ(x) and VarMZ(y) < VarDZ(y) | possible competition on y |
7.3 Correlated cross-equation shocks
A further assumption for the estimation of β in the ACE-β model is the assumption that eyx = 0 that is, that any individual-specific shocks that affect x (say, schooling) have an effect on fertility y only through x but not directly. In the first part of this paper in the context of the economic twins model we discussed that, if this assumption is not satisfied, an instrumental variable estimation can be used. The requirement for the instrument is that it predicts the within-MZ difference in schooling x and that it is not correlated with the unobserved determinants of fertility y.
Figure 8 shows the corresponding integration of the instrumental variable estimation in the ACE-β model, to which we refer as the ACE-β IV model. In the top part of Figure 8 the available instrument z is completely exogenous in the sense that it predicts x but is not correlated with any of the unobserved endowments that affect schooling x and fertility y. The bottom part of Figure 8 shows the more likely scenario for social-science applications of the ACE-β IV model of an instrument that is correlated with the endowments affecting schooling x and fertility y. The crucial advantage of the ACE-β IV approach in Figure 8, which is formally presented in Appendix A.3, is the ability—conditional on a valid instrument being available—to test the assumption that eyx = 0, and if is assumption is rejected, to estimate an ACE-β model that allows for eyx ≠ 0. That is, if a suitable instrument is available, the assumption that individual-specific influences on schooling x affect fertility y only through schooling and not directly can be relaxed. The ACE-β model in Figure 8 therefore allows the estimation of (i) the causal effect β of schooling x on fertility y, (ii) the contributions of genetic and social endowments to the variation and covariation of schooling x and fertility y within and across individuals, and (iii) the extent to which individual-specific factors that affect schooling affect fertility y through x as well as directly along the path eyx.
Figure 8. ACE-β IV model: combining the ACE-β model with instrumental variable estimation.
(Note: the coefficients for the paths between the latent variables and the phenotypes have been omitted for clarity of the diagram)
8 Application to the Minnesota Twins Data
We illustrate the models discussed earlier in this paper using analyses of the effect of schooling on three outcomes—self-reported health, schooling of the first spouse and fertility—for which the relationship with schooling has received considerable attention in the literature (Wolfe and Haveman 2003). The data used for these analyses is provided by a subset of the Minnesota Twins Registry (MTR) Data. The MTR is one of the largest birth-record based twins registries in the world; details of the sample and its characteristics are in Lykken et al. (1990). The specific data that we use consists of a socioeconomic survey conducted in 1994 of about 3,600 twins born in 1936–1955. The interesting features of these data include the availability of birth weight information that is obtained through a link with the birth registry, and the inclusion of a co-twin’s report about a twin’s schooling that will allow us to control for measurement error. These data have previously been used by Behrman et al. (1994, 1996) and Behrman and Rosenzweig (1999, 2002, 2004). We focus in our analyses on female twins only (same-sex MZ twins and same-sex DZ twins) with complete information on own schooling and the co-twin’s report of schooling. Descriptive statistics of our study population are provided in Table 7. Scripts and data for replicating the analyses presented in this section are available online at http://www.ssc.upenn.edu/~hpkohler.
Table 7.
Descriptive statistics for MTR study population
| MZ twins
|
DZ twins
|
|||||
|---|---|---|---|---|---|---|
| Mean | Std. Dev. | N | Mean | Std. Dev. | N | |
| Birth yeara | 1947 | 5.51 | 858 | 1946 | 5.82 | 682 |
| Schooling (years)a | 13.4 | 2.27 | 858 | 13.3 | 2.28 | 682 |
| Co-twin report of schoolinga | 13.4 | 2.20 | 858 | 13.1 | 2.08 | 682 |
| Self-reported healtha,b | 4.34 | 0.69 | 838 | 4.30 | 0.69 | 668 |
| Schooling (years) of 1st spousea,c | 13.4 | 2.30 | 484 | 13.2 | 2.25 | 406 |
| Fertility (# of children)a,d | 2.17 | 1.42 | 758 | 2.38 | 1.42 | 606 |
| Subset for twin pairs for within-MZ IV analysese | ||||||
| Birth weight (kg) | 2.51 | 0.47 | 672 | 2.65 | 0.49 | 516 |
| Mother age at birth of twins | 28.4 | 6.14 | 672 | 29.4 | 5.30 | 516 |
| Mother died before twins were age 30 | 0.033 | 0.18 | 672 | 0.027 | 0.16 | 516 |
| Schooling (years) | 13.6 | 2.31 | 672 | 13.3 | 2.27 | 516 |
| Fertility (# of children) | 2.13 | 1.39 | 672 | 2.30 | 1.35 | 516 |
Notes:
includes twins in pairs for whom complete information on (own) schooling and co-twin report of schooling is available;
twins in pairs for whom information on subjective health is available for both twins; subjective health is coded as 5 = excellent, 4 = good, 3 = fair, 2 = poor and 1 = bad;
twins in pairs in which both twins were ever married and for whom information on schooling of the first spouse is available for both twins;
twins in pairs for whom fertility is available for both twins;
twins in pairs for which data on schooling, co-twin report of schooling, fertility, mother age at birth of twins, mother mortality and birthweight are complete.
In our illustrations of the different methods for the analyses of twins data in this Section, we do not present any analyses that allow for social interactions on schooling among twins because the equal variance of schooling between DZ and MZ twins does not provide an indication that social interaction among twins is an important determinant of the schooling outcome in the study population. There is also no differential variation between MZ and DZ twins in health, fertility or schooling of the first spouse, thereby providing no indication that social interaction processes of the form outlined earlier in this paper (Section 7.2) are important for the outcomes considered in this section.
8.1 Within-MZ analyses of the effect of schooling on health, spouse’s schooling and fertility
Table 8 compares within-MZ analyses—with and without correction for measurement error—with standard OLS analyses for the relationship between schooling on the one hand and self-reported health, schooling of the first spouse and fertility, respectively. Because the twins were between 39–55 years old at the time of the survey, these outcomes reflect completed schooling and near-completed fertility.
Table 8.
The effect of schooling on health, spouse schooling and fertility: Comparison of OLS and within-MZ analyses (female twins only)
| MZ Twins
|
|||
|---|---|---|---|
| within-MZ | within-MZ with meas. error | OLS | |
|
Subjective Health (z-score)
| |||
| Schooling (z-score) | 0.007 (0.069) | 0.014 (0.103) | 0.110**(0.038) |
| Observations | 838 | 838 | 838 |
|
| |||
|
Spouse Schooling (z-score)
| |||
| Schooling (z-score) | 0.259** (0.081) | 0.285* (0.118) | 0.510** (0.044) |
| Observations | 484 | 484 | 484 |
|
| |||
|
Fertility (z-score)
| |||
| Schooling (z-score) | −0.239** (0.066) | −0.232* (0.092) | −0.220** (0.038) |
| Observations | 758 | 758 | 758 |
p-values:
p < .01,
p < .05,
p < .1. The analyses are based on complete MZ twin pairs (females only) with non-missing information on the respondent’s schooling, the co-twin’s report of the respondent’s schooling, and the outcome variable (subjective health, spouse’s schooling and fertility). For spouse’s schooling, only twin pairs where both twins have been married are included. All variables have been converted into z-scores with mean zero and a variance of one using cohort-specific estimates of the mean and standard-deviation for each variable.
In all analyses that are shown in Table 8, the twin’s schooling, health, fertility and schooling of the first spouse has been converted into z-scores with zero means and variances of one by first regressing each variable, and then the residual of this regression, on a quadratic function of birth year. Cohort-specific mean and standard deviations were then used to standardize each variable to a mean of zero and a variance of one using the cohort-specific mean and variance. In addition to removing secular cohort trends in schooling, health and fertility, this standardization of all variables renders the coefficients comparable across models and outcomes. A coefficient of .11, as is shown for the OLS analyses for health in Table 8, for example, suggests that a 1-standard deviation (SD) increase in schooling is associated with a .11 SD increase in subjective health.
Several interesting substantive and methodological issues emerge from our analyses in Table 8. First, in contrast to the extensive literature on health and schooling (Cutler et al. 2006; Cutler and Lleras-Muney 2007) that have documented a strong association—that has often been interpreted as a causal effect—between schooling and health (see also the OLS analyses for health in Table 8), the within-MZ analyses of schooling and subjective health in Table 8 show that the effect of schooling on health is essentially zero. This finding is unchanged after controlling for measurement error using a twin’s co-twin report of her schooling. Very similar results have also obtained by Behrman et al. (forthcoming) using data on Danish twins. While the within-MZ regression that underlies this result relies on an assumption that individual-specific “shocks” to schooling affect health only through schooling (i.e., the assumption that eyx = 0), it seems unlikely that the near-zero coefficient estimate in the within-MZ model is caused by a violation of this assumption. In particular, the most plausible violation of this assumption are individual-specific “shocks” such as an accident that affect schooling and health in the same direction (which would imply eyx > 0). Examples of such shocks are accidents that disrupt schooling and have long-term health consequences. If the true effect of schooling and health were positive, and in violation of the model assumptions eyx were positive (instead of eyx = 0) because such shocks are important, the within-MZ estimate would be biased upwards. This upward bias, however, is inconsistent with an within-MZ point estimate of almost zero if the true effect of schooling on health were positive.
This finding of a close-to-zero coefficient in the within-MZ analyses of schooling and health hence raises questions about the usual attribution to schooling of substantial positive effects on health-related behaviors and outcomes and the existence of an important causal schooling–health gradient. In terms of causal effects, despite the strong associations with schooling, the real strati-fication appears to be with regard to social and genetic endowments. “Better” endowments, thus, apparently tend to lead to more schooling and better self-reported health, and the resulting positive association between schooling and health does not appear to reflect causal effects of schooling towards improved health in the population studied here.
In contrast to the above findings for health, the within-MZ results in Table 8 suggest a significant effect of own schooling on schooling of a twin’s first spouse: a 1 SD increase in the twin’s own schooling would on average imply a .26 SD increase in the schooling of the first spouse. The presence of measurement error in schooling, which is exacerbated in within-MZ analyses, implies that this estimate might be biased downwards. Consistent with this expectation, the within-MZ analyses that control for measurement error find a somewhat stronger effect of .28 of own schooling on that of the first spouse. In both cases, however, the within-MZ analyses provide an estimate of the effect of own schooling on spouse education that is substantially below the association of .51 that is suggested by the OLS estimates. This finding therefore suggests that the cross-sectional association between own and spouse’s schooling results to a substantial extent from assortative mating on endowments: both own and spouse’s schooling are affected by unobserved social and genetic endowments that tend to move own and spouse’s schooling in the same direction. For example, if there is positive assortative mating in the marriage market on aspects such as “ability” or “motivation”, or if sorting on unobserved dimensions such as parents’ socioeconomic status, own and spouse’s schooling would tend to be correlated as a result of correlated endowments and OLS analyses are biased upwards. Consistent with such assortative mating on schooling-related endowments, the OLS estimate in Table 8 is between 80–95% above the estimated within-MZ effect of own schooling on spouse’s schooling, and arguably, the within-MZ estimates provide a better estimate of the causal effect of own on spouse’s schooling that suggests that a 1 SD increase in own schooling implies a .26–.28 SD increase in spouse’s schooling. Behrman and Rosenzweig (2002) report similar results.
The final set of our within-MZ analyses considers the relationship between schooling and fertility, where the within-MZ analyses suggest that a 1 SD increase in own schooling for women reduces fertility by about .24 SD. This estimate remains essentially unchanged if co-twin reports are used to control for measurement error in schooling. Moreover, the reduction in fertility as a result of schooling that is suggested by the within-MZ analyses is only marginally larger in magnitude than the association obtained from a OLS analyses of fertility and schooling, suggesting that unobserved social and genetic endowments affecting schooling are only weakly associated with the social/genetic endowments that affect (completed or near-completed) fertility.
In assessing this estimate of the negative effect of schooling on fertility that is revealed by the within-MZ estimate in Table 8, the possible robustness—or not—of the results with respect to the assumption eyx = 0 of the within-MZ model is an important consideration. In the context of fertility, individual-specific shocks that affect schooling and fertility in the opposite direction might be expected, such as for example, an unintended pregnancy during high-school/college education or an “unexpectedly” early marriage that disrupts schooling. In terms of our empirical model, if these and similar shocks are important determinants of both schooling and fertility, the path coefficient eyx would be negative in violation of the within-MZ model assumptions. As a result, the within-MZ estimate of the reduction in fertility as a result of schooling would be biased towards zero, and the true effect of schooling on fertility would be more negative than suggested by the within-MZ analyses.
The combination of instrumental variable estimation with within-MZ analyses is one strategy to explore the potential importance of a non-zero eyx path on the estimation results, provided that there is an instrumental variable(s) that predicts schooling, but affects fertility only through its effect on schooling. In the Minnesota Twins Data that are used in this paper, one possible instrument that predicts schooling and, arguably affects fertility only through schooling, is birth weight. Previous studies using within-MZ twins have found significantly effects of birth weight on schooling, though they have not addressed the question of possible direct effects on fertility beyond any indirect effects through schooling (Almond et al. 2005; Behrman and Rosenzweig 2004; Conley et al. 2003). The impact of birth weight on schooling arguably differs depending on various parental characteristics, such as mother’s age or whether mothers died before the child reached adulthood. Therefore we also interact birth weight with mother’s age at birth of the twins and an indicator variable for whether a twin’s mother died before the twins reached age 20. It is important to notice that the instruments—birth weight and its interactions with mother’s age at the birth of the twins and maternal mortality—are likely to be correlated with the social and genetic endowments of the twins. The instruments would therefore be not acceptable in standard IV analyses that do not control for endowments, but they may constitute valid instruments in within-MZ IV analyses because social and genetic endowments are controlled.
In our application using the Minnesota Twins Registry data, birth weight and its interactions significantly predict the z-score of schooling (as well as schooling directly), with the F(3,333)-statistic of the first-stage fixed-effect regression equal to 2.62 (p = .05) and the instruments explaining 2.3% of the within-MZ variation in schooling. While the F-statistic is statistically significant, a better predictive power of the instruments in the first-stage regression would clearly be desirable and our analyses are potentially subject to concerns about weak instruments (Staiger and Stock 1997; Stock 2010; Stock and Yogo 2002). But since finding suitable instruments that predict schooling differences among MZ twins is often challenging, as is the case in our application using the Minnesota Twins Registry data, we present our within-MZ IV analyses that allow an assessment of the potential biases that are incurred if the assumption of eyx = 0 is violated with an important cautionary note about potential concerns about weak instruments.
Table 9 presents the within-MZ IV regression results for the effect of schooling on fertility, using birth weight and its interactions as instruments for schooling in the within-MZ analyses. Clearly, the precision of the estimate for the effect of schooling substantially declines in the within-MZ IV estimates, in part due to the weak first-stage instruments. At the same time, the within-MZ IV estimate of the effect of schooling on fertility is about 0.84, suggesting that the reduction in fertility as a result of increased schooling might be substantially larger than is suggested by the within-MZ analyses (without IV). In particular, taking the within-MZ IV estimate in Table 9 at face value suggests that a 1 SD increase in schooling for women in the study population reduces fertility by about .84 standard deviation, about 3.5 times the effect indicated by the within-MZ analyses without instrumenting. This substantial increase in the magnitude of the fertility-reducing effect of schooling in the within-MZ IV estimates would be consistent with a considerable importance of individual-specific shocks—such as unintended early pregnancies—that affect schooling and fertility in opposite directions.
Table 9.
The effect of schooling on fertility: Within-MZ IV analyses
p-values:
p < .01,
p < .05,
p < .1. Notes: Instruments for schooling include birth weight (z-score) and interactions between birth weight and (a) mother’s age at birth of the twins and (b) an indicator that the twins’ mother died before the twins reached age 20. The within-MZ model is re-estimated for the same set of respondents for whom the instruments are available.
In summary, the different within-MZ analyses in Tables 8 and 9 illustrate a broad spectrum of results that are obtained from such analyses: For the relationship between schooling and health, the analyses suggest that the true effect of schooling on health might be zero, and that the observed strong association between schooling and health might the result of stratification on endowments that jointly affect schooling and health. Neither measurement error in schooling nor the presence of individual-specific shocks that jointly affect schooling and health are likely explanations for this finding. For schooling of the first spouse, which is an important indicator of marriage market outcomes, our within-MZ analyses show that more own schooling is likely to imply also substantially more schooling of the spouse. With controls for measurement error, our analyses suggest that a 1 SD increase in own schooling increases schooling of the spouse by about .28 SD. But our analyses also point to the presence of assortative mating on social and genetic endowments. In particular, these assortative mating processes imply that the cross-sectional association between own and spouse’s schooling is substantially higher—nearly 80% higher in our analyses—than the effect that is found in the within-MZ analyses. Finally, for fertility, both our OLS and within-MZ analyses in Table 8 point to an important reduction of fertility as a result of increased schooling. Because the within-MZ results might be an underestimate of the true reduction of fertility that is implied by more schooling, we use within-MZ IV analyses to explore the potential importance of individual-specific shocks that affect schooling and fertility in opposite directions. While we emphasize a cautionary note about possibly weak instruments in these analyses, the within-MZ IV results suggest a substantially larger reduction in fertility as a result of increased schooling than do the within-MZ analyses without instrumenting. This pattern suggests that, in the context of assessing the relationship between schooling and fertility, potential individual-specific shocks—such as unintended early pregnancies—that affect schooling and fertility in opposite directions might be an important aspect that cannot be ignored in within-MZ analyses.
8.2 ACE analyses for the relationship between schooling and health, spouse’s schooling and fertility
A limitation of the above within-MZ analyses is that they are not very informative about the nature of endowments, and the pathways of how genetic and social endowments affect the relationship between a twin’s schooling and the outcomes health, spouse’s schooling and fertility. In Tables 10–12 we therefore present univariate and multivariate ACE models for these phenotypes, including ACE-β models that are closely related to the within-MZ analyses discussed above. For each table, all analyses (with the exception of the instrumental variable model for fertility in Table 12) are estimated on the same sample so that differences in the estimates across the models are not the result of different samples. We also continue to use z-scores for all variables to remove secular cohort/age trends in the outcomes and to make the estimated model coefficients more comparable across different specifications and outcome variables.
Table 10.
Univariate, bivariate ACE and ACE-β models for schooling and health (z-scores)
| Univariate ACE | Bivariate ACE | ACE-β | ACE-β with Meas. Err. | ||
|---|---|---|---|---|---|
| Model | (1) | (2) | (3) | (4) | |
| axx | 0.678** (0.069) | 0.681** (0.067) | 0.681** (0.067) | 0.603** (0.064) | |
| ayx | — | 0.044 (0.099) | 0.031 (0.127) | 0.055 (0.156) | |
| ayy | 0.537** (0.127) | 0.534** (0.079) | 0.534** (0.079) | 0.549** (0.123) | |
| cxx | 0.439** (0.098) | 0.436** (0.096) | 0.436** (0.096) | 0.524** (0.07) | |
| cyx | — | 0.271* (0.131) | 0.263* (0.127) | 0.186 (0.118) | |
| cyy | 0.267 (0.213) | 0.000 (0.576) | 0.000 (0.58) | 0.124 (0.483) | |
| exx | 0.580** (0.020) | 0.579** (0.020) | 0.579** (0.020) | 0.466** (0.020) | |
| eyx | — | 0.011 (0.039) | — | — | |
| eyy | 0.821** (0.027) | 0.820** (0.026) | 0.820** (0.026) | 0.819** (0.027) | |
|
| |||||
| β | — | — | 0.019 (0.067) | 0.034 (0.093) | |
|
| |||||
| γ | — | — | — | 0.982** (0.018) | |
| σ2(xo) | — | — | — | 0.13** (0.013) | |
| σ2(xs) | — | — | — | 0.075** (0.012) | |
|
| |||||
|
|
0.465 | 0.469 | 0.469 | 0.425 | |
|
|
0.195 | 0.192 | 0.192 | 0.321 | |
|
|
0.279 | 0.278 | 0.278 | 0.297 | |
|
|
0.069 | 0.071 | 0.071 | 0.055 | |
|
| |||||
| N | 1,506 | 1,506 | 1,506 | 1,506 | |
p-values (for model coefficients only):
p < .01,
p < .05,
p < .1. N refers to individuals. All variables have been converted to z-scores with mean zero and a variance of one using cohort-specific estimates of both mean and variance of each variable. The subscripts x, y indicate the variables as: x = schooling; y = self-reported health.
Table 12.
Univariate, bivariate ACE and ACE-β models for schooling and fertility
| Univariate ACE | Bivariate ACE | ACE-β | ACE-β with Meas. Err. | ACE-β with IV | ACE-β with IV & eyx:= 0 | ||
|---|---|---|---|---|---|---|---|
| Model | (1) | (2) | (3) | (4) | (5) | (6) | |
| axx | 0.68** (0.072) | 0.682** (0.072) | 0.682** (0.072) | 0.618** (0.068) | 0.721** (0.076) | 0.721** (0.076) | |
| ayx | −0.231* (0.115) | −0.073 (0.14) | −0.071 (0.15) | 0.517 (0.38) | −0.001 (0.143) | ||
| ayy | 0.611** (0.105) | 0.565** (0.108) | 0.565** (0.107) | 0.559** (0.111) | 0.458** (0.138) | 0.481** (0.126) | |
| cxx | 0.424** (0.106) | 0.421** (0.107) | 0.421** (0.107) | 0.501** (0.079) | 0.384** (0.131) | 0.384** (0.131) | |
| cyx | — | 0.094 (0.179) | 0.192 (0.162) | 0.196 (0.124) | 0.459 (0.284) | 0.155 (0.190) | |
| cyy | 0.114 (0.474) | −0.069 (0.89) | 0.069 (0.873) | 0.108 (0.532) | 0.345+ (0.184) | 0.297 (0.201) | |
| exx | 0.574** (0.021) | 0.574** (0.021) | 0.574** (0.021) | 0.471** (0.021) | 0.573** (0.022) | 0.573** (0.022) | |
| eyx | — | −0.133 (0.037) | — | — | 0.448 (0.298) | 0† | |
| eyy | 0.745** (0.026) | 0.733** (0.026) | 0.733** (0.026) | 0.734** (0.026) | 0.742** (0.027) | 0.742** (0.027) | |
|
| |||||||
| β | — | — | −0.232** (0.064) | −0.275** (0.088) | −1.025* (0.512) | −0.265** (0.068) | |
|
| |||||||
| δ | — | — | — | — | 0.126** (0.045) | 0.126** (0.045) | |
| γ | — | — | — | 0.972** (0.019) | — | — | |
| σ2(xo) | — | — | — | 0.114** (0.013) | — | — | |
| σ2(xs) | — | — | — | 0.08** (0.012) | — | — | |
|
| |||||||
|
|
0.476 | 0.478 | 0.478 | 0.446 | 0.515 | 0.515 | |
|
|
0.185 | 0.183 | 0.183 | 0.294 | 0.144 | 0.144 | |
|
|
0.397 | 0.395 | 0.395 | 0.393 | 0.280 | 0.292 | |
|
|
0.014 | 0.014 | 0.014 | 0.016 | 0.099 | 0.090 | |
|
| |||||||
| N | 1,364 | 1,364 | 1,364 | 1,364 | 1,188 | 1,188 | |
p-values (for model coefficients only):
p < .01,
p < .05,
p < .1. N refers to individuals. All variables have been converted to z-scores with mean zero and a variance of one using cohort-specific estimates of both mean and variance of each variable. The subscripts x, y indicate the variables as: x = schooling; y = fertility. The instrument for schooling used in the extended ACE IV model is a linear combination of a twin’s birth weight and the interaction of birth weight with the mother’s age at the birth of the twins and an indicator of whether the twin’s mother died before the twins reached age 20. The weights for this linear combination were obtained from a within-MZ fixed-effect regression of schooling on birth weight and its interactions (i.e., the first-stage regression of the within-MZ IV approach).
The coefficient eyx in Model 6 is set to zero.
The univariate ACE model (Model 1) for the z-score of schooling (coefficients axx, cxx, and exx) in Table 10 indicates that schooling is strongly influenced by genetic endowments, resulting in a heritability estimate for schooling of about 47% ( ), with an important influence of social endowments (shared environments) that is consistent with about 20% of the variation in schooling in this study population ( ). Self-reported health, on the other hand, is less affected by social or genetic endowments. In particular, the univariate ACE model for health (coefficients ayy, cyy, and eyy in Table 10) suggests that about 28% of the variation in self-reported health is related to genetic endowments ( ), while 7% of the variation stems from social endowments such as parental characteristics ( ). Almost two thirds of the variation in self-reported health is attributed in the univariate ACE model to individual-specific factors that are not shared by twins.
The bivariate ACE model for schooling and heath (Model 2 in Table 10) provides the same estimates for the heritability (h2) and the variance contribution from social endowments (c2) for these outcomes, but it points to more complex underlying processes that shape the observed relationship between schooling and health. Most importantly, the bivariate ACE model suggests that an important source for the observed association between schooling and health stems from the fact that social endowments—e.g., parental characteristics or socioeconomic status—that affect schooling in early adulthood have long-term influences on self-reported heath. The coefficient of cyx = .27 in this model, for example, implies that about 76% of the observed correlation between schooling and health results from social endowments that are shared between twins, with genetic factors contributing about 19% to the observed correlation. Moreover, after accounting for the extent to which endowments jointly affect schooling and health, there are no unique contributions of social endowments to subjective health and the coefficient cyy is estimated to be insignificantly different from zero. The very small estimate for eyx suggests that individual factors affecting schooling are not associated with health once the endowments are controlled.
The ACE-β model (Model 3 in Table 10), which includes the possibility of a direct of effect β of schooling on health, confirms the findings of our earlier within-MZ analyses of the schooling–health relationship and also does not suggest a relevant direct effect of schooling on health after the influence of endowments is accounted for.
The ACE-β model with measurement error (Model 4) additionally identifies that schooling reports include some measurement error, with measurement error contributing 13% to the variance of own schooling and 8% to the variance in the co-twin’s report of schooling. Controlling for measurement error in schooling reduces somewhat the estimate for heritability of the “true” unobserved schooling of the twins, and it suggests social endowments contribute about 32%—about 50% more then the ACE-β model without measurement error—to the variation in schooling. But similar to our earlier within-MZ analyses, controlling for measurement error does not affect the conclusion of our analyses that there does not seem to be a direct effect of schooling on health in this study population.
Table 11 presents the different ACE analyses for the relationship between own schooling and schooling of the first spouse. The univariate ACE results for the subset of ever-married twins suggest a somewhat higher heritability and lower variance contribution of social endowments than found in our earlier analyses. For the schooling of the first spouse, the univariate ACE model (Model 1 in Table 11) suggests a “heritability” of 32%, implying that about a third of the variation in spouse schooling is related to genetic endowments that are shared by the twins and indicating a substantial extent of assortative mating on genetically determined traits (for related studies of assortative mating, see Buss 1984, 1985; Eckman et al. 2002; Schwartz and Mare 2005).
Table 11.
Univariate, bivariate ACE and ACE-β models for (own) schooling and schooling of first spouse
| Univariate ACE | Bivariate ACE | ACE-β | ACE-β with Meas. Err. | ||
|---|---|---|---|---|---|
| Model | (1) | (2) | (3) | (4) | |
| axx | 0.678** (0.084) | 0.577** (0.078) | 0.577** (0.078) | 0.559** (0.07) | |
| ayx | — | 0.257* (0.114) | 0.156 (0.135) | 0.087 (0.142) | |
| ayy | 0.547** (0.133) | 0.286* (0.124) | 0.286* (0.124) | 0.296* (0.118) | |
| cxx | 0.31+ (0.165) | 0.456** (0.088) | 0.456** (0.088) | 0.485** (0.076) | |
| cyx | — | 0.491** (0.099) | 0.412** (0.093) | 0.376** (0.092) | |
| cyy | 0.337+ (0.188) | 0.000 (0.162) | 0.000 (0.162) | 0.000 (0.163) | |
| exx | 0.56** (0.025) | 0.574** (0.026) | 0.574** (0.026) | 0.447** (0.026) | |
| eyx | — | 0.101* (0.044) | — | — | |
| eyy | 0.708** (0.031) | 0.719** (0.03) | 0.719** (0.03) | 0.717** (0.029) | |
|
| |||||
| β | — | — | 0.175* (0.076) | 0.254* (0.109) | |
|
| |||||
| γ | — | — | — | 0.996** (0.024) | |
| σ2(xo) | — | — | — | 0.121** (0.014) | |
| σ2(xs) | — | — | — | 0.072** (0.013) | |
|
| |||||
|
|
0.529 | 0.383 | 0.383 | 0.418 | |
|
|
0.111 | 0.239 | 0.239 | 0.315 | |
|
|
0.327 | 0.162 | 0.162 | 0.153 | |
|
|
0.124 | 0.264 | 0.264 | 0.272 | |
|
| |||||
| N | 890 | 890 | 890 | 890 | |
p-values (for model coefficients only):
p < .01,
p < .05,
p < .1. N refers to individuals. All variables have been converted to z-scores with mean zero and a variance of one using cohort-specific estimates of both mean and variance of each variable. The subscripts x, y indicate the variables as: x = schooling; y = schooling of first spouse. The analyses include only twin pairs in which both twins are ever-married and data on schooling of the first spouse are available.
The bivariate ACE model for spouse’s schooling (Model 2 in Table 11) indicates that there is a substantial overlap in the latent social and genetic endowments affecting own and spouse’s schooling. For example, the coefficient estimates of ayx = .26 and cyx = .49 suggest that about 34% of the observed correlation between own and spouse’s schooling is due to genetic endowments that affect both own schooling and spouse’s schooling through assortative mating, and 52% of the correlation is due to social endowments that affect both own and spouse’s schooling. After accounting for overlapping influences of social and genetic endowments, the bivariate ACE model no longer identifies social endowments that affect spouse’s schooling only, while there remain important genetic endowments that affect spouse’s schooling but not own schooling. All in all, the bivariate ACE model suggests somewhat lower heritabilities for both own and spouse’s schooling than the univariate ACE model, while social endowments make a somewhat stronger contribution to the variation in own and spouse’s schooling.
While the ACE-β model (Model 3 in Table 11) provides similar estimates for heritability h2 and the variance contribution of social endowments (c2) for both own and spouse’s schooling, the ACE-β model that allows for a direct effect of own schooling on spouse’s schooling suggests a different story regarding the underlying processes that lead to the observed association between own and spouse’s schooling. Foremost, and similar to the within-MZ analyses earlier in this paper, the ACE-β model (Model 3) suggests that an increase in own schooling has a direct effect on the spouse’s schooling. This effect is sizable in that a 1 SD in own schooling implies a .18 SD increase in spouse’s schooling in our analyses without controls for measurement error, and a .25 SD increase in the spouse’s schooling once measurement error is controlled.
Once this direct effect of own on spouse’s schooling is allowed, the ACE-β models (Models 3 and 4 in Table 11) reveal a different explanation than the bivariate ACE model about the underlying processes that lead to the pronounced association between own and spouse’s schooling that is well documented in many populations. Focusing on the ACE-β model with measurement error (Model 4), where these changes in interpretation are most clearly expressed, the introduction of a direct pathway β from own to spouse’s schooling leads to a substantial drop in the coefficient ayx that measures the extent to which the genetic endowments that a twins own schooling directly affect the schooling of the spouse. In contrast, the bivariate ACE model for the relationship between own and spouse’s schooling (Model 2) suggested that this effect is sizable and importantly contributes the observed covariance between these outcomes. The results of the ACE-β model (Model 4), however, imply that this pathway is relatively unimportant. In particular, while the ACE-β model with measurement error suggests that about 30% of the correlation between the unobserved “true” own schooling and spouse’s schooling is due to genetic factors, the primary pathway operates through schooling: the genetic endowments are an important source of variation in a twin’s own schooling, and these genetic factors affect spouse’s schooling primarily through the effect on twin’s own schooling. Specifically, in the ACE-β model with measurement error, only 11% of the correlation between own and spouse’s schooling is attributed to a direct effect of the genetic endowments for own schooling on spouse’s schooling, while 19% are due the indirect pathway in which affects a twin’s own schooling, and spouse’s schooling only through the effect on own schooling. Shared environmental factors that affect schooling account for about 57% of the correlation between own and spouse’s schooling, and three quarters of this contribution are accounted for by the direct effect cyx on spouse’s schooling of the social endowments for own schooling .
In terms of assortative mating in the marriage market, the bivariate and ACE-β model present two different scenarios (see also Behrman et al. 1994). The bivariate ACE model (Model 2) suggests strong assortative mating on unobserved genetic and social endowments—including for example aspects such as ability, personality characteristics, parental socioeconomic status—that directly affect a twin’s own schooling, and via assortative mating on these characteristics, also spouse’s schooling. In contrast, the ACE-β model (Models 3 and 4) emphasizes a direct effect β of own schooling on spouse’s schooling that may arise due to social processes such as assortative mating on observed schooling (rather than the latent determinants of schooling), bargaining in the marriage market where own schooling affects the ability to attract more-schooled spouses, or a marriage search process where educational institutions are an important source of potential partners. The results of Model 4 that control for measurement error, for example, imply that a 1 SD increase in own schooling increases spouse’s schooling by 1/4 SD. Once this direct effect of own on spouse’s schooling is accounted for, the ACE-β model suggests a substantially reduced extent of assortative mating on genetic endowments that affect a twin’s own schooling (such as for example genetic factors underlying ability). The ACE-β model continues to attribute a substantial fraction of the observed correlation between own and spouse’s schooling to social endowments that affect a twin’s own schooling (e.g., parental socioeconomic status), but to a lesser extent than is suggested in the bivariate ACE model because the bivariate ACE model does not allow for the possibility that these social endowments affect the spouse’s schooling through the twin’s own schooling.
Table 12 presents the results of our different ACE models for the relationship between schooling and fertility. The negative relationship between schooling and fertility, especially for women, has been widely documented across many populations (e.g., Kravdal and Rindfuss 2008) and the determinants and changes of this negative schooling–fertility relation have been the topic of extensive investigations (Kohler and Rodgers 2003).
The univariate ACE analyses of fertility (Model 1 in Table 12) yield an estimate of heritability h2 for fertility of about 40%, with social endowments providing a negligible contribution to the variation in (completed/near-completed) fertility. These conclusions from the Minnesota Twins Registry data are similar to findings obtained from Danish twins data and NLSY data (Rodgers and Doughty 2000; Rodgers et al. 2001a,b). In its univariate form, however, the ACE model is not informative about the processes that contribute to the negative association between schooling and fertility. To explain the observed negative association between schooling and fertility, the bivariate ACE model (Model 2 in Table 12) points in particular to the genetic endowments of schooling that exert a strong negative influence on fertility ayx = −.23. This model would therefore suggest that genetic factors that tend to increase schooling—e.g., the genetic factors affecting ability—have a direct negative effect on fertility through the path ayx. In addition, the bivariate ACE model suggests that individual-specific shocks to schooling have a strong direct effect on schooling (eyx = −.13), for instance, in the form of an unintended pregnancy that disrupts schooling and leads to an overall increase in completed fertility.
The limitation of this model that there is no direct effect of schooling on fertility is avoided in the ACE-β model (Model 3) that estimates a coefficient β suggesting that a 1 SD increase in schooling reduces fertility by .23 SD, which is very similar to our earlier results obtained from within-MZ analyses. Controlling for measurement error in schooling (Model 4) increases this negative effect of schooling on fertility to −0.27. Most importantly, and in contrast to the bivariate ACE model, the coefficient ayx in the ACE-β model with measurement error has become insignificant and small in magnitude, suggesting that the genetic factors affecting schooling ( ) do not affect fertility directly, but primarily indirectly through their effect on schooling.
The ACE-β IV model, which uses birth weight in interaction with mother’s age at the birth of twins and maternal mortality as instruments for schooling, provides a test of the assumption eyx = 0 that underlies the within-MZ and the ACE-β model. The ACE-β IV model (Model 6 in Table 12) provides an estimate of β = −1.02 that is very similar to our earlier within-MZ IV estimate in Table 9 and substantially larger than the effect of schooling on fertility that is estimated by the ACE-β model (Models 4 and 5 in Table 12). While there are some concerns about possibly weak instruments in these analyses that we recognize but cannot resolve with the data used for the analyses in this paper, the ACE-β IV analyses (Model 5) show that the null-hypothesis of eyx = 0 cannot be rejected. In the final column of Table 12 (Model 6) we therefore re-estimate the ACE-β IV model with the coefficient eyx constrained to zero. This final model, which is our preferred specification for the ACE-β IV model for the schooling–health relationship—suggests that a 1 SD increase in schooling reduces fertility by about .26 SD, which is an effect that is about 15% larger in magnitude that suggested by the ACE model without measurement error correction (Model 3). In addition, the final ACE-β IV estimates (Model 6) confirm our earlier conclusions that, once direct effects of schooling on fertility are allowed in the model specification, there is no longer evidence that the genetic endowments for schooling ( ) have a direct effect on fertility, and instead, these endowments affect fertility primarily through schooling, and through this pathway, account for about three-quarters of the negative association between schooling and fertility in the data.
Acknowledgments
We are grateful for the many helpful comments and suggestions provided by Jason Boardman, Joseph Rodgers and the participants of the Boulder conference. We also gratefully acknowledge the generous support for this research through NIH grants RO1 HD046144 and RO1 HD043417.
Appendix
A.1 Measurement error model
To formally represent measurement error in the ACE-β model (Figure 6, we distinguish between the “true”—but unobserved—values of the phenotypes, which are denoted as , and the observed phenotypes that are denoted as P. If the concern is particularly with respect to measurement error in schooling x, and the data contain both a twin’s own report of schooling, denoted , and a twin’s sibling’s report of his/her schooling, denoted , then the observed data for each twins pair can be written as . Moreover, the observed data P is related to the latent phenotypes P* as
| (23) |
where
and GME is a vector containing the random “measurement error component” in own and sibling’s report of schooling that is given as .
The variance/covariances among the observed phenotypes is then given as
| (24) |
| (25) |
where Var(GME) is variance of the random measurement error in own and sibling’s report of x that, due the assumption of independent measurement error across twins, is given by Var(GME) = ε[GMEGME′] = Diag(Var(eo), Var(es), 0, Var(eo), Var(es), 0).
A.2 Social interactions in the ACE-β model
Social interaction between twins within the same twins pair can be captured by modifying the matrix B in the ACE-β model to reflect both the effect of schooling x on fertility y as well as the interaction between the twins. We focus first on social interaction that affects the schooling attainment x. Similarly to the economic fixed-effects model, where we discussed social interactions in Section 4.4, interaction with respect to x between twins is represented by modifying the relation for the first phenotype x in Eq. 13 as follows:
| (26) |
where s (with |s| < 1) is the social interaction parameter. Stacking the observed phenotypes as P = (x1j, y1j, x2j, y2j)′, and redefining the matrix B to include the social interaction parameter s as
| (27) |
the relationships (18–19) continue to hold. Social interaction in the ACE-β model is therefore straight forward to implement, and the variance-covariance matrix of the observed phenotypes P can be obtained from Eqs. (18–19), using the matrix B as specified in Eq. (27). Since the inverse of I4 – B in this case is given by
which is no longer block-diagonal as in the ACE-β model without social interaction Eqs. (18), (19)) and (27) imply that MZ and DZ twins will have a different variance of x whenever s ≠ 0 (see also Table 5). This fact allows the ACE-β model to not only estimate the causal effect β of schooling x on fertility y, but also the extent s to which social interactions affect schooling.
Social interaction with respect to the primary outcome, fertility y, can be incorporated into the ACE-β model by specifying the matrix B as
| (28) |
Following similar steps as in the case of social interactions with respect to schooling x, the variance-covariance matrix of the observed phenotypes P can be obtained from Eqs. (18–19), using the matrix B as specified in Eq. (28). Because social interactions with respect to y imply a different variance of y for MZ and DZ twins, the parameter s can be estimated along with the other model parameters.
A.3 Instrumental variable estimation in the ACE-β model
The path-diagram for the instrumental variable estimation in the ACE-β model, which is given in Figure 8(b) for the case where the instruments are possibly correlated with the genetic and social endowments, can be obtained by stacking the observed phenotypes as P = (x1j, y1j, z1j, x2j, y2j, z2j,)′. We can then represent the ACE-β model with instrumental variables as
where
and
With the above notation, the variance/covariances among the observed phenotypes z, x and y can be written—similar to the ACE-β model in Eqs. (18–19)—as
| (29) |
| (30) |
where A = LaLa′, C = LcLc′, and E = LeLe′ and
| (31) |
| (32) |
Footnotes
An earlier version of this paper was presented at the conference on “Integrating Genetics and the Social Sciences” in Boulder, CO, June 2–3, 2010.
While not the focus of our discussion here, it is important to point out that there have been many other uses of twins data in the social sciences. Historically, for example, the predominant use probably has been for univariate heritability estimates of the ratio of genetic variance to phenotypic variance in a linear model. Also in economics the combination of identical and fraternal twins has been used to investigate how intrafamilial allocations (say, of schooling among children) respond to individual-specific endowments (e.g., Behrman et al. 1994). The birth of twins has also been used to represent unexpected increases in fertility and to estimate quantity-quality fertility models and to study the consequences of fertility on other life-course outcomes (Rosenzweig and Wolpin 1980a,b). Behrman, Kohler and Schnittker (2010) provide a comprehensive treatment of twins methods for social scientists that includes both conceptual and methodological discussions that are beyond the scope of this paper.
An extensive literature exists that discusses these assumptions and the potential implications of violations of these assumptions (e.g., Behrman et al. 2010; Derks et al. 2006; Guo 2005; Hobcraft 2003; Plomin et al. 2005). There also exist several ways to test or relax these assumptions if additional data are available (e.g., Behrman et al. 2010; Neale and Maes 2004; Plomin et al. 2005), including for example the incorporation of assortative mating if data on spouses is available, or the consideration of dominance genetic effects if additional sibling categories (half siblings, adopted children) are available.
See for instance Behrman and Wolfe (1987); Chamberlain and Griliches (1977); Griliches and Mason (1972); Hauser and Wong (1989) and Warren et al. (2002).
See Behrman and Taubman (1976) and Behrman et al. (1980) for early work on this issue.
This point holds even if some random assignment (e.g., of incentives for attending school) is used as an instrument to attempt to identify the impact of schooling x on fertility y. Such identification occurs only under the assumption that the random assignment does not affect the outcome y through other channels (e.g., financial wealth accumulation) than through x.
For a critical discussion of this key assumption, see Griliches (1979) and Bound and Solon (1999).
In addition, since siblings other than twins are of differential ages, the argument of sibling models that within-sibling estimates control for all relevant social endowments so that the path eyx in Figure 1 can reasonably be assumed to be zero is weaker than in the case of twins who are born at the same time and thus share factors such as parents’ ages, socioeconomic conditions, etc., all at the same age.
More generally, can also represent the effect of any other sibling’s specific endowments on i’s schooling attainment.
If the correlation in measurement error between siblings (ρε) is nonzero, , where ϕ = (1 − ρw)/(1 − ρx). Note that the measurement error bias in the within-sibling estimate is decreasing in ρw and is less in the within-sibling estimate than in the standard estimate if ρw > ρx. We are not aware of any estimates of ρw. But what appears to be random noise in cross-sectional data may have a family component if the measurement error is due to such unobserved factors as exaggeration or modesty or to failure to control for school quality, all of which may be shared by siblings.
Ashenfelter and Krueger also find that correcting for measurement error leads to larger estimates than found by conventional ordinary least squares models. Behrman, Rosenzweig and Taubman and subsequent studies using this method have yielded measurement-error corrected estimates that are usually less than the OLS estimates, suggesting that conventional cross-sectional estimates of the schooling-wage association are, in any case, too large.
For a detailed discussion of this ACE model and similar approaches for the study of twins and families, see for example Neale and Maes (2004).
The ACE model can be fit using any structural equation program, but some programs are better for samples of relatives. Mx (and more recently, its successor OpenMx) is perhaps the single most popular program for estimating behavioral genetics models, but other programs have functions that are also well-suited (Neale et al. 2006; OpenMx Development Team 2010). On their webpage, for example, M-Plus provides example scripts for assorted models using twins, including those discussed here. Likewise LISREL scripts are provided in Neale and Cardon (1992).
The ACE model can easily be generalized to other relatives by focusing on the correlation among the A factors, as for example, parents and offspring share 50% of genes, half siblings 25%, first-cousins 12.5%, and so on. Such models also require making assumptions regarding C, which are less definitive than assumptions regarding A. Identifying genetic influences also requires relatives who differ in their level of shared genetic variance, which means that surveys in which all members of a household are interviewed are usually not sufficient for calculating heritability, as the expected child-parent and child-child correlations are all 0.5.
The equal environments assumption requires that environmentally caused similarity for a particular phenotype be the same for both MZ and DZ twins and, thus, that the shared environment correlation between twins be identical for both types of twins. While some critics argue that this assumption is regularly and severely violated (Richardson and Norgate 2005), the validity of this assumption needs to be evaluated in the specific context. Empirical tests of the equal environment assumption often provide support for the acceptability of this assumption. According to the critics, for example, MZ twins experience more similar environments than DZ twins, thereby inflating differences between the two types of twins and, in turn, inflating estimates of heritability. In response to such concerns, the validity of the equal environments assumption has been evaluated using mislabeled twins (twins labeled DZ when they are in fact MZ) or and MZ twins who are in fact treated differently (Scarr 1968). Both methods rely on the idea that MZ twins who are treated more individually should show more differences than those who are treated more similarly. Studies using both methods provide evidence for the validity of the assumption. Physical similarity, for example, is unrelated to twin similarity in personality (Morris-Yates et al. 1990; Plomin et al. 1976) and concordance on many psychiatric disorders, with the notable exception of bulimia (Hettema et al. 1995). Plomin et al. (1976) find evidence that MZ twins who resembled each other more were less similar in personality, leading to a downwardly biased estimate of heritability. Kendler et al. (1993) explore concordance for several common psychiatric disorders as a function of real zygosity, as revealed by biological tests, and perceived zygosity, as reported by twins or their families. In their study, 15% of twin pairs (one or both members) disagreed with the zygosity assigned by investigators, but perceived zygosity had no bearing on concordance for psychiatric disorders, including three disorders commonly studied by sociologists (i.e., major depression, generalized anxiety, and alcoholism).
In addition to additive genetic factors, the model can easily be modified to include dominance effects; in standard twins data, however, additive genetic contributions cannot be distinguished from dominance genetic effects, except under the restrictive assumption of no shared environmental influences, and our discussion therefore focuses on the additive genetic model; for a more extensive discussion of how additive and dominance genetic influences can be incorporated in twins and sibling analyses, see Neale and Maes (2004).
Twins data that include information about the characteristics of spouses can potentially identify the extent of assortative mating and can include this aspect explicitly in the analyses (see Neale and Maes 2004). In addition, the assumption of no assortative mating in behavioral genetics analyses tends to be “conservative” in the sense that estimates of heritability in traditional behavioral genetics analyses will be biased towards zero if there is positive assortative mating.
In addition to the structural equation (ACE) approach to estimating heritability, DeFries and Fulker (1985) propose a method of estimating heritability (h2) and common environmental influences (c2) with twins data by a simple linear regression of a twin’s trait on the co-twin’s trait and the degree of genetic relatedness (see also Kohler and Rodgers 2000). In addition, several extensions of DeFries-Fulker (DF) analyses have been proposed that allow the consideration of genetic non-additivity (Waller 1994), observed differences in non-shared environment (Rodgers et al. 1994), and binary or censored observations (Kohler and Rodgers 1999).
This specification is also sometimes referred to as the Cholesky decomposition because it is based on a decomposition of the variance-covariance matrix into lower triangular matrices that is known as the “Cholesky decomposition”.
The presentation of the bivariate ACE model uses the “Cholesky decomposition approach” of presenting this model; while this is the most frequently used bivariate ACE specification, there are other specifications of the latent genetic and social endowments that are observationally equivalent (Neale and Cardon 1992; Neale and Maes 2004).
In order to identify β in the ACE-β model in Figure 4, additional moment conditions that link x (schooling) on the outcome y within the same individual would be required; while an extended ACE framework that adds additional sibling relationships (half-sibs, cousins, etc.) allows to identify more complex genetic models (e.g., see Neale and Maes 2004), these additional sibling categories do not provide additional moment conditions linking x and y within individuals that provide identification of the causal pathway β between x (schooling) on the outcome y in the ACE-β model in Figure 4.
In Figure 4, the condition of distinct latent influences (endowments and individual specific factors) for both x and y implies that all of the coefficients ayx, cyx and eyx are equal to zero. A direction of causality model would then try to separate whether the path between x and y is directed from x to y (x → y) or vice versa (y → x).
While eyx = 0 is a plausible assumption to achieve the identification of the model parameter in the ACE-β model, it is not the only possible assumption. Alternative assumptions are cyx = 0 or ayx = 0.
Although the path β might be seen in the ACE-β framework as absorbing the influence of the individual-specific factors along the cross-path eyx in the conventional ACE model, the interpretation of the two approaches is fundamentally different and the two specifications imply different moment conditions (see below) and can result in different estimates for all model parameters. In the ACE-β framework, β measures the direct causal effect of schooling (xij) on fertility (yij), and all individual-specific shocks to schooling affect fertility only through schooling. In the conventional ACE model, eyx measures the extent to which unobserved shocks that affect schooling also have an direct effect on fertility. Distinctions of this sort are informative, and a conventional ACE and an ACE-β model can lead to very different conclusions. In the empirical illustration we provide below, for instance, we show that the negative relationship between schooling and fertility is observed within individuals is attributed in the ACE model to a negative coefficient for the path ayx, that is, to genetic factors that have a positive effect on schooling and a negative effect on fertility. In the ACE-β model, the negative association between schooling and fertility is predominantly due to a causal negative effect β of schooling on fertility. The interpretation of the ACE-β results is therefore much more consistent with the social science literature on the interrelation between schooling and fertility (e.g., Kravdal and Rindfuss 2008).
Unique environmental influences affecting schooling x, however, are assumed to have no direct effect on fertility y, and in both approaches, unique environmental influences on schooling are assumed to affect fertility only through their effect on schooling.
It is important to point out that, while the path-diagram of the children-of-twins design (D’Onofrio et al. 2003) is isomorphic to that of the ACE-β framework in Figure 5, the focus of these models is distinctly different: the children of twins design focuses on the estimation of the causal connection between parental behaviors and child outcomes, using parents who are twins to provide partial control for parental genetic endowments that also affect these child outcomes; in contrast to this intergenerational perspective, the ACE-β model focuses on behaviors/outcomes that occur across the life-course of individuals, using the twins design to control for the genetic and social endowments ( and , and and ) that affect both xij (schooling) and y (fertility).
In some cases if the data include other sibling categories in addition to twins, dominance and additive genetic effects can be estimated; also, when the data include information on spouses, aspects of assortative mating can be considered.
While this definition of heritability would be identical between the ACE-β and the bivariate ACE model, the estimated heritability would differ because both models would generally yield different parameter estimates.
This follows by solving for the variance/covariance matrix of the observed phenotype P in the ACE-β model as given in Appendix A.2.
Contributor Information
Hans-Peter Kohler, Email: hpkohler@pop.upenn.edu, Professor of Sociology, 3718 Locust Walk, University of Pennsylvania, Philadelphia, PA 19104-6299, USA.
Jere R. Behrman, Email: jbehrman@econ.sas.upenn.edu, W. R. Kenan, Jr. Professor of Economics and Sociology, 3718 Locust Walk, University of Pennsylvania, Philadelphia, PA 19104-6297, USA
Jason Schnittker, Email: jschnitt@soc.upenn.edu, Associate Professor of Sociology, 3718 Locust Walk, University of Pennsylvania, Philadelphia, PA 19104-6299.
References
- Almond D, Chay KY, Lee DS. The costs of low birth weight. Quarterly Journal of Economics. 2005;120(3):131–1083. [Google Scholar]
- Amin V. Returns to education: Evidence from UK twins: Comment. American Economic Review. 2010 forthcoming. [Google Scholar]
- Amin V, Behrman JR. Evidence from a sample of US twins. London: Economics Department, Royal Holloway College, University of London; 2010a. Do more educated women have fewer children and delay childbearing? [Google Scholar]
- Amin V, Behrman JR. Teenage motherhood and later life socioeconomic and health outcomes: Evidence from US twin studies. London: Economics Department, Royal Holloway College, University of London; 2010b. [Google Scholar]
- Amin V, Behrman JR, Spector TD. Does more schooling improve health behaviors and health outcomes? Evidence from UK twins. London: Economics Department, Royal Holloway College, University of London; 2010. [Google Scholar]
- Angrist JD, Krueger AB. Does compulsory school attendance affect schooling and earnings. Quarterly Journal of Economics. 1991;106(4):979–1014. [Google Scholar]
- Ashenfelter O, Krueger A. Estimates of the economic return to schooling from a new sample of twins. American Economic Review. 1994;84(5):1157–1173. [Google Scholar]
- Ashenfelter O, Rouse C. Income, schooling and ability: Evidence from a new sample of identical twins. Quarterly Journal of Economics. 1998;113(1):153–284. [Google Scholar]
- Bearman P. Introduction: Exploring genetics and social structure. American Journal of Sociology. 2008;114(S1):v–x. [Google Scholar]
- Behrman JR, Hrubec Z, Taubman P, Wales TJ. Socioeconomic Success: A Study of the Effects of Genetic Endowments, Family Environment and Schooling. Amsterdam: North-Holland Publishing Company; 1980. [Google Scholar]
- Behrman JR, Kohler H-P, Jensen V, Pedersen D, Petersen I, Bingley P, Christensen K. Does more schooling reduce hospitalization and delay mortality? New evidence based on Danish twins. Demography. doi: 10.1007/s13524-011-0052-1. forthcoming. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Behrman JR, Kohler H-P, Schnittker J. Unpublished book manuscript. Population Studies Center, University of Pennsylvania; 2010. Social science methods for twin data. [Google Scholar]
- Behrman JR, Rosenzweig MR. Ability biases in schooling returns and twins: A test and new estimates. Economics of Education Review. 1999;18(2):159–167. [Google Scholar]
- Behrman JR, Rosenzweig MR. Does increasing women’s schooling raise the schooling of the next generation? American Economic Review. 2002;92(1):323–334. [Google Scholar]
- Behrman JR, Rosenzweig MR. Returns to birthweight. Review of Economics and Statistics. 2004;86(2):586–601. [Google Scholar]
- Behrman JR, Rosenzweig MR, Taubman P. Endowments and the allocation of schooling in the family and in the marriage market: The twins experiment. Journal of Political Economy. 1994;102(6):1131–1173. [Google Scholar]
- Behrman JR, Rosenzweig MR, Taubman P. College choice and wages: Estimates using data on female twins. Review of Economics and Statistics. 1996;73(4):672–685. [Google Scholar]
- Behrman JR, Taubman P. Intergenerational transmission of income and wealth. American Economic Review. 1976;66(2):436–440. [Google Scholar]
- Behrman JR, Wolfe BL. How does mother’s schooling affect family health, nutrition, medical care usage, and household sanitation? Journal of Econometrics. 1987;36(1–2):185–204. [Google Scholar]
- Bishop J. Reporting errors and the true return to schooling. Madison, WI: University of Wisconsin, mimeo; 1977. [Google Scholar]
- Björklund A, Jäntti M, Solon G. Influences of nature and nurture on earnings variation: A report on a study of various sibling types in Sweden. In: Bowles S, Gintis H, Groves MO, editors. Unequal Chances: Family Background and Economic Success. Princeton, NJ: Princeton University Press; 2005. pp. 145–164. [Google Scholar]
- Bonjour D, Cherkas LF, Haskel JE, Hawkes DD, Spector TD. Returns to education: Evidence from UK twins. American Economic Review. 2003;93(5):1799–1812. [Google Scholar]
- Bouchard T, Lykken D, McGue M, Segal N, Tellegen A. Sources of human psychological differences: The minnesota study of twins reared apart. Science. 1990;250:223–228. doi: 10.1126/science.2218526. [DOI] [PubMed] [Google Scholar]
- Bound J, Solon G. Double trouble: On the value of twins-based estimation of the return to schooling. Economics of Education Review. 1999;18(2):169–182. [Google Scholar]
- Brim OG, Baltes PB, Bumpass LL, Cleary PD, et al. National survey of midlife development in the United States (MIDUS), 1995–1996. Ann Arbor, MI: Inter-university Consortium for Political and Social Research; 1996. [Google Scholar]
- Buss D. Marital assortment for personality dispositions: Assessment with three different data sources. Behavior Genetics. 1984;14(2):111–123. doi: 10.1007/BF01076408. [DOI] [PubMed] [Google Scholar]
- Buss DM. Human mate selection. American Scientist. 1985;73(1):47–51. [Google Scholar]
- Chamberlain G, Griliches Z. More on brothers. In: Taubman P, editor. Kinometrics: Determinants of socioeconomic success within and between families. New York: North-Holland Publishing Co; 1977. pp. 97–107. [Google Scholar]
- Conley D, Bennett NG. Is biology destiny? Birth weight and life chances. American Sociological Review. 2000;65(2):458–467. [Google Scholar]
- Conley D, Strully K, Bennett N. NBER Working Paper No. 9901. 2003. A pound of flesh or just proxy? Using twin differences to estimate the effects of birth weight on (literal) life chances. [Google Scholar]
- Coolidge F, Thede L, Jang K. Are personality disorders psychological manifestations of executive function deficits? bivariate heritability evidence from a twin study. Behavior Genetics. 2004;34:75–84. doi: 10.1023/B:BEGE.0000009486.97375.53. [DOI] [PubMed] [Google Scholar]
- Cutler DM, Deaton AS, Lleras-Muney A. The determinants of mortality. Journal of Economic Literature. 2006;20(3):97–120. [Google Scholar]
- Cutler DM, Lleras-Muney A. Education and health: Evaluating theories and evidence. In: House J, Schoeni R, Kaplan G, Pollack H, editors. The Effects of Social and Economic Policy on Health. New York: Russell Sage Foundation; 2007. [Google Scholar]
- DeFries JC, Fulker DW. Multiple regression analysis of twin data. Behavior Genetics. 1985;15(5):467–73. doi: 10.1007/BF01066239. [DOI] [PubMed] [Google Scholar]
- Derks EM, Dolan CV, Boomsma DI. A test of the equal environment assumption (EEA) in multivariate twin studies. Twin Research and Human Genetics. 2006;9(3):403–411. doi: 10.1375/183242706777591290. [DOI] [PubMed] [Google Scholar]
- D’Onofrio BM, Goodnight JA, Van Hulle CA, Rodgers JL, Rathouz PJ, Waldman ID, Lahey BB. A quasi-experimental analysis of the association between family income and offspring conduct problems. Journal of Abnormal Child Psychology. 2009;37:415–429. doi: 10.1007/s10802-008-9280-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- D’Onofrio BM, Turkheimer EN, Eaves LJ, Corey LA, Berg K, Solaas MH, Emery RE. The role of the children of twins design in elucidating causal relations between parent characteristics and child outcomes. Journal of Child Psychology and Psychiatry. 2003;44(8):1130–1144. doi: 10.1111/1469-7610.00196. [DOI] [PubMed] [Google Scholar]
- Eaves LJ, Silberg JL, Maes HH. Revisiting the children of twins: Can they be used to resolve the environmental effects of dyadic parental treatment on child behavior? Twin Research and Human Genetics. 2005;8(4):283–290. doi: 10.1375/1832427054936736. [DOI] [PubMed] [Google Scholar]
- Eckman RE, Williams R, Nagoshi C. Marital assortment for genetic similarity. Journal of Biosocial Science. 2002;34(04):511–523. doi: 10.1017/s0021932002005114. [DOI] [PubMed] [Google Scholar]
- Freese J. Genetics and the social science explanation of individual outcomes. American Journal of Sociology. 2008;114(S1):S1–S35. doi: 10.1086/592208. http://www.journals.uchicago.edu/doi/pdf/10.1086/592208. [DOI] [PubMed]
- Gillespie NA, Martin NG. Direction of causation models. In: Everitt BS, Howell DC, editors. Encyclopedia of Statistics in Behavioral Science. John Wiley & Sons, Ltd; 2005. pp. 496–499. [Google Scholar]
- Gillespie NA, Zhu G, Neale MC, Heath AC, Martin NG. Direction of causation modeling between cross-sectional measures of parenting and psychological distress in female twins. Behavior Genetics. 2003;33(4):383–396. doi: 10.1023/a:1025365325016. [DOI] [PubMed] [Google Scholar]
- Griliches Z. Sibling models and data in economics: Beginnings of a survey. Journal of Political Economy. 1979;87(5):S37–64. [Google Scholar]
- Griliches Z, Mason WM. Education, income, and ability. Journal of Political Economy. 1972;80(3):74–103. [Google Scholar]
- Guo G. Twin studies: How much can they tell us about nature and nurture? Contexts. 2005;4:43–47. [Google Scholar]
- Guo G, Tong Y, Cai T. Gene by social context interactions for number of sexual partners among white male youths: Genetics-informed sociology. American Journal of Sociology. 2008;114(S1):S36–S66. doi: 10.1086/592207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harris J, Magnus P, Tambs K. The Norwegian Institute of Public Health Twin Panel: a description of the sample and program of research. Twin Research. 2002;5(5):415–423. doi: 10.1375/136905202320906192. [DOI] [PubMed] [Google Scholar]
- Harris KM, Halpern CT, Smolen A, Haberstick BC. The National Longitudinal Study of Adolescent Health (Add Health) twin data. Twin Research and Human Genetics. 2006;9(6):988–997. doi: 10.1375/183242706779462787. [DOI] [PubMed] [Google Scholar]
- Hauser RM, Wong RSK. Sibling resemblance and intersibling effects in educational attainment. Sociology of Education. 1989;62(3):149–171. [Google Scholar]
- Heath AC, Kessler RC, Neale MC, Hewitt JK, Eaves LJ, Kendler KS. Testing hypotheses about direction of causation using cross-sectional family data. Behavior Genetics. 1993;23(1):29–50. doi: 10.1007/BF01067552. [DOI] [PubMed] [Google Scholar]
- Heckman JJ. Econometric causality. NBER Working Paper No. 13934. 2008 URL http://www.nber.org.
- Hettema J, Neale M, Kendler K. Physical similarity and the equal-environment assumption in twin studies of psychiatric disorders. Behavior Genetics. 1995;25:327–335. doi: 10.1007/BF02197281. [DOI] [PubMed] [Google Scholar]
- Hobcraft JN. Reflections on demographic, evolutionary, and genetic approaches to the study of human reproductive behavior. In: Wachter KW, Bulatao RA, editors. Offspring: Human Fertility Behavior in Biodemographic Perspective. Washington, D.C: The National Academies Press; 2003. pp. 339–357. [PubMed] [Google Scholar]
- Keith LG, Papiernik E, Keith DM, Luke B, editors. Multiple Pregnancy: Epidemiology, Gestation, and Perinatal Outcome. New York: Parthenon; 1995. [Google Scholar]
- Kendler KS, Neale MC, Kessler RC, Heath AC, Eaves LJ. A test of the equal-environment assumption in twin studies of psychiatric illness. Behavior Genetics. 1993;23:21–27. doi: 10.1007/BF01067551. [DOI] [PubMed] [Google Scholar]
- Kiely JL, Kiely M. Epidemiological trends in multiple births in the United States, 1971–1998. Twin Research. 2001;4(3):131–133. doi: 10.1375/1369052012335. [DOI] [PubMed] [Google Scholar]
- Kohler HP, Behrman JR, Skytthe A. Partner + children = happiness? An assessment of the effect of fertility and partnerships on subjective well-being in Danish twins. Population and Development Review. 2005;31(3):407–445. [Google Scholar]
- Kohler HP, Rodgers JL. DF-like analyses of binary, ordered and censored variables using Probit and Tobit approaches. Behavior Genetics. 1999;29(4):221–232. [Google Scholar]
- Kohler HP, Rodgers JL. DF-analyses of heritability with double-entry twin data: Asymptotic standard errors and efficient estimation. Behavior Genetics. 2000;31(2):179–191. doi: 10.1023/a:1010253411274. [DOI] [PubMed] [Google Scholar]
- Kohler H-P, Rodgers JL, Wachter KW, Bulatao RA. Offspring: Human Fertility Behavior in Biodemographic Perspective. Washington, D.C: The National Academies Press; 2003. Education, fertility and heritability: Explaining a paradox; pp. 46–90. URL http://books.google.com/books?id=poXXt7ta73cC&pg=PA46. [PubMed] [Google Scholar]
- Kravdal Ø, Rindfuss R. Changing relationships between education and fertility: A study of women and men born 1940 to 1964. American Sociological Review. 2008;73(5):854–873. [Google Scholar]
- Lichtenstein P, De faire U, Floderus B, Svartengren M, Svedberg P, Pedersen NL. The swedish twin registry: a unique resource for clinical, epidemiological and genetic studies. Journal of Internal Medicine. 2002;252(3):184–205. doi: 10.1046/j.1365-2796.2002.01032.x. URL http://dx.doi.org/10.1046/j.1365-2796.2002.01032.x. [DOI] [PubMed]
- Lleras-Muney A. The relationship between education and adult mortality in the United States. Review of Economic Studies. 2005;72(1):189–221. [Google Scholar]
- Lundborg P. The health returns to education: What can we learn from twins? Tinbergen Institute Discussion Paper No. TI 08-027/3. 2008 URL http://ssrn.com/abstract=111368.
- Lykken D, Bouchard T, McGue MAT. The minnesota twin family registry - some initial findings. Acta Geneticae Medicae et Gemellologiae. 1990;39(1):35–70. doi: 10.1017/s0001566000005572. [DOI] [PubMed] [Google Scholar]
- Miller P, Mulvey C, Martin N. Family characteristics and the returns to schooling: Evidence on gender differences from a sample of Australian twins. Economica. 1997;64(253):119–136. [Google Scholar]
- Moffitt R. Remarks on the analysis of causal relationships in population research. Demography. 2005;42(1):91–108. doi: 10.1353/dem.2005.0006. [DOI] [PubMed] [Google Scholar]
- Moffitt RA. Issues in the estimation of causal effects in population research, with an application to the effects of teenage childbearing. In: Engelhardt H, Kohler H-P, Fürnkranz-Prskawetz A, editors. Causal Analysis in Population Studies. chap 2. Berlin: Springer Verlag, The Springer Series on Demographic Methods and Population Analysis; 2009. pp. 9–29. [Google Scholar]
- Morris-Yates A, Andrews G, Howie P, Henderson S. Twins: a test of the equal environments assumption. Acta Psychiatrica Scandinavica. 1990;81(4):322–326. doi: 10.1111/j.1600-0447.1990.tb05457.x. [DOI] [PubMed] [Google Scholar]
- Neale MC, Boker SM, Xie G, Maes HH. Mx: Statistical Modeling 2006 [Google Scholar]
- Neale MC, Cardon LR. Methodology for Genetic Studies of Twins and Families. London: Kluwer Academic Publishers; 1992. [Google Scholar]
- Neale MC, Maes HHM. Virginia Commonwealth University: Draft Manuscript. Virginia Institute for Psychatric and Behavioral Genetics; 2004. Methodology for Genetic Studies of Twins and Families. URL http://www.vipbg.vcu.edu/~vipbg/mx/book2004a.pdf. [Google Scholar]
- OpenMx Development Team. Openmx documentation: User guide. 2010 (Release 0.3.3-1264), URL http://openmx.psyc.virginia.edu.
- Page WF. The NAS-NRC Twin Registry of WWII military veteran twins. Twin Research. 2002;5(5):493–496. doi: 10.1375/136905202320906345. [DOI] [PubMed] [Google Scholar]
- Plomin R, DeFries JC, McClearn GE, McGuffin P. Behavioral Genetics. 4 New York: Worth Publishers; 2005. [Google Scholar]
- Plomin R, Defries JC, Mclearn GE. Behavioral Genetics. Freemann & Co; 1997. [Google Scholar]
- Plomin R, Willerman L, Loehlin JC. Resemblance in appearance and the equal environments assumption in twin studies of personality traits. Behavior Genetics. 1976;6:43–52. doi: 10.1007/BF01065677. [DOI] [PubMed] [Google Scholar]
- Richardson K, Norgate S. The equal environments assumption of classical twin studies may not hold. British Journal of Educational Psychology. 2005;75(3):339–350. doi: 10.1348/000709904X24690. [DOI] [PubMed] [Google Scholar]
- Rodgers JL, Doughty D. Genetic and environmental influences on fertility expectations and outcomes using NLSY kinship data. In: Rodgers JL, Rowe DC, Miller WB, editors. Genetic Influences on Human Fertility and Sexuality. Boston: Kluwer Academic Publishers; 2000. pp. 85–106. [Google Scholar]
- Rodgers JL, Hughes K, Kohler HP, Christensen K, Doughty D, Rowe DC, Miller WB. Genetic influence helps explain variation in human fertility outcomes: Evidence from recent behavioral and molecular genetic studies. Current Directions in Psychological Science. 2001a;10(5):184–188. [Google Scholar]
- Rodgers JL, Kohler HP, Kyvik K, Christensen K. Behavior genetic modeling of human fertility: Findings from a contemporary Danish twin study. Demography. 2001b;38(1):29–42. doi: 10.1353/dem.2001.0009. [DOI] [PubMed] [Google Scholar]
- Rodgers JL, Rowe D, Li C. Beyond natures versus nurture: DF analysis of nonshared influences on problem behavior. Developmental Psychology. 1994;30(3):374–84. [Google Scholar]
- Rosenzweig MR, Wolpin KI. Life-cycle labor supply and fertility: Causal inferences from household models. Journal of Political Economy. 1980a;88:328–348. [Google Scholar]
- Rosenzweig MR, Wolpin KI. Testing the quantity-quality fertility model: The use of twins as a natural experiment. Econometrica. 1980b;48(1):227–240. [PubMed] [Google Scholar]
- Rosenzweig MR, Wolpin KI. Natural “natural” experiments in economics. Journal of Economic Literature. 2000;38(4):827–874. [Google Scholar]
- Scarr S. Environmental bias in twin studies. Eugenics Quarterly. 1968;(15):34–40. doi: 10.1080/19485565.1968.9987750. [DOI] [PubMed] [Google Scholar]
- Schnittker J. Happiness and success: Genes, families, and the psychological effects of socioeconomic position and social support. American Journal of Sociology. 2008;114:S233–S259. doi: 10.1086/592424. [DOI] [PubMed] [Google Scholar]
- Schwartz CR, Mare RD. Trends in educational assortative marriage from 1940 to 2003. Demography. 2005;42(4):621–646. doi: 10.1353/dem.2005.0036. [DOI] [PubMed] [Google Scholar]
- Skytthe A, Kyvik K, Holm NV, Vaupel JW, Christensen K. The Danish Twin Registry: 127 birth cohorts of twins. Twin Research. 2002;5(5):352–357. doi: 10.1375/136905202320906084. [DOI] [PubMed] [Google Scholar]
- Staiger D, Stock JH. Instrumental variable regression with weak instruments. Econometrica. 1997;65(3):557–586. [Google Scholar]
- Stock JH. The other transformation in econometric practice: Robust tools for inference. Journal of Economic Perspectives. 2010;24(2):83–94. [Google Scholar]
- Stock JH, Yogo M. Testing for weak instruments in linear IV regression. NBER Technical Working Paper No. 284. 2002 URL http://www.nber.org/papers/t0284.
- Waller NG. A DeFries and Fulker regression model for genetic nonadditivity. Behavior Genetics. 1994;24(2):149–153. doi: 10.1007/BF01067818. [DOI] [PubMed] [Google Scholar]
- Warren JR, Sheridan JT, Hauser RM. Occupational stratification across the life course: Evidence from the Wisconsin Longitudinal Study. American Sociological Review. 2002;67(3):432–455. [Google Scholar]
- Willcutt EG, Pennington BF, Olson RK, DeFries JC. Understanding comorbidity: A twin study of reading disability and attention-deficit/hyperactivity disorder. American Journal of Medical Genetics Part B: Neuropsychiatric Genetics. 2007;144B(6):709–714. doi: 10.1002/ajmg.b.30310. [DOI] [PubMed] [Google Scholar]
- Winship C, Sobel M. Causal inferences in sociological studies. Mimeo: Harvard University; 2000. [Google Scholar]
- Wolfe B, Haveman R. Social and nonmarket benefits from education in an advanced economy. In: Kodrzycki Y, editor. Education in the 21st Century: Meeting the Challenges of a Changing World. Boston, MA: Federal Reserve Bank of Boston; 2003. [Google Scholar]