Abstract
We have used a realistic model for double stranded DNA and Monte Carlo simulations to compute the extension (mean span) of a DNA molecule confined in a nanochannel over the full range of confinement in a high ionic strength buffer. The simulation data for square nanochannels resolve the apparent contradiction between prior simulation studies and the predictions from Flory theory, demonstrating the existence of two transition regimes between weak confinement (the de Gennes regime) and strong confinement (the Odijk regime). The simulation data for rectangular nanochannels support the use of the geometric mean for mapping data obtained in rectangular channels onto models developed for cylinders. The comparison of our results with experimental data illuminates the challenges in applying models for confined, neutral polymers to polyelectrolytes. Using a Flory-type approach, we also provide an improved scaling result for the relaxation time in the transition regime close to that found in experiments.
1 Introduction
When a polymer is confined inside a channel whose dimensions are smaller than that polymer's mean span dimension in the bulk, the polymer chain extends along the channel axis. In the context of DNA, such two-dimensional (nanochannel) confinement is emerging as an important tool for single molecule genomics.1–8 Operating these devices entails imaging stretched DNA, so they provide a seemingly straightforward test of the theories for confined chains.1–3,9–12 At present, discrepancies exist among theory, experiment and simulation.9,13,14 In this paper, we bring theory and simulation into agreement. In doing so, we provide clear evidence for the existence of two transition regimes between the de Gennes and Odijk regimes.15 Moreover, comparison of our simulation results and experimental data highlights the challenges inherent in applying the scaling theories developed for neutral polymers to confined DNA.
The basic problem at hand is to compute the mean span dimension of a polymer confined in nanochannel of size D. Typical nanochannels used in experiments9 range from 30nm to 500nm. The polymer is characterized by its contour length L, bulk radius of gyration Rg, persistence length lp and effective width w. For the widely used model polymer λ-phage DNA (48.5 kilobase pairs), typical parameters are L ≅ 21μm and Rg ≅ 0.7μm when the DNA is stained with an intercalating dye.16,17 Since DNA is a polyelectrolyte, both its persistence length and effective width include an intrinsic, chemical component and an additional electrostatic contribution, the latter depending on the ionic strength of the solution.18–21 We restrict our analysis to high ionic strength buffers where long-range electrostatic interactions within polymer segments and between the polymer and channel walls are screened.3,16 As a result, we will use the commonly accepted value for the DNA persistence length, lp ≅ 53nm.22 The bare width of the double helix is 2 nm, but the effective width w is larger due to electrostatic interactions, even in relatively high ionic strength buffers.16,19 In our analysis, we will take the value w = 4.6nm suggested by Odijk.15 Based on Stigter's theory for the effective width,18,19 this value is appropriate for TBE 5×; the effective width for the buffer used in experiments9 (TBE 0.5×) is closer to 12 nm. We will return to the question of effective width when we compare our simulation results to experiments. In contrast to most synthetic polymers such as polyethylene, where lp ≅ 0.7nm and w ≅ 0.5nm,23 DNA has a much larger persistence length and a much higher segment aspect ratio lp/w.
Figure 1 depicts the present understanding of DNA extension in nanochannels. Most experimental data are analyzed in the context of the theories for two limiting cases that have been confirmed since by simulation.14,24–27 One limit is the deflection chain model (known as the Odijk regime),28 developed for the strong confinement limit D ≪ lp. As seen in Figure 1, the chain in the Odijk regime may be viewed as a sequence of deflection segments of typical length that undulate inside the channel. The intrinsic stiffness of DNA on the length scale of the channel prohibits backfolding. The mean extension is thus the number of deflection segments L/λ times the average projection of a deflection segment on the channel axis:
| (1) |
In the latter, θ ≅ D/λ → 0 is an average deflection angle and α = 0.09137±0.00007 is a universal prefactor.24,25
Figure 1.
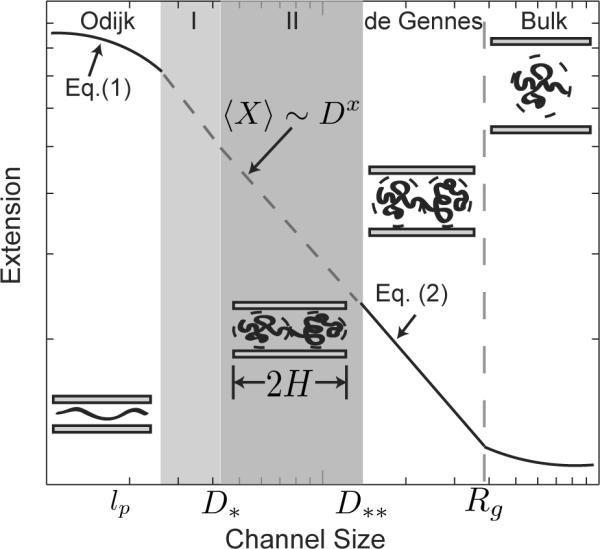
Schematic illustration of the different regimes of extension as a function of the channel size. The quantities D* and D** correspond to the transitions discussed in §2. The two shaded regions labeled I and II are the transition regimes described by Odijk;15 in what follows, region II will be referred to as the “extended de Gennes regime.” Various estimates for the exponent x are listed in Table 1. The schematics illustrate the DNA configuration under different degrees of confinement and the length scale H is discussed in §2.
The other limit is the blob model (known as the de Gennes regime)29–31 in which the chain is envisioned as the sequence of self-avoiding isometric compression blobs of diameter D sketched in Figure 1. On length scales smaller than D, segments of the chain are unaware of the presence of the confinement and follow the Flory statistics of an unperturbed excluded volume chain, whereupon blob theory predicts an mean equilibrium extension1,9
| (2) |
The assumptions used to derive Eq. (2), which we will review in §2, limit its applicability to down to a channel size , as indicated in Figure 1.15 The widely cited scaling exponent of −2/3 in Eq. (2) was obtained using a Flory exponent of v = 3/5. Sophisticated calculations32 for an excluded volume chain lead to v = 0.5877 ± 0.0006, whereupon the scaling in the de Gennes regime becomes
| (3) |
Naturally, once the channel becomes so large that the chain conformation is unaffected by the presence of the walls, as indicated at the largest channel diameters in Figure 1, the extension of the “confined” chain is the same as its bulk value.
The controversy surrounds the description of a chain in the transition between the de Gennes and Odijk regimes. As we can see in Table 1, theory, simulation and experiment have all revealed different exponents x in the scaling law for the extension, 〈X〉 ~ Dx. The issue is even more convoluted than a simple disagreement over the exponent. While a number of theories15,33 proposed that Eq. (2) extends into at least transition regime II, another theory35 suggested that no scaling law exists due to the depletion of segments from the blobs. Meanwhile, computer simulations13,14,36 suggested that the scaling in the transition regime is not universal, with the exponent depending on the total length of the chain. To further complicate the situation, the original analysis of experimental chain extension data9 assumed that one can simply extrapolate Eq. (1) and Eq. (2) into the transition regime, whereas a subsequent theory15 predicted that there are actually the two transition regimes indicated by the shading in Figure 1. Resolving the questions surrounding DNA extension in the transition from the Odijk regime to the de Gennes regime is a crucial issue, since many nanochannel devices for DNA stretching operate in this range.9 Such a resolution is the goal of our discourse.
Table 1.
Summary of scaling exponents 〈X〉 ~ Dx for the extension of DNA as a function of the channel size in the shaded transition regime of Figure 1. The Monte Carlo simulation data correspond to long chains (L/lp ≅ 40 and lp/w ≅ 20) for channels sizes ranging approximately from lp to 2lp. For the experimental data reported in the last four rows, the parameter D is the geometric average of the channel width and height, Dav. The rectangular channels range from Dav = 60–440 nm and the tapered channels range from Dav = 100–250 nm. The two different values for T4-DNA (166.7 kilobase pairs, L = 56.7 μm) correspond to different basepair-to-dye ratios.
| Approach | Exponent | Reference |
|---|---|---|
| Flory Theory (ν = 3/5) | −2/3 | Ref. 15,33 |
| Flory Theory (ν = 0.5877) | −0.7015 | Eq. (3) |
| Monte Carlo Simulation | −1 | Ref. 13,14 |
| λ,-DNA, rectangular channel | −0.85±0.05 | Ref. 9 |
| λ,-DNA, tapered channel | −0.85±0.01 | Ref. 34 |
| T4-DNA, tapered channel | −0.83±0.01 | Ref. 34 |
| T4-DNA, tapered channel | −0.78±0.01 | Ref. 34 |
2 Summary of the existing Flory theories
Before we proceed to our simulation study, it behooves us to recall the key results obtained by applying Flory theory29,37 to confined polymers, especially as there has been some confusion in the literature on the application of Flory theory to the de Gennes regime.38,39 We will briefly derive these results starting from the approach proposed by Jun et al.38 for the de Gennes regime. We recall that they derived a Flory-theory equivalent to the de Gennes blob model by considering effectively a one-dimensional walk of blobs inside the nanochannel
| (4) |
where the blob size D arises from scaling theory. As in the standard Flory theory, the first term in Eq. (4) is the elastic energy of the chain and the second term is the effective repulsion energy.23,40 The parameter β = 1/(kBT), with kB the Boltzmann constant and T the absolute temperature. Each blob, containing Lsub segments, is considered as an unperturbed excluded volume chain in both the de Gennes blob model and Eq. (4), whereupon the standard Flory theory for the size of an excluded volume chain gives40
| (5) |
Substituting the latter in Eq. (4) and minimizing with respect to the chain extension X yields Eq. (2). If we instead specify that Lsub ~ D1/v, we arrive at the scaling in Eq. (3).
The free energy in Eq. (4) is valid so long as the channel is large enough for the blobs to experience the excluded volume interactions that lead to Eq. (5). The critical chain length, L**, and channel size, D**, defining the boundary for the de Gennes regime are obtained at the crossover between ideal and excluded volume blobs,33,41
| (6) |
Thus, the chain must be longer than
| (7) |
in order to be able to form one of these excluded volume blobs, and the channel must be larger than15
| 8 |
so that this isometric blob indeed experiences excluded volume interactions and thus resides in the de Gennes regime. The later limits are equivalent to requiring that the repulsion energy between segments in a blob in the standard Flory theory, , be unity.
Let us now turn our attention to D < D**. The next regime is transition regime II in Figure 1, which we will refer to as the extended de Gennes regime. Odijk15 claimed that the extended de Gennes regime is valid for D* < D < D**, where the lower bound is
| (9) |
with c greater than unity. As we have highlighted in Figure 1, Odijk15 further proposed that an additional transition regime connects the extended de Gennes regime and the classic Odijk regime described by Eq. (1). Two of the goals of our analysis are to compute the value of c in Eq. (9) and the channel size for the lower bound of transition regime I.
Now let us compute the extension in the extended de Gennes regime (D* < D < D**). Following the existing models15,33 for transition regime II in Figure 1, the inset depicts the chain in the extended de Gennes regime as a string of anisometric (cylindrical) blobs, each of diameter D and length H (H > D). This anisometric blob, of contour length L*, swells in the axial direction along the channel to a distance H such that the chain is now at the cross-over between real and ideal chain behavior15
| (10) |
where the last term corresponds to the onset of excluded volume interactions (z ≅ 1 in the Flory theory). Solving the above equations yields
| (11) |
and
| (12) |
If we continue with the idea embodied in Eq. (4), the length of the chain in a blob Lsub is always L* and the size D is replaced by H, whereupon the Flory free energy is
| (13) |
Substituting Eq. (11) and Eq. (12) into Eq. (13) furnishes
| (14) |
which has often been taken for granted in the literature as the Flory energy of a confined chain.11,15,33,39 Minimizing Eq. (14) with respect to X again yields Eq. (2). Since each blob requires a contour length L*, then only chains which satisfy L > L* can be confined in the extended de Gennes regime. Note that Odijk15 derived the minimum channel size for the extended de Gennes regime in Eq. (9) from the confinement free energy of the Odijk regime.
One should not confuse the Flory free energies for the de Gennes and the extended de Gennes regimes: although they both predict the same mean equilibrium extension, only Eq. (4) is equivalent to the de Gennes blob model.38,39 However, if an experiment actually operates in the extended de Gennes regime, Eq. (14) can be safely applied.11
Note that Eq. (10) assumes the subchain inside an anisometric blob to be a flexible coil. In the context of the wormlike chain model, this requires L* 16lp, where the prefactor is obtained by comparing the end-to-end distance of a wormlike chain to that of a Gaussian coil. If we assume that the prefactor in Eq. (11) is unity, then this assumption requires
| (15) |
Using w ≅ 4.6nm and lp ≅ 53nm, we found that the flexible coil approximation for the subchain inside a blob may not be valid for , suggesting a possible value for the constant appearing in Eq. (9) for our model.
3 Polymer model and simulation methods
We have explored the different regimes of Figure 1 using a DNA model based on the classical wormlike chain.42 It is worth mentioning that although our approach is similar to that of Cifra et al.,13,14,36 there are explicit differences in the DNA model and the measure of the DNA extension. The chain consists of N beads connected by N − 1 inextensible rods of length l, with a corresponding contour length L = (N − 1)l. Let rj = (xj,yj,zj), j ∈ [1,N] be position of the jth bead and uj = (rj+1 − rj)/l, j ∈ [1,N − 1] be the unit vector along the jth rod. There are excluded volume repulsions between any two beads and bending penalties between any two adjacent rods. To compare with theory, we neglect possible long range electrostatic interactions within beads and between beads and walls. Such a model is appropriate for experiments using high ionic strength buffers.9
The total bending energy of the chain is obtained from converting the continuous wormlike chain model
| (16) |
to the approximate, discrete form42
| (17) |
where we used the relationship |uk+1 − uk|2 = 2(1 − uk · uk+1) for an inextensible rod with unit vector uk and length l. The steric excluded volume interaction between any two beads, i and j, separated by a distance rij is modeled by a purely repulsive Lennard-Jones potential of the Weeks-Chandler-Andersen (WCA) form,43 where
| (18) |
for rij < 21/6w, and UWCA(rij) = 0 otherwise. The energy and length scale in the WCA potential correspond to an excluded volume energy of kBT when two beads are separated by w, the effective width of the DNA. We fixed l = 21/6w so that w is a meaningful measure of the width of the chain. When the DNA is confined, we added a hard core potential3 that forbids any bead from approaching the channel surface closer than w/2, i.e.,
| (19) |
where h is the distance from the center of a bead to a channel surface. We used lp = 53nm22 and w = 4.6nm15 for most of our simulations. For comparison, we also simulated more flexible chains using lp = 5.3nm or lp = 23nm, keeping w = 4.6nm.
We define the extension, 〈X〉, as the mean span dimension along the channel direction, since the mean span is the parameter measured in the experiments:
| (20) |
Here, the center line of the channel is oriented along the x-axis, with the cross-section lying in the yz-plane. While the mean span is the most easily obtained metric for DNA when it is stretched in a nanochannel, measurements of the mean span for DNA in free solution normally suffer from significant error due to optical effects such as diffraction and blooming for such small objects.
Most prior simulations have considered other size parameters such as the end-to-end distance, or the component of the end-to-end distance parallel to the center line of the channel.13,14,36,44 As already demonstrated by Cifra,14 the use of different size parameters may result in quantitatively different results, even in the scaling exponent measured from simulation data. In our simulations, the mean span dimension along the channel direction is nearly the same as the end-to-end distance in the Odijk regime, but the difference grows as the channel dimension increases. In de Gennes blob theory for a chain squeezed in a tube,29 the length of tube R∥ occupied by the chain is the end-to-end distance (span) of a one-dimensional self-avoiding walk of blobs. In our view, the mean span dimension along the channel direction is a closer metric to R∥ than the end-to-end distance of the chain. The mean span also has the attractive feature that its fluctuations are much smaller than the end-to-end distance.
We used canonical ensemble Monte Carlo simulations to sample equilibrium configurations of the chain. First, we characterized our model DNA in free solution using the pruned-enriched Rosenbluth method.45,46 Our calculations are validated by comparing them with equivalent data produced by the Metropolis Monte Carlo method with elementary trial moves of reptation, crankshaft, and pivot.47–50 In the calculations of DNA extension in nanochannels, we used the Metropolis Monte Carlo method with reptation and crankshaft moves. Once a random initial configuration was generated inside the nanochannel, the system was equilibrated for about 107 steps. In production runs, chain configurations were sampled every 106 steps. Most of the presented results refer to an average of more than 104 configuration. The estimated error of ensemble averages is within the symbol size.
For channel sizes D greater than approximately Rg, we also used the method of confinement analysis from bulk structure to estimate chain extensions51
| (21) |
Here, Deff = D − w is the channel width accessible to the centerline of the DNA backbone, R(x) = xH(x) is the Ramp function, H(x) the Heaviside function, and X, Y , Z the span dimensions of a chain configuration in three orthogonal directions. This method has the advantage of obtaining 〈X〉 for a variety of channel widths solely by sampling equilibrium configurations in free space.
4 Results and discussion
4.1 Free solution
An important test of any DNA model is its predictive ability in free solution. Indeed, properly characterizing the free solution properties of a different model was a key step in demonstrating the agreement between theory, simulation and experiment for DNA confined in slit-like channels in the de Gennes regime.52 As seen in Figure 2, the simulation data for the root-mean-square end-to-end distance, Re, and radius of gyration, Rg, for the smaller chains, L/lp < 102, agree with the theoretical results for a wormlike chain without excluded volume.53 Moreover, as L/lp increases further, both Re and Rg begin to follow the scaling for a swollen chain. From Flory theory, this Gaussian-to-excluded-volume crossover33,41 should occur at a critical contour length L** given in Eq. (7). For our choices of lp and w,
| (22) |
The latter value matches the crossover in our simulation results, indicating that the numerical coefficient in Eq. (7) is close to unity.
Figure 2.
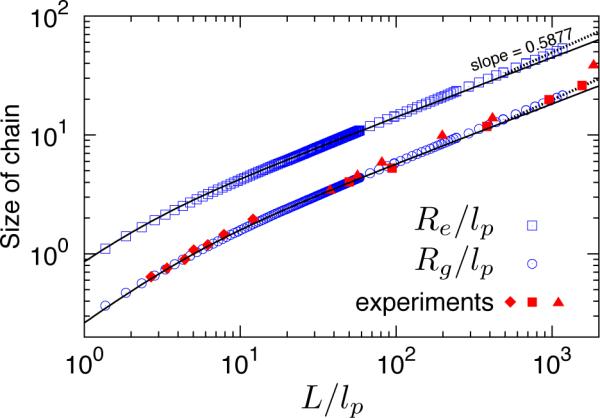
Bulk properties of the wormlike bead-rod model (w = 4.6nm and lp = 53nm): simulations (open symbols) vs. theory (solid lines: wormlike chain theory53 in the absence of excluded volume for Re and Rg, dashed lines: excluded volume chain scaling with ν = 0.5877) and experimental results for Rg (solid symbols; diamond: Godfrey and Eisenberg,54 square: Robertson et al.,56 triangle: Smith et al.55).
Besides being fully consistent with results from the wormlike chain theory, the model described here also reasonably captures several experimental data sets for the radius of gyration of DNA.54–56 However, we should note that (i) most of our data were obtained in the ideal wormlike chain regime and (ii) the radius of gyration for an excluded volume chain is only weakly dependent on the effective width, Rg ~ w1/5. As a result, the agreement with experiment only validates the order of magnitude for the effective width. For the calculations leading to Figure 2, we used the value w = 4.6nm cited by Odijk,15 since we will be devoting considerable effort to testing his scaling theory.15 As we will see later, a larger value of the effective width, w = 7nm, provides a more robust fit between our simulations and the experimental data. Such a change in w would not affect the data for the ideal chain in Figure 2 and only result in an 9% increase in the radius of gyration in the excluded volume regime.
Little is known about the mean span dimension, 〈X〉0, of wormlike chains in free solution except that 〈X〉0/L = 0.5 in the rod limit (L/lp → 0) and 〈X〉0/(2Rg) = 2/π1/2 in the flexible coil limit (L/lp → ∞) in the absence of excluded volume interactions.51 The simulation results reported in Figure 3 show that the fractional extension at the Gaussian-to-excluded-volume crossover contour length L** is approximately 0.1. Thus, the minimum extension of an unperturbed swollen chain is 0.1L** ≅ 500nm. This value roughly agrees with the estimate of D** in Eq. (8) using our choices of lp and w and a numerical coefficient of unity. Furthermore, Figure 3 indicates that 〈X〉0 is approximately 2Rg at L/lp = 102, and the ratio 〈X〉0/2Rg only changes slightly with increasing L/lp. Thus, one may approximate 〈X〉0 using available Rg-data in practice.
Figure 3.
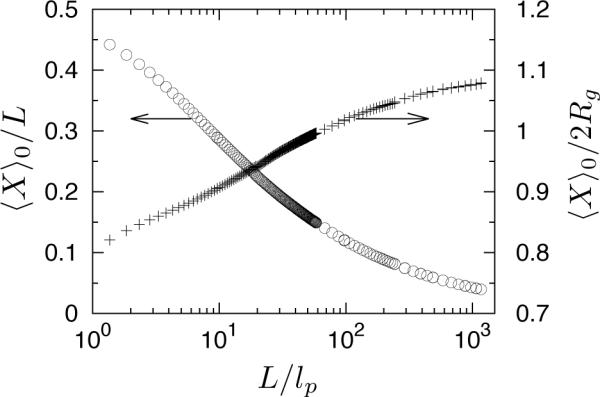
Bulk mean span dimensions 〈X〉0 of the wormlike bead-rod model (w = 4.6nm and lp = 53nm). The left y-axis: fractional extension in free solution, 〈X〉0/L. The right y-axis: size ratio 〈X〉0/(2Rg).
In our study of extension in nanochannels, it will also prove convenient to compare data for our semi-flexible DNA model to results obtained for a flexible chain with a persistence length lp = 5.3nm. Table 2 reports the simulated sizes of a flexible and a semi-flexible chain with L = 4.12μm. While the simulated data for lp = 53nm agree well with theory for an ideal wormlike chain, as we would expect from Figure 2, the simulation results for the flexible chain are much larger than those predicted by the theory for an ideal wormlike chain.53 The deviation with the theory is evidence for excluded volume interactions, which we would expect for the more flexible chain since L** ≅ 7nm ≪ L.
Table 2.
Bulk size properties of our model DNA (lp = 53nm) and that of a flexible chain (lp = 5.3nm): simulations vs. wormlike chain (WLC) theory. Other parameters: number of beads N = 800, contour length L = 4.12 μm, bead diameter w = 4.6nm and bond length l = 5.2nm. The exact result for the mean span dimension is not known for the wormlike chain model but should be close to 2Rg.
| lp (nm) | Re (nm) | Rg (nm) | 〈X〉0/2 (nm) | |
|---|---|---|---|---|
| 53 | simulation | 671.0±0.9 | 270.2±0.3 | 272.5±0.2 |
| WLC theory | 657.0 | 264.8 | ≅264.8 | |
|
| ||||
| 5.3 | simulation | 341.8±0.3 | 136.5 ±0.2 | 141.0±0.2 |
| WLC theory | 209.0 | 85.2 | ≅85.2 | |
4.2 Extension in nanochannels
4.2.1 Comparison with theory
Having established that the model captures the free solution properties of DNA, we proceed to test the theoretical predictions of the mean extension in a square nanochannel. The values for the number of beads N in our simulations are 100, 200, 500, and 800, corresponding to contour lengths L of 0.51μm, 1.03μm, 2.58μm, and 4.12μm, respectively. Although these chains (1.5 to 12 kilobase pairs using 0.34nm per base pair) are small compared to the DNA used in experiments,9,34 such as λ DNA (48.5 kilobase pairs), they illuminate the properties of the chain extension in the transition regime of Figure 1 while minimizing the computational cost. Since their contour lengths are below the Gaussian-to-excluded-volume crossover contour length of L**≅ = 5μm in Eq. (22), these chains cannot be described by the de Gennes blob model. In the context of Figure 1, these chains should crossover directly from their bulk extension to the transition regime as the channel size decreases.
Before proceeding to our analysis, it is useful to recapitulate two key points. First, although in our simulations, as is also the case in reality, the whole chain has to fit into the channel, the channel width in the theories refers only to the effective size accessible to the centerline of the DNA backbone. We therefore use the effective width
| (23) |
to compare experimental or simulation data with theories. Such a correction is negligible only when D ≫ w. Second, the extension data reported here correspond to the mean span dimension, rather than the end-to-end distance or some other measure of the chain size.
We begin by addressing first the importance of including excluded volume interactions in our simulations. Since all of our chains behave as ideal wormlike chains in free solution, one might be tempted to neglect excluded volume interactions between chain segments to accelerate the simulation of the confined chains. However, a key idea underlying the Flory theory is that a semi-flexible chain swells in confinement, even if the chain is short enough to behave ideally in free solution.33 To underscore the importance of excluded volume, Figure 4 plots the extension of the longest chain in our simulations with and without excluded volume interactions. In the bulk, both simulations yield the same extension, as expected. As the confinement increases, the interplay between bending stiffness and confinement results in an increase in extension due to excluded volume interactions. Nearly the same extension is obtained in the Odijk limit whether or not there are excluded volume interactions,24,25 but we need to go to substantially smaller values of Deff before the chain without excluded volume collapses onto Eq. (1). Here, the extension is driven almost entirely by the chain stiffness, consistent with the concept of a deflection segment.20 It appears that the excluded volume interactions are manifest for Deff/lp > 0.3. In the context of DNA, excluded volume interactions are important for channels down to around 15nm.
Figure 4.
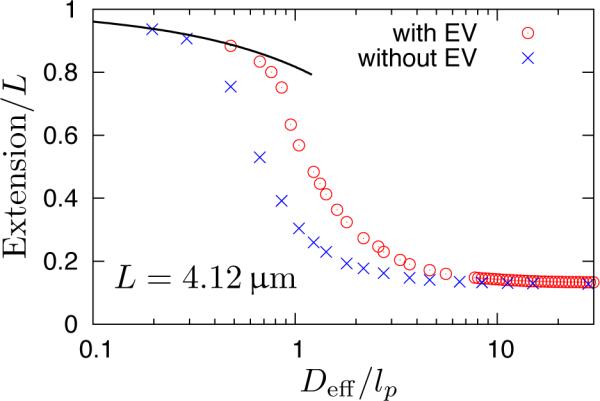
Extension of the wormlike bead-rod model in square nanochannels; circle: with excluded volume interactions, x: without excluded volume interactions. Other parameters: w = 4.6nm, lp = 53nm, N = 800 beads. Dashed line: theoretical prediction of Odijk's regime Eq. (1) with no adjustable parameters. Deff/lp = 1 corresponds to a real channel dimension of D = 57.6nm.
It is also interesting to note that for the phantom wormlike chain there is some discrepancy between our simulation results and Odijk's theory based on the formation of hairpins and hairpin tightening due to entropic depletion near channel walls.57 For instance, at Deff = lp = 53nm, theory57 predicts a global persistence length g = 43μm. For L = 4.12μm, such a chain would be highly stretched out, but our simulation data only suggest an extension of about 0.3L. The exact cause of such discrepancy is unclear to us; it may result from the finite length of DNA used in our simulation, or it could arise from the mechanical limit approximation used to derive g.57
Having convinced ourselves that excluded volume is important, let us now see how our simulation data in Figure 5 compare to the picture in Figure 1. For channel sizes smaller than approximately 30nm, our results coincide with Eq. (1) for the deflection chain model without any adjustable parameters. Moreover, the plateau values of the extension for large values of Deff/lp approach the free solution values for the mean span in Figure 3. These results obtained for limiting values of the channel size validate our overall calculation.
Figure 5.
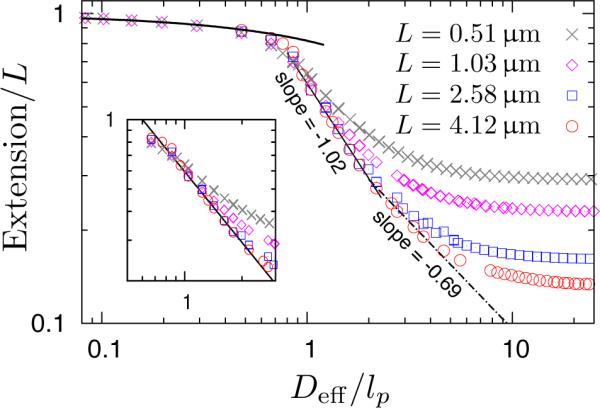
Extension of the wormlike bead-rod model (w = 4.6nm, lp = 53nm) in square nanochannels. The plateau values at large Deff/lp for the shorter chains agree with the free space data in Figure 3. Deff/lp = 1 corresponds to a real channel dimension of D = 57.6nm. The inset shows the region near Deff/lp = 1 in more detail. Symbols: simulations. Thicker solid line: theoretical prediction of Odijk's regime [Eq. (1)] with no adjustable parameters. Thinner solid line: power-law fit to the data with an exponent of −1.02 ± 0.01 for channel widths ranging from 60nm to 120nm. Dash-dotted line: power-law fit to the data with an exponent of −0.69 ± 0.03 for channel widths ranging from 120nm to 200nm.
As the channel size increases, the fractional DNA extension in the inset of Figure 5 appears to depend on the chain length. Such behavior, observed previously by Cifra et al. in simulations,13,14 was used to support a hypothesis of non-universal behavior in the transition regime. However, we recall that the chain extension must approach the value in the bulk when the channel size becomes large compared to the chain's radius of gyration. Since we have been able to simulate the extension of relatively long chains, it becomes apparent that the chain-length dependent extension simply reflects short chains diverging from a universal curve to their asymptotic mean span value in the bulk. The transition of our chains (L < L**) from the extended de Gennes regime to the bulk is a broad one, reminiscent of the similar transition from the de Gennes regime to the bulk for longer chains L > L**.27 The scaling law (or, as we will see, scaling laws) are independent of molecular weight for sufficiently long chains — the quantity that depends on molecular weight is the channel size D at which the confinement ceases to affect the chain extension. From a practical standpoint, we can safely treat the extension in the transition regime with universal scaling laws; it would be exceedingly difficult to obtain accurate fluorescence microscopy data such small chains, especially at extensions near 50%.
Let us now consider the chain with L = 2.58μm. Recall that Odijk15 predicted a transition regime between D ≪ lp, where the extension is described by Eq. (1), and some value D* given by Eq. (9). While we did observe a transition regime here, the extension does not correspond to the scaling predicted by Odijk.15 Rather, the fractional extension seems to have a power-law dependence on Deff with a best fit exponent of −1.02 in channel sizes ranging approximately from lp to 2lp. This scaling was also observed by Cifra for nearly the same channel size ranges.14 The origin of this scaling remains an open question. It does not appear to correspond to the “Regime 2A” or “Regime 2B” (Ref. 15) posited by Odijk; the ξ1-parameter defined in Eq. (8) of Ref. 15, computed for lp < Deff < 2lp, is greater than unity if we assume a numerical prefactor of unity. (This analysis is certainly rather crude as the numerical coefficient can be ≪ 1.) Although a scaling of 〈X〉 ~ D−1 has been predicted earlier for a channel-confined flexible chain in a θ-solvent (where the second virial coefficient disappears but the third virial coefficient is positive),58 it is questionable whether the same physics apply to semi-flexible chains. We should also point out that experimentally measuring the scaling exponent in this regime would be very challenging. The −1.02 slope only occurs over a range of Deff from 60nm to 120nm. Testing the scaling exponent would require a number of channels spanning this size range, which would be challenging and rather expensive to fabricate with the desired precision. Nevertheless, it is clear that (i) the chain with L = 2.58μm follows a scaling law 〈X〉 ~ D−1.02 in regime I of Figure 1 and (ii) our simulation data agree with prior results14 down to ≈ 20% extension.
We do not see any evidence that the chain with L = 2.58μm enters into an extended de Gennes regime (II in Figure 1) before transitioning to its bulk extension. This result is consistent with the Flory theory for the extended de Gennes regime. Recall that each anisometric blob in the extended de Gennes regime requires a contour length L* given by Eq. (11). For L = 2.58μm, the shift to the bulk behavior begins at a channel size Deff/lp ≅ = 2–4. The corresponding chain length per blob in the extended de Gennes regime for these channel sizes is L* ≅ = 0.68–1.7μm, neglecting any numerical prefactor. It appears that this chain is too short to form a series of anisometric blobs and thus only experiences transition regime I in Figure 1.
Only when we simulated a chain with L = 4.12μm did we have sufficient contour length (without ever crossing over into the de Gennes regime) to reconcile the disagreement between theory15 and simulation.14 For lp < D < 2lp, the extension data for L = 4.12μm collapse onto the results obtained for L = 2.58μm, indicating that (i) the scaling is not a function of molecular weight for chains that can actually be confined in this regime and (ii) the constant c ≈ 2 in Eq. (9) is slightly larger than unity, as predicted by Odijk15 and our estimate in Eq. (15) for the breakdown of the flexible coil assumption. As the channel size moves into the 120nm to 200nm range, where the L = 2.58μm chain begins the transition to its bulk extension, we found that the extension for the L = 4.12μm chain transitions to a different power law dependence on Deff. In this regime, the best fit exponent is −0.69 ± 0.03, in good agreement with the predicted exponent of −0.7015 in Eq. (3).
We believe that the data in Figure 5 confirm the theoretical predictions of the extended de Gennes regime by Brochard-Wyart et al.33 and Odijk15 because the contour length of our model DNA is so short that the chain itself is not in the region where we observe sensible excluded volume interactions in Figure 2, let alone any isometric blobs formed from a subsection of the chain. However, one might be tempted to argue that the scaling of −0.69 in regime II is an artifact of fitting a limited amount of data acquired in the transition between the slope of zero in the bulk and −1.02 in regime I of Figure 1. In other words, although the extension scaling is consistent with the prediction for the extended de Gennes regime, we have not demonstrated that we have the correct prefactor as well. There are infinitely many lines of slope −0.69; only one of these lines corresponds to the prediction for the extended de Gennes regime.
In principle, we could resolve the question by simulating a DNA chain of sufficient contour length to reach the de Gennes regime. Our claim would then be verified if the extension of this long chain agreed with (i) the scaling in the de Gennes regime for Deff > D** and (ii) the extension of the 4.12μm chain for Deff/lp ≈ 2. Unfortunately, the calculations become increasingly more expensive as the number of beads increases. We estimate that a DNA chain in the de Gennes regime would require a contour length of at least 30μm so that, if it formed two blobs, each blob would have enough contour length to be in the excluded volume regime of Figure 2.
Since such a long-chain simulation (6000 beads) is intractable with our computational resources, we took an alternate approach. Recall that the scaling laws for both the de Gennes and extended de Gennes regimes are given by Eq. (3). It is reasonable to assume that the extension at the crossover between these two contiguous regimes is continuous, implying that their scaling laws also have the same prefactor. Thus, if we can establish the prefactor for our wormlike chain model in the well established de Gennes regime and the continuity of the scaling law as we pass through D**, then we will know the prefactor for the more contentious extended de Gennes regime as well.
While we cannot simulate a DNA chain in the de Gennes regime, we can certainly simulate a more flexible chain (L = 4.12μm, w = 4.6nm) by changing the persistence length in Eq. (17) to lp = 5.3nm. For this smaller persistence length, the minimum channel size for the de Gennes regime, given by Eq. (8), is D** ≅ 6nm. We thus expect this more flexible chain to be in the de Gennes regime for channel sizes ranging from 20nm to 136.5nm (its bulk radius of gyration given in Table 2) and allow us to establish the prefactor for the de Gennes regime for our model. We also simulated an intermediate case (L = 4.12μm, w = 4.6nm, lp = 23nm). This chain is much longer than the value L** ≅ 575nm given by Eq. (7) and thus should cross-over between the de Gennes regime and the extended de Gennes regime at a channel size D** ≅ 115nm. This moderately flexible chain will allow us to establish the continuity of the extension at the cross-over between the de Gennes regime and the extended de Gennes regime.
Figure 6 shows that the extension obtained for lp = 5.3nm indeed is fit by a single power law dependence on Deff for channel sizes ranging from 20nm to 150nm. Moreover, the best fit exponent is −0.698 ± 0.001, which agrees with the Flory theory prediction in Eq. (3). As an aside, we point out that the calculation of this slope highlights the importance of using the effective width when comparing simulation/experiment with theory; had we used the overall channel width D instead of the effective width Deff, the best power law fit to the same data leads to an exponent of −0.800 ± 0.009. The data for lp = 23nm also collapse onto the same curve, with the transition between the extended de Gennes and de Gennes regime occurring near Deff/(wlp)1/2 ≅ 11. We thus confirm that the extension is continuous through the transition between regimes. Finally, when we plot the extension data for our original DNA chain with lp = 53nm in Figure 6, the data collapse over the relevant range of Deff/(wlp)1/2. As the extension data for lp = 53nm for (corresponding to channel sizes from 120 to 200 nanometers) in Figure 6 have both the magnitude and slope characterizing the de Gennes regime but do not satisfy the assumptions of that regime, we conclude that they must be in the extended de Gennes regime.
Figure 6.
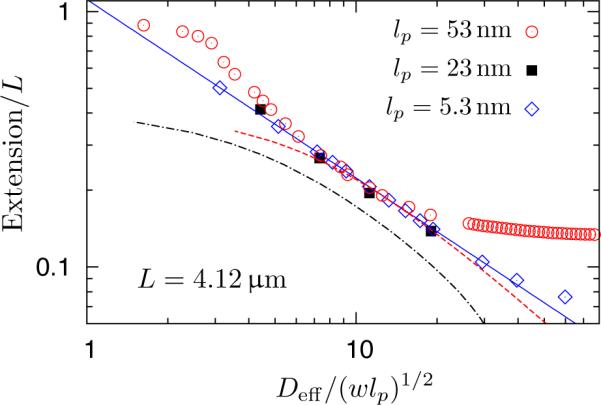
Extension of the wormlike bead-rod model (w = 4.6nm, L = 4.12μm) in square nanochannels. Circles: lp = 53nm. Squares: lp = 23nm. Diamonds: lp = 5.3nm. Solid line: a best power law fit to the simulation data of lp = 5.3nm, excluding the data points for the two widest channels (fitting function: y = axb with a = 1.113±0.002 and b = −0.698±0.001). Predictions the theory proposed Zhang et al.35 are shown for lp = 53nm (dashed line) and lp = 23nm (dash dotted line), respectively, using a common numerical constant C = 1.52 obtained by fitting their model to our simulation data for lp = 53nm; the numerical calculation of the extension with their model fails for lp = 5.3nm and w = 4.6nm because the theory is only valid for slender segments. Deff/(wlp)1/2 = 10 corresponds to a real channel dimension of D = 160.7nm for lp = 53nm, D = 107.4nm for lp = 23nm and D = 54.0nm for lp = 5.3nm.
To further support our claim, we also tested an alternate theory35 that supposes the blobs remain isometric but their statistics are corrected using the full Benoit-Doty equation59 for the unperturbed radius of gyration and an approximation for the swelling of the chain under weak excluded volume interactions. The latter theory includes a single free parameter, which we used in Figure 6 to obtain a good fit to the data for lp = 53nm. Unfortunately, as we see in Figure 6, this theory35 fails to predict the universal dependence of the extension on the dimensionless parameter Deff/(wlp)1/2.
4.2.2 Comparison with experiments
We now turn our attention to the comparison of our simulation results with experimental data.9,34 As we can see in Table 1, the values for the scaling exponents extracted from the experimental data in the transition regime deviate substantially from the theoretical predictions. In our discussion, we will focus primarily on the experimental data reported by Reisner et al.9 for λ DNA in a wide range of nanochannel sizes. The contour length of this polymer is sufficient for it to pass through the full range of regimes in Figure 1 as the channel size varies. Thus, in contrast to our simulations with lp = 53nm, we would expect the experiments to exhibit a de Gennes regime.
The first question we address is the role of the aspect ratio of the channel. While it is simple to create a square nanochannel in a simulation, the corresponding experiment is considerably more difficult. Thus, experiments have either been performed in D1-by-D2 rectangular channels9 or in a tapered channel34 where D1 remains constant and D2 varies slowly enough that it can be treated constant on the length scale of the polymer. To interpret the data in the context of either Eq. (1) or Eq. (2), the channel size D is replaced with the geometric average, Dav = (D1/D2)1/2. For small perturbations away from a square channel, this is a plausible approach. However, at some point the aspect ratio becomes large enough that we need to account for the anisotropy of the blobs. Indeed, for sufficiently large aspect ratio, the problem transitions from the configuration in a nanochannel to that in a nanoslit.
The aspect ratio is thus a possible explanation for the deviation between experiments and theory. To rule out this possibility, we simulated the extension of chains in a wide range of aspect ratios for three different values of the geometric averaged width, Dav. As we see in Figure 7, changing the aspect ratio only leads to very small deviations in the extension, even out to D1/D2 = 5. As the experiments of Reisner et al.9 used aspect ratios 1 to approximately 1.5 and the pertinent data from Persson et al.34 are for aspect ratios up to 6.25, it appears that the error in using Dav is commensurate with other experimental errors, in particular measuring the size of the channel in the first place. The one caveat is in the Odijk regime, where we observe consistent deviations between the theory for an isotropic channel and the data obtained for a rectangular channel with Dav = 30nm in Figure 7. Although the geometric mean is smaller than the persistence length, increasing the aspect ratio at a fixed Dav requires that the larger channel dimension become commensurate with the persistence length. As the Odijk regime is valid only for D1,D2 ≪ lp, we would expect to see deviations in rectangular channels. These deviations are small, so we can conclude from Figure 7 that the geometric mean is an appropriate choice.
Figure 7.

Extension of the wormlike bead-rod model (w = 4.6nm, lp = 53nm) in nanochannels of D1-by-D2 rectangular cross section. The geometric average of the channel size is Dav = (D1D2)1/2. Symbols are simulation data for three different contour lengths: L = 1.03μm for Dav = 30nm (diamond), L = 2.58μm for Dav = 60nm (square), and L = 4.12μm for Dav = 141.4nm (circle). Solid lines are smooth Bezier curves to approximate the data trend. The dashed line refers to predictions for the Odijk regime24,25 where we used Dav = 30nm, w = 4.6nm, and lp = 53nm.
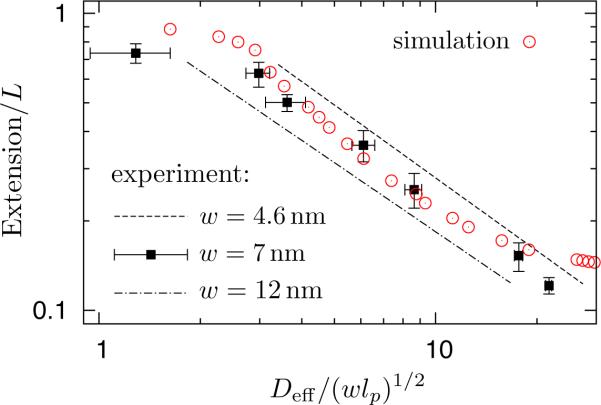
Having established that Dav is the correct metric, we decided to take a different approach to understand the difference between the theoretical and experimental results in Table 1. Let us assume the theory, and thus our simulations, are correct. In that case, we should be able to match any experimental data in the extended de Gennes regime (transition regime II) to our simulated data for L = 4.21μm and lp = 53nm by plotting the extension a function of Deff/(wlp)1/2. Moreover, since we showed in Figure 6 that the extended de Gennes regime and de Gennes regime have the same prefactor, experimental data in de Gennes regime should lie on a line extrapolated from our extended de Gennes regime data to larger channel diameters. We then treated the effective width for the experimental data as an adjustable parameter. Figure 8 shows the results for three different values of w, and the value w = 7.0nm appears to give a satisfactory fit. The experimental data for the three largest channels lie in either the de Gennes regime or the extended de Gennes regime, and their extensions agree with Eq. (3). The next three channel sizes (in decreasing order) are in transition regime I, while the smallest channel is the only one that appears to be in the Odijk regime. While our simulations provide a reasonable fit for the data in transition regime I, there is a substantial difference between Eq. (1) and the lone experiment in the Odijk regime. Given the paucity of data in the latter regime, we cannot identify with any certainty the reason for the discrepancy.
Figure 8.
Comparison of simulation (circle) and experimental data.9 The simulation data correspond to L = 4.12μm, w = 4.6nm and lp = 53nm in a square nanochannel, the same as that shown in Figure 6. The experimental data as a function of Deff = Dav − w were plotted using a persistence length lp = 57.5nm reported by Reisner et al.9 and different values for the effective width: w = 4.6nm (dashed line), w = 7.0nm (squared symbols) and w = 12nm (dash dotted line). For clarity, we only show the best power-law fits to the data for channel sizes ranging from 440nm to 60nm for w = 4.6nm and 12nm, a similar analysis to Reisner et al.9Deff/(wlp)1/2 = 10 corresponds to a real channel dimension of D = 160.7nm for w = 4.6nm and lp = 53nm and corresponds to D = 207.6nm for w = 7.0nm and lp = 57.5nm.
In Figure 8, the best agreement between experiments and simulation was obtained with an effective width of w = 7.0nm, which is somewhat smaller than the effective width w = 12nm produced by Stigter's theory18,19 for the buffer used in these experiments.9,16 Prior results give us reason to question the value (but not the order of magnitude) of Stigter's effective width; for DNA in slit-like confinement, combining Stigter's effective width theory with blob theory for the conformation captured the qualitative trends with ionic strength, but there were still quantitative differences between theory and experiment.16 While Stigter's theory is the only approach we know for estimating the effective width, it is not obvious that his model translates directly to our application. Stigter19 defined w such that the second virial coefficient for a system consisting of highly charged rods of some bare size a, oriented at right angles, matches the result for a system of neutral rods of size w. This choice makes sense for studying the solution thermodynamics of short, rod-like DNA. The Flory theory discussed in §2, as well as our simulation model, is predicated on the idea that each segment experiences a hard core repulsion if its separation from another segment is less than the distance w. While the appropriate value of w required to describe the configuration of a polyelectrolyte should be similar to that required to quantify the osmotic pressure, we do not see the theoretical basis for requiring that the values be identical. Indeed, we could equally as well propose that the effective width should be the quantity used to match the simulated extension to its experimental counterpart, which was the approach we pursued to create Figure 8. A deeper analysis could consider the the existence of depletion layers near channel walls and the induced orientational correlations between DNA segments.60 Alternatively, perhaps the best approach is to abandon the concept of an effective width entirely in favor of an explicit electrostatic interaction potential between segments, which seems to provide a good fit to experimental data in low ionic strength buffers.3
Our reinterpretation of the experimental data in Figure 8 points out a key issue in the computation of the exponents appearing in Table 1. If we assume that the simulations and theory are correct, then only the three largest channels actually lie in the de Gennes regime or the extended de Gennes regime. However, the exponent for the experiments9 was determined by assuming that a single power law fits the data for all but the smallest channel in Figure 8, corresponding to a lower bound of Dav = 69nm. Since several of these data points lie in transition regime I, where the scaling exponent is −1.02, it is unsurprising that the experimental exponents in Table 1 exceed the theoretical prediction. Rather, our analysis in Figure 8 indicates that the experiments agree with Eq. (3) so long as we remain within the range of validity of the corresponding Flory theory. This insight is a natural advantages of revisiting these experimental data after some time has passed; the theories for the extended de Gennes regime15,33 were published after the experimental data.9 Based on our analysis, analyzing the extended de Gennes regime requires data for channels larger than Dav ≈ 200nm. Such length scales are actually easier to reach than the sub-100 nm range.61
4.2.3 A comment on chain dynamics
In our study, we have focused entirely on the static properties of the chain under confinement. Since theoretical predictions of the mean extension are the same for both the de Gennes and extended de Gennes regimes, it is difficult to distinguish one from the other from the mean extension data alone. While there are only four different scaling laws for the chain configuration, there should be five regimes for the chain dynamics. This is because the confinement free energy for the de Gennes regime [Eq. (4)] and the extended de Gennes regime [Eq. (14)] lead to different effective Hookean spring constants for small fluctuations around the minimum free energy,38
| (24) |
For the de Gennes regime,1
| (25) |
whereas for the extended de Gennes regime,
| (26) |
Let us assume the same friction coefficient of the chain for these to regimes is proportional to the chain extension, ζ ~ 〈X〉. The corresponding relaxation time for the lowest vibration mode of the chain scales as
| (27) |
for the de Gennes regime, and
| (28) |
for the extended de Gennes regime. The latter scaling, τ ~ D−2/3, is closer to the experimental estimate9 of D−0.9±0.4 for channel sizes ranging from 140nm to 440nm than is the scaling of τ ~ D−1/3 for the de Gennes regime. However, as previous studies27,39,62–64 have revealed certain deviations from the scaling predictions of chain dynamics in the de Gennes regime [Eq. (27)], more studies are needed to validate Eq. (28) for the extended de Gennes regime.
The confinement free energy, and any corresponding dynamic properties, are ready evidence for the existence of an extended de Gennes regime. For example, Reccius et al.11 used the Flory free energy for the extended de Gennes regime, Eq. (14), to derive a model for DNA relaxation from a compressed state that describes their experimental data for λ-DNA in nanochannels of 100nm in width with a depth of 200nm. It is plausible that those experiments actually operated in the extended de Gennes regime. One also needs to be cautious in using dynamic data to identify a given regime. For example, experimental evidence that the mean equilibrium extension and the mean square fluctuations (which are estimated by kBT/keff) depend linearly on the chain length1 does not definitely prove that the experiment occurs in the de Gennes regime, since both Eq. (25) and Eq. (26) exhibit the same dependence on molecular weight.
5 Conclusions
Our results have confirmed Odijk's prediction15 of multiple transition regimes between deflection segments in strong confinement and isometric blobs in weak confinement. Table 3 summarizes, for each regime, the scaling law for the extension, the approximate value for the chain length required to enter the regime, and the relevant channel sizes. As the channel size increases, those chains that do not have sufficient contour length to remain on the universal curve begin a broad transition to their bulk extension. The latter effect explains the previous disagreements between theory and simulation, highlighted in Table 1. First, the apparent non-universal dependence on molecular weight near the end of the Odijk regime arises from chains that do not have sufficient length to enter transition regime I. If the chain is long enough, then the scaling exponent observed in previous simulations13,14 agrees with the result we obtained here for transition regime I. Second, when we simulated chains that possess enough contour length to enter the extended de Gennes regime (transition regime II), we recover the scaling predicted by Flory theory15,33 rather than the predictions of an alternate theory.35 In the context of the extension, the distinction between the de Gennes regime and extended de Gennes regime seems artificial, since both regimes are governed by the same scaling law and the extension must be continuous across the transition between regimes. However, the confinement free energies in the two regimes differ. We thus expect that the chain dynamics will allow us to distinguish between the two regimes. Such calculations are feasible but numerically intense.
Table 3.
Summary of the results for the different regimes of confinement in Figure 1. In the text, we normally refer to Transition II as the extended de Gennes regime. The minimum chain length is the size of the deflection segment or blob, as appropriate, and does not include numerical prefactors. The minimum chain length for entering regime I is unknown and there is no minimum chain length for the bulk. Based on Figure 3, the prefactor for the bulk extension should be between 1.5 and 2.2. The upper bound for D in the de Gennes regime is approximate.
| Regime | Extension (〈X〉) | Minimum Chain Length | Channel Size |
|---|---|---|---|
| Odijk | Eq. (1) | D 2/3 | D ≪ lp |
| I | D −1.02 | — | lp < D < 2lp |
| II | D (ν−1)/ν | ||
| de Gennes | D (ν−1)/ν | ||
| Bulk | Rg | — - | D > Rg |
We have also found reasonable agreement between our simulations and experimental data, provided that we use the effective width as a free parameter (albeit restricted to a region nearby the prediction from Stigter's theory18,19). Our results also support the use of the geometric average for mapping channels of rectangular cross-section onto square channels. Now that we are certain that there are, indeed, multiple transition regimes,15 it appears that there is no disagreement between theory and experiment. The limited extension data obtained from experiments in the extended de Gennes and the de Gennes regime are described by Eq. (3); including extension data from transition regime I tilts the slope to the higher value in Table 1. More experimental data in regimes governed by Eq. (3) would certainly strengthen our claim. Based on Figure 8, these data should be obtained in channels no smaller than Dav = 200nm. The corresponding dynamic data in such channels, measured either as a relaxation time or diffusion coefficient, should distinguish between the different regimes.
While we have made substantial progress in reconciling theory, simulation and experiments for DNA extension in nanochannels, our analysis leaves three intriguing, open questions. First, we do not have a theoretical basis for the scaling 〈X〉 ~ D−1.02 in transition regime I. As this scaling arises in both our model and a slightly different one14 in this size range, we suspect that it is a real scaling law, rather than a coincidence. Odijk15 predicted the existence of a transition regime between the Odijk regime and the extended de Gennes regime, but the scaling that we and Cifra14 observed does not seem to accord with Odijk's scaling theory. Second, there appears to be an inconsistency between the mechanical approximation for the global persistence length15,57 and the reduction in the chain extension after exiting the Odijk regime. It is possible that a single answer will resolve both of these open questions, since the predicted scaling law for transition regime I is intimately connected to the global persistence length.15 Third, the experimental data seem to be best fit with an effective width of 7 nm, which is somewhat smaller than the value of 12 nm predicted from Stigter's theory.18,19 We are optimistic that more experimental data, especially in the extended de Gennes regime, and detailed modeling of the electrostatic interactions of confined DNA3 will ultimately resolve this last question.
Acknowledgement
This work was supported by the NIH (R01-HG005216 and R21-RR031230) and was carried out in part using computing resources at the University of Minnesota Supercomputing Institute.
References
- (1).Tegenfeldt JO, Prinz C, Cao H, Chou S, Reisner WW, Riehn R, Wang YM, Cox EC, Sturm JC, Silberzan P, Austin RH. Proc. Natl. Acad. Sci. USA. 2004;101:10979–10983. doi: 10.1073/pnas.0403849101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (2).Jo K, Dhingra DM, Odijk T, de Pablo JJ, Graham MD, Runnheim R, Forrest D, Schwartz DC. Proc. Natl. Acad. Sci. USA. 2007;104:2673–2678. doi: 10.1073/pnas.0611151104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (3).Kim Y, Kim KS, Kounovsky KL, Chang R, Jung GY, dePablo JJ, Jo K, Schwartz DC. Lab Chip. 2011;11:1721–1729. doi: 10.1039/c0lc00680g. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (4).Chan EY, Goncalves NM, Haeusler RA, Hatch AJ, Larson JW, Maletta AM, Yantz GR, Carstea ED, Fuchs M, Wong GG, Gullans SR, Gilmanshin R. Genome Res. 2004;14:1137–1146. doi: 10.1101/gr.1635204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (5).Riehn R, Lu M, Wang Y-M, Lim SF, Cox EC, Austin RH. Proc. Natl. Acad. Sci. USA. 2005;102:10012–10016. doi: 10.1073/pnas.0503809102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (6).Das SK, Austin MD, Akana MC, Deshpande P, Cao H, Xiao M. Nucleic Acids Res. 2010;38:e177. doi: 10.1093/nar/gkq673. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (7).Meltzer RH, et al. Lab Chip. 2011;11:863–873. doi: 10.1039/c0lc00477d. [DOI] [PubMed] [Google Scholar]
- (8).Rasmussen KH, Marie R, Lange JM, Svendsen WE, Kristensen A, Mir KU. Lab Chip. 2011;11:1431–1433. doi: 10.1039/c0lc00603c. [DOI] [PubMed] [Google Scholar]
- (9).Reisner W, Morton KJ, Riehn R, Wang YM, Yu Z, Rosen M, Sturm JC, Chou SY, Frey E, Austin RH. Phys. Rev. Lett. 2005;94 doi: 10.1103/PhysRevLett.94.196101. 196101. [DOI] [PubMed] [Google Scholar]
- (10).Reisner W, Beech JP, Larsen NB, Flyvbjerg H, Kristensen A, Tegenfeldt JO. Phys. Rev. Lett. 2007;99 doi: 10.1103/PhysRevLett.99.058302. 058302. [DOI] [PubMed] [Google Scholar]
- (11).Reccius CH, Mannion JT, Cross JD, Craighead HG. Phys. Rev. Lett. 2005;95 doi: 10.1103/PhysRevLett.95.268101. 268101. [DOI] [PubMed] [Google Scholar]
- (12).Su T, Das SK, Xiao M, Purohit PK. PLoS ONE. 2011;6 doi: 10.1371/journal.pone.0016890. e16890. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (13).Cifra P, Benková Z, Bleha T. J. Phys. Chem. B. 2009;113:1843–1851. doi: 10.1021/jp806126r. [DOI] [PubMed] [Google Scholar]
- (14).Cifra P. J. Chem. Phys. 2009;131 doi: 10.1063/1.3271830. 224903. [DOI] [PubMed] [Google Scholar]
- (15).Odijk T. Phys. Rev. E. 2008;77 doi: 10.1103/PhysRevE.77.060901. 060901(R) [DOI] [PubMed] [Google Scholar]
- (16).Hsieh C-C, Balducci A, Doyle PS. Nano Lett. 2008;8:1683–1688. doi: 10.1021/nl080605+. [DOI] [PubMed] [Google Scholar]
- (17).Hsieh C-C, Doyle PS. Korea-Aust. Rheol. J. 2008;20:127–142. [Google Scholar]
- (18).Stigter D. J. Colloid Interface Sci. 1975;53:296–306. [Google Scholar]
- (19).Stigter D. Biopolymers. 1977;16:1435–1448. doi: 10.1002/bip.1977.360160705. [DOI] [PubMed] [Google Scholar]
- (20).Odijk T. J. Polym. Sci. B. 1977;15:477–483. [Google Scholar]
- (21).Skolnick J, Fixman M. Macromolecules. 1977;10:944–948. [Google Scholar]
- (22).Bustamante C, Marko JF, Siggia ED, Smith S. Science. 1994;265:1599–600. doi: 10.1126/science.8079175. [DOI] [PubMed] [Google Scholar]
- (23).Rubinstein M, Colby RH. Polymer Physics. Oxford University Press; NY: 2003. [Google Scholar]
- (24).Yang Y, Burkhardt TW, Gompper G. Phys. Rev. E. 2007;76 doi: 10.1103/PhysRevE.76.011804. 011804. [DOI] [PubMed] [Google Scholar]
- (25).Burkhardt TW, Yang Y, Gompper G. Phys. Rev. E. 2010;82 doi: 10.1103/PhysRevE.82.041801. 041801. [DOI] [PubMed] [Google Scholar]
- (26).Wall FT, Seitz WA, Chin JC, de Gennes PG. Proc. Natl. Acad. Sci. USA. 1978;75:2069–2070. doi: 10.1073/pnas.75.5.2069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (27).Jendrejack RM, Schwartz DC, Graham MD, de Pablo JJ. J. Chem. Phys. 2003;119:1165–1173. doi: 10.1063/1.1637331. [DOI] [PubMed] [Google Scholar]
- (28).Odijk T. Macromolecules. 1983;16:1340–1344. [Google Scholar]
- (29).de Gennes P. Scaling Concepts in Polymer Physics. Cornell University Press; Ithaca, NY: 1979. [Google Scholar]
- (30).Daoud M, de Gennes P. J. Phys. (Paris) 1977;38:85–93. [Google Scholar]
- (31).Brochard F, de Gennes PG. J. Chem. Phys. 1977;67:52–56. [Google Scholar]
- (32).Li B, Madras N, Sokal A. J. Stat. Phys. 1995;80:661–754. [Google Scholar]
- (33).Brochard-Wyart F, Tanaka T, Borghi N, de Gennes PG. Langmuir. 2005;21:4144–4148. doi: 10.1021/la0474114. [DOI] [PubMed] [Google Scholar]
- (34).Persson F, Utko P, Reisner W, Larsen NB, Kristensen A. Nano Lett. 2009;9:1382–1385. doi: 10.1021/nl803030e. [DOI] [PubMed] [Google Scholar]
- (35).Zhang C, Zhang F, van Kan JA, van der Maarel JRC. J. Chem. Phys. 2008;128 doi: 10.1063/1.2937441. 225109. [DOI] [PubMed] [Google Scholar]
- (36).Cifra P, Benkova Z, Bleha T. Faraday Discuss. 2008;139:377–392. doi: 10.1039/b716546c. [DOI] [PubMed] [Google Scholar]
- (37).Flory PJ. Principles of Polymer Chemistry. Cornell University Press; Ithaca, NY: 1953. [Google Scholar]
- (38).Jun S, Thirumalai D, Ha B-Y. Phys. Rev. Lett. 2008;101 doi: 10.1103/PhysRevLett.101.138101. 138101. [DOI] [PubMed] [Google Scholar]
- (39).Jung Y, Jun S, Ha B-Y. Phys. Rev. E. 2009;79 doi: 10.1103/PhysRevE.79.061912. 061912. [DOI] [PubMed] [Google Scholar]
- (40).Schaefer DW, Joanny JF, Pincus P. Macromolecules. 1980;13:1280–1289. [Google Scholar]
- (41).Moon J, Nakanishi H. Phys. Rev. A. 1991;44:6427–6442. doi: 10.1103/physreva.44.6427. [DOI] [PubMed] [Google Scholar]
- (42).Wang J, Gao H. J. Chem. Phys. 2005;123 doi: 10.1063/1.2008233. 084906. [DOI] [PubMed] [Google Scholar]
- (43).Weeks JD, Chandler D, Andersen HC. J. Chem. Phys. 1971;54:5237–5247. [Google Scholar]
- (44).Wagner F, Lattanzi G, Frey E. Phys. Rev. E. 2007;75 doi: 10.1103/PhysRevE.75.050902. 050902. [DOI] [PubMed] [Google Scholar]
- (45).Grassberger P. Phys. Rev. E. 1997;56:3682–3693. [Google Scholar]
- (46).de Pablo JJ, Yan Q, Escobedo FA. Annu. Rev. Phys. Chem. 1999;50:377–411. doi: 10.1146/annurev.physchem.50.1.377. [DOI] [PubMed] [Google Scholar]
- (47).Verdier PH, Stockmayer WH. J. Chem. Phys. 1962;36:227–235. [Google Scholar]
- (48).Wall FT, Mandel F. J. Chem. Phys. 1975;63:4592–4595. [Google Scholar]
- (49).Kumar SK, Vacatello M, Yoon DY. J. Chem. Phys. 1988;89:5206–5215. [Google Scholar]
- (50).Madras N, Sokal AD. J. Stat. Phys. 1988;50:109–186. [Google Scholar]
- (51).Wang Y, Peters GH, Hansen FY, Hassager O. J. Chem. Phys. 2008;128 doi: 10.1063/1.2842073. 124904. [DOI] [PubMed] [Google Scholar]
- (52).Chen Y-L, Graham MD, de Pablo JJ, Randall GC, Gupta M, Doyle PS. Phys. Rev. E. 2004;70 doi: 10.1103/PhysRevE.70.060901. 060901R. [DOI] [PubMed] [Google Scholar]
- (53).van der Maarel JRC. Introduction to Biopolymer Physics. World Scientific; Singapore: 2008. [Google Scholar]
- (54).Godfrey JE, Eisenberg H. Biophysical Chemistry. 1976;5:301–318. doi: 10.1016/0301-4622(76)80042-7. [DOI] [PubMed] [Google Scholar]
- (55).Smith DE, Perkins TT, Chu S. Macromolecules. 1996;29:1372–1373. [Google Scholar]
- (56).Robertson RM, Laib S, Smith DE. Proc. Natl. Acad. Sci. USA. 2006;103:7310–7314. doi: 10.1073/pnas.0601903103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (57).Odijk T. J. Chem. Phys. 2006;125 doi: 10.1063/1.2400227. 204904. [DOI] [PubMed] [Google Scholar]
- (58).Raphael E, Pincus P. J. Phys. II France. 1992;2:1341–1344. [Google Scholar]
- (59).Benoit H, Doty P. J. Phys. Chem. 1953;57:958–963. [Google Scholar]
- (60).Stroobants A, Lekkerkerker HNW, Odijk T. Macromolecules. 1986;19:2232–2238. [Google Scholar]
- (61).Cao H, Yu ZN, Wang J, Tegenfeldt JO, Austin RH, Chen E, Wu W, Chou SY. Appl. Phys. Lett. 2002;81:174–176. [Google Scholar]
- (62).Harden JL, Doi M. J. Phys. Chem. 1992;96:4046–4052. [Google Scholar]
- (63).Arnold A, Bozorgui B, Frenkel D, Ha B-Y, Jun S. J. Chem. Phys. 2007;127 doi: 10.1063/1.2799513. 164903. [DOI] [PubMed] [Google Scholar]
- (64).Graham MD. Annu. Rev. Fluid Mech. 2011;43:273–298. [Google Scholar]