Surface–Region Context in Optimal Multi-Object Graph-based Segmentation: Robust Delineation of Pulmonary Tumors

Abstract

Multi-object segmentation with mutual interaction is a challenging task in medical image analysis. We report a novel solution to a segmentation problem, in which target objects of arbitrary shape mutually interact with terrain-like surfaces, which widely exists in the medical imaging field. The approach incorporates context information used during simultaneous segmentation of multiple objects. The object–surface interaction information is encoded by adding weighted inter-graph arcs to the graph. A globally optimal solution is achieved by solving a single maximum flow problem in a low-order polynomial time. The method’s performance was evaluated in robust delineation of lung tumors in megavoltage cone-beam CT images in comparison with an expert-defined independent standard. The evaluation showed that our method generated highly accurate tumor segmentations. Compared with the conventional graph-cut method, our new approach provided significantly better results (p < 0.001). The Dice coefficient obtained by the conventional graph-cut approach (0.76 ± 0.10) was improved to 0.84 ± 0.05 when employing our new method for pulmonary tumor segmentation.

1 Introduction

Medical image segmentation allows analyzing medical image data in a quantitative manner, which plays a vital role in numerous biomedical applications. Recently, graph-based methods with a global energy optimization property have attracted considerable attentions (e.g., [1–3]). Despite their widespread use for image segmentation, they may have problem in the presence of multiple target objects with weak boundaries, similar intensity information and serious mutual interaction among each other [4].

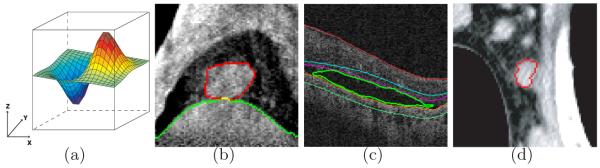
To solve the problem of multi-object segmentation with mutual interaction, Boykov et al. [5] developed a multi-region framework based on a graph cut method. An interaction term is added into the energy function, which incorporated the geometric interactive relationship between different regions. Their method is topologically flexible and shares some elegance with the level set methods. Li et al. [3] proposed an approach called “graph search” for globally optimal segmentation of multiple terrain-like surfaces(Fig.1(a)), which was successfully extended to a wide spectrum of applications [6, 4, 7, 8]. For each target surface a corresponding geometric graph is constructed. The relative position information between pairs of surfaces is enforced by adding weighted arcs between corresponding graphs. Multiple surfaces can be detected simultaneously in a globally optimal fashion by solving a single maximum flow problem in a transformed graph. Compared with the graph cut approach, this method requires no human interaction and provides easier way to incorporate shape prior information [9]. The major limitation of Li et al.’s family of the graph search method lies in the fact that it is non-trivial to deal with the region of complicated topology without an approximate segmentation of the region’s surface.

Fig. 1.

(a) The terrain-like surface intersects each (x, y)-column exactly one time. (b) Example slices of a lung tumor (red) in megavoltage cone-beam CT. The tumor is attached/adjacent to the diaphragm (green). (c) Example slices of a fluid-filled region (green) in retinal optical coherence tomography (OCT). The fluid region is surrounded by intraretinal layers. (d) Example slices of a lymph node (red) in X-ray CT data. The lymph node is connected to surrounding soft tissues.

In this paper, we consider a special structure consisting of mutually interacting terrain-like surfaces and regions of “arbitrary shape”. Here “arbitrary shape” means that the target region itself does not have any specific preferred shape. Mutual interaction exists between the pairs of the terrain-like surfaces and the regions in a way that their topological information and relative positions are usually known beforehand. Incorporating these interrelations into the segmentation plays a significant role for accurate segmentation when target surfaces and regions lack clear edge and have similar intensity distribution. Fig. 1(b),(c) and (d) show some typical medical imaging examples.

The main idea is to make use of the advantages from both the graph cut method [1] and Li et al.’s graph search method [3]. For regions of arbitrary shape we construct a corresponding graph following the graph cut method making use of its shape flexibility. For terrain-like surfaces the graph is built based on the graph search approach, which requires no initial seeds and provides good shape control. The key is to introduce an additional interaction term in the energy function, which can be implemented by adding inter-graph arcs between the pairs of different types of graphs, enforcing known interacting information between the target terrain-like surfaces and the regions of arbitrary shape. Then a globally optimal solution can be obtained by solving a single maximum flow problem, yielding the simultaneous segmentation of surfaces and regions.

Our paper is organized as follows. In Section 2 we describe our proposed framework in details. In Section 3-5 a quantitative and comparative performance evaluation over a representative number of experiments with Mega-Voltage Cone Beam CT (MVCBCT) images for lung tumor is performed. Section 6 presents concluding remarks.

2 Method

To simplify the presentation and to ease the understanding of our method, let us first consider the task of detecting one terrain-like surface and one region of arbitrary topology with mutual interaction between each other. Note that the same principles used for this illustration are directly applicable to multiple pairs of surfaces and regions with interactions between those two kinds of targets.

2.1 Energy function

Consider a volumetric image $\mathcal{I}(X,Y,Z)$ of size X×Y ×Z. For each (x, y) pair the voxel subset {v(x, y, z)ȣ0 ≤ z < Z} forms a column parallel to the z-axis, denoted by p(x, y). Each column has a set of neighborhoods for a certain neighbor setting ${\mathcal{N}}_c$[3]. A terrain-like surface of particular interest, denoted as S_T , is the surface that intersects each column p(x, y) at exactly one voxel. It can be defined as a function S_T (x, y), mapping each (x, y) pair to its z-value. The target region of arbitrary shape, denoted as R_A, includes all the voxels v inside the region. Fig. 2(a) shows one example 2-D slice from a 3-D image.

Fig. 2.

An example 2-D slice from a 3-D image. (a) The terrain-like surface S_T and the region of arbitrary shape R_A, S_T (p) = 2, S_T (q) = 3. (b) Incorporation of the interaction constraint that the region R_A tends to be positioned “lower” than the terrain-like surface S_T . For voxels v ∈ R_A and S_T (p) − z(v) < d (yellow voxels), a penalty w_v is given; d is set as 1. (c)The interaction constraint that R_A tends to be positioned “higher” than S_T . For voxels v ∈ R_A(l_v = 1) and z(v) − S_T (p) < d (yellow voxels), penalty w_v is given; d is set as 1.

To explain the employed cost function, let us start with the energy terms used for detecting the terrain-like surface, which are similar in form to those described in [9]. Suppose an edge-based cost c_v is assigned to each voxel v ∈ I, which is inversely related to the likelihood that the desired surface S_T indeed contains this voxel. For any pair of neighboring columns (p, q) ∈ $(p,q)\in \mathcal{N}$ a convex function penalizing the surface shape change of S_T on p and q is expressed as f_p,q(S_T (p) − S_T (q)). Then the energy term E_gs takes the form

$$E_{gs}\left(S_T\right)=\sum _{v\in S_T}{c}_v+\sum _{(p,q)\in {\mathcal{N}}_c}{f}_{p,q}\left(S_T\right(p)-S_T(q\left)\right).$$ (1)

For segmentation of the target region R_A we employ the well-known binary graph cut energy [1, 5]. Let l denote the binary variables assigned for each voxel, indexed as l_v over voxels v ∈ I. In our notation, l_v = 1 means that v belongs to the target region R_A and l_v = 0 means that v belongs to the background. The graph cut energy E_gc is expressed as

$$E_{gc}\left(R_A\right)=\sum _{v\in I}{D}_v\left(l_v\right)+\sum _{(v_i,v_j)\in {\mathcal{N}}_v}{V}_{i,j}(l_i,l_j),$$ (2)

where D_v is the data term measuring how well the label l_v fits the voxel v given the image data. ${\mathcal{N}}_v$ defines the neighboring relationship between voxels, and the boundary energy term V_i,j(l_i, l_j) is the penalty of assigning the neighboring voxels (v_i, v_j) to labels l_i and l_j, respectively.

As mentioned above, incorporation of known interrelations between terrain-like surface S_T and object R_A plays a key role for accurate segmentation. To enforce a priori object–surface interaction information, we add an interaction term E_interaction(S_T ,R_A) to our energy function and the energy function takes the form

$$E\left(S\right)=E_{gs}\left(S_T\right)+E_{gc}\left(R_A\right)+E_{\text{interaction}}(S_T,R_A).$$ (3)

Our objective is to find the optimal set S = {S_T ,R_A} such that the above energy is minimized.

2.2 Incorporation of geometric interactions

In this section, we specify the geometric interactions incorporated in our framework between the target surface S_T and the region R_A, and show how to enforce as the interaction energy term E_interaction(S_T ,R_A). We start with the case that the region R_A tends to be lower than the terrain-like surface S_T with a given distance d. For any violating voxels in R_A, a penalty is given. More specifically, let z(v) denote the z coordinate for voxel v. S_T (p) is the z-value for the surface S_T on column p, representing the “height” of the surface on that column. Then for any voxel v ∈ p, if v ∈ R_A and S_T (p) − z(v) < d, a penalty w_v is given (Fig.2(b)). Our interaction energy term takes the form

$$E_{\text{interaction}}(S_T,R_A)=\sum _{p\in \mathcal{I}}\sum _{\begin{array}{c}\hfill v\in p\hfill \\ \hfill S_T\left(p\right)-z\left(v\right)<d\hfill \end{array}}{w}_v{l}_v.$$ (4)

For the constraint that R_A is a priori expected to be positioned “higher” than the terrain-like surface S_T , a similar formulation is employed. For any voxel v ∈ p, if v ∈ R_A(l_v = 1) and z(v) − S_T (p) < d, a penalty w_v is given (Fig. 2(c)). Our interaction energy term then takes the form

$$E_{\text{interaction}}(S_T,R_A)=\sum _{p\in \mathcal{I}}\sum _{\begin{array}{c}\hfill v\in p\hfill \\ \hfill z\left(v\right)-S_T\left(p\right)<d\hfill \end{array}}{w}_v{l}_v.$$ (5)

2.3 Graph construction

Our graph transformation scheme formulates the energy minimization problem as a single computation of maximum flow in the graph.

For the graph cut energy term E_gc(S_T ) a sub-graph G_R(N_R,A_R) is built using the method described in [1]. Every voxel $v\in \mathcal{I}$ has a corresponding node n_R ∈ N_R. Two additional nodes, the source (object) s and the sink (background) t, are added. Each node n_R has one t-link to each of the source and sink, which enforces the data-term energy. Each pair of neighboring nodes is connected by an n-link, which encodes the boundary energy term. The minimum-cost s-t cut divides the graph G_R into two parts: All nodes belonging to the target object are included in the source set and all background nodes are in the sink set.

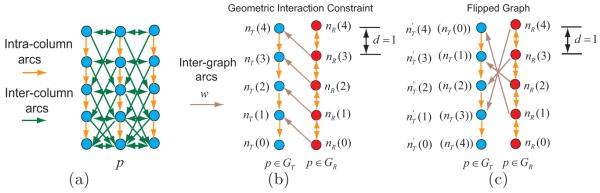
For the graph search energy term E_gs(S_T ) a sub-graph G_T (N_T ,A_T ) is constructed, which follows the method described in [10, 4]. Every node n_T (x, y, z) ∈ N_T corresponds to exactly one voxel $v(x,y,z)\in \mathcal{I}$. The positions of nodes reflect the positions of corresponding voxels in the image domain. Two types of arcs are added to the graph: (1) The intra-column arcs with +∞ weight serve to enforce the monotonicity of the target surface S_T ; and (2) the inter-column arcs incorporate the shape-prior penalties f_p,q between the neighboring columns p and q. Each node is assigned a weight w_n such that the total weight of a closed set in the graph G_T equals to the edge-cost term in E_gs. A typical graph G_T is shown in Fig. 3(a). Then, as in [10, 4], each node n_T is connected to either the source s by the arc with weight −w_n if w_n < 0 or the sink t by the arc with weight w_n if w_n > 0. Note that the source s and the sink t are the same nodes used in G_R for the implementation of the graph cut energy term. Using this construction, we merge the two sub-graphs G_R and G_T as a single s-t graph G. The original energy minimization can be achieved by solving a maximum flow problem in the graph. The target surface S_T can be defined by the minimum-cost s-t cut in the graph. All nodes in G_T above surface S_T belong to the sink set and all nodes on or below S_T belong to the source set of the cut [10].

Fig. 3.

(a) Graph construction of G_T (N_T ,A_T ) for the graph search energy term E_gs(S_T ). Two types of arcs are introduced: intra-column arcs (yellow arrows) and inter-column arcs (green arrows). (b) Incorporation of geometric interaction constraints by adding inter-graph arcs (brown arrows). The region R_A tends to be lower than the terrain-like surface S_T with a distance of d = 1; n_T (i) and n_R(i) correspond to the same voxel in original image. (c) The flipped graph for constraints that R_A tends to be higher than the surface S_T with a distance of d = 1. $n_T^{\prime }\left(i\right)$ and n_R(Z−i−1) correspond to the same voxel in the original image.

To incorporate geometric interaction constraints, additional inter-graph arcs are added between two sub-graphs. We begin with the case that region R_A tends to be lower than the terrain-like surface S_T with a given distance d. If n_R(x₁, y₁, z₁) in the subgraph G_R belongs to the source set (labeled as “object”) and n_T (x₁, y₁, z₁+d) in the subgraph G_T belongs to the sink set, which indicates that S_T (x₁, y₁)−z₁ < d, a penalty w contributes to the objective energy function. That can be enforced by adding a directed arc with a weight of w from each node n_R(x, y, z) to n_T (x, y, z + d), as shown in Fig. 3(b).

To enforce the constraint that R_A tends to be higher than S_T with distance d, a “flip” operation is involved. A transformed graph $G_T^{\prime }(N_T^{\prime },A_T^{\prime })$ is constructed, in which a node $n_T^{\prime }(x,y,z)$ corresponds to a voxel v(x, y,Z − z − 1) in the image $\mathcal{I}$. The interaction penalty is given by adding a directed arc with weight w from n_R(x, y, z) to $n_T^{\prime }(x,y,Z-z+d-1)$, which is associated with the voxel v(x, y, z − d) in original image. Fig. 3(c) shows the flipped graph.

Once the graph is constructed, a globally optimal solution can be found by solving a single maximum flow problem, which minimizes the total energy E(S) in a low-order polynomial time.

3 Application for lung tumor segmentation on MVCBCT image

In this section, we exemplify the application of our method on lung tumor segmentation from MVCBCT images. MVCBCT is a promising technique used in clinic for daily imaging of patients [11] for lung tumor radiotherapy. Successful segmentation of lung tumors from the respiratory correlated 3-D images reconstructed from the projection data of MVCBCT scans can provide important information of tumor motion and volume changes, which allows better delineation of lung tumors for radiation therapy [12, 13].

Here we mainly focus on the segmentation of the primary lung tumor from the reconstructed MVCBCT images, which is a very challenging work. First, the quality of the MVCBCT images is poor. Serious noise interference exists. Second, the lung tumor is frequently located next to the lung surface, the adjacent tissues have a similar intensity profile, and no clear boundary exists in-between. To overcome those difficulties, our new approach was employed for simultaneous segmentation of the lung primary tumor and the adjacent boundary.

3.1 Initialization

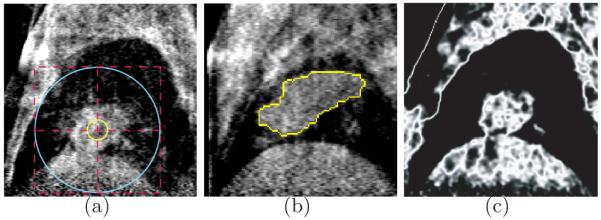
As the initialization step, one center point and two radii were required as the user input, from which two spheres were generated. The smaller one was required to be completely inside the tumor and the larger one was required to be completely outside the tumor. Fig. 4(a) shows a typical example. The segmentation was then conducted on the bounding box area of the larger sphere.

Fig. 4.

(a) One typical example of the initialization step in sagittal view. The yellow sphere lies inside the tumor and the blue sphere completely contains the tumor. The cross point indicates the given center point. (b) The tumor (yellow) lies adjacent to both the diaphragm and the upper boundary of the lung. (c) The cost image for data term of the graph cut energy. The higher intensity value indicates the larger probability that the voxel belongs to the tumor.

3.2 Simultaneous segmentation of lung boundary and tumor

The graph is constructed using the method described in Section 2.3, which contains two sub-graphs: G_T for lung boundary detection and G_R for tumor segmentation. To construct G_T , the user also need to interactively define the direction from which the tumor is adjacent to the lung boundary. In certain cases the tumor may be adjacent to the lung surface from two directions, as shown in Fig. 4(b). In this situation, we segment the tumor and two boundary surfaces together. Three sub-graphs are constructed accordingly: G_T1 and G_T2 for detection of lung boundaries from two directions; G_R for tumor segmentation. The geometric interactions are enforced between two pairs of graphs: (G_T1, G_R) and (G_T2, G_R).

Cost design for G_T

For lung boundary detection a gradient-based cost function was employed for edge-based costs. The negative magnitude of the gradient of the image $\mathcal{I}$ was computed at each voxel: $c(x,y,z)=-\mid \nabla \mathcal{I}\mid$. Note that the intensities inside the lung are generally lower than surrounding tissues, a Sobel kernel was used to favor a bright-to-dark or dark-to-bright transition depending on the direction of the target surface. A second order shape prior penalty was employed with the form: f(h) = β·h², where β was a constant parameter. The shape prior penalty penalized the change of the surface topology: h = S_T (p) − S_T (q) between neighboring columns p and q.

Cost design for G_R

For tumor detection the data term D_v for voxel v was designed as follows: For all voxels lying inside of the smaller circle, which belong to the object, D_v(l_v = 1) = 0, D_v(l_v = 0) = +∞. Similarly, for all voxels outside the larger circle D_v(l_v = 1) = +∞, D_v(l_v = 0) = 0. For all other voxels the intensity distribution for tumor followed Gaussian distribution. The mean intensity value $\stackrel{‒}{i}$ and the standard deviation value σ were obtained from all the voxels inside of the smaller circle. For voxel v with intensity i_v the data term was given as

$$D_v(l_v=1)=-\log \mathit{Pr}(i_v\mid l_v=1)\propto \frac{{(i_v-\stackrel{‒}{i})}^2}{{\sigma }^2},$$ (6)

$$D_v(l_v=0)=-\log (1-\mathit{Pr}(i_v\mid l_v=1\left)\right)\propto -\log (1-\exp (-\frac{{(i_v-\stackrel{‒}{i})}^2}{{\sigma }^2}\left)\right).$$ (7)

A typical cost image for data term is shown in Fig. 4(c).

For the boundary penalty a gradient-based cost function was used with the similar form as described in [1]

$$w_{ij}=-\log (1-\exp (\frac{-{\mid \nabla \mathcal{I}\mid }^2(i,j)}{2{\sigma }_g^2}\left)\right),$$ (8)

where w_ij corresponds to the weight of the n-link arc between neighboring voxels v_i and v_j; ${\mid \nabla \mathcal{I}\mid }^2(i,j)$ denotes the squared gradient magnitude.

Cost design for interaction constraint

For the geometric interaction constraint we required that the minimum distance between the target tumor and the lung boundary be at least one. A hard constraint is enforced with d = 1 and w_v = +∞.

4 Experimental Methods

The performance evaluation of the reported method was carried in 20 MVCBCT scans obtained from three patients with non-small cell lung cancer. Each set of patient MVCBCT scans was acquired longitudinally over eight weeks of radiation therapy treatment. For each scan two volumetric images were reconstructed, one for full-exhalation phase and one for full-inhalation phase, resulting in 40 images [13]. The size of the reconstructed images was 128 × 128 × 128 voxels with cubic voxel sizes of 1.07 × 1.07 × 1.07 mm³. Out of the 40 datasets, 2 were rejected for poor image quality by experts prior to any work reported here [13] and our experiments were conducted on the remaining 38 datasets.

Surfaces of lung tumors were obtained by expert manual tracing as reported in [13] and served as the independent standard for assessing segmentation correctness of our approach. The employed values of the above-described segmentation method parameters were selected empirically. The same parameter values of β = 5, d = 1, and σ_g = 10 were applied to all analyzed datasets.

The segmentation performance was assessed using the Dice similarity coefficient (DSC). DSC = 2∣V_m⋂V_c∣/(∣V_m∣ + ∣V_c∣), where V_m denotes the volume of the independent standard and V_c denotes the volume of the computer-determined object. All DSC values were computed in 3-D.

To determine the performance of our novel surface-and-region segmentation approach in comparison with a conventional approach of solely using a graph cut method to detect the tumor without simultaneously segmenting associated lung boundary surfaces, these two approaches were applied to all 38 MVCBCT images with identical spherical initialization (Fig. 4) and the obtained DSC performance indices were compared for the two methods. Statistical significance of the observed differences was determined using Student t-test for which p value of 0.05 was considered significant.

5 Results

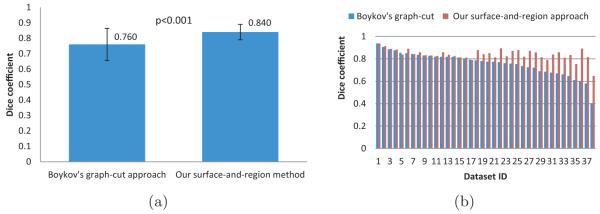
Our simultaneous surface–region segmentation method as well as Boykov’s conventional graph-cut segmentation method were applied to all 38 MVCBCT images for which the independent standard was available. Our approach achieved tumor segmentation correctness characterized by DSC = 0.840 ± 0.049 while the conventional approach yielded statistically significantly lower segmentation performance of DSC = 0.760 ± 0.104 (p < 0.001). Fig. 5(a) displays these overall results graphically as Mean±stdev.

Fig. 5.

Quantitative and comparative performance evaluation based on computed DSC in 38 volumetric MVCBCT images. (a) Overall tumor segmentation performance of Boykov’s graph cut approach and our new surface-and-region method. (b) Dice coefficients for all 38 datasets ordered according to the performance of the conventional graph-cut approach (blue). Note the uneven character of the segmentation performance for the conventional method compared to the highly-robust segmentation performance of the new approach.

Fig. 5(b) shows the pairwise performance comparisons for all 38 datasets, ordered according to the performance of the conventional approach. Fig. 5(b) thus clearly demonstrates that the performance of the conventional method is very uneven in the analyzed data set. In contrary, our new approach not only shows an overall improvement of the segmentation, it also demonstrates that the segmentation performance is very similar for all tumors in the entire set of the 38 analyzed images, thus showing a markedly higher robustness of the new approach resulting from the incorporation of image-based surface context.

Fig. 6 shows a typical outcome of our new tumor segmentation method and gives visual comparison with the independent standard. Fig. 7 shows tumor segmentation results obtained using the two compared methods in a difficult image, in which the tumor is closely adjacent to the lung surface from two directions. Fig. 7(b) shows a segmentation failure of the conventional approach while Figs. 7(c,d) show correctly segmented tumor using our new method.

Fig. 6.

Typical tumor segmentation examples. (a) one 2-D slice of 3-D MVCBCT image with outlines of spherical initialization. (b) Manual segmentation of the lung tumor − independent standard. (c) Simultaneous region-and-surface segmentation of the diaphragm (green) and the lung tumor (blue) using our new approach showing excellent segmentation performance − DSC = 0.878. (d) The 3-D representation of the diaphragm (green) and the tumor (blue).

Fig. 7.

Performance comparison in a difficult image. (a) Independent standard obtained by manual segmentation and shown in one 2-D slice of the 3-D volume. (b) Tumor segmentation failure resulting from the conventional graph cut method − DSC = 0.689. (c) Tumor segmentation obtained using our new method − segmented lung surfaces are shown in yellow and green, tumor surface is in blue − DSC = 0.814.

Current non-optimized implementation requires about 5 minutes on a Linux workstation (3 GHz, 32 GB memory). The run time decreases to less than 10 s when working with downsampled images for which voxel sizes doubled along each of the x, y, and z directions with only a limited segmentation performance penalty (DSC₂ = 0.826 ± 0.046).

6 Discussion and Conclusion

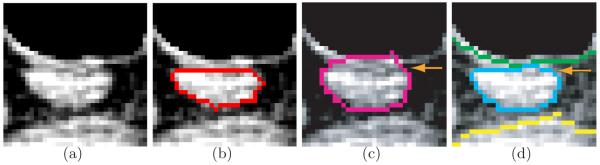
We presented a novel graph-based framework incorporating surface-region context information to solve the segmentation problem of a special structure having target objects of arbitrary topology mutually interacting with terrain-like surfaces, which widely exists in medical imaging fields. The proposed approach was successfully applied to lung tumor segmentation in MVCBCT. The result shows the power of our algorithm. To demonstrate the diverse applications of our framework, we also applied our method to lymph node segmentation in CT image. Fig. 8 shows an illustrative result.

Fig. 8.

Feasibility examples of lymph node segmentation in X-ray CT data. (a) One 2-D slice from 3-D CT image. (b) Manual segmentation of lymph node boundaries. (c) Segmentation failure resulting from the conventional graph-cut method. (d) Simultaneous region–surface segmentation of the lymph node (blue) and surrounding tissues (green and yellow) using our new approach showing excellent segmentation performance. The improvement is indicated by the arrow.