Abstract
The thermochemical properties ΔH o n , ΔS o n, and ΔG o n for the hydration of sodiated and potassiated monosaccharides (Ara = arabinose, Xyl = xylose, Rib = ribose, Glc = glucose, and Gal = galactose) have been experimentally studied in the gas phase at 10 mbar by equilibria measurements using an electrospray high-pressure mass spectrometer equipped with a pulsed ion beam reaction chamber. The hydration enthalpies for sodiated complexes were found to be between −46.4 and −57.7 kJ/mol for the first, and −42.7 and −52.3 kJ/mol for the second water molecule. For potassiated complexes, the water binding enthalpies were similar for all studied systems and varied between −48.5 and −52.7 kJ/mol. The thermochemical values for each system correspond to a mixture of the α and β anomeric forms of monosaccharide structures involved in their cationized complexes.
Key words: Hydration energies, Cationized monosaccharides, High-pressure mass spectrometry
Introduction
Carbohydrates constitute the most abundant and structurally diverse class of biological compounds in nature. They are important in numerous processes, such as energy storage, molecular recognition, and mediation in many biological functions [1–3]. Carbohydrates form part of the backbone of RNA and DNA molecules, and they are also linked to proteins and lipids as glycoproteins and glycolipids [4]. The complex functions of carbohydrate molecules are attributed to their outstanding conformational variety and flexibility. Noncovalent interaction between carbohydrates and neighboring molecules, such as metal ions, water, or other noncovalently bound molecules, can effectively stabilize favored conformations of these complexes and play a vital role in molecular recognition processes. Therefore, exploration and characterization of water–carbohydrate interactions as well as noncovalently bound metal ion-carbohydrate systems and their microhydrated complexes is an essential step in understanding the origins of the biochemical functionality of carbohydrates. Sodium and potassium cations are involved in the transport of amino acids and monosaccharides across cell membranes, and play an important role in physiologic and pathologic processes in the extracellular environment.
A number of techniques, such as NMR [5, 6], neutron-scattering [7], terahertz absorption spectroscopy [8], and computer simulations [8–11] have been used to study the dynamics and hydration properties of different monosaccharide units and short oligosaccharides in water.
Water interactions with a variety of carbohydrate molecules have also been studied in the gas phase in the absence of solvent effects to enable the intrinsic behavior of the system to be examined and evaluated in detail. Such gas phase studies eliminate the effects of the surrounding solvent that complicate and may mask behavior of the system in the condensed phase. Hydrogen bonding and the conformational structures of phenyl-substituted mono- and oligosaccharides and their hydrated complexes have been widely investigated by Simons and co-workers [12–17] by a combination of mass-selected resonant two-photon ionization (R2PI), UV hole burning, IR-dip, spectroscopy experiments, and computation through molecular mechanics, density functional theory (DFT) and ab initio calculations. These studies reveal that the water binding site(s) to the preferred carbohydrate conformations and structures of their hydrated complexes are dominated by cooperative hydrogen bonding.
A number of studies have been conducted on the interaction of monosaccharides with alkali ions in the gas phase. Bothner et al. characterized monosaccharide/alkali cation (Li+, Na+, K+, Rb+, or Cs+) complexes of D-glucose, D-galactose, D-mannose, D-fructose, and a deuterated analog of glucose, 6,6-D-glucose-d2, using different mass spectrometric techniques and molecular modeling [18]. Cerda and Wesdemiotis [19] used the kinetic method and ab initio calculations to investigate the thermochemistry and structures of sodiated mono- and disaccharide stereoisomers. Their results indicate that each saccharide solvates the sodium ion differently, depending on the donor groups available. More recently, Heaton and Armentrout [20] investigated the sodium cation complexes of arabinose, xylose, glucose, and galactose using a guided ion beam tandem mass spectrometer equipped with an electrospray ionization source, and quantum chemical calculations. They found that the experimental Na+ binding affinities follow the trend arabinose < xylose < glucose < galactose.
Because biomolecules and metal ions are surrounded by water in living systems, interactions of their complexes with water molecules are of significant importance in understanding the molecular mechanisms involved in biological processes. The structures and energetics of hydrated amino acid/alkali cation complexes have been studied using blackbody dissociation (BIRD) experiments [21–29], guided ion beam studies [30–32], high-pressure mass spectrometry [33, 34], infrared multiple photon dissociation (IRMPD) spectroscopy [29, 35], and calculations [21–32, 35, 36]. Very recently, Fridgen and co-workers [37–39] used IRMPD spectroscopy in combination with computational methods to determine the structures of singly hydrated nucleobase/alkali cation complexes. In this study, we present the first experimental results on the water binding energies to the monosaccharide/cation complexes, AraX+, XylX+, RibX+, GlcX+, and GalX+, where X = Na or K. These results were obtained from high-pressure mass spectrometry equilibria measurements in the gas phase.
Experimental
The experiments were performed with a home-made 60° magnetic sector high-pressure mass spectrometer (HPMS) using a pulsed ion-beam ESI ion source, which has been previously described in detail [40]. Briefly, cationized monosaccharides were obtained by electrospray from a silica capillary (15 μm i.d.; 150 μm o.d.). A solution containing ~2.0 mM monosaccharide in water/methanol (1:1) and NaCl or KI was supplied to the capillary by a syringe pump at a rate of 0.8 μL/min. The samples studied were purchased from Aldrich Chemical Co. (Steinheim, Germany). The clustered ions were desolvated by a dry nitrogen gas counter-current and in a heated (~80°C) pressure-reducing capillary through which they were introduced into the fore-chamber, and then deflected toward a 3-mm orifice in the interface plate leading to the reaction chamber (RC). Ions drifting across the RC toward the exit slit under the influence of a weak electric field (2 V/cm at 10 mbar) were hydrated and reached equilibrium prior to being sampled to the mass analysis section of the mass spectrometer. Ion detection was provided by a secondary electron scintillation detector of the Daly type with an aluminum conversion dynode using a short rise-time photomultiplier (Hamamatsu R-647-04;). The output pulses of the multiplier were counted using a multichannel scaler with dwell-time per channel of 1 μs.
Mass spectra were registered with continuous ion sampling, while for equilibrium determination the ion beam was injected into the RC in a pulsed mode by applying short pulses (+45 V, 90 μs) to the deflection electrode with repetition of 1 ms. Typically, several thousand injection pulses were sufficient to accumulate a reasonable signal of the ion arrival time distribution (ATD) for each mass on the multichannel scaler (Figure 1).
Figure 1.
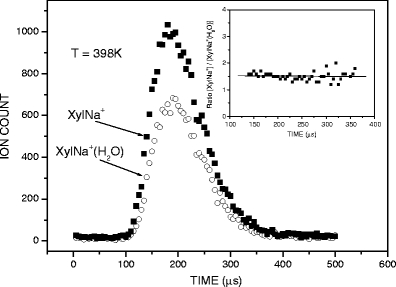
Arrival time distributions of the reactant, XylNa+, and product, XylNa+(H2O), ions. The inset shows the ratio of ion intensities, [XylNa+]/[XylNa+(H2O)] , as a function of ion residence time
The reagent gas mixture consisting of pure N2 as the carrier gas at about 10 mbar and a known partial pressure of water vapor (0.02–0.20 mbar) was supplied to the RC via the heated reactant gas inlet (RGI) at a flow rate of ~100 mL/min. The pressure was measured with an MKS capacitance manometer attached near the inlet of the RGI. The amount of water introduced into the N2 gas flow was kept constant throughout the temperature-dependent measurements of the equilibrium constants. Water concentrations were controlled continuously with a calibrated temperature and humidity transmitter (Delta OHM, type DO 9861T; Italy) inserted into the carrier gas flow line. The RC temperature was monitored by an iron-constantan thermocouple which was embedded close to the ion exit slit; the temperature could be varied from ambient to 300 °C by electrical heaters.
Results
The equilibrium constants K n-1,n Equation (1) for the association reaction Equation (2)
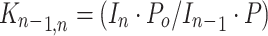 |
1 |
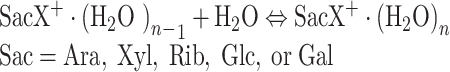 |
2 |
were determined from the measured ATD peak areas of the ions SacX+·(H2O)n and SacX+·(H2O)n–1, whose ratio, I n/I n–1, is taken to be equal to the ion concentration ratio, and P is the known partial pressure of H2O (in mbar). The standard pressure P o is 1000 mbar. Equilibrium attainment was checked by comparing the ATDs of the reactant and product ions, and testing the ion intensity ratio of [SacX+·(H2O)n-1]/[SacX+·(H2O)n] as a function of ion residence time. This is illustrated in Figure 1 for the pair of ions XylNa+ and XylNa+·(H2O), while the inset shows the ratio of their intensity as a function of time. Clearly, within the error limits and the limits of statistical noise, the ratio of [XylNa+]/[XylNa+·(H2O)] remains essentially constant, suggesting that the system is at equilibrium under the present experimental conditions.
The equilibrium constants, K
n–1,n , as functions of temperature for the SacNa+·(H2O)n and SacK+·(H2O) systems, are shown in the van’t Hoff plots of Figures 2 and 3. The standard enthalpy, 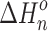 , and entropy,
, and entropy, 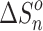 , changes for each equilibrium Equation (2), obtained from the slope and intercept of the van’t Hoff plot, are shown in Tables 1 and 2. The data for lower case n are given in the tables, since determining the hydration enthalpies for higher hydration steps requires temperatures below room temperature, which are not accessible with the present reaction chamber. The reported
, changes for each equilibrium Equation (2), obtained from the slope and intercept of the van’t Hoff plot, are shown in Tables 1 and 2. The data for lower case n are given in the tables, since determining the hydration enthalpies for higher hydration steps requires temperatures below room temperature, which are not accessible with the present reaction chamber. The reported 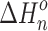 and
and 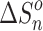 values are the averages of at least three measurements and the uncertainty corresponds to the standard deviation of the linear least-squares fit. The free energy,
values are the averages of at least three measurements and the uncertainty corresponds to the standard deviation of the linear least-squares fit. The free energy, 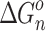 , was obtained from
, was obtained from 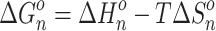 .
.
Figure 2.
van’t Hoff plots of equilibrium constants for the gas-phase reactions  : (a) n = 1, and (b) n = 2.
: (a) n = 1, and (b) n = 2.
Figure 3.
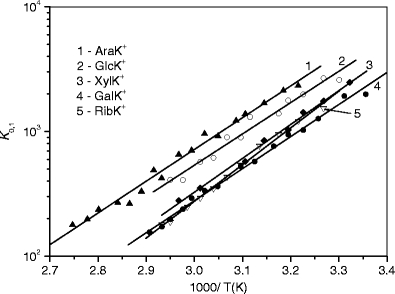
van’Hoff plots of equilibrium constants for the gas-phase reactions SacK+ + H2O < = > SacK+(H2O).
Table 1.
Experimental enthalpies, entropies, and free energy valuesa for the hydration of the sodiated monosaccharides
| Ion | n |
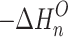 (kJ/mol) (kJ/mol) |
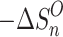 (J/mol K) (J/mol K) |
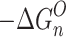 (kJ/mol)b (kJ/mol)b
|
D(Sac-Na+) (kJ/mol) |
|---|---|---|---|---|---|
| AraNa+ | 1 | 57.3(2) | 74.9(2) | 35.0(3) | 170c; 173d |
| 2 | 43.1(2) | 79.5(6) | 19.4(4) | ||
| XylNa+ | 1 | 56.1(2) | 76.6(5) | 33.3(4) | 171c; 183d |
| 2 | 44.8(3) | 84.1(7) | 19.7(5) | ||
| RibNa+ | 1 | 57.7(1) | 87.9(4) | 31.5(2) | 176c |
| 2 | 52.3(1) | 113.0(6) | 18.6(3) | ||
| GlcNa+ | 1 | 54.0(1) | 73.6(6) | 32.0(3) | 174c; 183d |
| 2 | 51.0(2) | 113.0(4) | 17.0(3) | ||
| GalNa+ | 1 | 46.4(1) | 64.4(2) | 27.4(2) | 177c; 205d |
| 2 | 42.7(2) | 87.9(4) | 16.5(3) |
Table 2.
Experimental enthalpies, entropies, and free energy valuesa for the hydration of the potassiated monosaccharides
| Ion | –ΔH O (kJ/mol) | –ΔS O (J/mol K) | –ΔG O (kJ/mol)b |
|---|---|---|---|
| AraK+ | 49.4(1) | 92.0(4) | 22.0(2) |
| XylK+ | 52.3(2) | 108.0(5) | 20.0(3) |
| RibK+ | 52.7(2) | 113.8(7) | 18.8(4) |
| GlcK+ | 48.5(2) | 92.9(8) | 20.8(4) |
| GalK+ | 49.8(1) | 101.3(3) | 19.6(2) |
Standard pressure is 1000 mbar
aUncertainties in parentheses
b –ΔG O at 298 K
Discussion
SacNa+(H2O)1,2
As mentioned above, in the present experiments ions are generated by electrospray from the aqueous-methanol solution. In solution, monosaccharides exist in an equilibrium between several different tautomeric and anomeric forms. These various forms have different free energies and, in general, the tautomeric equilibrium is dominated by conformers of six-membered (pyranoid) ring structures. In an aqueous solution, Ara, Xyl, Glc, and Gal exist predominantly (≥94%) or exclusively in the 1C4 (Ara) and 4C1 (Xyl, Glc, and Gal) pyranoid ring conformations [41, 42], (Scheme 1), and their equilibrium occurs between the α and β anomers at the carbon atom C-1.
Scheme 1.

Ring conformations of the monosaccharides considered in this work, indicating the numbering convention of carbon atoms [19]. The oxygen bonded to the carbon follows the same number convention
The equilibrium mixture of Rib contains structures of both pyranoid (4C1 and 1C4) and furanoid (five-membered) rings in the approximate ratio 4:1, with each of these tautomers having α and β anomers [41]. Therefore, one can expect that the SacX+ complexes formed in electrospray droplets and then transported into the reaction chamber for each system represent a mixture of their conformational forms.
Heaton and Armentrout [20] determined the ground state (GS) and low energy structures for the α and β anomeric forms of the AraNa+, XylNa+, GlcNa+ and GalNa+ complexes at the B3LYP/6-311 + G(d,p) level with single-point energies calculated at the B3LYP, B3P86, and MP2(full) levels of theory using a 6-311+G(2d,2p) bases set. A schematic representation of the GS structures for these complexes showing sodium cation coordination by the oxygen sites can be seen in Scheme 2.
Scheme 2.
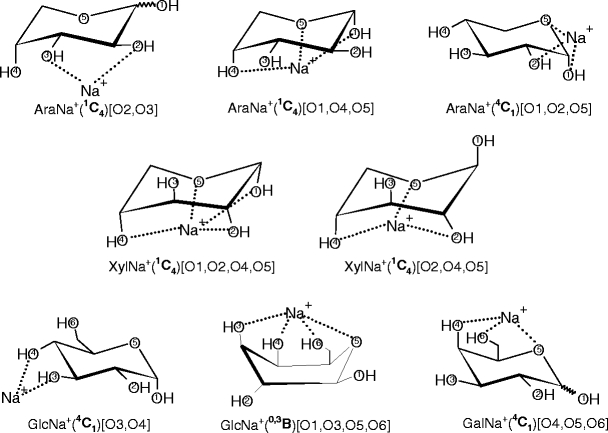
Schematic representation of the ground state structures of the α and β anomeric forms of the sodiated monosaccharide complexes obtained in the theoretical calculations [20]
For XylNa+, GlcNa+, and GalNa+, the calculations [20] at all three levels of theory predict the same GS conformers for each complex shown in Scheme 2. For AraNa+, these calculations predict that the GSs of the bidentate binding conformers, 1C4 [O2, O3], are in the range of 0–0.3 kJ/mol and 0–1.0 kJ/mol for the α and β forms, respectively. The GSs determined [20] for the tridentate binding orientations, α-AraNa+(1C4)[O1,O4,O5] and β-AraNa+(4C1)[O1,O2,O5], are in the range of 0–3.3 kJ/mol and 0–5.3 kJ/mol, respectively. The population analysis by Heaton and Armentrout [20] indicate that the GS structures obtained for the XylNa+, β-GalNa+, and α-GlcNa+ systems are predominant in equilibrium at 298 K, and their excited conformers comprise <1% (for XylNa+ and β-GalNa+), and ~3% (for α-GlcNa+) of the total population. In contrast, excited conformers of AraNa+ comprise 11%–47% of the total population and 1%–20% for the β-GlcNa+ and α-GalNa+ systems (depending on level of theory) [20]. For RibNa+, the most stable α and β conformers computationally predicted [19] at the HF/6-31G* level have 1C4 ring with [O1,O2,O4,O5] and [O2,O4,O5] binding geometry, respectively. The numbering of atoms and nomenclature used here are consistent with the literature [19, 20].
It is likely that the GS structures and very low-lying excited conformations of SacNa+, as discussed above, correspond to the precursor ions for hydration in the present study. It seems reasonable to assume that in the singly hydrated systems, SacNa+(H2O), the water molecule binds directly to the sodium cation of SacNa+, as illustrated schematically below for the hydration of the GS tridentate conformations predicted for the α and β forms of AraNa+.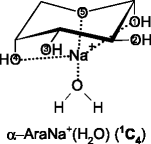
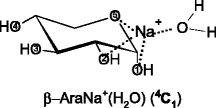
Based on the structural characterization of SacNa+ as the precursors to hydrated structures, one can say that the water binding energies to these complexes measured in the present experiments for each system correspond to a mixture of the precursor ions discussed above. Table 1 shows that with the exception of GalNa+, for all systems studied, the hydration enthalpies (−ΔH
o
1) of the first water molecule are very similar (within ~3 kJ /mol), and very close to that of the fourth water molecule (57.7 ± 4 [43]; 54.8 ± 6 [44] kJ/mol) in the Na+(H2O)n system. This suggests that the solvation effect provided by Ara, Xyl, Rib, and Glc on a sodium ion in the SacNa+ systems is comparable to that of three water molecules in the Na+(H2O)n cluster. This observation is in line with a multidentate (≥2) coordination of Na+ in the AraNa+, XylNa+, GlcNa+, and GalNa+ complexes predicted by Heaton and Armentrout [20]. For GalNa+(H2O), the water binding enthalpy is smaller than that for other SacNa+(H2O) systems (Table 1). This is expected because both the α and β GSs of Gal bind [20] the sodium cation more tightly than other monosaccharides studied here. Figure 4 shows the plot of the hydration free energies ( ), Table 1, versus the corresponding Na+ affinities of monosaccharides [20]. As can be seen, there is a fair linear relationship between these values. An analogous correlation was also found [33, 34] for the binding energies of water to the cationized amino acids (AAs), AANa+, and AAK+. This effect can be rationalized by direct interaction of the water molecule with the Na+ ion in the SacNa+(H2O) system, and as a consequence of charge delocalization from Na+ to the monosaccharide moiety, resulting in a lower electrostatic interaction between Na+ and H2O. The charge density on Na+ in SacNa+ is expected to decrease as the Na+ affinity of the monosaccharide increases.
), Table 1, versus the corresponding Na+ affinities of monosaccharides [20]. As can be seen, there is a fair linear relationship between these values. An analogous correlation was also found [33, 34] for the binding energies of water to the cationized amino acids (AAs), AANa+, and AAK+. This effect can be rationalized by direct interaction of the water molecule with the Na+ ion in the SacNa+(H2O) system, and as a consequence of charge delocalization from Na+ to the monosaccharide moiety, resulting in a lower electrostatic interaction between Na+ and H2O. The charge density on Na+ in SacNa+ is expected to decrease as the Na+ affinity of the monosaccharide increases.
Figure 4.
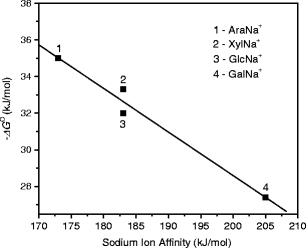
Correlation between hydration free energies, –ΔG o, and corresponding sodium ion affinity of monosaccharides. T = 298 K. The sodium ion affinity values are taken from ref. [20]
Generally, the observed binding energies of the second water molecule in SacNa+(H2O)2 are smaller than those of the first one (Table 1). This result can be explained by increasing steric crowding and decreasing effective charge on the sodium ion when the next water molecule is added to the SacNa+(H2O) complex. As shown in Table 1, the –ΔH o 2 values for all of the systems investigated here vary between 42.7 ± 2 and 52.3 ± 1 kJ/mol, such that they are within the range of the binding energies reported in the literature for the binding of the fifth water molecule in the Na+(H2O)n complex, 44.4–51.5 kJ/mol [43, 45]. This observation could indicate that the second water in the SacNa+(H2O)2 systems is coordinated directly to the sodium ion, although the slightly higher values of both –ΔH o 2 and –ΔS o 2 for RibNa+(H2O)2 and GlcNa+(H2O)2 may suggest that the second H2O in these two complexes is bound more tightly than in others, possibly because of the H-bonded interaction with the monosaccharide moiety.
SacK+(H2O)
As expected, the enthalpy change values for the association of H2O to the SacK+ complexes are lower than those for SacNa+ (Tables 1 and 2). These results are fully in line with the predominating direct electrostatic interaction between the water molecule and alkali metal cation in these systems. Because the ionic radius of K+ is larger than Na+, its charge density becomes smaller and, therefore, the electrostatic interaction of H2O with SacK+ is weaker compared with SacNa+. The –ΔH o and –ΔG o values found for SacK+(H2O) are identical within the combined error bars (Table 2), and very similar to the corresponding experimental values of 49.4 and 18.4 kJ/mol, respectively, reported in the literature [43] for the fourth water in the K+(H2O)n system. This indicates that similarly to the SacNa+(H2O) systems discussed above, the solvation effect provided by the monosaccharides in SacK+(H2O) is comparable to that of three water molecules in the corresponding K+(H2O)n system.
Conclusions
Hydration of sodiated and potassiated monosaccharides (arabinose, xylose, ribose, glucose, and galactose) produced by electrospray from an aqueous-methanol solution have been investigated by pulsed high-pressure mass spectrometry. The thermochemical values measured here for each solvated system correspond to a mixture of the monosaccharide structures involved in the SacX+ complexes. Thermochemical information indicates that the solvation effects of Ara, Xyl, Rib, Glc, and Gal on both Na+ and K+ ions are comparable to that of three water molecules in Na+(H2O)n and K+(H2O)n, respectively, which is consistent with metal cation coordination in the most stable conformations as calculated [20] for the SacNa+ complexes. A good correlation was found between the free energy changes for the attachment of the first water molecule to the AraNa+, XylNa+, GlcNa+ and GalNa+ complexes and the sodium cation binding affinities to the corresponding monosaccharides [20].
Open Access
This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
References
- 1.Varki A. Biological Roles of Oligosaccharides: All of the Theories are Correct. Glycobiology. 1993;3:97–130. doi: 10.1093/glycob/3.2.97. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Lis H, Sharon N. Lectins: Carbohydrate-Specific Proteins that Mediate Cellular Recognition. Chem. Rev. 1996;98:683–720. doi: 10.1021/cr940413g. [DOI] [PubMed] [Google Scholar]
- 3.Gabius H-J, André S, Jiménez-Barbero J, Rüdiger H. Chemical Biology of the Sugar Code. Chem. BioChem. 2004;5:740–764. doi: 10.1002/cbic.200300753. [DOI] [PubMed] [Google Scholar]
- 4.Dwek RA. Glycobiology: Toward Understanding the Function of Sugars. Chem. Rev. 1996;96:683–720. doi: 10.1021/cr940283b. [DOI] [PubMed] [Google Scholar]
- 5.Girlich D, Lüdemann H-D. Molecular Mobility of the Water Molecules in Aqueous Sucrose Solutions, Studied by 2H-NMR relaxation. Z. Naturforsch. C. 1994;49:250–257. [Google Scholar]
- 6.Rampp M, Buttersack C, Lüdemann H-D. c, T-Dependence of the Viscosity and the Self-Diffusion Coefficients in Some Aqueous Carbohydrate solutions. Carbohydr. Res. 2000;328:561–572. doi: 10.1016/S0008-6215(00)00141-5. [DOI] [PubMed] [Google Scholar]
- 7.Magazů S, Villari V, Migliardo P, Maisano G, Telling MTF. Diffusive Dynamics of Water in the Presence of Homologous Disaccharides: A Comparative Study by Quasi-Elastic Neutron Scattering. J. Phys. Chem. B. 2001;105:1851–1855. doi: 10.1021/jp002155z. [DOI] [Google Scholar]
- 8.Heugen U, Schwaab G, Bründermann E, Heyden M, Yu X, Leitner DM, Havenith M. Solute-Induced Retardation of Water Dynamics Probed Directly by Terahertz Spectroscopy. Proc. Natl. Acad. Sci. U.S.A. 2006;103:12301–12306. doi: 10.1073/pnas.0604897103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Liu Q, Brady JWJ. Anisotropic Solvent Structuring in Aqueous Sugar Solutions. Am. Chem. Soc. 1996;118:12276–12286. doi: 10.1021/ja962108d. [DOI] [Google Scholar]
- 10.Lee SL, Debenedetti PG. A Computational Study of Hydration, Solution Structure, and Dynamics in Dilute Carbohydrate Solutions. J. Chem. Phys. 2005;122:204511. doi: 10.1063/1.1917745. [DOI] [PubMed] [Google Scholar]
- 11.Eriksson M, Lindhorst TK, Hartke B. Differential Effects of Oligosaccharides on the Hydration of Simple Cations. J. Chem. Phys. 2008;128:105105. doi: 10.1063/1.2873147. [DOI] [PubMed] [Google Scholar]
- 12.Çarçabal P, Jockusch RA, Hünig I, Snoek LC, Kroemer RT, Davis BG, Gamblin DP, Compagnon I, Oomens J, Simons JP. Hydrogen Bonding and Cooperativity in Isolated and Hydrated Sugars: Mannose, galactose, glucose, and Lactose. J. Am. Chem. Soc. 2005;127:11414–11425. doi: 10.1021/ja0518575. [DOI] [PubMed] [Google Scholar]
- 13.Cocinero EJ, Stanca-Kaposta EC, Scanlan EM, Gamblin DP, Davis BG, Simons JP. Conformational Choice and Selectivity in Singly and Multiply Hydrated Monosaccharides in the Gas Phase. Chem. Eur. J. 2008;14:8947–8955. doi: 10.1002/chem.200800474. [DOI] [PubMed] [Google Scholar]
- 14.Cocinero EJ, Gamblin DP, Davis BG, Simons JP. The Building Blocs of Cellulose: The Intrinsic Conformational Structures of Cellobiose, Its Epimer, Lactose, and Their Singly Hydrated Complexes. J. Am. Chem. Soc. 2009;131:11117–11123. doi: 10.1021/ja903322w. [DOI] [PubMed] [Google Scholar]
- 15.Çarçabal P, Patsias Th, Hünig I, Liu B, Kaposta EC, Snoek LC, Gamblin DP, Davis BG, Simons JP. Spectral Signatures and Structural Motifs in Isolated and Hydrated Monosaccharides: Phenyl α- and β-L-Fucopyranoside. Phys. Chem., Chem. Phys. 2006;8:129–136. doi: 10.1039/b514301b. [DOI] [PubMed] [Google Scholar]
- 16.Stanca-Kaposta EC, Gamblin DP, Cocinero EJ, Frey J, Kroemer RT, Fairbanks AJ, Davis BG, Simons JP. Solvent Interactions and Conformational Choice in a Core N-Glycan Segment: Gas Phase Conformation of the Central, Branching Trimannose Unit and Its Singly Hydrated Complex. J. Am. Chem. Soc. 2008;130:10691–10696. doi: 10.1021/ja801892h. [DOI] [PubMed] [Google Scholar]
- 17.Cocinero EJ, Stanca-Kaposta EC, Dethlefsen M, Liu B, Gamblin DP, Davis BG, Simons JP. Hydration of Sugars in the Gas Phase: Regioselectivity and Conformational Choice in N-Acetyl Glucosamine and Glucose. Chem. Eur. J. 2009;15:13427–13434. doi: 10.1002/chem.200901830. [DOI] [PubMed] [Google Scholar]
- 18.Bothner B, Carmitchel L, Staniszewski K, Sonderegger M, Siuzdak G. Biomolecule Structure Characterization in the Gas Phase Using Mass Spectrometry. Spectroscopy. 2002;16:71–79. [Google Scholar]
- 19.Cerda BA, Wesdemiotis C. Thermochemistry and Structures of Na+ Coordinated Mono- and Disaccharide Stereoisomers. Int. J. Mass Spectrom. 1999;189:189–204. doi: 10.1016/S1387-3806(99)00085-8. [DOI] [Google Scholar]
- 20.Heaton AL, Armentrout PB. Experimental and Theoretical Studies of Sodium Cation Interactions with D-Arabinose, Xylose, Glucose, and Galactose. J. Phys. Chem. A. 2008;112:10156–10167. doi: 10.1021/jp804113q. [DOI] [PubMed] [Google Scholar]
- 21.Jockusch RA, Lemoff AS, Williams ER. Hydration of Valine–Cation Complexes in the Gas Phase: On the Number of Water Molecules Necessary to Form Zwitterions. J. Phys. Chem. A. 2001;105:10929–10942. doi: 10.1021/jp013327a. [DOI] [Google Scholar]
- 22.Jockusch RA, Lemoff AS, Williams ER. Effect of Metal Ion and Water Coordination on the Structure of a Gas-Phase Amino Acid. J. Am. Chem. Soc. 2001;123:12255–12265. doi: 10.1021/ja0106873. [DOI] [PubMed] [Google Scholar]
- 23.Lemoff AS, Bush MF, Williams ER. Binding Energies of Water to Sodiated Valine and Structural Isomers in the Gas Phase: The Effect of Proton Affinity on Zwitterion Stability. J. Am. Chem. Soc. 2003;125:13576–13584. doi: 10.1021/ja034544n. [DOI] [PubMed] [Google Scholar]
- 24.Lemoff AS, Williams ER. Binding Energies of Water to Lithiated Valine: Formation of Solution-Phase Structure In Vacuo. J. Am. Soc. Mass Spectrom. 2004;15:1014–1024. doi: 10.1016/j.jasms.2004.04.001. [DOI] [PubMed] [Google Scholar]
- 25.Lemoff AS, Bush MF, Williams ER. Structures of Cationized Proline Analogues: Evidence for the Zwitterionic Form. J. Phys. Chem. A. 2005;109:1903–1910. doi: 10.1021/jp0466800. [DOI] [PubMed] [Google Scholar]
- 26.Lemoff AS, Bush MF, Wu C-C, Williams ER. Structures and Hydration Enthalpies of Cationized Glutamine and Structural Analogues in the Gas Phase. J. Am. Chem. Soc. 2005;127:10276–10286. doi: 10.1021/ja051743t. [DOI] [PubMed] [Google Scholar]
- 27.Lemoff AS, Wu C-C, Bush MF, Williams ER. Binding Energies of Water to Doubly Hydrated Cationized Glutamine and Structural Analogues in the Gas Phase. J. Phys. Chem. A. 2006;110:3662–3669. doi: 10.1021/jp055662v. [DOI] [PubMed] [Google Scholar]
- 28.Lemoff AS, Bush MF, O’Brien JT, Williams ER. Structures of Lithiated Lysine and Structural Analogues in the Gas Phase: Effects of Water and Proton Affinity on Zwitterionic Stability. J. Phys. Chem. A. 2006;110:8433–8442. doi: 10.1021/jp057436r. [DOI] [PubMed] [Google Scholar]
- 29.Bush MF, Prell JS, Saykally RJ, Williams ER. One Water Molecule Stabilizes the Cationized Arginine Zwitterions. J. Am. Chem. Soc. 2007;129:13544–13553. doi: 10.1021/ja073796b. [DOI] [PubMed] [Google Scholar]
- 30.Ye SJ, Moision RM, Armentrout PB. Sequential Bond Energies of Water to Sodium Glycine Cation. Int. J. Mass Spectrom. 2005;240:233–248. doi: 10.1016/j.ijms.2004.09.019. [DOI] [Google Scholar]
- 31.Ye SJ, Moision RM, Armentrout PB. Sequential Bond Energies of Water to Sodium Proline Cation. Int. J. Mass Spectrom. 2006;253:288–304. doi: 10.1016/j.ijms.2006.05.008. [DOI] [Google Scholar]
- 32.Ye SJ, Armentrout PB. Guided Ion Beam and Theoretical Studies of Sequential Bond Energies of Water to Sodium Cysteine Cation. Phys. Chem. Chem. Phys. 2010;12:13419–13433. doi: 10.1039/c0cp00302f. [DOI] [PubMed] [Google Scholar]
- 33.Wincel H. Hydration Energies of Sodiated Amino Acids from Gas-Phase Equilibria Determinations. J. Phys. Chem. A. 2007;111:5784–5791. doi: 10.1021/jp0721595. [DOI] [PubMed] [Google Scholar]
- 34.Wincel H. Hydration of Potassiated Amino Acids in the Gas Phase. J. Am. Soc. Mass Spectrom. 2083;2007:18. doi: 10.1016/j.jasms.2007.09.006. [DOI] [PubMed] [Google Scholar]
- 35.Kamariotis A, Boyarkin O, Mercier SR, Beck RD, Bush MF, Williams ER, Rizzo TR. Infrared Spectroscopy of Hydrated Amino Acids in the Gas Phase: Protonated and Lithiated Valine. J. Am. Chem. Soc. 2006;128:905–916. doi: 10.1021/ja056079v. [DOI] [PubMed] [Google Scholar]
- 36.Remko M, Fitz D, Rode BM. Effect of Metal Ions (Li+, Na+, K+, Mg2+, Ca2+, Ni2+, Cu2, and Zn2+) and Water Coordination on the Structure and Properties of L-Histidine and Zwitterionic L-Histidine. Amino Acids. 2010;39:1309–1319. doi: 10.1007/s00726-010-0573-8. [DOI] [PubMed] [Google Scholar]
- 37.Gillis EAL, Rajabi K, Fridgen TD. Structures of Hydrated Li+-Thymine and Li+-Uracil Complexes by IRMPD Spectroscopy in the N–H/O–H Stretching Region. J Phys. Chem. A. 2009;113:824–832. doi: 10.1021/jp809993k. [DOI] [PubMed] [Google Scholar]
- 38.Rajabi K, Gillis EAL, Fridgen TD. Structures of Alkali Metal Ion–Adenine Complexes and Hydrated Complexes by IRMPD Spectroscopy and Electronic Structure Calculations. J. Phys. Chem. A. 2010;114:3449–3456. doi: 10.1021/jp9098683. [DOI] [PubMed] [Google Scholar]
- 39.Gillis EAL, Fridgen TD. The hydrated Li+-Adenine–Thymine complex by IRMPD Spectroscopy in the N–H/O–H Stretching Region. Int. J. Mass Spectrom. 2010;297:2–8. doi: 10.1016/j.ijms.2010.04.005. [DOI] [Google Scholar]
- 40.Wincel H. Hydration of Gas-Phase Protonated Alkylamines, Amino Acids, and Dipeptides Produced by Electrospray. Int. J. Mass Spectrom. 2006;251:23–31. doi: 10.1016/j.ijms.2005.12.036. [DOI] [Google Scholar]
- 41.Franks F. Physical Chemistry of Small Carbohydrates-Equilibrium Solution Properties. Pure Apll. Chem. 1987;59:1189–1202. doi: 10.1351/pac198759091189. [DOI] [Google Scholar]
- 42.Jiang Y, Hu M, Li S, Wang J, Zhuo K. Thermodynamics of the Interaction of RbCl with Some Monosaccharides (D-glucose, D-galactose, D-xylose, and D-arabinose) in Aqueous Solutions at 298.15 K. Carbohydr. Res. 2006;341:262–269. doi: 10.1016/j.carres.2005.11.006. [DOI] [PubMed] [Google Scholar]
- 43.Džidi I, Kebarle P. Hydration of the Alkali Ions in the Gas Phase. Enthalpies and Entropies of Reactions M+(H2O)n-1 + H2O = M+(H2O)n. J. Phys. Chem. 1970;74:1466–1474. doi: 10.1021/j100702a013. [DOI] [Google Scholar]
- 44.Dalleska NF, Tjelta BL, Armentrout PB. Sequential Bond Energies of Water to Na+(3s0), Mg+ (3s1), and Al+ (3s2) J. Phys. Chem. 1994;98:4191–4195. doi: 10.1021/j100066a045. [DOI] [Google Scholar]
- 45.Tang IN, Lian MS, Castleman AW., Jr Mass Spectrometric Study of Gas-Phase Clustering Reactions: Hydration of the Monovalent Strontium ion. J. Chem. Phys. 1976;65:4022–4027. doi: 10.1063/1.432854. [DOI] [Google Scholar]


