Abstract
Linking demographic and genetic dispersal measures is of fundamental importance for movement ecology and evolution. However, such integration can be difficult, particularly for highly fecund species that are often the target of management decisions guided by an understanding of population movement. Here, we present an example of how the influence of large population sizes can preclude genetic approaches from assessing demographic population structuring, even at a continental scale. The Australian plague locust, Chortoicetes terminifera, is a significant pest, with populations on the eastern and western sides of Australia having been monitored and managed independently to date. We used microsatellites to assess genetic variation in 12 C. terminifera population samples separated by up to 3000 km. Traditional summary statistics indicated high levels of genetic diversity and a surprising lack of population structure across the entire range. An approximate Bayesian computation treatment indicated that levels of genetic diversity in C. terminifera corresponded to effective population sizes conservatively composed of tens of thousands to several million individuals. We used these estimates and computer simulations to estimate the minimum rate of dispersal, m, that could account for the observed range-wide genetic homogeneity. The rate of dispersal between both sides of the Australian continent could be several orders of magnitude lower than that typically considered as required for the demographic connectivity of populations.
Keywords: approximate Bayesian computation, gene flow, migration rate, population size, power test
1. Introduction
Dispersal is one of the most fundamental, yet least understood, concepts in population biology and ecology [1]. Dispersal characteristics in combination with population size give populations their patterns in space and time. Assessing dispersal is of obvious importance in disciplines such as conservation biology, in which informed management decisions based on an understanding of population structure and movement, or lack thereof, must be made to help preserve species threatened by small population sizes (e.g. [2]). At the opposite end of the spectrum are pest and invasive species whose large population sizes and dispersal ability can threaten both ecological and agricultural systems. Precise knowledge of population movement in these cases can guide management decisions aimed at more effectively monitoring, controlling and ultimately preventing outbreaks or invasions (e.g. [3]).
While dispersal rate (sometimes referred to as migration rate) and population size have traditionally been estimated by direct methods such as capture–mark–recapture, more recent methods have used spatial genetic structure [4]. In spite of the difficult challenge of linking genetics and demographic population parameters (e.g. [5]), molecular studies have been widely used to provide insights into patterns of connectivity and movement among populations of a variety of taxa. Microsatellite loci have been considered markers of choice owing to high levels of variation, especially for highly fecund and mobile species (e.g. [6]). Population genetic surveys of invasive species have examined processes such as colonization dynamics and range expansion within the introduction areas (e.g. [7] for vertebrates and [8] for invertebrates). Additionally, microsatellites have been used for pest species to study the origins and/or subsequent movements of individuals emanating from outbreak populations (e.g. [9–11]).
These microsatellite studies investigating dispersal patterns of invasive and pest populations are particularly important as guides to set appropriate scales for management (e.g. [3,11]). Management units are usually defined as populations whose dynamics (e.g. growth rate) depend largely on local recruitment rather than dispersal [12,13]. However, there is no general framework for determining the dispersal rate at which populations become demographically correlated [14,15]. Yet knowing whether dispersal rates are sufficient to synchronize population dynamics and therefore outbreak occurrences between populations can be useful for the delineation of management units [16,17]. The threshold for synchrony in population dynamics is often considered to occur at a dispersal rate of 0.1 (e.g. [18,19]; see [15,20] for use in molecular ecology studies). Management of economically important species can also utilize different definitions of population connectivity—in particular the degree to which gene flow affects evolutionary processes (e.g. the evolution of insecticide resistance [9])—but such genetic connectivity will not be considered here.
The use of population genetics for estimating demographic connectivity, however, is not necessarily as straightforward as it may initially seem. This is because genetic differentiation scales with levels of gene flow (Nem), which is quantified as the product of the effective population size (Ne) and the fraction of dispersers entering the population each generation (m). An important consequence of the above is that levels of gene flow high enough to homogenize genotypic frequencies do not necessarily indicate demographic connectivity between populations. Gene flow owing to tens of migrants per generation is usually sufficient to prevent all but minor allele frequency differences [15,21]. Given that gene flow also depends on population size (Ne), such a level of genetic exchange may actually represent a very small fraction of dispersers (m) entering the population. When population sizes are large, the dispersal rate high enough to homogenize genotypic frequencies might still be much lower than the 10 per cent rate required to induce synchrony in population dynamics [18,19]. Therefore, a failure to detect population structure then raises an important question in terms of managing populations: can a dispersal rate, m, between populations be sufficient to cause them to be genetically indistinguishable, yet insufficient to couple their dynamics? Addressing this question requires an understanding of the relative contribution of population size (i.e. Ne) and dispersal rate (i.e. m) to estimates of genetic differentiation. The relationship between these two variables becomes particularly important when considering highly fecund species, such as insect pests characterized by outbreaking populations containing millions if not billions of individuals.
The Australian plague locust, Chortoicetes terminifera, is one of Australia's most significant agricultural pests and can be found across most of the continent. Chortoicetes terminifera is an endemic species that can experience huge increases in local population density, with individuals actively aggregating and forming migratory bands and swarms that can damage pastures and crops [22]. Given its broad geographical range and potential to mass migrate, an improved understanding of its movement patterns and population dynamics is of critical importance to its management. Locust populations have been monitored independently in Western Australia (by the Western Australia Department of Agriculture) and in the four eastern states of Australia (by the Australian Plague Locust Commission), largely assuming low demographic connectivity between populations from both sides of the continent [23,24]. However, the demographic independence of outbreak events at the continental scale has been questioned since the first report of simultaneous locust plagues in 1999–2000 at both the eastern and western extremes of the species's distribution [25]. In contrast, a recent time-series analysis of C. terminifera population growth rates recorded between 1987 and 2010 showed a lack of synchrony across the eastern states of Australia and a demographic structuring congruent with geography and climate in this region (K. Berthier, S. J. Simpson, E. Deveson, M.-P. Chapuis & G. A. Sword, unpublished data). Because uncertainty remains about the rate and significance of C. terminifera movements at the continental scale, despite detailed ecological studies, investigation of spatial molecular structure may represent a useful alternative. Although cuticular hydrocarbon profiles [26] and B chromosomes [27] have not revealed any population structure across C. terminifera's range, the possibility of genetic population structure has not been examined to date using highly variable molecular markers.
Here, we used microsatellite loci to assess genetic variation in 12 C. terminifera population samples spanning most of the species's range. Our primary goal was to check for genetic differentiation between locust populations from the eastern states of Australia versus those from Western Australia and how such differentiation, or lack thereof, translated into rates of dispersal. We first computed traditional summary statistics to evaluate levels of genetic diversity in C. terminifera and the existence of population structure across the entire Australian continent. We then investigated how these observed levels of genetic diversity translated in terms of the population-scaled mutation rate (Θ) by using an approximate Bayesian computation (ABC) method [28,29]. Finally, given these Bayesian estimates, we used computer simulations based on the coalescent [30] to estimate the rates of migration (m) that could account for levels of genetic structure we observed.
2. Material and methods
(a). Population sampling, genotyping and basic statistics
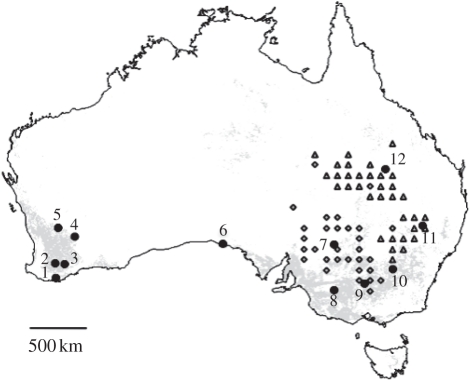
We collected a total of 12 population samples (22–35 diploid nymphs per sample) between October 2005 and March 2007, covering much of the distribution of C. terminifera (figure 1). The sampling included five population samples from Western Australia (ID 1–5), and seven from the eastern states of South Australia (ID 6), New South Wales (ID 7–11) and Queensland (ID 12). The geographical distances between population samples varied from 76 to 3047 km. Most of the locusts came from inland agricultural areas where high-density populations were sampled during upsurge periods as part of monitoring campaigns conducted by the Australian Plague Locust Commission and the Western Australia Department of Agriculture (figure 1). In states from eastern Australia, 15 plagues persisting for 1 or 2 years have been recorded since the 1920s, with the last event in 2004–2005, during our sampling. There have been five major plagues in which numerous regions across several states including Western Australia were affected by swarms.
Figure 1.
Geographical origin of sampled populations of the Australian plague locust. The map was generated using Quantum GIS (QGIS) 0.11.0 (http://www.qgis.org). Grey areas represent croplands based on the Land Cover Map for Australia in the year 2000 [31]. Triangles and diamonds, respectively, represent populations from the demographically independent northeastern and southwestern areas (i.e. the upper level of demographic structuring inferred from hierarchical clustering and cross-correlation analyses of density time series across eastern states of Australia).
Seven microsatellite loci (CT096, CT106, CT128, CT278, CT318, CT358 and CT401) were genotyped using fluorescently labelled PCR primers and an ABI 3130 DNA sequencer (Applied Biosystems), as described by Chapuis et al. [32]. To minimize genotyping errors, a minimum of two replicate PCRs per sample per locus were conducted. Alleles were scored using Genetic Profiler 1.0 software (Amersham Biosciences). Alleles included in the final consensus genotypes were observed at least twice; if observed only once, an additional PCR replicate was conducted. One negative and eight positive controls (samples with known genotypes) were included in each run of 96 PCR reactions to check for potential contamination and standardize genotyping across experiments.
We did not detect any significant linkage disequilibrium between all pairs of microsatellite loci in all population samples using exact G-tests in Genepop 4.0 (p > 0.054; [33]). We tested for and estimated the null allele prevalence as previously described by Chapuis et al. [34] and detailed in the electronic supplementary material. We calculated expected heterozygosity (HE) [35] averaged over loci and population samples. We tested for genotypic differentiation among population samples by using the exact G-test of heterogeneity of genotypic frequencies implemented in Genepop 4.0 [33]. The level of differentiation between population samples was quantified by computing pairwise estimators of FST [36] following Chapuis & Estoup [37] and using the package FreeNA (http://www1.montpellier.inra.fr/URLB). These population genetic analyses are little affected by the presence of null alleles [34,37] (see the electronic supplementary material).
(b). Bayesian inference of the population-scaled mutation rate
We then investigated how the high levels of genetic diversity observed within the 12 sampled C. terminifera populations translated in terms of the population-scaled mutation rate (Θ). Under the coalescent model, only the product 4NeμR of the effective population size and the mutation rate of the microsatellite repeat region (μR) can be estimated, unless additional information on μR is available. Estimates of germline mutation rates in microsatellites from insect genomes are scarce [38–40], and unknown in the Orthoptera.
To this end, we used the ABC method [28] implemented in DIYABC [29] because, to our knowledge, it is the single exception in implementing the elaborate generalized stepwise mutation (GSM) model [41] (see also [42]) among likelihood-based approaches for estimating population parameters (e.g. [43]). These other methods postulate a stepwise mutation model [44] that has been shown to be too simplistic and insufficient to explain all observed microsatellite data [42]. Another microsatellite evolutionary feature handled by DIYABC, and particularly relevant to our C. terminifera dataset, is the presence of mutations in the flanking region leading to the presence of even and uneven allele sizes. In addition, ABC circumvents the difficulty of convergence of the Markov chain Monte Carlo exploration used in full likelihood-based approaches [29] while comparing in terms of statistical efficiency of inferences, at least when dealing with simple evolutionary scenarios [28]. Statistics summarizing genetic diversity within population samples included the mean number of alleles (A), the mean expected heterozygosity (HE) and the variance of allele sizes in base pairs (V). Independently, for each population sample, we produced a reference table containing five million simulated datasets generated from a simple model in which a single population of constant size Ne was sampled. With these datasets, we then used a local linear regression to estimate the posterior distribution of Θ. For use in local linear regression, we took the 1000 (0.5‰) simulated datasets closest to our real dataset and applied a logit transformation to parameter values.
With regard to model parameters, we chose a uniform prior bounded between 5 × 103 and 5 × 106 for Ne. Mutations in the repeat region of each locus followed a symmetric GSM model [41], with a maximum range of 60 contiguous allelic states. Prior values for the mean mutation rate (μR) were drawn in a uniform distribution bounded between 10−5 and 10−4. By drawing mutation rates for each locus independently from a gamma distribution (mean = μR and shape = 2), we allowed for large mutation rate variance across loci (i.e. range of 10−6 to 10−3). This reflected uncertainty on germline mutation rates of dinucleotide microsatellites from insect genomes (i.e. two species of insect studied to date: 6.3 × 10−6 [38] and 9.3 × 10−6 [39] in Drosophila melanogaster, and 10−3 in the ant Camponotus consobrinus [40]). We also considered mutations that insert or delete a single nucleotide to the microsatellite sequence. We used default values for any other mutation model settings. Further details on model parametrization are supplied in the electronic supplementary material. The electronic supplementary material also provides results of sensitivity analyses, in particular to prior values for the mean mutation rate and null alleles, as well as measures of performance for our ABC analysis.
(c). Assessing the power to detect departure from panmixia as a function of migration
We used computer simulations based on the coalescent [30] to assess the power of the exact G-test of heterogeneity of genotypic frequencies to detect two panmictic populations of equal effective size Ne and exchanging migrants at a rate m each generation. Exact tests were computed with a Markov chain method in Genepop 4.0 [33] and the type I error α was considered at a conventional 0.05 level. For each m value tested, we simulated 100 genotype datasets and calculated the percentage of times the false null hypothesis (i.e. panmixia) was rejected (i.e. statistical power P = 1 − β, with β the type II error). Simulated datasets had 29 diploid individuals per population and seven independent microsatellite loci with null alleles, reflecting the sample values in our real C. terminifera dataset. We also mimicked the global comparisons made in our real C. terminifera dataset by simulating datasets with six samples for each of the two panmictic populations. The total of 12 simulated samples mimicked those we collected at different sites in each of the two regions (i.e. the eastern states of Australia and Western Australia).
Regarding model parameters, we used a population-scaled mutation rate Θ of 100, which plausibly explained the observed heterozygosity values at C. terminifera microsatellite markers according to DIYABC inferences (§3). By approaching the lower 2.5 per cent quantile of the DIYABC posterior distributions, this value is also very conservative regarding assessment of the power to detect departure from panmixia. Mutations were simulated as described for the Bayesian inferences, with slight modifications. We modelled mutations in the primer-binding sites that can lead to the presence of null alleles, as described by Chapuis & Estoup [37]. Other details on mutation parameter settings are provided in the electronic supplementary material.
3. Results
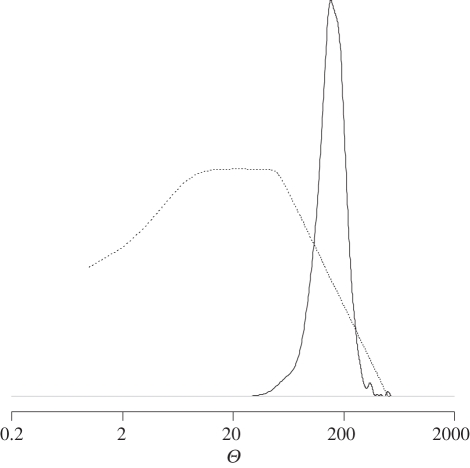
Mean and standard deviations over loci and population samples of the expected heterozygosity were 0.933 ± 0.056 in our real C. terminifera dataset (see the electronic supplementary material for HE values for each population sample). We investigated how these remarkably high levels of genetic diversity observed within the 12 sampled C. terminifera populations translated in terms of the population-scaled mutation rate Θ = 4NeμR (see figure 2 for the density estimate of the posterior distribution from the ABC treatment on population sample 1). Variation of posterior distributions between population samples was relatively small for our parameter of interest (see the electronic supplementary material). Therefore, we hereafter report the mean estimates and 2.5 and 97.5 per cent quantile values averaged over all 12 population samples. Our results indicate that the observed levels of genetic diversity within C. terminifera corresponded to very large values of Θ, with a mode estimate of 155 and a relatively narrow confidence interval (CI) of 87–314. This result was robust to changes in prior distribution for the mean mutation rate μR and conservative regarding impact of null alleles (see the electronic supplementary material). The lower 2.5 per cent limit of the CI (87) indicated that a very conservative range of the long-term C. terminifera effective population size was 21 750–3452 382 diploid individuals, when considering the highest and lowest germline mutation rates estimated in insects to date (10−3 [40] and 6.3 × 10−6 [38]).
Figure 2.
Density estimates of the DIYABC posterior distribution sample for Θ = 4NeμR of C. terminifera population sample 1. Ne is the effective population size and μR the mean mutation rate of the repeat region. The continuous and discontinuous lines correspond to the posterior and prior distributions, respectively.
We failed to detect any genotypic differentiation among populations sampled across the entire continental range of C. terminifera. This was the case in each of the 66 pairwise comparisons between population samples (p > 0.063), as well as when considering all population samples (p = 0.847; see the electronic supplementary material). Accordingly, 62 confidence intervals of pairwise FST estimates included zero (see the electronic supplementary material). For the four exceptions, the magnitude of difference between population pairs was minor, being less than or equal to 0.01—see population pairs 1–12 (FST = 0.003; 0.001–0.005), 2–11 (FST = 0.004; 0.001–0.007), 2–7 (FST = 0.005; 0.002–0.008) and 7–12 (FST = 0.006; 0.001–0.010).
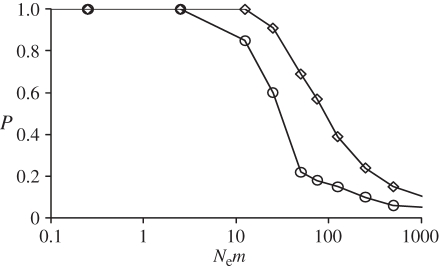
We used computer simulations to investigate the minimum number of migrants per generation (i.e. Nem) that could explain the absence of differentiation observed between populations sampled from eastern states of Australia and from Western Australia. Global exact tests performed on simulated datasets, with similar characteristics to our real dataset, erroneously accepted the null hypothesis of panmixia (i.e. committed a type II error β) with a probability of 10 per cent when populations exchanged 25 effective migrants per generation (figure 3). Similarly, the probability of committing a type II error β exceeded 10 per cent from levels of gene flow of 10 migrants per generation when comparing a single pair of population samples. Power of both the global and pairwise exact tests fell below 70 per cent for gene flow values of Nem greater than 50.
Figure 3.
Power of the exact G-test of heterogeneity of genotypic frequencies, as computed in Genepop 4.0 [33], for detecting two populations exchanging migrants at a rate m. The statistical power P = 1 − β, with β the type II error (see text for more details). Circles represent pairwise comparisons (one sample per population) and diamonds represent global comparisons on 12 samples (six per population). The model considers two populations exchanging migrants at a rate m and of equal effective size Ne. One hundred simulated genotype datasets were generated for each value of m. Simulated datasets contain samples of 29 diploid individuals genotyped at seven independent microsatellite loci. The population-scaled mutation rate Θ = 4NeμR was set to 100. The null allele frequency values were similar to those observed on average for C. terminifera microsatellite markers (i.e. 0.19). See text and electronic supplementary material for more details.
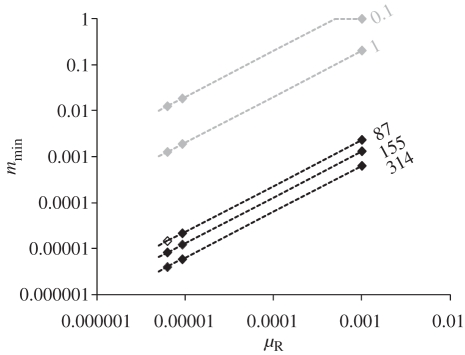
Taken together, the results that (i) power to detect two populations dramatically declined when the populations exchanged more than 50 migrants given the characteristics of the C. terminifera dataset, and (ii) C. terminifera lived in populations of a minimum of 21 750 effective individuals, indicated that a very conservative estimate of the minimum migration rate per generation that could explain the observed absence of genetic differentiation between locust populations separated by 3047 km across the Australian continent was 2.3 × 10−3 (i.e. 50/21 750). Figure 4 shows that a migration rate necessary to maintain genetic homogeneity would be even smaller for larger and more realistic effective population sizes. For instance, using the mode Bayesian estimate for Θ (155) and an average mutation rate of 10−4 provided a realistic estimate of the effective population size of about half a million individuals, in which case we would expect a minimum exchange rate as small as 1.3 × 10−4 to homogenize genotypes between populations on opposite sides of the continent.
Figure 4.
Lower limit of the migration rate range (mmin) necessary to maintain genetic homogeneity as a function of the mean mutation rate of microsatellite repeat regions (μR) for values of Θ (i.e. 4NeμR) estimated using DIYABC in C. terminifera populations (black) or studied in Waples & Gaggiotti's [15] simulations (grey). We considered that power to detect two panmictic populations was poor (i.e. chance to observe genetic homogeneity was high) when the populations exchange more than 50 migrants. See text for more details. Diamonds represent the three germline estimates of dinucleotide microsatellite mutation rate in insects [38–40].
4. Discussion
We detected no genetic structure for Australian plague locust populations covering a large part of the species's range in our analysis of microsatellite variation. In contrast, genetic differentiation between geographical localities is a common trend observed in most living species [45]. Complete lack of any genetic differentiation at microsatellite markers and across the entire range of a species is very rare in terrestrial species, including insects [46], but has been more frequently observed in marine species (e.g. [47]). It is of interest to note that locust species share some key attributes with marine invertebrates and fish, including life histories characterized by high fecundity with the potential for huge population sizes, as well as the capacity for long-distance dispersal, with long-winged adult locust and planktonic larvae movements driven by prevailing winds and ocean currents, respectively.
Although a lack of genetic structure across a species range is rare, the failure to detect genetic differentiation at finer scales is not uncommon. Despite the relatively high resolution of microsatellite loci, the studies on pest and invasive populations of invertebrate species often report a lack of genetic structure in threatened areas [8–11]. Similarly, a low degree of genetic differentiation among many fish populations is commonly reported in marine studies (reviewed in [48]). There are several non-exclusive explanations for the failure of microsatellite markers to detect genetic structure. The first is that microsatellite markers do not allow the detection of structure that may actually be present owing to limits on statistical power imposed by the relatively small numbers of markers typically used. Accordingly, additional computer simulations showed that genetic heterogeneity could be detected despite twofold and fourfold more migrants by increasing the number of genotyped microsatellite loci from the seven used in the present study to 30 and 100, respectively (see the electronic supplementary material).
Alternatively, it may be that there really is genetic homogeneity among populations across large geographical scales. There are several possible explanations for such a pattern. In introduced species, homogeneity may be due to the recent and rapid spreading of invasive populations from a unique source population (e.g. [49]), and/or sufficiently large effective sizes of newly successful populations, preventing genetic drift and differentiation since introduction (i.e. shared ancestral polymorphism; e.g. [8]). However, in species occupying their native ranges, shallow genetic structuring across broad regions has primarily been explained by high levels of gene flow (Nem). In pests, the propensity to outbreak may itself play a major role in intensifying gene flow and homogenizing genetic variation, even over continental scales [34,50]. Levels of gene flow high enough to maintain genetic homogeneity in terrestrial pest and marine populations have often been explained by their presumed high dispersal rate or distance (e.g. [10]; see [48] for marine literature). Consequently, the demographics of genetically non-differentiated populations have sometimes been interpreted as tightly linked, connected as a single panmictic group (e.g. [11,47]). This interpretation has led to the controversial conclusion that management units should be delineated at scales at least similar to that for which genetic homogeneity was observed (e.g. [11,51]; for debate and review, see [14]).
Importantly, homogenizing levels of gene flow do not necessarily indicate demographic dependence [15] or synchrony [20] between populations. The Australian plague locust is a stark illustration of this fact. A clear demographic structure was recently observed in this species that distinguished northeastern and southwestern populations across the same eastern region of Australia that was sampled in this study (figure 1). Growth rates in these demographic areas were strongly impacted by local recruitment, being primarily dependent on rainfall patterns, whereas the contribution of immigration was insufficient to couple their dynamics, as evidenced by the lack of observed synchrony between these areas. This study also suggested that outbreaks in northeastern and southwestern populations could possibly be due to different time lag responses to tropical and temperate rainfall regimes, respectively. Thus, the risk of outbreaks and the potential need for management actions within one of the focal areas cannot reliably be extrapolated to the other. Taken together, the combined population genetic and dynamic data illustrate that although dispersal rates between Australian plague locust populations cause them to be genetically indistinguishable, they can still nonetheless be demographically distinct. By dissecting the relative contribution of population size and dispersal rate to estimates of genetic differentiation, our results have allowed us to reconcile these apparently conflicting patterns.
Computer simulations using datasets that mimicked our actual data and sampling regime showed that the power to detect two distinct populations (e.g. on the western and eastern sides of Australia) dramatically declined when the populations exchanged more than 50 migrants per generation (figure 3). This suggests that populations located in eastern states of Australia and those from Western Australia were connected by a seemingly high level of gene flow (considering the distances involved) of at least 50 migrants per generation. This result parallels the results of Waples & Gaggiotti [15], who showed that power to detect distinct populations drops beyond levels of gene flow of 25 migrants per generation when assessed by Fisher's exact tests on allelic frequencies simulated under standard microsatellite genotyping effort and various population models. Given that gene flow also depends on population size (Ne), such a level of genetic exchange may actually represent a very small fraction of dispersers (m) entering the population.
The relationship between these two variables (Ne and m) becomes particularly important when considering highly fecund species. Very large population sizes are a feasible explanation for why the Australian plague locust population samples had a noticeably high mean expected heterozygosity of 0.933. The ABC treatment to examine population parameters indicated notably large long-term values of the population-scaled mutation rate Θ in C. terminifera populations, conservatively estimated at about 100. Germline mutation rates in Orthoptera are unknown, but the few available studies in insects indicated a range of 6.3 × 10−6 to 10−3. In light of these parameter values, our inferences suggest that the minimum long-term effective population sizes in which Australian plague locusts persist range anywhere from tens of thousands to a few million individuals. Typical values of effective population size are about one order of magnitude less than actual adult population sizes in insects [52]. Demographic factors such as variance in reproduction and living in crowds are predicted to further lower the ratio of effective to actual population size [52]. Importantly, in outbreaking species, the long-term effective population size is also expected to be closer to the size during remission periods than to that during outbreak periods [53]. Thus, our inferences suggest that Australian plague locusts persist, even during non-outbreak periods, in populations of hundreds of thousands of adults or more, which is likely to be in the upper range of most orthopteran species' population sizes. During outbreak periods, the population sizes resulting from successive generations of breeding in these already large remission populations would be truly massive.
The estimates of C. terminifera population sizes combined with computer simulations provide critical insight into the relationship between genetic and demographic connectivity across its range. The very large population sizes overwhelmingly affected levels of genetic differentiation among populations and hampered appreciation of the levels of dispersal between them. Indeed, given the very large sizes of the C. terminifera populations, even dispersal rates (m) of the order of 10−5 between populations located in western and in eastern Australian states could result in a number of effective migrants of 50 (Nem), which is sufficient to homogenize genotypic frequencies (figure 4). At the other end, the most conservative minimum exchange rate to homogenize genotypes between study populations on opposite sides of the continent just slightly exceeded 10−3 (i.e. by using the 2.5% lower limit of our Bayesian estimate for Θ and the highest germline mean mutation rate reported for insect microsatellites so far; figure 4). The actual dispersal rate will probably be greater than our minimum estimate range, but cannot be quantified using the methods employed here owing to the observed genetic homogeneity among populations. The threshold for synchrony in population dynamics is often considered to occur at a migration rate of 0.1, which is several orders of magnitude higher than our minimum estimates [18,19]. Therefore, despite the fact that Australian plague locust populations are genetically homogeneous, a population genetics approach alone simply cannot determine whether they are demographically connected.
Our conclusion about detecting population structure in the face of dispersal differed somewhat from that of Waples & Gaggiotti [15], who also examined the performance of exact tests. The authors concluded that there was moderate power to detect significant structure among populations exchanging effective migrants at a rate as high as 0.2 per generation. This discrepancy is because they considered, in accordance with their species of interest, values for the population-scaled mutation parameter Θ varying from 0.1 to 1, whereas the value of Θ for Australian plague locust populations considered here can number in the hundreds (figure 4). The relatively low range of Θ considered in other population genetics studies (e.g. [15]) may reflect the fact that a large proportion of the population genetics and conservation genetics literature focuses on vertebrates, most (but not all) of which live in smaller population sizes than invertebrates and will therefore have smaller Θ values. In broader terms, what is most important to stress here is that when population sizes (Ne) are large, a non-significant difference in genotypic frequencies between populations does not provide any evidence that their dynamics are connected or synchronized. Conversely, for large populations, a significant test of genotypic differentiation should be a reliable indication that migration is far below the threshold for population dynamics uncoupling, or even independence [15,54]. Although directly relevant to C. terminifera in Australia, this example applies to a variety of population genetics analyses of other mobile and fecund species. Indeed, this situation echoes challenges encountered in the study of marine organisms that occur in apparently unstructured populations spread across vast areas (reviewed in [48]) and may occur in a large number of outbreaking insects [9–11,50]. These insights between genetic homogeneity and demographic connectivity of large populations are timely, considering the recent growth of population genetics studies focused on pest or fish management (e.g. [48,55]).
Clearly, an accurate understanding of effective sizes of wild populations is required to appreciate the extent to which genetics data can be used to estimate ecological connectivity within species. Our study highlights some potentially important constraints on the application of population genetic approaches to the study of movement ecology and its application to the management of organisms with very large populations. Although there are considerable challenges involved in the analysis of the population genetics of large populations, it is important to remember that populations are dynamic in space and time. As such, in many species there are likely to be critical windows during which analyses will be more informative, such as when populations are subjected to drastic founder effects. This might occur in the initial phases of invasion of introduced species, or at the time of outbreak declines, or during recession periods in pest species, resulting in populations displaying less allelic variation and some degree of genetic differentiation. Of particular interest for future study of the Australian plague locust will be the stability of the observed pattern of range-wide genetic homogeneity over time, in particular during periods of outbreak versus remission, as well as with more intensive sampling of potentially divergent populations, since our sampling of the species range was not exhaustive. The potential still exists for genetically distinct populations in environments at the periphery of the core range (figure 1). In such areas, the locust populations may be subject to bottlenecks and isolated from the main core populations, at least during remission periods [56].
Acknowledgements
M.-P.C. gratefully acknowledges funding by a Marie-Curie Outgoing Fellowship within the Sixth European Community Framework Programme (MOIF-CT-2006-040033). This study was conducted as part of Australian Research Council Linkage Project grant no. LP0669080 to S.J.S. and G.A.S. in partnership with the Australian Plague Locust Commission. We benefited from constructive comments on an earlier version of the manuscript from Réjane Streiff and Arnaud Estoup (CBGP, France), and two anonymous reviewers.
References
- 1.Wiens J. A. 2001. The landscape context of dispersal. In The evolution of dispersal (eds Clobert J., Dhondt A., Danchin E., Nichols J.), pp. 96–109 Oxford, UK: Oxford University Press [Google Scholar]
- 2.Telfer S., Piertney S. B., Dallas J. F., Stewart W. A., Marshall F., Gow J. L., Lambin X. 2003. Parentage assignment detects frequent and large-scale dispersal in water voles. Mol. Ecol. 12, 1939–1949 10.1046/j.1365-294X.2003.01859.x (doi:10.1046/j.1365-294X.2003.01859.x) [DOI] [PubMed] [Google Scholar]
- 3.Cullingham C. I., Pond B. A., Kyle C. J., Rees E. E., Rosatte R. C., White B. N. 2008. Combining direct and indirect genetic methods to estimate dispersal for informing wildlife disease management decisions. Mol. Ecol. 17, 4874–4886 10.1111/j.1365-294X.2008.03956.x (doi:10.1111/j.1365-294X.2008.03956.x) [DOI] [PubMed] [Google Scholar]
- 4.Rousset F. 2001. Genetics approaches to the estimation of dispersal rates. In The evolution of dispersal (eds Clobert J., Dhondt A., Danchin E., Nichols J.), pp. 18–28 Oxford, UK: Oxford University Press [Google Scholar]
- 5.Peacock M. M., Ray C. 2001. Dispersal in Pikas (Ochotona princeps): combining genetic and demographic approaches to reveal spatial and temporal patterns. In The evolution of dispersal (eds Clobert J., Dhondt A., Danchin E., Nichols J.), pp. 43–56 Oxford, UK: Oxford University Press [Google Scholar]
- 6.Zhang D. X., Yan L. N., Ji Y. J., Kang L., Hewitt G. M., Huang Z. S. 2003. Isolation, characterization and cross-species amplification of eight microsatellite DNA loci in the migratory locust (Locusta migratoria). Mol. Ecol. Not. 3, 483–486 10.1046/j.1471-8286.2003.00485.x (doi:10.1046/j.1471-8286.2003.00485.x) [DOI] [Google Scholar]
- 7.Estoup A., Beaumont M., Sennedot F., Moritz C., Cornuet J. M. 2004. Genetic analysis of complex demographic scenarios: spatially expanding populations of the cane toad, Bufo marinus. Evolution 58, 2021–2036 [DOI] [PubMed] [Google Scholar]
- 8.Kim K. S., Sappington T. W. 2005. Genetic structuring of western corn rootworm (Coleoptera: Chrysomelidae) populations in the United States based on microsatellite loci analysis. Environ. Entomol. 34, 494–503 10.1603/0046-225X-34.2.494 (doi:10.1603/0046-225X-34.2.494) [DOI] [Google Scholar]
- 9.Endersby N. M., Hoffmann A. A., McKechnie S. W., Weeks A. R. 2007. Is there genetic structure in populations of Helicoverpa armigera from Australia? Entomol. Exp. Appl. 122, 253–263 10.1111/j.1570-7458.2006.00515.x (doi:10.1111/j.1570-7458.2006.00515.x) [DOI] [Google Scholar]
- 10.Sallé A., Arthofer W., Lieutier F., Stauffer C., Kerdelhué C. 2007. Phylogeography of a host-specific insect: genetic structure of Ips typographus in Europe does not reflect past fragmentation of its host. Biol. J. Linn. Soc. 90, 239–246 10.1111/j.1095-8312.2007.00720.x (doi:10.1111/j.1095-8312.2007.00720.x) [DOI] [Google Scholar]
- 11.Schrey N. M., Schrey A. W., Heist E. J., Reeve J. D. 2008. Fine-scale genetic population structure of southern pine beetle (Coleoptera: Curculionidae) in Mississippi forests. Environ. Entomol. 37, 271–276 10.1603/0046-225X(2008)37[271:FGPSOS]2.0.CO;2 (doi:10.1603/0046-225X(2008)37[271:FGPSOS]2.0.CO;2) [DOI] [PubMed] [Google Scholar]
- 12.Moritz C. 1995. Uses of molecular phylogenies for conservation. Phil. Trans. R. Soc. Lond. B 349, 113–118 10.1098/rstb.1995.0097 (doi:10.1098/rstb.1995.0097) [DOI] [Google Scholar]
- 13.Moritz C. 2002. Strategies to protect biological diversity and the evolutionary processes that sustain it. Syst. Biol. 51, 238–254 [DOI] [PubMed] [Google Scholar]
- 14.Palsbøll P., Berube M., Allendorf F. 2007. Identification of management units using population genetic data. Trends Ecol. Evol. 22, 11–16 10.1016/j.tree.2006.09.003 (doi:10.1016/j.tree.2006.09.003) [DOI] [PubMed] [Google Scholar]
- 15.Waples R. S., Gaggiotti O. E. 2006. What is a population? An empirical evaluation of some genetic methods for identifying the number of gene pools and their degree of connectivity. Mol. Ecol. 15, 1419–1439 10.1111/j.1365-294X.2006.02890.x (doi:10.1111/j.1365-294X.2006.02890.x) [DOI] [PubMed] [Google Scholar]
- 16.De Valpine P., Scranton K., Ohmart C. P. 2010. Synchrony of population dynamics of two vineyard arthropods occurs at multiple spatial and temporal scales. Ecol. Appl. 20, 1926–1935 10.1890/09-0468.1 (doi:10.1890/09-0468.1) [DOI] [PubMed] [Google Scholar]
- 17.Liebhold A., Koenig W. D., Bjørnstad O. N. 2004. Spatial synchrony in population dynamics. Ann. Rev. Ecol. Evol. Syst. 35, 467–490 10.1146/annurev.ecolsys.34.011802.132516 (doi:10.1146/annurev.ecolsys.34.011802.132516) [DOI] [Google Scholar]
- 18.Hastings A. 1993. Complex interactions between dispersal and dynamics—lessons from couples logistic equations. Ecology 74, 1362–1372 10.2307/1940066 (doi:10.2307/1940066) [DOI] [Google Scholar]
- 19.Sherratt T. N., Lambin X., Petty S. J., MacKinnon J. L., Coles C. F., Thomas C. J. 2000. Use of coupled oscillator models to understand synchrony and travelling waves in populations of the field vole (Microtus agrestis) in northern England. J. Appl. Ecol. 37, 148–158 10.1046/j.1365-2664.2000.00472.x (doi:10.1046/j.1365-2664.2000.00472.x) [DOI] [Google Scholar]
- 20.Koizumi I., Yamamoto S., Nomoto K., Maekawa K. 2008. Synchrony in local population dynamics of stream-dwelling Dolly Varden: do genetically similar groups show similar demography? Popul. Ecol. 50, 367–377 10.1007/s10144-008-0108-2 (doi:10.1007/s10144-008-0108-2) [DOI] [Google Scholar]
- 21.Slatkin M. 1987. Gene flow and the geographic structure of natural populations. Science 236, 787–792 10.1126/science.3576198 (doi:10.1126/science.3576198) [DOI] [PubMed] [Google Scholar]
- 22.Gray L. J., Sword G. A., Anstey M. L., Clissold F. J., Simpson S. J. 2009. Behavioural phase polyphenism in the Australian plague locust (Chortoicetes terminifera). Biol. Lett. 5, 306–309 10.1098/rsbl.2008.0764 (doi:10.1098/rsbl.2008.0764) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Deveson E. D., Drake V. A., Hunter D. M., Walker P. W., Wang H. K. 2005. Evidence from traditional and new technologies for northward migrations of Australian plague locusts (Chortoicetes terminifera) (Walker) (Orthoptera: Acrididae) to western Queensland. Austral Ecol. 30, 928–943 10.1111/j.1442-9993.2005.01536.x (doi:10.1111/j.1442-9993.2005.01536.x) [DOI] [Google Scholar]
- 24.Hunter D. M. 2004. Advances in the control of locusts (Orthoptera: Acrididae) in eastern Australia: from crop protection to preventive control. Aust. J. Entomol. 43, 293–303 10.1111/j.1326-6756.2004.00433.x (doi:10.1111/j.1326-6756.2004.00433.x) [DOI] [Google Scholar]
- 25.APLC 2000. Australian Plague Locust Commission annual report 1998–99. Canberra, Australia: Department of Agriculture, Fisheries and Forestry [Google Scholar]
- 26.Hooper G. H. S., Brown W. V., Lacey M. J., Hunter D. 1996. Cuticular hydrocarbons of the Australian plague locust, Chortoicetes terminifera (Walker) (Orthoptera: Acrididae), collected from widely separated geographical locations. Aust. J. Entomol. 35, 257–262 10.1111/j.1440-6055.1996.tb01400.x (doi:10.1111/j.1440-6055.1996.tb01400.x) [DOI] [Google Scholar]
- 27.Gregg P. C., Webb G. C., Adena M. A. 1984. The dynamics of chromosomes B in populations of the Australian plague locust, Chortoicetes terminifera (walker). Can. J. Genet. Cytol. 26, 194–208 [Google Scholar]
- 28.Beaumont M. A., Zhang W., Balding D. J. 2002. Approximate Bayesian computation in population genetics. Genetics 162, 2025–2035 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Cornuet J. M., Santos F., Beaumont M. A., Robert C. P., Marin J.-M., Balding D. J., Guillemaud T., Estoup A. 2008. Inferring population history with DIY ABC: a user-friendly approach to approximate Bayesian computation. Bioinformatics 24, 2713–2719 10.1093/bioinformatics/btn514 (doi:10.1093/bioinformatics/btn514) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Hudson R. R. 1990. Gene genealogies and the coalescent process. In Oxford surveys in evolutionary biology (eds Futuyama D., Antonovics J.), pp. 1–44 Oxford, UK: Oxford University Press [Google Scholar]
- 31.Mayaux P., Bossard K. 2003. GLC2000 database. European Commission Joint Research Centre. See http://ies.jrc.ec.europa.eu/global-land-cover-2000. [Google Scholar]
- 32.Chapuis M.-P., Popple J.-A., Simpson S. J., Estoup A., Martin J.-F., Steinbauer M. L. M., Sword G. A. 2008. Eight polymorphic microsatellite loci for the Australian plague locust, Chortoicetes terminifera. Mol. Ecol. Resour. 8, 1414–1416 10.1111/j.1755-0998.2008.02204.x (doi:10.1111/j.1755-0998.2008.02204.x) [DOI] [PubMed] [Google Scholar]
- 33.Rousset F. 2008. GENEPOP'007: a complete re-implementation of the GENEPOP software for Windows and Linux. Mol. Ecol. Resour. 8, 103–106 10.1111/j.1471-8286.2007.01931.x (doi:10.1111/j.1471-8286.2007.01931.x) [DOI] [PubMed] [Google Scholar]
- 34.Chapuis M.-P., Lecoq M., Loiseau A., Piry S., Sword G. A., Michalakis Y., Estoup A. 2008. Do outbreaks affect genetic population structure? A worldwide survey in Locusta migratoria, a pest plagued by microsatellite null alleles. Mol. Ecol. 17, 3640–3653 10.1111/j.1365-294X.2008.03869.x (doi:10.1111/j.1365-294X.2008.03869.x) [DOI] [PubMed] [Google Scholar]
- 35.Nei M. 1987. Molecular evolutionary genetics. New York, NY: Columbia University Press [Google Scholar]
- 36.Weir B. S. 1996. Genetic data analysis II: methods for discrete population genetic data. Sunderland, UK: Sinauer Associates [Google Scholar]
- 37.Chapuis M.-P., Estoup A. 2007. Microsatellite null alleles and estimation of population differentiation. Mol. Biol. Evol. 24, 621–631 10.1093/molbev/msl191 (doi:10.1093/molbev/msl191) [DOI] [PubMed] [Google Scholar]
- 38.Schlötterer C., Ritter R., Harr B., Brem G. 1998. High mutation rate of a long microsatellite allele in Drosophila melanogaster provides evidence for allele-specific mutation rates. Mol. Biol. Evol. 15, 1269–1274 [DOI] [PubMed] [Google Scholar]
- 39.Schug M. D., Hutter C. M., Wetterstrand K. A., Gaudette M. S., Mackay T. F., Aquadro C. F. 1998. The mutation rates of di-, tri- and tetranucleotide repeats in Drosophila melanogaster. Mol. Biol. Evol. 15, 1751–1760 [DOI] [PubMed] [Google Scholar]
- 40.Crozier R. H., Kaufmann B., Carew M. E., Crozier Y. C. 1999. Mutability of microsatellites developed for the ant Camponotus consobrinus. Mol. Ecol. 8, 271–276 10.1046/j.1365-294X.1999.00565.x (doi:10.1046/j.1365-294X.1999.00565.x) [DOI] [PubMed] [Google Scholar]
- 41.Zhivotovsky L. A., Feldman M. W., Grishechkin S. A. 1997. Biased mutations and microsatellite variation. Mol. Biol. Evol. 14, 926–933 [DOI] [PubMed] [Google Scholar]
- 42.Ellegren H. 2000. Microsatellite mutations in the germline: implications for evolutionary inference. Trends Genet. 16, 551–558 10.1016/S0168-9525(00)02139-9 (doi:10.1016/S0168-9525(00)02139-9) [DOI] [PubMed] [Google Scholar]
- 43.Hey J., Nielsen R. 2007. Integration within the Felsenstein equation for improved Markov chain Monte Carlo methods in population genetics. Proc. Natl Acad. Sci. USA 104, 2785–2790 10.1073/pnas.0611164104 (doi:10.1073/pnas.0611164104) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Kimura M., Ohta T. 1978. Stepwise mutation model and distribution of allelic frequencies in a finite population. Proc. Natl Acad. Sci. USA 75, 2868–2872 10.1073/pnas.75.6.2868 (doi:10.1073/pnas.75.6.2868) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Avise J. C. 1994. Molecular markers, natural history and evolution. New York, NY: Chapman and Hall [Google Scholar]
- 46.Beveridge M., Simmons L. W. 2006. Panmixia: an example from Dawson's burrowing bee (Amegilla dawsoni) (Hymenoptera: Anthophorini). Mol. Ecol. 15, 951–957 10.1111/j.1365-294X.2006.02846.x (doi:10.1111/j.1365-294X.2006.02846.x) [DOI] [PubMed] [Google Scholar]
- 47.Hoarau G., Rijnsdorp A. D., Van der Veer H. W., Stam W. T., Olsen J. L. 2002. Population structure of plaice (Pleuronectes platessa L.) in northern Europe: microsatellites revealed large-scale spatial and temporal homogeneity. Mol. Ecol. 11, 1165–1176 10.1046/j.1365-294X.2002.01515.x (doi:10.1046/j.1365-294X.2002.01515.x) [DOI] [PubMed] [Google Scholar]
- 48.Palumbi S. R. 2003. Population genetics, demographic connectivity, and the design of marine reserves. Ecol. Appl. 13, S146–S158 10.1890/1051-0761(2003)013[0146:PGDCAT]2.0.CO;2 (doi:10.1890/1051-0761(2003)013[0146:PGDCAT]2.0.CO;2) [DOI] [Google Scholar]
- 49.Ciosi M., Miller N. J., Kim K. S., Giordano R., Estoup A., Guillemaud T. 2008. Invasion of Europe by the western corn rootworm, Diabrotica virgifera virgifera: multiple transatlantic introductions with various reductions of genetic diversity. Mol. Ecol. 17, 3614–3627 10.1111/j.1365-294X.2008.03866.x (doi:10.1111/j.1365-294X.2008.03866.x) [DOI] [PubMed] [Google Scholar]
- 50.Chapuis M. P., Loiseau A., Michalakis Y., Lecoq M., Franc A., Estoup A. 2009. Outbreaks, gene flow and effective population size in the migratory locust, Locusta migratoria: a regional-scale comparative survey. Mol. Ecol. 18, 792–800 10.1111/j.1365-294X.2008.04072.x (doi:10.1111/j.1365-294X.2008.04072.x) [DOI] [PubMed] [Google Scholar]
- 51.Querouil S., et al. 2007. High gene flow in oceanic bottlenose dolphins (Tursiops truncatus) of the North Atlantic. Conserv. Genet. 8, 1405–1419 10.1007/s10592-007-9291-5 (doi:10.1007/s10592-007-9291-5) [DOI] [Google Scholar]
- 52.Frankham R. 1995. Effective population-size adult population-size ratios in wildlife—a review. Genet. Res. 66, 95–107 10.1017/S0016672300034455 (doi:10.1017/S0016672300034455) [DOI] [PubMed] [Google Scholar]
- 53.Motro U., Thomson G. 1982. On heterozygosity and the effective size of populations subject to size changes. Evolution 36, 1059–1066 10.2307/2408083 (doi:10.2307/2408083) [DOI] [PubMed] [Google Scholar]
- 54.Avise J. C. 1995. Mitochondrial-DNA polymorphism and a connection between genetics and demography of relevance to conservation. Conserv. Biol. 9, 686–690 10.1046/j.1523-1739.1995.09030686.x (doi:10.1046/j.1523-1739.1995.09030686.x) [DOI] [Google Scholar]
- 55.Schwartz M. K., Luikart G., Waples R. S. 2007. Genetic monitoring as a promising tool for conservation and management. Trends Ecol. Evol. 22, 25–33 10.1016/j.tree.2006.08.009 (doi:10.1016/j.tree.2006.08.009) [DOI] [PubMed] [Google Scholar]
- 56.Bonizzoni M., Guglielmino C. R., Smallridge C. J., Gomulski M., Malacrida A. R., Gasperi G. 2004. On the origins of medfly invasion and expansion in Australia. Mol. Ecol. 13, 3845–3855 10.1111/j.1365-294X.2004.02371.x (doi:10.1111/j.1365-294X.2004.02371.x) [DOI] [PubMed] [Google Scholar]