Constraints on food chain length arising from regional metacommunity dynamics

Abstract

Classical ecological theory has proposed several determinants of food chain length, but the role of metacommunity dynamics has not yet been fully considered. By modelling patchy predator–prey metacommunities with extinction–colonization dynamics, we identify two distinct constraints on food chain length. First, finite colonization rates limit predator occupancy to a subset of prey-occupied sites. Second, intrinsic extinction rates accumulate along trophic chains. We show how both processes concur to decrease maximal and average food chain length in metacommunities. This decrease is mitigated if predators track their prey during colonization (habitat selection) and can be reinforced by top-down control of prey vital rates (especially extinction). Moreover, top-down control of colonization and habitat selection can interact to produce a counterintuitive positive relationship between perturbation rate and food chain length. Our results show how novel limits to food chain length emerge in spatially structured communities. We discuss the connections between these constraints and the ones commonly discussed, and suggest ways to test for metacommunity effects in food webs.

1. Introduction

An important puzzle in ecology is how food web topology, and in particular food chain length, is determined [1–8]. Food chain length is a measure of the number of feeding links between resources and top predators (e.g. [9]). Ecological theory has long tried to understand why food chains should have limited length [3,5,10,11]. For instance, the energetic constraint hypothesis [3] invokes imperfect transfers of energy and resources along food chains, whereas the dynamics constraint hypothesis [11,12] considers that long food chains are more vulnerable to perturbation than short ones.

Recent empirical studies have identified three major determinants of food chain length: productive space, disturbance and ecosystem size [13]. While confirming the roles of resource limitation and perturbation, these results argue against single explanations, and also stress the need to incorporate space in theoretical models. Indeed, despite ample evidence that food chain length correlates with habitat area or ecosystem size [14–17], spatial processes are still understudied in theoretical models of food webs [18,19]. Models have incorporated trait evolution [20] or adaptive foraging [21], but the assumption of homogeneous and well-mixed communities has remained the rule.

Here, we apply the metacommunity framework to food webs [22] to study how habitat patchiness and extinction–colonization dynamics affect food chain length. It has been suggested that, even in the absence of other constraints, regional processes can set a theoretical limit on food chain length [19,23]. We propose to determine this limit quantitatively in a general model where: (i) the form of disturbance can be either patch-level perturbation or species-specific extinction; (ii) predators can have any type of top-down effect on the colonization and extinction rates of prey populations; and (iii) dispersal can be non-random, i.e. predator (or prey) propagules possess some level of habitat selection.

We find that metacommunity dynamics can set an effective limit to food chain length in the absence of other constraints. Our model predicts that: (i) food chain length is more limited when species-specific processes rather than patch-level catastrophes cause extinction; (ii) top-down control of extinction is more critical to food chain length than top-down control of colonization; (iii) strong negative top-down control of colonization can produce counterintuitive patterns, such as food chain length increasing with perturbation rate, or decreasing with foraging efficiency; and (iv) food chain length can be very variable in space, so that the average chain length can be much smaller than the maximum. We discuss connections between metacommunity constraints on food chain length and earlier non-spatial theories, suggesting that a spatial framework can help reconcile hypotheses commonly brought up as rivals.

2. Model

(a). Metacommunity dynamics

We use a multi-trophic extension of Levins' metapopulation model [24] describing the occurrences of species in patches of a metacommunity connected by dispersal. This represents a relatively simple approach to the dynamics of spatialized food webs [25]. So far, few studies have considered trophic interactions in this patch dynamics framework. For instance, Holt [23] addressed the issue of spatial persistence, the possibility of alternative equilibria [19] and Melian & Bascompte [26] studied the resistance to habitat loss, all for tri-trophic food chains.

We consider food chains with an arbitrary number of trophic levels, and the proportion of patches harbouring exactly i trophic levels is noted p_i. There may be several species sharing preys and predators at each level, in which case they are averaged into a single trophic species [7]. We make the assumption that consumers at level i persists only in patches where level i − 1 is found. This does not rule out feeding links between non-adjacent levels, but means that level i needs prey i − 1 in order to maintain viable local populations. Thus, patches with level i necessarily contain all lower levels (1 to i − 1). The regional occupancy of level i is q_i = ∑_j≥i p_j. The first trophic level is considered a primary producer to which all habitat is available (i.e. q₀ = 1).

Although such a model is quite naturally expressed in terms of p_i [19], we express it in terms of q_i to highlight its connections to Levins' [24] model:

2.1

Here 〈c_i〉 is the colonization rate by trophic level i from an average occupied patch; μ is the patch-level perturbation rate (e.g. hurricanes on tropical islands or severe drought in ponds); and 〈e_i〉 is the perceived extinction rate of trophic level i in an average occupied patch.

Equation (2.1) has the structure of a metapopulation model with three important differences. First, the habitat available to trophic level i is q_i−1, the occupancy of level i − 1. Second, there are two distinct sources of population disturbance: perturbation (μ) and extinction 〈e_i〉. These two processes are confounded in monotrophic models [27], but differ in multitrophic metacommunities: while perturbation removes all trophic levels from a patch, extinction occurring at some trophic level leaves all lower levels in the patch. Third, colonization and extinction rates (〈c_i〉 and 〈e_i〉) are functions of the metacommunity state as soon as there is habitat selection and/or top-down effects, as explained below.

(b). Definition of extinction rates

We assume that every trophic level goes extinct from an occupied patch at some intrinsic extinction rate e_i. As predators cannot persist without prey, any trophic level experiences not only its own extinction rate, but also those of all lower levels. Extinction rates can also be modulated by the presence of predators in a patch: predation is indeed likely to alter extinction rates through a variety of consumptive and non-consumptive effects. Hence, if trophic level i has rate e_i in patches where it does not suffer predation, it has a rate e_i + e_TD in all other patches. Parameter e_TD quantifies the top-down control of predation on extinction, and can have any sign. Under these assumptions, the perceived extinction rate is:

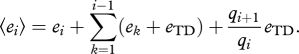2.2

The first term is the intrinsic extinction rate of the focal trophic level, the second term is the sum of the extinction rates of all lower levels, and the third term represents top-down control of extinction: it introduces a dependency on the metacommunity state, as only patches with predators (representing a fraction q_i+1/q_i of occupied patches) are affected. We also investigated a formulation with within-patch trophic cascades instead (electronic supplementary material, appendix B).

(c). Definition of colonization rates

As for extinction, we assume that each trophic level emits propagules at rate c_i from predator-free patches, and at rate c_i + c_TD from patches with predators. Parameter c_TD quantifies top-down control on colonization. We further consider the possibility of habitat selection during dispersal, whereby predator propagules can maximize the odds to settle in ‘hospitable’ (i.e. occupied by prey) patches. We assume that if a propagule samples a patch without prey on its first attempt, it redirects to a hospitable patch with probability φ. Here, φ quantifies the efficiency of habitat selection. These assumptions yield the following expression for c_i:

2.3

The first parenthesis represents the intrinsic colonization rate and top-down control of colonization, and the second parenthesis quantifies the increase in colonization rate caused by habitat selection: if the propagule first sampled a patch devoid of prey (probability 1 − q_i−1), then it has some chance (φ) to resample only patches with prey (q_i−1 at the denominator). We also investigated alternate formulations with within-patch trophic cascades and habitat selection by prey rather than predators (electronic supplementary material, appendix B).

(d). Determination of food chain length

Because food chain length varies in space, we studied both the maximum chain length observed in the metacommunity and the spatially averaged chain length. The latter may better reflect the value that would be measured with finite sampling effort. It is also closer to some definitions of food chain length that take into account the relative importance of feeding links, not just their existence [9,28].

The positive equilibrium of equations (2.1) to (2.3) can be computed efficiently without resorting to simulations (electronic supplementary material, appendix A). We determined the maximum feasible chain length as the longest possible chain in which all trophic levels have occupancy larger than some threshold δ. This threshold represents the lowest detectable occupancy, or the lowest viable occupancy when there is a finite number of patches. We used δ = 10⁻⁴ for numerical analyses. The average chain length was computed as ∑_i>0 ip_i/q₁.

Our model allows for arbitrary rates (c_i and e_i) at each trophic level, which represent many free parameters. Although these rates might show consistent trends across trophic levels (e.g. in relation to body size; [29,30]), intuition is limited and data are scarce (these are per-patch rates: extinction is not just mortality, and colonization is not just fecundity). In this article, we will retain the baseline assumption that all trophic levels have identical rates, i.e. c_i = c and e_i = e. The observed constraints on food chain length thus emerge entirely from regional metacommunity dynamics, rather than intrinsic differences between trophic levels. Departures from the baseline assumption are discussed below.

3. Results

(a). Perturbation- versus extinction-limited chains

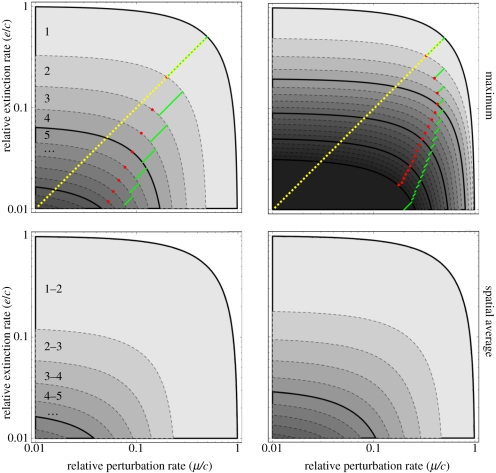
Both perturbation (μ) and extinction (e) rates can set strong constraints on maximum chain length if high enough, but the latter sets stronger constraints than the former (figure 1). This is revealed by the asymmetry of the contour lines in figure 1: e.g. in the absence of habitat selection, it takes μ ≈ 0.1c to limit the maximum chain length to 6, whereas it takes only e ≈ 0.03c. The red dots in figure 1 locate the pairs (μ,e), such that it would take the same relative increase of any rate to decrease the maximum chain length by 1: chain length is thus more strongly limited by extinction to the left of these dots, and by perturbation to their right. Red dots fall well below the e = μ line (dotted yellow line), especially for long food chains. With perfect habitat selection (φ = 1), perturbation and extinction are unsurprisingly less efficient at limiting food chain length, but extinction rate more strongly limits food chain length. Note that chain lengths above 6 or 7 are unrealistically larger than values observed in nature [16]. This indicates that with insufficient local turnover (e.g. e less than 5–15% of the colonization rate; figure 1), metacommunity dynamics are unlikely to be a dominant control on food chain length; additional (local) constraints should be invoked.

Figure 1.

The effect of perturbation (μ) and extinction (e) in limiting food chain length. Remember that perturbation is the simultaneous eradication of all trophic levels in a patch; while extinction occurs by definition independently at different trophic levels. Darker shades of grey indicate that longer food chains can persist (white, no species persists as μ + e > c). Upper graphs, maximum food chain length; lower graphs, spatially averaged food chain length. Left-hand graphs no habitat selection (φ = 0) and right-hand graphs perfect habitat selection (φ = 1). Yellow lines indicate where μ = e. Green lines indicate where the top trophic level experiences extinction rate equal to the perturbation rate. Red dots represent values where food chain length is limited equally by perturbation and extinction, i.e. it takes exactly the same relative increase of μ or e to reduce chain length by one. Other parameters: e_TD = c_TD = 0.

Extinction more readily limits food chain length than perturbation as predators cannot persist without prey, and thus cumulate the extinction rates of all lower levels (equation (2.2)). Such a ‘snowball’ effect implies that the experienced extinction rate increases with trophic level, whereas the risk of perturbation remains the same at all levels. However, this effect is mitigated by the fact that extinctions do not affect all trophic levels at once, thus preserving a higher fraction of available habitats for top predators, whereas perturbation wipes out all trophic levels in a patch. This can be seen in figure 1: an equal relative sensitivity of maximal chain length to perturbation and extinction (red dots in figure 1) is always achieved for perturbation rates lower than the cumulated extinction rate of the top predator (i.e. on the left of green lines in figure 1). If the snowball effect were the only determinant of the differences between perturbation and extinction, we would expect red dots and green lines to coincide. This mitigation of the snowball effect is weak though, especially in long food chains (figure 1), and a given extinction rate (e) is always stronger than a similar rate of perturbation (μ) at limiting food chain length (red dots always fall right of the yellow line in figure 1).

As the snowball effect increases the extinction rate experienced by upper trophic levels, it is particularly efficient at counteracting the effects of habitat selection. From equation (2.3), it is apparent that habitat selection causes the effective colonization rate to increase with trophic level: top predators, whose hospitable habitat is necessarily scarcer than that of lower levels, benefit relatively more from habitat selection. Snowballing extinction rates affect top predators more heavily, and thus counteract habitat selection more efficiently than perturbation, which affects all levels indiscriminately. Thus, the effects of perturbation and extinction become more asymmetrical with stronger habitat selection (figure 1).

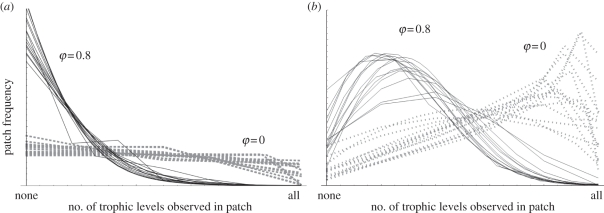
The average food chain length is always lower than the maximum one (figure 1). This difference is especially pronounced with strong habitat selection: whereas habitat selection can increase maximum chain length manifold, it barely increases the spatial average. The asymmetry between perturbation and extinction effects is weaker when one considers the spatial average rather than the maximum. To understand this, we can look at the distribution of chain length (i.e. the distribution of p_i values; figure 2). There are robust differences between food chains that are limited primarily by perturbation versus extinction (see the electronic supplementary material, appendix A for analytical insights). In perturbation-limited chains, the distribution of chain length is flat or decreasing, whereas in extinction-limited chains it has a mode at some intermediate, often quite high value. Note that in both cases, habitat selection increases the skewness of the distribution, and hence the discrepancy between the average and the maximum, by introducing a fat tail. In other words, habitat selection allows many additional trophic levels to persist (increasing the maximum chain length), but as these have relatively small occupancies, the average length is little affected. Habitat selection by prey rather than predators has a similar, but much weaker, effect on chain length (electronic supplementary material, appendix B).

Figure 2.

The distribution of patch types when food chain length is limited primarily by (a) perturbation or (b) extinction. The number of trophic levels present in a patch (i) was standardized between 0 and its regional maximum, while patch frequency (p_i) was normalized so that the area below each curve is one. In each panel two sets of curves are shown: 15 with no habitat selection (φ = 0) and 15 with φ = 0.8. Curves correspond to random parameters drawn uniformly in (0.08, 0.5) for μ, in (0.001, 0.1) for e, in (−e, e), for e_TD for (−1, 0.2), for c_TD and in (10⁻⁵, 10⁻³) for δ, except that e (μ) was fixed to zero in a.

(b). Top-down effects: extinction versus colonization

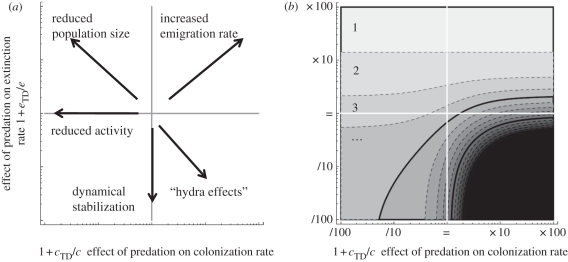
The top-down control effects on extinction and colonization rates can be multifarious (figure 3). Predation, by lowering population densities, would cause the extinction rate to increase (low population density implies high stochasticity) and the colonization rate to decrease (low population density implies low recruitment and thus low propagule emission) with increasing trophic level. The opposite pattern, albeit less documented, is also possible: there may be a stabilizing effect of predators on population dynamics [19] or ‘hydra effects’ [31], whereby predation increases average prey population density, potentially decreasing the extinction rate and/or increasing the colonization rate. Non-consumptive effects can also have contrasting impacts: colonization and extinction rates may increase owing to emigration from high-risk patches [32], but colonization may also decrease because of increased vigilance and/or decreased activity levels [33].

Figure 3.

Effect of top-down control of colonization (c_TD) and extinction (e_TD) on maximal food chain length. At the centre of the graph, c_TD = e_TD = 0, and the range of values amounts to dividing or multiplying the rates by a factor of 100. Contour lines as in figure 1 (dashed lines at every added trophic level; solid lines every four added levels). (a) represents potential mechanisms generating different signs for c_TD (abscissas) and e_TD (ordinates). For instance, increased emigration rate owing to the presence of a predator would generate positive c_TD and e_TD. Other parameters: μ = e = 0.1; φ = 0.5.

We investigated all possibilities regarding the signs of c_TD and e_TD (figure 3). In the most intuitive scenario (c_TD < 0 and e_TD > 0; upper left quadrant), c_TD has a much weaker effect than e_TD at limiting food chain length. The same holds if the two kinds of top-down control work in opposite directions: c_TD > 0 and e_TD > 0 (upper right quadrant) or c_TD < 0 and e_TD < 0 (lower left quadrant). A predation-driven increase/decrease of colonization rate does not efficiently compensate the effect of a predation-driven increase/decrease of extinction rate. Indeed, affecting prey extinction rate causes a twofold feedback on the predator by altering (i) the fraction of hospitable habitat, and (ii) the experienced extinction rate through the snowball effect (equation (2.2)). Top-down control of colonization generates only the first sort of feedback. In the least plausible scenario (c_TD > 0 and e_TD < 0; lower right quadrant), the two top-down controls act synergistically to suppress the constraint on food chain length. The resulting food chains ultimately become regionally unstable though, which sets another type of constraint on length ([19]; electronic supplementary material, appendix A). Similar conclusions are reached about the spatial average of chain length (not shown), or when within-patch trophic cascades are introduced in the model (electronic supplementary material, appendix B).

(c). Specificities of top-down control of colonization

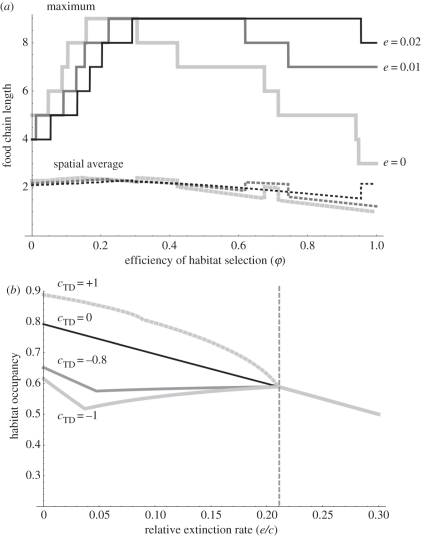
Although top-down control of colonization has a much weaker effect than top-down control of extinction, the former can generate unique, and unexpected, behaviours (figure 4). These occur for highly negative values of c_TD (c_TD ≈ −c), i.e. when predation almost suppresses the emission of propagules. First, in contrast to the general result (figure 1), there can be a non-monotonic effect of the efficiency of habitat selection (φ) on the maximum and/or average food chain length (figure 4a). Increasing φ above some optimal value (about 0.3 in figure 4) can reduce the maximum chain length, even below the value observed at φ = 0. The non-monotonic effect of φ can persist with frequent perturbations (high μ), but is easily suppressed by increased extinction rates (e; figure 4a), or equivalently, by top-down control of extinction (positive e_TD values). Therefore, increasing e (or e_TD) can increase food chain length (figure 4a). Again, this is not observed in any other situation. These atypical properties correspond to top predators imposing strong negative effects on the basal levels, while compensating for the scarcity of hospitable patches through efficient habitat selection. As explained above, snowballing extinction rates are most detrimental to upper trophic levels and can thus counteract even strong habitat selection. This explains why atypical behaviours are suppressed when extinction rates are increased (figure 4a). Interestingly, prey habitat selection never has such a detrimental effect on chain length (electronic supplementary material, appendix B).

Figure 4.

Properties of metacommunities with strong top-down control of colonization. (a) Increasing the efficiency of habitat selection (φ) is detrimental to food chain length (maximum and spatial average) with c_TD = −1. Three cases, corresponding to increasing extinction rates (e) are presented. The discontinuous changes in average chain length mirror the discrete changes in maximum food chain length. (b) Increasing the extinction rate (e) can be beneficial to habitat occupancy (q_i). Abrupt changes in the curves correspond to discrete changes in the number of trophic levels, top predators being lost as e increases. Beyond the vertical line, only one species persists and top-down effects no longer play any role. Other parameters: μ = 0.1; e_TD = 0.01;φ = 0.1.

Strong top-down control of colonization rate can also produce counterintuitive effects of extinction rate on total habitat occupancy, i.e. the proportion of non-empty patches (q₁). Although Levins' metapopulation model classically predicts that extinction is detrimental to occupancy, this does not hold for multi-trophic metacommunities. When c_TD is sufficiently negative (smaller than about −0.75c), e or e_TD have non-monotonic effects on total occupancy, irrespective of habitat selection (figure 4b). Increasing extinction rate decreases occupancy only when the number of trophic levels is odd, otherwise it has a beneficial effect. Hence, increasing extinction rates sequentially decreases and increases occupancy, with inversions corresponding to the loss of top predators (figure 4b). This is an instance of a regional trophic cascade, which is similar to classical trophic cascades but involves spatial occupancy rather than population density. Unsurprisingly, incorporating classical (within-patch) trophic cascades in the model exacerbates these regional cascade patterns (see electronic supplementary material, appendix B).

4. Discussion

(a). Food chain length in metacommunities

Both maximum and average food chain length were found to have stringent upper limits in metacommunities, as soon as extinction–perturbation rates are not too small when compared with colonization rates. The first reason is that as predators are restricted to patches where prey is found, a finite number of trophic levels can persist regionally, as anticipated by Holt [23]. The second reason is the snowball effect: when extinction is owing to species-specific processes (e.g. chance extinction owing to demographic stochasticity) rather than patch-specific processes, the perceived extinction rate increases with trophic level. This effect is supported empirically: at a small scale, Cronin [34] found that 25 per cent of the higher extinction rate of parasitoid local populations was explained by local extinction of their hosts, while the intrinsic extinction rates (e values) of the two species did not differ significantly. At larger scales, co-extinction of herbivorous insects because of host plant extinction is thought to be common [35]. Whereas earlier theoretical analyses overlooked this snowball effect ([19,22]; see [25]), we showed here that it can severely constrain food chain length, and also alter the effects of habitat selection. Hence, attention should be paid to the source of population disturbance (extinction versus patch perturbation) when studying food webs in metacommunities.

The two mechanisms that limit food chain length in a metacommunity have connections to those commonly discussed in the literature. Decreasing available habitat with trophic level is a spatial analogue of the energetic constraint hypothesis [3], substituting regional prey occupancy to local resource as a limiting factor. As such, it conforms to the view that productive space and ecosystem size are important determinants of food chain length [13]. Extinction (e) introduces the snowball effect as a second constraint on food chain length. This effect is a variation on the theme of dynamics constraints [11,12] applied at the patch level: longer food chains are less persistent locally, which makes them less frequent at the regional level. Interestingly, snowballing extinction rates also lower habitat occupancy, and thus amplify the first constraint (reduced available habitat) for upper trophic levels. This shows that these two aspects of food chain limitation (resource limitation versus dynamical constraints), perceived as alternatives in most non-spatial theories (but see [36]), are intertwined in metacommunities.

(b). Top-down effects and habitat selection

We investigated how regional constraints on food chain length are affected by top-down control and by habitat selection (i.e. non-random dispersal). Top-down effects are equally likely to alter extinction or colonization rates (figure 3a), but predictions depend strongly on which rate is affected. Food chain length is much more sensitive to top-down control of extinction than of colonization. The reason is that top-down control of extinction contributes to the snowball effect: its effects thus accumulate along trophic chains. By contrast, top-down control of colonization affects only the occupancy of impacted trophic levels (by modifying their colonization ability), and this effect is not cumulative. In other words, top-down control of colonization alters only the first constraint on food chain length (limited habitat availability), whereas top-down control of extinction alters both.

Habitat selection generates a frequency-dependent increase of the effective colonization rate of predators. Top predators, whose prey is scarcer, benefit most from it. As expected, this almost always results in higher maximum chain length, but has a comparatively smaller effect on the average food chain length in the metacommunity. Indeed, efficient habitat selection can allow many high trophic levels to persist, but these have low occupancy. As a consequence, most patches still harbour shorter food chains, and the spatially averaged food chain length is little affected. Another consequence is that even though efficient habitat selection can virtually eliminate any regional constraint on maximum chain length, a small reduction in the number of patches in the metacommunity (and thus in the smallest feasible regional occupancy, our parameter δ) would imply the collapse of many trophic levels at once, which is not expected with weak habitat selection [26]. These are situations where ecosystem size would be a primary determinant of food chain length [17]. Interestingly, habitat selection by prey does not have the same properties.

Although top-down control of colonization generally has moderate effects on food chain length, it can produce unique patterns. First, a negative correlation between habitat selection and food chain length may emerge in metacommunities with a very strong top-down suppression of colonization (c_TD ≈ −c). Second, top-down suppression of colonization can cause the fraction of non-empty patches to increase with extinction rate (figure 4). This is caused by regional trophic cascades equivalent to classical trophic cascades. These results imply that seemingly beneficial changes (e.g. more efficient habitat selection) could adversely affect key metacommunity properties (such as food chain length). It is plausible that predation can reduce colonization in many cases (e.g. by reducing local population sizes; see figure 3a), but it is unknown whether this effect can be strong enough in natural systems. Looking for these atypical patterns allows the evaluation of the role of metacommunity dynamics in shaping food webs, and specifically the importance of top-down control of colonization.

(c). Model extensions

Our model is one of the first applications of the metacommunity framework to food web issues. We have considered simple food chains only as a logical first step, but natural food webs are typically more complex [7,16]. More realistic food web topologies could readily be included in our modelling framework, at the expense of tractability [25,26]. This would allow consideration of other sources of variation in food chain length in food webs, e.g. if omnivores can persist locally even without their preferred prey and thus have different trophic positions in different patches [28]. The latter effect would reduce the control of predator occupancy by prey, allowing predators to colonize more patches and to persist despite extinction of the preferred prey. It would alleviate the two constraints of food chain length that we have identified, while decreasing average colonization/increasing average extinction rates (under the reasonable assumption that omnivores endure some cost when feeding on non-preferred prey; [26]). Which effect would prevail is not clear.

Other factors that could alleviate the regional constraint on food chain length include a systematic decrease of extinction rates, or increase in colonization rates, with trophic level. The first possibility is at odds with the general pattern of top predators having lower population size (and thus higher extinction risk), as echoed by their greater susceptibility to habitat fragmentation [37], a situation that would instead strengthen the snowball effect. Furthermore, as extinction rates cannot be negative, the experienced extinction rate can at best stay constant with trophic level, and the perturbation-only scenario we have considered applies. Increased colonization rates may appear more realistic. It should be noted that predator habitat selection effectively generates an accelerating increase in the effective colonization rates with trophic position. It is thus unlikely that any reasonable trend of increasing intrinsic colonization rate would cause stronger deviations than perfect habitat selection (φ = 1). Of course, it could cumulate with the latter. Note that the trends on extinction and colonization that seem most plausible are both increasing, and thus would tend to cancel out. Perhaps, more importantly, we assumed that all trophic levels perceive spatial structure with the same grain. This seems appropriate when patch structure is environmentally enforced, e.g. for aquatic food webs in isolated ponds. In other cases, the definition of a patch may vary with trophic level [22].

(d). Link to empirical data

Our model can be readily parametrized for specific systems, such as experimental mesocosms with controlled patch structure. Fitting intrinsic rates for the focal species would allow strong inference, by isolating the effects of metacommunity dynamics from idiosyncratic differences among trophic levels, a pervasive confounding effect in this type of study [37]. General insights can also be gained from observational data. We found that the spatial distribution of chain length differs qualitatively between food chains limited primarily by perturbation or extinction. Metapopulation occupancies for a bark-fungus-moth-fly food chain are reported in the study of Komonen et al. [38], from which a convex decreasing distribution of p_i values can be reconstructed. This points to perturbation limitation with significant levels of habitat selection (figure 2a)—a probable scenario for this system. In an arctic archipelago (M. Zalewski, W. Ulrich & A. V. Uvarov 2010, unpublished data), average species occupancy decreases linearly with trophic level, suggesting perturbation limitation and no habitat selection (figure 2a). Appropriate datasets combining spatial occupancies and trophic relationships are unfortunately still scarce.