Unraveling networks of co-regulated genes on the sole basis of genome sequences

Abstract

With the growing number of available microbial genome sequences, regulatory signals can now be revealed as conserved motifs in promoters of orthologous genes (phylogenetic footprints). A next challenge is to unravel genome-scale regulatory networks. Using as sole input genome sequences, we predicted cis-regulatory elements for each gene of the yeast Saccharomyces cerevisiae by discovering over-represented motifs in the promoters of their orthologs in 19 Saccharomycetes species. We then linked all genes displaying similar motifs in their promoter regions and inferred a co-regulation network including 56 919 links between 3171 genes. Comparison with annotated regulons highlights the high predictive value of the method: a majority of the top-scoring predictions correspond to already known co-regulations. We also show that this inferred network is as accurate as a co-expression network built from hundreds of transcriptome microarray experiments. Furthermore, we experimentally validated 14 among 16 new functional links between orphan genes and known regulons. This approach can be readily applied to unravel gene regulatory networks from hundreds of microbial genomes for which no other information is available except the sequence. Long-term benefits can easily be perceived when considering the exponential increase of new genome sequences.

INTRODUCTION

The analysis of gene regulatory networks is a key to understand gene function and genome evolution. Bioinformatics methods have been developed to infer gene regulatory networks, on the basis of high-throughput data sets such as microarray expression profiles (1–4) or starting from some prior knowledge, e.g. a library of known transcription factor (TF) binding motifs (5). However, such approaches are restricted to organisms in which prior information about gene regulation is available. Given the ever-increasing pace of sequencing, a great challenge for modern biology will be to infer genetic networks on the sole basis of genome sequences, by using ab initio methods to discover cis-regulatory elements in the promoters of all genes.

Several motif discovery algorithms have been developed to detect over-represented motifs in promoters of co-regulated genes of a single organism (6–10) and have also been applied at a multi-genome level to detect phylogenetic footprints, i.e. motifs conserved across promoters of orthologous genes (11–20). The discovered motifs can then be clustered using specific algorithms (21,22), or be used to establish pairwise relationships between genes (23–25). Such regulon inference approaches have initially been tested with the very few genomes available at that time, and the results have been shown to match known regulons or functional classes (21,22). A systematic assessment of the predictive power of such network inference methods is however still missing. In addition, previous approaches were essentially producing groups of genes based on motif clustering, and thereby failed to capture the complexity of regulatory networks, where genes can be regulated by multiple factors. In addition, novel regulations predicted in those studies have not been submitted to experimental validation.

In this article, we propose a new method to directly infer co-regulation networks from genome sequences without any prior knowledge about regulation: we first apply a footprint discovery algorithm (20) to predict TF binding motifs for each gene of a genome, we then infer a co-regulation network by linking genes with similar footprints. We performed a systematic in silico evaluation of the results by comparing the co-regulations predicted in the genome of Saccharomyces cerevisiae to three reference data sets: annotated regulons (26,27), a co-expression network derived from microarray data (28) and physical associations between TF and their target promoters detected by ChIP-on-chip (29). We further proceed to the experimental validation of a selected set of predictions. The high predictive value of the method opens promising perspectives for the discovery of regulatory interactions in poorly characterized organisms.

METHODS

Genomes

Fungal genomes (Supplementary Table S1) were downloaded from National Center for Biotechnology Information (NCBI) (http://www.ncbi.nlm.nih.gov/), from the web site maintained by Jason Stajic (http://fungal.genome.duke.edu/) and from the BROAD institute web site (http://www.broad.mit.edu/). All genomes were made available on the Regulatory Sequence Analysis Tools (RSAT) web site (http://rsat.ulb.ac.be/rsat/) (30).

Ortholog detection

Pairwise similarities between gene products were detected by running BLAST with all the translated sequences of S. cerevisiae (‘query organism’) against those of each genome of the reference taxonomical group (Saccharomycetes, ‘reference taxon’). The bi-directional best hits (BBHs) are considered as putative orthologs with an E-value smaller than 10⁻⁵.

Phylogenetic footprint discovery

Starting from a set of input genes and their orthologous clusters, the upstream sequences were collected from the start codon up to the upstream neighbor gene, with a maximal length of 800 bp. These distances were chosen based on our previous analysis (9) of the distributions of annotated sites in the TRANSFAC database (26).

For each gene of S. cerevisiae, we collected the promoters of all orthologs in 19 species belonging to the class Saccharomycetes. Promoter sequences were purged to mask redundant fragments among the promoters of orthologs of a single gene. A fragment is defined as redundant if it matches a previous segment of the same promoter set over at least 40 bp, with at the most three substitutions. These purged sequences were used to detect over-represented motifs, using the pattern-discovery program dyad-analysis (10). The program counts the number of occurrences of each dyad, i.e. pair of trinucleotides separated by a spacing comprised between 0 and 20 bp. All occurrences of each dyad are counted, in order to account for the frequent existence of multiple TF binding sites in a same promoter. Since dyads with a spacing of 0 correspond to hexanucleotides, the method is also able to discover non-spaced motifs. The program dyad-analysis assesses the significance of each dyad by comparing the observed occurrences in the orthologs of a single gene with those expected by chance, according to a given background model. For this analysis, we used the ‘taxfreq’ background model (20), where the prior probability of each dyad is estimated by computing the frequency observed for this dyad in the promoters of all genes of all organisms of the reference taxon. For each dyad, the risk of false positive (nominal P-value) is computed using the binomial distribution.

A multi-testing correction is then applied by computing an E-value (Eval = Pval × D), where D is the number of distinct dyads analyzed in one set of orthologous promoters, and the E-value is converted to a significance score sig_B = −log₁₀(Eval). For each gene, we selected all the dyads with sig_B ≥ 0, which corresponds to an upper threshold of 1 on the E-value.

An organism-specific filtering was applied by considering only the dyads found in the promoter of S. cerevisiae. For each query gene, the analysis is thus restricted to a few tens or hundreds of dyads instead of the 43 680 possible dyads. This option has a double effect of lowering the rate of false positives (by filtering out dyads that are irrelevant for the promoter of the query organism) and increasing the sensitivity (by strongly lowering the correction term D in the computation of the E-value).

Alternative metrics for measuring the similarity between dyad significance profiles

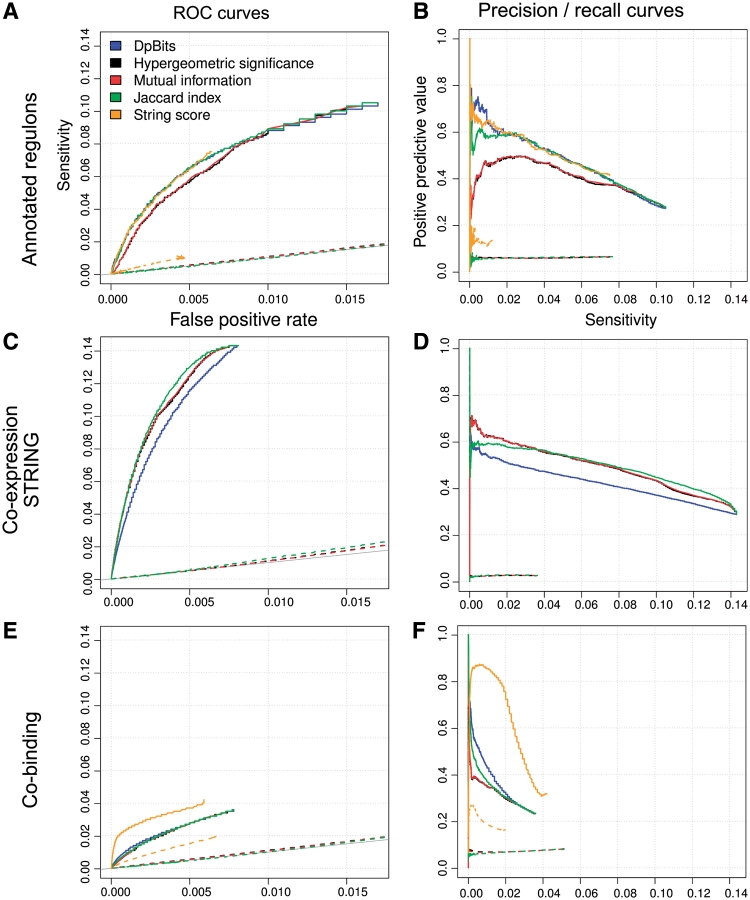
A motif involved in the binding of a given TF will also be occasionally discovered in promoters of other genes. We thus need to define a criterion to infer co-regulation between genes based on the similarities between dyad significance profiles, that emphasizes the most significant motifs (supposedly cis-regulatory signals), while minimizing spurious motifs (noise). Four alternative metrics were evaluated to score the similarity between dyad significance profiles: Jaccard similarity (JS), Hypergeometric significance (sig_H), mutual information (MI), and dot product bits (DPbits, Figure 1E). The comparison between the different metrics is presented in Supplementary Figures S2 and S3, showing an almost perfect correspondence between MI and sig_H, and strong differences between all the other pairs of metrics.

Figure 1.

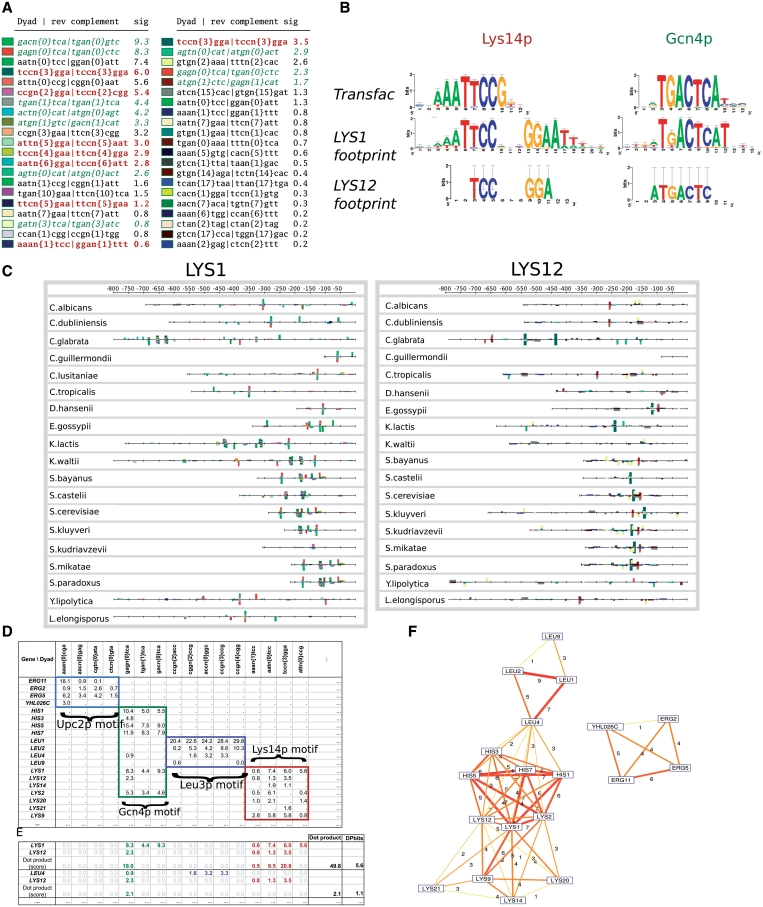
Description of the method to infer co-regulation networks by phylogenetic footprint discovery. (A) Over-represented dyads in promoters of LYS1 (left) and LYS12 (right) orthologs in Saccharomycetes. Sig: binomial significance. Bold brown and green italics characters highlight the dyads matching the motifs bound by Lys14p (WWWTCCRnYGGAWWW) and Gcn4 (TGAGTCA) (38). (B) Sequence logos built from the over-represented dyads matching the Gcn4p and the Lys14p motifs compared to the reference motif (TRANSFAC). (C) Feature maps showing the location of the over-represented dyads in the promoters of orthologs for LYS1 (left) and LYS12 (right). Each box indicates an exact match for a dyad, with a height proportional to the binomial significance. (D) Subset of the dyad significance matrix selected for illustrating the correspondences between dyads and genes. The full matrix comprises 3585 rows (genes) and 33 276 columns (dyads). Values indicate the binomial significance sig_gj of each dyad (j) in the phylogenetic footprints of each gene (g). Negative significance values are denoted by a dot, and are replaced by a zero value for further computation. Boxes highlight groups of dyads that match the motif annotated for a given regulator (Upc2p, Gcn4p, Leu3p and Lys14p). (E) Detail of computation of the DPbits score. (F) Co-regulation network built by tracing an edge between each pair of genes having a strictly positive DPbits score. Edge thickness and color gradient (yellow–red) are proportional to the DPbits.

Notation: Let a and b be two genes. We denote hereafter A and B as the sets of significant dyads [i.e. dyads with a positive binomial significance (sig_B)] in their respective profiles, with N_a = |A| and N_B = |B| the number of significant dyads. Let C be the intersection between the sets A and B, with N_c = |C| be the number of common dyads between profiles of genes a and b. We further define N_D as the total number of dyads in the significance profiles of all the genes (N_D = 22 565 for the yeast data set).

Jaccard similarity

The Jaccard similarity (JS) is a classical metric for comparing the two sets A and B. It is computed as the ratio between the intersection and the union of the two sets.

Hypergeometric significance

The hypergeometric P-value (Pval_H) indicates the probability to observe at least N_C dyads in common between two random selections of sizes N_A and N_B, respectively.

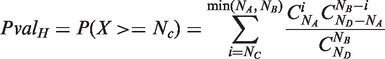where X is a random variable representing the number of common dyads between two profiles, and N_c is the actual value observed in a given comparison. Pval_H can be interpreted as the risk of false positive for one given pair of genes, i.e. the risk to erroneously consider as significant the intersection between the sets (A and B) of dyads selected in their respective phylogenetic footprints. Since the same significance test is performed successively for each pair of genes, we perform a multi-testing correction by multiplying this nominal P-value by the number of tests.

where T is the number of pairwise comparison between gene profiles [T = N_G(N_G−1)/2 = 15 593 320], N_G = 5585 being the number of genes in the dyad profiles matrix.

Mutual information

The mutual information (MI) is computed from the binary profiles indicating whether a given dyad is significant in the promoters of orthologs for a given gene. The mutual information MI = I(A, B) is defined according to Shannon’s information theory.

In this formula, H(A) and H(B) are the entropies of gene profiles A and B, respectively.

whereas H(A, B) is the joint entropy of A and B.

The probability P(A) of profile A is computed as the fraction of significant dyads in this profile [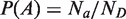]. The other probabilities are estimated in a similar way.

DPbits score

The dot product bits (DPbits) score is the only metric that takes into account the actual values of sig_B (all the other considered metrics rely on binary profiles). The dyad significance matrix (Figure 1D) was built by collecting the significant dyads (columns) detected in promoters of orthologs for each yeast gene (rows).

where x_gj indicates the sig_B of the dyad j for the gene g. Negative significance values were replaced by 0 to avoid masking the few significant dyads of each gene by the negative contribution of the vast majority of non-significant dyads. Taking into account the actual values of the sig_B returned by the dyad-analysis, we computed the dot product between each pair of significance profiles.

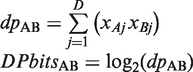A dyad j will contribute to the dot product only if it is significant in both genes A (x_Aj > 0) and B (x_Bj > 0). The DPbits score requires not only for two genes to have the same selection of dyads, but also to have a coincidence between their highest-scoring sig_B values.

Inference of a co-regulation network

In a co-regulation network, each node represents a gene, and an edge is added between genes sharing similar motifs. To detect which gene pairs present similar motifs, we used the program compare-classes (31) to compute the DPbits score, as well as three various similarity metrics (see above). The possible number of edges of this network increases quadratically with the number of genes (N), with a maximum of E_max = N(N − 1)/2 edges. Since the yeast genome contains N_G = 5876 protein-coding genes, the network can contain up to T = 17 260 750 edges. A co-regulation network was built by linking any pair of genes having at least one significant (sig_B ≥ 0) dyad in common. This network was used to evaluate the impact of parameters on the sensitivity and false positive rate (FPR) (see below).

After having evaluated the four alternative metrics, we decided to use the DPbits score for further investigation. The inferred co-regulation network was then generated by linking pairs of genes having at least two dyads in common and whose DPbits score is at least 1. The condition of having at least two dyads in common reduces the sensitivity, but reduces the rate of false positives due to spurious matches of a single dyad. This condition still permits to detect pairs of genes having a single motif in common, since the motifs returned by dyad-analysis are generally composed of several mutually overlapping dyads (10).

Reference networks

To assess the relevance of the inferred co-regulation network, we performed network comparisons with three reference networks, respectively. (i) The annotated co-regulation network was built by linking pairs of genes belonging to the same annotated regulon. These regulons were collected from the TRANSFAC database (26) complemented by Simonis et al. (27). For this collection, factor–gene interactions were taken into consideration only if they had been proven by individual experiments (in silico inferences and high-throughput experiments were thus discarded). (ii) The co-expression reference network was obtained from the STRING database (http://string.embl.de) (32). (iii) The co-binding reference network was derived from a genome-wide location analysis characterized with the ChIP-on-chip method (29), where we selected the gene/TF associations with P < 0.001. This network was built by linking any pair of genes whose promoters’ is bound by the same TF.

Co-regulation network assessment

The program compare-graphs (31) was used to calculate the intersection (in terms of edges) between two graphs (e.g. inferred co-regulation versus annotated regulons). The sizes of these networks and the results of their comparison are summarized in Table 1. Performance statistics (Sn, PPV) were computed with the program roc-stats, which takes as input a set of scored elements, each one annotated as true positive (TP, i.e. elements present in both predictions and reference), false positive (FP, i.e. predicted while absent from the reference) or false negative (FN, i.e. present in the reference but missing in the predictions). After having sorted the predictions by score, the rates of FP, TP and FN are computed for each possible score value, and the program computes the derived validation statistics. The Sensitivity is the proportion of the reference set covered by the predictions (above a given score threshold): Sn = TP/(TP + FN). The positive predictive value (PPV) is the fraction of predicted elements supported by the reference set: PPV = TP/(TP + FP). The FPR is the fraction of non-reference elements erroneously predicted as positive: FPR = FP/(FP + TN). For example, when the inferred co-regulation network (predictions) is compared to the annotated regulons (reference network), TP is the number of predicted co-regulations whose genes belong to a same regulon, FP is the number of predicted co-regulations that are not found in a same annotated regulon, FN is the number of annotated gene pairs missed by the predictions and TN is the number of gene pairs that are neither annotated nor predicted as co-regulated. Performance curves (Sn/PPV, precision/recall, receiver operating characteristic (ROC)) were drawn with the statistical package R (http://www.r-project.org/).

Table 1.

Size of the inferred and annotated data sets

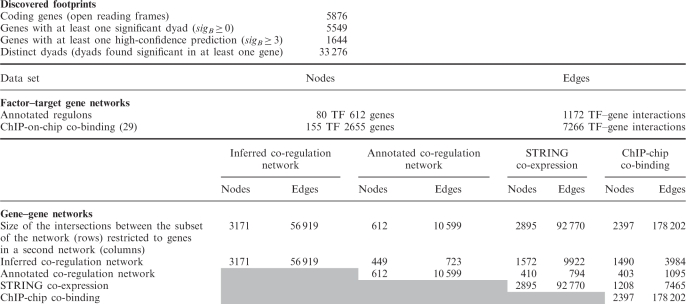Discovered footprints (top), i.e. motifs over-represented in the promoters of orthologous genes. Reference data sets indicating interactions between TFs and their target genes (middle). Annotated regulons were used to build the co-regulation network, whereas the ChIP-on-chip results were used to build the co-binding network. Comparison between inferred and reference networks (bottom). The diagonal indicates the size (nodes and edges) of each network; the other cells indicate the size of the pairwise intersections between networks.

The area under the curve (AUC) was computed for each ROC curve using the trapezoidal approximation. As is frequently the case with bioinformatics data, computing an AUC of the full range of an ROC curve (FPR from 0 to 1) is misleading, because the majority of this range is irrelevant for prediction purposes (33). We thus restricted the computation of the AUC to informative values of FPR (Table 2). The area under the ROC curve was computed for FPR ranging from 0 to a given threshold (5 × 10⁻⁴, 5 × 10⁻³, 1 × 10⁻² or 1.5 × 10⁻²), and divided by the maximal area in the same range (the area that would be obtained with a 100% sensitivity). Note that the AUC values are very small by construction, since the computation is restricted to the left-bottom corner of the ROC curve. The numbers should thus be interpreted as relative values for comparing two metrics rather than as absolute measures of the performances.

Table 2.

Areas under the ROC curves of Figure 2 (A, C and E) at different FPR threshold values

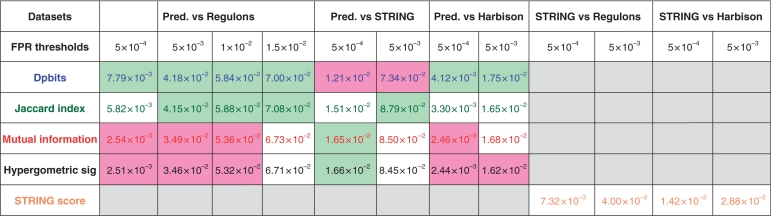Text colors correspond to the curves in Figure 2. Background colors highlight the maximal (green) and minimal (pink) values for each column (differences <2% of the max AUC are ignored). Cells for which the AUC calculation is not pertinent are left empty (gray).

Random controls

Two types of negative controls were performed: (i) motif permutations, by shuffling the rows and columns of the dyad significance matrix; and (ii) network permutation, by shuffling the edges of inferred or reference networks. For the performance curves, random expectation values were estimated by computing networks from the permuted dyad significance matrix. Network permutation was used when no matrix was available (e.g. for comparing STRING co-expression to co-binding network).

Functional enrichment

The program compare-classes was used to compare the clusters of direct neighbors of unknown genes to Gene Ontology (GO) functional classes.

RNA preparation and quantitative reverse transcription–PCR

The yeast strains and oligonucleotide primers used in this study are provided in Supplementary Table SIII. Total RNA was purified as previously described (34). Quantitative reverse transcription–PCR (qRT–PCR) experiments were carried out using the RT-RTCK05 and RT-SN10-05 kits (Eurogentec, Belgium). We performed three independent experiments and computed the mean and standard error for each triplicate. Mean comparisons between treated/mutant versus untreated/wild-type were performed with the Student’s t-test (Prism 5.0 statistical software; Graphpad, San Diego, CA, USA). Differences were considered as significant when P < 0.05 (*) or P < 0.01 (**).

Chromatin immuno-precipitation

Chromatin immuno-precipitation (ChIP) was performed as previously described (35). Mbp1-HA protein was immunoprecipitated with 12CA5 antibody bound to IgG magnetic beads (Dynabead; Dynal Biotech ASA, Oslo, Norway). Immunoprecipitated DNA was analyzed by quantitative real-time PCR on an ABI Prism 7000 machine (Applied Biosystems, Foster City, CA, USA). Relative quantification using a standard curve method was performed and the occupancy level for a specific fragment was defined as the ratio of immunoprecipitated over total DNA. For this we used the Platinum SYBR Green PCR Super Mix-UDG with ROX (Invitrogen). The value 1.0 was arbitrarily given to the reference signal provided by amplifying the GAL1 gene used as negative control.

Availability

Bioinformatics analysis was performed by combining the RSAT (30) and the Network Analysis Tools (NeAT) (31). Supplementary methods, scripts and results are available on the RSAT web server (http://rsat.ulb.ac.be/rsat/data/published_data/coregulation_networks/).

RESULTS

Gene-wise discovery of phylogenetic footprints

A crucial parameter for footprint discovery is the choice of the appropriate taxonomical level. As previously observed for bacteria (20), taxonomical levels that are too narrow return a poor sensitivity. Whereas, taxonomical levels that are too wide reduce the signal-to-noise ratio, and may increase the rate of false positives due to the heterogeneity of the background sequences. We applied footprint discovery at various taxonomical levels: Fungi, Saccharomycetes, Saccharomycetales, Saccharomycetaceae, Saccharomyces. For each gene of S. cerevisiae, we identified putative orthologs in the considered taxon (Supplementary Table SI), collected their upstream non-coding sequences and discovered phylogenetic footprints by detecting over-represented spaced motifs (dyads) (20) with all possible spacing values from 0 to 20. Spaced motifs are of particular importance for microbial regulation, since they are characteristic of several classes of TFs, such as the fungal Zn(2)–Cys(6) binuclear cluster, covering 56 TFs in S. cerevisiae (36) or the bacterial Helix-Turn-Helix, found in more than 150 TF in Escherichia coli (37). The footprint discovery method based on dyad detection was validated in a previous study (20), where we predicted cis-regulatory motifs for each gene of E. coli by detecting footprints at all taxonomical levels, and identified the optimal parameters for detecting relevant motifs. An important strength of the approach is that the sig_B returned by the footprint discovery algorithm provides a reliable estimate of the risks of false positive, thereby enabling application of stringent criteria to select the most reliable motifs. The most significant footprints were found at the level of Saccharomycetes, and we retained this taxon for further analysis.

To illustrate the method, Figure 1A–C shows the significant dyads found in the promoters of orthologs for the genes LYS1 and LYS12. Both genes are involved in lysine biosynthesis. Dyads are grouped by pairs of reverse complements, because yeast cis-regulatory elements are generally strand-insensitive. Among the 43 680 possible dyads, only 30 reach a positive sig_B score (sig_B ≥ 0) for LYS1, and 24 for LYS12. For LYS1, the most significantly over-represented dyad (GACTCA | TGAGTC) reaches a significance of 9.3, corresponding to an E-value of 10^−9.3= 5.01 × 10⁻¹⁰. At this level of significance, the random expectation is of one false positive every 5.01 × 10⁻¹⁰ trials. The dyads detected in the LYS12 footprints are less significant, but still very unlikely to result from chance (sig_B = 3.5, corresponding to an E–value of 3.16 × 10⁻⁴). For both genes, the top-scoring dyads match either the canonical Lys14p binding motif WWWTCCRnYGGAWWW (38) (third dyad for LYS1 and first for LYS12) or the motif bound by Gcn4p (TGAGTCA), the general amino acid controlling factor (the two top-scoring dyads for LYS1; the third dyad for LYS12). As already shown in our previous publications, the dyad-analysis program generally returns groups of mutually overlapping dyads that can be assembled to form a larger motif (10). Figure 1B shows the sequence logos of the position-specific scoring matrix obtained by assembling the dyads detected in the promoters of the LYS1 and LYS12 orthologs. The multi-genome feature maps (Figure 1C) show that the significant dyads are generally found in clusters of mutually overlapping instances, indicating that the individual dyads reveal complementary fragments of a same motif.

In summary, the most significant dyads discovered in these two LYS genes correspond to sub-sequences of the motifs bound by the TFs lysine regulator (Lys14p) and the general control of amino acid metabolism (Gcn4p). However, the footprints of those two genes show some differences in the precise composition and significance of the individual dyads. In the next section, we introduce a new method for detecting similarities between phylogenetic footprints defined as partly overlapping sets of score-associated dyads such as those shown in Figure 1A.

Unraveling the co-regulation network by linking genes with similar footprints

Gene-wise discovered footprints can be summarized in a matrix of dyad significance profiles, where each cell gives the binomial significance (sig_ij) of a given dyad (column j) for a given gene (row i). The values are left blank for dyads falling below the significance threshold (sig_B ≤ 0) for a given gene. The fragment of this gene/dyad matrix, shown in Figure 1D, illustrates that genes involved in a similar function (e.g. ergosterol, lysine or histidine biosynthesis) are generally characterized by similar dyads, albeit with different significance values. We tested four alternative metrics to measure the similarity between the phylogenetic footprints of two genes, in terms of dyad composition (Jaccard similarity, mutual information, hypergeometric significance) or dyad significance (DPbits) and evaluated the respective performances of those metrics (Figure 2). When the inferred network is compared to either the annotated regulons (Figure 2A and B) or the ChIP-on-chip data (Figure 2E and F), the DPbits and Jaccard index outperform the hypergeometric P-value and the Mutual Information (see Table 2 for quantitative comparisons). In contrast, when the inferred co-regulation network is compared to the STRING co-expression network (Figure 2C and D), the DPbits score has a lower sensitivity than the other metrics. We performed a negative control by measuring the same metrics in randomized dyad significance matrices (50 permutations per control, dotted curves in Figure 2). As expected, the negative controls are aligned along the diagonal of the ROC curves (grey lines). The choice among those metrics is not trivial, since their respective performances vary depending on the reference set. However, since our goal is to predict co-regulation (i.e. the fact that two genes are recognized and regulated by the same TFs), we tend to consider the annotated regulons and co-binding networks as more directly related to the question. Thus, we finally retained the DPbits score. A reason for the relatively good performances of the DPbits score may be that it takes into account the sig_B score of the dyads, whereas the three other metrics only consider the presence or absence of a dyad in the footprints of a given gene.

Figure 2.

Comparison between scoring metrics. The ability of different scoring metrics to predict co-regulation is evaluated by comparing their performances on receiver operating characteristic (ROC) curves (A, C, E) and precision-recall curves (B, D, F), using the different reference networks: annotated regulons (A, B), STRING co-expression (C, D) or ChIP-on-chip co-binding (E, F), respectively. Each curve represents one of the metrics used for comparing dyad profiles. Dotted lines: negative controls performed by permuting the cells of the dyad significance matrix (50 permutations per curve). Orange curves indicate the correspondences between the STRING co-expression network and the annotated regulons (A, B) or ChIP-on-chip co-binding network (D, E), respectively. The STRING network interactions are weighted according to their co-expression score derived from Pearson's correlation coefficient (L. J. Jensen, personal communication). For the STRING co-expression network, the negative control was performed by permuting the edges of the original network (50 repetitions).

Figure 1E shows how the DPbits score is computed between a pair of rows (genes) of the significance matrix. The DPbits score is computed in the same way for each pair of genes. In the sub-network linking, the subset of genes of Figure 1, groups of functionally related genes are densely interconnected by highly weighted edges (Figure 1F). Interestingly, the inferred network also contains inter-module connections revealing the general control of three amino acid pathways (leucine, histidine and lysine) by the TF Gcn4p. This small sample network, thus, reflects the capability of our approach to detect relationships between genes regulated by multiple TFs. We also notice a separate module regrouping three ERG genes with the orphan gene YHL026C indicating that these genes may be regulated by the same factor. The latter gene is annotated in SGD as ‘Putative protein of unknown function’. The similarity between its phylogenetic footprints and those of three ERG genes suggest that YHL026C may be transcriptionally controlled by sterols, a hypothesis that has been tested experimentally (see below).

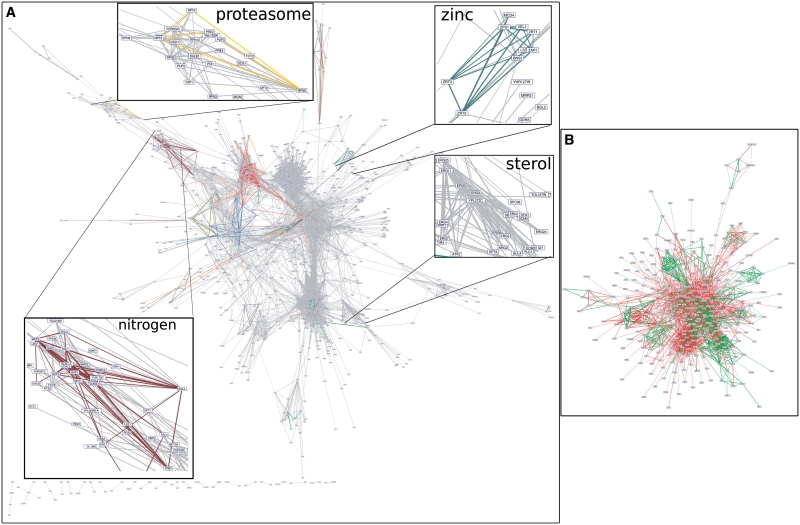
When the same procedure is applied to each of the 5876 protein-coding genes of S. cerevisiae, the footprint discovery algorithm returns at least one significant dyad (sig_B ≥ 0) for 5585 genes (95%), among which 1638 (27.8%) have a high-confidence prediction (sig_B ≥ 3). The complete co-regulation network derived from this significance matrix (5585 genes × 33 276 dyads) links 3171 genes by 56 919 predicted co-regulations (Figure 3).

Figure 3.

Co-regulation network inferred by phylogenetic footprint discovery. (A) High-scoring layer (DPbits ≥ 5) of the co-regulation network inferred between all yeast genes. Edge thickness reflects the prediction score. Insets highlight areas of the network corresponding to groups of functionally related genes. Each color corresponds to one annotated regulon. (B) Subset of the inferred network restricted to the 612 genes of the reference data set (80 regulons, DPbits ≥ 1). Green edges: co-regulations already supported by annotations; non-supported predictions, combining novel predictions and false positives.

Reference networks: co-regulation (regulons), co-expression (microarrays) and co-binding (ChIP-on-chip)

To evaluate the reliability of the predicted network, we compared it to three reference networks (Table 1) obtained from complementary types of information. The first reference network was built from a collection of annotated regulons (i.e. lists of target genes regulated by each TF). Annotated regulons were collected from the TRANSFAC database (26) and complemented by literature searches as described in a previous work (27). For the sake of comparison with the inferred (gene–gene) co-regulation network, the factor–gene interaction network (list of regulons) was converted into a gene–gene interaction network (hereafter called annotated co-regulation network) by linking any pair of genes regulated by the same TF.

The second reference network, called the co-binding network, was derived from a genome-wide detection of binding sites for 155 TFs, performed with the ChIP-on-chip technology (29), by linking pairs of genes whose promoters are bound by common TFs. This network is in principle more comprehensive than the annotated co-regulation network, but it is also more likely to contain false positive relationships, since it results from a systematic application of a high-throughput technology. Furthermore, the binding of a TF in the upstream region of a gene does not always correspond to a bona fide regulatory effect (e.g. the factor may bind in the intergenic region of two divergently transcribed genes, but regulate only one of them).

A third reference network has been extracted from the STRING database (28). This network was built by linking genes having similar expression profiles in a compendium of microarray experiments.

It should be noted that the three reference networks represent different types of information (protein–DNA binding or expression) and have different levels of reliability. The annotated regulons cover a subset of the known regulations found in the literature, which themselves represent a subset of the existing interactions. In addition, we only retained the annotations reporting individual experiments, and discarded in silico predictions and high-throughput experiments. This data set thus represents a ‘high-confidence’ subset of the existing regulatory interactions, and we should expect that predictive methods would reveal true interactions that are missing in this reference collection (and thus improperly considered as ‘false positives’). In contrast, the co-binding network relies on high-throughput detection of TF binding regions, which is known to return a non-negligible rate of false positives. Using this data set as the golden standard will thus lead to an over-estimation of the rate of false negative (interactions present in the annotations, but not predicted). This remark holds true for the co-expression network, which was built from gene expression data.

For the first two reference networks, it is of note (29) that the conversion from a set of factor–gene interactions (regulons or binding targets) to a gene–gene network has an important effect (Supplementary Figure S1): as the number of edges per regulon increases in a quadratic way with the number of regulated genes, highly connected TFs (global TFs) generate very large cliques. For example, the 54 targets of Zap1p are linked by (54 × 53)/2 = 1431 edges. In total, the three most pleiotropic TFs (Msn2p, Msn4p and Zap1p) cover 14% of the nodes (genes) and 34% of the edges (co-regulations) in the annotated co-regulation network.

Top-scoring predictions correspond to annotated regulons

For the sake of comparison with the annotated network, we selected all co-regulations predicted between the 612 genes found in at least one annotated regulon (for non-annotated gene, it is not possible to estimate whether predictions are correct or not). Among those, three-quarters of the 60 most significant gene pairs (44/60 = 73%) are already annotated as members of the same regulon. As a negative control, we performed 50 random permutation tests of the dyad significance matrix, derived a co-regulation network from each permuted matrix and compared the 60 top-scoring gene pairs of with the annotated regulons. Only 8 out of those 50 control networks contained one annotated pair of co-regulated genes, and none contained more than one.

In addition, 13 other gene pairs (22%) are involved in some common function, suggesting they may correspond to actual co-regulations, despite not being annotated in the regulon data set (Table 3). Only 3 (5%) of the 60 top-scoring predictions have no prior evidence of co-regulation. These may either correspond to false predictions, or to actual regulations not yet documented. Noticeably, two out of these three gene pairs (LEU1-TPO1 and LEU1-ACO1) include LEU1, a target gene of the Leu3p TF, and the high significance score of the Leu3p binding motif in the footprints of two other genes make them potential new targets of leucine regulation. In summary, almost all of the 60 top-scoring predictions correspond to valid pairs of co-regulated genes.

Table 3.

Top-ranking predicted co-regulations

Gene 1	Gene 2	DPbits	Jaccard, %	Hypersig	Mutual info	Annotated regulon	Co-expression	Similar function
LEU2	LEU1	10.2	16.2	22.7	0.00203	LEU3
RNR1	RAD27	10.0	12.2	12.3	0.00129			DNA replication and repair
RNR1	CDC21	9.9	9.8	4.6	0.00077	MBP1
SWI4	RNR1	9.6	4.9	1.5	0.00035	SWI6
RNR1	CDC6	9.3	3.9	2.3	0.00029	MBP1
LEU1	BAT1	9.3	11.5	13.1	0.00135		1	Branched amino acid metabolism
RNR1	RAD53	9.2	13.7	9.9	0.00114	SWI6
YKR075C	HXT3	9.2	4.9	6.0	0.00085			Regulated by glucose
ZRT2	ZPS1	9.2	27.1	25.5	0.00221	ZAP1
YKR075C	HXT2	9.2	11.0	29.4	0.00246	MIG1
GAL10	GAL1	9.1	39.7	53.2	0.00413	GAL4	1
SST2	FUS1	9.0	14.7	5.7	0.00085	MOT3	1
RNR1	CLB5	8.9	1.7	4.0	0.00017	SWI6
PCK1	FBP1	8.8	5.8	8.2	0.00100	CAT8	1
RAD27	CDC21	8.7	7.4	1.8	0.00058		1	DNA replication and repair
SWI4	RAD27	8.7	4.8	1.6	0.00035			DNA replication and cell cycle regulation
FTR1	FIT2	8.7	4.2	2.8	0.00063			Iron transport and homeostasis
HIS7	ARG3	8.6	5.9	0.3	0.00047	GNC4
RNR1	ABF1	8.6	6.4	2.8	0.00064			DNA replication and repair
TPO1	LEU1	8.6	3.2	1.4	0.00035
LEU1	ILV5	8.6	5.7	3.2	0.00066	LEU3
MEP2	DUR1,2	8.6	23.8	7.2	0.00095	GLN3
ZRT3	ZRT2	8.6	10.9	5.5	0.00083	ZAP1
MEP2	DAL1	8.6	4.5	1.3	0.00037	GLN3
DAL4	DAL1	8.5	23.6	38.3	0.00309	GLN3
GAL2	GAL1	8.5	4.1	1.2	0.00036	GAL4
SWI4	CDC21	8.5	25.0	10.0	0.00115	SWI6
RAD27	CDC6	8.5	6.5	1.7	0.00056			DNA replication and repair
LEU1	GDH1	8.4	6.2	9.8	0.00111	LEU3	1
DUR1,2	DAL1	8.4	9.4	6.3	0.00089	GLN3
LEU1	ILV3	8.4	7.6	5.6	0.00083	LEU3	1
MEP2	DAL4	8.3	4.8	1.2	0.00037	GLN3
SWI4	CDC6	8.3	8.0	1.3	0.00054	SWI6
RNR1	CLB6	8.3	6.3	1.5	0.00055			DNA replication and repair
HXT3	HXT2	8.3	5.8	5.2	0.00080	CYC8
PCK1	ICL1	8.2	6.7	9.2	0.00107	CAT8
RAD53	RAD27	8.2	9.1	4.1	0.00073			DNA repair
CDC6	CDC21	8.2	7.0	0.4	0.00043	SWI6
HIS1	ARG3	8.2	7.0	1.5	0.00056			Amino acid metabolism
PCK1	MDH2	8.2	6.7	10.0	0.00113	CAT8
RNR3	RNR1	8.2	6.2	10.4	0.00116	TUP1
LEU1	ILV2	8.2	6.1	2.9	0.00064	LEU3	1
RAD27	ABF1	8.2	37.8	61.5	0.00470			DNA replication and repair
GAL2	GAL10	8.1	4.9	0.5	0.00042	GAL4
HXT4	HXT2	8.1	6.9	10.2	0.00114	MIG1
ZRT2	ZRT1	8.1	12.2	6.1	0.00087	ZAP1
DUR1,2	DAL4	8.1	10.0	6.5	0.00090	GLN3
RAD53	CDC21	8.1	26.3	7.6	0.00099	MBP1
ZRT2	VEL1	8.0	9.1	3.1	0.00066	ZAP1
HXT6	HXT2	8.0	6.7	6.5	0.00089			Hexose transporters
SWI4	RAD53	8.0	10.3	0.2	0.00047	SWI6
LEU1	ACO1	8.0	1.8	4.7	0.00013
LEU4	LEU1	8.0	5.1	2.5	0.00061	LEU3	1
LEU1	BAP2	8.0	2.4	2.9	0.00025	LEU3	1
PRB1	MEP2	7.9	0.9	4.7	0.00014	GLN3
YKR075C	HXT4	7.9	3.8	2.6	0.00061	MIG1
CLB5	CDC6	7.9	2.5	2.2	0.00030	SWI6
PDE2	DED1	7.9	21.4	41.3	0.00330
TRP3	ARG3	7.9	6.9	1.4	0.00055	GCN4
CLB5	CDC21	7.9	2.2	2.1	0.00031	SWI6

Top-ranking predictions of co-regulation in Saccharomyces cerevisiae, ordered by DPbits score, completed with the alternative scores (Jaccard, hypergeometric significance and mutual information). Gene pairs regulated by a same TF (annotated regulons) are highlighted in bold. Italics indicate gene pairs that are not annotated as regulated by a common TF, but which are involved in similar functions. Note that in our quantitative evaluation, these pairs are labeled as ‘false positive’ (FP), despite their very likelihood to be co-regulated. White background corresponds to gene pairs with no evidence of co-regulation or functional relationship.

Inferred co-regulations have a good PPV

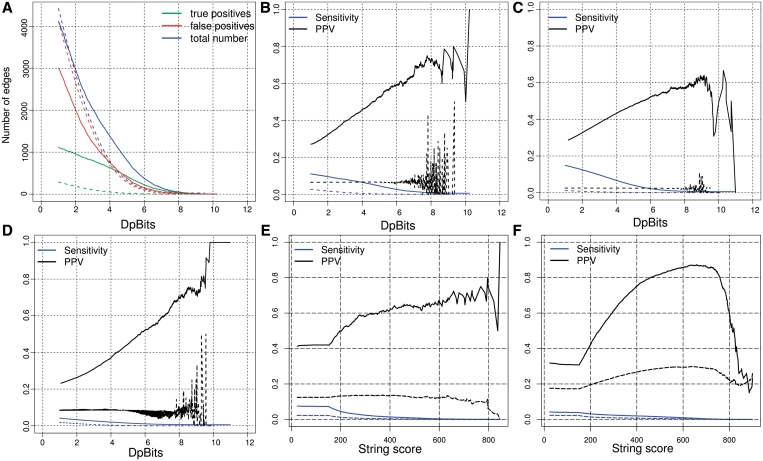
We applied a systematic evaluation of the predicted co-regulations by estimating the sensitivity (Sn, i.e. the fraction of known co-regulations covered by the predictions) and the PPV (i.e. the fraction of predictions corresponding to actual co-regulations). For this evaluation, we selected the 4121 links having a DPbits score of at least 1 between the 612 genes of the annotated regulons, and compared this network to the three reference networks. It should be noted that TF databases only cover a subset of the published literature, which itself reflects a part of existing regulations. Thus, it is likely that a fraction of our predictions are unduly counted as false positives in our evaluation. The PPV curves should be considered as lower bounds for the actual PPV. The number of predicted co-regulations decreases rapidly when the threshold on DPbits increases (Figure 4A). Interestingly, the number of true predictions decreases slower than the false predictions. The reliability (PPV) of predicted co-regulations increases with the DPbits score, at the cost of sensitivity (Sn): when the threshold on DPbits increases from 1 to 5, the number of predicted co-regulations drops from 4121 to 798, but the PPV rises from 27% to 53% (Figure 4B). Altogether, the evaluation shows that the DPbits score is positively correlated with PPV and thus provides a good estimation of the reliability of predicted co-regulations. Since the PPV reaches 50% for the high-scoring predictions (DPbits ≥ 5) of the evaluation set (annotated regulon), we are highly confident that a substantial fraction of the 13 060 high-scoring predictions inferred in the whole genome correspond to actual co-regulations.

Figure 4.

Correspondences between inferred co-regulation network and three ‘reference’ networks: annotated regulons, microarray co-expression (STRING) and co-binding (ChIP-on-chip), respectively. (A) Impact of the score threshold on the size of the co-regulation network (restricted to the subset of interactions between genes found in at least one annotated regulon) and on its correspondence with annotated regulons. Note that some of the ‘false positives’ may correspond to actual co-regulations not yet documented in the database. (B) Sn and PPV curves as a function of the DPbits score of the predicted interactions. Inferred co-regulation versus annotated regulons. (C) Inferred co-regulation versus STRING co-expression. (D) Inferred co-regulation versus ChIP-on-chip. (E) STRING co-expression versus annotated regulons. (F) STRING co-expression versus ChIP-on-chip. Dotted lines: negative controls performed by permuting the cells of the dyad significance matrix (50 permutations per curve) (A–D) or by permuting the edges of the original network (50 repetitions) (E–F).

The sensitivity of the predictions strongly depends on regulon size

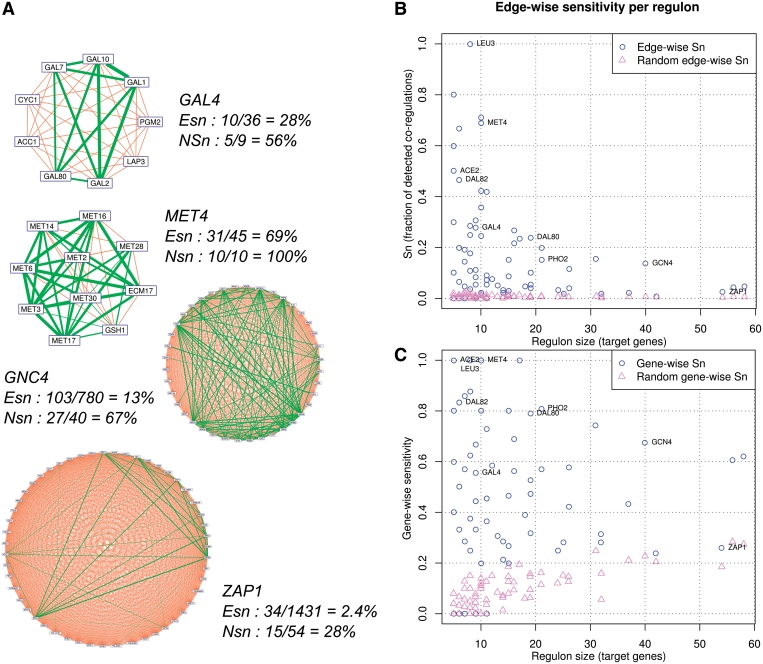
At first sight, the sensitivity seems rather weak (Figure 4B): even with the lowest score threshold (DPbits ≥ 0), the inferred network covers no more than 10.5% of the edges derived from annotated regulons (1117 in 10 599). This apparent lack of sensitivity is largely due to a few highly connected TF, which generate large cliques in the reference network (e.g. Zap1p, Gcn4p in Figure 5A; Table 4). However, regulon inference does not require a full coverage of all the edges between genes regulated by a same TF: a partial coverage of the intra-regulon edges may already provide sufficient information to collect a good fraction or even all of its nodes. For example, the Met4p regulon encompasses 10 genes, which can be linked by a maximum of 45 co-regulation edges (Figure 5A). Footprint detection only covers 31 (69%) of those edges, but these are sufficient to establish a dense network linking the 10 target genes of Met4p. Similarly, the Gcn4p regulon includes 40 genes that can be linked by 780 edges. Even though no more than 103 (13%) of those edges are detected by footprint detection, these edges link 27 of the 40 target genes (67%). In complement to the edge-wise sensitivity (Figure 5B), we define a node-wise sensitivity (Figure 5C) indicating, for each TF, the fraction of its target genes linked to another of its target genes by at least one edge. Both edge-wise and node-wise estimations plots show that the sensitivity strongly decreases when regulon size increases. Not surprisingly, node-wise sensitivity gives much higher estimates than edge-wise sensitivity (Table 4). Of course, the random expectation is also higher for node-wise than for edge-wise sensitivity, as confirmed by our negative controls (triangles in Figure 5C). However, since the primary goal of the method is to predict regulons, the node-wise sensitivity can be considered as a more direct estimate of the performances than edge-wise sensitivity.

Figure 5.

Impact of regulon size on sensitivity. (A) Gene–gene cliques generated by specific (GAL4, MET4) and global (GCN4, ZAP1) TFs. Correctly predicted co-regulations (true positives) are highlighted in green, with edge thickness proportional to the DPbits score. Orange edges indicate false negatives (FN), i.e. existing co-regulations missing from the predicted co-regulation network. Edge-wise sensitivity (E_sn) is the fraction of correctly predicted edges. Node-wise sensitivity (N_sn) is the fraction of target genes linked by at least one prediction. (B, C) Impact of regulon size (abscissa) on edge-wise (b) and gene-wise (c) sensitivity, respectively. All numerical values are provided in Table 4.

Table 4.

Coverage of co-regulation interactions per annotated regulon

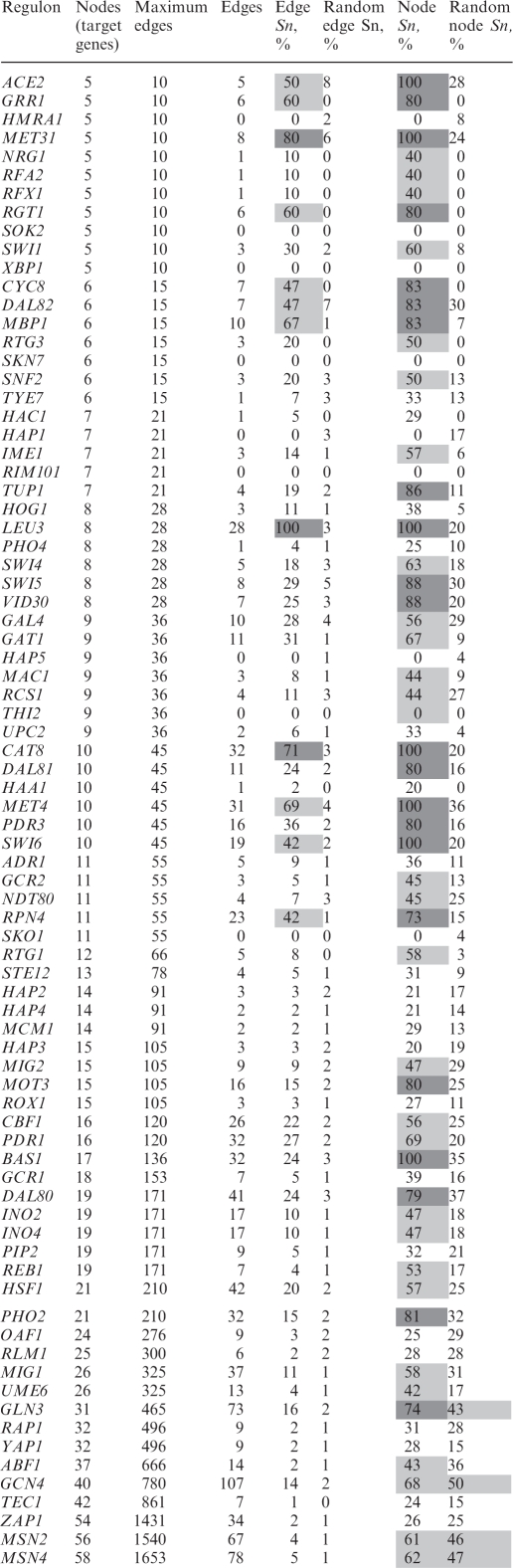For each annotated regulon, the maximal number of intra-regulon edges (M) is computed as M = n × (n1)/2, where n is the number of genes (nodes) in the regulon. ‘Edge sensitivity’ indicates the fraction of intra-regulon edges covered by the predictions. ‘Node sensitivity’ is the fraction of nodes linked to at least one other gene of the regulon. The random expectations were estimates by computing edge and node sensitivity in a network randomized by shuffling edges between nodes (five permutations). Color code for the background. Dark grey: >70%; light grey: >40%.

All these observations confirm that our method better predicts the cis-regulatory elements bound by specific than by global TFs.

The inferred co-regulation network is as accurate as a co-expression network derived from hundreds of microarray experiments

We extended the evaluation of the inferred co-regulation network by comparing it with the STRING co-expression network. Before interpreting the results, it should be stressed that co-regulation and co-expression reflect distinct aspects of transcriptional regulation. Two genes are considered co-regulated if they are direct targets of the same TF(s). Co-expression denotes expression under similar conditions, and may result from a direct co-regulation, or from more complex causes such as an action of independent factors, regulation cascades, etc. Thus, the co-expression network cannot be considered as a golden standard for inferred co-regulation. Nevertheless, it is interesting to analyze the overlap between those two networks.

When the inferred co-regulation network is compared either to the STRING co-expression network (Figures 2C, 3D and 4 C) or to the co-binding network (Figures 2E, 3 F and 4D), the same general trends are observed as discussed above for the annotated co-regulation network: a rather weak overall sensitivity, but fairly good PPV. Here as well, the PPV of the predicted co-regulation increases with the DPbits score, showing that similarities between predicted phylogenetic footprints reliably predict co-expression.

It is well known that transcriptome data might be noisy, and there are many issues with the choice of normalization, similarity measurements and clustering procedures. We wondered to which extent the STRING co-expression data set would correspond to the annotated co-regulation network. Interestingly, the STRING co-expression network shows similar figures of merit as our inferred co-regulation network (Figures 2A and B, 4B and E): the PPV of the STRING network is reasonably good (41% fits some annotated regulon), and increases with the score, whereas the sensitivity is rather poor (7.5% for the whole network) and rapidly drops when the STRING score increases above 170 (Figure 4E). It thus seems that our network inferred only by in silico analysis of phylogenetic footprints gives as good results as a network derived from several hundreds of microarray experiments.

When the chip-on-chip ‘co-binding’ network is used as reference to evaluate the inferred co-regulation (Figure 4D) or the STRING co-expression (Figure 4F) networks—the sensitivity (∼4%) is still lower than that for the annotated regulons, which is not surprising since the high-throughput ChIP-on-chip data produce a huge co-binding network of 178 202 edges, i.e. ∼17 times larger than the annotated co-regulation network (Table 1). Despite the low sensitivity, the PPV shows a regular increase with the DPbits score (Figure 4D), confirming the interest of this metric to estimate the reliability of predicted co-regulations. The ROC curves show that the ChIP-on-chip network is better recovered by the STRING co-expression data than by the inferred co-regulation (Figure 2E and F, Table 2).

In summary, the co-regulation network inferred from the sole analysis of genome sequences performs at least as well as a microarray-derived co-expression network.

Interestingly, the predicted co-regulation and STRING co-expression network recover different fractions of the annotated regulons (Table 1C, Supplementary Figure S4): whereas STRING recovers 794 of the annotated co-regulations and 723 of our predictions, their intersection covers 175 annotated co-regulations only, i.e. 13% of their union (1342 annotated co-regulation). The inference of co-regulation and the analysis of co-expression thus seem to reveal complementary parts of the annotated co-regulation network.

Experimental tests confirm the links between fourteen orphan genes and their regulatory family

After having verified that high-scoring predictions generally reveal pairs of co-regulated genes, we used the complete inferred network to identify a reasonable set of testable hypotheses about regulation. We selected genes of unknown function (orphan), collected their direct neighbors (i.e. the genes linked to them in the inferred co-regulation network) and retained the neighbor sets significantly enriched for some functional class of GO (39). On this basis, we selected four co-regulation modules containing one or more orphan genes, and carried out experiments to validate their co-regulation experimentally (Figure 6).

Figure 6.

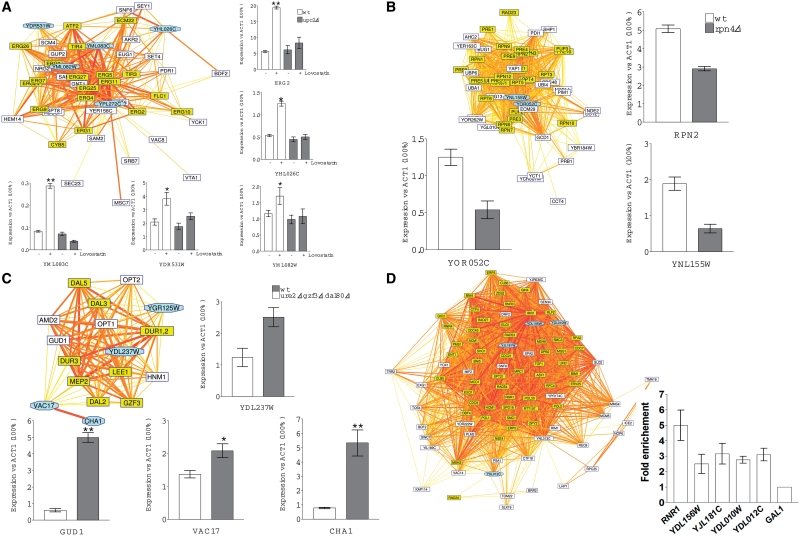
Experimental validation of selected inferred regulations by qRT–PCR and ChIP analyses. Each panel shows a cluster of neighbor genes in the inferred network, together with the experimental measurement of the transcriptional responses. (A) Effect of Lovastatin and UPC2 deletion on RNA levels of four potentially Upc2 regulated genes, using ERG2 as control. Lovastatin (40 µg/ml) was added to the cultures for 16 h before cell harvesting. RNA levels were quantified by qRT–PCR and data were expressed versus the actin gene (ACT1) used a non-regulated reference. (B) Effect of the RPN4 deletion on two potentially Rpn4 regulated genes using RPN2 as a positive control. Cells were grown on the YPD medium; experiments were performed as in (A). (C) Derepressing effect of the triple ure2 gzf3 dal80 mutations on the RNA levels of four genes potentially subject to nitrogen catabolite repression. Cells were grown on glutamine as the sole nitrogen source. Experiments were performed as in (A). (D) ChIP PCR analysis of four potentially Mbp1 regulated genes. Mbp1-HA expressing cells were grown on YPD and the promoter occupancy by Mbp1 was monitored by ChIP for RNR1 (a known target gene of Mbp1) and the four indicated genes. Data were expressed versus the GAL1 gene used as a reference. Color code for the network clusters: genes known to be submitted to a common regulation are highlighted in yellow. Cyan-shaded octagonal boxes indicate genes submitted for experimental validation.

We first considered a neighbor set of 48 genes, 16 of which are involved in uptake and biosynthesis of sterols (ERG genes) and 3 in sphingolipid biosynthesis (Figure 6A). In cells deprived of sterols, these genes are up-regulated by Upc2p, a TF binding to the sterol response element (SRE) TCGTATA (40). The inferred cluster included 12 ERG genes (Supplementary Table SII), linked to several orphan genes among which YDR531W, YHL026C and the pair of divergently transcribed genes YML082W-YML083C. The most significant footprints detected in these genes contain the motif TCGTTTag, which corresponds to the annotated SRE. The inferred co-regulation thus suggests that these four orphan genes might be regulated by sterols. To test this hypothesis, we grew wild-type and upc2Δ mutant cells with or without lovastatin, a compound causing sterol depletion, and used qRT–PCR to monitor the relative RNA levels of these genes. An ERG2 was used as a positive control and the actin gene (ACT1) as a normalizing reference. The results clearly show Upc2-dependent induction of ERG2 in response to lovastatin. The four tested orphan genes displayed similar expression changes, thereby indicating that they belong to the Upc2 regulon.

Rpn4p is a transcriptional activator binding to the GGTGGCAAA sequence present in the upstream non-coding sequence of most genes encoding proteasome subunits. In an rpn4Δ mutant, the expression level of these genes is typically reduced about twofold (41). The inferred co-regulation network contains a cluster of densely connected genes coding for proteasome subunit genes, together with the two orphan genes YNL155W and YOR052C (Figure 6B), and whose footprints include the Rnp4p motif (Supplementary Table SII). The qRT–PCR results clearly show that both genes are expressed in a manner very similar to the proteasomal subunit RPN2 gene, with a reduced expression in the rpn4Δ mutant (Figure 6B). Interestingly, both YNL155W and YOR052C products contain a conserved AN1-type zinc-finger motif also present in the human protein AIRAP, an arsenite-inducible protein found to be associated with, and to stimulate, the 19 S regulatory particle of the proteasome, thereby counteracting the toxic effect of arsenic on protein structure (42). Furthermore, YNL155W is also up-regulated by arsenic (43). These results strongly suggest that Ynl155wp and Yor052cp represent possible functional orthologs of AIRAP.

The expression of many genes involved in nitrogen catabolism decreases to low levels when good nitrogen sources (e.g. glutamine) are provided in the growth medium. This regulation termed the nitrogen catabolite repression (NCR) is mediated by a combination of three negative factors (Ure2p, Gzf3p and Dal80p) preventing the trans-acting factors Gln3p and Nil1p from activating transcription through cis-acting sequences containing GATAA motif (44). The neighborhood of NCR-target genes in the inferred network includes two divergently transcribed gene pairs each containing a known NCR-target (GUD1 and CHA1). We were interested in determining whether each associated gene (YDL237W and VAC17) is also under NCR control as they had not been fished out in any genome-wide inventory of NCR-target genes (45–47). We used qRT–PCR to monitor the relative RNA levels of the four genes (Figure 6C). As expected, GUD1 and CHA1 were derepressed in ure2Δ gzf3Δ dal80Δ triple mutant cells grown on glutamine, an expression profile typical of NCR-target genes. The VAC17 and YDL237W genes were also significantly derepressed in the triple mutant strain, though to a lower extent than the GUD1 and CHA1 genes. As Vac17p is a vacuole-specific receptor for myosin (Myo2p), it remains uncertain whether its apparent weak NCR control is physiologically relevant.

Finally, we examined four other genes of an unknown function (YDL010W, YDL012C, YJL181W and YDL156W) from an inferred co-regulation set regrouping several Mbp1 target genes (Figure 6D). Mbp1p is a DNA-binding protein associating with Swi6p to form the MBF complex [Mlu1 cell cycle box (MCB) binding factor] involved in transcriptional control of several genes during the G1/S transition (48). Although these four genes have never been shown to be regulated by Mbp1p, their expression profiles show similarities to other genes under MBF control (49). To determine whether these four genes represent actual MBF target genes, we performed a ChIP–PCR analysis to monitor their possible association with an HA-tagged Mbp1 protein. The RNR1 gene was used as positive control (29) and GAL1 as a negative control. The results (Figure 6D) show that Mbp1p associates with the upstream regions of RNR1, YDL156W and YJL181W, possibly also YDL010W and YDL012C. These genes thus represent probable new Mbf1p target genes, and their products are possibly involved in G1/S transition.

We also tested the response to stress in amino acid for a pair of divergently transcribed genes YHR020W and DED81, which were grouped with many Gcn4p targets, but the result was negative.

In summary, by combining predicted regulatory elements and GO annotation, we could suggest a hypothetical regulation for 16 orphan genes, 14 of which were supported by experiments.

DISCUSSION

This study shows that a set of genome sequences from related organisms can be used as sole input for predicting cis-regulatory elements of individual genes and to infer co-regulation between gene pairs. Importantly, the method relies on ab initio pattern discovery in promoter sequences of orthologous genes (phylogenetic footprint), and does not require any prior knowledge about regulation, such as annotated TF binding motifs or gene expression data. By comparing predicted groups of co-regulated genes to functional classes (e.g. GO classes), a putative function and regulation can further be assigned to uncharacterized genes.

The co-regulation network inferred in the yeast S. cerevisiae was extensively evaluated in various ways. We first showed that almost all of the top-ranking predictions correspond to pairs of genes previously known to be co-regulated or involved in the same function (Table 3). We then performed a systematic in silico validation of the accuracy of the predictions, and showed that the DPbits score gives a good indication of their reliability (Figure 4, Table 4). The comparison between inferred groups of co-regulations and annotated regulons showed a good ability for inferring links between the target genes of specific TFs, but a weakness for detecting large regulons controlled by global TFs (Figure 5). It has been shown recently that global regulators consistently display low levels of binding specificity (50) and consequently the binding sites of a given TF can differ from each other, so that even if they were perfectly predicted, it might still be very difficult to link them. Noticeably, although our method relies only on genome sequences, its figures of merit are comparable to those of the STRING co-expression network derived from several hundreds of microarray experiments. Finally, we selected 16 interesting cases of orphan genes appearing to be linked to some regulons, and 14 of these predictions were confirmed by experimental testing. This experimental validation of course concerns only a tiny fraction of the inferred co-regulations network, which certainly contains many more correctly predicted regulations. The validation however demonstrates that the in silico method proposed here not only re-discovers previously known interactions, but also provides a valuable set of new hypotheses about regulation, even for the genome of one of the best studied model organism.

An important strength of our approach is that the sig_B returned by the footprint discovery algorithm provides a reliable estimate of the risks of false positives (20), enabling a more stringent criterion for selecting the most reliable motifs. Similarly, we show that the DPbits score ranks the infer co-regulations in a relevant manner, with a steady enrichment of correct predictions with increasing scores.

Our method can readily be applied to decipher the wiring of transcriptional regulatory networks in hundreds of microbial organisms for which no other information is available than the raw genome sequence, and to analyze the evolution of these networks. Its long-term benefits can easily be perceived to catch the pace of the exponential increase of genome and metagenome sequences that will result from the new high-throughput sequencing technologies.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online

FUNDING

R.J. and S.B. are supported by a doctoral grant from the Fonds pour la Recherche dans l’Industrie et l’Agriculture (FRIA) allowed by the Belgian Fond National de la Recherche Scientifique (FNRS). R.J. is also supported by a postdoctoral grant from the Wiener-Anspach Foundation. S.B. is chargé de recherches at the FNRS de la Communauté Française de Belgique. F.A.-S. is supported by the Actions de Recherche Concertées de la Communauté Française de Belgique (ARC grant number 04/09-307). This project and funding for open access charge were partly supported by the Belgian Program on Interuniversity Attraction Poles, initiated by the Belgian Federal Science Policy Office, project P6/25 (BioMaGNet). The BiGRe laboratory is supported the MICROME Collaborative Project funded by the European Commission within its FP7 Programme, under the thematic area ‘BIO-INFORMATICS—Microbial genomics and bio-informatics’ (contract number 222886-2).

Conflict of interest statement. None declared.