Abstract
We show that the cAMP receptor protein (Crp) binds to DNA as several different conformers. This situation has precluded discovering a high correlation between any sequence property and binding affinity for proteins that bend DNA. Experimentally quantified affinities of Synechocystis sp. PCC 6803 cAMP receptor protein (SyCrp1), the Escherichia coli Crp (EcCrp, also CAP) and DNA were analyzed to mathematically describe, and make human-readable, the relationship of DNA sequence and binding affinity in a given system. Here, sequence logos and weight matrices were built to model SyCrp1 binding sequences. Comparing the weight matrix model to binding affinity revealed several distinct binding conformations. These Crp/DNA conformations were asymmetrical (non-palindromic).
INTRODUCTION
Conformational selection refers to how functional proteins interact by folding along one of several overall energetically down-hill paths to form one of multiple possible structures termed conformers (1). According to conformational selection, multiple populations of the same biological molecule form because the protein in one conformer population is folded differently from that of the same protein populating another conformer population. We proceed as if protein/DNA complexes also undergo conformational selection (2). This hypothesis is testable because populations of distinct conformers attain equilibrium in the absence of catalysis such that the affinity of the protein and DNA comprising protein/DNA conformer complexes can be quantified experimentally.
A generalized two conformer scenario clarifies conformational selection by bending DNA along one of two paths across an essentially spherical protein surface such as the cAMP receptor protein (Crp). These two paths can be formed with (i) a planar conformer wherein DNA bends around the protein's equatorial plane and (ii) a non-planar solenoid conformer wherein DNA bends at angles to the equatorial plane [see (3) for an illustration]. The length L of DNA contacted in the planar conformer by an essentially spherical protein is less than that for the non-planar conformer. The non-planar length of DNA contact is greater because a first order solenoid follows a corkscrew-like path wrapping around a spherical protein. Contact length is not limited to the equator. Greater contact length allows higher binding affinity due to increased electrostatic interactions (4) relative to that of the planar conformer. Because the path that DNA takes across the protein surface must be unique to each conformer, the major groove accessibility relative to the bound protein surface will also be unique to each of these two generalized planar and non-planar conformers. Sequence logos form sinusoidal conservation patterns (5) showing how major groove accessibility relative to the bound protein surface is involved in DNA sequence conservation. It follows that sequence logos should be able to distinguish sinusoidal curves between planar and non-planar DNA bending paths across the protein surface.
DNA sequence conservation has been measured according to the method of Hertz and Stormo (6) for calculating a relative weight score (Ws) of a DNA segment, and by the method of Schneider and Stephens (7) for calculating and displaying bit values and relative conservation frequencies as a sequence logo. The higher the bit value of a position, the lower is the entropy contributed by that position. According to the method of Hertz and Stormo (6), collected DNA segment sequences are aligned and recorded as a position-specific scoring matrix (PSSM) (8). A PSSM serves as a ‘scanning’ matrix and is required to calculate a relative weight score (Ws) for each window of length L at each position of a DNA sequence along a genome. This method allows the collection of high scoring sequence segments of length L that can be aligned to generate an ‘output’ matrix from those aligned sequences. The higher the Ws value, the higher the protein/DNA binding affinity. The method of Schneider and Stephens (7) requires a set of aligned sequences to calculate bit values and relative conservation frequencies. These are graphically displayed as a sequence logo. A sine curve generated by this method is reflected by the logo and indicates major groove accessibility relative to the bound protein surface (5). However, each method returns a different value for the parameter ‘information content’. Instead of addressing this difference (9–11), we will show how to use both seamlessly in concert.
Ws (or a weight score equivalent) is the parameter traditionally plotted on the x-axis to compare against a protein's binding affinity on the y-axis of a scatter plot. This plot tests if DNA sequence and binding affinity are correlated so that affinity can be predicted from the DNA sequence. For protein/DNA complexes lacking DNA bending, R2 = 0.98, where R is the correlation coefficient (11–13). Currently, 98% of the sequence-dependent affinity changes can be calculated. These proteins do not bend DNA, thereby maintaining the same length of DNA contacting the bound protein no matter how conformational selection changes the conformer [in essence (13)]. Using current methods, however, R2 ≤ 0.74 for proteins that bend DNA such as Crp, but this is true only for low affinity sites (14). If Ws versus the full affinity spectrum is considered, the correlation is further reduced giving R2 ∼ 0.45–0.60 (15) and has not improved over the past 23 years [excluding methods, which employ subdivision by affinity or transcription activity ranges, e.g. see (16)]. While performing DNA sequence Ws versus affinity comparisons, conformers were not always recognized and grouped separately [though it has been mentioned (17)].
DNA positions −6 and +5 (defined in Figure 1A) of Crp/DNA complexes are primary kink conformer indicators. They form either smooth bend, or kinked conformations observed in crystal structures (18). Each participates in bending DNA ∼ 40° (19). The bases at these positions are generally not bound by Crp. They are predominantly free from Crp bonding enthalpy contributions such that entropy is the major factor for conserving base identities at these positions. Entropy of these bases decreases because the motion of these bases is restrained by kinking against a neighboring base at positions −5 or +4. Accordingly, kinking conserves the base identity at primary kink positions −6 and +5 via selection of the resultant conformer function at the time and place where primary kink conformations are formed. This causes the conserved base to display as a large letter in sequence logos quantifying entropy in bits. Hence, coincident conservation of a primary kink and another element can be identified if these elements are associated, occurring together in any given Crp binding site. Alternatively, if smooth-bend and flanking flexible bend elements are associated, positions −6 or +5 should have low bit values while flanking flexible bends should have high bit values. Omagari et al. (20) first suggested that DNA regions flanking the core 16 bp binding site could influence Synechocystis sp. PCC 6803 cAMP receptor protein (SyCrp1)/DNA affinity. Others have shown that flanking flexible bends are important for binding (4,19,21–33). To our knowledge, however, studies relating flanking flexible bends and primary kinks have not been reported (22).
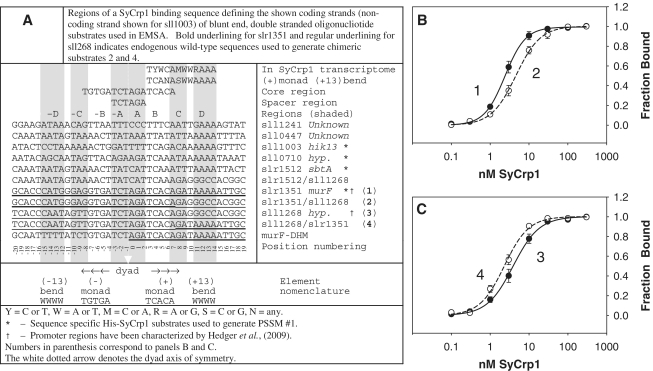
Figure 1.
DNA binding substrates used and distinct His-SyCrp1 affinities for endogenous and chimeric substrates containing either (+13)AAAA or (+13)GGCC. (A) DNA binding substrate sequences and nomenclature. (B and C) Titration curves for His-SyCrp1 binding to the endogenous wild-type slr1351 (closed circles; 1) and sll1268 (closed circles; 3) substrates are compared with their respective chimeric substrates slr1351/sll1268 (open circles; 2) and sll1268/slr1351 (open circles; 4) listed in panel A. The fraction of bound DNA is shown as a function of the concentration of His-SyCrp1. The solid and dashed lines are obtained by a nonlinear regression best fit to the three-parameter Hill equation, n = 3 ± SE (see also Supplementary Table S31). Binding reactions and electrophoresis were performed at 22°C. Reactions contained His-SyCrp1 at the indicated concentrations, 0.1 nM radiolabeled substrate, 20 µM cAMP and reaction buffer only. The non-specific competitor Rndm. was omitted.
In this work, we approached a model base distribution of SyCrp1 binding sites to generate a PSSM, a hypothetical base distribution. This PSSM, the result of many previous hypotheses, matrix operations and stability rounds is itself a de novo hypothesis. Using this PSSM model to calculate Ws, we find that flanking flexible bends determine different binding conformers. This finding enabled the development of algorithms to mathematically relate Ws and binding affinity by identifying the primary kink contribution to affinity of the relevant flanking flexible bend-dependent conformer. These comparisons rely upon sequence logos to serve as both a metric parameter for programming and as a human-readable guide to the DNA bending code. Researchers can follow both the DNA sequence distribution and the sine curves tracing the logo contour of double stranded DNA (dsDNA) major groove accessibility relative to the bound protein surface. The methods described here were cut-and-paste procedures, thanks to publically available web servers.
MATERIALS AND METHODS
Element nomenclature
‘AAAA’ or ‘TTTT’ bp stacks act essentially as ‘hinges’ and are canonical flexible bend elements (24,27,34). Dyads within Escherichia coli Crp (EcCrp) sites are often flanked by a tract containing a contiguous stack of four A:T bp steps termed flanking flexible ‘bend’ here (21,23). We have used the term ‘bend’, but these can also form flexible kinks such as for TA steps bent by EcoRV (35). These two secondary DNA ‘bends’ (∼5–10° or more) centered on positions −10 or +10 (19) are defined here as ‘(±10)WWWW’ where weak (W) bases are adenine (A) or thymine (T) and (±x) indicates the bp center of the tract relative to the dyad axis of symmetry. For example, the sequence ‘TGTGATCT*AGATCACAWW*WW’ contains the (+10)bend, (+10)WWWW, centered 10 bp from the dyad axis of symmetry [note the 10 bp spacing between the asterisk positions corresponding to the dyad axis and (+10)WWWW]. Consequently, our nomenclature describes symmetry about the dyad axis but contains no zero (0) position. Conversely, our position numbering system does contain a zero position in the figures. To differentiate between the two dsDNA strands, the left to right 5′ to 3′ sequence representation relative to the downstream transcribed gene as displayed according to current conventions is termed ‘conventional strand’ here. Hence, the reverse complement is the reverse complement relative to the conventional strand. Genomic Synechocystis dsDNA substrates tested here are mostly named according to the target gene. These dsDNA substrates are not italicized (e.g. the 40′mer slr1351).
PSSM #3 derivation
PSSM #3 was a de novo hypothesis. Given how hypothesis generation is not amenable to method or result reporting, Introduction in Supplementary Data (Supplementary Figures S1–3) and tables (Supplementary Tables S1–S30) describing and documenting PSSM #3 derivation is provided.
Genome-wide computational sequence analysis
Computation was performed by programs embedded in freely available web servers at (http://rsat.ulb.ac.be/rsat/) (36), (http://seqtool.sdsc.edu/CGI/BW.cgi) (37) and (http://weblogo.berkeley.edu/logo.cgi) (21). The pDraw program (http://www.acaclone.com/) (38) was used for plasmid and primer organization and design. BioBIKE (http://www.Biobike.org) (39) was used for comparisons between annotated cyanobacterial genomes. Regression fitting was performed with Sigma Plot; otherwise, windows-installable freeware and web servers were used exclusively. Functional annotation of Synechocystis sp. Pasteur Culture Collection of Cyanobacteria (PCC) 6803 was obtained from Cyanobase (40).
Stability rounds were performed with a scanning matrix resulting in a list of output sequences (of length L equal to that of the scanning matrix) that were aligned with the Consensus (6) program (pi = 40% G:C) forcing one match per sequence to generate a tab formatted output matrix to copy-paste special-text into Excel. To minimize computational load for genome-wide matrix scans, Genome-Wide Patser (6) performed all genome-wide search functions (e.g. scanning matrix) most often specifying the default pi = 40% G:C and Ws cutoff = 7. The output gene list was copied into Retrieve Sequence (36) to collect the 400 bp upstream of the annotated start site the same as for Patser. These regions are termed ‘intergenic regions’ for simplicity. Thus limited to a smaller sequence data set than that of all upstream intergenic regions, the Patser-identified intergenic regions were then pasted into the (full options) Matrix-Scan (6) sequence window using the No-ORF (no-open reading frame) background pi option to scan using a tab formatted matrix. Pseudo-counts = 1 distributed proportionally to residue priors and pseudo-frequency = 0.01. The program PSSM-convert (http://www.phisite.org/pssm-convert/pssm-convert.htm) was run to check proper matrix tab formatting by converting a count matrix to a sequence logo equal to the Weblogo v2.8.2 (http://weblogo.berkeley.edu/logo.cgi) and Sequence Logos (http://genome.tugraz.at/Logo/) servers when small sample correction is not selected (allowing interlogo comparisons). Data sets of <80 kb were pasted directly into Matrix-Scan bypassing Patser. Matrix-Scan (6) calculated all Ws scores presented here. If a plot (from highest to lowest) of Ws values for collected intergenic sequences exhibited a discontinuity (i.e. a break in the curve) at some value greater than Ws = 7, then the Ws cutoff was defined at or above that discontinuity. Markov chains were not employed.
Logo sine curve fitting
Fitting was accomplished by tracing the conservation curvature of sequence logos using sine curves of various periodicities starting with 0° at the dyad axis of symmetry, which corresponds to a point where the minor groove is centered on the dyad axis of symmetry. Periods of 8.5 or 10.6 bp/period (5,41,42) provided approximate fits to different conformers. The sine curve amplitude values shown here are arbitrary fits to the logo curvature and do not follow from Shannon entropy. Minima were often centered on T-stacks. Maxima were often centered on A-stacks.
Protein purification and electromobility gel shift assay
Masayuki Ohmori (Saitama University) provided pCGA used to overexpress histidine-tagged SyCrp1. A method for purification using nickel and mono-Q columns, binding reactions and EMSA has been previously described (43). This was essentially reproduced and has been described in detail (44).
All 32P end-labeled dsDNA substrates were prepared by slow cooling to anneal boiled ssDNA complementary pairs and then gel purified with UV shadowing prior to 32P labeling with polynucleotide kinase as referenced above. dsDNA substrates were then assayed by EMSA in the absence of protein to ensure that the preparations used did not show banding above the free 40-mer dsDNA band upon overexposure of autoradiograms. All reactions contained 20 μM cAMP unless noted.
Rapid amplification of cDNA ends
The +1 start site of transcription was determined by rapid amplification of cDNA ends (RACE) analysis using 1.0 µg total RNA harvested from photoautotrophically grown log-phase acclimated cultures (except for sbtA) as was previously described (45). See the ‘Results’ section for sbtA culture conditions and primers used. Sequencing was performed at the California State University Northridge sequencing facility.
RESULTS
Importance of the flanking flexible (+13)bend element for binding
The difference between His-SyCrp1 affinity for slr1351 and the lower affinity for sll1268 dsDNA substrates (Figure 1A) previously reported (20) was almost completely accounted for by exchanging positions from +8 to +19 in slr1351 for those in sll1268. This exchange essentially replaced the (+13)AAAA bend from the slr1351 substrate with G:C base pairing and resulted in decreased His-SyCrp1 affinity (Figure 1B). Conversely, the addition of (+13)AAAA to sll1268 increased binding affinity (Figure 1C). These differences were statistically significant (Supplementary Table S31).
These endogenous and chimeric (+)monad (+13)AAAA bend substrates were also tested for cAMP-dependent and sequence-specific binding along with the murF-DHM object for bioinformatics to confirm cAMP dependent and sequence-specific binding (Supplementary Figures S4–S5).
(+)Monad (+13)bend associated promoters determined by RACE
The +1 transcriptional start sites (TSS) for sll1003, sll0710 and slr1512 were determined by RACE (Supplementary Figure S6, also listing all known SyCrp1 target promoters) to confirm that predicted SyCrp1 sites were upstream of the +1 TSS. Promoter activators such as Crp bind upstream of the +1 TSS. The predicted SyCrp1 sites were also upstream of a +1 TSS when a TSS was present, but no TSS was detected for sll0710.
Conformer predictions
The conformer identification (Figure 2) process began with sll1003, sll0710 and slr1512. These three (+)monad (+13)bend DNA sequences along with the dyad (+13)bend sequence slr1351 were used to initiate the process for deriving the PSSM #3 major binding mode model containing all of the conformers shown. The Introduction in Supplementary Data (Supplementary Figures S1–S3) details the PSSM #3 derivation.
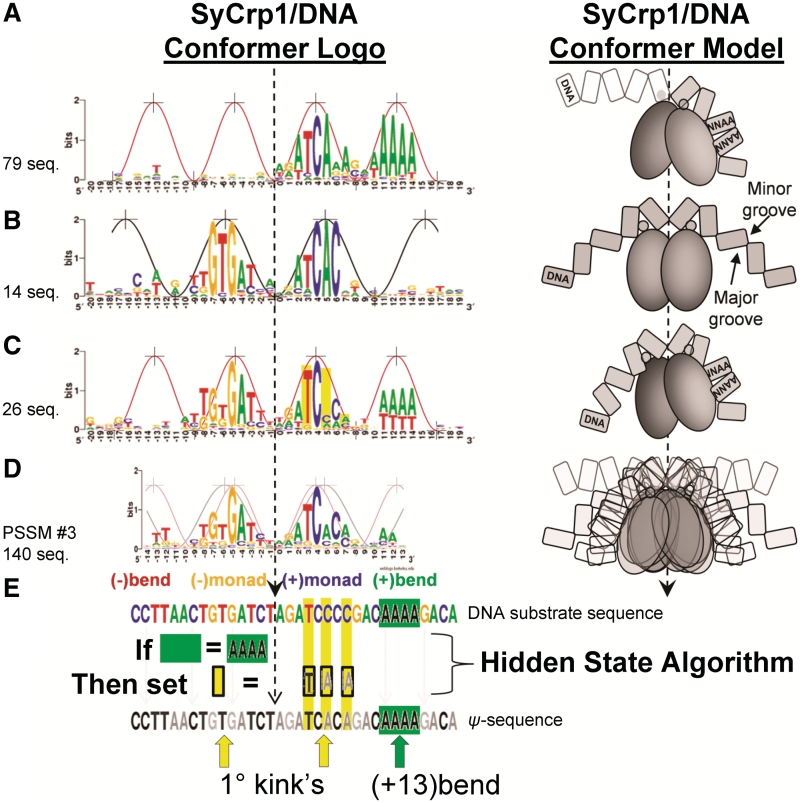
Figure 2.
Three distinct SyCrp1/DNA conformer logos (left) with the corresponding conformer model (right) contributing to the major binding mode PSSM #3 model. The ∼10.6 [black, wide peaks (5,41,42)] and 8.5 (red, narrow peaks) bp/period sine curves are aligned to the contour of the logos. (A)PSSM #1.3, a (+)monad (+13)bend conformer (non-planar, 17.7 bits positions −20 to +19). The strand contributing to the logo is the highest scoring strand orientation collected with the scanning PSSM #1.2 (Supplementary Table S32). In the conformer model (Right), DNA indicated with white fill is less conserved than DNA indicated with grey fill. Note: the protein's F-helix (small grey circle) on the left does not necessarily contact the major groove. (B) Dyad conformer (planar, 22.9848 bits positions −20 to +19). The sequences aligned are endogenous class II SyCrp1 substrates previously suggested (46) and upstream of the open reading frames sll1247, sll1520, sll1941, slr1667, slr1732, slr0442, sll1268, sll1371, sll1261, slr0869, slr1805, sll1924, slr0316 and slr2127. Sequences were aligned in the conventional strand orientation as shown (see ‘Materials and Methods’ section). (C) Dyad (+13)bend conformer (non-planar, 21.7 bits positions −20 to +19) aligned in the conventional strand orientation (see Supplementary Introduction). Slr1351 is the highest affinity known SyCrp1 binding locus and also a Dyad (+13)bend conformer. (D) PSSM #3 (Supplementary Table S34) (neither planar nor non-planar, 16.0 bits positions from −14 to +13). The PSSM #3 model considered here estimates the major binding mode. PSSM #3 includes both conventional and reverse complement strands for each of 70 loci giving 140 aligned sequences. Thus, all conformer models (right) are represented in both conventional and reverse complement orientations. PSSM #3 calculating positive Ws for all sequences in each functional conformer is represented by the PSSM #3 conformer model (right) showing all conformers overlaid. In the schematic conformer models, the DNA is labeled, the flanking flexible bends (if present) are labeled and SyCrp1 consists of representative F-helix circles atop homodimeric ovoids. (E) ‘Filling in the hole’, a HS algorithm. The ‘hole’ is at position +5. An endogenous DNA substrate sequence containing a flanking flexible bend is operated upon by the HS algorithm to generate a ψ-sequence changing primary kink-associated positions +3, +5 and +7 (yellow bars in panels C and E) to the most frequently occurring base identity at those positions. The primary kink positions −5 and −6 (yellow arrow) and a canonical flanking flexible bend (green arrow, green box, positions from +11 to +14) are shown. The dashed arrows indicate the dyad axis of symmetry.
The proposed SyCrp1/DNA conformations (Figure 2) were clearly distinguished by DNA sequence. Each of the (+)monad (+13)bend (Figure 2A and Supplementary Table S32), dyad [Figure 2B, (46)] and dyad (+13)bend (Figure 2C and Supplementary Table S33) conformers provided sequence logo fitting to either of two sine curves. The PSSM #3 logo fit neither curve but was an average tracing midway between the two curves (Figure 2D).
PSSM #3 (Supplementary Table S34) consists of several ‘minor’ binding modes. One minor mode is the set of folding paths or dynamic interactions required to form a single conformer type. A single conformer type is specific to a single hidden state (HS) algorithm (see below). The major binding mode includes all bound DNA sequences for a closed system (e.g. an isolated bacterium or in vitro evolution) because it includes each of the minor binding modes describing the folding paths to each conformer.
A HS model
The energetic states that distinguish conformers formed by bending DNA are not comparable using traditional means because the position-specific bit value of a given conformer's PSSM is distinct from any other conformer-specific PSSM. Moreover, distinct binding modes are not globally informative unless all conformers share associated elements within the major mode of binding. The hidden state (HS) model hypothesizes that minor binding modes can be brought into register and considered within a single major mode PSSM by following a strict Boolean HS algorithm to account for conformation-specific element associations that contribute to position-specific bit value differences between conformers.
A HS algorithm is an ‘IF-THEN’ statement. The ‘IF’ statement identifies the minor binding mode. A minor mode contains the folding paths that can be taken by a single dsDNA in complex with Crp to achieve the final conformer. The ‘THEN’ statement translates that DNA sequence into a pseudo-sequence (ψ-sequence) so it may be comparable with sequences from other minor binding modes. Here, the ‘IF’ statement identifies flanking flexible bends while the ‘THEN’ statement acts upon position −6 or +5 of monad sequences. A HS algorithm is Boolean and treats all sequences the same to generate a ψ-sequence, from which a PSSM ψ-score (Wψs) can be generated for each real sequence.
A ‘fill in the hole’ HS algorithm
A ‘fill in the hole’ operation is a HS algorithm (Figure 2E). When the (+13)bend (boxed in Figure 2E) was found flanking a dyad sequence, the (+)primary kink position +5 was not conserved leaving a ‘hole’ in the sequence logo (yellow bar at the primary kink position +5 in Figure 2E, also see Introduction in Supplementary Data). The hole is the missing information at position +5 of Figure 2C relative to Figure 2A and B. The logos of conformers having a flanking flexible bend have a hole at position +5 (Figure 2C). The logos of conformers lacking a flanking flexible bend lack the hole at position +5 (Figure 2B). The logic follows: ‘IF’ the sequence has a flanking flexible bend, ‘THEN’ filling in the hole should make the resultant ψ-sequences comparable. Moreover, when the sequence logo contour formed a sine curve, the curve suggested folding into a functional conformer along certain minor mode folding paths. So if a logo contour contained both a (+13)bend, and a hole at position +5, then a ‘fill in the hole’ operation was conducted by changing the primary DNA sequence at the hole position +5 to the most frequently occurring base in the major mode model PSSM #3. At position +5, this base is ‘A’.
A HS algorithm forms the basis for using experimentally determined binding affinities to validate the PSSM #3 model. If the primary kink base identity is not highly relevant because any base is just as relevant as another in the presence of a flanking flexible bend element, then a HS algorithm should improve the Ws versus affinity correlation of the resultant ψ-sequence Wψs.
ΔΔG and a reference standard
Information of binding for the catabolite activator protein (ICAP) (15,47) has been the highest affinity EcCrp binding DNA substrate sequence for most of the history of Crp experimentation. Consequently, ICAP has become a reference standard. The strength of Crp binding to any dsDNA substrate is usually expressed as an affinity difference ΔΔG, the change in Gibbs free energy relative to that of a standard such as ICAP. The ΔΔG values shown in this work here were independently quantified Crp/DNA affinity differences relative to the affinity of the Crp/ICAP complex (20,34).
A position's bit value has sometimes been less than those of adjacent positions, leaving a ‘hole’ in the logo [e.g. EBNA1(5) positions −6 and +7]. Following from Shannon entropy (48,49), the base in this ‘hole’ should experience a freedom of occupancy greater than that of adjacent bases (10). Accordingly, an experimental test for ‘filling in the hole’ at Crp/DNA primary kink positions was performed by quantifying ΔΔG relative to ICAP.
His-SyCrp1/DNA variation in ΔΔG: validation of the PSSM #3 model in Synechocystis
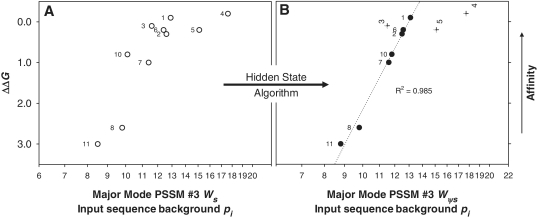
Individual sequence Ws calculated with PSSM #3 were plotted against ΔΔG values (Figure 3) measured by Omagari et al. (20) to experimentally validate the PSSM #3 major mode model. These dsDNA substrates include all known endogenous SyCrp1 binding substrates. The correlation coefficient was low (R2 = 0.652) for a log-linear relationship (Figure 3A). To define this HS algorithm, a flexible bend was defined as (±13)WW (where W = T or A) instead of (±13)WWWW because (±)bends in this data set were not highly conserved (by design). When the HS algorithm was carried out to ‘fill in the hole’, the relationship y = 17.7 − 6.793lnx then described a strong and significant positive correlation (Figure 3B) for ΔΔG and PSSM #3 calculated Wψs (R2 = 0.985, F1,5 = 161.8, P < 0.0001, α = 0.05). The HS algorithm and the resultant Wψs values are listed in Supplementary Table S35. Given the experimentally determined affinity data, the PSSM #3 model was validated because it accounted for 98.5% of the DNA sequence-dependent variation in ΔΔG.
Figure 3.
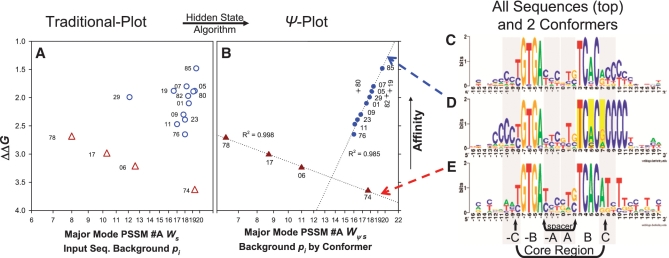
Affinity (ΔΔG) versus weight score (Ws) comparison of all 10 published endogenous SyCrp1 binding sites validating the PSSM #3 model. Traditional (open symbols) and Ψ-plots (closed symbols) for both dyad and dyad (+13)bend His-SyCrp1/DNA conformers are shown. Substrate ΔΔG values relative to ΔG for ICAP were obtained from experiments performed by Omagari et al. (20). PSSM #3 was the scanning matrix for calculating all scores. The highest score fitting to PSSM #3 (either strand orientation) is shown using all 10 input sequences as the background pi. (A) PSSM #3 used to calculate Ws for all known SyCrp1 sequence-specific binding substrates (open circles). (B) PSSM #3 calculated ψ-scores (Wψs) of ψHis-SyCrp1 (closed circles and crosses) by application of a HS algorithm. Specific ψ-sequences, ΔΔG values and PSSM #3 calculated ψ-scores are clearly listed in Supplementary Table S35. Outliers (crosses) are labeled vertically and not included in the R2 value because they are distinct from the major mode trendline. The R2 value for the major mode trendline (dotted) was obtained by fitting to y = y0 + alnx. ΔΔG is the same for any given substrate in each plot. Substrates are labeled as previously (20). Here, 4 = slr1351 and 2 = sll1268 substrates from Figure 1A. Note logarithmic scaling of the abscissa.
A negative control algorithm was: (i) if NOT (-13)WW then set positions +5 and +7 (TCA5CA7) equal to ‘A’, and (ii) reciprocate (i.e. set positions −6 and −8 equal to ‘T’) for the inverted side. This HS algorithm negative-control decreased the log linear correlation coefficient R2 from 0.652 to 0.381 as expected. These control and experimental results were consistent with the HS assumption that any base in primary kink associated positions +3 (if positions +5 and +7 are the most frequently occurring base identity), +5 and +7 was just as relevant as the most frequently occurring base for binding affinity in the presence of a (+13)bend element.
The PSSM #3 relationship to known SyCrp1 binding substrates
PSSM #3 predicted all 10 previously tested and published endogenous SyCrp1 binding substrates (Figure 3) (20), and failed to predict sll0702 (PSSM #3 Ws = 0.3). Exclusion of the sll0702 substrate sequence was critical because biochemical position substitution data obtained by Omagari et al. (20) predicted the aforementioned substrates (including sll0702), but could not demonstrate His-SyCrp1 binding to the sll0702 substrate. Further, the right half (positions 0–19) of PSSM #3 (Supplementary Table S34) yielded Ws > 0 (most >7) for all (+)monad (+13)bend substrates (PSSM #1, #1.2 and #1.3; see Introduction in Supplementary Data) listed in Supplementary Table S32. The core 16 bp of PSSM #3 yielded Ws > 0 for all dyad substrates (Figure 2B), and PSSM #1.3 calculated positive Ws values for the experimentally bound substrates comprising PSSM #1 (data not shown). Indeed, the information relevant to the DNA binding code was retained in accordance with Shannon entropy because we could recollect the experimentally verified substrate sequences sll1003, sll0710 and slr1512 from the genome by scanning with the final matrices.
EcCrp/XD-DNA variation in ΔΔG: validation of the HS model in E. coli
A HS algorithm was tested (Figure 4A and B; Supplementary Table S36) with sequence and affinity data collected by Lindemose et al. (34) who performed systematic evolution of ligands by exponential enrichment (SELEX) to collect a wide sampling of all EcCrp/DNA conformers possible with 40-mer modified dsDNA. Accordingly, all DNA substrates retained by SELEX are known and make up the sequence alignment of PSSM #A (Figure 4C). The sequence alignment of PSSM #A models a known major mode of binding. It is the real and only DNA sequence distribution of a whole system (the SELEX Crp/XD-DNA system) that exists. There are no other DNA substrates in the system. Moreover, the PSSM #A sequence alignment distribution (Figure 4C) is known, and is not hypothetical; it includes all binding sites and requires no validation.
Figure 4.
Affinity (ΔΔG) versus weight score (Ws) comparison validating the HS model. Traditional (open symbols) and Ψ-plots (closed symbols) for dyad (triangles) and dyad (+10)bend (circles and crosses) EcCrp/XD-DNA sequence-specific conformers. Substrate ΔΔG values relative to ΔG for ICAP were obtained from experiments performed by Lindemose et al. (34). PSSM #A was the scanning matrix for calculating all scores. The highest score fitting to PSSM #A (either strand orientation) is shown. (A) PSSM #A calculated Ws of dyad (open triangles) and dyad (+10)bend substrates (open circles). (B) PSSM #A calculated ψ-scores (Wψs) of ψEcCrp/XD-DNA for dyad (closed triangles) and dyad (+10)bend substrates (closed circles and crosses). Each set of conformer-specific sequences scored (e.g. the circles) make up the input sequence background pi for scoring that conformer. Specific ψ-sequences, ΔΔG values, and PSSM #A calculated ψ-scores are clearly listed in Supplementary Table S36. Outliers (crosses) are labeled vertically and not included in the R2 value because they are distinct from a trendline. R2 shown for trend lines (dotted) was obtained by fitting to y = y0 + anlnx. ΔΔG is the same for any given substrate in each graph. The point for the highest affinity substrate is G8.85 = 85 and labels correspond to the G8.## clones as described (34). Note logarithmic scaling of the abscissa. For the XD-DNA shown, G = X and A = D. (C) The entire sequence distribution constituting the major binding mode illustrated as PSSM #A (25.7 bits). All 49 unique sequences of the SELEX system make up this logo. The EcCrp/XD-DNA complex affinities for 26 dsDNA substrates with these unique sequences were determined, leaving 23 sequences having unknown affinities. (D) The dyad (+10)bend conformer illustrated as PSSM #A1 (33.5 bits). The 14 sequences that contain (+10)CCCC make up this logo. A total of 12 affinities were determined (circles and crosses in A and B). (E) The dyad conformer illustrated as PSSM #A2 (31.2 bits). The seven sequences that contain ≤2 X/C bp's total in both (+ and −10)NNNN tracts make up this logo. A total of four affinities were determined (triangles in panels A and B). The reported bit values span between positions −16 and +16. The logos in C and D are not ψ-sequences. Base positions and arbitrary regions shaded in gray are labeled as in Figure 1A. Flanking flexible bend proximal primary kink associated positions +3, +5 and +7 (yellow bars) are where ψ-sequence changes were performed.
All guanine and adenine bases were substituted with xanthine (X) and 2-6-diaminopurine (D) base analogues thereby exchanging the minor-groove amino filling group (XD-DNA). The result was ‘C's’ in the flanking flexible bends (Figure 4C–E) as discussed previously (34).
The Lindemose et al. (34) sequence data distinctly separated by conformers attained via minor modes of binding within one major binding mode (Figure 4C–E). When a single substrate contained multiple sequence elements such as a dyad with either (+10 and −10)bends or only one (±10)bend, a HS algorithm was required to improve the correlation of weight score and ΔΔG (circles in Figure 4A and B).
A HS algorithm (circles in Figure 4B) improved the correlation of weight score and ΔΔG. The relationship y = y0 + anlnx described a high positive correlation of ΔΔG and PSSM #A calculated Wψs (R2 = 0.985, F1,7 = 531.1, P < 0.0001, α = 0.05). The HS algorithm and the resultant Wψs values are listed in Supplementary Table S36. The HS model hypothesis was the only unknown in this experiment (PSSM #A was known). Given the experimentally determined affinity data, the HS model was validated because it accounted for 98.5% of the DNA sequence-dependent variation in ΔΔG.
The conformer-specific nature of HS algorithms
The major binding mode model PSSM #A (Figure 4C) contained three minor modes of binding (Supplementary Tables S37–40). A dyad (+10)bend conformer (PSSM #A1; Figure 4D), a dyad conformer (PSSM #A2; Figure 4E) and a third minor mode conformer (PSSM #A3), which is not shown, but contributes 10 affinity-quantified substrate sequences to PSSM #A (Supplementary Table S37). These 10 sequences required the HS algorithm: if ‘C’ within (−10)NNNN, then set ‘C’ equal to ‘G’ to yield a highly correlated (R2 > 0.905) relationship (data not shown). ΔΔG and PSSM #A calculated Wψs were therefore highly correlated within all minor binding modes. Moreover, the three conformers in this SELEX system each required a distinct HS algorithm.
Several controls were performed using alternate HS algorithms. Alternate parameters, such as ‘if (+10)CCCC then set positions −6 and −8 “T−8GT−6GA” equal to “T”’, decreased the correlation coefficient for these negative controls as expected (data not shown). These control and experimental (Figure 4) results were consistent with the HS assumption that any base in primary kink position +5 is just as relevant as the most frequently occurring base for binding affinity (e.g. ICAP) in the presence of a (+10)bend element.
A HS algorithm is malleable. It can follow nonlinear state paths to include conformer-specific transition probabilities bypassing both: (i) functional conformers not selected naturally and (ii) possible forbidden transition zone encounters in 5′ to 3′ linear Eigen sequence space (50) and Markov (51) state-transition paths (Supplementary Figures S8 and S9).
Outliers
R2 values including the circles and crosses (outliers) in Figures 3B and 4B were 0.698 and 0.541, respectively. These variances were unequal as expected for comparing genomic sequences evolved in a supercoiled system and SELEX sequences evolved in a linear dsDNA system (14). The outliers that evolved in the Synechocystis genome were farther from the trendline (Figure 3B) than the outliers that evolved in the SELEX system (Figure 4B). Previous methods could not clearly distinguish outliers and instead excluded all high affinity Crp/DNA complexes such that the few remaining low affinity sites fit (R2 = 0.74) the model (14). The PSSM and HS models tested here fit (R2 = 0.985) 70 and 80% of the SyCrp1 (Figure 3B) and EcCrp (Figure 4B) data, respectively. This fit spanned the full affinity range, and allowed for the identification of obvious outliers.
DISCUSSION
This article validates the SyCrp1 PSSM #3 model. This model was based upon identifying mutually conserved structural DNA sequence elements such as monads, kinks and flanking flexible bends. The DNA sequences of the three (+)monad (+13)bend sites and the dyad (+13)bend site initiating PSSM #3 construction were starting suggestions that enabled scanning and output matrix methods to reiteratively hone in on mutually conserved monad and bend elements. These elements describe distinct conformer structures that, in turn, account for bent DNA binding affinity. Even if the four sites initiating PSSM #3 construction are not acceptable, we have quantitatively accounted for all 10 genomic sequences of currently published linear B-form DNA segments that bind SyCrp1 (20). In accordance with Shannon entropy, both the scanning and the resultant output matrices contained the four initiating sites. Further, our PSSM #3 model excluded those sites that do not bind in vitro, but were previously predicted to bind (20,44,46,52). Clearly, the four initial sites were a sufficient starting collection for PSSM construction. Previous experimental and predictive methods that do not initiate PSSM construction with so few sites had overlooked distinct protein/DNA conformers and the relationship of binding affinity versus DNA sequence information. Since 98% of the sequence-dependent affinity changes can be calculated due to the finding of multiple bent protein/DNA conformers here, the sequence-dependent affinity changes describing both bent and unbent-protein/DNA complexes are now comparably correlated (i.e. R2 ≥ 0.98). Specifically, the finding of distinct Crp/DNA conformers validates the PSSM #3 model by solving for the correlation of binding affinity (quantified experimentally) versus DNA sequence information (calculated with the PSSM #3 model).
Transcription factors that do not bend DNA upon binding differ from those that do; they are limited by how much protein surface can contact a length L of DNA. These contacts with unbent-dsDNA are amenable to the traditional approach of finding a weight matrix within L for E. coli. Such a weight matrix accurately predicts binding affinities in E. coli. Due to this success in the well-characterized cellular model E. coli, this same method is used to scan and discover similar binding sites in other less well characterized bacterial genomes by assuming the predictions will be comparable with those experimentally verified for E. coli. This approach has failed for transcription factors that bend DNA. An evolutionary scenario explains this failure. Historical mutation(s) resulting in AT-rich tracts flanking the dyad (Figure 2C) 16 bp = L core Crp recognition sequence has allowed the DNA to wrap further around the SyCrp1 protein, interact with a protein surface area formerly neglected by the dyad conformer (Figure 2B) and relinquish base contacts previously used to bind the (−)monad (absent in Figure 2A). The bent DNA evolved outside the old confines of L. Historical attempts to remain within the confines of L while ignoring the conformers suggested by L-flanking sequences have led to the low R2 correlation coefficients because flanking sequences modify the function within L. Our approach does not presuppose binding sites as objects confined to the limits of L, but instead follows evolutionary selection whereby insertions, deletions and transpositions that would select against a L limited binding site were tested as a hypothesis (53); if the resulting gene regulation conferred fitness less than that of neighboring cells, then the hypothesis was rejected via evolutionary selection. Most evolutionary tests were failures but the successes did contain pieces of previous binding sites that provide links to relate distinct SyCrp1 binding conformers. Outlined in the Supplementary Introduction is a bioinformatics method of hypothesis testing that starts with a few binding sequences and, similar to evolution, tests many hypotheses, most being dead ends. The results of the method are, of necessity, discontinuous; the dead ends can not be published. Eventually the method accumulated a wide sampling of genomic sequences that participate in SyCrp1 sequence-specific binding according to a PSSM model.
Evolution can explain how flanking flexible bends influence the primary kink base identity at position +5. Ψ-Plots test the explanation. First, PSSMs and HS algorithms require DNA Ws or bit value calculations to predict binding affinity. Ws is calculated according to a PSSM composed of all available binding sequences (11). This score is based on the distance in sequence space from a hypothetical attractor (50), a best guess at the ultimately strongest binding sequence. Different conformers have different attractors. For example, the dyad (triangles in Figure 4B) has one attractor, while the dyad (+10)bend (circles in Figure 4B) has another attractor. The PSSM major mode model is an average of both. The HS model overcomes this comparison problem by allowing all binding sequences to contribute to a new global PSSM (e.g. major mode PSSM #3) Ws calculation using a ψ-sequence data set, but with the conformer-specific energetically irrelevant positions changed to the most frequently occurring base by the ‘fill in the hole’ operation, a strict Boolean HS algorithm. An evolutionary scenario explains why this works. The major binding mode involves the dyad core region (Figure 2B) of 16 bp wherein position +5 is energetically relevant because kinking against a neighboring base decreases entropy. When the 16 bp Crp core recognition region obtained AT-rich flanking sequences in the past, the relevant +5 position was changed into a functionally irrelevant position within this new conformer because the kink was disrupted by supercoiling. This formed a smooth bend instead of a kink, increasing entropy at position +5. Then, the base identity distribution drifted, accumulating base substitutions in the absence of selective pressure. Such substitutions drastically lower the global PSSM scores for sequences in this conformer group. The HS algorithm simply changes these back to the most frequently occurring base identity in the major mode model, essentially reversing evolution, and returns a high R2 value. By allowing a universal (major mode) PSSM to be applied to all sequences, a thermodynamic landscape can be created that allows interconformer energetic comparisons within a ψ-sequence data set. Thus, Ψ-plots test conformer predictions with HS algorithms that reverse engineer evolution.
The presence or absence of the primary kink defines Crp HS algorithms. We would expect molecular motions to show wide positional occupancy of the base in position +5 most proximal to a flanking flexible bend because of the low bit value of the primary kink position +5. Dyad (+13)bend conformers (Figure 2C) show no evidence for a primary kink at position +5 because the bit value at this position is low. A kink position should be highly conserved having a high bit value because a kink is a low entropy configuration that should show adjacent position comparable (e.g. positions +4 and +6 adjacent to kink position +5) bit values following parallel to a sine curve (5,21). The SyCrp1/dyad (+13)bend conformer's primary kink position +5 forms a ‘hole’ (Figure 2C) that does not follow parallel to a sine curve thereby causing an asymmetrical, non-palindromic distribution. Peter von Hippel and Otto G. Berg also identified the non-palindromic distribution of Crp sites (15). The dyad conformer (Figure 2B) does contain primary kinks, and the HS algorithm is ‘no change’.
The EcCrp/XD-DNA thermodynamic landscape shown as a Ψ-plot demonstrates conformational selection entirely due to the primary DNA sequence differences between dyad and dyad (+10)bend conformers indicated with the colored arrows in Figure 4. These sequences are sufficiently distinct to allow a priori conformer identification with sequence logos (Figure 4D and E). Wψs and affinity are negatively correlated when dyad conformers are selected (triangles in Figure 4B), but positively correlated when dyad (+10)bend conformers are selected (circles in Figure 4B). Such a negatively correlated relationship (Wψs increases as affinity decreases) must be due to XD-substituted DNA because Wψs and affinity are positively correlated when EcCrp (14) or SyCrp1 (Figure 3) are bound to regular DNA in any conformation. EcCrp/XD-DNA affinity can be explained if the flanking flexible bend proximal to a primary kink functions antagonistically with that kink position in the dyad conformer. Most of these dyad conformer sequences contain flanking flexible bends to some extent. This increases Ws, but the positioning of these bends is not conserved, and does not increase logo bit values because these bends do not span all the (+10)WWWW positions. However, if the primary kink is instead a smooth bend, then that smooth bend and the proximal flanking flexible bend function cooperatively as for the dyad (+10)bend conformer. Thus, the negative thermodynamic relationship of these two conformers (Figure 4A and B) shows how sequence elements of these two conformers function together to control affinity. Moreover, the Ψ-plot and logos of EcCrp/XD-DNA shows how primary kinks with flanking flexible bends elicit a difference in function from that of smooth bends with flanking flexible bends. These functional differences result from conformational selection (e.g. minor binding modes) and are as distinct as the logos of each conformer.
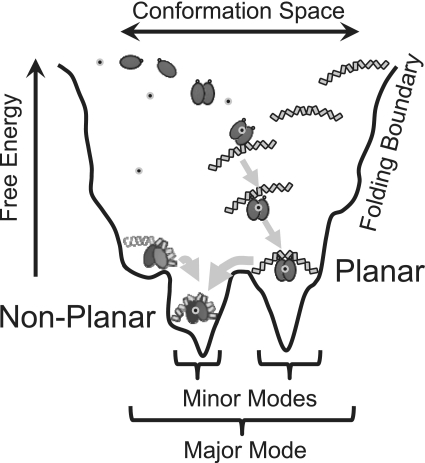
The (±13)bend is located out of phase (i.e. ±13 instead of ±10) with the primary kinks for SyCrp1/regular DNA complexes. These flanking flexible (±13)bend and primary kink DNA elements cannot bend toward each other in a planar configuration as suggested for a (+10)bend (34), but must direct the SyCrp1/DNA conformer to bend DNA in a non-planar and left-handed solenoid configuration. This bending occurs because the extra three positions (from ±10 to ±13) rotate the ‘hinge’ orientation 127° (i.e. orientation of the flanking flexible bend) relative to the canonical core region containing the primary kinks (3). Flanking flexible (±13)bend positioning thus determines the ‘hinge’ orientation of the flanking flexible bend and is clearly distinguished in sequence logos between SyCrp1/DNA mostly planar dyad (Figure 2B) and non-planar dyad (+13)bend (Figure 2C) conformers. Each conformer has a distinct attractor energetically comparable using the major mode HS model (Figure 3B). The logos of these conformers fit distinctly different sine curve periods as would be expected of distinct planar and non-planar DNA wrapping conformers because changing the DNA conformation changes the DNA path follows across the surface of a protein thereby changing major groove accessibility at the bound protein surface. Such structures may be relevant to transcription activation. They could be modulated by non-specific binding (54), photo-entrained diurnal superhelical density oscillations (55), local DNA gyrase influence (56) or chromosomal acclimation to diurnal feeding schedules by increasing superhelical density (57). Given how conformational selection occurs while bending between planar and non-planar DNA paths, an allosteric switch between these paths seems a plausible mechanism for transcription regulation. Moreover, the data presented here do not necessarily support an absolutely planar DNA bending conformer, but our results do differentiate between two different DNA wrapping conformers. DNA wrapping configurations are formed through a combination of conformational capture and induced fit (58) steps along a folding path. These configurations must be formed sequentially when linear dsDNA is bent because dyad (+)bend conformers are of higher affinity than dyad conformers. This finding indicates that monads must first bend DNA towards Crp before flanking flexible bends are close enough to the Crp surface for the relatively short-range electrostatic interactions at flanking flexible bends to be formed with Crp thereby increasing affinity. Thus, we propose a generalized conformational selection model for SyCrp1/DNA illustrated diagrammatically as a folding funnel (Figure 5).
Figure 5.
Schematic folding funnel for SyCrp1 conformational selection with linear B-form DNA substrates in vitro. Planar (class II) dyad and non-planar dyad (+13)bend or non-planar (+)monad (+13)bend conformers are represented as in Figure 2. The cAMP molecule is represented with small grey circled black dots. In this model, SyCrp1 cAMP-independent binding has not yet been rejected, but has been rejected for EcCrp due to cAMP-dependent induced fit changes to the C-helix secondary structure. Attaining a bound state is dynamic in this model. SyCrp1 must exhibit conformational entropy (61) leading to conformational-capture (33) because the DNA sequence determines the sequential minor mode folding paths (arrows) leading to the lowest energy conformer. In vivo DNA topology landscapes impose additional influences due to imposed supercoiling and flanking chromatin.
As with evolution, our method scans the genome in a self-referential and reiterative manner to hone in on the mutually conserved sequence elements that define conformers, even if only one conformer type is formed. This allows optimization of scanning PSSMs and HS algorithms against an experimental sampling. A first iteration is shown as a means of validating a SyCrp1 PSSM model (Figure 3B). Ψ-Plots empirically test and show how this first iteration fits the data well. Such fitting could be improved by reiterating major mode PSSM generation using Wψs and a cutoff value generated by the Ψ-plot in Figure 3B. Sequential reiteration in this way would test putative conformers with the ψ-sequence changes giving high R2 values by reiteratively approaching a Ψ-plot-testable Wψs cutoff value. Approaching in this way should approximate a cutoff value required for computational objectivity (57). As an alternative to Ws, individual information provides a natural thermodynamic cutoff in bits (9,59) consistent with sequence logo calculations. Though we did not calculate such cutoffs and opted instead for conservatively high Ws cutoff values, we were able to find unifying conformer relationships because the DNA sequence and topology directs protein binding preferences during evolution by reiteratively referencing the host genome with protein binding events. DNA wraps around a protein following certain available folding paths reflected in sequence logos. The multiple ways, in which Crp binds to and bends DNA are described as minor binding modes requiring a specific set of mutually conserved sequence elements to direct DNA wrapping. By defining the mutually conserved conformer DNA sequence elements with HS algorithms, Ψ-plots confirm that the thermodynamic parameters of minor binding modes are quantifiably related at the major mode level.
Here, we have identified functionally distinct Crp/DNA conformers and provided relevant Synechocystis PSSMs that can be pasted into publically available web servers (see the Supplementary Introduction). These conformers are relevant because flanking flexible bend element positioning (Figure 2B and C) ‘…presumably sets the rotational phasing of the DNA’ (60). The HS model developed here supports conformer distinctions while providing a fundamental basis for accurately unifying molecular information theory and thermodynamics as these apply to DNA bending proteins.
SUPPLEMENTARY DATA
Supplementary Data are available in NAR Online.
FUNDING
This research was funded by the United States National Science Foundation (MCB 0093327 to M.L.S.); United States National Institute of Health (5 SO6 GM048680 and 1 SC1 GM093998 to M.L.S.). Funding for open access charge: College of Science and Mathematics, Biology Department, CSU Northridge.
Conflict of interest statement. None declared.
Supplementary Material
ACKNOWLEDGEMENTS
We thank Timothy R. O'Connor, Virginia Oberholzer-Vandergon, Zhengchang Su and Stan Metzenberg for discussion, Araceli Vasquez for sbtA expression data, and the NAR reviewers for forbearance.
REFERENCES
- 1.Lange OF, Lakomek NA, Fares C, Schroder GF, Walter KF, Becker S, Meiler J, Grubmuller H, Griesinger C, de Groot BL. Recognition dynamics up to microseconds revealed from an RDC-derived ubiquitin ensemble in solution. Science. 2008;320:1471–1475. doi: 10.1126/science.1157092. [DOI] [PubMed] [Google Scholar]
- 2.Bae S, Kim D, Kim KK, Kim YG, Hohng S. Intrinsic Z-DNA Is Stabilized by the Conformational Selection Mechanism of Z-DNA-Binding Proteins. J. Am. Chem. Soc. 2010;133:668–671. doi: 10.1021/ja107498y. [DOI] [PubMed] [Google Scholar]
- 3.Ohyama T. Intrinsic DNA bends: an organizer of local chromatin structure for transcription. Bioessays. 2001;23:708–715. doi: 10.1002/bies.1100. [DOI] [PubMed] [Google Scholar]
- 4.Kapanidis AN, Ebright YW, Ludescher RD, Chan S, Ebright RH. Mean DNA bend angle and distribution of DNA bend angles in the CAP-DNA complex in solution. J. Mol. Biol. 2001;312:453–468. doi: 10.1006/jmbi.2001.4976. [DOI] [PubMed] [Google Scholar]
- 5.Schneider TD. Strong minor groove base conservation in sequence logos implies DNA distortion or base flipping during replication and transcription initiation. Nucleic Acids Res. 2001;29:4881–4891. doi: 10.1093/nar/29.23.4881. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Hertz GZ, Stormo GD. Identifying DNA and protein patterns with statistically significant alignments of multiple sequences. Bioinformatics. 1999;15:563–577. doi: 10.1093/bioinformatics/15.7.563. [DOI] [PubMed] [Google Scholar]
- 7.Schneider TD, Stephens RM. Sequence logos: a new way to display consensus sequences. Nucleic Acids Res. 1990;18:6097–6100. doi: 10.1093/nar/18.20.6097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Turatsinze JV, Thomas-Chollier M, Defrance M, van Helden J. Using RSAT to scan genome sequences for transcription factor binding sites and cis-regulatory modules. Nat. Protoc. 2008;3:1578–1588. doi: 10.1038/nprot.2008.97. [DOI] [PubMed] [Google Scholar]
- 9.Schneider TD. Measuring molecular information. J. Theor. Biol. 1999;201:87–92. doi: 10.1006/jtbi.1999.1012. [DOI] [PubMed] [Google Scholar]
- 10.Schneider TD. Information content of individual genetic sequences. J. Theor. Biol. 1997;189:427–441. doi: 10.1006/jtbi.1997.0540. [DOI] [PubMed] [Google Scholar]
- 11.Fields DS, He Y, Al Uzri AY, Stormo GD. Quantitative specificity of the Mnt repressor. J. Mol. Biol. 1997;271:178–194. doi: 10.1006/jmbi.1997.1171. [DOI] [PubMed] [Google Scholar]
- 12.Carlson CD, Warren CL, Hauschild KE, Ozers MS, Qadir N, Bhimsaria D, Lee Y, Cerrina F, Ansari AZ. Specificity landscapes of DNA binding molecules elucidate biological function. Proc. Natl Acad. Sci. USA. 2010;107:4544–4549. doi: 10.1073/pnas.0914023107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Drawid A, Gupta N, Nagaraj VH, Gelinas C, Sengupta AM. OHMM: a Hidden Markov Model accurately predicting the occupancy of a transcription factor with a self-overlapping binding motif. BMC Bioinformatics. 2009;10:1–26. doi: 10.1186/1471-2105-10-208. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Nagaraj VH, O'Flanagan RA, Sengupta AM. Better estimation of protein-DNA interaction parameters improve prediction of functional sites. BMC. Biotechnol. 2008;8:1–11. doi: 10.1186/1472-6750-8-94. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Berg OG, von Hippel PH. Selection of DNA binding sites by regulatory proteins. II. The binding specificity of cyclic AMP receptor protein to recognition sites. J. Mol. Biol. 1988;200:709–723. doi: 10.1016/0022-2836(88)90482-2. [DOI] [PubMed] [Google Scholar]
- 16.Kinney JB, Murugan A, Callan CG, Jr, Cox EC. Using deep sequencing to characterize the biophysical mechanism of a transcriptional regulatory sequence. Proc. Natl Acad. Sci. USA. 2010;107:9158–9163. doi: 10.1073/pnas.1004290107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Roulet E, Busso S, Camargo AA, Simpson AJ, Mermod N, Bucher P. High-throughput SELEX SAGE method for quantitative modeling of transcription-factor binding sites. Nat. Biotechnol. 2002;20:831–835. doi: 10.1038/nbt718. [DOI] [PubMed] [Google Scholar]
- 18.Napoli AA, Lawson CL, Ebright RH, Berman HM. Indirect readout of DNA sequence at the primary-kink site in the CAP-DNA complex: recognition of pyrimidine-purine and purine-purine steps. J. Mol. Biol. 2006;357:173–183. doi: 10.1016/j.jmb.2005.12.051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Lawson CL, Swigon D, Murakami KS, Darst SA, Berman HM, Ebright RH. Catabolite activator protein: DNA binding and transcription activation. Curr. Opin. Struct. Biol. 2004;14:10–20. doi: 10.1016/j.sbi.2004.01.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Omagari K, Yoshimura H, Suzuki T, Takano M, Ohmori M, Sarai A. DeltaG-based prediction and experimental confirmation of SYCRP1-binding sites on the Synechocystis genome. FEBS J. 2008;275:4786–4795. doi: 10.1111/j.1742-4658.2008.06618.x. [DOI] [PubMed] [Google Scholar]
- 21.Crooks GE, Hon G, Chandonia JM, Brenner SE. WebLogo: a sequence logo generator. Genome Res. 2004;14:1188–1190. doi: 10.1101/gr.849004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Zhang S, Xu M, Li S, Su Z. Genome-wide de novo prediction of cis-regulatory binding sites in prokaryotes. Nucleic Acids Res. 2009;37:e72. doi: 10.1093/nar/gkp248. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Bai G, McCue LA, McDonough KA. Characterization of Mycobacterium tuberculosis Rv3676 (CRPMt), a cyclic AMP receptor protein-like DNA binding protein. J. Bacteriol. 2005;187:7795–7804. doi: 10.1128/JB.187.22.7795-7804.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Travers AA. The structural basis of DNA flexibility. Philos. Transact. A Math. Phys. Eng. Sci. 2004;362:1423–1438. doi: 10.1098/rsta.2004.1390. [DOI] [PubMed] [Google Scholar]
- 25.Pyles EA, Chin AJ, Lee JC. Escherichia coli cAMP receptor protein-DNA complexes. 1. Energetic contributions of half-sites and flanking sequences in DNA recognition. Biochemistry. 1998;37:5194–5200. doi: 10.1021/bi972450i. [DOI] [PubMed] [Google Scholar]
- 26.Pyles EA, Lee JC. Escherichia coli cAMP receptor protein-DNA complexes. 2. Structural asymmetry of DNA bending. Biochemistry. 1998;37:5201–5210. doi: 10.1021/bi972451a. [DOI] [PubMed] [Google Scholar]
- 27.Haran TE, Mohanty U. The unique structure of A-tracts and intrinsic DNA bending. Q. Rev. Biophys. 2009;42:41–81. doi: 10.1017/S0033583509004752. [DOI] [PubMed] [Google Scholar]
- 28.Lin SH, Lee JC. Determinants of DNA bending in the DNA-cyclic AMP receptor protein complexes in Escherichia coli. Biochemistry. 2003;42:4809–4818. doi: 10.1021/bi027259+. [DOI] [PubMed] [Google Scholar]
- 29.Zhurkin VB, Lysov YP, Ivanov VI. Anisotropic flexibility of DNA and the nucleosomal structure. Nucleic Acids Res. 1979;6:1081–1096. doi: 10.1093/nar/6.3.1081. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Bellomy GR, Mossing MC, Record MT., Jr Physical properties of DNA in vivo as probed by the length dependence of the lac operator looping process. Biochemistry. 1988;27:3900–3906. doi: 10.1021/bi00411a002. [DOI] [PubMed] [Google Scholar]
- 31.Coulombe B, Burton ZF. DNA bending and wrapping around RNA polymerase: a ‘revolutionary’ model describing transcriptional mechanisms. Microbiol. Mol. Biol. Rev. 1999;63:457–478. doi: 10.1128/mmbr.63.2.457-478.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Alvarez M, Rhodes SJ, Bidwell JP. Context-dependent transcription: all politics is local. Gene. 2003;313:43–57. doi: 10.1016/s0378-1119(03)00627-9. [DOI] [PubMed] [Google Scholar]
- 33.Dixit SB, Andrews DQ, Beveridge DL. Induced fit and the entropy of structural adaptation in the complexation of CAP and lambda-repressor with cognate DNA sequences. Biophys. J. 2005;88:3147–3157. doi: 10.1529/biophysj.104.053843. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Lindemose S, Nielsen PE, Mollegaard NE. Dissecting direct and indirect readout of cAMP receptor protein DNA binding using an inosine and 2,6-diaminopurine in vitro selection system. Nucleic Acids Res. 2008;36:4797–4807. doi: 10.1093/nar/gkn452. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Hancock SP, Hiller DA, Perona JJ, Jen-Jacobson L. The Energetic Contribution of Induced Electrostatic Asymmetry to DNA Bending by a Site-Specific Protein. J. Mol. Biol. 2010;406:285–312. doi: 10.1016/j.jmb.2010.12.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.van Helden J. Regulatory sequence analysis tools. Nucleic Acids Res. 2003;31:3593–3596. doi: 10.1093/nar/gkg567. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Subramaniam S. The Biology Workbench–a seamless database and analysis environment for the biologist. Proteins. 1998;32:1–2. [PubMed] [Google Scholar]
- 38.Tippmann HF. Analysis for free: comparing programs for sequence analysis. Brief. Bioinform. 2004;5:82–87. doi: 10.1093/bib/5.1.82. [DOI] [PubMed] [Google Scholar]
- 39.Elhai J, Taton A, Massar JP, Myers JK, Travers M, Casey J, Slupesky M, Shrager J. BioBIKE: a Web-based, programmable, integrated biological knowledge base. Nucleic Acids Res. 2009;37:28–32. doi: 10.1093/nar/gkp354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Nakamura Y, Kaneko T, Hirosawa M, Miyajima N, Tabata S. CyanoBase, a www database containing the complete nucleotide sequence of the genome of Synechocystis sp. strain PCC6803. Nucleic Acids Res. 1998;26:63–67. doi: 10.1093/nar/26.1.63. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Rhodes D, Klug A. Sequence-dependent helical periodicity of DNA. Nature. 1981;292:378–380. doi: 10.1038/292378a0. [DOI] [PubMed] [Google Scholar]
- 42.Peck LJ, Wang JC. Sequence dependence of the helical repeat of DNA in solution. Nature. 1981;292:375–378. doi: 10.1038/292375a0. [DOI] [PubMed] [Google Scholar]
- 43.Yoshimura H, Hisabori T, Yanagisawa S, Ohmori M. Identification and characterization of a novel cAMP receptor protein in the cyanobacterium Synechocystis sp. PCC 6803. J. Biol. Chem. 2000;275:6241–6245. doi: 10.1074/jbc.275.9.6241. [DOI] [PubMed] [Google Scholar]
- 44.Hedger J, Holmquist PC, Leigh KA, Saraff K, Pomykal C, Summers ML. Illumination stimulates cAMP receptor protein-dependent transcriptional activation from regulatory regions containing class I and class II promoter elements in Synechocystis sp. PCC 6803. Microbiology. 2009;155:2994–3004. doi: 10.1099/mic.0.028035-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Argueta C, Yuksek K, Patel R, Summers ML. Identification of Nostoc punctiforme akinete-expressed genes using differential display. Mol. Microbiol. 2006;61:748–757. doi: 10.1111/j.1365-2958.2006.05263.x. [DOI] [PubMed] [Google Scholar]
- 46.Xu M, Su Z. Computational prediction of cAMP receptor protein (CRP) binding sites in cyanobacterial genomes. BMC Genomics. 2009;10:23–39. doi: 10.1186/1471-2164-10-23. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Ebright RH, Ebright YW, Gunasekera A. Consensus DNA site for the Escherichia coli catabolite gene activator protein (CAP): CAP exhibits a 450-fold higher affinity for the consensus DNA site than for the E. coli lac DNA site. Nucleic Acids Res. 1989;17:10295–10305. doi: 10.1093/nar/17.24.10295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Pierce JR. An introduction to information theory: symbols, signals and noise. New York: Dover Publications; 1980. [Google Scholar]
- 49.Shannon CE. A mathematical theory of communication. Bell System Tech. J. 1948;27:379–656. [Google Scholar]
- 50.Eigen M, Winkler-Oswatitsch R, Dress A. Statistical geometry in sequence space: a method of quantitative comparative sequence analysis. Proc. Natl Acad. Sci. USA. 1988;85:5913–5917. doi: 10.1073/pnas.85.16.5913. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Eddy SR. What is a hidden Markov model? Nat. Biotechnol. 2004;22:1315–1316. doi: 10.1038/nbt1004-1315. [DOI] [PubMed] [Google Scholar]
- 52.Ochoa de Alda JA, Houmard J. Genomic survey of cAMP and cGMP signalling components in the cyanobacterium Synechocystis PCC 6803. Microbiology. 2000;146:3183–3194. doi: 10.1099/00221287-146-12-3183. [DOI] [PubMed] [Google Scholar]
- 53.Kidd JM, Graves T, Newman TL, Fulton R, Hayden HS, Malig M, Kallicki J, Kaul R, Wilson RK, Eichler EE. A human genome structural variation sequencing resource reveals insights into mutational mechanisms. Cell. 2010;143:837–847. doi: 10.1016/j.cell.2010.10.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Lin S, Riggs AD. The general affinity of lac repressor for E. coli DNA: implications for gene regulation in procaryotes and eucaryotes. Cell. 1975;4:107–111. doi: 10.1016/0092-8674(75)90116-6. [DOI] [PubMed] [Google Scholar]
- 55.Vijayan V, Zuzow R, O'Shea EK. Oscillations in supercoiling drive circadian gene expression in cyanobacteria. Proc. Natl Acad. Sci. USA. 2009;106:22564–22568. doi: 10.1073/pnas.0912673106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Prakash JS, Sinetova M, Zorina A, Kupriyanova E, Suzuki I, Murata N, Los DA. DNA supercoiling regulates the stress-inducible expression of genes in the cyanobacterium Synechocystis. Mol. Biosyst. 2009;5:1904–1912. doi: 10.1039/B903022k. [DOI] [PubMed] [Google Scholar]
- 57.Philippe N, Crozat E, Lenski RE, Schneider D. Evolution of global regulatory networks during a long-term experiment with Escherichia coli. Bioessays. 2007;29:846–860. doi: 10.1002/bies.20629. [DOI] [PubMed] [Google Scholar]
- 58.Vertessy BG, Orosz F. From ‘fluctuation fit’ to ‘conformational selection’: evolution, rediscovery and integration of a concept. Bioessays. 2011;33:30–34. doi: 10.1002/bies.201000068. [DOI] [PubMed] [Google Scholar]
- 59.Gadiraju S, Vyhlidal CA, Leeder JS, Rogan PK. Genome-wide prediction, display and refinement of binding sites with information theory-based models. BMC Bioinformatics. 2003;38:1–13. doi: 10.1186/1471-2105-4-38. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Kahn JD, Crothers DM. Protein-induced bending and DNA cyclization. Proc. Natl Acad. Sci. USA. 1992;89:6343–6347. doi: 10.1073/pnas.89.14.6343. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Tzeng SR, Kalodimos CG. Dynamic activation of an allosteric regulatory protein. Nature. 2009;462:368–372. doi: 10.1038/nature08560. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.