An improved objective evaluation measure for border detection in dermoscopy images

Abstract

Background

Dermoscopy is one of the major imaging modalities used in the diagnosis of melanoma and other pigmented skin lesions. Owing to the difficulty and subjectivity of human interpretation, dermoscopy image analysis has become an important research area. One of the most important steps in dermoscopy image analysis is the automated detection of lesion borders. Although numerous methods have been developed for the detection of lesion borders, very few studies were comprehensive in the evaluation of their results.

Methods

In this paper, we evaluate five recent border detection methods on a set of 90 dermoscopy images using three sets of dermatologist-drawn borders as the ground truth. In contrast to previous work, we utilize an objective measure, the normalized probabilistic rand index, which takes into account the variations in the ground-truth images.

Conclusion

The results demonstrate that the differences between four of the evaluated border detection methods are in fact smaller than those predicted by the commonly used exclusive-OR measure.

Invasive and in situ malignant melanoma together comprise one of the most rapidly increasing cancers in the world. Invasive melanoma alone has an estimated incidence of 62,480 and an estimated total of 8420 deaths in the United States in 2008 (1). Early diagnosis is particularly important as melanoma can be cured with a simple excision if detected early.

Dermoscopy, also known as epiluminescence microscopy, is a non-invasive skin imaging technique that uses optical magnification and either liquid immersion and low angle-of-incidence lighting or cross-polarized lighting, making subsurface structures more easily visible when compared with conventional clinical images (2). Dermoscopy allows the identification of dozens of morphological features such as pigment network, dots/globules, streaks, blue-white areas, and blotches (3). This reduces screening errors, and provides greater differentiation between difficult lesions such as pigmented Spitz nevi and small, clinically equivocal lesions (4). However, it has been demonstrated that dermoscopy may actually lower the diagnostic accuracy in the hands of inexperienced dermatologists (5). Therefore, in order to minimize the diagnostic errors that result from the difficulty and subjectivity of visual interpretation, the development of computerized image analysis techniques is of paramount importance (6).

Automated border detection is often the first step in the automated or semi-automated analysis of dermoscopy images (7). It is crucial for the image analysis for two main reasons. First, the border structure provides important information for accurate diagnosis as many clinical features such as asymmetry, border irregularity, and abrupt border cutoff are calculated directly from the border. Second, the extraction of other important clinical features such as atypical pigment network (6), globules (8), and blue-white areas (9) critically depends on the accuracy of border detection. Automated border detection is a challenging task due to several reasons:

• low contrast between the lesion and the surrounding skin,

• irregular and fuzzy lesion borders,

• artifacts and intrinsic cutaneous features such as black frames, skin lines, blood vessels, hairs, and air bubbles,

• variegated coloring inside the lesion, and

• fragmentation due to various reasons such as scar-like depigmentation.

Numerous methods have been developed for border detection in dermoscopy images (10). Recent approaches include fuzzy c-means clustering (11–13), gradient vector flow snakes (14), thresholding followed by region growing (15, 16), meanshift clustering (17), color quantization followed by spatial segmentation (18), statistical region merging (SRM) (19), two-stage k-means clustering followed by region merging (20), and contrast enhancement followed by k-means clustering (21). Some of these studies used subjective visual examination to evaluate their results. Others used objective measures including Hance et al.’s (22) exclusive-OR (XOR) measure, sensitivity and specificity, precision and recall, error probability, and pixel misclassification probability (23). These measures require borders drawn by dermatologists, which serve as the ground truth. In this paper, we refer to the computer-detected borders as automatic borders and those determined by dermatologists as manual borders.

In a recent study, Guillod et al. (23) demonstrated that a single dermatologist, even one who is experienced in dermoscopy, cannot be used as an absolute reference for evaluating border detection accuracy. In addition, they emphasized that manual borders are not precise, with inter-dermatologist borders and even intra-dermatologist borders showing significant disagreement, so that a probabilistic model of the border is preferred to an absolute gold-standard model.

Only a few of the above-mentioned studies used borders determined by multiple dermatologists. Guillod et al. (23) used 15 sets of borders determined by five dermatologists over a minimum period of 1 month. They constructed a probability image for each lesion by associating a misclassification probability with each pixel based on the number of times it was selected as part of the lesion. The automatic borders were then compared against these probability images. Iyatomi et al. (15, 16) modified Guillod et al.’s method by combining the manual borders that correspond to each image into one using the majority vote rule. The automatic borders were then compared against these combined ground-truth images. Celebi et al. (19) compared each automatic border against multiple manual borders independently.

In this paper, we evaluate the performance of five recent automated border detection methods on a set of 90 dermoscopy images using three sets of manual borders as the ground truth. In contrast to prior studies, we use an objective criterion that takes into account the variations in the ground-truth images.

The rest of the paper is organized as follows. The second section reviews the objective measures used previously in the border detection literature. The third section describes a recent measure that takes into account the variations in the ground-truth images. The fourth section presents the experimental setup and discusses the results obtained, while the last section concludes the paper.

Material and Methods

Review of Objective Measures for Border Detection Evaluation

All of the objective measures mentioned in ‘Introduction’, except for Guillod and colleagues probabilistic measure, are based on the concepts of true/false positive/negative defined in Table 1. For example, if a lesion pixel is detected as part of the background skin, this pixel is considered to be a false negative (FN). On the other hand, if a background pixel is detected as part of the lesion, it is considered as a false positive (FP). Note that in the remainder of this paper, true positive (TP), FN, FP, and true negative (TN) will refer to the number of pixels that satisfy these criteria.

TABLE 1.

Definitions of true/false positive/negative

	Detected pixel
Actual pixel	Lesion	Background
Lesion	True positive (TP)	False negative (FN)
Background	False positive (FP)	True negative (TN)

‘Actual’ and ‘detected’ pixels refer to a pixel in the manual border and the corresponding pixel in the automatic border, respectively.

XOR measure

The XOR measure, first used by Hance et al. (22) quantifies the percentage border detection error as

$$\begin{array}{cc}\text{Error}\hfill & =\frac{\text{Area}(\text{AB}\oplus \text{MB})}{\text{Area}(\text{MB})}\times 100\%\hfill \\ \hfill & =\frac{\text{FP}+\text{FN}}{\text{TP}+\text{FN}}\times 100\%\hfill \end{array}$$ (1)

where AB and MB are the binary images obtained by filling the automatic and manual borders, respectively, ⊕ is the XOR operation that gives the pixels for which AB and MB disagree, and Area (I) denotes the number of pixels in the binary image I. The drawback of this composite measure is that it tends to favor larger lesions due to the size term in the denominator.

Sensitivity and specificity

Sensitivity (TP rate) and specificity (TN rate) are commonly used evaluation measures in medical studies. In our application domain, the former corresponds to the percentage of correctly detected lesion pixels, whereas the latter corresponds to the percentage of correctly detected background pixels. Mathematically, these measures are given by

$$\begin{array}{cc}\text{Sensitivity}\hfill & =\frac{\text{TP}}{\text{TP}+\text{FN}}\times 100\%\hfill \\ \text{Specificity}\hfill & =\frac{\text{TN}}{\text{FP}+\text{TN}}\times 100\%\hfill \end{array}$$ (2)

Note that an automatic border that encloses the corresponding manual border will have a perfect (100%) sensitivity. On the other hand, an automatic border that is completely enclosed by the corresponding manual border will have a perfect specificity. Therefore, it is crucial not to interpret these measures in isolation from each other.

Precision and recall

Precision (positive predictive value) and recall are commonly used evaluation measures in information retrieval studies. Precision refers to the percentage of correctly detected lesion pixels over all the pixels detected as part of the lesion and is defined as

$$\text{Precision}=\frac{\text{TP}}{\text{TP}+\text{FP}}\times 100\%$$ (3)

Recall is equivalent to sensitivity as defined in Eq. (2). Note that as in the case of sensitivity and specificity, precision, and recall measures should be interpreted together.

Error probability

Error probability refers to the percentage of pixels incorrectly detected as part of the lesion or background over all the pixels. It is calculated as

$$\text{Error probability}=\frac{\text{FP}+\text{FN}}{\text{TP}+\text{FN}+\text{FP}+\text{TN}}\times 100\%$$ (4)

The drawback of this composite measure is that it disregards the distributions of the classes. For example, consider a small lesion of size 20,000 pixels in a large image of size 768 × 512 pixels. An automatic border of size 40,000 pixels that encloses the manual border for this lesion will have an error probability of about 5% despite the fact that the automatic border is twice as large as the manual border.

Pixel misclassification probability

In Guillod et al. (23), the probability of misclassification for a pixel (i, j) is defined as

$$p(i,j)=1-\frac{n(i,j)}{N}$$ (5)

where N is the number of observations (manual+automatic borders), and n (i, j) is the number of times pixel (i, j) was selected as part of the lesion. For each automatic border, the detection error is given by the mean probability of misclassification over the pixels inside the border

$$\text{Error}=\frac{{\displaystyle {\sum }_{(i,j)\in \mathit{\text{AB}}}}p(i,j)}{\text{TP}+\text{FP}}\times 100\%$$ (6)

Error measures used in previous studies

Table 2 compares recent border detection methods based on their evaluation methodology: the number of human experts who determined the manual borders, the number of images used in the evaluations (and the diagnostic distribution of these images if available), and the measure used to quantify the border detection error. It can be seen that:

• Recent studies used objective measures to validate their results, whereas earlier studies relied on visual assessment.

• Only five out of 19 studies involve more than one expert in the evaluation of their results.

• XOR measure is the most commonly used objective error function despite the fact that it is not trivial to extend this measure to capture the variations in multiple manual borders.

TABLE 2.

Evaluation of border detection methods

References	Year	# Experts	# Images (distribution)	Error measure (value)
(13)	2009	1	100 (70 b/30 m)	Sensitivity (78%) and Specificity (99%)
(19)	2008	3	90 (65 b/25 m)	XOR (10.63%)
(20)	2008	1	67	XOR (14.63%)
(21)	2008	1	100 (70 b/30 m)	XOR (2.73%)
(24)	2007	1	50	Error probability (16%)
(24)	2007	1	50	Error probability (21%)
(18)	2007	2	100 (70 b/30 m)	XOR (12.02%)
(15)	2006	5	319 (244 b/75 m)	Precision (94.1%) and Recall (95.2%)
(17)	2006	NR	117	Sensitivity (95%) and Specificity (96%)
(14)	2005	2	100 (70 b/30 m)	XOR (15.59%)
(25)	2003	0	NR	NR
(12)	2002	0	600	Visual
(26)	2001	0	NR	NR
(27)	2000	5	30	Visual
(28)	2000	1	30	Visual
(11)	1999	1	400	Visual
(29)	1999	1	300	Visual
(30)	1998	1	57	XOR (36.50%)
(30)	1998	1	57	XOR (24.71%)

b, benign; m, melanoma; XOR, exclusive-OR.

Proposed Measure for Border Detection Evaluation

The objective measures reviewed in the previous section share a common deficiency. They do not take into account the variations in the manual borders. Given an automatic border, the XOR measure, sensitivity and specificity, precision and recall, and error probability can only be defined with respect to a single manual border. Therefore, it is not possible to use these measures with multiple manual borders. Although the methods described in (15, 16, 23), and (19) allow the use of multiple manual borders; these methods do not accurately capture the variations in the manual borders. For example, using Guillod and colleagues measure an automated border that is entirely enclosed by the manual borders would get a very low error. Iyatomi and colleagues method discounts the variation in the manual borders by simple majority voting, while Celebi and colleagues approach does not produce a scalar error value, which makes comparisons more difficult.

In this paper, we propose to use a recent, more elaborate probabilistic measure, namely the normalized probabilistic rand index (NPRI) (31) to evaluate border detection accuracy. We first describe the probabilistic rand index (PRI) (32). Consider a set of manual segmentations {S₁, …,S_K} of an image X = {x₁, …, x_N} consisting of N pixels. Let S_test be the segmentation that is to be compared with the manually labeled set. We denote the label of point x_i by $l_i^{S_{\text{test}}}$ in segmentation S_test and by $l_i^{S_k}$ in the manually segmented image S_k.

The motivation behind the PRI is that a segmentation is judged as ‘good’ if it correctly identifies the pairwise relationships between the pixels as defined in the ground-truth segmentations. In addition, a proper segmentation quality measure should penalize inconsistencies between the test and ground-truth label pair relationships proportionally to the level of consistency between the ground-truth label pair relationships. Based on this, the PRI is defined as

$$\mathit{\text{PRI}}(S_{\text{test},}\{S_k\})=\frac{{\displaystyle {\sum }_{\stackrel{i,j}{{\displaystyle i<j}}}}{c}_{\mathit{\text{ij}}}{p}_{\mathit{\text{ij}}}+(1-c_{\mathit{\text{ij}}})(1-p_{\mathit{\text{ij}}})}{\left(\begin{array}{c}\hfill N\hfill \\ \hfill 2\hfill \end{array}\right)}$$ (7)

where I(․) is a boolean function defined as

$$I(t)=\{\begin{array}{cc}1,\hfill & t=\text{true}\hfill \\ 0,\hfill & t=\text{false}\hfill \end{array}$$

c_ij ∈ {0, 1} denotes the event of a pair of pixels x_i and x_j having the same label in the test image S_test

$$c_{\mathit{\text{ij}}}=I(l_i^{S_{\text{test}}}=l_j^{S_{\text{test}}})$$ (8)

Note that the denominator in Eq. (7) denotes the number of possible distinct pixel pairs. Given the K manually labeled images, we can compute the empirical probability of the label relationship of a pixel pair x_i and x_j by

$$p_{\mathit{\text{ij}}}=\frac{1}{K}{\displaystyle \sum _{k=1}^K}I(l_i^{S_k}=l_j^{S_k})$$ (9)

The PRI is always within the interval [0, 1], and an index of 0 or 1 can only be achieved when all of the ground-truth segmentations agree or disagree on every pixel pair relationship. A score of 0 indicates that every pixel pair in the test image has the opposite relationship as every pair in the ground-truth segmentations, while a score of 1 indicates that every pixel pair in the test image has the same relationship as every pair in the ground-truth segmentations.

The PRI has one disadvantage. Although the index values are in [0, 1], there is no expected value for a given segmentation. That is, it is impossible to know if any given score is good or bad. In addition, the score of a segmentation of one image cannot be compared with the score of a segmentation of another image. The NPRI addresses this drawback by normalizing the PRI as follows:

$$\text{Normalized index}=\frac{\text{Index}-\text{Exp}.\text{ index}}{\text{Max}.\text{ index}-\text{Exp}.\text{ index}}$$ (10)

The maximum index is taken as 1 while the expected value of the index is calculated as follows:

$$E[\text{PRI}(S_{\text{test},}\{S_k\})]=\frac{{\displaystyle {\sum }_{\stackrel{i,j}{{\displaystyle i<j}}}}p{\prime }_{\mathit{\text{ij}}}{p}_{\mathit{\text{ij}}}+(1-p{\prime }_{\mathit{\text{ij}}})(1-p_{\mathit{\text{ij}}})}{\left(\begin{array}{c}\hfill N\hfill \\ \hfill 2\hfill \end{array}\right)}$$ (11)

Let Φ be the number of images in the entire data set, and K_ϕ be the number of ground-truth segmentations of image ϕ. Then p′_ij can be expressed as

$$p{\prime }_{\mathit{\text{ij}}}=E[c_{\mathit{\text{ij}}}]=\frac{1}{\mathrm{\Phi }}{\displaystyle \sum _{\varphi }}\frac{1}{K_{\varphi }}{\displaystyle \sum _{k=1}^{K_{\varphi }}}\mathrm{I}\left(l_i^{S_k^{\varphi }}=l_j^{S_k^{\varphi }}\right)$$ (12)

Because in the computation of the expected values no assumptions are made with regards to the number or size of regions in the segmentation, and all of the ground-truth data is used, the NPR indices are comparable across images and segmentations.

Results and Discussion

The proposed evaluation method was tested on a set of 90 dermoscopy images (23 invasive malignant melanoma and 67 benign) obtained from the EDRA Interactive Atlas of Dermoscopy (2), and three private dermatology practices (19). The benign lesions included nevocellular nevi and dysplastic nevi.

Manual borders were obtained by selecting a number of points on the lesion border, connecting these points by a second-order B-spline and finally filling the resulting closed curve. Three sets of manual borders were determined by dermatologists Dr William Stoecker, Dr Joseph Malters, and Dr James Grichnik using this method.

Five recent automated border detection methods were included in the experiments. These were orientation-sensitive fuzzy c-means method (11), dermatologist-like tumor extraction algorithm (DTEA) (15, 16), meanshift clustering method (17), modified JSEG method (JSEG) (18), and the SRM (19). Table 3 gives the mean and standard deviation errors as evaluated by the commonly used XOR measure [Eq. (1)]. The best results, i.e. the lowest mean errors, in each row are shown in bold.

TABLE 3.

XOR measure statistics: mean (standard deviation)

Dermato- logist	Diagnosis	OSFCM	DTEA	MS	JSEG	SRM
W. S.	Benign	22.995 (12.614)	10.513 (4.728)	11.527 (9.737)	10.832 (6.359)	11.384 (6.232)
	Melanoma	28.311 (15.245)	11.853 (5.998)	13.292 (7.418)	13.745 (7.590)	10.294 (5.838)
	All	24.354 (13.449)	10.855 (5.081)	11.978 (9.193)	11.577 (6.772)	11.106 (6.120)
J. M.	Benign	25.535 (11.734)	10.367 (3.771)	10.802 (6.332)	10.816 (5.227)	10.186 (5.683)
	Melanoma	26.743 (14.508)	10.874 (5.016)	12.592 (7.202)	12.981 (6.316)	10.500 (8.137)
	All	25.843 (12.426)	10.496 (4.101)	11.259 (6.571)	11.370 (5.570)	10.266 (6.351)
J. G.	Benign	27.506 (12.789)	12.091 (5.220)	12.224 (7.393)	12.257 (6.588)	10.561 (5.152)
	Melanoma	27.574 (15.836)	12.675 (6.865)	12.168 (7.479)	13.414 (7.379)	10.411 (5.860)
	All	27.523 (13.538)	12.240 (5.650)	12.210 (7.373)	12.553 (6.775)	10.523 (5.308)

XOR, exclusive-OR; OSFCM, orientation-sensitive fuzzy c-means method; DTEA, dermatologist-like tumor extraction algorithm; MS, meanshift clustering method; JSEG, modified JSEG method; SRM, statistical region merging method.

It can be seen that the results vary significantly across the border sets, highlighting the subjectivity of human experts in the border determination procedure. Overall, the SRM method achieves the lowest mean errors followed by the DTEA and JSEG methods. It should be noted that, with the exception of SRM, the error rates increase in the melanoma group which is possibly due to the presence of higher border irregularity and color variation in these lesions. With respect to consistency, the best methods are DTEA followed by the SRM and JSEG methods.

Table 4 shows the border detection quality statistics as evaluated by the proposed NPRI measure. Note that, in this table, higher mean values indicate lower border detection errors, whereas higher standard deviation values indicate lower consistency, respectively.

TABLE 4.

NPRI measure statistics: mean (standard deviation)

Diagnosis	OSFCM	DTEA	MS	JSEG	SRM
Benign	0.520 (0.247)	0.785 (0.079)	0.774 (0.137)	0.775 (0.114)	0.785 (0.109)
Melanoma	0.520 (0.258)	0.783 (0.108)	0.762 (0.161)	0.748 (0.141)	0.811 (0.092)
All	0.520 (0.248)	0.784 (0.087)	0.771 (0.142)	0.768 (0.122)	0.791 (0.105)

OSFCM, orientation-sensitive fuzzy c-means method; DTEA, dermatologist-like tumor extraction algorithm; MS, meanshift clustering method; JSEG, modified JSEG method; SRM, statistical region merging method; NPRI, normalized probabilistic rand index.

It can be seen that the ranking remains the same: SRM and DTEA are still the most accurate and consistent methods. However, using the NPRI measure, the differences between the methods have become smaller. In addition, this measure considers the variations in the manual borders simultaneously and produces a scalar value, which makes comparisons among methods much easier.

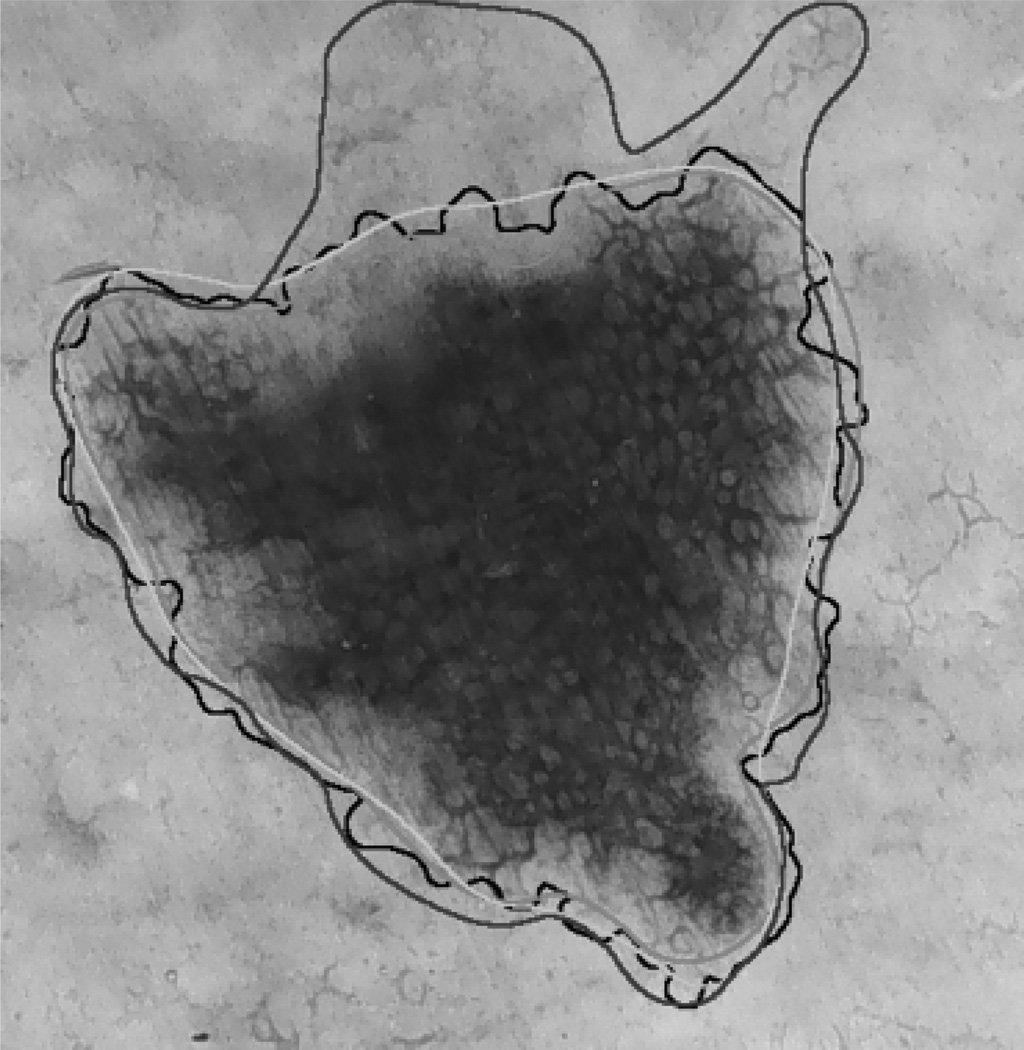
Figure 1 illustrates one advantage of using the NPRI measure. Here the manual borders are shown in red, green, and blue, whereas the border determined by the DTEA method is shown in black. The border detection errors with respect to the red, green, and blue borders calculated using the XOR measure are 10.872%, 9.342%, and 20.958%, respectively. It can be concluded that, with respect to the first two dermatologists, the DTEA method has an average accuracy (see Table 3). On the other hand, with respect to the third dermatologist, the automatic method is quite inaccurate. The NPRI value in this case is 0.814, which is above the average over the entire data set (see Table 4). This was expected, because this measure does not penalize the automatic border in those regions where dermatologist agreement is low.

Fig. 1.

Sample border detection result.

Conclusion

In this paper, we evaluated five recent automated border detection methods on a set of 90 dermoscopy images using three sets of manual borders as ground truth. We proposed the use of an objective measure, the NPRI, which takes into account variations in the ground truth. The results demonstrated that the differences between four of the evaluated border detection methods were in fact smaller than those predicted by the commonly used XOR measure. Future work will be directed towards the expansion of the image set and the inclusion of more dermatologists in the evaluations.