Generating Text from Functional Brain Images

Abstract

Recent work has shown that it is possible to take brain images acquired during viewing of a scene and reconstruct an approximation of the scene from those images. Here we show that it is also possible to generate text about the mental content reflected in brain images. We began with images collected as participants read names of concrete items (e.g., “Apartment’’) while also seeing line drawings of the item named. We built a model of the mental semantic representation of concrete concepts from text data and learned to map aspects of such representation to patterns of activation in the corresponding brain image. In order to validate this mapping, without accessing information about the items viewed for left-out individual brain images, we were able to generate from each one a collection of semantically pertinent words (e.g., “door,” “window” for “Apartment’’). Furthermore, we show that the ability to generate such words allows us to perform a classification task and thus validate our method quantitatively.

1. Introduction

Over the last decade, functional magnetic resonance imaging (fMRI) has become a primary tool for identifying the neural correlates of mental activity. Traditionally, the aim of fMRI experiments has been to identify discrete, coherent neuroanatomic regions engaged during specific forms of information processing. More recently, it has become clear that important information can be extracted from fMRI by attending instead to broadly distributed patterns of activation. The application of machine learning techniques for pattern classification (Pereira et al., 2009) has enabled impressive feats of “brain reading,” making it possible to infer the semantic category of an object viewed by an experimental participant, to track the process of memory retrieval, to predict decisions or mistakes, or even (controversially) to detect lies (Mitchell et al., 2004; Davatzikos et al., 2005; Haynes and Rees, 2006; Norman et al., 2006).

In all of these cases, the key step involves assigning each brain image to one in a small set of discrete categories, each occurring within both a training set and a test set of images. More recently (Mitchell et al., 2008) and (Kay et al., 2008) have extended this approach applying sophisticated forward models to predict brain activation patterns induced by stimuli from outside the initial training set, thus enabling a more-open ended form of classification.

Even more strikingly, a few recent studies have demonstrated the feasibility of a generative approach to fMRI decoding, where an artifact is produced from a brain image. Concrete examples include reconstructing a simple visual stimulus (Miyawaki et al., 2008), a pattern of dots mentally visualized by the subject (Thirion et al., 2006) and generating a structural and semantic description of a stimulus scene, which could then be used to find a similar scene in a very large image database (Naselaris et al., 2009).

The success of this work leads to the question of what may be produced from a brain image if the mental content is not amenable to pictorial rendering. This paper attempts to answer this question by introducing an approach for generating a verbal description of mental content. We began with brain images collected while subjects read the names of concrete items (e.g., house) while also seeing line drawings of the item named; subjects were instructed to think about the item being shown, its properties, purpose, etc. From these brain images we generated words pertaining to the relevant concept (e.g., “door,”“window,”“home”). This is a simplified form of the description task that ignores syntax and word order, but a very common approach in machine learning done on text data (Mitchell, 1997; Blei et al., 2003). We show that the quality of the words generated can be evaluated quantitatively, by using them to match the brain images with corresponding articles from the online encyclopedia Wikipedia.

2. Materials And Methods

2.1. Data

We re-used the fMRI data¹ from Mitchell et al. (2008) and hence we will only provide a summary description of the dataset here. The stimuli were line drawings and noun labels of 60 concrete objects from 12 semantic categories with five exemplars per category, adapted from an existing collection (Snodgrass and Vanderwart, 1980); see Figure 1 for a depiction of the “Table” stimulus. The entire set of 60 stimulus items was presented six times, randomly permuting the sequence of the 60 item on each presentation. Each item was presented for 3 s, followed by a 7 s rest period, during which the participants were instructed to fixate. When an item was presented, the participant's task was to think about the properties of the object. To promote their consideration of a consistent set of properties across the six presentations, they were asked to generate a set of properties for each item prior to the scanning session (for example, for the item castle, the properties might be cold, knights, and stone). Each participant was free to choose any properties they wished, and there was no attempt to obtain consistency across participants in the choice of properties.

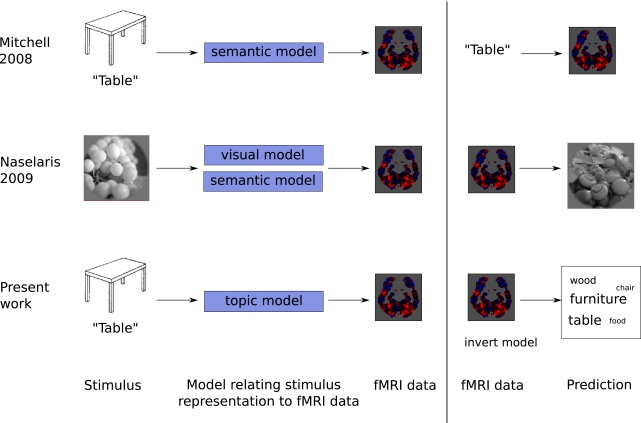
Figure 1.

The approach we follow to generate text (bottom) parallels that used in Naselaris et al. (2009) (middle, adapted from that paper), by having three stages: creating a model of how stimuli will be represented in the brain, learning how to predict fMRI data in response to the stimuli, given the model, and inverting the process to make a prediction for fMRI data not used to fit the model.

Nine subjects participated in the fMRI study. Functional images were acquired on a Siemens Allegra 3.0T scanner at the Brain Imaging Research Center of Carnegie Mellon University and the University of Pittsburgh using a gradient echo EPI pulse sequence with TR = 1000 ms, TE = 30 ms, and a 60° flip angle. Seventeen 5-mm thick oblique-axial slices were imaged with a gap of 1 mm between slices. The acquisition matrix was 64 × 64 with 3.125-mm × 3.125-mm × 5-mm voxels. Initial data processing was performed using Statistical Parametric Mapping software (SPM2, Wellcome Department of Cognitive Neurology, London, UK). The data were corrected for slice timing, motion, and linear trend, and were temporally filtered using a 190 s cutoff. The data were spatially normalized into MNI space and resampled to 3 mm × 3 mm × 6 mm voxels. The percent signal change (PSC) relative to the fixation condition was computed at each voxel for each stimulus presentation. A single fMRI mean image was created for each of the 360 item presentations by taking the mean of the images collected 4, 5, 6, and 7 s after stimulus onset (to account for the delay in the hemodynamic response). Each of these images was normalized by subtracting its mean and dividing by its SD, both across all voxels.

2.2. Approach

At the procedural level, our approach followed a set of steps analogous to those employed in Naselaris et al. (2009) to reconstruct visual stimuli from fMRI data, but tailored to the task of mapping from fMRI to text:

1. We began with a corpus of text – Wikipedia articles – and used it to create a topic model (Blei et al., 2003), a latent factor representation of each article; this is, in essence, a representation of the concept the article is about. The task used to obtain our fMRI data entails thinking about the concept prompted by a stimulus, and hence we use the representation learned from text as an approximation of the mental representation of the concept. This is analogous to the way (Naselaris et al., 2009) takes a corpus of naturalistic images and represents them in terms of a combination of latent factors representing visual aspects and semantic content.

2. Learn a mapping from each latent factor in the model from Step 1 to a corresponding brain image that captures how the factor gives rise to sub-patterns of distributed brain activity, using a training set of brain images.

3. Finally, for each brain image in a new, test set, the mapping from Step 2 can be used to infer a weighting over latent factors. Given this, the generative model from Step 1 can be inverted in order to map from the latent factor representation to text, in the shape of a probability distribution over words. In Naselaris et al. (2009), the model is inverted and used to assign probability to images.

The first step is present also in Mitchell et al. (2008), which relies on a postulated semantic representation of the stimulus. In contrast with them, the semantic model we use to represent the mental content while thinking of a concept is learned from the text corpus through unsupervised learning.

2.2.1. Semantic model: topics as latent factors

The approach we used for producing latent factors is called latent Dirichlet allocation (LDA), and it can be applied to a text corpus to produce a generative probabilistic model; this is known, colloquially, as a topic model, as it represents each document by the probabilities of various topics being present and each topic by a probability distribution over words.

Our use of topic models had a dual motivation. First, as generative statistical models, topic models support Bayesian inversion, a critical operation in the approach described above. Second, it has been suggested that the latent representations discovered by topic models may bear important similarities with human semantic representations (Griffiths et al., 2007). This encourages the idea that the latent factors discovered by learning the topic models in our study would bear a meaningful relationship to patterns of neural activation carrying conceptual information.

There are multiple approaches for learning features from text data, with latent semantic analysis (LSA, Landauer and Dumais, 1997) being perhaps the best known, and a tradition of using them to perform psychological tasks or tests with word stimuli (see Steyvers et al., 2005; Griffiths et al., 2007; or Murphy et al., 2009) for applications to EEG, for instance, Liu et al. (2009) for semantic features learned from a matrix of co-occurrences between the 5000 most common words in English, to perform the same prediction task as Mitchell et al. (2008). The differences between LDA and LSA are discussed in great detail in Griffiths et al. (2007), so we will only provide a brief outline here. Both methods operate on word-document/paragraph co-occurrence matrices. They both place documents in a low-dimensional space, by taking advantage of sets of words appearing together in multiple documents. Each dimension corresponds thus to some pattern of co-occurrence, a singular vector of the co-occurrence matrix in LSA and a topic word probability distribution in LDA. The major difference is that LSA is not a generative model and, furthermore, the way that singular vectors are created forces them to be orthogonal, a constraint that does not reflect any aspect of the text domain but just mathematical convenience. LDA, in contrast, allows one to interpret the topic probabilities as the probability that a word came from the distribution for a particular topic. LSA places documents in an Euclidean space, whereas LDA is placing them in a simplex, making the presence of some topics detract from the presence of others (something useful for us, as we will show later).

We learned our topic model on a corpus derived from a set of 3500 Wikipedia pages about concepts deemed concrete or imageable. These were selected using classical lists of words (Paivio et al., 1968; Battig and Montague, 1969), as well as modern revisions/extensions thereof (Clark and Paivio, 2004; Van Overschelde, 2004), and considering scores of concreteness or imageability, as well as subjective editorial ranking if scores were not available. We then identified the corresponding Wikipedia article titles (e.g., “airplane” is “Fixed-wing aircraft”) and also compiled related articles which were linked to from these (e.g., “Aircraft cabin”). If there were words in the original lists with multiple meanings we included the articles for at least a few of those meanings. We used Wikipedia Extractor² to remove HTML, wiki formatting and annotations and processed the resulting text through the morphological analysis tool Morpha³ (Minnen et al., 2001) to lemmatize all the words to their basic stems (e.g., “taste,” “tasted,” “taster,” and “tastes” all become the same word).

The resulting text corpus was processed with topic modeling (Blei et al., 2003) software⁴ to produce several models, excluding words that appeared in a single article or were in a stopword list. We ran the software varying the number of topics allowed from 10 to 100, in increments of 10, setting the α parameter to 25/#topics (as suggested in other work modeling a large text corpus for semantic purposes; Griffiths et al., 2007, though a range of multiples of the inverse of the number of topics yielded comparable experiment results).

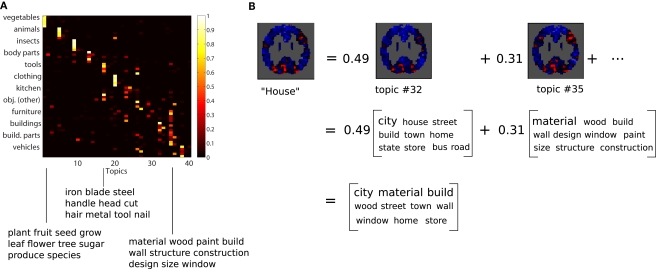
The model produced contains a representation of each of the 3500 articles in terms of the probabilities of each topic being present in it; these are our latent factor loadings. To each topic corresponds a probability distribution over individual words; the top 10 most probable words for each topic are shown in Table 1. Within those 3500 are 60 articles about the 60 concepts in Mitchell et al. (2008), and the factor loadings for these are presented in Figure 2A. Each column in the figure corresponds to a topic, each row to an article (a small subset of the articles used), with articles grouped into general categories, as labeled on the left. Below, the figure shows the 10 most highly weighted words for three topics. The pattern of topic weightings makes clear that the model has captured the category structure implicit in the corpus; through unsupervised learning, several topics have aligned with specific semantic categories (e.g., topic 1 with the vegetable category). The representation is sparse but most concepts have multiple topics in their representation.

Table 1.

The top 10 most probable words according to each topic in the 40 topic model used in Figure 2A (topic ordering is slightly different).

Topic	Top 10 words
1	Plant fruit seed grow leaf flower tree sugar produce species
2	Color green light red white blue skin pigment black eye
3	Light drink lamp wine beer bottle water produce valve pipe
4	Drug chemical acid opium cocaine alcohol substance produce form reaction
5	School university student child education college degree state train Unite
6	Animal species cat wolf breed hunt dog male wild human
7	Water metal form temperature carbon process air element iron salt
8	Vehicle wheel gear car aircraft passenger speed drive truck design
9	Market party state country price government political trade people economic
10	Water ice rock river surface form sea ocean wind soil
11	Species bird egg fish insect female ant live feed bee
12	Language book write art century form story character word publish
13	War military force army weapon service submarine soviet world train
14	Blood cause disease patient treatment infection health risk increase pain
15	Church bishop pope catholic priest roman soap cardinal religious time
16	Cell muscle body brain form tissue human organism bone animal
17	Ship fish boat water vessel sail design build ski bridge
18	Iron blade steel handle head cut hair metal tool nail
19	Film image camera digital shotgun movie lens magazine rifle gun
20	Wear horse woman clothe saddle century dress fashion ride trail
21	Law state court legal police crime person act Unite criminal
22	Smoke chocolate light tobacco sign speed cigaret cigar state traffic
23	key lock switch machine needle tube bicycle type knit design
24	Card record information service company product datum process program credit
25	State cross head salute plate model symbol portrait scale circus
26	Love sexual god woman people pyramid death sex religion evil
27	Coin gold silver issue currency stamp state dollar value bank
28	Game play player ball team sport rule football hit league
29	Fuel engine gas energy power oil hydrogen heat rocket produce
30	Woman marriage god word christian child term jesus family gender
31	Fiber sheep wool cotton fabric weave hamlet pig produce silk
32	City build house store street town state home road bus
33	Tea tooth pearl kite shoe culture wear tattoo jewelry form
34	Earth sun star planet moon solar time orbit day comet
35	Material wood paint build wall structure construction design size window
36	Human social study people culture theory individual nature behavior term
37	Power station train signal line locomotive radio steam electric frequency
38	Food diamond cook meat bread coffee sauce chicken kitchen eat
39	Measure scale angle [formula theory object unit energy line property
40	Music instrument play string band bass sound note player guitar

Figure 2.

(A) Topic probabilities for the Wikipedia articles about the 60 concepts for which we have fMRI data. Each concept belongs to one of 12 semantic categories, and concepts are grouped by category (five animals, five insects, etc.). Note that the category structure visible is due to how we sorted the columns for display; the model is trained in an unsupervised manner and knows nothing about category structure. Note also that there are topics that are not probable for any of the concepts, which happens because they are used for other concepts in the 3500 concept corpus. Below this are the top 10 most probable words in the probability distributions associated with three of the topics. (B) The decomposition of the brain image for “House” into a weighted combination of topic basis images. The weights allow us to combine the corresponding topic word distributions into an overall word distribution (top 10 words shown).

Topic probabilities for all 3500 concepts and topic word distributions can be examined in detail through am interactive model browser available online⁵.

2.2.2. Learning a mapping between topics and their patterns of brain activation

Armed with the topic model, we used ridge regression to establish a mapping between each topic and a corresponding pattern of brain activation. We averaged the trial brain images described earlier for all presentations of each of the 60 concepts in our dataset, yielding 60 examples images. We use these (selecting a subset of the voxels and reserving two images at a time for the test set, as further explained below) as prediction targets and the set of topic probabilities describing the corresponding Wikipedia articles (shown in Figure 2A) as regression inputs. This decomposes into a set of independent regression problems, one per voxel, where the regression weights are the value of the pattern of activation for each topic at that voxel. The regression weights effectively represent each topic in terms of a basis image, or representative pattern of brain activation. This makes it possible to decompose the fMRI image for any stimulus object into a set of topic-specific basis images, with combination weights quantifying the contribution of the relevant topic, as illustrated in Figure 2B. The regression problems are described more rigorously in Section A.3 of the Appendix.

2.2.3. Predicting topic probabilities from example images

We start by taking known topic probabilities and brain images for concepts and learning a basis image for each topic. Each topic defines a probability distribution over words, the most probable of which are shown under the topic basis images in Figure 2B. Combined, they define an overall probability distribution over words for a concept (for more details see Section A.2 of the Appendix. The process can be reversed and topic probabilities estimated from new, previously unseen concept brain images, using the basis images. Those topic probabilities can be used to combine the topic word probability distributions into a word probability distribution about the new image, which is what we use to generate text.

The process of estimating the topic probabilities is a regression problem, with the vector of values across all voxels in the new image being predicted as a linear combination of the topic basis images; it also requires the constraint that regression weights be between 0 and 1, as they have to be valid probabilities. This is described more rigorously in Section A.3 of the Appendix.

3. Results

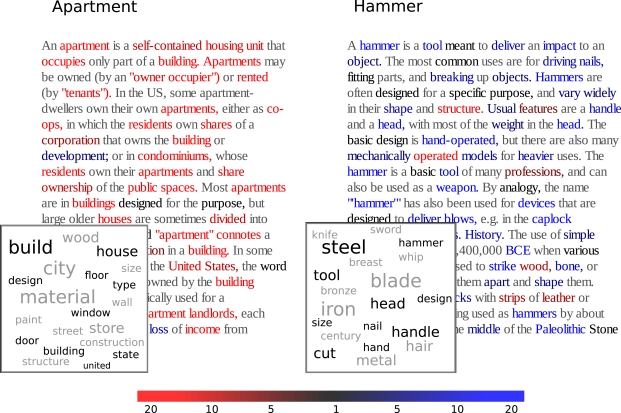
Using the approach described in the previous section, we can generate word probability distributions – or text output according to them – from the brain images of each of the 60 concepts. We do so in a cross-validated fashion, learning the basis images from all concepts in training set and generating the distributions for those in the test set, as described in more detail below. An illustrative example is presented as part of Figure 3. The data shown are based on brain images collected during presentation of the stimuli apartment and hammer for one of the participants. The tag clouds shown in the figure indicate the words most heavily weighted in their respective output distribution. As in this case, text outputs for many stimuli appeared strikingly well aligned with the presumptive semantic associations of the stimulus item. Full results for all 60 concepts are available for inspection online (see text footnote 5).

Figure 3.

The inset under each article shows the top words from the corresponding brain-derived distribution [10 which are present in the article (black) and 10 which are not (gray)]. Each word of the two articles is colored to reflect the ratio p_apartment (word)/p_hammer(word) between the probabilities assigned to it by the brain-derived distributions for concepts “apartment” and “hammer” (red means higher probability under “apartment,” blue under “hammer,” gray means the word is not considered by the text model).

To more objectively evaluate the quality of the text generated for each stimulus, we used a classification task where the word distributions derived from the brain images for each pair of concepts (test set) were used to match them with the two corresponding Wikipedia pages. The classification was done by considering the total probability of all the words in each Wikipedia article under each probability distribution, and selecting the article deemed most probable.

The idea is illustrated in Figure 3, for the stimuli apartment and hammer. The text for each of the corresponding Wikipedia articles is presented in colors that indicate the likelihood ratio for each word, given the fMRI-derived text for each stimulus. In this case, each output text matched most closely with the appropriate Wikipedia article. This, indeed, was the case for the majority of stimulus pairs. Plots comparable to Figure 3 for all concept pairs are available online (see text footnote 5).

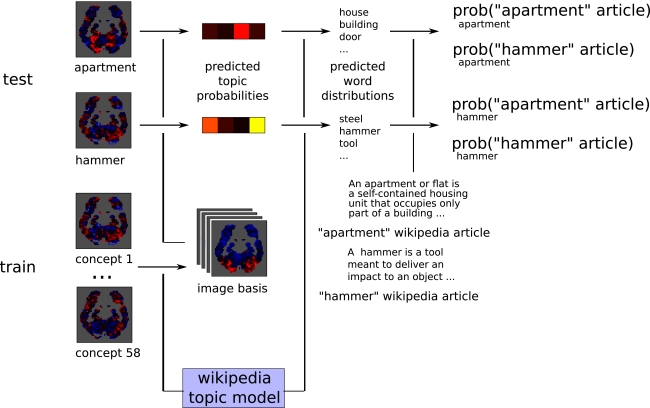
The classification process is illustrated in Figure 4 and consists of the following steps:

Figure 4.

Classification procedure for the “apartment” and “hammer” example images.

1. leave out one pair of concepts (e.g., “apartment” and “hammer”) as test set.

2. use the example images for the remaining 58 concepts, together with their respective topic probabilities under the model, as the training set to obtain a set of basis images (over 1000 stable voxels, selected in this training set).

3. for each of the test concepts (for instance, “apartment”):

   • predict the probability of each topic being present from the “apartment” example image.

   • obtain an “apartment”-brain probability distribution for that combination of topic probabilities.

   • compute the probability of “apartment” article and “hammer” article under that distribution, respectively p_apartment (“apartment”) and p_apartment (“hammer”).

4. assign the article with highest probability to the corresponding test concept, and the other article to the other concept (this will be correct or incorrect).

The steps are repeated for every possible pair of concepts, and the accuracy is the fraction of the pairs where the assignment of articles to example images was correct. For voxel selection we used the same reproducibility criterion used in Mitchell et al. (2008), which identifies voxels whose activation levels across the training set examples of each concept bear the same relationship to each other over epochs (mathematically, the vector of activation levels across the sorted concepts is highly correlated between epochs). These voxels came from all across temporal and occipital cortex, as shown in Table 2 in the Appendix, indicating that the learned basis image associated with a topic is related to both semantic and visual aspects of it.

Table 2.

Average number of voxels selected from each cortical AAL ROI over all leave-two-out folds.

AAL ROI	P1	P2	P3	P4	P5	P6	P7	P8	P9
Angular_L	3	3	7	2	2	7	8	6	1
Angular_R	2	5	7	2	3	4	3	11	15
Calcarine_L	47	56	41	34	63	29	42	53	19
Calcarine_R	38	47	65	50	33	27	25	32	27
Caudate_L	0	0	0	0	1	7	7	1	4
Caudate_R	0	0	0	0	0	7	5	0	4
Cingulum_ant_L	0	4	0	0	7	4	1	4	2
Cingulum_ant_R	0	0	0	2	1	2	0	0	1
Cingulum_mid_L	4	2	2	3	6	2	2	3	6
Cingulum_mid_R	0	3	1	0	4	4	4	1	5
Cuneus_L	0	6	9	26	9	6	7	7	11
Cuneus_R	17	20	23	18	9	22	5	10	14
Frontal_inf_oper_L	7	6	3	15	0	6	9	5	1
Frontal_inf_oper_R	0	2	1	4	1	7	2	6	10
Frontal_inf_orb_L	2	5	1	3	1	9	5	4	8
Frontal_inf_orb_R	0	3	1	2	11	3	1	1	4
Frontal_inf_tri_L	2	22	16	23	9	3	9	6	7
Frontal_inf_tri_R	0	4	1	12	14	19	6	2	12
Frontal_mid_L	3	4	7	3	16	23	13	21	13
Frontal_mid_R	1	1	11	5	9	21	7	2	12
Frontal_sup_L	3	15	6	15	15	20	7	14	12
Frontal_sup_medial_L	1	4	0	0	12	8	4	7	16
Frontal_sup_medial_R	0	1	1	1	3	15	1	4	10
Frontal_sup_R	0	0	5	16	17	15	4	2	11
Fusiform_L	74	50	38	39	50	24	46	35	39
Fusiform_R	94	40	46	44	57	53	54	25	28
Hippocampus_L	0	0	1	0	3	7	9	0	0
Hippocampus_R	0	3	2	1	2	1	10	3	0
Lingual_L	29	30	32	33	34	36	33	38	9
Lingual_R	24	51	36	24	40	28	40	46	17
Occipital_inf_L	36	39	27	9	24	24	16	34	22
Occipital_inf_R	11	13	22	5	16	30	15	8	21
Occipital_mid_L	130	67	118	63	67	72	57	94	68
Occipital_mid_R	73	58	54	42	22	17	54	34	37
Occipital_sup_L	15	9	7	49	19	7	12	14	32
Occipital_sup_R	29	23	46	15	17	27	19	20	31
Parahippocampal_L	2	2	1	1	1	6	2	6	1
Parahippocampal_R	4	1	4	1	12	6	7	2	0
Parietal_inf_L	21	23	27	37	13	18	27	25	28
Parietal_inf_R	2	1	0	12	4	2	3	8	8
Parietal_sup_L	19	25	4	19	21	15	12	26	13
Parietal_sup_R	17	36	6	19	8	2	12	18	28
Postcentral_L	30	8	39	20	6	17	17	10	4
Postcentral_R	0	3	4	6	3	15	4	0	14
Precentral_L	6	21	3	46	7	8	33	18	7
Precentral_R	0	1	3	14	2	13	8	1	8
Precuneus_L	1	17	53	9	23	7	18	10	21
Precuneus_R	21	12	27	27	20	3	16	2	16
Supp_motor_Area_L	3	1	0	37	3	9	2	4	0
Supp_motor_Area_R	0	5	2	10	2	12	4	4	2
Supramarginal_L	9	4	12	34	2	8	11	23	10
Supramarginal_R	0	6	0	14	0	9	5	3	4
Temporal_inf_L	13	18	5	5	10	5	12	27	11
Temporal_inf_R	41	16	10	5	19	10	10	10	21
Temporal_mid_L	29	29	12	7	30	30	31	39	28
Temporal_mid_R	24	21	9	8	37	18	14	13	17
Temporal_sup_L	0	1	2	4	5	7	14	17	14
Temporal_sup_R	0	3	1	1	3	6	9	12	3
Not_labeled	50	67	65	65	50	73	80	94	65

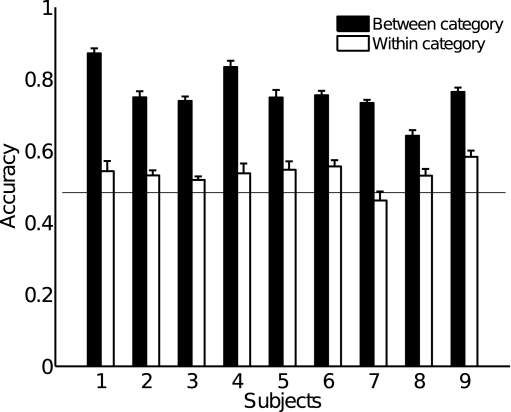
Overall classification accuracies for each subject are shown in Figure 5, averaged across the results from models using 10–100 topics to avoid bias; this will be somewhat conservative, as models with few topics perform poorly. Results were statistically significant for all subjects, with p-values calculated using a conservative Monte Carlo procedure being less than 0.01. More details about voxel selection and statistical testing are provided in Section A.1 of the Appendix.

Figure 5.

Average classification accuracy across models using 10 to 100 topics, for each of 9 subjects (chance level is 0.5); the accuracy is broken down into classification of concept pairs where concepts are in different categories (“Between”) and pairs where the category is the same (“Within”). Error bars are across numbers of topics, chance level is 0.5.

As the figure shows, classification performance was best when the comparison was between concepts belonging to different semantic categories. This indicates that the text outputs for semantically related concepts tended to be quite similar, which would in turn suggest that the topic probability representations giving rise to word distributions were similar. This could be because our data are too noisy to extract different representations for those related concepts, or an intrinsic limitation of the semantic model we extracted from text.

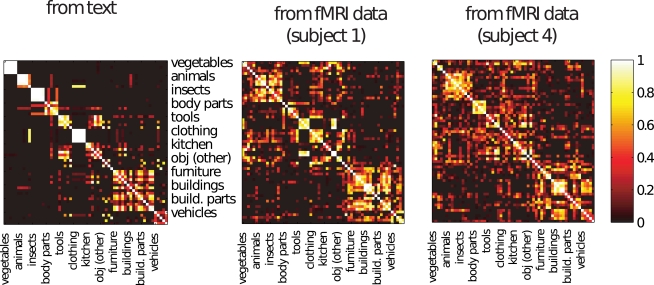
In order to examine this question, we first considered the pattern of similarity across concepts – correlation of their respective topic representations – derived solely from text, shown on the left of Figure 6. The right of the figure shows the correlation between the topic representations predicted from each pair of brain images when they were in the test set. The close resemblance between the two matrices indicates that the fMRI-derived text reflected the semantic similarity structure inherent in the stimulus set. The high correlations apparent in the Wikipedia-based matrix also indicate a possible explanation for the relatively weak within-category classification performance we obtained, since our text-generation procedure can only pick up on distinctions if they are made by the underlying topic model. The marginal within-category classification performance may thus reflect the limited granularity of our topic models, rather than a fixed limitation of the overall technique.

Figure 6.

Left: Similarity between the topic probability representations of each concept learned solely from text, with concepts grouped by semantic category. Right: Similarity between the topic probability representations predicted from the brain images for each pair of concepts, when they were being used as the test set, for the two best subjects with the highest classification accuracy. These were obtained using a 40 topic model, the general pattern is similar for the other subjects. Note that the representations for concepts in the same category are similar when obtained from brain images and that this is also the case when those representations are derived from text.

4. Discussion

We have introduced a generative, multivariate approach for producing text from fMRI data. Even as we draw on aspects of the approaches used in Mitchell et al. (2008) and Naselaris et al. (2009), our method differs from these in various ways. The most important are the fact that we generate text pertaining to mental content, rather than a pictorial reconstruction of it, and, furthermore, we do this by inverting a model of semantic representations of concrete concepts that was learned from text data in an unsupervised manner.

We have shown that we can generate a probability distribution over words pertaining to left-out novel brain images and that the quality of this distribution can be measured quantitatively through a classification task that matches brain images to Wikipedia articles. Our results indicate that performance at this task is mainly constrained by the quality of the model learned from text, suggesting that one might be able to improve within-category discrimination accuracy by learning a finer-grained model.

Given that we do not have to specify verbs to obtain semantic features and that we can thus obtain models with any number of topics (up to certain practical constraints), there is a lot of room for further improvement. One possibility would be to have topics correspond to semantic features at a finer grain than “category.” An example could be a “made of wood” topic that would place heavy probability on words such as “brown,” “grain,” “pine,” “oak,” etc. In this situation, there would be far more topics, each spreading probability over fewer words; each concept would be represented by assigning probability to more of these topics than is currently the case. It is conceptually straightforward to modify parameters of topic models to yield this and other characteristics in each model, and we are currently working on this direction.

The present work serves as a proof of concept, subject to considerable limitations. In order to simplify the problem, we focused only on representations of concrete objects. It is therefore an open question how the present technique would perform on a wider range of semantic content; this would include more abstract concepts and relationships between concepts, for instance. The semantic model in our case can be learned from any sub-corpus of Wikipedia, so any concept for which there is an article can be represented in terms of semantic features, regardless of whether it is concrete or abstract. It remains to be seen whether the topics learned are reasonable for abstract concepts, and that is also a research direction we are pursuing.

A second important simplification was to ignore word order and grammatical structure. Although this is a conventional step in text-analysis research, a practical method for text generation would clearly require grammatical structure to be taken into account. In this regard, it is interesting to note that there have been proposals (Griffiths et al., 2005, 2007; Wallach, 2006) of approaches to enriching topic model representations by considering word dependency and order. Integrating such a modeling approach into the present approach to fMRI analysis might support more transparently meaningful text outputs.

It would be possible to use the semantic features defined in Mitchell et al. (2008) to both generate words and classify articles. One would need to tally, for each of the 25 verbs, which words occur within a five token window of it; this vector of counts would then have to be normalized into a probability distribution. Given a vector of semantic feature values, we would again normalize the vector to be a probability distribution. To classify, we would have to take the further step of combining the word probability distributions of all the verbs according to their respective probabilities in the normalized semantic feature vector. This distribution would then be used to compute the probability of each article.

We think that this could work for generating words, to some extent. These would, however be restricted to words occurring close to the verb in text, rather than any words pertaining to the concept the verb is associated with; these words might come from anywhere in an article about the concept, in our approach. This issue would also affect the probability distributions over words associated with each verb, which are necessary for doing classification. Furthermore, we would be using one ad hoc distribution (over semantic features) to combine other ad hoc distributions (over words). Whereas this is not necessarily a problem, it should be contrasted with the straightforward process of estimating topic probabilities for each concept and word distributions for each topic and then using these by inverting the model.

If this approach can be further developed, it may offer an advance over previous efforts to decode patterns of neural activation into language outputs, either letter-by-letter (Birbaumer, 2006) or word-by-word (Kellis et al., 2010), with possible clinical implications for conditions such as locked-in syndrome (Owen et al., 2006; this would require showing generalization beyond a single experiment, of course).

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

A. Appendix

A.1. Classification experiment

A.1.1. Selection of stable voxels

The reproducibility criterion we used identifies voxels whose activation levels across the training set examples of each concept bear the same relationship to each other over epochs (mathematically, the vector of activation levels across the sorted concepts is highly correlated between epochs). As pointed out elsewhere (Mitchell et al., 2008), we do not expect all – or even most – of the activation to be differentially task related, rather than uniformly present across conditions, or consistent between the various presentations of the same noun stimulus. We chose to use 1000 rather than 500 reproducible voxels, as the results were somewhat better (and still comparable with 2000 voxels, say), but it's legitimate to consider how sensitive the results are to this choice. Given that the reproducibility criterion for selecting voxels is essentially a correlation computation, one can find a threshold at which the null hypothesis of there being no correlation has a given p-value, using the Fisher transformation. For instance, given that 59 voxel values are compared across 6 × 5 per pairs of runs, observed correlation r = 0.1 has a p-value of 0.01 if the true correlation ρ = 0. Using this threshold gives us a different number of voxels in each subject, ranging from approximately 200 to well over 2000, but the results are still very similar to those obtained with 1000 voxels.

The voxels selected come from regions of interest (ROIs) all across temporal and occipital lobes, as shown in Table 2 with labels from the AAL atlas (Tzourio-Mazoyer et al., 2002); this indicates that we are using both visual and semantic information in learning the relationship between topic probabilities and brain activation.

A.1.2. Testing dependent classification results in our situation

In the experiment described in the paper we have one classification decision for each possible pair of concepts (1770 in total). Those decisions are not independent, as each concept appears in 59 pairs. The expected accuracy under the null hypothesis that the classification was being made at random is still 50%, but the variance is not what the same as in the case where examples are independent (see Pereira et al., 2009 for details about the usual procedure). So how can we get this distribution?

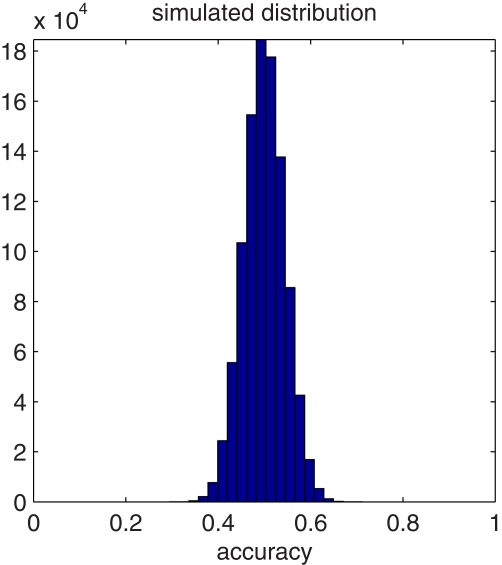
The ideal would be to use a permutation test, but the whole process for each permutation takes at least a few minutes, so doing enough permutations to get a low p-value is too computationally expensive. Instead we simulated a distribution of classification results under the null hypothesis, introducing dependencies between them, with one simulation run proceeding as follows. For each concept pair (i,j), we draw a number from a uniform distribution in the [0,1] interval and take that to be the similarity score for the article j under the brain distribution for concept i. We then use these as the scores for matching, using the algorithm described earlier.

Figure A1 has a histogram of the accuracy results from a simulation with 1000000 iterations. Based on the percentiles of this distribution, the p-values for our classification results would be similar to those obtained with a binomial distribution if we had approximately 150 independent classification decisions. The p-values under this distribution of the results averaging across multiple topics are below 0.00001 for eight of nine subjects, and 0.003 for subject 8.

Figure A1.

Distribution of classification results under our simulated null hypothesis.

A.2. Topic models

The construction of our corpus is described in detail in the Section 2. Here we provide a brief description of key aspects of topic models (Blei et al., 2003) for the purposes of this paper, which pertain to the LDA software we used (http://www.cs.princeton.edu/∼blei/topicmodeling.html).

Latent Dirichlet allocation models each document w (a collection of words) as coming from a process where the number of words N and the probabilities of each topic being present υ are drawn. Each word w is produced by selecting a topic z (according to probabilities υ), and drawing from the topic-specific probability distribution p(w|z) over words. In the process of learning a model of our corpus, a vector of topic probabilities is produced for each article/concept, and the topic-specific distributions are learned. The topic probabilities are what we use as the low-dimensional representation of each concept.

Given the probabilities υ for a concept, we can combine the topic-specific distributions over words into a single distribution

$$p(w|\theta )=p(w|topic1){\theta }_1+\dots +p(w|topicK){\theta }_k$$

i.e., the more probable a topic is the more bearing it has in determining what the probability of a word is. In the paper this is used to convert the topic probabilities estimated from a test set brain image into a word distribution corresponding to that image.

Note also that, since the topic probabilities add up to 1, the presence of one topic trades off with the presence of the others, something that is desirable if expressing one brain image as a combination of basis images (otherwise one might expect to have multiple ways for the same basis images to be combined to yield a similar result).

A.3. Basis image decomposition

The procedure depicted in Figure 4 has two steps that require solving optimization problems. The first is learning a set of basis images, given example images for 58 concepts and their respective topic probabilities. The second is predicting the topic probabilities present in an example image, given a set of basis images. The following sections provide notation and a formal description of these two problems.

A.3.1. Notation

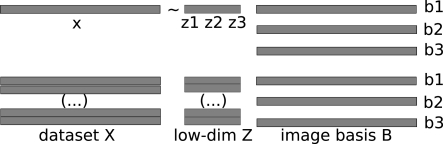
As each example is a 3D image divided into a grid of voxels, it can be unfolded into a vector x with as many entries as voxels containing cortex. A dataset is a n × m matrix X where row i is the example vector x_i. Each example x will be expressed as a linear combination of basis images b₁, …, b_K of the same dimensionality, with the weights given by the topic probability vector z = [z₁, …, z_K], as depicted on the top of Figure A2. The low-dimensional representation of dataset X is a n × K matrix Z where row i is a vector z_i and the corresponding basis images are a K × m matrix B, where row k corresponds to basis image b_k, as shown on the bottom of Figure A2.

Figure A2.

Top: each brain image can be written as a row vector, and the combination as a linear combination of three row vectors. Bottom: A dataset contains many such patterns, forming a matrix X where rows are examples and whose low-dimensional representation is a matrix Z.

A.3.2. Learn basis images given example images and topic probabilities

Learning the basis images given X and Z can be decomposed into a set of independent regression problems, one per voxel j, i.e., the values of voxel j across all examples, X(:,j), are predicted from Z using regression coefficients β = B(:,j), which are the values of voxel j across basis images. Any situation where linear regression was infeasible because the square matrix in the normal equations was not invertible was addressed by using a ridge term with the trade-off parameter set to 1. Hence, for voxel j, we solve:

$$\underset{\beta }{\max }\left|\right|X_{:,j}-Z\beta |{|}_2\left(+\lambda \left|\right|Z|{|}_2\right)$$

A.3.3. Predict topic probabilities given example images and basis images

Predicting the topic probability vector z = Z_i,: for an example x = X_i,: is a regression problem where x′ is predicted from B′ using regression coefficients z′. The prediction of the topic probability vector is done under the additional constraint that the values need to be greater than or equal to 0 and add up to 1, as they are probabilities. We used CVX (Grant and Boyd, 2009) to solve for topic vector z:

$$\begin{array}{ll}{\max }_{\beta }\left|\right|Xi,:-zB|{|}_2\hfill & \text{Subject\hspace{0.17em}\hspace{0.17em}to:}\hfill \\ \hfill & {\forall }_j{z}_j>=0\hfill \\ \hfill & {\displaystyle \sum _j{z}_j=1}\hfill \end{array}$$