Control and Reversal of the Electrophoretic Force on DNA in a Charged Nanopore

Abstract

Electric field-driven transport of DNA through solid-state nanopores is the key process in nanopore-based DNA sequencing that promises dramatic reduction of genome sequencing costs. A major hurdle in the development of this sequencing method is that DNA transport through the nanopores occurs too quickly for the DNA sequence to be detected. By means of all-atom molecular dynamics simulations, we demonstrate in this communication that velocity of DNA transport through a nanopore can be controlled by the charge state of the nanopore surface. In particular, we show that the charge density of the nanopore surface controls the magnitude and/or direction of the electro-osmotic flow through the nanopore and thereby can significantly reduce or even reverse the effective electrophoretic force on DNA. Our work suggests a physical mechanism to control DNA transport in a nanopore by chemical, electrical or electrochemical modification of the nanopore surface.

1. Introduction

It has become possible to manufacture nanometer-size pores in thin solid-state membranes [1] and use such pores as single molecule detectors [2,3] to reveal the type and composition of biomolecules dissolved in an electrolytic solution. In a typical measurement, an external electric field drives charged biomolecules from one side of the membrane to the other, through the nanopore, one molecule at a time. The presence of a biomolecule in a nanopore alters the nanopore ionic current, revealing some information about the biomolecule. In the case of long a DNA molecule, this process sequentially exposes its fragments to the nanopore volume, which potentially can be used to determine the nucleotide sequence of DNA [4]. A major obstacle for realizing this principle in practice is that DNA moves through the pore too fast for its sequence to be detected. Extensive efforts have been directed toward developing methods to reduce the velocity of DNA transport, including changing the temperature, viscosity and ion concentration of the solvent [5], fine-tuning the nanopore size and material [6,7], and rapidly switching the transmembrane bias [8]. Several theoretical studies have suggested methods to control DNA motion by switching the electrostatics potentials acting on the DNA molecule [9–11]. Using all-atom molecular dynamics simulations (MD), we demonstrate in this work the possibility of electro-kinetic control of the DNA motion by adjusting the charge of the nanopore surface.

2. Method

All MD simulations were performed using the program NAMD [12], TIP3P model of water [13], CHARMM parameters for ions [14], and AMBER parm94 force field [15] for DNA and a custom force field [16,17] for Si₃N₄. We have previously shown that the above combination of parameters accurately describes the distribution of ions around DNA and the electrophoretic force on DNA in an uncharged nanopore [18]. Figure 1 illustrates a typical simulation system. The atomic scale model of the 3-nm-radius nanochannel used in this study was cut from a hexagonal prism of crystalline Si₃N₄ membrane 6.0-nm on side and 6.4-nm thickness. In all simulations, atoms of Si₃N₄ were harmonically restrained to their initial positions in the crystalline solid. Atoms at the Si₃N₄ surface were assigned a uniform excess charge to produce the surface charge density. Five channels were constructed to have the uniform surface charge density σ between −0.34 and 0.34 e/nm², where e is the charge of a proton. After placing a poly(dA₂₀) · poly(dT₂₀) DNA duplex in the nanochannel, 0.1 M or 1 M KCl electrolyte was added in the amount required to produce the same solvent density as in a free volume of the electrolyte equilibrated at 1 bar and 310K. The Si₃N₄ solid and the DNA duplex were made effectively infinite by imposing periodic boundary conditions in all three dimensions. The simulations of the electrophoretic force were conducted in the NVT ensemble. Long-range Coulomb interactions were computed using the PME method [19]. The temperature was maintained at 310 K using the Langevin [20] thermostat applied to the atoms of the Si₃N₄ solid [18].

Figure 1.

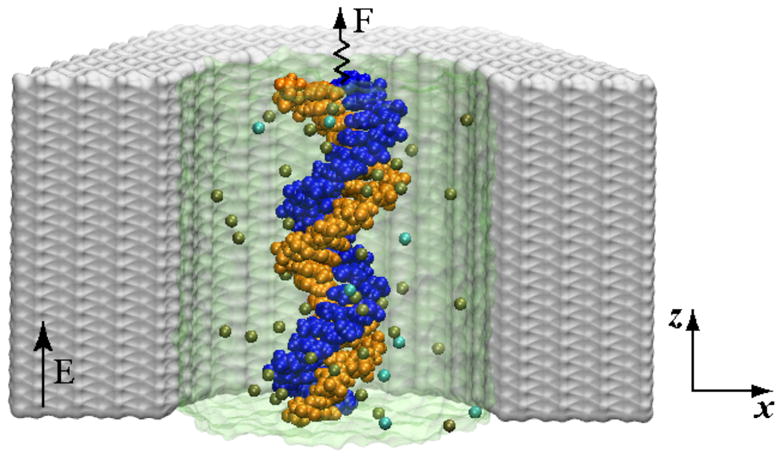
Simulation system: A cut-away view of a crystalline Si₃N₄ nanochannel (grey) containing a DNA molecule (blue and orange) and KCL electrolyte. The water is shown as a semi-transparent surface, K⁺ and Cl⁻ ions are shown as tan and cyan spheres. The position of the DNA’s center of mass is restrained by a harmonic potential. The displacement of the DNA in an electric field reveals the effective force.

Following a method described previously [18], each system was simulated for about 30 ns under a constant external electric field of 78 mV/nm directed along the DNA molecule. In all simulations, the DNA was radially restrained to the center of the nanochannel. Ions within 5 Å of the Si₃N₄ surface were harmonically pushed away from the surface [18], mimicking the effect of an oxidized layer or a polymer coating [6,7]. These restraints were required to prevent ion adhesion to the surface of the channel and thus maintain constant concentration of mobile ions. The center of mass of the DNA’s phosphorous atoms was harmonically restrained along the axis of the nanochannel. In our setup, positive values of the restraining force correspond to DNA displacements in the direction opposite the external electric field.

3. Results and discussions

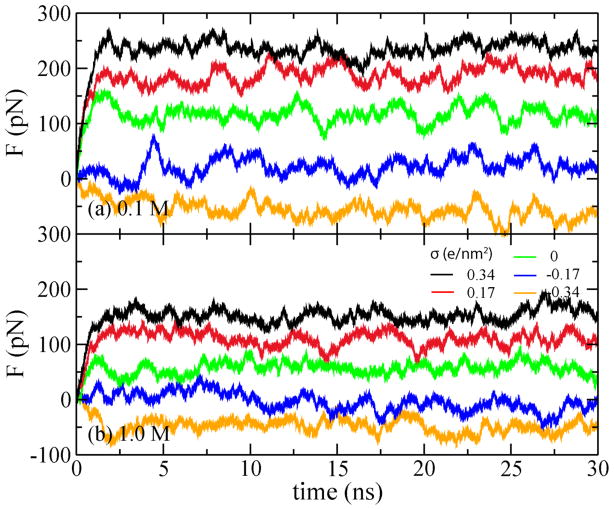
In our simulations of the effective force, the center of mass of the DNA’s phosphorus atoms was restrained using a harmonic spring with the spring constant of 1 pN/Å. Under the influence of the external electric field, the DNA was observed to change its position until the force of the harmonic spring balanced the effective force of the electric field. Figure 2 plots the restrain force versus the simulation time for all simulation systems. Each simulation lasted about 30 ns; the restrain force saturated in less than 2 ns. In all simulations, the strength of the external electric field was 78 mV/nm. Note that when σ = −0.34 e/nm², the spring force is negative, indicating reversal of the effective driving force.

Figure 2.

Restrain force on DNA versus simulation time. In each panel, the color of the lines corresponds to the surface charge density of −0.34, −0.17, 0, 0.17 to 0.34 e/nm², from bottom to top. Here e is the charge of a proton.

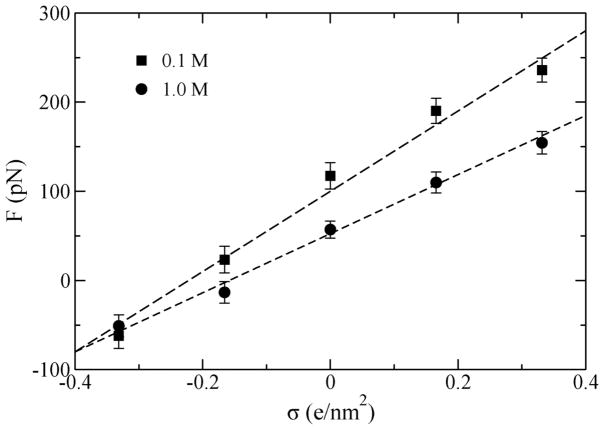
The dependence of the steady-state restraining force F (the stall force) on the charge density of the Si₃N₄ surface is shown in Figure 3. The stall force (balancing the effective force) increases linearly with the surface charge density σ. Hence, the effective electrophoretic force driving DNA transport through nanopores increases with σ as well, so does the speed of DNA transport. At some negative values of σ, the stall force F changes its sign, indicating that DNA could move in the field direction, similar to the behavior observed during inversion of the DNA charge [21,22]. Changing the bulk ion concentration from 1 to 0.1 M, increases the slope of F(σ) dependence, likely due to a stronger electrostatic screening effect in the 1.0 M KCl electrolyte. Note, that when σ approaches −0.4 e/nm², the stall force becomes independent of the ion concentration.

Figure 3.

The stall force (F) on DNA in a nanopore versus the nanopore surface charge density (σ). The direction of the force depends on σ.

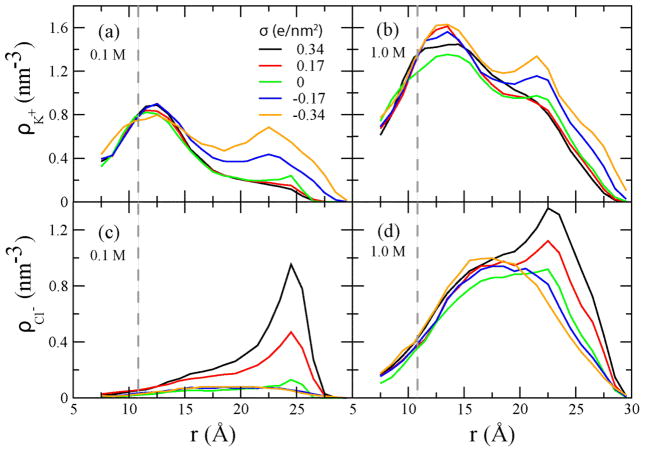
To determine the microscopic origin of the observed phenomena, we characterized the distribution of ions in the simulated systems. Figure 4 shows that ions of both types accumulate near oppositely charged surfaces and their concentration rapidly decays with the distance, in accordance with the Debye screening mechanism. Near the DNA molecule (which is negatively charged), the density of counterions (K⁺) is high, which is seen as peaks in the ion density plots, Figure 4(a, b). The density of co-ions (Cl⁻) is depleted near the DNA surface, Figure 4(c, d). In a 1.0 M electrolyte, co-ions are found closer to DNA than in the 0.1M case, which is consistent with the concentration dependence of the Debye screening length. Similar behavior is observed near the charged wall of the nanochannel: the density of ionic species carrying the charge opposite to the charge of the surface has a local maximum near the wall. As these ions are not specifically bound to DNA or the nanochannel surface, the application of an external electrostatic field produces surface currents, which in turn produce the electro-osmotic flow of water along the DNA and nanochannel surfaces.

Figure 4.

Radial distributions of K⁺ (a, b) and Cl⁻ (c,d) ions computed as the number density averaged over concentric cylindrical shells around DNA. The dashed lines indicate the approximate location of the DNA surface.

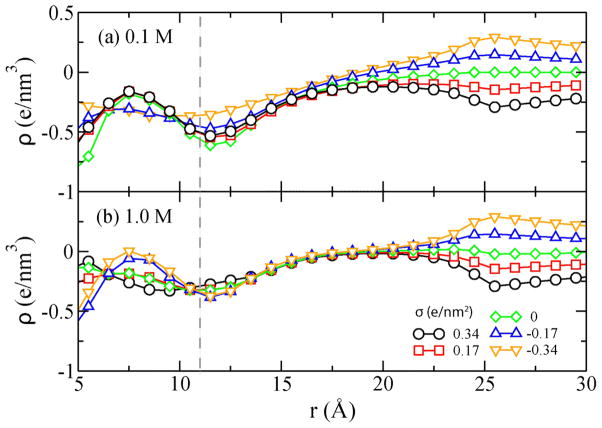
Figure 5 plots the cumulative charge density ϱ(r)=Σ_r<RQ(r)/V(r) as a function of the distance from the DNA center. In the above formula, Q is the charge of an atom (DNA or ion) inside a cylinder with radius R and V is the volume of the cylinder. Because each simulation system is, overall, neutral, ϱ (r=3nm) = −2σ/3 e/nm³. The plot clearly shows that within the Debye length of the DNA surface (1.0 and 0.3 nm for 0.1 and 1M solution, respectively), the cumulative charge is negative, and hence inversion of the DNA charge does not take place. Therefore, the observed dependence of F on σ cannot be explained by electrostatic overscreening of the DNA charge. Note that at 0.1M, the Debye layers of the DNA and the channel wall overlap, and hence the charge density ϱ near DNA is slightly affected by the charge density σ on the pore surface. At 1.0 M, the Debye layers do not overlap and the cumulative charge density ϱ near the DNA surface (r = 12 Å) is independent of σ, as shown in Figure 5b.

Figure 5.

Cumulative charge density (ϱ) versus the distance from the DNA center (r). The dashed line indicates the approximate location of the DNA surface.

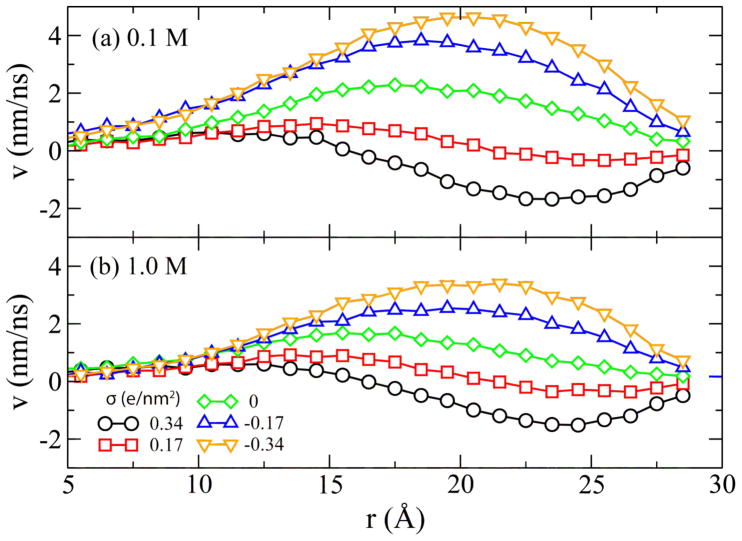
We have recently demonstrated that the effective force on DNA in an uncharged nanopore is determined by the electro-osmotic flow (EOF) of counter ions near the DNA surface [13]. In the case of a charged nanopore, one can expect to observe a superposition of the EOF near the DNA surface and the EOF near the channel surface. In Figure 6, we plot the velocity profile of the EOF versus distance from the DNA center. For the negatively charged pores, the directions of both EOFs coincide, and hence the resulting flow velocity is greater than in the uncharged pore (σ=0). This leads to increased hydrodynamic drag on the DNA, which reduces the effective electrophoretic force. For highly charged and electrically negative pores, the hydrodynamic drag can become greater than the force of the external electrostatic field on bare DNA. In this case, the effective electrophoretic force reverses its direction. When σ>0, the EOF near the pore surface partially cancels out the EOF near the DNA surface, reducing the overall hydrodynamic drag on DNA and thus increasing the effective electroporetic force. The behavior described above is qualitatively consistent with a continuum theory of the electrophoretic force in a nanopore [23,24].

Figure 6.

Water flow velocity (v) versus the distance from the DNA center (r).

Figure 6 also indicates that the flow profile is more sensitive to the variation of the surface charge at a lower bulk ion concentration, consistent with a stronger dependence of the stall force on the surface charge, Figure 2. Hence, the hydrodynamic screening effect [18] qualitatively explains the simulated dependence of the stall force on the surface charge. Also qualitatively, the apparent linear dependence of the stall force on the surface charge can be explained by a linear superposition of the electro-osmotic flow in an empty (charged) nanochannel and the electrophoretic mobility of DNA in free electrophoresis. As the velocity of both types of flow are linearly proportional to the zeta potentials of the respective surfaces [25], a linear change in the nanopore surface’ zeta potential (due to the change of its charge density) can produce a linear variation of the effective force, and the first reversal should occur when the two zeta potentials becomes equal. The reversal of the effective driving force on DNA also indicates that DNA can be surprisingly loaded into or driven through a solid-state nanopore even along the electric field direction because of the electroosmotic flow on a negatively charged pore surface. Future simulations will be directed toward building a quantitative theoretical model of these phenomena.

4. Conclusions

We have demonstrated that the effective driving force on DNA in a nanopore can be controlled by the nanopore’s surface charge. Furthermore, we have shown that the direction of the electrophoretic force in a negatively charged nanopore could be reversed, which, in principle, could allow for real-time, local control over the DNA motion in a nanopore. In practice, the surface charge density can be adjusted by chemical means, for example, by changing the solvent’s pH [26,27] or electrically, by embedding metallic or semiconductor electrodes within the nanopore structure and modifying the surface charge by changing the electrostatic potential of the electrodes [28–30]. The same electrodes could be used, in principle, to detect the presence of DNA [31,32], enabling feedback control of the DNA transport through a solid-state nanopore.