Optimal regulatory strategies for metabolic pathways in Escherichia coli depending on protein costs

Analysis of optimal strategies for the control of metabolic pathways in Escherichia coli reveals that the extent of transcriptional regulation reflects an evolutionary trade-off between the minimization of response time and protein costs.

Abstract

While previous studies have shed light on the link between the structure of metabolism and its transcriptional regulation, the extent to which transcriptional regulation controls metabolism has not yet been fully explored. In this work, we address this problem by integrating a large number of experimental data sets with a model of the metabolism of Escherichia coli. Using a combination of computational tools including the concept of elementary flux patterns, methods from network inference and dynamic optimization, we find that transcriptional regulation of pathways reflects the protein investment into these pathways. While pathways that are associated to a high protein cost are controlled by fine-tuned transcriptional programs, pathways that only require a small protein cost are transcriptionally controlled in a few key reactions. As a reason for the occurrence of these different regulatory strategies, we identify an evolutionary trade-off between the conflicting requirements to reduce protein investment and the requirement to be able to respond rapidly to changes in environmental conditions.

Introduction

In recent years, the increasing availability and decreasing prices of experimental techniques in molecular biology have led to an explosion in the number of available experimental data sets (Ishii et al, 2007; Lu et al, 2007; Faith et al, 2008; Bennett et al, 2009; Lewis et al, 2010). These data sets cover a broad range of aspects of cellular systems, for example, transcript levels, protein abundances, metabolite concentrations or fluxes of a large number of metabolic reactions. However, analytical methods to integrate these data sets into a comprehensive understanding of organisms have lagged behind (Palsson and Zengler, 2010) and, thus, there is a great need for theoretical tools that allow us to build more comprehensive models of cellular mechanisms (Heinemann and Sauer, 2010). Whole-cell models of metabolism have been shown to be a suitable framework to simplify this integration (Feist and Palsson, 2008; Oberhardt et al, 2009; Lewis et al, 2010; Ruppin et al, 2010).

Using these large-scale models of metabolism to analyze transcriptomic data sets, a number of recent studies have been able to show a link between the structure of metabolic networks and their transcriptional regulation (Stelling et al, 2002; Ihmels et al, 2004; Reed and Palsson, 2004; Kharchenko et al, 2005; Schwartz et al, 2007; Notebaart et al, 2008; Seshasayee et al, 2009; Marashi and Bockmayr, 2011). However, the extent to which transcriptional regulation controls metabolism has not yet been analyzed in detail despite of a large body of earlier theoretical work on the control of metabolism (Heinrich and Schuster, 1996). Although there is a relationship between the structure of metabolism and its regulation, the results from some of these studies indicate that it is not very strong (Stelling et al, 2002; Reed and Palsson, 2004; Notebaart et al, 2008; Marashi and Bockmayr, 2011). Indeed, the picture emerges that transcriptional regulation of metabolism is less pervasive than was previously thought (Heinemann and Sauer, 2010).

In our study, which integrates a large array of experimental and bibliomic data sets, we analyzed the extent to which transcriptional regulation controls metabolism in Escherichia coli. As experimental data sets, we used gene-expression profiles of E. coli from the Many Microbe Microarrays Database (M^3D; Faith et al, 2008) and genome-wide protein abundance data (Lu et al, 2007). We used bibliomic data sets on the transcriptional regulatory network controlling metabolism stored in RegulonDB (Gama-Castro et al, 2008) and EcoCyc (Keseler et al, 2005), information on the post-translational regulation of enzymes (allosteric regulation and phosphorylation) from EcoCyc and Phosida (Gnad et al, 2007).

Using these data sets, we show that there are large differences in the degree of transcriptional control between different subsystems of metabolism. While some pathways show a strong coexpression of the corresponding enzymes, there appears to be no coexpression in other pathways. In order to explain these observations, we used dynamic optimization on a simple model of a linear pathway to identify a regulatory program that allows the flux through a pathway to be controlled. For the optimization we used the minimization of transcriptional regulatory interactions and protein costs as an objective function. ‘Cost’ of a particular protein refers to the total weight of this protein present in the cell. The results of the optimization show that for tight control of flux, initial and terminal reactions in a pathway need to be transcriptionally regulated and that this regulatory program is used in particular to control pathways with low abundance and thus low costs of enzymes. In contrast, in pathways with highly abundant and thus costly enzymes, all enzymes are predicted to be transcriptionally regulated.

Analyzing the positional regulation within pathways showing a low degree of coexpression of enzymes, we can confirm the utilization of the predicted minimal regulatory program and find that regulation at initial pathway positions is exerted mainly through post-translational means. Thus, the extent of transcriptional regulation is even further reduced through post-translational regulation. Moreover, we confirm that the occurrence of the different regulatory programs is related to the costs of enzymes within a pathway. Finally, we show that the cost-dependent control of metabolic pathways can be explained by a subtle balance between two conflicting evolutionary objectives: the pressure to be able to react as quickly as possible to a change in environmental conditions and the requirement to minimize the enzyme investment necessary to achieve this response.

Results

Identification of elementary flux patterns

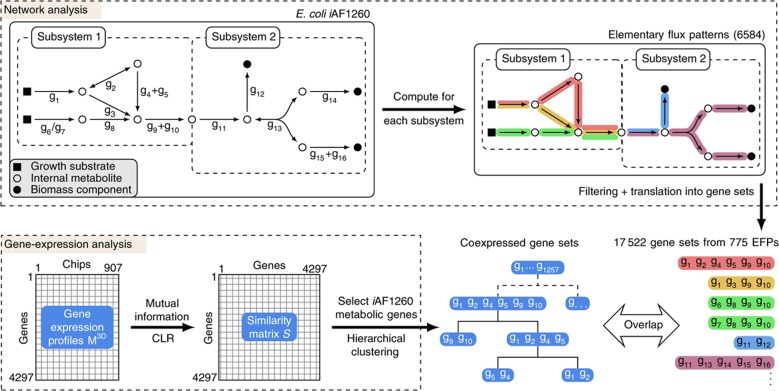
An outline of our approach to identify coexpressed elementary flux patterns is shown in Figure 1. Our analysis is based on the genome-scale metabolic network of E. coli, iAF1260 (Feist et al, 2007). We allowed for the unconstrained inflow and outflow of every metabolite that can be taken up by the cell in order to model the set of conditions under which the microarray data have been obtained (see Materials and methods).

Figure 1.

Outline of the analysis. Elementary flux patterns were identified for each metabolic subsystem and then translated into the corresponding gene sets using the gene–protein–reaction associations of the model. Gene sets were compared on a subsystem basis to sets of coexpressed genes determined from a large compendium of microarrays from the Many Microbe Microarrays Database (M^3D). In the schematic depiction of iAF1260, gene–protein–reaction associations are shown below the reactions. In case of ‘/’ isoenzymes are catalyzing a reaction, in the case of ‘+’ a protein complex catalyzes a reaction. EFPs, elementary flux patterns.

In order to identify reactions that need to be regulated in a similar manner, we computed the elementary flux patterns of the 35 biochemically annotated subsystems of iAF1260 (Table I). Elementary flux patterns (Kaleta et al, 2009) are defined as the basic routes of physiological feasible fluxes through a particular subsystem of metabolism. Hence, they correspond to basic metabolic routes through each subsystem.

Table 1. Subsystems defined in the model iAF1260.

Alanine and aspartate metabolism

Alternate carbon metabolism*

(Metabolism of various carbon sources)

Anaplerotic reactions

(Supply of tricarboxylic acid cycle precursors)

Arginine and proline metabolism*

Cell envelope biosynthesis*

Citric acid cycle*

Cofactor and prosthetic group biosynthesis*

(Biosyntheses of flavin adenine dinucleotide (FAD), NAD(P), protoheme, pyridoxal 5-phosphate, riboflavin, siroheme, quinones, tetrahydrofolate, thiamin and undecaprenyl diphosphate)

Cysteine metabolism*

Folate metabolism

Glutamate metabolism

Glycerophospholipid metabolism*

(Biosyntheses of cardiolipin and phosphatidylethanolamine)

Glycine and serine metabolism*

Glycolysis/gluconeogenesis*

Glyoxylate metabolism

Histidine metabolism*

Inorganic ion transport and metabolism*

Lipopolysaccharide biosynthesis/recycling*

Membrane lipid metabolism*

(Fatty acid biosynthesis and oxidation)

Methionine metabolism*

(Metabolism of methionine and S-adenosyl-L-methionine)

Methylglyoxal metabolism*

Murein biosynthesis*

Murein recycling*

Nitrogen metabolism*

Nucleotide salvage pathway*

Oxidative phosphorylation

Pentose phosphate pathway*

Purine and pyrimidine biosynthesis*

Pyruvate metabolism*

Threonine and lysine metabolism*

Transport, inner membrane*

Transport, outer membrane

Transport, outer membrane porin*

tRNA charging

Tyrosine, tryptophan and phenylalanine metabolism*

Valine, leucine and isoleucine metabolism*

We obtained a total of 6584 elementary flux patterns (see Supplementary Information S2 for a list). We translated the elementary flux patterns into the gene sets encoding the enzymes catalyzing them and performed several filtering steps in order to remove elementary flux patterns, which either gave rise to the same gene set or translated into a gene set of size one. After this final filtering step, 775 elementary flux patterns remained (see Supplementary Information S3 for a size distribution). Due to this filtering, no elementary flux patterns remained in eight subsystems, which mainly contain very small elementary flux patterns that did not translate into gene sets of size of at least two. For a detailed discussion of this issue see Supplementary Information S2. The 27 subsystems for which elementary flux patterns remained are listed in Table I.

Elementary flux patterns are moderately coexpressed

Using a compendium of uniformly normalized microarray data sets from the Many Microbe Microarrays Database (M^3D; Faith et al, 2008), we used mutual information with the context likelihood of relatedness algorithm (CLR; Faith et al, 2007) to compute coexpression values. This method showed superior performance over several tested association scores (Supplementary Information S4). Next, based on these values, hierarchical clustering was used to obtain a coexpression tree of metabolic genes. We verified whether the coexpression tree reflects known regulatory entities in E. coli metabolism by testing for every set of metabolic genes contained either within an operon, a transcription unit or a regulon, if it significantly overlaps with a node in the coexpression tree. Here, by ‘regulon’ we refer to a set of genes that is transcriptionally regulated by the same entity, like a transcription factor or a small RNA. We found that the gene sets of 84% of the operons, 83% of the transcription units and 88% of the regulons are significantly coexpressed. Thus, the coexpression tree reflects known regulatory entities in E. coli metabolism.

In order to detect elementary flux patterns that are significantly coexpressed (i.e. catalyzed by proteins that are coexpressed), the corresponding gene sets were compared with the nodes of the coexpression tree. We found that in total, 112 of the 775 elementary flux patterns (14.5%) are significantly coexpressed. For an overview of the distribution of the size of coexpressed elementary flux patterns as well as their corresponding gene sets, see Supplementary Information S3.

Degree of coexpression of pathways strongly varies between subsystems of metabolism

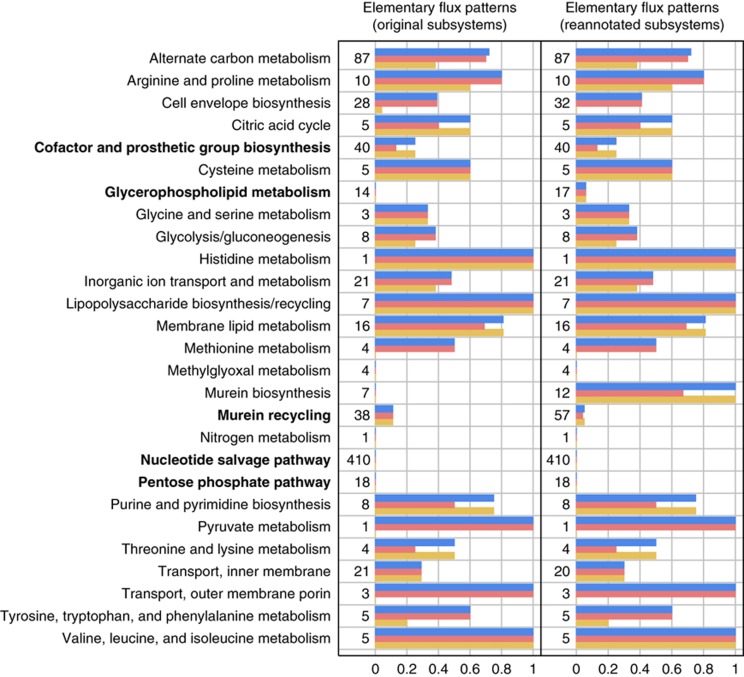
To identify the reasons for a low coordination in the expression of enzymes in a large number of elementary flux patterns, we analyzed the coexpression on a subsystem basis. We found that the fraction of coexpressed elementary flux patterns strongly varies between the functionally annotated subsystems of E. coli (Figure 2). While most elementary flux patterns in subsystems concerning amino-acid biosynthesis, nucleotide biosynthesis, alternate carbon metabolism and cell membrane metabolism are coexpressed, only few elementary flux patterns are coexpressed in subsystems, such as cofactor metabolism, glycerophospholipid metabolism and nucleotide salvage pathways.

Figure 2.

Coexpression and transcriptional coregulation of elementary flux patterns on a subsystem basis. The fraction of coexpressed (orange bars) and transcriptionally coregulated (red bars) elementary flux patterns is indicated for every subsystem containing at least one elementary flux pattern. Blue bars indicate the fraction of elementary flux patterns that were found to be coexpressed or transcriptionally coregulated (i.e. a union of both sets). The number of elementary flux patterns pertaining to each subsystem is indicated in front of every plot. Transcriptionally sparsely regulated subsystems are indicated in bold. Numbers are given before and after subsystem reannotation. Source data is available for this figure at www.nature.com/msb.

Source data for figure 2 ^{(2KB, txt)}

Next, we analyzed the transcriptional coregulation to test if the microarray data set used is comprehensive. We refer to an elementary flux pattern as transcriptionally coregulated if it significantly overlaps with a gene set representing known regulatory entities of E. coli (operons, transcription units and regulons), obtained from RegulonDB. As depicted in Figure 2, for most subsystems the elementary flux patterns that were found to be coexpressed are also transcriptionally coregulated. The addition of the few regulatory interactions affecting translation leads to only one more significantly transcriptionally or translationally coregulated elementary flux pattern.

It remains that there are several subsystems in which only few or no elementary flux patterns are coexpressed or transcriptionally coregulated (Figure 2). Using a maximum of 25% of coexpressed or transcriptionally coregulated elementary flux patterns as a threshold, this encompasses the ‘Cofactor and Prosthetic Group Biosynthesis’, ‘Glycerophospholipid Metabolism’, ‘Murein Biosynthesis’, ‘Murein Recycling’, ‘Nucleotide Salvage Pathway’ and ‘Pentose Phosphate Pathway’ subsystems. We refer to these subsystems as transcriptionally sparsely regulated (TSR) subsystems. We did not consider the two TSR subsystems ‘Methylglyoxal Metabolism’ and ‘Nitrogen Metabolism’, because they only contain a few, short elementary flux patterns.

To understand why we found a low degree of coexpression or coregulation in the TSR subsystems, we analyzed the elementary flux patterns they contain in more detail. In particular, we analyzed how sensitive the elementary flux patterns are to the random addition of reactions to the subsystem (Supplementary Information S5). We found that some of these subsystems do not accurately reflect the pathways they contain. For instance, the subsystem ‘Glycerophospholipid Metabolism’ contains cytoplasmatic and periplasmatic reactions but does not contain the exchange reactions across the inner membrane required to link both parts of this subsystem. Instead, these reactions were part of the subsystem ‘Transport Inner Membrane’. Thus, we added the corresponding reactions to ‘Glycerophospholipid Metabolism’. Moreover, reactions of murein biosynthesis were distributed across the subsystems ‘Cell Envelope Biosynthesis’, ‘Murein Recycling’ and ‘Murein Biosynthesis’, while several reactions of ‘Murein Recycling’ were contained in the subsystem ‘Murein Biosynthesis’ (Supplementary Information S5).

After remedying these problems, we recomputed the elementary flux patterns within all affected subsystems and determined those that are significantly coexpressed or coregulated (Figure 2). We found that reactions of murein biosynthesis are indeed coexpressed and coregulated. In our previous analysis, the part of murein biosynthesis that shows the strongest coexpression belonged to ‘Cell Envelope Biosynthesis’ while ‘Murein Biosynthesis’ only contained the terminal reactions of murein biosynthesis. However, there was no principal change in the coexpression and coregulation of elementary flux patterns within the remaining five TSR subsystems. After the reannotation of subsystems, we found a total of 805 elementary flux patterns of which 123 are significantly coexpressed (15.3%).

Consequently, the list of TSR subsystems was reduced to the five subsystems: ‘Cofactor and Prosthetic Group Biosynthesis’, ‘Glycerophospholipid Metabolism’, ‘Murein Recycling’, ‘Nucleotide Salvage Pathway’ and ‘Pentose Phosphate Pathway’. Overall, on a subsystem level, on average 7% of the elementary flux patterns within the TSR subsystems and on average 69% of the elementary flux patterns of the non-TSR subsystems are coexpressed or coregulated.

Identification of a minimal transcriptional regulatory strategy for controlling metabolic pathways

The fact that we have not identified coexpression of most elementary flux patterns in the TSR subsystems indicated that transcriptional regulation within these subsystems does not affect all enzymes belonging to a pathway simultaneously. To understand the mechanisms behind this observation, we used dynamic optimization to identify a regulatory program that allows to control the flux through a metabolic pathway with a minimal number of transcriptional regulatory interactions.

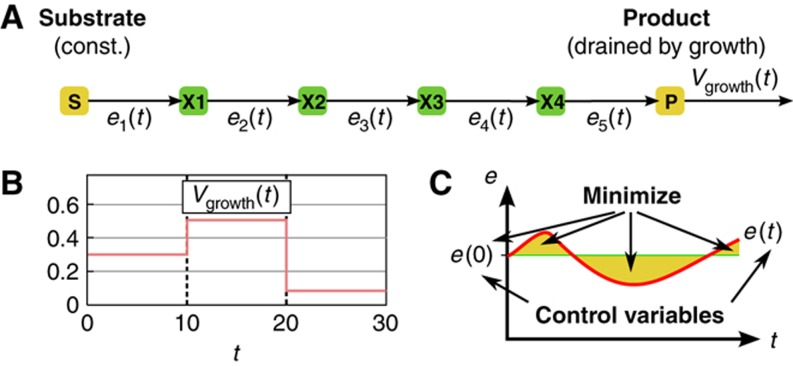
To this end, we constructed a simple kinetic model of a linear metabolic pathway comprising five enzymatic steps that convert a source compound s into a product p (Figure 3A). To take into account a drain on the product by bacterial growth or a subsequent pathway, a dilution reaction was incorporated. In order to simulate the environmental changes to which E. coli needs to adapt, we assumed that the dilution of the product changes at two time points (Figure 3B). The aim of the optimization was to identify a regulatory program in the form of a time course of enzyme concentrations e₁(t), …, e₅(t), which keeps the concentration of p(t) within a certain range and avoids the accumulation of intermediates to toxic concentrations. By defining the objective function, we searched for a regulatory program that minimizes two objectives: the change in enzyme concentrations through transcriptional regulatory interactions and the enzyme costs, that is, the initial enzyme concentrations (Figure 3C). The relative contribution of both factors to the objective function can be adjusted by a weighting factor σ that is multiplied by the sum of initial enzyme concentrations.

Figure 3.

Optimization problem to identify a minimal transcriptional regulatory program. (A) Linear pathway that converts a substrate s into a product p which is drained through v_growth. (B) Dilution of the product during the simulation. (C) The optimizer controls the initial concentration as well as the time course of the enzymes e₁, …, e₅. The objective function is to minimize, for all enzymes, the deviations from the initial concentrations plus the initial concentration (costs) of the enzymes.

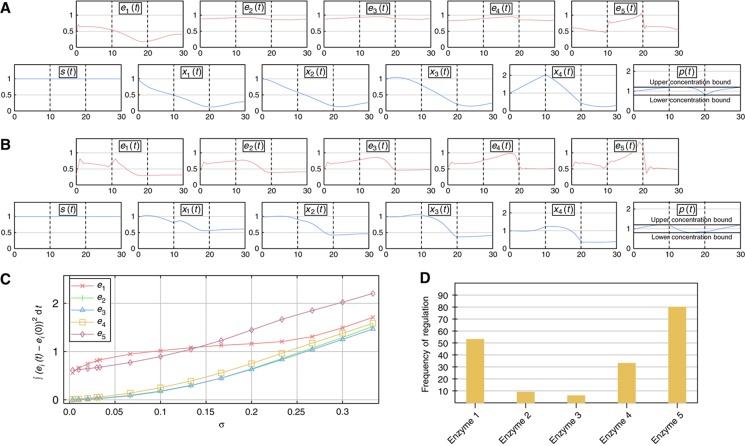
The results of this optimization are displayed in Figure 4A. As shown in this figure, the optimal solution gives rise to a regulatory program in which, in particular, the concentrations of the initial and terminal enzymes of the pathway change while the concentrations of intermediate enzymes stay relatively constant. We call this pattern sparse transcriptional regulation of a metabolic pathway. Using several subsequent optimizations, as described in Supplementary Information S6, we analyzed the role of the individual enzymes in this minimal regulatory program.

Figure 4.

Optimal regulatory programs. (A) Optimal regulatory program if the weight of the enzyme costs in the objective function is low (σ=1/30). (B) Corresponding optimal regulatory program for a high weight of enzyme costs (σ=1/3). (C) Absolute changes in enzyme concentrations in the course of the simulation for different weights of protein costs in the objective function. Changes in the concentration of enzymes from their initial concentration are measured as the integral of the absolute deviation from the initial concentration in the course of the simulation (yellow area in Figure 3). (D) Frequency of regulation at different pathway positions for randomly chosen kinetic parameter values over 100 samples. Source data is available for this figure at www.nature.com/msb.

Source data for figure 4A ^{(25.7KB, txt)}

Source data for figure 4B ^{(13.2KB, txt)}

Source data for figure 4C ^{(1.6KB, txt)}

Source data for figure 4D ^{(525B, txt)}

Changes in the concentration of the first enzyme are predominantly used to regulate flux into the pathway and, moreover, the concentration of intermediates in order to prevent their accumulation. Most importantly, through transcriptionally regulating the final enzyme, a more precise control of the flux out of the pathway and, hence, into the product is achieved. In principle, it would be possible to have control over the flux through the pathway while only regulating the initial enzyme. However, there is a certain time delay before changes in the concentration of the initial enzyme affect flux through the final reaction (Supplementary Information S6). Thus, a transcriptional regulation at the initial and terminal locations is especially suited to longer pathways.

Analyzing the concentrations of intermediate enzymes, we found that they are adjusted to the level necessary to achieve the maximal required flux through the pathway. If remaining above a certain threshold, their concentrations can even vary without affecting the flux through the pathway, since this is controlled by the initial and terminal enzymes (Supplementary Information S6). Hence, transcriptionally regulating pathways in initial and terminal reactions is sufficient to control the flux through a pathway as well as the concentration of the product of the pathway.

In order to assess the influence of the kinetic parameters of the individual enzymes on the regulatory pattern that was identified, we performed 100 optimizations in which the catalytic activities and half-saturation constants of all enzymes were uniformly drawn from the interval [0,2]. Subsequently, we determined those enzymes whose cumulative absolute concentration changes were above a threshold value (see Materials and methods). These enzymes were defined to be the regulated enzymes. We found that, depending on the parameter values, the regulation of enzymes other than the initial and terminal enzymes is optimal. In Figure 4D, the frequency at which different enzymes were regulated for randomly drawn parameter values is shown. While a regulation of initial and terminal enzymes within a pathway is not required in all cases, we observe that the frequency of transcriptional regulation increases strongly toward the beginning and end of pathways. The reasons for this increase are, as discussed above, that transcriptional regulation at initial and terminal positions confers the highest level of control on flux through the pathway and into the product.

Moreover, we investigated the influence of the weighting factor σ in the objective function on the observed pattern of regulation (Figure 4B and C). We observed that with increasing costs of initial enzyme concentrations, changes in the concentration of intermediate enzymes are more marked. We call this pattern of a transcriptional regulation of all enzymes within a pathway pervasive transcriptional regulation. These results show that with increasing enzyme costs, there will be a shift from transcriptional regulation of initial and terminal enzymes to regulation of all enzymes.

Specific patterns of regulation in TSR subsystems

After identifying a minimal transcriptional regulatory program that allows control of flux through metabolic pathways, we verified whether the utilization of this program could help to explain the missing coexpression of enzymes along pathways in the TSR subsystems.

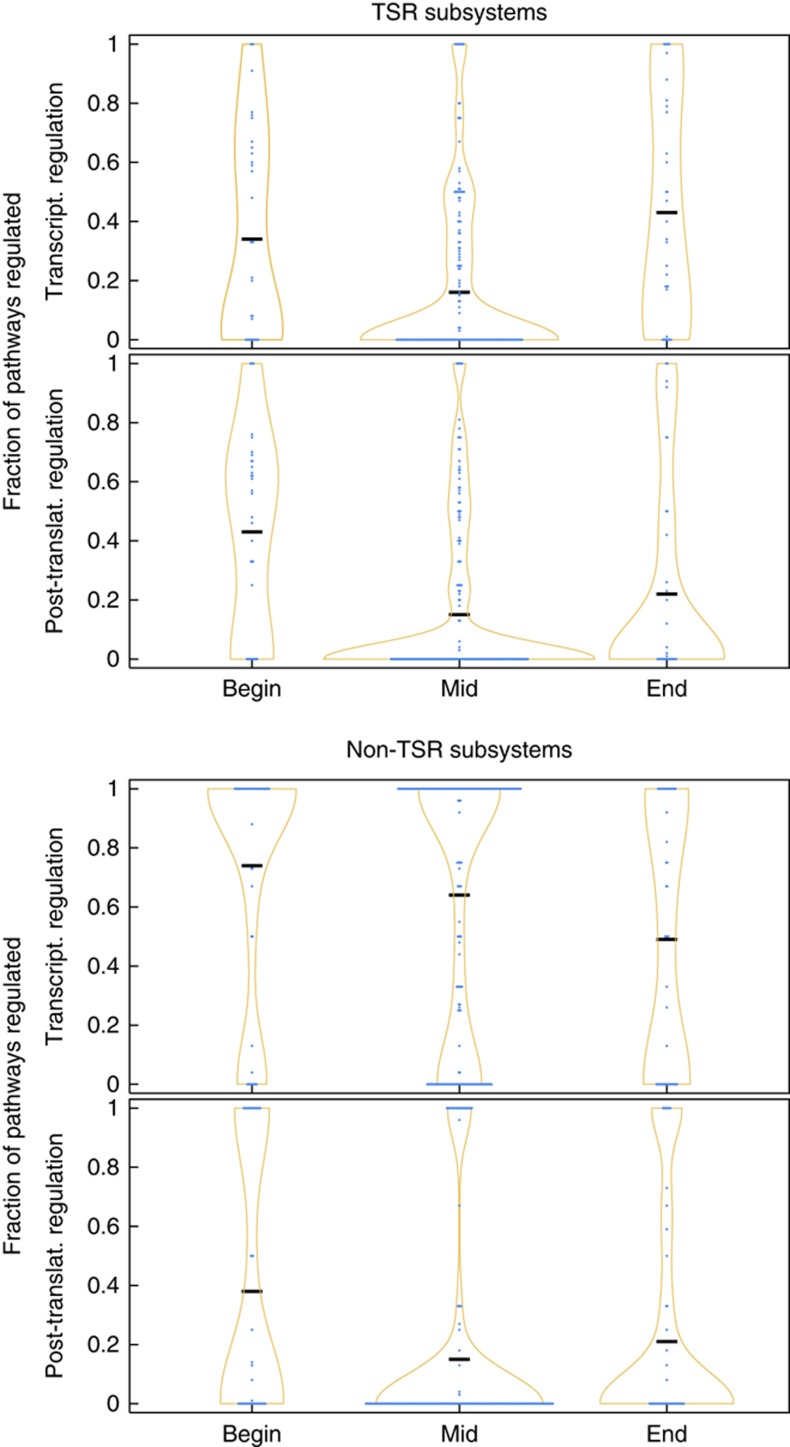
To this end, we performed a pathway position-based analysis of elementary flux patterns in the TSR subsystems. Thus, we identified for each elementary flux pattern the sequence of reactions along the corresponding pathway (using an approach outlined in Supplementary Information S7). Then, for each specific pathway length, we computed how often a given position in each pathway contains a reaction catalyzed by a transcriptionally regulated protein. Please note that for simplicity, we have included the few proteins that are translationally regulated in this list. Hence, by transcriptional regulation, we also refer to the translationally regulated proteins. Subsequently, we classified each reaction, depending on whether it is the first, last or an intermediate reaction within a pathway. The distribution of the occurrence of transcriptional regulation at different pathway positions is depicted in Figure 5. We observed a statistically significant increase in transcriptional regulatory interactions at the beginning and the end of pathways, compared with intermediate reactions (Mann–Whitney–Wilcoxon test, P-value=8.7 × 10⁻⁴ and P-value=4.7 × 10⁻⁶, respectively).

Figure 5.

Positional regulation of pathways. Violin plots of the density distribution of transcriptional and post-translational regulation at different pathway positions in different sets of subsystems. ‘Begin’ corresponds to the first reaction in pathways, ‘End’ to the last reaction in pathways and ‘Mid’ to the remaining reactions. Elementary flux patterns were grouped on a per subsystem basis according to the length of the pathways identified in them. For each subsystem and each pathway length, the fraction of pathways that are regulated at the specified position has been determined (blue dots). If several pathway lengths gave rise to the same fraction of regulated pathways, the corresponding number of dots is arranged horizontally. Ochre lines correspond to the density distribution of the values and black bars to the means of the distributions. ‘TSR subsystems’ correspond to elementary flux patterns from transcriptionally sparsely regulated subsystems and ‘non-TSR subsystems’ to elementary flux patterns from the remaining subsystems. Positional regulation for each pathway length in both groups of subsystems and in each TSR subsystem is provided in Supplemental Information S8. Source data is available for this figure at www.nature.com/msb.

Source data for figure 5 ^{(64.3KB, txt)}

However, a leave-one-out cross-validation on the level of subsystems showed that the subsystem ‘Murein Recycling’ has a strong contribution to the significance of the transcriptional regulation at the initial position of pathways. Without this subsystem, the transcriptional regulation at initial positions is no longer significant (Mann–Whitney–Wilcoxon test, P-value=4.3 × 10⁻¹). Thus, we checked whether there is another mechanism regulating pathways at initial positions. We did observe a statistically significant increase in post-translational regulation at the beginning of pathways (Mann–Whitney–Wilcoxon test, P-value=7.5 × 10⁻⁷) (Figure 5). This pattern remains significant if the subsystem ‘Murein Recycling’ is not taken into account (Mann–Whitney–Wilcoxon test, P-value=4.7 × 10⁻³, see Supplementary Information S8 for an overview of the statistical tests). Consequently, control of initial enzymes is exerted by post-translational and transcriptional regulation while regulation at the end of pathways is exerted through transcriptional regulation. The post-translational regulation at the beginning of pathways is reminiscent of the classical picture of feedback regulation through the product of a pathway. The common explanation is that such a feedback regulation allows to accurately regulate the flux through a pathway. This is in line with our observation that the regulation of initial enzymes, which we observed in the optimization, is used to regulate the flux into the pathway in order to avoid accumulation of intermediates.

We performed the same analysis for the non-TSR subsystems (Figure 5). Here, we did not find a significant decrease in the occurrence of transcriptional regulation at intermediate positions, but most enzymes within pathways were found to be transcriptionally regulated (pervasive regulation). However, there is no apparent difference in the post-translational regulation at initial and terminal positions between TSR and the other subsystems (Mann–Whitney–Wilcoxon test, P-value=0.41 and P-value=0.59, respectively). In consequence, there is also a statistically significant increase in post-translational regulation at initial positions (Mann–Whitney–Wilcoxon test, P-value=2.0 × 10⁻⁶).

A further prediction of the minimal transcriptional regulatory program is that intermediate enzymes of pathways are constitutively expressed, since they do not need to be transcriptionally controlled. At a pathway level, this effect can already be observed from the very low fraction of intermediate enzymes that are transcriptionally regulated in TSR subsystems (Supplementary Figure S20). We additionally tested this assumption by computing the average variance of the gene-expression profiles for every subsystem over all the microarray experiments contained in M^3D. We found that the TSR subsystems rank among those subsystems with the lowest variance in gene expression (Supplementary Information S9). This is a strong indicator that there is a large number of enzymes within these subsystems that are constitutively expressed.

TSR subsystems contain pathways with low-cost enzymes

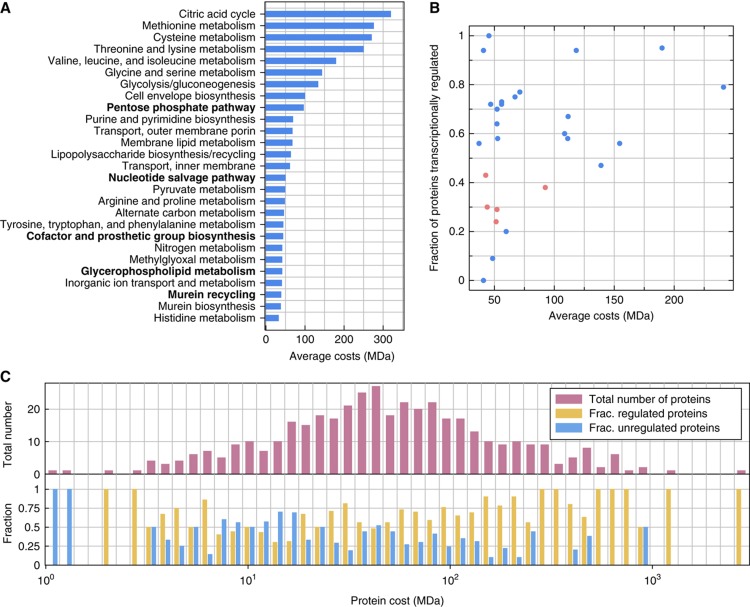
Another important prediction of the optimization is that with increasing enzyme costs there should be a shift from sparse to pervasive transcriptional regulation. To verify this prediction, we analyzed an expanded data set of experimentally measured protein abundances (Lu et al, 2007) (see Materials and methods for details). Here, we define the protein cost as the total mass of this protein present in the cell. We determined the total mass of all enzymes in E. coli for which quantitative abundance data were available (413 proteins). This mass is computed as the number of instances of the protein being present in the cell multiplied by the individual mass of the protein. Hence, the cost of a protein is measured as the molecular weight of all its instances present in the cell in Dalton. We computed the costs of protein expression for each subsystem by first determining the average costs of the proteins catalyzing the reactions of each elementary flux pattern. Then, we computed the average of these values over all elementary flux patterns for each subsystem. Apart from ‘Pentose Phosphate Pathway’, the four remaining TSR subsystems rank within the lower half of the list of subsystems sorted according to the average protein costs of each elementary flux pattern (Figure 6A). Thus, as predicted, sparse transcriptional regulation appears to be favored in subsystems with low-cost enzymes. Another interesting observation from the analysis of enzyme costs is that amino-acid biosynthetic pathways tend to be catalyzed by costly enzymes. For some amino-acid biosynthetic pathways in E. coli, a sequential activation of the enzymes of the corresponding pathways has been observed (Zaslaver et al, 2004), which has been explained by a reduction of time toward product formation (Klipp et al, 2002; Zaslaver et al, 2004; Bartl et al, 2010). Expanding upon these previous works, our results indicate that a sequential activation of proteins within a pathway is particularly relevant if the enzymes of the pathway are costly (i.e. present in a high total mass). This leads to the hypothesis that with increasing total protein mass, there is a shift from sparse transcriptional regulation to fine-tuned transcriptional regulation of all enzymes within a pathway.

Figure 6.

Cost-dependent regulation of pathways and proteins. (A) Average costs of proteins of elementary flux patterns of each subsystem measured as total mass in Megadalton (MDa). TSR subsystems are indicated in bold. (B) The average costs of proteins within each subsystem (x axis) plotted against the fraction of transcriptionally regulated proteins in each subsystems (y axis). Each dot corresponds to one subsystem (magenta dots represent TSR subsystems). (C) Histogram of the costs of proteins. In the upper plot, the number of proteins in each bin is indicated. In the lower plot, the fraction of proteins that are and are not transcriptionally regulated is indicated. For a histogram of the total number of proteins per bin and a plot in which protein costs are replaced by codon adaptation indices see Supplementary Information S11. Source data is available for this figure at www.nature.com/msb.

Source data for figure 6A ^{(1.2KB, txt)}

Source data for figure 6B ^{(1.4KB, txt)}

Source data for figure 6C ^{(1.3KB, txt)}

These results led us to hypothesize that there is a general difference in the transcriptional regulation of proteins depending on their costs. To test this assumption, we constructed a histogram of the costs of regulated and unregulated proteins (Figure 6C). This figure shows that low-cost enzymes are less likely to be transcriptionally regulated in E. coli. This observation is statistically significant: a Mann–Whitney–Wilcoxon test shows that there is a difference in the costs distribution of transcriptionally regulated and non-regulated proteins (P-value=2.3 × 10⁻⁵). A similar observation can be made from Figure 6B in which the average costs of proteins within each subsystem are plotted against the fraction of proteins that are transcriptionally regulated. While there are subsystems containing proteins with low average costs in which most of the proteins are transcriptionally regulated, there are no subsystems with high average protein costs in which only few proteins are transcriptionally regulated.

We performed a similar test in order to elucidate whether post-translationally regulated proteins show a different cost distribution than proteins not known to be post-translationally regulated. Prior to this test, we removed all proteins from the set of post-translationally regulated proteins that are reported to be phosphorylated in the Phosida database, since the gel-based method that was used to detect phosphorylated proteins appears to be strongly biased toward proteins present in high total mass (the median of the total masses of all proteins found to be phosphorylated is three-fold higher than the median of the total masses of proteins with detected masses) (Macek et al, 2008). Using a Mann–Whitney–Wilcoxon test, there is no significant difference in the costs distribution between proteins that are post-translationally regulated and those that are not (P-value=0.45). Thus, protein costs appear not to influence the likelihood of a protein being post-translationally regulated. This is in line with the observation that there is no apparent difference in post-translational regulation between TSR and the other subsystems.

A trade-off between cost minimization and response time minimization explains observed patterns of regulation

The general tendency for costly enzymes to be more likely to be transcriptionally regulated shows that there is a mechanism leading to a more pronounced transcriptional control of these enzymes. An explanation for the underlying principles is a trade-off between the minimization of protein investment and the minimization of response time. This trade-off corresponds to the two cellular objectives to reduce the expression of unnecessary proteins and to reduce the time that is required to respond to changes in the environment. The reduction of response time is particularly relevant, for instance, in response to a stress or after a shift into a growth medium that supports higher growth rates. The trade-off can be explained by the fact that the best minimization of the cost of a protein is achieved by limiting its expression to situations where it is needed. However, a response on a transcriptional level is usually very slow, and in the order of minutes (Zaslaver et al, 2004).

Regardless of the costs of the enzymes, the cell needs to be able to precisely tune the flux through each pathway. According to our optimization analysis and the observation in E. coli, this is optimally achieved through pervasive transcriptional regulation of all enzymes within a pathway, if protein costs are high (non-TSR subsystems). In contrast, sparse transcriptional regulation of initial and terminal enzymes is optimal in cases where protein costs are low (TSR subsystems).

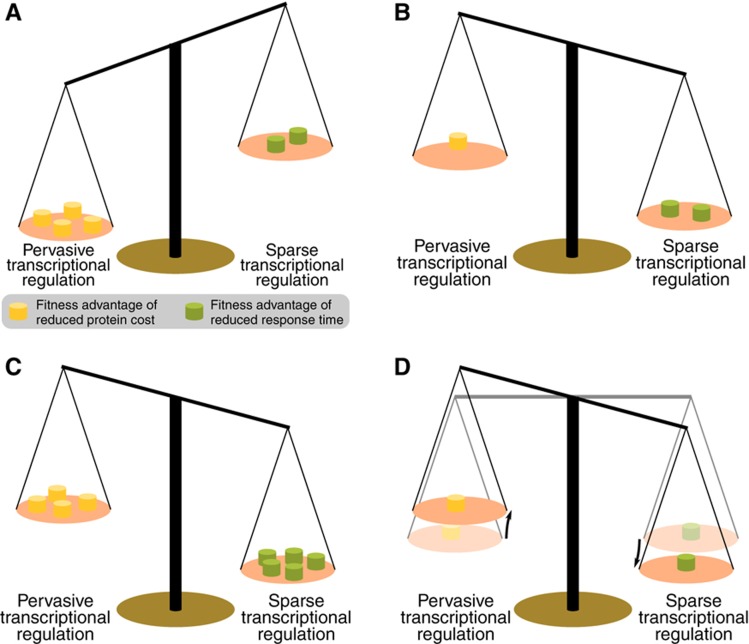
In the context of the trade-off between cost minimization and response time minimization, the first case corresponds to a situation in which the fitness advantage of minimization of protein costs is higher than the fitness advantage of reduced response time (Figure 7A).

Figure 7.

Evolutionary trade-off between protein costs and response time optimization. (A) If protein costs are very high, reducing the costs of unnecessary proteins confers a higher fitness advantage. (B) If protein costs are low, a higher fitness advantage is achieved through a reduced response time. (C) Even if protein costs are high, a sparse transcriptional regulation can be advantageous if the flux through a pathway needs to be adjusted very quickly. (D) If the fitness advantages of reduced protein costs or reduced response time are small, the need to control the flux through a pathway favors the regulation of pathways at initial and terminal positions.

The second case corresponds to two different situations. On the one hand, if the fitness advantage of a reduced response time is higher than the fitness advantage of a reduced protein cost, a constitutive expression of enzymes is advantageous (Figure 7B). This condition is more easily fulfilled by pathways with small enzyme costs. However, an extreme case is the pentose phosphate pathway whose enzymes are very costly. This pathway produces reducing equivalents for a large number of biosynthetic pathways. Hence, it is required for the activity of these pathways. As can be seen from our analysis, being able to quickly adapt the flux through the pentose phosphate pathway confers a higher fitness advantage than reducing the high protein cost through transcriptional regulation (Figure 7C). The observation that flux through the pentose phosphate pathway is only regulated to a small extent through transcriptional regulation is in line with earlier experimental observations (Fong et al, 2006). On the other hand, for some pathways the fitness advantage that could be achieved through following either of the cellular objectives can be very small, in particular if enzyme costs are low (Figure 7D). Consequently, the evolutionary pressure to develop a fine-tuned transcriptional control of all enzymes in the corresponding pathway is low. However, in both situations, the requirement to be able to regulate the flux through a pathway remains. The best control of flux through a pathway can be achieved through regulation of initial and terminal enzymes, so these are predominantly regulated.

Discussion

We have examined global patterns in the regulation of metabolic pathways in E. coli, which can be characterized by elementary flux patterns, a novel concept for the analysis of pathways in genome-scale metabolic networks. Our analysis showed that apart from the classical picture of a pervasive transcriptional regulation of all enzymes within a metabolic pathway, also another regulatory pattern of sparse transcriptional regulation exists in which only initial and terminal reactions are regulated. Both regulatory patterns allow for a precise control of the flux into and out of metabolic pathways. The preference for pervasive or sparse transcriptional regulation can be explained by a trade-off between protein cost minimization and response time minimization. Pathways that are catalyzed by highly abundant and thus costly proteins are predominantly controlled through pervasive transcriptional regulation, while pathways catalyzed by enzymes with low abundance are controlled through sparse transcriptional regulation. However, if immediate control over a pathway is required, sparse transcriptional regulation occurs even if the corresponding enzymes are costly.

The identified trade-off is similar to the trade-off between rate (amount produced per time) and yield (amount produced per carbon source molecule) of different ATP producing pathways (Pfeiffer et al, 2001). While a high rate leads to a low yield, that is, a waste of the carbon source, a high yield allows for a more complete utilization of the carbon source but the overall amount of ATP produced per unit time is lower. In the context of our results, pervasive transcriptional regulation corresponds to an economization of resources while sparse transcriptional regulation corresponds to a waste of resources. If resources are scarce, pervasive transcriptional regulation should be the predominant mode of control of metabolic pathways. In contrast, if an organism is confronted with frequent changes between nutrient-rich/nutrient-poor environments or is constantly growing in nutrient-rich environments, sparse transcriptional regulation should dominate. The ability to quickly shift between different uptake pathways (low response time) through sparse transcriptional regulation would be of great selective advantage despite the high cost of constitutive protein expression, especially in frequently changing environments.

In our work, we used a combination of tools from network inference, pathway detection and dynamic optimization to integrate knowledge from transcriptomic, proteomic and bibliomic data on a large scale. This integrative approach, which we based on a genome-scale metabolic network and the concept of elementary flux patterns, gave us novel insights into the global principles behind different regulatory patterns in the control of metabolism in E. coli. Moreover, our work shows that genome-scale models of metabolism allow for integration of a large number of very diverse experimental data sets on an unprecedented scale. Due to the rapidly growing availability of such data sets (Ishii et al, 2007; Lu et al, 2007; Bennett et al, 2009), we are certain that knowledge of global principles governing the architecture of the regulatory network affecting the metabolism in E. coli will become much more detailed in the near future.

Materials and methods

Data

Metabolic network

Our analysis is based on the genome-scale metabolic model of E. coli, iAF1260 (Feist et al, 2007). For the computation of elementary flux patterns, we split all reversible reactions into irreversible forward and backward steps. Additionally, we modified the metabolic network as described in Notebaart et al (2008): First, we removed the biomass reaction containing a compound reaction consuming all the metabolites required for a reproduction of the cell and replaced it with individual outflow reactions. Second, we allowed the unconstrained inflow and outflow of every compound for which there exists an exchange reaction to simulate the variety of conditions under which the utilized microarray data have been obtained. This is justified for two reasons. First, the largest fraction of the microarray data in M^3D, 363 of 466 experiments, has been obtained from cells grown on a rich medium that can be simulated in this way. Second, as explained in Supplementary Information S1, adding an inflow and an outflow of every metabolite that can be taken up by the cell in principle allows modeling of every possible combination of growth media. This is due to the fact that the elementary flux patterns of every possible growth medium can be generated as set unions of elementary flux patterns computed on this medium. Thus, the elementary flux patterns obtained from this medium are the building blocks of elementary flux patterns on any possible growth medium.

Gene-expression data

We used a gene-expression data set from version 4, build 6 of the Many Microbe Microarrays Database (M^3D, http://m3d.bu.edu; Faith et al 2008), which encompasses data, which has been uniformly normalized using RMA (Irizarry et al, 2003), from 907 Affymetrix microarray chips from 466 experiments.

Known regulatory structure of E. coli

Data on the operonic structure, transcription units and transcription factor—gene interactions have been obtained from RegulonDB 6.4 (Gama-Castro et al, 2008). Data about other regulatory mechanisms that affect the expression of genes like attenuation, translational regulation or RNA silencing have been obtained from EcoCyc version 13.1 (Keseler et al, 2005). For data on post-translational regulation of enzymes, EcoCyc and Phosida (Gnad et al, 2007) have been used. Reactions within EcoCyc with information on the regulation of enzyme activity through small compounds (indicated by ‘Regulation-of-Enzyme-Activity’ and the attribute ‘Physiologically relevant’) were mapped to the corresponding enzymes/enzyme complexes, which catalyze the reactions. For information on post-translational protein modifications we used Phosida, which contains data from a genome-scale identification of phosphorylated proteins in E. coli (Macek et al, 2008).

Cost estimation for proteins in E. coli

Abundance data for 450 proteins in E. coli, grown on glucose minimal medium, has been documented in Lu et al (2007). Since these data were obtained on glucose minimal medium, the pathways for the production of all biomass components of E. coli can be considered to be active. Additionally, using abundance data from 2D-gel electrophoresis provided by Lu et al (2007) and estimating missing protein abundances using an imputation procedure building on known protein complex stoichiometries, we obtained abundance data for a total of 758 proteins (Supplementary Information S10). The total mass of a particular protein (number of instances of the protein multiplied by the mass of the individual proteins) was used as a reference for the cost associated to the production of each protein. For proteins for which no mass has been measured, we used the median of the total protein mass of all proteins: 40.9 Megadalton (except in Figure 6C). This was necessary in order to reduce bias due to proteins that were not detected. The average costs of proteins belonging to elementary flux patterns of a subsystem (Figure 6A) were obtained by translating all elementary flux patterns of this subsystem into gene sets and calculating the average costs of proteins for each gene set individually.

Determination of coexpressed gene sets

In order to determine the sets of coexpressed genes, we used mutual information in combination with the CLR algorithm (Faith et al, 2007). To estimate mutual information, we used a b-spline estimator (bin size of 10, spline degree of 3) based on the work of Daub et al (2004). Next, we applied CLR with the implemented ‘plos’-method to estimate the significance of every mutual information value returning z-scores (for more details see Faith et al, 2007). Only genes that are included in the iAF1260 model were retained (metabolic genes). In the case of M^3D (version 4, build 6), a set of 1257 metabolic genes was selected (three genes out of a total of 1260 metabolic genes are not included in this build). Distance measures were obtained by subtracting each z-score from the maximum z-score for any two metabolic genes. Using average linkage, this distance measure was used as input for an agglomerative hierarchical clustering to build a coexpression tree using MATLAB (http://www.mathworks.com/). We tested the performance of mutual information in comparison to several versions of Pearson correlation (Supplementary Information S4). Confirming previous results based on the quality of inferred gene-regulatory networks (Faith et al, 2007), we found that mutual information in combination with CLR outperformed Pearson correlation based methods.

Elementary flux pattern analysis

Elementary flux patterns have been introduced as a new tool for pathway analysis in subsystems of genome-scale metabolic networks (Kaleta et al, 2009). A flux pattern is defined as a set of reactions of a subsystem of a metabolic network that is part of a physiological feasible pathway through the entire network. A feasible pathway corresponds to a flux vector that fulfills the steady-state condition and uses reactions only in the thermodynamically feasible directions. A flux pattern is called elementary if it is not the combination of other flux patterns, that is, if it cannot be written as set union of other flux patterns. For a formal definition of elementary flux patterns see Kaleta et al (2009).

Computation of elementary flux patterns

We used the 35 biochemically annotated subsystems defined in the model iAF1260 for the computation of elementary flux patterns. Of these we did not consider the subsystem ‘tRNA Charging’, as this subsystem contains only blocked reactions. We were able to compute all elementary flux patterns for 33 of the remaining 34 subsystems. In the subsystem, ‘Cell Envelope Biosynthesis’, an integer solution had been found prior to termination of the algorithm but optimality could not be proved. This indicates that some elementary flux patterns have not been detected in this subsystem (for algorithmic details see Kaleta et al, 2009). The mixed-integer linear programming problems were solved using Coin-OR Cbc version 2.4 (Lougee-Heimer, 2003) and IBM ILOG CPLEX version 12.2 (http://www.ibm.com/software/integration/optimization/cplex, freely available for academic purposes through the IBM Academic Initiative). For the number of elementary flux patterns in each subsystem see Supplementary Information S2.

Transformation of elementary flux patterns into gene sets

In order to compare elementary flux patterns with sets of coexpressed genes, we translated the corresponding sets of reactions into minimal sets of genes encoding the proteins that catalyze them. For this purpose, we used the gene–protein–reaction associations contained within iAF1260, which are Boolean expressions describing the enzymes catalyzing each reaction. In the case where one reaction can be catalyzed by two (iso-) enzymes, the corresponding genes are linked by an OR. If several proteins make up a multienzyme complex that is required for a reaction to proceed, the corresponding proteins are linked by an AND. For an example of the transformation of elementary flux patterns into gene sets, see Figure 1.

After translating the elementary flux patterns into gene sets, we performed several filtering steps. First, we removed those elementary flux patterns in which less than two reactions were annotated for a gene. Second, elementary flux patterns that translated into a set containing less than two genes were removed. This case can arise, for instance, if several reactions contained in an elementary flux pattern are catalyzed by the same gene. Third, if several elementary flux patterns translated into the same gene set(s), we merged them into a single elementary flux pattern,

Comparison of gene sets

To obtain coexpressed or transcriptionally coregulated elementary flux patterns, each translated gene set was compared with each coexpressed gene set of the calculated coexpression tree or to each known regulatory entity (operon, transcription unit or regulon). To compare gene sets, we used a procedure described in Schwartz et al (2007). The comparison of the two gene sets is based on the number of common genes. The hypergeometric distribution was used to test the statistical significance of the intersection. Every comparison of two gene sets of size n and m with an intersection of size k results in a P-value that corresponds to the probability of obtaining the corresponding overlap from two randomly drawn gene sets:

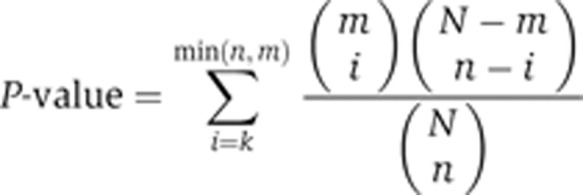For the total population N, we used the value of 1260, which is the number of metabolic genes within iAF1260. False discovery rate control was used for multiple testing correction by applying the Benjamini–Hochberg–Yekutieli procedure, which considers dependencies in the data due to overlapping gene sets (Benjamini and Yekutieli, 2001). The calculated and ordered P-values were compared with local α values α_i:

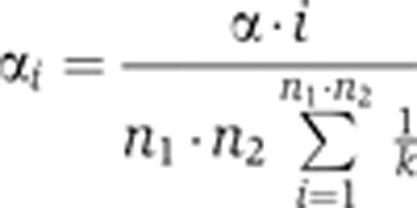A global α value=0.05 was used. The total number of comparisons is given by the product of n₁ and n₂, which are the number of either of the two types of gene sets (e.g. the number of interior nodes of the coexpression tree and the number of translated gene sets from elementary flux patterns of one subsystem).

Algebraic formulation of the optimization problem

The metabolic pathway is described by

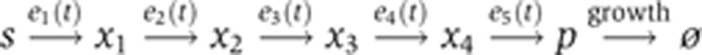with the kinetics

with

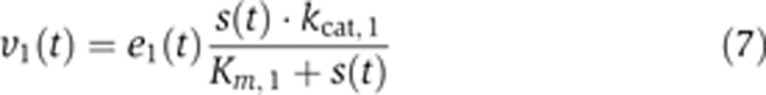and

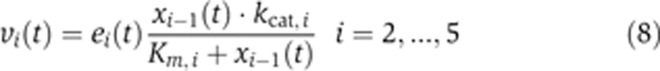and

and

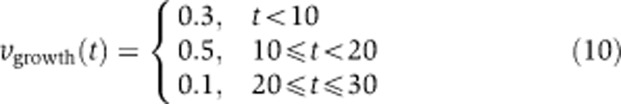Given this model, the objective function

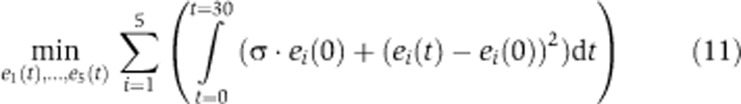with

is minimized subject to the constraints

with

To identify a minimal regulatory program, we built a model of a linear metabolic pathway that converts a substrate s via four intermediates x₁, …, x₄ into a product p. The individual reactions are catalyzed by five enzymes e₁, …, e₅ modeled by irreversible Michaelis–Menten–Kinetics with unit rate constants. Moreover, the concentration of s was assumed to be constant, while there is a constant drain on p through a dilution reaction v_growth. In the course of the simulation, which was performed for 30 (arbitrary) time units, the velocity of v_growth was changed according to Equation (10).

The aim of the optimization was to identify a transcriptional regulatory program by adjusting the time courses e₁(t), …, e₅(t) of enzymes (including their initial concentrations) such that the concentration of p(t) remains within a range (Equation (13)) around its initial concentration of p(0)=1 (which was also the initial concentration of the other metabolites). Moreover, we assumed that the sum of concentrations of intermediates is constrained to a value of Ω in order to avoid their accumulation to toxic levels (Equation (14)) (Schuster and Heinrich, 1987).

For the optimization, we assumed that the cell tries to achieve two objectives: (1) to minimize the total operation costs, that is the initial enzyme concentration multiplied by the duration (since protein needs to be constantly renewed during growth) and (2) to keep the enzyme concentrations during the operation as invariable as possible from their initial values. This means the initial enzyme concentration can be regarded as an optimal operating point. These objectives can be realized by defining the objective function given by Equation (11) where the first term represents the cost minimization and the second term the minimization of the deviation of the enzyme time courses from their initial concentration. The importance of both objectives is adjusted by a weighting factor σ.

This represents a non-linear dynamic constrained optimization problem for which an analytical solution cannot be obtained. Therefore, we used an efficient numerical method, which is an extension of the quasi-sequential approach (Hong et al, 2006) with improved convergence properties (Bartl et al, 2011). Since it is a gradient-based approach, to avoid local optima, we solved the problem in each case 100 times with randomly initialized starting values and show only the solution with the minimal value of the objective function. For an analysis of alternative local optima with higher objective function values, see Supplementary Information S6.

Influence of randomized kinetic parameters

To test the influence of random parameter values, we performed 100 optimization runs in which the kinetic parameters of the reactions were chosen randomly from the interval [0,2]. After the optimization, we defined an enzyme to be regulated if the total deviation from the initial concentration was above a threshold value of 0.1. The principal distribution of regulatory events did not alter on changing this threshold value. For an overview of the results of individual runs see Supplementary Information S6.

Supplementary Material

Supplementary Information

Supplementary Figures S1–29, Supplementary Tables S1–6