Development of a Complex Parent-Metabolite Joint Population Pharmacokinetic Model

Abstract

This study aimed to develop a joint population pharmacokinetic model for an antipsychotic agent in development (S33138) and its active metabolite (S35424) produced by reversible metabolism. Because such a model leads to identifiability problems and numerical difficulties, the model building was performed using the FOCE-I and the Stochastic Approximation Expectation Maximization (SAEM) estimation algorithms in NONMEM and MONOLIX, respectively. Four different structural models were compared based on Bayesian information criteria. Models were first written as ordinary differential equations systems and then in closed form (CF) to facilitate further analyses. The impact of polymorphisms on genes coding for the CYP2C19 and CYP2D6 enzymes, respectively involved in the parent drug and the metabolite elimination were investigated using permutation Wald test. The parent drug and metabolite plasma concentrations of 101 patients were analyzed on two occasions after 4 and 8 weeks of treatment at 1, 3, 6, and 24 h following daily oral administration. All configurations led to a two compartment model with back-transformation of the metabolite into the parent drug and a first-pass effect. The elimination clearance of the metabolite through other processes than back-transformation was decreased by 35% [9–53%] in CYP2D6 poor metabolizer. Permutation tests were performed to ensure the robustness of the analysis, using SAEM and CF. In conclusion, we developed a complex joint pharmacokinetic model adequately predicting the impact of CYP2D6 polymorphisms on the parent drug and its metabolite concentrations through the back-transformation mechanism.

INTRODUCTION

For most drugs undergoing biotransformation, the process results in the formation of a more polar metabolite that is pharmacologically inactive and is eliminated more rapidly than the parent drug (1). For some drugs however, the metabolite may be pharmacologically active and/or produce adverse effects. Joint pharmacokinetic (PK) modeling accounts for the uncertainties in the data and allows feedback from the metabolite data to the parent drug data to influence the estimation. Thus, more and more studies now use this approach (2–4). Also, joint modeling allows to correctly evaluate and predict the impact of drug–drug interactions, and in the case of reversible metabolic systems, it is the only way to properly assess covariate effects.

However, such models can rapidly gain in complexity and present parameter identifiability problems and numerical difficulties in terms of estimation. To solve the issue of structural identifiability, it is important to identify the parameters or “apparent” parameters that can be estimated (3), and for the sake of parameter interpretation or covariate analysis, it might be needed to make some assumptions on the parameters (e.g., fixing one parameter to a given value) (4). Also, instability during the estimation is likely to result in solutions at local minima which may lead to biased parameter estimates and potentially wrong conclusions. Furthermore, numerical issues are likely to arise depending on the algorithms used for estimation in nonlinear mixed effect models (NLMEM). The First-Order Conditional Estimation with Interaction (FOCE-I) algorithm (5), which is implemented in the NONMEM software (6), has been shown to encounter numerical difficulties even on simple single-response models (7,8). Yet, more robust alternatives have been proposed that avoid simplifying the equation for the likelihood, such as the Stochastic Approximation Expectation Maximization (SAEM) algorithm (9) implemented in the MONOLIX (10) and S-ADAPT (11) software. The NONMEM software remains though the most popular tool in population PK analysis because of its superior flexibility in the pharmaceutical field with tools such as NMTRAN. MONOLIX was only recently provided with a similar model translator called MLXTRAN. Of note, the SAEM algorithm was recently implemented in NONMEM software version 7.2.

During its development, an innovative antipsychotic agent from SERVIER research, the (12), was shown to produce a metabolite which was also an active compound, called S35424, through hydrolytic cleavage by hydrolases, as assessed in human microsomes (Fig. 1). Preclinical studies in rat and monkey supported the existence of a back-transformation of the metabolite into the parent drug, and this was further confirmed in a microdose study in man. Such reversible metabolism explained why both compounds showed similar terminal plasma half-life although the parent compound only slightly accumulates while the metabolite accumulates to a much larger extent (AUC accumulation ratio of 3). In addition to hydrolases, other metabolism pathways were identified for the parent drug involving CYP3A4 and, to a lesser extent, CYP2C19. The active metabolite was mainly metabolized through CYP2D6. Both CYP2C19 and CYP2D6 are encoded by highly polymorphic genes and these polymorphisms are known to have an impact on the course of many therapeutic drugs (13). Therefore, the effects of CYP2D6 and CYP2C19 polymorphisms on the PK of the parent compound and the metabolite were investigated in a phase II study using NLMEM. Drug plasma concentrations profiles were documented in patients at two occasions for the parent drug and its metabolite along with genotypes for five polymorphisms of the CYP2D6 gene and two polymorphisms of the CYP2C19 gene. In previous works, we have shown through simulations that asymptotic tests to detect a gene effect in NLMEM require a correction for type I error inflation on designs with unbalanced genotypes and/or including a small number of subjects (8,14). This slight inflation can be handled by permutation tests (15). However, such computing intensive approaches require a fast estimation method, all the more when the structural and variability models become complex.

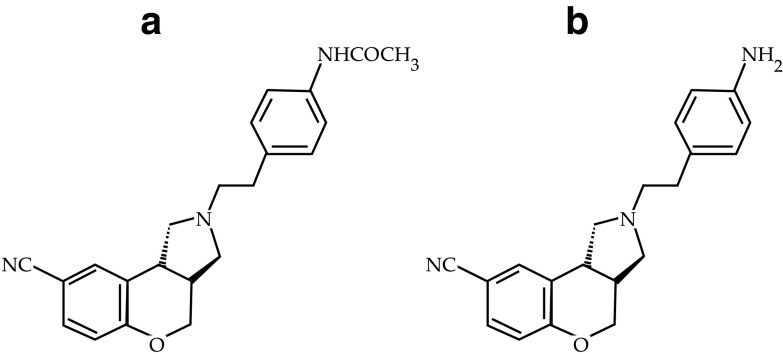
Fig. 1.

a Chemical structure of the parent drug: S33138 and b its active metabolite: S35424

The aim of the present work was thus to develop a joint population PK model for the antipsychotic and its metabolite after oral administration based on the data of the phase II study and to test for genetic effects. Because of the model complexity (reversible metabolism), the building of the model was performed using FOCE-I in NONMEM and SAEM in MONOLIX, in parallel. Furthermore, in order to alleviate the computational burden of permutation tests in the analysis of the genetic effect of CYP2D6 and CYP2C19 polymorphisms, models were encoded in ordinary differential equations (ODE) system and closed-form solutions (CF). Finally, both internal and external model evaluations were performed, the latter using the data from a phase I study. It is noteworthy that external evaluation provides the most stringent method for assessing the predictive ability of the developed model (16).

MATERIALS AND METHODS

Pharmacokinetic Studies

The data used for model building came from a pilot, phase II, international, multicentre, randomized, double-blind, parallel-group study assessing the effect of the abovementioned antipsychotic drug compared to a gold-standard medication. In this study, 120 patients were randomly allocated to four groups receiving for 8 weeks, either 5, 10, or 20 mg of the novel antipsychotic or the gold-standard medication (risperidone). Both treatments were administered orally and once a day in the morning before breakfast. Four blood samples were collected on two occasions, i.e., 4 and 8 weeks after treatment initiation (W4 and W8). The sampling times were set empirically as the following: prior to drug administration and then 1, 3, and 6 h after drug administration. On the day of the sampling, the date and exact time of each blood sample were reported along with the date and exact time of the drug administration as well as those of the previous administration. Those exact times were used for the modeling.

For the external model evaluation, we used the data from a phase I randomized, double-blind tolerance study versus placebo with repeated increasing oral doses. Thirty healthy male volunteers were randomly divided into three groups: in each group, 8 subjects received repeated once-a-day oral administrations of the parent drug at the dose of 10, 20, or 30 mg respectively, while two other subjects received the placebo. In this study, blood concentrations were documented at steady state after 14 days of treatment with the following sampling times: prior to drug administration and then 0.33, 0.66, 1, 1.5, 2, 3, 4, 8, and 12 h after drug administration. The exact times of blood collection were also recorded.

Concentration Measurements and Genetic Polymorphisms

In both studies, the plasma concentrations of the antipsychotic and its active metabolite were determined using a validated method involving solid-phase extraction followed by reverse phase liquid chromatography with mass spectrometry—mass spectrometry detection (LC/MS-MS).

The intra/inter-day accuracy was 97.8%/101.7% for the parent drug and 93%/101.3% for the metabolite; the intra/inter-day precision was 4.7%/5.6% for the parent drug and 6.1%/8.6% for the metabolite and the recovery was 71% for the parent and 65.4% for the metabolite. Typical retention times of the chromatography were about 1.6 min for S33138 and the internal standard and 2.0 min for S35424, respectively. The limits of quantification were 0.56 and 0.44 nmol L⁻¹ for the parent drug and its metabolite, respectively.

In the phase II study, blood samples were taken at the selection visit in order to determine the patient's genotype of CYP 2D6*3, *4, *6, *7, and *8 alleles and of CYP 2 C19*2 and *3 alleles, while in the phase I study, a phenotyping test (dextromethorphan administration) was performed at the selection visit to ensure that all the persons involved were CYP2D6 intermediate or extensive metabolizers. All samples were stored at −20°C and blood samples of included patients were sent on a regular basis to a central laboratory for analysis.

Joint Pharmacokinetic Model

Here, we present the analysis of concentration-time profiles from patients treated with the novel antipsychotic only (excluding patients treated with the reference medication). Concentrations were expressed in nanomoles per liter for the joint modeling of the parent drug and its metabolite; molecular weights were respectively 319.4 and 361.4 g mol⁻¹. Data below the limit of quantification as well as concentrations considered as non-reliable given time or dosing information were treated as missing data and were excluded from the analysis.

Four different structural models of increasing complexity were investigated: their structural representations are shown in Fig. 2 along with the definition of related parameters. The first model, on the left end of Fig. 2, is a two compartment model where the dose is absorbed into the parent compartment at a rate K_ap, and the parent drug (S33138) is either eliminated from the system with a clearance CL_po or is transformed with a clearance CL_pm into a metabolite (S35424) which is eliminated from the system with a clearance CL_mo. Panhard et al. used such a model to jointly analyze nelfinavir and M8 concentrations (3). In the second model from the left on Fig. 2, S35424 can, in addition, be transformed back to the parent with a clearance CL_mp. The existence of a back-transformation of S35424 into S33138 was supported by preclinical studies in rat and monkey and further confirmed in a microdose study in man. This microdose study included five healthy volunteers in a cross-over design where they received an oral dose of S33138 plus an additional intravenous dose of C¹⁴S35424 or C¹⁴S33138 depending on the period with two groups of sequence composed of three and two subjects, respectively. Substantial concentrations of C¹⁴S33138 were measured after administration of C¹⁴S35424. Moreover, back-transformation of the metabolite into the parent drug is a well-known process for numerous amines. A similar model was used to describe the increased hydrolysis of tesaglitazar metabolite into tesaglitazar via biliary circulation in renally impaired subjects (17). In the third model from the left on Fig. 2, a first-pass effect has been considered: the dose not only enters into the parent compartment at a rate K_ap but also enters into the metabolite compartment at a rate K_am. This model, although less physiological, is parsimonious because the fraction of dose transformed into the metabolite is driven by the two absorption rate constants. The last model on the right end of Fig. 2, includes a dose apportionment independent of the rate constant values (K_ap and K_am) with a fraction F_p of the dose leading to the parent and a fraction 1-F_p leading to the metabolite prior to reach the plasma. Such presystemic formation of an interconversion metabolite is mentioned in the extensive review on reversible metabolic systems from Cheng and Jusko (18). For identifiability purposes, the fraction of dose available after absorption (f) was set to 1.

Fig. 2.

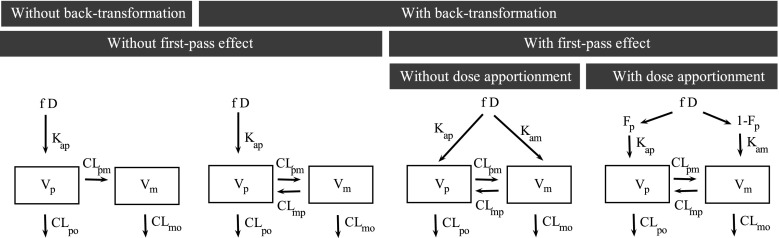
Schematic representation of the four tested structural models. f fraction of dose after absorption, D the dose, F _p fraction of parent reaching systemic circulation after absorption, K _ap absorption constant for the parent, K _am absorption constant for the metabolite, V _p volume of distribution for the parent, V _m volume of distribution for the metabolite, CL _po clearance of the parent by other pathways, CL _pm clearance of the parent into the metabolite, CL _mo clearance of the metabolite by other pathways, CL _mp clearance of back-transformation of the metabolite into the parent drug

Also for all these models, it is noteworthy that all PK parameters cannot be estimated in the present study, since only an oral administration of the parent drug was performed. Estimating all PK parameters requires that both the parent drug and the metabolite be given by the intravenous route in addition to the oral administration of the parent compound (18). It results that only “apparent” parameters can be estimated. The following parameters were identified for the last model: V_p/F_p, V_m/(1 − F_p), E₁ = k_po + k_pm, E₂ = k_mo + k_mp, k_pmF_p/(1 − F_p), and k_mp(1 − F_p)/F_p. An alternative parameterization is given in APPENDIX. As our objective was here to assess the impact of genetic covariates on specific clearances (CL_mo for CYP2D6 and CL_po for CYP2C19), it was necessary to make an assumption on the parameters to estimate all clearances separately (and not global clearances divided by the corresponding volume). Thus, we chose to set V_m equal to V_p. In this respect, F_p, V_p, and the clearance estimates presented here are tagged by an asterisk (*) as a reminder of their reliance on the assumption made on volumes. All drug transfers between compartments were modeled as linear processes.

Population parameter estimation was performed in parallel with the FOCE-I and SAEM algorithms implemented in the NONMEM and MONOLIX softwares, respectively. The first algorithm performs an approximation of the model with a first-order linearisation around the individual predictions of the random effects. In contrast, the second algorithm is a stochastic version of the well-known expectation maximization algorithm, where the individual random effects are the missing variables. In the expectation step, the individual parameters are simulated using a Monte Carlo Markov Chain approach and then used to compute a stochastic approximation of the conditional expectation of the complete loglikelihood which is the loglikelihood of the complete data, i.e., the observations and the imputed individual parameter estimates at the current iteration of the SAEM algorithm. Then, the complete loglikelihood is maximized to obtain the updated estimates of the population parameters. In NONMEM, the convergence of the FOCE-I algorithm is achieved when all parameters have the required number of significant digits, while in expectation maximization-like methods, the definition of convergence is usually left to the user discretion. In MONOLIX, additionally to the visual inspection of convergence graphics, stopping rules are available which are based on the absence of decrease of the complete loglikelihood sequence during the stochastic step and small variability between subsequent population parameter estimates and estimates of the complete loglikelihood during the cooling step.

In both NONMEM and MONOLIX, the Fisher information matrix and the loglikelihood of the model were obtained by linearization of the model around the predictions of the individual parameters. In NONMEM, we used the OPTION UNCONDITIONAL in the covariance step to overcome the convergence issue as well as the OPTION MATRIX = R and MATRIX = S when needed.

The models were encoded through ODE as well as using the corresponding CF solution derived using the Laplace transform approach (19,20) (see APPENDIX). For the models encoded with ODE system, data were fitted using the ADVAN5 routine in the NONMEM software version 7.2 and MLXTRAN with the STIFF option in MONOLIX version 2.4. For the models with a dose apportionment, we used the ADVAN6 routine because of an issue in the ADVAN5 routine to be fixed in the next version of NONMEM. For the models encoded in CF solution, data were fitted using the PRED routine in the NONMEM software version 7.2 and the model building function of MONOLIX version 2.4.

In NONMEM, the number of digits required for convergence (SIG) was set to its default value of 3 for ADVAN5 and to 3 or 2 for ADVAN6 with a fortran 95 compiler. With ADVAN6, we set the number of significant digits for the predicted values (TOL) to 6 and the number of significant digits for the objective function (SIGL) to 6 in the estimation step and TOL = 6 with SIGL = 6 in the covariance step, following guidance from (6); with ADVAN5 the TOL option is not required. In MONOLIX, the algorithm settings were left to the default values; the maximal numbers of stochastic (K1) and cooling (K2) iterations were set to 500 and 200, respectively, with use of automatic stopping rules and only one markov chain (nmc).

The structural model was determined on the data collected at W4 only, and all the systems were considered at steady state with a 24-h dosing interval. We used an exponential model for the between-subject variability to ensure positivity of the individual PK parameters and a logit model to force 0 ≤ F_p ≤ 1. Along the structural model selection, random effects for all parameters but f were assumed to follow a normal distribution with a diagonal variance matrix. A combined error model with an additive component a and multiplicative coefficient b was used for the parent drug and the metabolite. Model selection was performed using the Bayesian information criteria (21): BIC = −2 L + P_poplog(N), where L is the loglikelihood of the model, P_pop is the number of population parameters which includes the fixed effects and the variance components, and N is the number of subjects. BIC allows to compare both nested and non-nested models such as those including F_p or not. In order to compare the NONMEM and MONOLIX output, we retrieved −2 L for each model by adding n_tot × log(2π) to the objective function estimate, n_tot being the total number of observations. Also in the present work, we used N rather than n_tot in the BIC penalizing term, as the observations are dependent within each subject (22,23).

Once the structural model was selected, parsimonious error models (additive and proportional) were tested using the likelihood ratio test (LRT). To capture clearance and volume correlations due to bioavailability variation, between-subject variance was estimated on f. Next, between-subject variance (ω²) nullity was tested using an LRT with, as a reference distribution, a mixture of a χ² distribution with 0 degree of freedom and χ² distribution with 1 degree of freedom (24). Finally, data at W8 were added to the dataset and forward inclusion of within-subject variances (γ²) was performed on parameters with non-null between-subject variance.

Covariate Model

A linear dose effect was systematically investigated on f and F_p parameters using the Wald test. The dose was analyzed as a continuous covariate with 10 mg as the reference dose, so that f and F_p of subject i at occasion k were predicted as described in Eqs. (1) and (2).

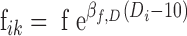1

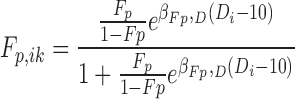2

Also, linear effects of the CYP2D6 and CYP2C19 polymorphisms were investigated following a forward selection based on the Wald test with a significance threshold at 5%. Both genetic covariates were analyzed by means of a phenotypic binary categorization; poor metabolizer (PM) versus the reference class the extensive metabolizer (EM), so that the parameter θ of subject i at occasion k was predicted as described in Eq. (3), where β_{θ,CY P ∗} was non-null for patients CYP* EM and 0 otherwise.

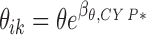3

The classification was performed as follows: carriers of two rare allele were classified as PM (25).

In order to correct the inflation of the Wald type I error shown to occur on unevenly distributed genotypes (14), final p values were assessed using permutations (15). The null hypothesis of the permutation test is that the mean value of the parameter θ would be the same whatever the CYP2D6 and CYP2C19 status, while the alternative is that the mean value would be different between the poor and extensive metabolizers. More specifically, 1,000 datasets were generated by permuting the rows of the covariate matrix from the original dataset. For each covariate, one Wald statistic, 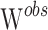, was estimated from the original data and one Wald statistic, 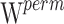, was estimated from each of the 1,000 datasets. Thus, we obtained 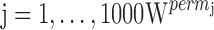. The permutation p value was the proportion: 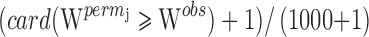. As the patients were sampled on two occasions, we also computed a metric representing the genetic component of variability 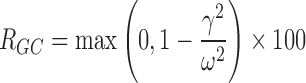(26) for each model parameter with non-null within-subject variance. This component gets closer to 100% when the between-subject variance for the parameter under study is larger than its within-subject variance, so that the variability for this parameter is more likely to be explained by a genetic covariate.

As mentioned previously, the covariate analysis was performed with the assumption V_m = V_p. As the parameter estimates are dependent on this assumption, we have also derived apparent parameters that are independent of any assumption made: 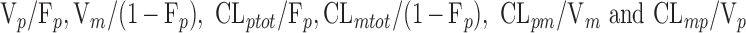(see APPENDIX). The fixed effects and between-subject standard deviation of these apparent parameters were derived by simulation using our final parameter estimates.

Model Evaluation

An internal model evaluation was performed on both occasions as well as an external model evaluation which only considered one occasion. For the internal model evaluation before the addition of the genetic effect, we performed visual predictive check plots where the 90% confidence intervals around the 5th, 50th, and 95th prediction percentiles from 250 simulated datasets were overlaid to the 5th, 50th, and 95th percentiles of the observed data binned using the theoretical sampling times (27). Then after the addition of the genetic effect, we computed the normalized prediction distribution errors (npde), i.e., the observation percentiles within the empirical distribution obtained from the model simulations, decorrelated and normalized using the inverse function of the normal cumulative density function (28).

For the external evaluation of the model after the addition of the genetic effect, we computed the npde and performed a visual predictive check plots where the 5th, 50th, and 95th predicted percentiles from 250 simulated datasets were overlaid to the observed 5th, 50th, and 95th percentiles of the observed data binned using the theoretical sampling times (27).

For the internal and the external model evaluation based on npde, 1,000 datasets were simulated and we used the R npde package (29) for the calculations.

RESULTS

Data

The phase II study dataset combining the observed profiles at both occasions contained 101 patients. Thirty-five patients had a dose of 5 mg, 31 had a dose of 10 mg, and 35 had a dose of 20 mg. The average [range] age in the population was 40 years [22–64], the average weight 69.0 kg [43.6–120.0], and 53.5% were men. Among the 101 patients, 12 patients were classified as CYP2D6 PM and 2 were classified as CYP2C19 PM. Four of the CYP2D6 PM patients received a dose of 5 mg, six received a dose of 10 mg, and two received a dose of 20 mg. The two CYP2C19 PM patients received a dose of 5 and 20 mg, respectively. Genotype information was not available in two patients.

On W4, 355 and 358 concentrations were measured for the parent drug and the metabolite, respectively, in 97 patients, 81 of whom had a complete profile of four samples for both compounds. On W8, 271 and 268 concentrations were measured for the parent drug and the metabolite, respectively, in 71 patients, 51 of whom had a complete profile for both compounds. Sixty-seven patients had concentration-time profiles at both W4 and W8. Only 8 concentrations out of 1,252 (less than 1%) were below the limit of quantification and were discarded from the analysis.

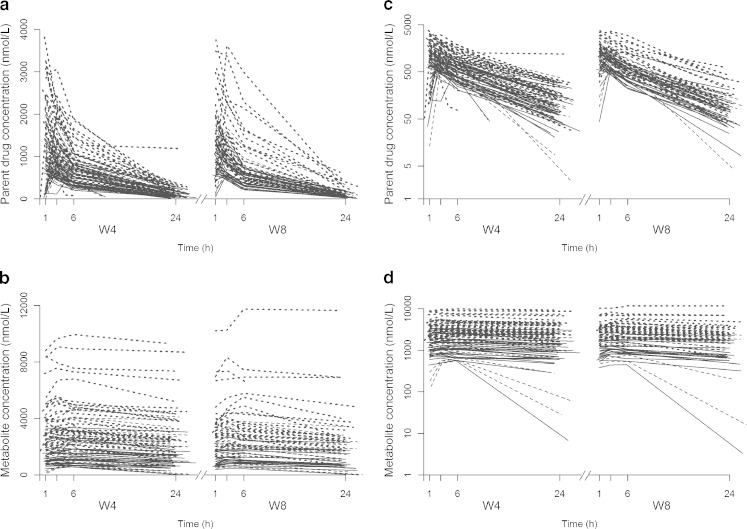
Figure 2 displays the observed concentrations for the parent drug and the metabolite on both normal and semi-log scales versus the time at W4 and W8, revealing a much larger accumulation for the metabolite than for the parent drug.

In the external evaluation dataset, the average age was 28 years [18–45], the average weight 72.5 kg [63.0–99.3] and all patients were men. Eight patients had a dose of 10 mg, eight had a dose of 20 mg, and seven had a dose of 30 mg. After 2 weeks of repeated oral doses, 203 concentrations were measured for the parent drug and the metabolite in 23 healthy volunteers, 20 of whom had a complete profile of ten samples for both compounds. No concentrations were below the limit of quantification.

Structural and Variability Models

Using FOCE-I in NONMEM and SAEM in MONOLIX, convergence was achieved for all models with both coding conditions (ODE or CF). However, with FOCE-I in NONMEM, standard error estimates could only be obtained for the models with dose apportionment in ODE.

Table I reports the BIC along with the error model variance component estimates as well as the computation time for the four structural models investigated plus the model with K_ap  = K_am, using both software and codings on data at W4. Confirming pre-existent knowledge, the addition of the back-transformation mechanism greatly improved the model with a 100-U drop in BIC. The addition of a first-pass effect led to a 40-U decrease in BIC further lowered with the inclusion of an additional F_p term for the dose apportionment. Estimates of error model components were quite close across algorithms and coding with the exception of the additive coefficient for the parent drug. Yet, the relative standard error (RSE) obtained with FOCE-I in NONMEM and/or MONOLIX for this parameter was always very large (data not shown). For the most complex model, computation times dramatically decreased when using CF instead of ODE irrespective of the software (53.8 h to 22.2 min using NONMEM and 2.42 h to 0.6 min using MONOLIX).

Table I.

Bayesian Information Criteria (BIC)

		BIC	a p	b p	a m	b m	Time
Without interconversion	FOCE-I ODE	10,357	5.82	0.35	89.2	0.05	0.31
	CF	10,368	4.00	0.36	96.4	0.05	0.14
	SAEM ODE	10,352	27.60	0.30	105.0	0.05	0.98
	CF	10,359	28.80	0.30	89.2	0.05	0.01
With interconversion	FOCE-I ODE	10,241	0.34	0.34	76.2	0.05	0.50
Without first-pass effect	CF	10,260	1.64	0.35	85.8	0.05	0.16
	SAEM ODE	10,253	0.06	0.34	74.1	0.06	1.37
	CF	10,245	0.02	0.34	70.0	0.05	0.01
With first-pass effect	FOCE-I ODE	10,196	2.84	0.34	71.6	0.05	0.60
Without dose apportionment	CF	10,206	2.97	0.35	74.9	0.05	0.27
	SAEM ODE	10,212	0.08	0.34	74.8	0.05	1.40
	CF	10,215	0.37	0.34	75.3	0.05	0.01
With dose apportionment	FOCE-I ODE	10,186	2.47	0.34	55.90	0.05	53.8
Different absorption rates	CF	10,196	2.44	0.35	53.0	0.05	0.37
	SAEM ODE	10,176	0.57	0.32	58.3	0.05	2.42
	CF	10,196	0.27	0.33	54.0	0.05	0.01
With dose apportionment	FOCE-I ODE	10,149	3.65	0.31	51.30	0.05	35.4
Similar absorption rates	CF	10,166	3.17	0.32	51.20	0.05	0.45
	SAEM ODE	10,141	−0.01	0.32	57.90	0.05	2.37
	CF	10,152	0.09	0.32	52.20	0.05	0.01

Residual error model coefficient estimates and the computing time for the four structural models and the model with similar absorption rates, encoded in ordinary differential equations (ODE) and closed form (CF) using both the FOCE-I and the SAEM algorithms implemented in NONMEM and MONOLIX, respectively, on data at W4

a additive coefficient in nanomoles per liter, b multiplicative coefficient, time computing time in hour

The fixed effect estimates were similar when using ODE or CF for the same model and estimation algorithm, as shown in Table II. The median and maximal relative differences on clearances were respectively 0% and 47% with FOCE-I and 3% and 45% with SAEM in MONOLIX. For the two models without first-pass effect, the FOCE-I estimates were always included in the confidence intervals of the SAEM estimates. Whereas for the model with first-pass effect but no dose apportionment, the FOCE-I estimates for the volumes and all clearance but CL_mp* did not fall within the confidence intervals of the SAEM estimates. For the model with dose apportionment and similar absorption rates, the confidence intervals of the FOCE-I estimates in ODE always included the FOCE-I estimates in CF and overlapped with the confidence intervals of the SAEM estimates. However, with FOCE-I, the clearance of the parent by other pathways (CL_po*) was greater than the clearance of transformation of the parent into the metabolite (CL_pm*), while with SAEM CL_po* > CL_pm*. Also with FOCE-I, the clearance of the metabolite by other pathways (CL_mo*) was similar to the clearance of transformation of the metabolite into the parent (CL_mp*), while with SAEM CL_mo* > CL_mp*.

Table II.

Fixed Effect Estimates

F ap			K ap		K am		V p (=V m)a		CL apo		CL apm		CL amo		CL amp
			(h−1)		(h−1)		(L)		(L h−1)		(L h−1)		(L h−1)		(L h−1)
Without interconversion	FOCE-I ODE	–	–	99.0	NE	–	–	25.2	NE	0.19	NE	2.66	NE	0.61	NE	–	–
	CF	–	–	99.0	NE	–	–	25.0	NE	0.28	NE	2.56	NE	0.59	m	–	–
	SAEM ODE	–	–	46.7	133	–	–	23.0	4	0.57	27	2.06	6	0.46	7	–	–
	CF	–	–	29.2	120	–	–	23.7	4	0.31	39	2.40	6	0.54	7	–	–
With interconversion	FOCE-I ODE	–	–	74.9	NE	–	–	20.9	NE	1.28	NE	2.70	NE	0.38	NE	0.17	NE
Without first-pass effect	CF	–	–	99.0	NE	–	–	20.9	NE	1.37	NE	2.67	NE	0.38	NE	0.17	NE
	SAEM ODE	–	–	65.6	132	–	–	20.9	4	1.00	22	2.95	6	0.40	11	0.20	9
	CF	–	–	101.0	171	–	–	20.8	5	0.99	21	2.91	7	0.42	10	0.18	9
With first-pass effect	FOCE-I ODE	–	–	1.5	NE	0.3	NE	17.4	NE	2.55	NE	1.34	NE	0.18	NE	0.19	NE
Without dose apportionment	CF	–	–	1.5	NE	0.3	NE	17.3	NE	2.53	NE	1.31	NE	0.18	NE	0.19	NE
	SAEM ODE	–	–	5.4	52	0.5	44	20.8	4	0.70	24	2.36	7	0.48	8	0.11	15
	CF	–	–	11.4	77	0.7	71	20.8	4	1.02	20	2.39	8	0.42	10	0.16	12
With dose apportionment	FOCE-I ODE	0.82	NE	1.87	NE	1.88	NE	17.0	NE	2.54	NE	1.21	14	0.18	NE	0.18	NE
Different absorption rates	CF	0.82	NE	1.92	NE	2.05	NE	17.0	NE	2.45	NE	1.24	NE	0.20	NE	0.18	NE
	SAEM ODE	0.86	2	20.2	84	5.9	87	18.4	5	1.39	15	1.76	9	0.34	12	0.13	12
	CF	0.83	3	22.0	101	7.6	121	18.3	5	1.44	15	1.80	10	0.35	12	0.15	12
With dose apportionment	FOCE-I ODE	0.81	2	1.8	40	–	–	16.5	10	2.58	34	1.16	41	0.18	66	0.18	21
Similar absorption rates	CF	0.81	NE	2.0	NE	–	–	16.6	NE	2.48	NE	1.20	NE	0.19	NE	0.17	NE
	SAEM ODE	0.87	2	7.5	46	–	–	18.9	4	1.15	18	2.06	8	0.39	10	0.14	11
	CF	0.85	2	9.3	54	–	–	19.4	4	0.80	23	2.33	7	0.46	8	0.13	14

Their RSE (%, in grey) for the four structural models and the model with similar absorption rates, encoded in ordinary differential equations (ODE), and closed form (CF) using both the FOCE-I and the SAEM algorithms implemented in NONMEM and MONOLIX, respectively, on data at W4

NE not estimated

^aEstimates that rely on the assumption that V _m = V _p

Table III displays the between-subject standard deviation estimates of the four structural models as well as the model with similar absorption rates. The between-subject standard deviation estimates showed greater discrepancies using ODE or CF for the same model and estimation algorithm. Indeed, the median and maximal relative difference on clearance standard deviation estimates were respectively 0% and 150% with FOCE-I in NONMEM and 1.8% and 44% with SAEM in MONOLIX. As for the similarity based on the confidence intervals of the FOCE-I and/or SAEM estimates, the pattern was similar to that for the fixed effect. Of note with FOCE-I, 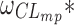and 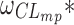estimates were very close to zero, while zero was either included in, or very close to the boundaries of the corresponding confidence intervals of the corresponding SAEM estimates.

Table III.

Between-Subject Standard Deviation

ωF ap			ωK ap		ωK am		ωV p (= ωV m)a		ωCL apo		ωCL apm		ωCL amo		ωCL amp
Without interconversion	FOCE-I ODE	–	–	0.05	NE	–	–	0.21	NE	2.04	NE	0.30	NE	0.51	NE	–	–
	CF	–	–	0.06	NE	–	–	0.20	NE	1.70	NE	0.29	NE	0.51	NE	–	–
	SAEM ODE	–	–	2.18	47	–	–	0.28	14	1.46	12	0.30	15	0.44	10	–	–
	CF	–	–	1.60	61	–	–	0.31	13	1.60	18	0.37	12	0.52	8	–	–
With interconversion	FOCE-I ODE	–	–	3.35	NE	–	–	0.27	NE	0.95	NE	0.20	NE	0.60	NE	0.05	NE
Without first-pass effect	CF	–	–	0.04	NE	–	–	0.25	NE	0.88	NE	0.21	NE	0.60	NE	0.00	NE
	SAEM ODE	–	–	2.66	39	–	–	0.23	17	1.09	12	0.21	27	0.62	9	0.31	40
	CF	–	–	2.94	46	–	–	0.31	12	0.98	13	0.24	22	0.59	9	0.28	50
With first-pass effect	FOCE-I ODE	–	–	0.01	NE	0.32	NE	0.28	NE	0.55	NE	0.02	NE	0.90	NE	0.01	NE
Without dose apportionment	CF	–	–	0.01	NE	0.29	NE	0.28	NE	0.55	NE	0.05	NE	0.87	NE	0.01	NE
	SAEM ODE	–	–	0.66	70	0.66	57	0.30	12	1.12	13	0.20	30	0.55	9	0.36	56
	CF	–	–	0.68	96	0.76	78	0.27	14	0.90	12	0.23	28	0.57	9	0.29	62
With dose apportionment	FOCE-I ODE	0.00	NE	0.00	NE	1.37	NE	0.31	NE	0.54	NE	0.00	NE	0.91	NE	0.00	NE
Different absorption rates	CF	0.00	NE	0.00	NE	1.42	NE	0.33	NE	0.54	NE	0.00	NE	0.86	NE	0.00	NE
	SAEM ODE	0.44	46	2.13	32	1.51	57	0.36	12	0.78	10	0.20	46	0.64	9	0.30	51
	CF	0.12	21	2.00	39	4.89	21	0.30	12	0.75	11	0.15	89	0.60	9	0.41	30
With dose apportionment	FOCE-I ODE	0.01	235	1.12	52	–	–	0.34	37	0.53	76	0.06	3579	0.91	54	0.01	117
Similar absorption rates	CF	0.01	NE	1.15	NE	–	–	0.35	NE	0.54	NE	0.05	NE	0.85	NE	0.01	NE
	SAEM ODE	0.07	34	1.66	22	–	–	0.31	12	0.10	10	0.20	36	0.54	10	0.34	43
	CF	0.07	37	1.96	22	–	–	0.29	12	0.12	12	0.14	61	0.53	9	0.49	28

RSE (%, in grey) for the four structural models and the model with similar absorption rates, encoded in ordinary differential equations (ODE) and closed form (CF) using both the FOCE-I and the SAEM algorithms implemented in NONMEM and MONOLIX respectively, on data at W4

NE not estimated, ω between-subject standard deviation

^aEstimates that rely on the assumption that V _m = V _p

The model selection proceeded similarly using either FOCE-I in NONMEM or SAEM in MONOLIX and ODE or CF, with the selected model including a back-transformation mechanism and a first-pass effect with an F_p parameter for the dose apportionment. Both absorption/formation rate constants were difficult to estimate across models due to the combination of a ten times ratio with the elimination rates and limited plasma data early after dose administration. Thus, we investigated a reduced model with similar absorption/formation rate constants for the parent drug and the metabolite. The BIC decreased by 30 U so that we kept this model for subsequent analyses. The RSE on the absorption rate constant in this model were about 15% with FOCE-I in NONMEM in ODE and 46% and 54% with SAEM in ODE and CF, respectively. Given the shorter computation time and the possibility to obtain standard error estimates, the MONOLIX software with the model encoded in closed-form solution was used in the following.

A proportional and a combined error model were selected for the parent drug and its metabolite, respectively, with estimates for the multiplicative component about 30% and 6%. Of note, in the model including the f parameter, the BIC was reduced by 100 U using a diagonal-covariance matrix for the random effects compared to a full matrix where the smallest and largest correlation estimates were −0.09 and 0.71, respectively. Then, estimation of between-subject variance was found to improve BIC for all parameters except the fraction of dose that escaped first-pass effect (F_p*), CL_mp*, and CL_pm*. Once included the data at W8, the absorption constant rate had to be fixed to its estimate on data at W4 for stability purposes. Only the within-subject variance of the CL_po* was significantly different from 0.

Covariate Model

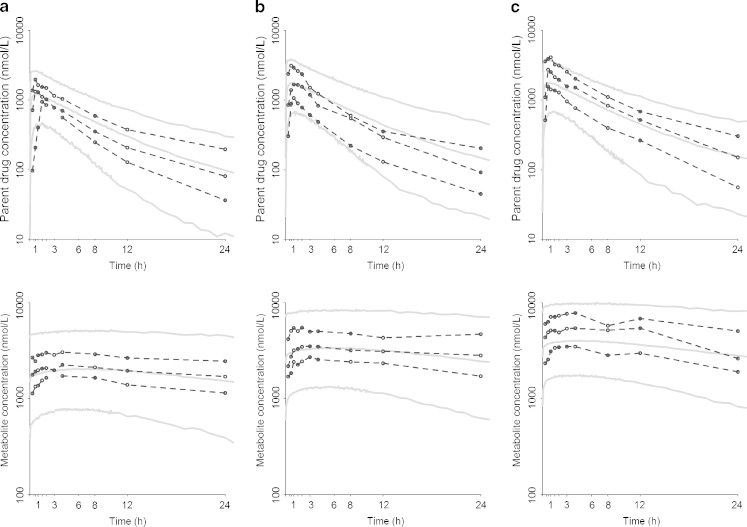
It appears that the f* and F_p* were 10% and 22% higher for a 5-mg dose and 19% and 33% lower for a 20-mg dose, respectively (both p values <10⁻³). The population parameter estimates of the basic model not including the genetic covariate and their RSE are given in Table IV for the 101 patients of the phase II study. Figure 3 represents the visual predictive check (VPC) plots obtained for each compound at both occasions and for the three doses. The predictions from the model described adequately the observed high and median concentration profiles of both molecules for the three doses. However, the model seems to predict less well the low concentration-time profiles, with a systematic overprediction at time 1 h for the parent together with an underprediction of the ensuing times for the 5 mg dose on both occasions and the 10-mg dose at W8. For the metabolite, the VPC plots indicate a misfit for the low concentration-time profiles for the 10 mg dose at W4. It is noteworthy though that some of these misfits might be explained by some atypical individual profiles (see Fig. 4c, d), which drive the lower observed percentile estimates at doses 5 and 10 mg.

Table IV.

Population Pharmacokinetic Parameters of the Parent Drug and Its Active Metabolite for the Model Without and With the Genetic Covariate

	Without the genetic covariate		With the genetic covariate
	(N = 101)		(N = 99)
f	1.00	–	1.00	–
β f,D a (nmol−1)	−0.02	28	−0.02	24
F ap	0.85	2	0.87	2
β Fp,D a (nmol−1)	−0.04	29	−0.06	27
K a (h−1)	8.06	–	8.06	–
V a (L)	19.2	4	19.4	5
CL apo (L h−1)	0.84	11	0.67	11
CL apm (L h−1)	1.94	5	2.09	5
CL amo (L h−1)	0.46	6	0.50	7
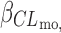CY P 2D6 a (log(L h−1))	−	−	−0.42	40
CL amp (L h−1)	0.09	12	0.09	12
ω f a	0.25	13	0.27	12
ω Ka a	1.50	21	1.41	25
ω V a	0.19	18	0.26	13
ωCL apo	0.52	29	0.46	38
ωCL amo	0.51	8	0.50	8
γCL apo	0.79	12	0.82	12
b p	0.31	3	0.30	3
a m (nmol−1)	66.9	14	66.5	14
b m	0.06	9	0.06	9

Estimates and relative standard errors (in grey,%) using the SAEM algorithm in MONOLIX and encoding in closed form

V = V _p = V _m

ω Between-subject standard deviation, γ within-subject standard deviation, a additive coefficient in nanomoles per liter, b multiplicative coefficient, a _p was fixed to 0

^aEstimates that rely on the assumption that V _m = V _p

Fig. 3.

Confidence interval visual predictive check plots of the selected structural and variability model including the dose effect, on a semi-log scale. The 90% confidence interval around the 5th, 50th, and 95th prediction percentiles from 250 simulated datasets are overlaid on the observed 5th, 50th, and 95th percentiles for the parent drug (top) and the metabolite (bottom) at W4 and W8 for a dose of a 5, b 10, and c 20 mg

Fig. 4.

a, b Spaghetti plot of the observed concentrations of parent drug and metabolite versus time collected on two occasions, 4 and 8 weeks after the treatment onset (W4 and W8) on a normal c, d and semi-log scale. The solid lines represent profiles from patients with a dose of 5 mg, dashed lines profiles from patients with a dose of 10 mg and dotted lines profiles from patients with a dose of 20 mg

The genetic effect analysis indicated that CL_mo* was decreased by 34% (p value = 0.015, Wald test by permutation) in CYP2D6 PM patients The population parameters of the model including the genetic covariate and their RSE are given in Table IV for the 99 patients with available genotyping for the CYP2D6 polymorphisms. Based on these estimates for a CYP2D6 EM patients at a dose of 10 mg, the following estimates could be derived for the apparent parameters (with between-subject, and when applicable, within-subject standard deviation in brackets) V_p/F_p = 22.34 (0.42) L, V_m/(1 − F_p) = 145.27 (0.42) L, CL_ptot/F_p = 3.19 L h⁻¹ (1.58 and 0.83 L h⁻¹), CL_mtot/(1 − F_p) = 4.40 L h⁻¹ (0.65 L h⁻¹), CL_pm/V_m = 0.11 h⁻¹ (0.28 h⁻¹), and CL_mp/V_p = 0.004 h⁻¹ (0.28 h⁻¹). Figure 5 represents the distribution of the concentrations at each dose level between PM and EM. The rise in metabolite concentration levels in CYP2D6 poor metabolizers compared to extensive metabolizers appeared clearly in all dose groups, while for the parent drug, the impact was only noticeable at the 20-mg dose. The between-subject standard deviation for CL_mo* was only slightly decreased with the incorporation of the covariate. However, it is noteworthy that there were only 12 CYP2D6 PM patients in this study. Following Özdemir definition (26), R_GC was computed only for CL_po* because it was the only parameter with non-null within-subject variance. In this study, the R_GC for CL_po* was equal to 0 as 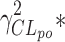was superior to 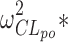, and indeed, no genetic effect was found on this parameter. No effect of the CYP2C19 polymorphisms was found, probably due to the small number of PM.

Fig. 5.

a Boxplots of the parent drug b and metabolite concentrations in the study at the three dose levels. The 10th percentile corresponds to the lower whisker, the 25th percentile to the lower hinge, the median to the thick bar, the 75th percentile to the upper hinge, and the 90th percentile to the upper whisker

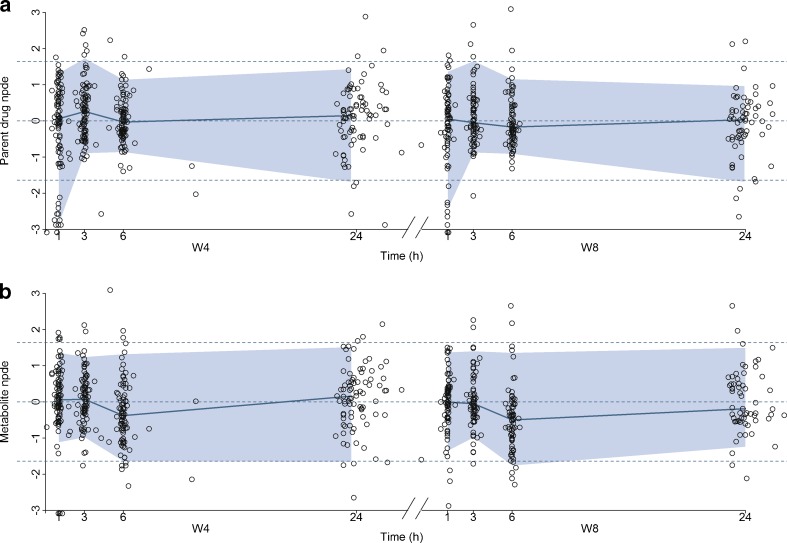
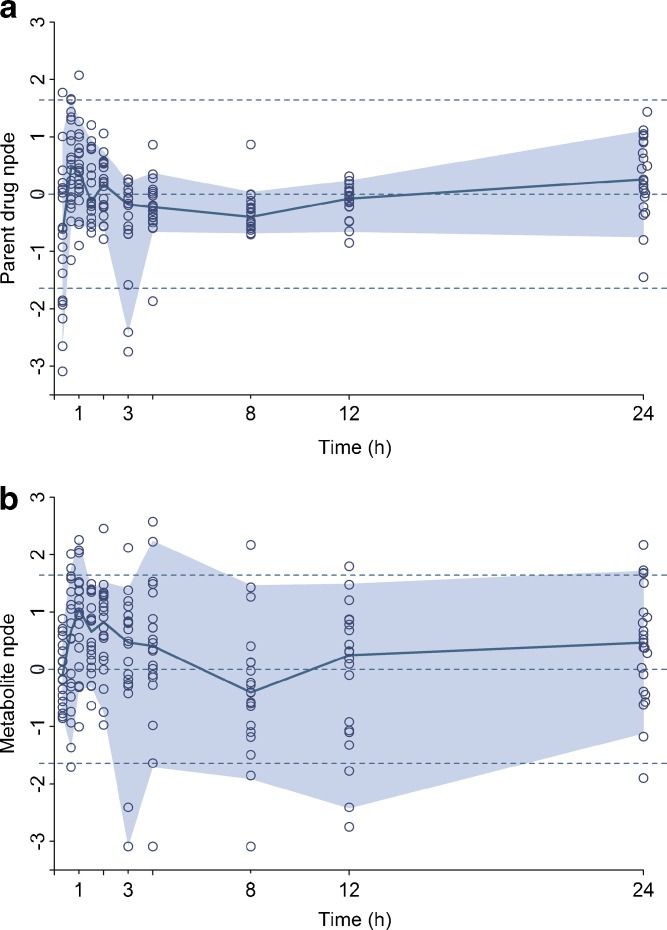
Figure 6 displays the npde from the model including the genetic covariate versus time for the parent drug and the metabolite on both occasions in the original dataset. For the parent, the npde at 3, 6, and 24 h were evenly distributed around 0 with the colored area formed by the 90% interval almost confounded with the dashed lines that represent the 5th and 95th percentiles of the normal distribution. Yet at time 1 h on both occasions, the npde showed a deviation which was previously observed on the visual predictive check plots and the corresponding global tests p values given in the output of the npde calculation were below 0.001. The bias at time 1 h might be explained by the existence of a few patients with a slower absorption whose S33138 profile is not accurately described by the model. For the metabolite, the npde appeared randomly distributed around 0 and within the required boundaries but the corresponding global tests p values were also below 0.001. Figures 7 and 8 present respectively the npde and a visual predictive check plots from the model including the genetic covariate versus time for the parent drug and the metabolite in the external evaluation dataset. The npde for the parent drug tended to be below zero, especially in the first times but remained above the 5th percentiles of the normal distribution. Also, the colored area formed by the 90% interval was somewhat narrower than expected and the corresponding global tests p values were below 0.001. Similarly on the visual predictive check plots, the 5th and 95th predicted percentiles were respectively lower and higher compared to the observed percentiles, especially for the 95th percentiles of the parent drug at the 20-mg dose. Nevertheless, the observed and predicted median was satisfactorily close.

Fig. 6.

Normalized prediction distribution errors versus time from the final covariate model using the model building dataset for the parent drug (a) and the metabolite (b) at W4 and W8. The corresponding 90% interval and the median are overlaid on the plot, and the dashed lines represent the 90% interval and median of the normal distribution

Fig. 7.

Normalized prediction distribution errors versus time from the final covariate model using the external evaluation dataset for the parent drug (a) and the metabolite (b). The corresponding 90% interval and the median are overlaid on the plot, and the dashed lines represent the 90% interval and median of the normal distribution

Fig. 8.

Classic visual predictive check plots of the final covariate model using the external evaluation dataset for the parent drug (top) and the metabolite (bottom) on a semi-log scale. The plain lines in grey represent the 5th, 50th, and 95th predicted percentiles and the dark dots jointed by dashed lines represent the 5th, 50th, and 95th observed percentiles for the parent drug (top) and the metabolite (bottom) for a dose of a 10, b 20, and c 30 mg

In conclusion, the final model provided sensible predictions of the observations despite some difficulties in capturing the lower concentration profiles in patients and an overprediction of the variability in healthy volunteers. Due to these misspecifications, the model was rejected based on the npde global test. However, the heterogeneity in absorption at 1 h could be tackled in future analyses using mixture models to account for the diet or other unknown factors, and healthy volunteers are known to be a less heterogeneous population than patients. This model, involving back-transformation and first-pass effect, had thought to be parsimonious given the study design.

DISCUSSION

In the present work, we compared four different structural models to describe the concentration-time profiles of a novel antipsychotic and its active metabolite obtained at two occasions. We used the FOCE-I algorithm in NONMEM and the SAEM algorithm in MONOLIX to fit the data using models encoded both in ODE and CF solutions. With the final selected model, we investigated the effect of the metabolizer status as defined by CYP2D6 and CYP2C19 polymorphisms on the PK of the parent drug and its metabolite.

The PK of both compounds was reasonably well described by a model including a back-transformation mechanism and a first-pass effect with an additional term for the dose apportionment. Cheng and Jusko (18) defined the acetylation of the metabolite to form back its acetylated parent as a known process for numerous amines, in their extensive review on reversible metabolic systems. They also mentioned the occurrence of presystemic formation of an interconversion metabolite and the consequences in determining the rates and extents of drug absorption and presystemic formation of an interconversion metabolite. In addition, this reference work lists several formulas to derive PK parameters for compounds with interconversion metabolite(s), based on AUC ratio and/or numerical deconvolution after a separate analysis of the parent and/or metabolite profiles. Here, we chose to model both compounds jointly, to provide PK parameter-fixed effects and variance estimates in patients. In the present study, the back-transformation process provided a mechanism-based explanation for the long terminal plasma half-life observed for the parent drug with reduced accumulation at steady state. Actually, the terminal plasma half-lives derived from our model for the parent drug and metabolite were similar, yet the parent drug showed an effective half-life of 8.5 h, i.e., four times faster than that of the metabolite (32.7 h) (30). The first-pass effect, on the other hand, allowed to capture the early bump observed in the metabolite data. Auclair et al. also showed that adding a first-pass effect in their model allowed to fit metabolite concentrations that appeared quicker or at the same time as the parent drug (25). Such a first-pass effect through amidases in the gut and the liver has already been observed in more dramatic proportions for the experimental anti-convulsant related to lidoca¨ıne, D2624 (31). In our final model, the rate of appearance of the metabolite, Kam was set to the absorption rate of the parent drug K_ap. We explain this finding by the fact that the absorption rate of the parent drug would be rate limiting due to the very quick formation of the metabolite. Duffull et al. also reported this phenomenon for ivabradine and its metabolite in (32).

Thorough mathematical investigations were required to identify the apparent PK parameters which are presented here for the final and more complex model (first-pass effect with back-transformation of the metabolite) in the APPENDIX of the article. Yet, interpretation of apparent PK parameters is not always straightforward, and they may not allow proper covariate analysis. For instance, the effect of CYP2D6 was expected on CL_mo only, given prior knowledge, with no impact on CL_mp so using the apparent parameter CL_mtot/(1 − F_p) would not have been appropriate. For this reason, we have decided to make an assumption on volumes in order to be able to estimate all clearances separately. By convenience, we chose to set the volumes equal as this allowed estimation of between and within-subject variability on parent and metabolite volumes. This assumption was judged reasonable since the ratio of 1 is in the range of volumes ratios estimated from the microdose study and gives estimates for the bioavailability and the percentage of dose undergoing back-transformation close to those obtained from the microdose study where clearances of all processes were identifiable. The microdose study gave a median [range] volume of distribution of 78 L [60–287] for the parent and 48 L [30–129] for the metabolite, with a volume ratio of 2.4 [0.5–6]. It is obvious that Fp, Vp and clearance estimates depend on the assumption we made on the ratio of volumes, but setting the volumes ratio to 2.4 in the final model did not markedly impact the results of the analysis apart a significant higher estimate for the percentage of dose undergoing back-transformation (10% instead of 5%) which is less in agreement with the microdose study results.

In silico measures of log P = 2.29 and 2.36, log D (pH 7.4) = 1.24 and 1.32 and pKa1 = 8.46 and 8.46 (tertiary amine) between respectively the parent and the metabolite were similar with the exception of pKa2 = 12.43 (amide) and 4.73 (primary amine). This information neither supported nor infirmed the assumption on the ratio of volumes. Moreover, the volume of distribution also depends on the compound affinity for transporters or tissues as well as its binding ability to plasma proteins. In the present analysis, models with saturable elimination were not investigated as neither the prior knowledge on the compounds nor the goodness of fit plots suggested the existence of such a process. Also, models with a central and peripheral compartment for the parent and metabolite were not evaluated because of the sparse study design which would have not enabled robust estimation.

Here, two estimation algorithms implemented in two softwares were used for data analysis. As regulatory authorities encourage the use of new estimation algorithms, this work addresses a current and relevant issue with a comparison of both softwares on such a complex model and using both codings. The SAEM algorithm has been recently implemented in NONMEM version 7. Yet, we chose its implementation in MONOLIX because it has been thoroughly evaluated compared to the more recent NONMEM one. Both algorithms led to the selection of the same structural model whatever the coding approach. However, substantial differences between the standard deviation estimates were observed across codings for the same model and same estimation algorithm. An extensive comparison of both softwares performances has been already performed and is currently available on the MONOLIX website (http://software.monolix.org/sdoms/software/index.php?/evaluation.html). However, the models investigated were less advanced and all considered only one response. In the present work, using two estimation algorithms was a complementary investigation, and a proper comparison would require simulations from known parameters and models. Taking these limitations into account, some differences in parameter estimates were observed. Among the two software, the absorption rate estimates were those that differed the most, but they were also the most difficult to evaluate. The lack of sampling times early after dose administration led to poorly estimable absorption rate constants. Yet, we chose not to fix these parameters for the structural model building because this was the first modeling of S33138 and S35424 pharmacokinetics performed in patients and this population can greatly differ from healthy volunteers. Also, we were comforted in our decision by the consistency in the BIC and other parameter estimates. Difficulties were met to obtain SEs with FOCE-I in NONMEM despite using several sets of different initial conditions; however, we did not systematically investigate initial conditions (this could be done using hypercube sampling in the multi-dimensional space of parameter). Non-parametric bootstrap can be performed to obtain an empirical distribution of the parameter uncertainty, but in the present work, we have performed permutation-based Wald tests to correct for the departure from asymptotic conditions. Both procedures are computationally intensive and are facilitated by the use of closed-form solutions which provides an important gain of time. While NONMEM easily handles steady-state concentrations with model encoded in ODE, MLXTRAN in MONOLIX version 2.4 requires the user to add dummy lines of dose to mimic the path to steady state. The difference in computation time using this coding approach would thus increase with the number of subjects and the time to reach steady state.

CYP2D6 is an important catalyst of the oxidation of various antipsychotic agents: chlorpromazine, thioridazine, risperidone, and haloperidol (33). Recently, significantly higher risperidone and 9-hydroxyrisperidone (its active metabolite) plasma concentrations have been observed in Korean CYP2D6 PM (34). Here, both the metabolite and the parent drug showed a higher plasma exposure (AUC) in CYP2D6 PM patients compared to EM patients. This indicates that the back-transformation of the metabolite to the parent affects the disposition of the parent drug although concerning only 6% of the dose (30). Hamrén et al. have also described the impact of metabolite decreased elimination on parent drug concentrations in the presence of a reversible metabolism; in patients with impaired renal function, the decreased renal elimination of the tesaglitazar metabolite (acyl glucuronide) causes an increase of the metabolite in plasma, which leads to increased amounts of metabolite undergoing back-transformation and subsequently an accumulation of tesaglitazar (17). In this respect, despite some limitations of the model (i.e., its apparent difficulty in capturing the lower concentration profiles in patients), the present work opens some perspectives for the ongoing development of the antipsychotic. The occurrence of CYP2D6 PM is higher in Caucasians (5–10%) than in East Asians (about 1%) (35) and the CYP2D6 activity is lower in Chinese EM compared to Caucasians (35) due to the CYP2D6*10 allele. Thus, additional investigations should be useful to assess the impact of CYP2D6 polymorphisms in populations other than Caucasians. As the model does not correctly predict the variability in healthy volunteers, it may not be used for comparison of Caucasian and Asian healthy volunteers. However, it may be used as a model for Caucasian patients. Indeed, despite the lack of intravenous data in patients and identifiability problems, the present model gives sensible predictions of the concentrations of the parent drug and the metabolite in patients and of the effect of CYP2D6 on plasma exposure.

CONCLUSION

Using both algorithms and coding, we developed a complex joint pharmacokinetic model of interest for further developments of an antipsychotic and its metabolite. This model enabled us to evidence the CYP2D6 polymorphisms influence on the elimination of the active metabolite and adequately predict its impact on the parent drug levels through a back-transformation mechanism.

APPENDIX

In all the equations below, C_p is the parent drug concentration in plasma and C_m is the active metabolite concentration in plasma following a single oral administration of a dose D of the parent drug.

The ordinary differential equation system and the corresponding closed-form solution correspond to the last model on the right-hand side of Fig. 2, with similar absorption rates K_a = K_ap = K_am.

Ordinary Differential Equation System

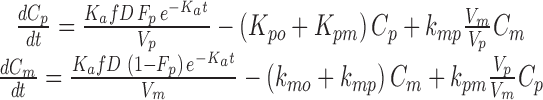4

In the ordinary differential equation system (4), f is the fraction of dose after absorption, D is the dose, F_p is the fraction of parent reaching systemic circulation after absorption, K_a is the absorption constant for the parent and the metabolite, V_p is the volume of distribution for the parent, V_m is the volume of distribution for the metabolite, k_po is the parent rate constant of elimination by other pathways (=CL_po/V_p), k_pm is the parent rate constant of transformation into the metabolite (=CL_pm/V_p), k_mo is the metabolite rate constant of elimination by other pathways (=CL_mo/V_m), and k_mp is the metabolite rate constant of back-transformation into the parent (=CL_mp/V_m).

Closed-Form Solutions

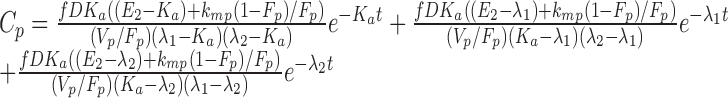5

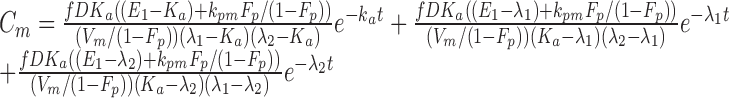6

In both Eqs. (5) and (6), E₁ is the parent drug total rate constant of elimination (=k_po + k_pm), E₂ is the metabolite total rate constant of elimination (=k_mo + k_mp), and λ₁ and λ₂ are the initial and terminal slopes of elimination, respectively defined in Eqs. (7) and (8).

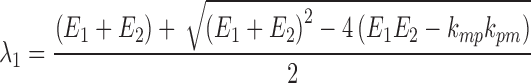7

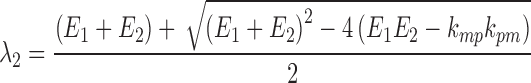8

Parameter Identifiability

From the model slopes, the following parameters may be identified: K_a, λ₁, and λ₂. From the model intercepts, we can identify the following equations:

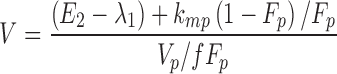9

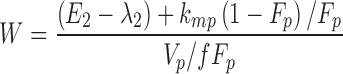10

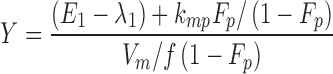11

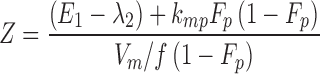12

From (7) and (8) we can write:

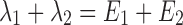13

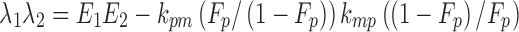14

This yields a system of six equations, where V, W, Y, and Z are four reals like λ₁ and λ₂. We can estimate the following parameters: V_p/f F_p, V_m/f (1 − F_p), E₁ = k_po + k_pm, E₂ = k_mo + k_mp, k_pmF_p/(1 − F_p) and k_mp(1 − F_p)/F_p, with the following solutions:

15

where 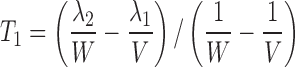and 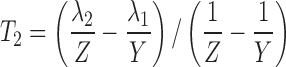. Alternatively, the following parameterization may be used instead:

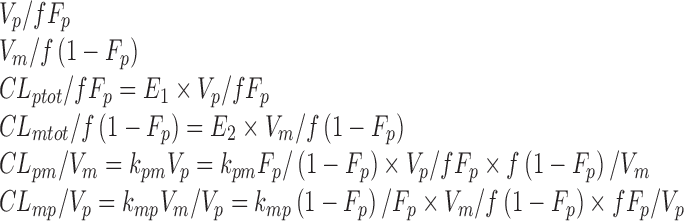16