A Fast Method for Testing Covariates in Population PK/PD Models

Abstract

The development of covariate models within the population modeling program like NONMEM is generally a time-consuming and non-trivial task. In this study, a fast procedure to approximate the change in objective function values of covariate–parameter models is presented and evaluated. The proposed method is a first-order conditional estimation (FOCE)-based linear approximation of the influence of covariates on the model predictions. Simulated and real datasets were used to compare this method with the conventional nonlinear mixed effect model using both first-order (FO) and FOCE approximations. The methods were mainly assessed in terms of difference in objective function values (ΔOFV) between base and covariate models. The FOCE linearization was superior to the FO linearization and showed a high degree of concordance with corresponding nonlinear models in ΔOFV. The linear and nonlinear FOCE models provided similar coefficient estimates and identified the same covariate–parameter relations as statistically significant or non-significant for the real and simulated datasets. The time required to fit tesaglitazar and docetaxel datasets with 4 and 15 parameter–covariate relations using the linearization method was 5.1 and 0.5 min compared with 152 and 34 h, respectively, with the nonlinear models. The FOCE linearization method allows for a fast estimation of covariate–parameter relations models with good concordance with the nonlinear models. This allows a more efficient model building and may allow the utilization of model building techniques that would otherwise be too time-consuming.

INTRODUCTION

The aim of covariate modeling is generally to reduce unexplained parameter variability, improve the predictability of the models, and/or to increase understanding of the studied system. The covariates explored as predictors are of many different types, e.g., demographic factors, laboratory values, disease characteristics, habits, and concomitant therapy-related and study-related factors. The identification of covariate models, i.e., the relationship between the parameters of the models and covariates, within the population modeling program like NONMEM is a time-consuming and non-trivial task. Many different approaches exist for building covariate models, for example automatic screening and directed implementation based on clinically expected relations. Regardless of the approach taken, the improvement of the goodness-of-fit to data, expressed through the change in the objective function value (OFV) is an important determinant of the relationship.

In order to facilitate the identification of parameter–covariate relations Maitre et al. (1) suggested a plot of empirical Bayes estimates of a parameter from a model without covariates versus covariates. When an individual’s data are sparse in parameter information, shrinkage toward the population average parameter will occur (2). This distorts the covariate–parameter relation and may make it appear either stronger or weaker than it truly is. The approach does not handle situations of time-varying covariates as only single covariate and parameter values per subject are explored. Mandema et al. (3) presented an automated generalized additive models (GAM) approach in which the individual empirical Bayes estimates parameters are regressed against covariates to identify possible covariate relations which are then subsequently tested in nonlinear mixed effect models. However, the GAM approach suffers the same disadvantages of empirical Bayes estimates versus covariates plot as mentioned above.

Recognizing the shortcomings of the identification method based on empirical Bayes estimates, Jonsson and Karlsson (4) developed a method based on the analysis of the observed data using a first-order (FO) approximation of the influence of covariates on parameters. The method showed promising properties in identifying parameter–covariate relations. However, this FO linearization method was never incorporated in software, and soon after its introduction, shortcomings of the FO approximation for model selection become evident (5), while in the same studies, the first-order conditional estimation (FOCE) method, with interaction when called for, showed good model discrimination properties when the test statistic was based on the change in objective function value. In the present work, we present a method based on FOCE linearization which is an extension of the previous FO linearization method. The FOCE linearization method is outlined and compared with the corresponding nonlinear models; the relative merits compared with the FO linearization method are also investigated.

METHODS

Population Model and Linearization

In a nonlinear mixed effects model framework, it is often assumed that the data can be described by

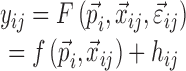1

where y_ij is the ith individual’s jth observation, 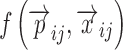is a model that relates the independent variables 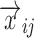and the ith individual’s vector of model parameters 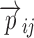to the observations, and h_ij is the residual error. Usually, the residual term h_ij is modeled as a function of 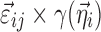, where 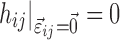, , 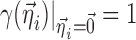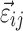is assumed as symmetrically distributed with the variance–covariance matrix Σ, and 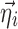is assumed as symmetrically distributed with mean 0 and variance–covariance matrix Ω. Normally, γ depends only on some elements of 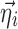, and often, there is no dependence at all, i.e., 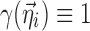. Common forms are 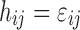(additive error), 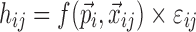(proportional error), or a combination of the two.

The vector of model parameters 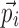can be modeled as

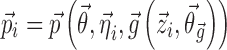2

where 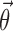are the typical values of the parameters in the population, 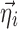describes the inter-individual and inter-occasion variation of 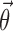, and 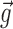is a function of additional population parameters 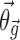, which are specific to the function 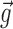, and covariates 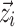such as age, gender, and clinical laboratory measurements. Commonly, the inter-individual variation of P_ki is described using the following models:

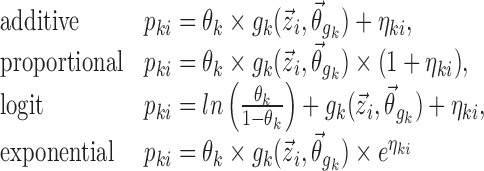3

In the above examples, the same indexing is used for p and η, illustrating the common situation that the elements of 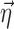are unique to their respective parameters, but this assumption is not required for the proposed method. The covariate functions are defined so that the value of p_ki will be the same as if no covariate effects are included at all when the effect parameters 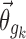are 0, or when the covariates 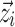are equal to that of the typical individual. Specifically, this means that 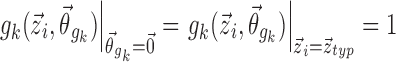for covariate functions which are multiplicative with respect to p_k, as with additive, proportional, or exponential models for inter-individual variation, and 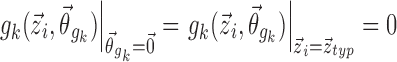for covariate functions which are additive with respect to p_k, as with the logit model.

The FO and FOCE algorithms of NONMEM use a first-order Taylor expansion of F arou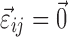nd and 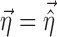, where 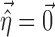with the FO method and 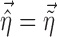, where 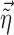are the empirical Bayes estimates of 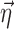, when the FOCE method is used. In NONMEM, F is first linearized around :

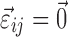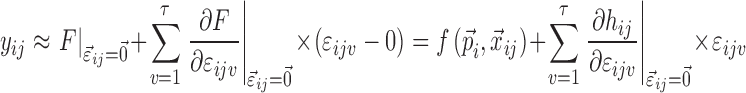4

In the FO and FOCE algorithms, Eq. 4 is then linearized around 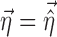. In the method proposed in this work, Eq. 4 is linearized both arou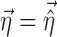nd and 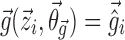in the following way:

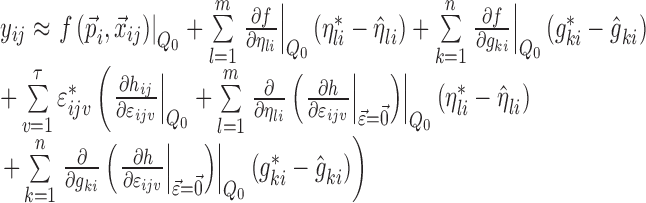5

where 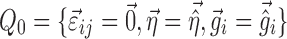; m is the number of elements in 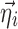; n is the number of elements in 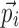; and 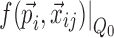is the model prediction based on 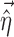, , 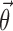and 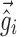. Equation 5 reduces to the linearization used in the FO and FOCE algorithms if 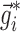is set to 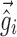, i.e., there is no linearization around .

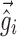Only the parameters marked with an asterisk in Eq. 5 are not known after the minimization or single-point evaluation from the original nonlinear model. Partial derivatives with respect to η_li and ε_ijv are outputs by NONMEM, and formulas for the partial derivatives with respect to g_ki can be derived from the expressions for 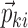and the error model using the chain rule as follows:

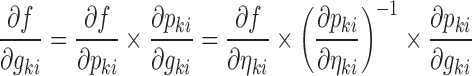6

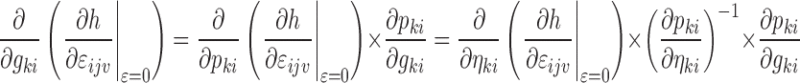7

where the expressions for 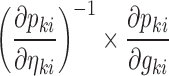are easily derived using Eq. 3. In Eqs. 6 and 7, it is assumed that each element of 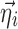affects at most one element of 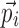. Without this assumption, the derivation strategy remains the same, but the expressions will include sums over k and l and require solving a linear system of equations (not shown). In this work, we have only tested models where the assumption holds.

It is necessary in the proposed method that all parameterizations of the covariate function fulfill the requirement that 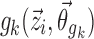has no effect on p_ki for the typical individual because 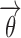are fixed in the linearized Eq. 5.

For covariate functions which are additive or multiplicative with respect to p_k, the covariate functions 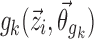are parameterized as Eqs. 8 or 9, respectively.

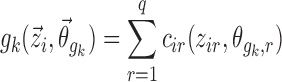8

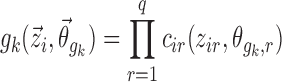9

where z_ir is the ith individual’s covariate value. Examples of 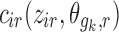for continuous covariate parameterizations are:

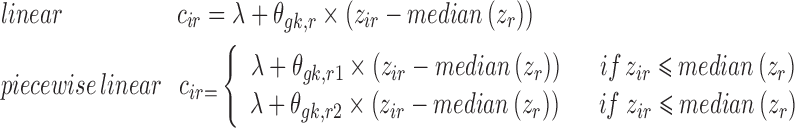10

where λ is 0 for g_k which are additive and 1 for multiplicative g_k, and is estimated in Eq. 5 and is a measure of the change in parameter value per unit change in the covariate. For multiplicative g_k, the

11

parameterizations can also be used.

For categorical covariates with levels a and b, c_ir is parameterized as:

12

where f_a is the fraction of individual with a as the value of the covariate. The centering method in Eq. 12 requires that categorical covariates are bivariate.

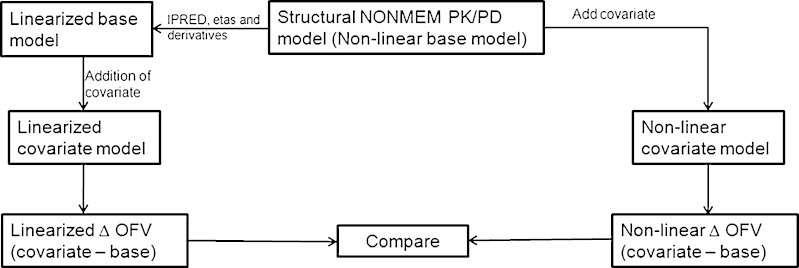
The two steps involved in the current method are the development of a linearized base model and the addition of covariates to the linearized base model. The linearized base model is developed by extracting PRED (FO), IPRED (FOCE), and first partial derivatives of the individual predictions with respect to etas from the conventional nonlinear mixed effect base model (Fig. 1, left side). In the next step, the covariates are added to the linearized base model. If desired, the base model can also include pre-selected covariates.

Fig. 1.

Schematic representation of the steps involved in the linearization approach and comparison with nonlinear models for the inclusion of a covariate

The linearized and nonlinear base models under FO and FOCE approximations were fit to the observed data. This step was performed in order to assure that linearization is correctly performed and the results are the same as the nonlinear base model. Also, the linearized covariate and nonlinear covariate models were fit to the observed data using both FO and FOCE approximations. The schematic representation of the method and comparisons is shown in Fig. 1. An example of a NONMEM model file for univariate testing is shown in Appendix 1. The calculations were performed in NONMEM (version 7) (6) running on Linux cluster with CentOS 5.5 × 86 operating system and gfortran, version 4.5.0, compiler from GCC.

Datasets

Both the simulated and real datasets were used to compare the FO and FOCE linearization methods with the corresponding nonlinear method.

Simulated Dataset

In order to test the sensitivity of the method to the quality of the dataset, both rich and sparse sampling techniques were employed. The simulated continuous covariate was tested for inclusion in both the linear and nonlinear models for the 100 datasets for each condition.

1. Rich sampling: A one-compartment IV bolus model was used to simulate the datasets of 100 individuals with five samples per individual. The samples were collected at 2, 4, 6, 8, and 10 h post-dose. The mean (inter-individual variability) CL and V were 30 L/h (30% CV) and 100 L (30% CV), respectively, without any covariate parameter relation. One hundred datasets were simulated using these conditions, and in parallel, a normally distributed covariate (COV1), unrelated to the pharmacokinetic data, was simulated. The mean and CV of COV1 was set to 80 and 20%, respectively.

2. Sparse sampling: A one-compartment IV bolus model was used to simulate the datasets of 50 individuals with two samples (1 and 10 h post-dose) and 50 individuals with one sample (50% 1 h post-dose and remaining 10 h post-dose). Simulations were performed as in the example above.

3. Docetaxel dataset: The structural model describing docetaxel-induced myelosuppression as reported in (7) was used for simulation. Briefly, the model consists of a compartment representing stem cells and progenitor cells, three transit compartments with maturing cells, and a compartment representing circulating neutrophils. A negative feedback between circulating neutrophils and the proliferation rate was included in the model. The true model comprises three different univariate scenarios, namely: (a) effect of α1-acid glycoprotein (AAG) on baseline neutrophil concentrations (NEU_t0); (b) effect of age on NEU_t0; and (c) effect of previous chemotherapy (PC) on SLOPE. The following fixed effects parameter estimates were used for simulation: 5.20 × 10⁹ cells/L (NEU_t0); 84.1 h (mean transition time, MTT); 0.144 (γ); 14.6 L/μmol (SLOPE); and 0.4710, 0.004, and 0.216 (coefficients for AAG, age, and PC, respectively). A log-normal distribution was assumed for inter-individual variability (η, IIV).The residual variability (ε) was 42% (proportional error). The IIVs (CV%) for NEU_t0, MTT, γ, and SLOPE were 28%, 14%, 15%, and 45%, respectively. All random effects variables (η and ε) were assumed to be symmetrically distributed with zero mean and variance ω² or σ², respectively. Since the model is computationally intensive, only ten datasets (n = 10) were simulated for each scenario using these conditions (FOCE approximation) and the design of the original reported study (7).

Real Dataset

In the current work, the pharmacokinetic structural model was adopted from the literature and only the covariate models were explored.

1. Phenobarbital (8): The dataset contains 155 observations from 59 subjects ranging from one to six samples per subject. The structural model describing the data was a one-compartment model with IIV on both (CL) and volume of distribution (V). Both weight and APGAR score were treated as continuous covariates. The covariates were tested on CL and V.

2. Moxonidine (9): The dataset contains 1,022 observations from 74 patients. The base model describing the data was a one-compartment model parameterized in CL, V, and Ka with IIV and inter-occasion variability (IOV) on CL, V, and Ka. Four dichotomous covariates including concomitant medications (digoxin, diuretic, and ace inhibitors), sex, and one continuous covariate (age) was considered in this study. The covariates were tested on CL and V. Also, the base model considered in this analysis already had creatinine clearance on CL and weight on V. The other remaining covariates were added to it using both the linear and nonlinear FO and FOCE methods.

3. Pefloxacin (3,10,11): The dataset contains 337 observations (plasma concentrations) from 74 critically ill patients obtained after multiple IV infusions of pefloxacin. The plasma samples were withdrawn at three different occasions ranging from 2.5 to 14 days. A one-compartment model with IIV and IOV on CL and V was used to describe the data. Weight, age, creatinine clearance bilirubin (millimoles per liter), and systolic blood pressure were treated as continuous whereas sex and center were treated as dichotomous covariates. All the covariates were tested on CL and V.

4. Dofetilide (12): The dataset comprises 9,548 observations from 1,438 patients. A total of 43 covariates including demographics, concomitant medications, biochemical markers, and clinical status were tested on CL. The model describing the data was a one-compartment model with first-order absorption with IIV on CL, V, and Ka.

5. Docetaxel (13): The dataset contains 3,553 neutrophil observations from 601 patients. Two continuous (age and AAG) and three dichotomous covariates (performance status (PERF), PC, and sex) were tested on NEU_t0, MTT, and SLOPE. The model consists of five compartments in series: a compartment representing proliferative cells, three compartments representing maturation, and a compartment representing circulating neutrophils. The transfer between compartments is first-order. Docetaxel acts nonlinearly on the proliferative cells. A negative feedback between circulating neutrophils and the proliferation rate is included in the model. Further details of the pharmacokinetic–pharmacodynamic models are described elsewhere (7).

6. Tesaglitazar(14): The population pharmacokinetic–pharmacodynamic (PK/PD) model relating tesaglitazar exposure, fasting plasma glucose (FPG), hemoglobin (Hb), and glycosylated hemoglobin (HbA1c) overtime in patients with type 2 diabetes mellitus was used for covariate analysis. The dataset contains 4,035, 3,115 and 1,548 observations for FPG, Hb, and HbA1c, respectively from 412 patients. The model describes the life span of red blood cells through a transit compartment model. The impact of drug treatment on FPG is characterized through an indirect response model, and FPG influences the glycosylation rate of Hb in a nonlinear manner. The effect of sex was tested on EC_50FPG and rate constant for the release of RBCs (K_inRBC), whereas the effect of sex and age was tested on EC₅₀ dilution.

Model Comparisons

For both FO and FOCE linearizations, the covariate models were compared with the conventional nonlinear models in terms of difference in objective function values (ΔOFV). The covariate screening was performed using a univariate search. The ΔOFV between two nested models is approximately χ²-distributed, and the critical ΔOFV for α = 0.05 at 1 degree of freedom is 3.84. The ΔOFV between the covariate and base models for both the linear and nonlinear models are calculated and are represented graphically by a plot of linear ΔOFV (covariate–base) versus nonlinear ΔOFV (covariate–base).

In the current work, the performance of the linearization models to the nonlinear mixed effect models with respect to the importance of covariate–parameter relations is compared based on the similarity of ΔOFV. Additionally, as an illustration, it was compared whether the significance of the covariate–parameter relations based on the likelihood ratio test (p < 0.05) would differ if based on the linear or nonlinear model. In this comparison, the nonlinear models are treated as providing the correct answer, and the outcome of the comparison is referred to as “true” if the linear models provide the same result as the nonlinear model and “false” otherwise. Outcome is “statistically significant” if the covariate is significant and “not statistically significant” otherwise.

RESULTS

Simulated Dataset

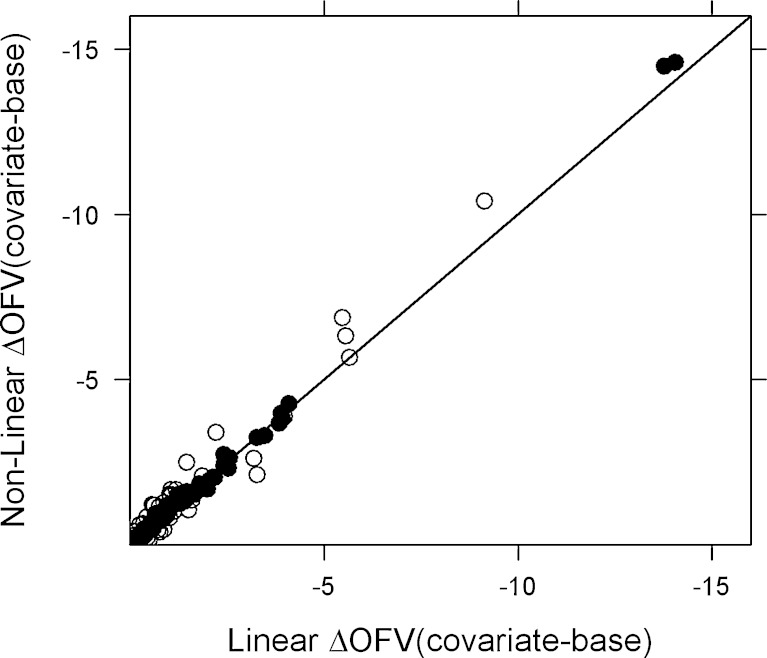
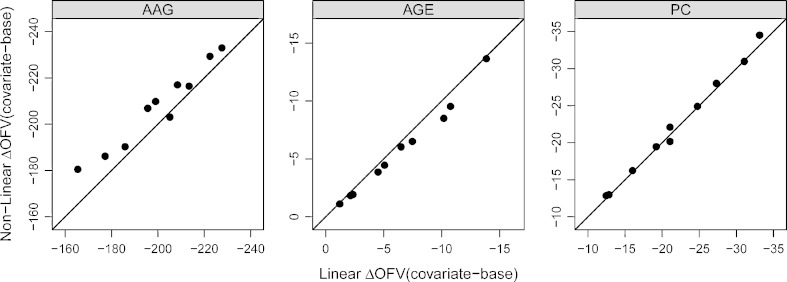
For both rich and sparse one-compartment data, excellent agreement was obtained between the linearized FOCE and nonlinear models as assessed by ΔOFV’s. In the case of rich data and FOCE, the non-statistically significant relations identified by the nonlinear and linear methods were 96% and 94%, respectively, whereas for sparse data, the non-statistically significant relation identified by both the linearized and nonlinear methods was 95%. A plot of linearized ΔOFV (covariate–base) versus nonlinear ΔOFV (covariate–base) is shown in Fig. 2. The ΔOFV (covariate–base) between the linear and nonlinear models are very similar for the simulated docetaxel dataset (Fig. 3).

Fig. 2.

Correlation in ΔOFV (covariate model–base model) between the nonlinear models and linearized models (FOCE) for 100 datasets. The filled circles (rich) and open circles (sparse) represent ΔOFV of the linear model in FOCE versus the nonlinear model in FOCE

Fig. 3.

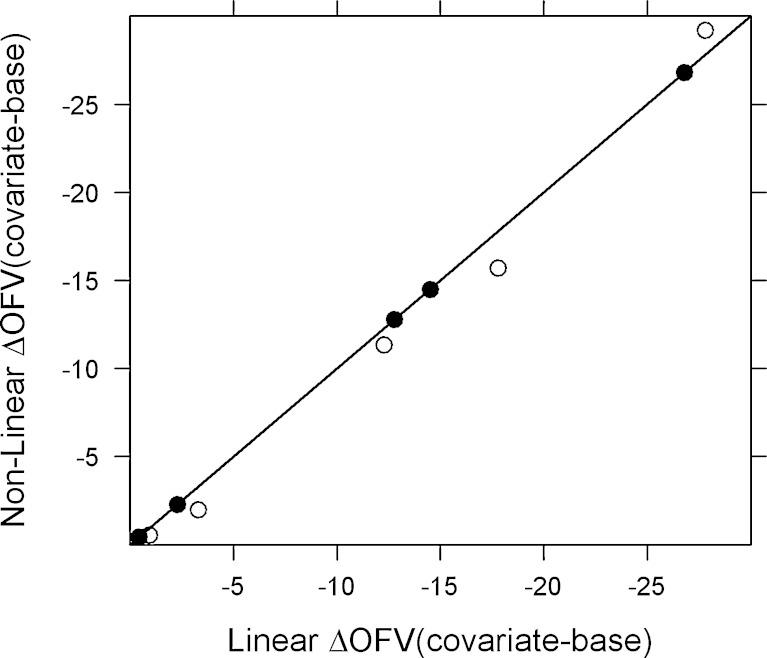
Simulated docetaxel dataset: The vertical and horizontal axes in each panel represent ΔOFV (covariate model–base model) between the nonlinear models and linearized models (FOCE), respectively, for ten datasets. The filled circles represent ΔOFV of the linear model in FOCE versus the nonlinear model in FOCE. The left, center, and right panels represent the effect of AAG on NEU_t0, effect of age on NEU_t0, and effect of PC on SLOPE, respectively

Comparison of Covariate Coefficient from Linear and Nonlinear Models

The three different simulated true models (docetaxel dataset) reflect strong, intermediate, and weak covariate effect scenarios. The effect of AAG and age on NEU_t0 and PC on SLOPE are examples of strong, weak, and intermediate effects, respectively. The true coefficients for AAG, PC, and age are 0.471, 0.216 and, 0.004, respectively. The mean ± SD coefficients for AAG, PC, and age from the nonlinear models are 0.480 ± 0.046, 0.216 ± 0.037, and 0.004 ± 0.001, respectively, whereas for the linear models in the same order are 0.422 ± 0.018, 0.191 ± 0.030, and 0.004 ± 0.001. The mean coefficients and the corresponding drop in ΔOFV (Fig. 3) are very similar for the linear and nonlinear models, suggesting similar magnitude of covariate effect.

Real Dataset

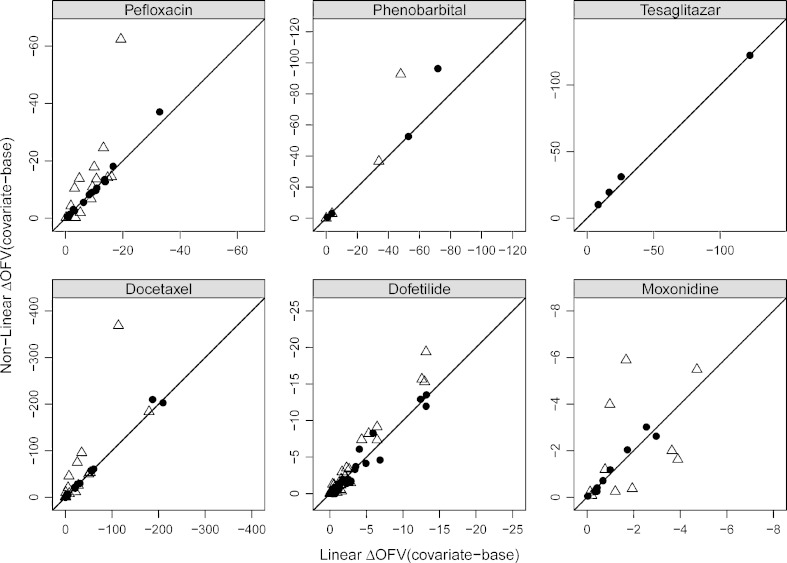
A brief summary of the statistically significant (α = 0.05, df = 1) covariate identified by a univariate search using different methods for real datasets is included in Table I. In all the investigated real datasets, the FOCE linearization performs better than the FO linearization (Fig. 4, filled circles (FOCE) versus open triangles (FO)). For all the covariate–parameter relations (phenobarbital dataset), a good (FO) or excellent (FOCE) agreement was obtained between the linear and nonlinear models, except for the effect of weight on V (ΔOFV >60) as shown in Fig. 4. In the case of the moxonidine dataset, none of the covariates were identified as statistically significant by FOCE approximation (linear and nonlinear methods). Excellent agreement was obtained between the linearized and nonlinear methods (FOCE) for moxonidine, pefloxacin, dofetilide, docetaxel, and tesaglitazar datasets (Fig. 4)

Table I.

Summary of Statistically Significant (α = 0.05) Covariate–Parameter Relations Identified By Different Methods

Datasets	FO		FOCE
	Nonlinear mixed effect models	Linearized	Nonlinear mixed effect models	Linearized
Phenobarbital	Weight on CL and V	Weight on CL and V	Weight on CL and V	Weight on CL and V
Moxonidine	ACE and Age on CL.	ACE on CL.	None	None.
Pefloxacin	Bilirubin, creatinine clearance, sex, and weight on CL and V; age, center, and systolic blood pressure on V	Bilirubin, center, creatinine clearance and sex on both CL and V; age on CL and weight on V	Bilirubin, center, creatinine clearance and sex on both CL and V; age on CL and weight on V	Bilirubin, center, creatinine clearance and sex on both CL and V; age on CL and weight on V
Dofetilide	Age, sex, ACE, loop diuretics, thiazide diuretics, alkaline phosphatase and alanine transaminase on CL	Age, sex, ACE, loop diuretics, thiazide diuretics, alkaline phosphatase and alanine transaminase on CL	Age, sex, ACE, loop diuretics, thiazide diuretics, alkaline phosphatase and alanine transaminase on CL	Age, sex, ACE, loop diuretics, thiazide diuretics, alkaline phosphatase and alanine transaminase on CL
Docetaxel	Age, AAG, PC, PERF and sex on NEUt0 and SLOPE, and age on MTT.	Age, AAG, PC, PERF and sex on NEUt0 and SLOPE, and age on MTT	Age, AAG, PC, PERF and sex on NEUt0 and SLOPE, and PCC and sex on MTT	Age, AAG, PC, PERF and sex on NEUt0 and SLOPE, and PCC and sex on MTT
Tesaglitazar	–	–	Sex and age on EC50 dilution, sex on EC50FPG, and K inRBC	Sex and age on EC50 dilution, sex on EC50FPG, and K inRBC

Fig. 4.

Real datasets: each panel represents a dataset. The vertical and horizontal axes in each panel represent ΔOFV (covariate model–base model) between the nonlinear models and linearized models, respectively. The filled circles represent ΔOFV of the linear model in FOCE versus the nonlinear model in FOCE; open triangles represent ΔOFV of the linear model in FO versus the nonlinear model in FO

Effect of Covariate Parameterization

In all of the above examples, the covariates were linear centered. In order to demonstrate that the FOCE linearization can also be used for other covariate parameterizations, the moxonidine dataset was used as an example. The effect of age and weight (WT) were tested on CL and V, whereas the effect of CLCR was tested on CL. The univariate screening was performed using both power and exponential parameterizations (Eq. 11). The ΔOFV’s (covariate–base) between the linear and nonlinear models are very similar for both power and exponential parameterizations using the FOCE method (Fig. 5).

Fig. 5.

Filled and open circles represent ΔOFV of the linear model in FOCE versus the nonlinear model in FOCE using exponential and power parameterizations, respectively

DISCUSSION

The proposed FOCE approximation for the addition of covariates provides essentially the same information regarding improvement in goodness of fit and covariate coefficients as the corresponding conventional nonlinear models. The OFV as the main measure of goodness of fit is most often used in the likelihood ratio test as a component in covariate model selection. The FOCE linearization is superior in performance to the corresponding FO approximation, but computationally as efficient with similar run times between the FO and FOCE linearizations. The method saves time because it does not depend on the complexity of the structural model and only depends on the number of covariates, the number of parameter–covariate relationships, and the size of the data. On the other hand, the run times for the nonlinear mixed effect models (conventional method) will also depend on the complexity of the structural model. This is exemplified by the time required to fit the tesaglitazar dataset with four parameter–covariate relationships (univariate). The time required to fit all the models with the current method (FOCE linearization) was 5.1 min compared with 151.6 h with the conventional method.

The approximation will be less accurate for strong covariate relations; for example, in the case of the phenobarbital data, the difference in OFV (ΔOFV) between the covariate (effect of weight on V) and the base model for nonlinear models is −96.33, whereas ΔOFV for the corresponding linearized model is −71.87. However, both relations are clearly significant and their importance will be identified in either case. It is possible that this difference in strong effects could be reduced by employing a second-order Taylor expansion around random effects. However, for the reason given, we have not prioritized the development of such a refinement as the FOCE approximation is sufficiently accurate for weaker covariate relationships. This is important since the outcomes of the hypothesis tests for relations that are close to the statistical significance limit is then likely to be the same for the nonlinear and linearized models.

The advantage of the FOCE linearization compared with the nonlinear method is that of shorter run times. The advantages of the linearization compared with graphical and other methods based on empirical Bayes estimates are: (a) all the steps involved in model building are within the same population modeling program; (b) multiple parameter–covariate relationships can be tested simultaneously; (c) the ΔOFV criterion used to judge the significance of covariate effect has familiar meaning; (d) it does not depend on posterior Bayes estimates of individual parameter values (to a larger extent than the FOCE method itself); and (e) it is suitable for time-varying covariates.

The derivatives and predictions can be obtained from the base models with or without covariates. If it is known a priori that a particular covariate is important, it can be included in the model before other covariates are tested using the linearization procedure. In the current study, phenobarbital, pefloxacin, and docetaxel datasets are examples of the former, whereas moxonidine, dofetilide, and tesaglitazar are examples of the latter. The derivatives and predictions for the moxonidine and dofetilide datasets are obtained from base models with effect of creatinine clearance on CL and weight on V.

Although the performance for the FOCE linearization method in this work was illustrated using single parameter–covariate relations, we anticipate its use and usefulness in model building procedures. One such procedure is the stepwise forward/backward search further discussed below. Some methods rely on the building of a “full” model, simultaneously incorporating all covariate–parameter relations of interest. The method proposed here may be used to get initial estimates for a full model which can be used as a final model or as a starting point for Wald’s approximation method analysis (15). This can be done by including all the covariates of interest and developing a full linearized model. The final parameter estimates from the linearized model can then be used as an initial estimate for the full model. The full model initial parameter estimates developed in this manner may be more stable and less likely to get trapped in local minima. In this, as in other uses of the linearization method during covariate model building, we envisage that at least the final model will be reanalyzed with the estimation of all parameters using a nonlinear method.

The FO and FOCE linearization methods are completely automated and implemented in PsN (Perl-speaks–NONMEM), version 3.2.6 and later (16). The “-linearize” option of the stepwise covariate model building (scm) module in PsN can be used to develop linearized covariate models. The generated models and script can then be used for manually directed investigations or in automated univariate search or forward addition/backward deletion stepwise model building. It should be noted that the method per se does not depend on a specific p value or difference in OFV and that it can be used for a fast evaluation of any covariate model, not only as part of scm. The “-derivatives_update” option can be used to recalculate derivatives and predictions after the addition (or deletion) of each covariate–parameter relation. This option will increase computational time as it requires a re-estimation of model parameters from the nonlinear mixed effect model after the addition of each covariate. Alternatively, the same predictions and derivatives can be used throughout a stepwise model building procedure or at least until the model resulting from the forward step.

Although not performed in the current study, the shorter run time allows users to perform computer-intensive tasks such as bootstraps and cross-validation. These procedures may improve the robustness of covariate model building, but presently often is performed, if at all, only on the final model. This in turn can also provide information about the stability of the covariate model, i.e., predictive performance at different model sizes and the possible presence of influential individuals.

CONCLUSIONS

The performance of linearized FOCE was better than the linearized FO. The linearized models can provide information on ΔOFV that is very similar to that of nonlinear models, but with substantially reduced run times. In the current work, the linearization methods were applied to single parameter–covariate relations. However, the linearization methods have been implemented in software such that they can be explored or used in common model building methods.

Appendix 1

1. Nonlinear Base Model

$PROBLEM PHENOBARB additive model

$ABBREVIATED COMRES = 2

$INPUT ID TIME AMT WT APGR DV

$DATA PHENO.dta IGNORE = @

$SUBROUTINE ADVAN1 TRANS2

$OMEGA 0.228 ; variance for ETA(1), initial estimate

$OMEGA 0.146 ; variance for ETA(2), initial estimate

$PK

TVCL = THETA(1) ; typical value of CL

TVV = THETA(2)

CL = TVCL*EXP(ETA(1)) ; individual value of CL

V = TVV*EXP(ETA(2)) ; individual value of V

S1 = V

$ERROR

IPRED = F; individual prediction

IRES = DV − F; individual residual

W = THETA(3); additive residual error

IWRES = IRES/W; individual weighed residual

Y = IPRED + W*EPS(1)

$THETA (0,0.005); 1. TVCL (lower-bound initial estimate)

$THETA (0,1.45); 2. TVV (lower-bound initial estimate)

$THETA (1E−16, 5)

$SIGMA 1 FIX ; initial estimate

$ESTIMATION METHOD = 1 MAXEVAL = 9999; FOCE calculation method

$TABLE ID DV MDV IPRED = OPRED WG11G21 ETA1 ETA2 APGR WT NOPRINT

NOAPPEND ONEHEADER FILE = derivatives_covariates.dta

2. Linear Base Model

$PROBLEM PHENOBARB additive model

$INPUT ID DV MDV OPR WG11G21 OET1 OET2 APGR WT

$DATA derivatives_covariates.dta IGNORE = @

$PRED

BASE1 = G11*(ETA(1)-OET1)

BASE2 = G21*(ETA(2)-OET2)

IPRED = OPR + BASE1 + BASE2

Y = IPRED + EPS(1)*W

$OMEGA 0.19788; variance for ETA(1), initial estimate

$OMEGA 0.201374; variance for ETA(2), initial estimate

$SIGMA 1; initial estimate

$ESTIMATION METHOD = 0, MAXEVALS = 9999

3. Linearized Base Model with Covariate: Effect of Weight on Clearance

$PROBLEM PHENOBARB additive model

$INPUT ID DV MDV OPR WG11 G21 OET1 OET2 APGR WT

$DATA derivatives_covariates.dta IGNORE = @

$PRED

CWT1 = THETA(1)*(WT-1.3) ; median(wt) = 1.3

BASE1 = G11*(ETA(1)-OET1)

BASE2 = G21*(ETA(2)-OET2)

BASE3 = G11*CWT1 ; Effect of Weight on CL

IPRED = OPR + BASE1 + BASE2 + BASE3

Y = IPRED + EPS(1)*W

$THETA 0.1;

$OMEGA 0.19788; variance for ETA(1), initial estimate

$OMEGA 0.201374; variance for ETA(2), initial estimate

$SIGMA 1; initial estimate

$ESTIMATION METHOD = 0, MAXEVALS = 9999