Pooled Exposure Assessment for Matched Case-Control Studies

Abstract

Exposure assessment using biologic specimens is important for epidemiology but may become impracticable if assays are expensive, specimen volumes are marginally adequate, or analyte levels fall below the limit of detection. Pooled exposure assessment can provide an effective remedy for these problems in unmatched case-control studies. We extend pooled exposure strategies to handle specimens collected in a matched case-control study. We show that if a logistic model applies to individuals, then a logistic model also applies to an analysis using pooled exposures. Consequently, the individual-level odds ratio can be estimated while conserving both cost and specimen. We discuss appropriate pooling strategies for a single exposure, with adjustment for multiple, possibly continuous, covariates(confounders)and assessment of effect modification by a categorical variable. We assess the performance of the approach via simulations and conclude that pooled strategies can markedly improve efficiency for matched as well as unmatched case-control studies.

Exposure assessment in epidemiology, particularly for biomonitoring and surveillance, often involves measurement of multiple analytes from stored biologic specimens. Assay expense, however, sometimes constrains the number of subjects and/or chemicals examined. Studies may also suffer from inadequate specimen volumes and from analyte levels below the assay’s limit of detection(LOD). For example, out of 148 chemicals assessed in specimens collected in 1999–2002, the US Centers for Disease Control and Prevention (CDC) provided no summary measures (e.g. geometric means or percentiles)for 22% of the chemicals and only a limited summary for another 41%¹. As the author explained, “These estimates could not be reported … either because of an extremely low exposure level or an insufficient quantity of body fluid or tissue.”²

Pooled exposure assessment can alleviate the three issues of assay expense, analyte levels below the LOD, and specimens with inadequate volumes. The idea is to partition individuals into disjoint pooling sets, combine small equal-volume aliquots from individuals in each pooling set, and then assay one pooled specimen per set instead of one per person. The exposure level of a pooled specimen is the arithmetic mean for the individuals in the pool. Pooling reduces both the number of assays and the specimen volume required from each subject. Thus, pooling depletes less of the biospecimen resource and enables inclusion of more people and more exposures within a given budget.

Specimen pooling was introduced during World War II for efficiently screening military inductees for syphilis³ and was later employed for other infectious diseases.^4–6 Pooling was used to estimate the prevalence and incidence of HIV ⁷ while protecting the privacy of individuals, and to assess diagnostic accuracy of biomarkers.⁸ DNA pooling has been proposed for identification of susceptibility loci in large-scale association studies.⁹

Another useful application of pooling is to estimate the relative odds associated with exposure based on a case-control study.¹⁰ After stratification on disease status(and possibly on covariates), individuals in each stratum are randomly partitioned into pooling sets before assay. With this strategy, the unit of analysis becomes the pooling set, rather than the individual participant. Nevertheless, a modified logistic regression allows valid and efficient maximum-likelihood estimation of the same odds ratio (OR) parameter for the exposure-disease relationship as would be estimated with exposure data from individuals. Pooling makes efficient use of a fixed assay budget with very little loss of statistical power. Moreover, if including an additional subject is relatively inexpensive compared with conducting an additional assay, then pooling can substantially improve power by enabling more people to be studied.

Matching,^11–12 along with conditional logistic regression analysis, remains a widely used technique for controlling confounding and increasing efficiency in case-control studies. For assay-based exposure assessment, matched case-control studies face the same issues of expense, LOD and limited specimen volume as unmatched studies. In this article, we extend the pooled exposure strategies of Weinberg and Umbach¹⁰ for use with matched case-control studies. We show that, when pooling sets are appropriately constructed and exposure is measured in pooled specimens, conditional logistic regression using pooled measurements estimates the same exposure odds ratio parameter as with exposure measured in individuals. Such an approach would be useful for exploratory as well as confirmatory studies of exposure and disease assessment. For example, it could have been applied in studies of serum vitamin D concentration and breast cancer,¹³ the association between blood lead level and ADHD in children,¹⁴ or the association between PCB and non-Hodgkins lymphoma.¹⁵

Methods

Pooled analysis of exposure alone

Let U denote the level of a continuous exposure of interest and D (1 for cases and 0 for controls)denote the disease status. To simplify the exposition we first consider a pair-matched case-control study. Assume the following logistic model for the i^th of N matched pairs:

$$\text{logit}Pr(D=1\mid U=u,i)={\alpha }_i+\beta u,i=1,2,\text{K},\text{N}$$ (1)

where β denotes the log odds ratio (OR) associated with unit increase in exposure and α_i denotes the pair-specific baseline log odds of disease. Based on (1), the contribution of the i^th matched pair to the conditional logistic regression likelihood is:

$$\frac{e^{\beta u_{1,i}}}{e^{\beta u_{0,i}}+e^{\beta u_{1,i}}}$$ (2)

and is free of α_i. This likelihood formulation extends readily to matched sets with more than one control per case.

A simple pooling strategy to allow estimation of β begins by randomly partitioning the matched pairs into sets of pairs. For simplicity, suppose that every set contains g pairs, where N=gk, for some integer k. For each such set of pairs, equal-volume aliquots from the g case specimens are combined to form a single pooled case specimen, and the corresponding g control specimens are pooled to form a single pooled control specimen. There are now k pairs of pools instead of N pairs of individuals. If we index the g specimens in a typical pooling set by i∈{1, 2, 3, … g}, the measured exposure in a pooled specimen is $\overline{U}=\frac{1}{g}{\displaystyle \sum _{i=1}^g}{U}_i$ where U_i denotes the level for the i^th specimen. A logistic model for individuals induces a logistic model for pooling sets.¹⁰ Application of a similar argument (see Appendix) shows that by treating the pairs of pools as if they were pairs of individuals and using $V=g\times \overline{U}={\displaystyle \sum _{i=1}^g}{U}_i$ as the exposure assigned to a pooled specimen, a conditional logistic model for pooling sets is induced as shown below.

Suppose that one of the following two events is observed: (1) A(v₁, v₀): the case set had V=v₁ and the control set had V=v₀, or (2) A(v₀, v₁): the case set had V=v₀ and the control set had V=v₁. Using the results from the Appendix, the contribution of each pair of pools to a conditional logistic likelihood is the conditional probability of A(v₁, v₀) given {v₁, v₀}, namely:

$$\frac{Pr(A(v_1,v_0))}{Pr(A(v_1,v_0))+Pr(A(v_0,v_1))}=\frac{e^{\beta v_1}}{e^{\beta v_1}+e^{\beta v_0}}.$$ (3)

This likelihood contribution for a pair of pooled specimens, as seen by comparison with (2), is that of a standard conditional logistic model for a matched case-control study except that the exposure variables reflect the sum of individual exposures in the pools or g times the measured exposure in the pools. Consequently, maximum likelihood estimation with pooled specimens uses exactly the same procedure as with individual specimens; standard statistical packages estimate both the log OR and its standard error(SE)by treating g times the measured exposure in a pooled specimen as though it were an individual-level exposure. Because we multiplied the measured exposure by g, there is no explicit dependence on g. Hence, the same general model holds when the pooling sets of pairs contain different numbers of pairs.

Pooled analysis of exposure and a confounder

Let W represent a confounder that can vary across individuals within a matching stratum. We assume the usual logistic model for the i^th stratum:

$$\text{logit}Pr(D=1\mid U=u,W=w,i)={\alpha }_i+\beta u+\gamma w,i=1,2,\text{K},\text{N}.$$

Because pooling sets are formed without considering the values of the confounder, confounders enter the model for pooling sets in the same way as exposures do, as the sum of the individual contributions within the set. Accordingly, let $Z={\displaystyle \sum _{i=1}^g}{W}_i$ be a summed confounder. Its value might be derived from another assay of the pooled specimen itself or by summing values recorded for the individuals who contributed to the pool. Continuous covariates need not be categorized, but categorical covariates should be summed as separate dummy variables. Let z₁ and z₀ be values of the summed confounder for a case and a control set, respectively. A derivation that parallels the one for the exposure-only analysis shows that the contribution to the conditional logistic likelihood by a matched pair of pools is:

$$\frac{e^{\beta v_1+\gamma z_1}}{e^{\beta v_1+\gamma z_1}+e^{\beta v_0+\gamma z_0}}.$$

Hence, both β and γ and their SEs can be estimated by standard conditional logistic regression tools.

Allowing for possible effect modification by a covariate

Stratum-specific effect modifier

Consider a dichotomous potential effect modifier W that is stratum-specific in having the same value for both individuals in the i^th pair, and suppose that the following model holds:

$$\text{logit}Pr(D=1\mid U=u,W=w,i)={\alpha }_i+\beta u+\gamma w+\theta wu,i=1,2,\text{K},\text{N}.$$

Here, γ denotes the log OR associated with W in the absence of exposure and θ assesses the change in the log OR for exposure when the level of W changes. For this stratum-specific effect modifier, we assemble sets of pairs by partitioning at random within each level of the effect modifier and then separately pooling case specimens and pooling control specimens within each set of pairs. The contribution of each pair of pools to a conditional logistic likelihood is:

$$\frac{e^{\beta v_1+\gamma gw+\theta v_{1}w}}{e^{\beta v_1+\gamma gw+\theta v_{1}w}+e^{\beta v_0+\gamma gw+\theta v_{0}w}}=\frac{e^{\beta v_1+\theta v_{1}w}}{e^{\beta v_1+\theta v_{1}w}+e^{\beta v_0+\theta v_{0}w}}.$$ (4)

Thus, β and θ and their SEs are estimated using conditional logistic regression as before and correspond to the parameters for individual-level data. However, γ cannot be estimated from either unpooled (g=1) or pooled data because, with stratum-specific W, the value of gw is the same for the case-and the control-pool in each paired pool. This approach also works for a categorical effect modifier or a categorized version of a continuous one.

Subject-specific effect modifier

For a categorical effect modifier W that instead can vary across individuals within a stratum, a modified pooling strategy is needed to assess effect modification. Concordant case-control pairs (where the case and the control have the same value of W) are subject to pooling as described in section 2.2.1 while W-discordant case-control pairs are left unpooled. This strategy results in a likelihood contribution that incorporates a term involving subject specific levels of W for the discordant pairs in the exponents of(4), so that parameters β, θ and γ are estimated via conditional logistic regression.

Pooling strategy for m:n matched studies and further generalizations

The pooling strategy for a pair-matched study is readily extended to a matched study where each matching stratum contains m cases and n controls. Here, too, we randomly partition the matched strata into sets of strata. Suppose a set of g matched strata have been grouped for pooling. One forms m case pools each having g case specimens, one specimen sampled at random without replacement from each stratum in the set, and n control pools each having g control specimens in a similar way (Figure 1). If n and m have a common divisor, p, one could alternatively pool to form m/p pooling sets for cases and n/p pooling sets for controls, by including a randomly selected p cases (controls) from each of the g strata in each pooling set for cases (controls) (Figure 2). In this way each subject (case or control) from a particular stratum contributes to exactly one pooled specimen, and the pooled data retain the m:n (or m/p: n/p) matched structure.

Figure 1.

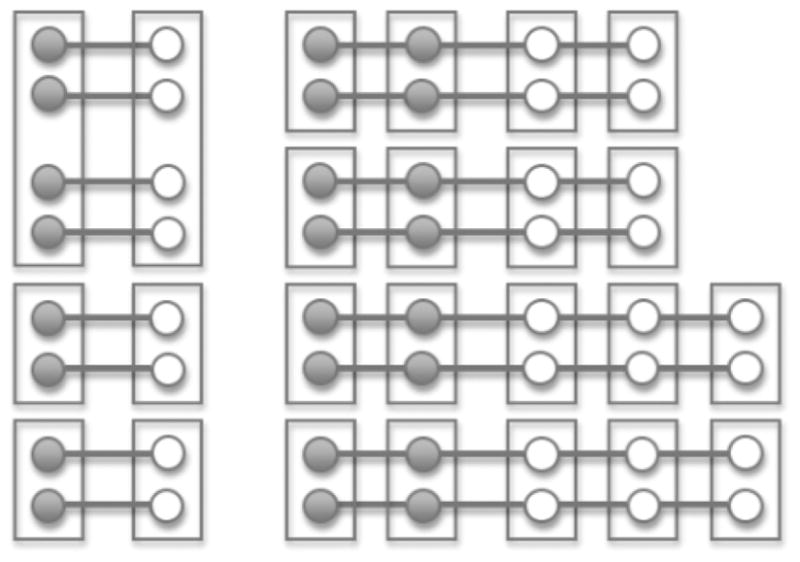
Schematic of a pooling strategy for matched case-control studies with a mixed matching strategy. Filled circles represent the cases, empty circles represent the controls, and a line joins the cases and controls in each matched stratum. Boxes surround the specimens pooled. There are 8 strata with 1:1 case-control matching, 4 strata with 2:2 matching and 4 strata with 2:3 matching. One pool of size g = 4 and two pools of size g = 2 are formed for the 1:1 matched strata. Two pools each of size g = 2 are formed for the 2:2 and 2:3 matched strata.

Figure 2.

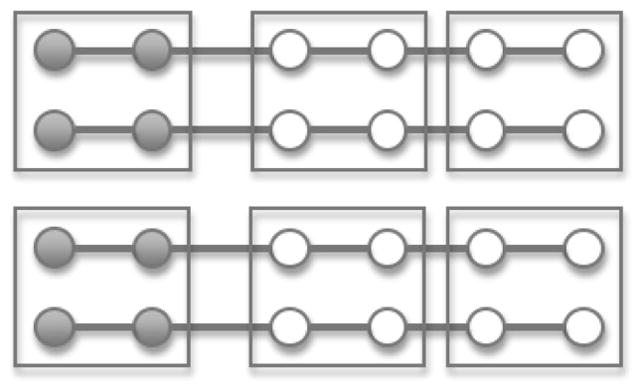
Schematic of a pooling strategy for an m:n matched case-control study where m and n have a common divisor. Filled circles represent the cases, empty circles represent the controls, and a line joins the cases and controls in each matched stratum. Boxes surround the specimens pooled. There are 4 strata with 2:4 case-control matching. A case pool is formed by combining four cases from two strata. Control pools are formed similarly. Note that the number of subjects (case or control) from each stratum should be the same for both the case pools and the control pools within a particular set of strata.

For complex designs where not every stratum contains the same number of cases or of controls(e.g., if the matching factor is sibship), a similar pooling strategy will again work, with the proviso that all strata that are assigned to any pooling set must have the same structure, i.e., the same number of cases and the same number of controls (Figure 1). For such complex pooling designs, conditional logistic regression can still be employed.

Simulation Studies

We examined the performance of our approach via simulations. In each study, we simulated 10,000 data sets to compare results from conditional logistic regression based on individual versus pooled exposure measurements. We specified distributions for exposure, covariates and stratum-specific intercept parameters α_i; we also specified values for the odds ratio parameters. For each matching stratum, we simulated an α_i and any stratum-specific covariates; for each subject within a stratum, we simulated an exposure and any individual covariates. With these values, we determined each subject’s probability of disease through the specified logistic model, and we assigned disease status based on a Bernoulli trial with that disease probability. We retained strata with the desired case-control ratio up to the desired sample size. We then randomly partitioned these matching strata into pooling sets of strata according to the relevant pooling strategy; the pooled exposure value was the average of the individual values. The same simulated data were used for analyses based on individual and on pooled exposures for each simulation.

Exposure effects only

Our first design used 1:1 matching and comprised 240 case-control pairs (480 subjects, 480 individual assays). We considered pools of size 2, 3, 4, 5 and 6, which would require 240, 160, 120, 96 and 80 assays, respectively, saving as much as 5/6 of the direct assay costs. We generated the stratum-specific intercepts, α_i, from a normal distribution with mean -3 and variance 2. We generated log-normal exposures by exponentiating normal random variables with mean 0 and variance 1. We studied three values of β:0, 0.08 and −0.08. For this design, results based on pooled exposure were generally comparable to those based on individual exposure measurements in terms of parameter estimate, model-based variance, coverage, power and type I error (Table 1, eTable 1 (http://links.lww.com/)). All scenarios, including analyses based on unpooled data, demonstrated some bias in the estimation of β but the bias, as well as the discrepancy between empirical and average model-based variance, increased with the pool size g. Regardless of pool size, the model-based variance was slightly smaller than the empirical variance. Nonetheless, the confidence interval coverage was slightly larger than the nominal level of 0.95 for pool sizes up to six. The results were similar for other exposure distributions or when the exposure was associated with the stratum-specific intercept (data not shown).

Table 1.

Results based on 10,000 simulated data sets for estimation and testing of exposure log odds ratio (OR) β using a design with 1:1 matching and N=240 strata (pairs).

		Pool sizea
β	Estimates	1	2	4	6
0.08	Mean of β̂	0.084	0.085	0.087	0.089
	Empirical standard errorb of β̂	0.047	0.048	0.051	0.055
	Model-based standard errorc of β̂	0.046	0.047	0.050	0.053
	Powerd	0.510	0.512	0.511	0.506
	Coverage of nominal 95% C.I.e	0.952	0.953	0.956	0.959
−0.08	Mean of β̂	−0.085	−0.086	−0.088	−0.091
	Empirical standard error of β̂	0.053	0.055	0.058	0.062
	Model-based standard error of β̂	0.053	0.054	0.057	0.060
	Power	0.391	0.389	0.390	0.390
	Coverage of nominal 95% C.I.	0.956	0.958	0.962	0.965

^apool size = 1 means standard analysis based on unpooled or individual exposure measurements.

^bsquare root of the empirical variance from 10,000 simulated data sets; divide by 100 to get the standard error of the mean β̂.

^csquare root of the average model-based variance. For sufficiently large N, this value is proportional to the expected length of the Wald confidence interval.

^dPower based on likelihood ratio tests.

^enominal 95% confidence intervals were calculated using model-based standard error (Wald intervals).

Using a similar pair-matched design, we also compared the power of pooled analysis with that of unpooled analysis for a fixed number of subjects and alternatively for a fixed number of assays (by including additional individuals) for several values of β based on 1000 simulations each for a log-normally distributed exposure. For a fixed sample size of 120 case-control pairs, the power of pooled analysis was comparable with that of the unpooled analysis regardless of pool size (Figure 3A). Though the number of assay determinations went from 240 (unpooled analysis) to 40 (pooled analysis with g=6), the power curves were almost indistinguishable. When instead the number of assays was held at 120 pairs, power increased substantially with pool size (Figure 3B). The number of pairs included also increased with pool size from 120 case-control pairs in an unpooled analysis (g=1) to 720 pairs for a pooled analysis with g=6.

Figure 3.

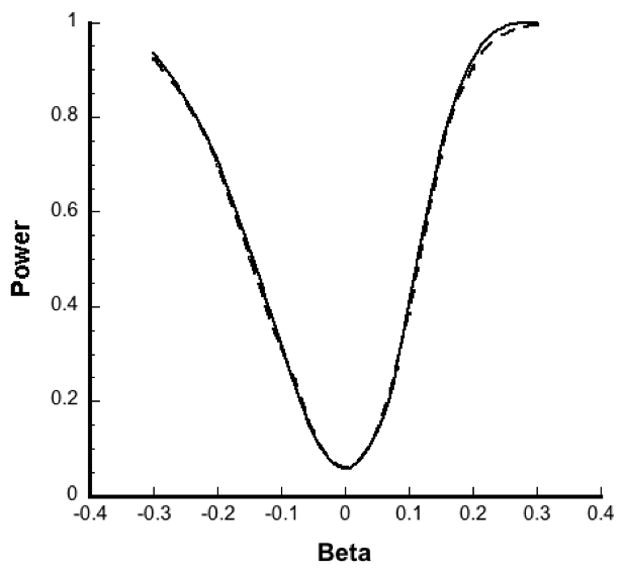
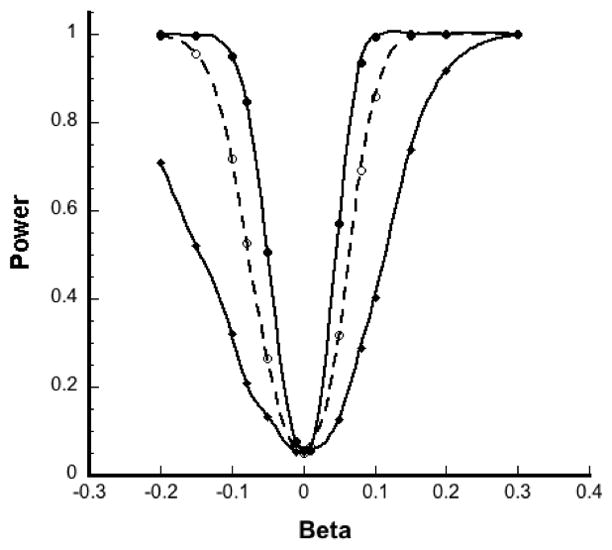
Simulated power curves (averaged over 1000 simulations) for β for unpooled and pooled analysis of exposure. (A) Power of unpooled analysis (solid line) and pooled analysis with g = 6 (dashed line) when sample size was fixed at 120 case-control pairs. (B) Power of unpooled analysis (solid line with diamonds), pooled analysis with g = 2 (dashed line) and g = 6 (solid line with bullets) when number of assays was fixed at 120 pairs, with α = 0.05.

A second scenario involved more complex structures; we considered a total of 240 matched case-control strata, 120 with 1:1, 90 with 1:2, 30 with 1:3 matching, totaling N=630 individuals. We created pools of size 4, 3, and 2 for the 1:1, 1:2, and 1:3matched strata, respectively. Thus, the pooled analysis needed only 210 assays. The distribution of the exposure and the stratum-specific intercepts were the same as in the first scenario. Results based on pooled exposure assessment were again comparable to results based on individual exposure measurements(Table 2). The pooled analysis produced estimates of β that were slightly more biased than those produced by the unpooled analysis. The type I error rate based on a likelihood ratio test of β = 0 was higher for the pooled analysis than for the unpooled analysis; however, the confidence interval coverage was close to the nominal 0.95.

Table 2.

Results based on 10,000 simulated data sets for estimation and testing of exposure log OR β using a design with 120 1:1, 90 1:2 and 20 1:3 matched case-control strata (total 630 subjects).

		Unpooled Analysisa	Pooled Analysisb
β	Characteristic
0.0	Mean of β̂	−0.002	−0.002
	Empirical standard errorc of β̂	0.043	0.046
	Model-based standard errord of β̂	0.042	0.044
	Type I Errore (nominal 0.05)	0.053	0.060
	Coverage of nominal 95% C.I.f	0.959	0.957
0.08	Mean of β̂	0.083	0.087
	Empirical standard error of β̂	0.041	0.045
	Model-based standard error of β̂	0.040	0.043
	Power	0.612	0.614
	Coverage of nominal 95% C.I.	0.951	0.950
−0.08	Mean of β̂	−0.085	−0.089
	Empirical standard error of β̂	0.050	0.055
	Model-based standard error of β̂	0.050	0.052
	Power	0.443	0.450
	Coverage of nominal 95% C.I.	0.952	0.951

^apool size = 1 means standard analysis based on unpooled or individual exposure measurements.

^bpool sizes were 4, 3, and 2 for 1:1, 1:2, and 1:3 matched case-control strata, respectively.

^csquare root of the empirical variance based on 10,000 estimates; divide by 100 to get the standard error of the mean β̂.

^dsquare root of the average model-based variance. For sufficiently large N, this value is proportional to the expected length of the Wald confidence interval.

^e5Type I error and power based on likelihood ratio tests.

^fnominal 95% confidence intervals were calculated using model-based standard error (Wald intervals).

Subject-specific confounder

Next, we considered a design with 240 case-control pairs that included a binary subject-specific confounder, W, having a population prevalence of 0.3. The exposure U was log normal, with its log having expectation 0.3*W and variance 1. The stratum-specific intercept, α_i, was drawn from a normal distribution with mean -3 and variance 2. The log OR for W was γ = 0.4 and we varied β. Parameter estimates, type I error, power and coverage for both β and γ based on pooled measurements, especially for pools of size 2 and 3, were comparable to results based on individual measurements(Table 3, eTable 2 (http://links.lww.com/)). The bias again increased with pool size.

Table 3.

Results based on 10,000 simulated data sets for estimation and testing of log OR β for a continuous exposure and g for a dichotomous confounder using a design with 1:1 matching and N=240 strata(pairs).

		Pool sizea
True values	Estimates	1	2	4	6
β = 0.08	Mean of β̂	0.086	0.087	0.090	0.093
	Empirical standard errorb of β̂	0.043	0.045	0.051	0.057
	Model-based standard errorc of β̂	0.043	0.045	0.049	0.054
	Powerd	0.597	0.586	0.563	0.539
	Coverage of nominal 95% C.I.e	0.954	0.955	0.958	0.964
γ = 0.4	Mean of γ̂	0.403	0.410	0.426	0.445
	Empirical standard error of γ̂	0.206	0.215	0.241	0.276
	Model-based standard error of γ̂	0.205	0.214	0.235	0.262
	Power	0.510	0.498	0.485	0.464
	Coverage of nominal 95% C.I.	0.951	0.954	0.956	0.964
β = −0.08	Mean of β̂	−0.084	−0.085	−0.088	−0.092
	Empirical standard error of β̂	0.049	0.051	0.056	0.062
	Model-based standard error of β̂	0.049	0.050	0.054	0.059
	Power	0.450	0.445	0.439	0.428
	Coverage of nominal 95% C.I.	0.956	0.957	0.960	0.962
γ = 0.4	Mean of γ̂	0.405	0.412	0.427	0.446
	Empirical standard error of γ̂	0.205	0.214	0.238	0.268
	Model-based standard error of γ̂	0.205	0.212	0.230	0.252
	Power	0.519	0.512	0.502	0.494
	Coverage of nominal 95% C.I.	0.955	0.955	0.958	0.964

^apool size = 1 means standard analysis based on unpooled or individual exposure measurements.

^bsquare root of the empirical variance based 10,000 estimates; divide by 100 to get the standard error of the mean β̂.

^csquare root of the average model-based variance. For sufficiently large N, this value is proportional to the expected length of the Wald confidence interval.

^dPower based on likelihood ratio tests.

^enominal 95% confidence intervals were calculated using model-based standard error (Wald intervals).

We also considered a design with a continuous confounder. We assumed that the log of the exposure (U) and the log of the confounder variable (W) were bivariate normal with E(log(U)) = E(log(W)) = 0, Var(log(U)) = Var(log(W)) = 1 and correlation between log(U) and log(W) = 0.5. The stratum-specific intercept, α_i, was drawn from a normal distribution with mean -3 and variance 2 as before. The log OR for W was γ = 0.2, and we varied β. Parameter estimates, type I error, power and coverage for both β and γ based on pooled measurements, especially for pools of size 2 and 3, were comparable to results based on individual measurements(eTable 3 (http://links.lww.com/)). The bias again increased with pool size.

Stratum-specificeffect modifier

We next considered a binary effect modifier W (population prevalence 0.3) that was concordant across individuals within each of 960 matched pairs. Exposure U had the lognormal distribution with its log having expected value 0.3*W and variance 1. The stratum-specific intercept, α_i, had a normal distribution with mean −5 and variance 1. We considered a range of values for β, γ and θ. Similar to ourprevious results, biases in the parameter estimates from pooled analysis for smaller pool sizes (g = 2 or 3) were small and comparable to those for unpooled estimates(Table 4 and eTable 4 (http://links.lww.com/) for g =0.0; additional data not shown). In general, the estimates of β were less biased than were estimates of θ. For example, for β =−0.2 the average estimate based on the unpooled analysis was −0.201 and the average estimate based on pools of size 6 was −0.207. By contrast, the unpooled estimate of θ=−0.3 was −0.312 and the pooled estimate when g = 6 was −0.398.

Table 4.

Results based on 10,000 simulated data sets for estimation and testing of log OR β for a continuous exposure and q for effect modification by a dichotomous stratum-specific factor using a design with 1:1 matching and N=960 strata(pairs). The log OR for the main effect of the effect modifier, γ, was 0.00 for these simulations.

		Pool sizea
Parameters		1	2	4	6
β = −0.2	Mean of β̂	−0.201	−0.202	−0.204	−0.207
	Empirical standard errorb of β̂	0.040	0.043	0.046	0.049
	Model-based standard errorc of β̂	0.040	0.041	0.044	0.048
	Powerd	1.000	1.000	1.000	1.000
	Coverage of nominal 95% C.I.e	0.948	0.949	0.951	0.958
θ = −0.3	Mean of θ̂	−0.312	−0.324	−0.346	−0.398
	Empirical standard error of θ̂	0.109	0.129	0.185	0.343
	Model-based standard error of θ̂	0.112	0.131	0.180	0.305
	Power	0.885	0.840	0.737	0.607
	Coverage of nominal 95% C.I.	0.963	0.958	0.960	0.956
β = 0.2	Mean of β̂	0.202	0.203	0.206	0.209
	Empirical standard error of β̂	0.025	0.028	0.034	0.042
	Model-based standard error of β̂	0.025	0.028	0.034	0.043
	Power	1.000	1.000	1.000	1.000
	Coverage of nominal 95% C.I.	0.951	0.951	0.959	0.964
θ = −0.3	Mean of θ̂	−0.311	−0.313	−0.320	−0.327
	Empirical standard error of θ̂	0.059	0.062	0.071	0.082
	Model-based standard error of θ̂	0.061	0.064	0.071	0.080
	Power	1.000	1.000	1.000	1.000
	Coverage of nominal 95% C.I.	0.963	0.960	0.962	0.968

^apool size = 1 means standard analysis based on unpooled or individual exposure measurements.

^bsquare root of the empirical variance based 10,000 estimates; divide by 100 to get the standard error of the mean β̂.

^csquare root of the average model-based variance. For sufficiently large N, this value is proportional to the expected length of the Wald confidence interval.

^dPower based on likelihood ratio tests.

^enominal 95% confidence intervals were calculated using model-based standard error (Wald intervals)

Subject-specificeffect modifier

We simulated 480 matched pairs and a binary effect modifier W that was not always concordant within pairs. The distribution of W, U and α was the same as in the previous scenarios and we considered a range of values for β, γ, and θ. The results from pooled analysis were again comparable with those based on unpooled analysis (Table 5 and eTable 5 (http://links.lww.com/)for γ =0.0; additional data not shown).

Table 5.

Results based on 10,000 simulated data sets for estimation and testing of log ORs β,γ and q for effect modification by a dichotomous subject-specific factor using a design with 1:1 matching and N=240 strata(pairs).

		Pool sizea
Parameters		1	2	4	6
β = −0.5	Mean of β̂	−0.510	−0.513	−0.520	−0.524
	Empirical standard errorb of β̂	0.085	0.092	0.106	0.118
	Model-based standard errorc of β̂	0.085	0.092	0.106	0.117
	Powerd	1.000	1.000	1.000	1.000
	Coverage of nominal 95% C.I.e	0.950	0.952	0.953	0.951
γ = 0.0	Mean of γ̂	0.011	0.011	0.006	0.001
	Empirical standard error of γ̂	0.266	0.275	0.286	0.292
	Model-based standard error of γ̂	0.263	0.271	0.282	0.288
	Type I Error (nominal 0.05)d	0.053	0.053	0.053	0.052
	Coverage of nominal 95% C.I.	0.949	0.950	0.950	0.950
θ = −0.2	Mean of θ̂	−0.213	−0.214	−0.210	−0.205
	Empirical standard error of θ̂	0.174	0.184	0.197	0.203
	Model-based standard errorof θ̂	0.171	0.180	0.191	0.198
	Power	0.239	0.219	0.197	0.186
	Coverage of nominal 95% C.I.	0.949	0.950	0.948	0.949
β = 0.5	Mean of β̂	0.509	0.512	0.518	0.522
	Empirical standard error of β̂	0.072	0.082	0.099	0.110
	Model-based standard error of β̂	0.071	0.081	0.098	0.109
	Power	1.000	1.000	1.000	1.000
	Coverage of nominal 95% C.I.	0.952	0.950	0.953	0.948
γ = 0.0	Mean of γ̂	−0.012	−0.011	−0.007	−0.002
	Empirical standard errorof γ̂	0.244	0.252	0.264	0.272
	Model-based standard error of γ̂	0.239	0.247	0.259	0.267
	Type I Error (nominal 0.05)	0.054	0.057	0.056	0.055
	Coverage of nominal 95% C.I.	0.948	0.945	0.946	0.947
θ = −0.2	Mean of θ̂	−0.197	−0.199	−0.203	−0.207
	Empirical standard error of θ̂	0.099	0.107	0.120	0.129
	Model-based standard error of θ̂	0.098	0.106	0.119	0.128
	Power	0.536	0.488	0.427	0.392
	Coverage of nominal 95% C.I.	0.954	0.956	0.956	0.954

^apool size = 1 means standard analysis based on unpooled or individual exposure measurements.

^bsquare root of the empirical variance based 10,000 estimates; divide by 100 to get the standard error of the mean β̂.

^csquare root of the average model-based variance. For sufficiently large N, this value is proportional to the expected length of the Wald confidence interval.

^dType I error and power based on likelihood ratio tests.

^enominal 95% confidence intervals were calculated using model-based standard error (Wald intervals)

Discussion

Currentlarge-scale studies focus on screening multiple biomarkers to improve risk assessment, prediction and management of disease. Such efforts require assaying stored biospecimens from several thousand subjects to measure levels of numerous biomarkers. Most, if not all, of these biomarkers turn out to be unassociated with the disease,¹⁶ resulting in loss of bio-resources that may be irreplaceable. In such situations, specimen pooling offers a practical strategy that not only reduces overall assay cost but also conserves specimens for future analyses of additional biomarkers yet to be identified as informative.

A pooling strategy was proposed earlier to estimate the individual-level odds ratio associated with a continuous exposure in unmatched or frequency-matched case-control studies.¹⁰ We extended that work and showed that unbiased estimation of the individual-level odds ratio parameter can be based on pooled exposure measurements for a fine-matched case-control study. If pooling sets are formed in a way that maintains the matching, a conditional logistic model applies, and OR scan be estimated using standard software. Unlike the method of Weinberg and Umbach,¹⁰ no offset adjustment is needed. Confounder effects can be estimated similarly and, in the presence of a potential effect modifier, only pairs with concordant values of the effect modifier should be pooled.

Conditional logistic regression involves likelihood-based inference, and the unbiasedness of estimates and the validity of tests and confidence intervals require a large number of observations in the analysis. With small numbers, bias can be severe.¹⁷ We observed some bias, generally away from the null, which increased as the pool size increased. This bias is attributable to the decreasing number of pooling sets, which reduces the effective sample size. Increasing the number of strata in our simulations by ten-fold eliminated detectable bias (data not shown). Nevertheless, when employing pooled exposure assessment, one should consider this issue and may need to adopt alternative estimators to cope with small numbers.¹⁷

Pooled analysis may also be applicable to exposures measured externally in the environment rather than in blood or serum specimens. Environmental exposures such as pesticides, arsenic, or lead can be measured in household dust, tap water, or ambient air. Depending on the medium (dust or water, say) samples from different sources could be combined on a weight or volume basis to form a pooled sample, and exposure assessed in the pooled sample would be used for estimation of odds ratios as outlined here.

The approach we have described might be useful for case-control studies with alternative matching schemes, e.g., randomized recruitment^18–19 or counter-matching.²⁰ In such designs, pools should additionally be stratified by first-stage or screening variables. The implications of pooling in such designs remain to be explored.

Pooling presents both advantages and limitations and may not be the best approach for every study. As mentioned before, when a small fraction of specimens falls under the LOD, then pooling may further reduce this fraction, because a mean of g sample values has the same mean but smaller variance than an individual value. For example, if the exposure is distributed as a standard log-normal random variable and the LOD is 0.431, then 20% of the individually-measured exposures fall below the LOD. If 3 random subjects were pooled, then only about 3.4% of the pooled observations would fall below the LOD. In contrast, when a large proportion of specimens fall under the LOD (for example, if the population mean is actually below the LOD for the assay), then pooling can even exacerbate the problem.

Another limitation worth noting is that transformations are difficult to accommodate in a set-based analysis. The argument in the eAppendix (http://links.lww.com) remains correct if, in the underlying logistic model (1), u is replaced by some non-linear function of u such as log(u), u², or, generically, h(u). Then, the variable v₁= Σu_1i in the likelihood contribution (3) becomes $v_1^{\ast }=\sum h(u_{1i})$, with a similar redefinition for v₀. The resulting likelihood contribution for pools is still correct. However, a difficulty arises because what is actually measured in a pooled specimen, namely, the average of the g constituent individual concentrations, allows one to measure Σu_1i but not Σh(u_1i). Naïvely substituting h(Σu_1i) for Σh(u_1i) leads to bias because the two differ. Hence, one cannot employ pooled analysis to estimate coefficients for a non-linear transformation of exposure. Under the null hypothesis of no exposure effect(β = 0), however, the likelihood contribution of (3) is 0.5 even for the naïve substitution. Thus, a pooled analysis can still provide a valid test of the null hypothesis for a non-linear transformation of exposure, even though it cannot provide an unbiased estimate of the effect. A related feature is that one can test departures from the assumed linear relationship between log-odds of disease and exposure by testing whether additional polynomial terms improve fit; however, if fit improves, the additional terms lack meaningful interpretations.

Another limitation is that effect-modifiers must be identified and accommodated a priori in the formation of pooling sets. Post-hoc analysis of effect modification between the exposure and another variable would require that the pooling be designed afresh. Continuous effect modifiers, even when known in advance, would require categorization, leading to coarsening and possibly loss of power. Multiple effect modifiers require that pooling be done within strata defined by cross-classified levels of effect modifiers. For example, if both age (young vs. old) and sex (male vs. female) are considered potential effect modifiers, then pooling sets are formed separately within the four age-sex groups. On the other hand, if additional covariates are confounders but not potential effect modifiers, the pooling sets are formed at random, without regard to the age and sex variables, and the value of the confounder for a pool is assigned by summing over values measured on individuals in the pool.

These limitations not withstanding, pooling strategies can greatly reduce the cost of a matched study, both in money and in depletion of irreplaceable specimens, while incurring minimal loss of statistical power or precision.