Abstract
An important element determining the time requirements of Born-Oppenheimer molecular dynamics (BOMD) is the convergence rate of the self-consistent solution of Roothaan equations (SCF). We show here that improved convergence and dynamics stability can be achieved by use of a Lagrangian formalism of BOMD with dissipation (DXL-BOMD). In the DXL-BOMD algorithm, an auxiliary electronic variable (e.g., the electron density or Fock matrix) is propagated and a dissipative force is added in the propagation to maintain the stability of the dynamics. Implementation of the approach in the self-consistent charge density functional tight-binding method makes possible simulations that are several hundred picoseconds in lengths, in contrast to earlier DFT-based BOMD calculations, which have been limited to tens of picoseconds or less. The increase in the simulation time results in a more meaningful evaluation of the DXL-BOMD method. A comparison is made of the number of iterations (and time) required for convergence of the SCF with DXL-BOMD and a standard method (starting with a zero charge guess for all atoms at each step), which gives accurate propagation with reasonable SCF convergence criteria. From tests using NVE simulations of C2F4 and 20 neutral amino acid molecules in the gas phase, it is found that DXL-BOMD can improve SCF convergence by up to a factor of two over the standard method. Corresponding results are obtained in simulations of 32 water molecules in a periodic box. Linear response theory is used to analyze the relationship between the energy drift and the correlation of geometry propagation errors.
INTRODUCTION
Classical molecular dynamics simulations with the potential energy of part or the entire system evaluated “on-the-fly” by a quantum-mechanical method are playing an increasing role in chemistry, physics and biology.1, 2 This type of approach is referred to as Born-Oppenheimer molecular dynamics (BOMD). Although the earliest application of BOMD goes back to 1973,3 there were only a few BOMD simulations in the intervening years4 until 1985, when Car and Parrinello introduced an alternative approach (CPMD) for determining the potential energy by quantum mechanics;5 i.e., extra classical variables were associated with the electrons and the computational efficiency for each dynamic step was significantly improved, especially for applications with a large number of basis functions. However, the smaller step size required for CPMD versus BOMD makes the two methods competitive. Furthermore, due to the use of a fictitious mass for the electrons, artifacts are unavoidably introduced in the resultant spectrum computed by CPMD,6, 7 e.g., there is a fictitious mass dependence of the vibrational frequencies.8 Recently, a modified formalism, called Ehrenfest dynamics,9 in which a complex term depending on the wavefunctions and their velocities are inserted into Lagrangian to maintain the orthogonality among orbitals, is being explored, but its performance still remains to be determined.9, 10 Both BOMD and CPMD with the potential energy of only part of the system determined by quantum mechanics and the rest obtained from an empirical force field, in what is called combined quantum mechanical and molecular mechanical (QM/MM) molecular dynamics, have been extended into many fields. This approach is of particular importance for reactions in an extended medium (e.g., in solution or in enzymes).11 An early example is the BOMD study of the Cl–, CH3Cl exchange reaction in aqueous solution with a semiempirical QM potential.12
BOMD, which we consider further here, can be based on any quantum mechanical method, the most popular of which are density functional theory (DFT),13 Hartree–Fock theory (HF),14 and semiempirical quantum mechanical methods (SE).15, 16, 17 All these methods have a high order scaling with respect to the number of atoms in the quantum system, which is due to the matrix diagonalization and construction of Fock matrices. The slow step in BOMD is the convergence of the SCF iterations so that considerable effort is being invested to accelerate this aspect of the method.18, 19, 20, 21, 22, 23 The new algorithms extrapolate electronic variables (e.g., the Fock matrix) to accelerate SCF convergence.21 Two types of extrapolations have been used. The first is “time” extrapolation, in which the electronic variables are explicit functions of time. An example is Fock matrix dynamics (FMD).21, 22 In FMD, the Fock matrix is assumed to be a polynomial function of time and the coefficients of the polynomial are found from the initial n steps (n is the polynomial order). For the first n steps, conventional BOMD is propagated without Fock matrix extrapolation and after the first n steps, the electronic variables at a new time step (i.e., the next geometry in the dynamics) are obtained from their values at previous time steps. These new electronic variables are then used as the initial guess in the SCF optimization. This has been found to significantly improve SCF convergence.20, 21 The second category is “geometric” extrapolation, in which the geometry of the current step is approximated as linear combination of previous step geometries and the electronic variables are extrapolated with the same linear combination of steps.19, 20 In the least-square fitting of molecular orbital coefficients method,20 the coefficients of the linear combination are obtained by the direct inversion in the iterative subspace method.24 Both the time and geometric extrapolation algorithms have demonstrated encouraging acceleration of the SCF convergence, but the lack of stability of the dynamical propagation calculated with these algorithms can create problems.22
To achieve dynamics stability and efficient SCF convergence, one of the authors (Niklasson and his co-workers) developed a time-reversible Born-Oppenheimer molecular dynamics (TR-BOMD), in which the time reversibility of the calculated density is explicitly conserved by introducing an auxiliary density.25, 26 A two-step procedure is used in which the actual density is determined from the auxiliary density, which is perfectly reversible and remains close to the Born-Oppenheimer density by introducing an update filter.25 With such an approach, the propagated density is close to the converged density. Thus, the SCF convergence efficiency is significantly improved, while the time reversibility of the densities aids in preserving the stability of the dynamics; details are given in Refs. 25 and 26. This approach has been generalized to an extended Lagrangian formalism (XL-BOMD), in which the auxiliary variables (i.e., the densities) are treated on an equal footing with other nuclear degrees of freedom.27 Although the XL-BOMD formalism has similarities to the CPMD, no fictitious mass is associated with the auxiliary variable in the former, eliminating artifacts arisen in the latter. Moreover, the generalization to a Lagrangian formalism enables the use of higher-order symplectic schemes (e.g., the Verlet algorithm), which makes possible time steps on the order of those standard in molecular dynamics simulations with an empirical potential energy function.28
An important drawback resulting from the time reversibility is that the error/noise propagates without cancellation in XL-BOMD, so that the energy drift of successive steps tends to accumulate and cause instability of the dynamics.29 Besides the numerical errors arising from truncation in the dynamical propagation, errors in XL-BOMD can originate from the only finite convergence of SCF and round off errors, which introduce inaccurate forces. Previous BOMD studies have been limited to a few picoseconds where energy conservation is easier to achieve; for a very clear discussion, see Ref. 29. The effect is expected to become more serious for longer simulations, such as those investigated here for the first time.
Inspired by an idea from conventional Langevin dynamics30 (i.e., having a damping term to counteract the effects of noise and maintain thermal equilibrium) and the algorithm of Kolafa et al.,31 a damping term has been introduced into the propagation of auxiliary variables. This term is a function of the electronic variables from previous steps. With this additional term, increased stability of dynamics has been obtained, while the acceleration of SCF convergence is preserved.29 This method is referred to as DXL-BOMD in the present paper.
The encouraging results from DXL-BOMD based HF (Ref. 29) and DFT (Ref. 32) stimulated us to combine the DXL-BOMD algorithm with the density-functional tight-binding method (DFTB).17, 33 Such a combination is of particular importance11, 34 because the DFTB method is generally several orders of magnitude faster than the DFT method, so that much longer simulation times can be achieved. This makes possible the calculation of dynamics of interest for evaluating conformational changes and the free energies of various processes, which cannot be achieved in a reliable fashion with DFT, given the present computational limitations. Further, from a more technical viewpoint, such longer simulations can make clear the deficiencies in the DXL-BOMD method and motivate improvements. In this paper, we describe the implementation of the DXL-BOMD algorithm with DFTB method and present some test results.
In Sec. 2, the theory of DFTB and DXL-BOMD are summarized to make the current manuscript self-contained. Section 3 presents computational details. In the Sec. 4, the results from C2F4 and amino acid molecules are presented as well as the comparison of algorithms based on an extrapolation of charges and the Fock matrix. Results from condensed water systems are also discussed in this section. Based on the test results and the current implementation of DXL-BOMD, the conclusion is made in the Sec. 5.
THEORY
In this section, we first review DFTB theory used in the present paper. Then, the DXL-BOMD method that were used previously in DFT32 and Hartree-Fock BOMD.29 These are included to make the paper self-contained.
Density functional tight-binding method
The DFTB method is a second-order approximation of density functional theory (DFT) energy with respect to variation of the atomic charges.17 Mulliken charges35 are utilized to account for the inter-atomic charge interactions due to its simplicity. In addition, only valence electrons are explicitly treated in the DFTB method, as in most other semiempirical methods.15 The total energy (closed-shell) of DFTB can be written as
| (1) |
Here, P is the one electron density matrix and h0 is the diatomic Hamiltonian matrix. The elements of h0 are parameterized based on diatomic calculation from density functional theory. In practice, the PBE functional36 has been used in these calculations. The matrix elements as a function of evenly distributed interatomic distances are interpolated by spline functions from precomputed values on evenly distributed grids. The Mulliken charge is computed via
| (2) |
where ZA is the nuclear charge of atom A. The overlap matrix S is parameterized via an approach similar to that used for h0 and γAB is a function that depends on the Hubbard values of atom A, B and their distance; at large distances, γAB converges to 1/R form (the standard Coulomb charge interaction kernel). VAB is the repulsive potential between atom A and atom B, which is parameterized to match the potential energy curves as a function of the A-B distance calculated with DFTB to those from DFT for a set of molecules. The repulsive potential between any two atoms is also parameterized on spatially evenly distributed grid points and the required values are interpolated by spline functions from these grid point values. From the total energy expression, the DFTB method can be considered to be a self-consistent charge extended Hückel method37 since only parameterized diatomic one electron Hamiltonian matrix elements and overlap matrix elements are required.
In the DFTB program, SCF starts either from zero charge guess (ZRC), i.e., all atoms are assumed to have zero charges at the first iteration of SCF, or from the converged SCF results at the previous geometry (PRC). After that, the charges are updated iteratively until the absolute total energy difference value at successive iterations is less than a preset threshold. In contrast to the ab initio methods or DFT methods, where the most time consuming part is in computing the integrals to update Fock matrix at each step, the main computational bottleneck in the DFTB method (as well as for other semiempirical methods) is the diagonalization of the Fock matrix, i.e., solving the Roothaan equations. Consequently, reducing the number of iterations in SCF procedure can significantly improve the computational efficiency.
In principle, the SCF procedure is an optimization problem, which is solved in the DFTB program with the modified Broyden method38, 39, 40 The approximate inverse electronic Hessian is updated from information obtained from previous iterations, i.e., a rank-n update (n is the number of previous iterations used). This method performs efficiently in optimization problems of the present type and thus is used here.39, 40, 41
Extended equations of motion for Born-Oppenheimer molecular dynamics with dissipation
In our previous work,27, 29 the propagation equations for both nuclei and the auxiliary variable(s) have been derived from an extended Lagrangian in the limit of zero fictitious masses associated with the auxiliary variables. An alternative and more direct way to arrive at the same equations is given here. The auxiliary variables are assumed to be harmonic oscillators that oscillate around the converged electronic variables while the nuclei propagate according to the Newtonian dynamics on Born-Oppenheimer potential energy surface. In the current study, the atomic Mulliken charges are used as auxiliary variables. The equations of motion for the nuclei and the auxiliary variables can be written straightforwardly as
| (3) |
| (4) |
Here, R represents the nuclear coordinates; , the second derivative of coordinates with respect to time; and U[R; D] is the self-consistent electronic ground state potential energy. The quantity D is the converged charge vector at the given nuclear configuration and the symbol C represents an auxiliary charge variable. ω is the parametric frequencies of auxiliary variable vibrations, which will be discussed in the following text. The Eqs. 3, 4 are equivalent to the Eqs. 7, 8, respectively, in our previous study using the extended Lagrangian formulation of Born-Oppenheimer molecular dynamics.29 From Eq. 3, it is clear that the dynamics of the nuclear degrees of freedom, R, is not affected by the auxiliary degree of freedom C. This differs from CPMD,6 and eliminates the artifacts introduced by the fictitious degree of freedom in that approach.
Since the variable C(t) evolves in a harmonic potential centered around the ground state solution D(t), C(t) will remain close to the self-consistent solution D(t) if appropriate values of ω2 are chosen in Eq. 4. It is natural, therefore, to use C(t) as the initial guess for D(t) at each nuclear configuration in the SCF optimization procedure, i.e.,
| (5) |
This choice often reduces the number of SCF iterations, compared with those required when one uses as the initial guess the zero charge vector. More importantly, because C(t) is a dynamical variable that can be integrated with a time-reversible scheme, the SCF optimization in Eq. 5 retains the time reversal symmetry in the underlying electronic propagation.25, 27 By contrast, in regular BOMD, the SCF procedure is nonlinear and irreversible, so that the time reversal symmetry of the electronic propagation is broken unless exact convergence to the SCF value is achieved. In any case, better convergence would be required for the same behavior of the dynamics; this is considered in the results section.25, 27 Because the broken time reversibility of the electronic degrees of freedom leads to the energy drift,21, 22 it is expected that conservation of time reversibility will improve the results.
However, a problem with the use of time reversible dynamics is that any noise introduced in the dynamical steps tends to accumulate, rather than average out, and again causes an energy drift in the simulations.29, 32 For resolving this issue, dissipative forces have been introduced into the propagated auxiliary variables, C, while maintaining the time reversibility as accurately as possible, so that the nuclear motion is not significantly perturbed.29 The conservation of time reversibility in this formulation is similar to the approach used by Kolafa et al.31 If the numerical noise is represented by η(t), then Eq. 4 is modified to
| (6) |
Using a Langevin dynamics like approach, the noise accumulation can be balanced by the addition of a dissipative force term, Fdiss. The equation of motion of the auxiliary degree of freedom becomes
| (7) |
where α is a small coupling constant and the inverse mass parameter μ−1 is introduced to give the correct dimensionality. In the conventional Langevin dynamics, the Fdiss term is chosen to be on the order of , but this would give rise to large deviations from the time-reversible microcanonical dynamics. Thus, Fdiss is chosen to retain time reversal symmetry to a higher order than linear, as we describe below.
Here, we reproduce the construction of Fdiss described in Ref. 29, so that the time-reversal symmetry is broken to only a small degree when C(t) is propagated. The construction of Fdiss is analogous to the classical Verlet scheme. Cn−k is expanded in a Taylor series about Cn, i.e.,
| (8) |
where at t = tn and K is the total number of steps. From Eq. 8, it is clear that with certain coefficients, the linear combination of the Taylor expansion of Cn−k could be chosen to cancel the odd order terms of δt, which give rise to the broken time-reversal symmetry. For example, in the classical Verlet scheme, the k = ±1 are combined to remove all odd order terms. With the appropriate linear combination, the second time derivative of C(t) becomes
| (9) |
where Oeven(δt4) and Oodd(δt(2K − 3)) are the leading even and odd order of the error in the expansion, respectively; the constant dK and expansion coefficients ck are chosen such that Eq. 12 is satisfied (see below). If the dissipative force term satisfies
| (10) |
time reversal symmetry is expected to be retained to high order in δt and thus have only a minor effect on the energy conservation during the dynamics for sufficiently small values of δt. The time reversal order in the dissipative force term is determined by K, as shown in Eq. 10, which will be used to distinguish different integration schemes in our analysis.
From Eqs. 7, 10, the propagation of C(t) is given, using the Verlet algorithm, by
| (11) |
where α now corresponds to α/dK. To employ these equations, the parameters κ, α and ak have to be determined. As can be seen from Eq. 12, the highest odd time order retained in the expansion is equal to 2K−5 (only odd term contributes to time irreversibility). In the rest of the paper, we refer to the value of 2K−5 as the order of DXL-BOMD. For example, the algorithm with K = 4 is called 3rd order DXL-BOMD. An optimized set was found in the previous study of DXL-BOMD with DFT (see Table I in Ref. 29).29, 32 Using this parameter set, it has been shown the propagation of the auxiliary variables C does well conserve the total energy of a system for the tested time (4 ps). Here we employ the same parameters for DFTB with the assumption that they should be appropriate for DFTB as well as for DFT/HF. Of course, the results provide a check on the assumption as well as a validation of DFTB.
Linear response theory
To interpret the observed energy drift in Section 4, a linear response theory estimate is made.As derived previously,28, 30, 42 the energy drift rate, , of an equilibrium system under perturbation of an external force by of the form
| (12) |
is equal to
| (13) |
In Eq. 12, ω represents the frequency of the applied force, Re represents the real part of a complex number, and A is the response to the applied force. In the current investigation, A is the atomic displacement error vector of all atoms due to f(t) and f(t) is the extra force from the finite convergence of the SCF and/or round-off error. Although the exact form of f(t) is not known, we assume it can be represented by Eq. 12 for simplicity.
COMPUTATIONAL DETAILS
The default SCF optimization was carried out by a modified Broyden method.39, 40 The SCF convergence criterion is based on the energy difference between successive iterations. The default SCF energy convergence threshold criterion is 10−8 hartree, but different SCF threshold values were tested. In current studies, threshold values in the range of 10−4 to 10−8 hartree were used. Molecular dynamics is propagated by use of Verlet algorithm.
For the C2F4 molecule, the system was equilibrated with the temperature kept at 500 K for 100 ps using velocity scaling with a scaling probability of 10%. The SCF convergence criterion used at each step was 10−8 hartree. The time step was 20 a.u. (0.484 fs). After equilibration, the temperature scaling was removed, i.e., a microcanonical ensemble simulation was performed and the system was integrated for another 100 ps with different SCF convergence criteria and with different algorithms for charge/Fock matrix extrapolation.
In addition, 20 natural amino acid molecules were tested in vacuum, all of which are neutral with a neutralized acid or base, if present. They include alanine, arginine, asparagine, aspartic, cysteine, glutamic, glutamine, glycine, histidine (Nɛ is protonated), isoleucine, leucine, lysine, methionine, phenylalanine, proline, serine, threonine, tryptophan, tyrosine, and valine molecules. First, 40 ps canonical ensemble simulation was carried out for each molecule using velocity scaling to keep the temperature at 298 K. Then, a 100 ps microcanonical ensemble simulation was performed for each molecule. The time step was 20 a.u. (0.484 fs) for all molecules.
The liquid water system was first simulated by CHARMM,43 in which 32 water molecules are in a periodic cubic box. The classical TIP3P (Refs. 43 and 44) water model was applied with the constraint of O−H bond using SHAKE algorithm.45 First, the system was simulated for 500 ps at 298 K under NPT ensemble using Langevin piston method.46 Then, it was followed by 500 ps NVT ensemble simulation under 298 K. In NVT ensemble simulations, the cubic box side lengths are fixed at 9.862 Å, which is equivalent to the experimental measured water density of 997 kg/m3. These pre-equilibrated systems using classical force fields were then used as starting configurations for 200 ps equilibration under NVT ensemble using simple velocity scaling with a scaling probability of 10% in the DFTB program. Afterwards, 500 ps NVE ensemble simulations using DFTB potential energy functions were done, from which the latter 300 ps segments were used in following analysis.
RESULTS AND DISCUSSION
Conventional approaches
C2F4
To be able to compare with previous investigations,21, 22, 25, 27 C2F4 is chosen as the test molecule for the SCC−DFTB molecular dynamics study. The parameters for fluoride were generated and added to the existing DFTB parameter set. Although a stringent test of the new parameters was not performed, their quality is not important for the present purpose.
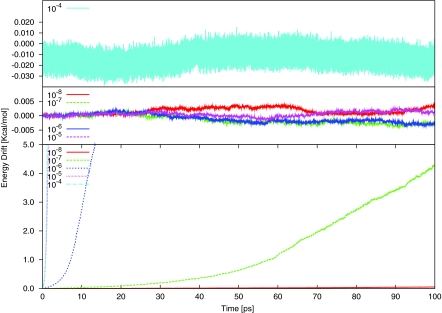
As a criterion for the stability of the molecular dynamics simulations, the total energy drift is plotted in Fig. 1. We note that the time period of the dynamics is 100 ps, in contrast to most earlier studies, which are restricted to within 10 ps.20, 21 The results using the zero charges (ZRC) (top panel) are stable for values of the convergence criterion below 10−4 hartree; of the latter values, large energy fluctuation occurs although there is no overall drift. By contrast, for the PRC calculations, although the energy fluctuations are small, there is significant energy drift. Such behavior using methods similar to PRC has been shown before for DFT and HF methods25, 29 and is also known from the work of other groups.21, 22, 25, 27, 32
Figure 1.
Energy drift of C2F4 in Kcal/mol during 100 ps microcanonical ensemble simulation with SCC-DFTB at 500 K in the standard approach; the scales are different in the two panels. Top and middle panels show the results from the molecular dynamics with the initial guess of zero charge (ZRC) for each atom at every new nuclear configuration while the bottom panel shows the results with the initial guess from previous converged charges (PRC). The legends on the left side of each panel indicate the SCF convergence criterion in unit of hartree.
Equation 13 shows that in linear response theory, the energy drift is linearly proportional to the autocorrelation function ⟨A(0)A(t)⟩ of the deviation in the atomic displacements. In ZRC case, since the SCF starts from zero charge, the error in the total energy due to finite convergence in the SCF at each step is independent of the previous steps. Correspondingly, the deviation of atomic displacements from the exact value (i.e., A) at each successive step is independent of other steps. Thus, the energy drift remains small, although it is not exactly zero. With PRC, in contrast to ZRC, the energy drift increases with time. This is due to the correlation between A values at different time steps. Even with 10 −7 hartree as the SCF convergence criterion, a significant systematic drift of the total energy is observed (see Fig. 1). The decrease with a tighter SCF threshold can also be understood from Eq. 13, in which the energy drift is proportional to the square of the force amplitude |fω|2, and the force amplitude is expected to be linearly proportional to the SCF energy convergence criterion.
The above results make clear that it is necessary to be careful when choosing the SCF convergence threshold value for the PRC case. In many studies,47, 4810−7 hartree has been used; this is also the default value in CHARMM.49 Although such a value does not cause a large energy drift in the current simulation to C2F4, the energy drift continuously increases as the simulation time increase (i.e., the energy drift over 100 ps dynamics is about 5 Kcal/mol). We note that with PRC, even an SCF criterion of 10−6 hartree shows no appreciable energy drift over the “standard” 2 ps simulation time. This may introduces errors in the calculated values of the system properties. Nevertheless, PRC is frequently used because it reduces the number of iterations relative to ZRC required to attain a given SCF convergence value (see Table 1). For all 5 different SCF energy convergence criteria studies, the average number of SCF iterations using PRC is smaller than that using ZRC, e.g., 10−7 hartree is used as the SCF energy convergence criterion, the number of iterations required on average is 5.3 for the PRC approach while the number is 9.4 for ZRC. As the convergence criterion is tightened, the number of iterations will increase and the relative difference in numbers of required cycles between PRC and ZRC will decrease.
Table 1.
The average number of SCF iterations of C2F4 in microcanonical ensemble simulation using SCC-DFTB at 500 K with different extrapolated DXL-BOMD algorithms and conventional approaches. Here, “PRC” denotes the algorithm use previous step converged charges as the initial guess of the current step geom. “ZRC” represents the algorithm that always starts from zero charge for each atom at every time step. The number under DXL-BOMD is higher odd order term remained in DXL-BOMD algorithms.
| DXL-BOMD |
|||||||||
|---|---|---|---|---|---|---|---|---|---|
| SCF energy criteria [hartree] | PRC | ZRC | 1 | 3 | 5 | 7 | 9 | 11 | 13 |
| 10−6 | 5 22 | 8.09 | 2.57 | 2.00 | 2.00 | 2.00 | 2.00 | 4.37 | 4.99 |
| 10−7 | 5.34 | 9.41 | 4.77 | 4.71 | 4.70 | 4.68 | 4.69 | 4.88 | 5.73 |
| 10−8 | 6.05 | 10.18 | 5.29 | 5.25 | 5.22 | 5.21 | 4.96 | 4.97 | 5.93 |
| 10−9 | 7.28 | 10.70 | 5.45 | 5.27 | 5.68 | 5.48 | 5.64 | 5.54 | 7.05 |
| 10−10 | 7.94 | 10.91 | 6.63 | 6.33 | 6.23 | 6.30 | 6.29 | 6.44 | 7.66 |
Amino acid molecules
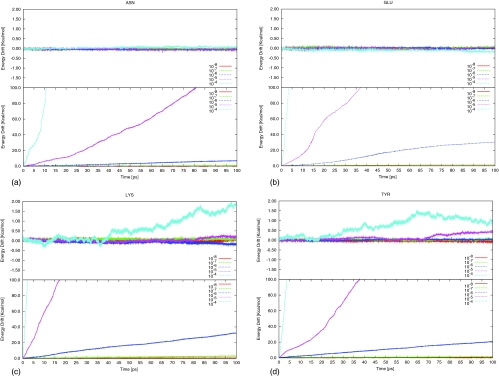
20 natural amino acids were simulated for 100 ps using both PRC and ZRC at 298 K. Only results from Asn, GluH, Lys, and Tyr are shown in Fig. 2; the other amino acids show similar features.
Figure 2.
Energy drift in Kcal/mol of amino acid molecules under microcanonical ensemble simulations under 298 K using SCC-DFTB. (a) Asparagine (neutral), (b) glutamic acid (neutral), (c) lysine (neutral), and (d) tyrosine. For each amino acid, the upper panel corresponds to ZRC while the lower panel to PRC.
Use of ZRC shows some new features, as shown in Fig. 2. For Asn and Lys the behavior is similar to C2F4, i.e., a stable energy is achieved for all threshold values. By contrast, GluH and Tyr appear to be very stable if a Hartree threshold value of 10−5 or better is used. With PRC, the results for the amino acids shown in Fig. 2 behave similarly to those of C2F4. In all four molecules, the energy drift using 10−4 hartree threshold value increases quickly; in 10 ps the drift is more than 100 kcal/mol. As discussed above, this is due to errors introduced by the finite SCF convergence and more particularly to the accumulation of errors in the successive steps, in accord with Eq. 13. When the hartree threshold is set to 10−8, the energy drift is smaller than 1 kcal/mol in 100 ps, again similar to C2F4. From these results, it appears that with PRC and conventional methods, a value of 10−7 hartree or smaller should be used as the SCF convergence criteria in term of energy drift. In addition, it is noticed that ZRC used here is similar to superposition of atomic density guess (SAD) by Herbert et al.22 while PRC is similar to the guess using previous MOs (PMO). The difference between ZRC and SAD or PRC and PMO is ZRC/PRC are concerned with charge variables while SAD/PMO are concerned with one electron density matrix. This difference is not essential and thus the performance are quite close to each other between ZRC and SAD or PRC and PMO.
DXL-BOMD
In this section, we use DXL-BOMD method and compare the results with those obtained in Sec. 1 based on the conventional methods.
C2F4
DXL-BOMD was introduced to reduce the number SCF iterations without introducing errors in molecular dynamics. It does so by extrapolating electronic variables from previous steps as in Eq. 11. In Table 1, the number of SCF iterations required to satisfy given convergence criteria are listed for conventional BOMD and for DXL-BOMD. From 3rd order to 9th order DXL-BOMD, only two SCF iterations are required when using 10−6 hartree as threshold values. This is in contrast to the fact that 5.2 SCF iterations are required on average for PRC. As total energy fluctuations are utilized as SCF convergence criteria, two is the least possible number of SCF iterations that is required. As a result, DXL-BOMD here provides the optimal method that's possible to accelerate SCF convergence.
Certainly, when a tighter SCF energy convergence criterion is applied, more SCF iterations will be required. This is definitely true for DXL-BOMD as well. As shown in Table 1, the number of SCF iterations increases almost logarithmically with the decrease in energy convergence criterion. This result reflects the superlinear convergence property of the modified Broyden method applied to electronic energy optimization.39
Despite the fact that all results using DXL-BOMD converged faster than PRC, there are appreciable difference between different orders of DXL-BOMD algorithms. For example, only 5.25 SCF iterations are needed when using 5th order DXL-BOMD, while 5.93 are needed when using 13th order DXL-BOMD. In general, it is found that using 3rd/5th/7th order DXL-BOMD requires fewer SCF iterations than other orders of DXL-BOMD, i.e., 1st, 9th, 11th and 13th order DXL-BOMD. We believe this somewhat surprising behavior arises from a better balance between the “noise” force and the dissipative force in Eq. 7 for 3rd/5th/7th order DXL-BOMD methods than for other orders. The extrapolated variables (i.e., charges) are closer to the true value at the next time step for these orders of DXL-BOMD. A similar trend is observed for the amino acids. However, additional analysis is required to verify this explanation.
Although it is critical to reduce the number of SCF iterations in practical calculations, it is also important to maintain the stability of the dynamics as discussed in Sec. 4A. In Table 2, the total energy drift values of C2F4 are shown. Due to the reasons mentioned in Sec. 4A, the energy drift from PRC is large even when using relatively higher threshold values, e.g., 10−6 hartree. Compared to PRC, all DXL-BOMD algorithms perform much better. In fact, several DXL-BOMD algorithms like 3rd/5th/7th order algorithms have results close to those from ZRC. These results are consistent with those in our previous paper. Among these DXL-BOMD algorithms, it's found that 3rd/5th/7th order algorithms are better than others in terms of total energy drift. This is attributed to a better balance between noise and damping terms retained in 3rd/5th/7th order algorithms.
Table 2.
Total energy drift of C2F4 in microcanonical ensemble simulation using SCC-DFTB at 500 K with different extrapolated DXL-BOMD algorithms and conventional approaches. Here, “PRC” denotes the algorithm use previous step converged charges as the initial guess of the current step geom. “ZRC” represents the algorithm that always starts from zero charge for each atom at every time step. The number under DXL-BOMD is higher odd order term remained in DXL-BOMD algorithms. The energy drift is taken as the different between the average energy of first 1000 steps and the final 1000 steps. The energy unit is 10−3 Kcal·mol−1 ps−1.
| DXL-BOMD |
|||||||||
|---|---|---|---|---|---|---|---|---|---|
| SCF energy criteria [hartree] | PRC | ZRC | 1 | 3 | 5 | 7 | 9 | 11 | 13 |
| 10−6 | 429.06 | −0.03 | 0.80 | 0.03 | 0.03 | −0.02 | 5.42 | −0.04 | 1.04 |
| 10−7 | 42.61 | −0.02 | 0.10 | 0.08 | 0.03 | 0.06 | 0.22 | −0.05 | 0.17 |
| 10−8 | 0.51 | 0.03 | 0.04 | 0.00 | 0.06 | 0.04 | 0.00 | 0.02 | 0.07 |
| 10−9 | 0.03 | 0.01 | −0.01 | 0.06 | 0.03 | 0.01 | 0.00 | 0.03 | 0.01 |
| 10−10 | 0.04 | 0.08 | 0.05 | 0.05 | −0.01 | −0.03 | 0.03 | −0.01 | −0.03 |
Amino acid molecules
For the four representative amino acids, i.e., asparagine, glutamic acid, lysine, and tyrosine, the numbers of average SCF iterations are still less than those using PRC with the same SCF convergence criteria (see Table 3). This is consistent with those results of C2F4. Since the number of SCF iterations using the DXL-BOMD algorithms is one or two less than that using PRC, there is a significant reduction in terms of the total SCF time. In general, the SCF iteration number using DXL-BOMD is only about half of those using ZRC, which is apparently favorable in terms of computational efficiency concern. Here, it is found again that 3rd/5th/7th order algorithms usually require less number of SCF iterations than other DXL-BOMD algorithms, which is consistent with the results of C2F4. This observation has been attributed to the better balance between noise and damping terms from these three algorithms.
Table 3.
The average number of SCF iterations of amino acid molecules in microcanonical ensemble simulation for 100 ps using SCC-DFTB at 298 K with different extrapolated DXL-BOMD algorithms and conventional approaches. Here, “PRC” denotes the algorithm use previous step converged charges as the initial guess of the current step geom. “ZRC” represents the algorithm that always starts from zero charge for each atom at every time step. The number under DXL-BOMD is higher odd order term remained in DXL-BOMD algorithms.
| ASN | DXL-BOMD |
||||||||
|---|---|---|---|---|---|---|---|---|---|
| SCF energy criteria [hartree] | PRC | ZRC | 1 | 3 | 5 | 7 | 9 | 11 | 13 |
| 10−6 | 5.53 | 10.82 | 4.58 | 4.50 | 4.35 | 4.36 | 4.35 | 4.52 | 5.94 |
| 10−7 | 7.11 | 12.14 | 5.64 | 5.55 | 5.54 | 5.53 | 5.49 | 5.48 | 8.00 |
| 10−8 | 8.58 | 13.87 | 7.21 | 6.96 | 6.85 | 6.83 | 6.80 | 6.78 | 8.57 |
| 10−9 | 9.70 | 15.21 | 8.76 | 8.63 | 8.59 | 8.59 | 8.56 | 8.56 | 9.71 |
| 10−10 | 11.02 | 16.67 | 9.89 | 9.75 | 9.74 | 9.73 | 9.71 | 9.70 | 10.68 |
| GLU | DXL-BOMD |
||||||||
| SCF energy criteria [hartree] |
PRC |
ZRC |
1 |
3 |
5 |
7 |
9 |
11 |
13 |
| 10−6 | 6.10 | 11.29 | 4.52 | 4.31 | 4.20 | 4.18 | 4.27 | 4.58 | 5.48 |
| 10−7 | 7.59 | 13.25 | 5.93 | 5.81 | 5.78 | 5.77 | 5.76 | 5.78 | 7.83 |
| 10−8 | 8.98 | 14.75 | 7.89 | 7.61 | 7.56 | 7.56 | 7.53 | 7.44 | 8.89 |
| 10−9 | 9.94 | 16.16 | 9.36 | 9.27 | 9.11 | 9.08 | 9.09 | 9.06 | 9.91 |
| 10−10 | 11.41 | 17.33 | 10.41 | 10.21 | 10.16 | 10.21 | 10.18 | 10.21 | 10.79 |
| LYS | DXL-BOMD |
||||||||
| SCF energy criteria [hartree] |
PRC |
ZRC |
1 |
3 |
5 |
7 |
9 |
11 |
13 |
| 10−6 | 6.02 | 10.56 | 4.63 | 4.41 | 4.38 | 4.40 | 4.45 | 4.58 | 5.34 |
| 10−7 | 7.40 | 11.71 | 5.84 | 5.74 | 5.70 | 5.70 | 5.70 | 5.72 | 7.20 |
| 10−8 | 8.36 | 13.37 | 7.33 | 7.12 | 6.94 | 6.99 | 6.90 | 7.06 | 8.44 |
| 10−9 | 9.29 | 14.33 | 8.63 | 8.57 | 8.47 | 8.49 | 8.45 | 8.48 | 9.79 |
| 10−10 | 10.80 | 15.63 | 9.64 | 9.56 | 9.53 | 9.50 | 9.50 | 9.55 | 10.52 |
| TYR | DXL-BOMD |
||||||||
| SCF energy criteria [hartree] |
PRC |
ZRC |
1 |
3 |
5 |
7 |
9 |
11 |
13 |
| 10−6 | 5.64 | 10.09 | 4.38 | 4.23 | 4.13 | 4.20 | 4.25 | 4.57 | 5.93 |
| 10−7 | 7.42 | 11.85 | 5.93 | 5.77 | 5.68 | 5.69 | 5.71 | 5.78 | 7.63 |
| 10−8 | 8.89 | 14.30 | 7.88 | 7.25 | 7.24 | 7.20 | 7.10 | 7.29 | 8.97 |
| 10−9 | 10.19 | 15.79 | 9.26 | 9.04 | 8.93 | 8.91 | 8.90 | 8.91 | 10.17 |
| 10−10 | 11.72 | 17.26 | 10.63 | 10.47 | 10.40 | 10.37 | 10.42 | 10.32 | 11.57 |
Besides the average number of SCF iterations, the total energy drift values are presented in Table 4. As noticed before, PRC results show significant energy drift compared with other algorithms. Only when very small SCF threshold values, i.e., less than 10−7 hartree, are the energy drift values comparable to other algorithms. Although 1st, 9th, 11th, and 13th order DXL-BOMD algorithms show relatively large energy drift values compared to those from ZRC when using 10−6 hartree SCF threshold value, the energy drift values from 3rd/5th/7th DXL-BOMD algorithms are favorable.
Table 4.
Total energy drift of amino acid molecules in microcanonical ensemble simulation for 100 ps using SCC-DFTB at 298 K with different extrapolated DXL-BOMD algorithms and conventional approaches. Here, “PRC” denotes the algorithm use previous step converged charges as the initial guess of the current step geom. “ZRC” represents the algorithm that always starts from zero charge for each atom at every time step. The number under DXL-BOMD is higher odd order term remained in DXL-BOMD algorithms. The energy drift is taken as the different between the average energy of first 1000 steps and the final 1000 steps. The energy unit is 10−3 Kcal·mol−1 ps−1.
| ASN | DXL-BOMD |
||||||||
|---|---|---|---|---|---|---|---|---|---|
| SCF energy criteria[hartree] | PRC | ZRC | 1 | 3 | 5 | 7 | 9 | 11 | 13 |
| 10−6 | 68.25 | −0.37 | 5.77 | 0.07 | −0.75 | −1.31 | 2.43 | 3.51 | 1.46 |
| 10−7 | 6.73 | 0.25 | 0.28 | −0.40 | 0.37 | 0.00 | 0.57 | −0.10 | −0.98 |
| 10−8 | 0.44 | −0.14 | 0.19 | 0.06 | 0.17 | −0.61 | −0.28 | −0.28 | 0.03 |
| 10−9 | 1.33 | −0.07 | −0.51 | −0.16 | −0.98 | −0.39 | −0.39 | −0.25 | 0.43 |
| 10−10 | −0.42 | −0.32 | −0.29 | −0.63 | −0.07 | −0.15 | −0.30 | −0.08 | 0.13 |
| GLU | DXL-BOMD |
||||||||
| SCF energy criteria[hartree] |
PRC |
ZRC |
1 |
3 |
5 |
7 |
9 |
11 |
13 |
| 10−6 | 303.10 | 0.30 | 14.77 | −0.44 | −0.35 | 0.92 | 6.09 | 11.10 | −0.12 |
| 10−7 | 15.16 | 0.84 | 1.99 | −0.20 | −0.89 | 1.00 | 0.04 | 1.30 | −0.73 |
| 10−8 | 1.94 | 0.37 | −0.92 | −0.09 | 0.62 | 0.40 | 2.00 | −0.85 | 1.65 |
| 10−9 | −0.21 | −0.58 | 0.08 | −0.22 | 0.92 | −1.41 | 0.42 | 1.25 | −1.51 |
| 10−10 | 1.33 | 1.08 | 0.17 | 0.83 | 0.85 | 1.05 | 0.10 | −0.79 | 1.11 |
| LYS | DXL−BOMD |
||||||||
| SCF energy criteria[hartree] |
PRC |
ZRC |
1 |
3 |
5 |
7 |
9 |
11 |
13 |
| 10−6 | 321.69 | −2.05 | 38.11 | −2.33 | −0.43 | −3.15 | 10.26 | 19.61 | 6.36 |
| 10−7 | 28.81 | 0.24 | 4.84 | −0.86 | 1.77 | −0.96 | 2.06 | 1.24 | 8.27 |
| 10−8 | 2.36 | 0.26 | 0.06 | −0.70 | 0.42 | 2.75 | 0.76 | 1.44 | 0.52 |
| 10−9 | 0.93 | −0.07 | −1.08 | 0.71 | 1.54 | −0.18 | −0.15 | −0.53 | −0.62 |
| 10−10 | 1.19 | 0.60 | 0.12 | −1.07 | −0.41 | 1.07 | −0.65 | −0.01 | 0.45 |
| TYR | DXL-BOMD |
||||||||
| SCF energy criteria[hartree] |
PRC |
ZRC |
1 |
3 |
5 |
7 |
9 |
11 |
13 |
| 10−6 | 207.20 | 0.42 | 13.27 | 1.27 | 0.49 | 0.08 | 3.99 | 14.21 | 32.82 |
| 10−7 | 15.22 | 0.57 | 1.97 | −0.44 | 0.87 | −0.47 | 0.61 | 2.74 | 8.01 |
| 10−8 | 1.51 | −0.69 | 0.81 | 0.45 | 0.08 | 0.47 | 0.38 | 0.55 | 0.11 |
| 10−9 | 0.29 | −0.44 | 1.14 | 1.08 | 0.85 | 0.05 | 0.35 | 0.37 | 0.95 |
| 10−10 | −1.07 | −0.15 | 0.51 | 1.30 | 0.68 | 0.39 | 1.20 | 0.40 | 0.01 |
Fock matrix extrapolation
Although only charge extrapolation results are presented in Secs. 4B1, 4B2, any electronic variable could be extrapolated under our DXL-BOMD scheme in principle. Beside the charge variable discussed in Secs. 4A, 4B1, 4B2 wavefunction, density matrix, Fock matrix could also be selected as the extrapolated variable. However, when extrapolating wavefunctions, one should be cautious to maintain a consistent gauge of the wavefunctions at each geometric step.20, 32 The gauge consistency issue arises due to the invariance of unitary rotations in the occupied orbital space. This issue is not present in charge or Fock matrix element extrapolation.19, 32 In the current section, the results from Fock matrix element DXL-BOMD algorithms will be presented.
As Fock matrix elements are explicitly computed in SCC-DFTB, it is interesting to compare the performance between the auxiliary dynamics using Fock matrix elements and atomic Mulliken charges. In Table 5, the difference of the average number of SCF iterations between Fock matrix element extrapolation and charge extrapolation is tabulated. A negative number means using Fock matrix element extrapolation requires fewer SCF iterations than using charge extrapolation. In general, the two different algorithms show similar performance. This indicates that the charge extrapolation is at least as efficient as the Fock matrix element extrapolation in term of the number of SCF iterations. If only 3rd, 5th, and 7th order DXL-BOMD algorithms are considered, these two different extrapolation algorithms have even closer performance.
Table 5.
The average number difference of SCF iterations of amino acid molecules in microcanonical ensemble simulation for 100 ps using SCC-DFTB at 298 K with different extrapolated DXL-BOMD algorithms between for Fock matrix element and for charge (nFock−ncharge). The number under DXL-BOMD is higher odd order term remained in DXL-BOMD algorithms.
| ASN | DXL-BOMD |
||||||
|---|---|---|---|---|---|---|---|
| SCF energy criteria[hartree] | 1 | 3 | 5 | 7 | 9 | 11 | 13 |
| 10−6 | 0.07 | 0.07 | 0.20 | 0.15 | 0.43 | 0.55 | −0.61 |
| 10−7 | 0.05 | 0.03 | −0.01 | 0.00 | 0.24 | 0.89 | −1.34 |
| 10−8 | 0.09 | −0.04 | 0.02 | −0.04 | 0.43 | 1.23 | −0.33 |
| 10−9 | 0.10 | 0.07 | 0.04 | 0.04 | 0.30 | 0.65 | −0.30 |
| 10−10 | 0.02 | 0.08 | 0.02 | 0.01 | 0.18 | 0.62 | 0.00 |
| GLU | DXL-BOMD |
||||||
| SCF energy criteria[hartree] |
1 |
3 |
5 |
7 |
9 |
11 |
13 |
| 10−6 | 0.38 | 0.23 | 0.43 | 0.41 | 0.69 | 0.62 | −0.09 |
| 10−7 | 0.12 | 0.08 | 0.18 | 0.10 | 0.43 | 1.16 | −0.54 |
| 10−8 | 0.37 | 0.33 | 0.35 | 0.28 | 0.62 | 1.13 | −0.20 |
| 10−9 | 0.01 | −0.09 | 0.11 | 0.02 | 0.36 | 0.83 | 0.16 |
| 10−10 | 0.15 | 0.14 | 0.04 | −0.02 | 0.27 | 1.03 | 0.69 |
| LYS | DXL-BOMD |
||||||
| SCF energy criteria[hartree] |
1 |
3 |
5 |
7 |
9 |
11 |
13 |
| 10−6 | −0.05 | 0.09 | 0.01 | −0.07 | 0.22 | 0.31 | −0.26 |
| 10−7 | −0.10 | −0.08 | −0.05 | −0.10 | 0.01 | 0.40 | −0.62 |
| 10−8 | −0.35 | −0.41 | −0.32 | −0.37 | 0.30 | 0.56 | −0.60 |
| 10−9 | −0.15 | −0.24 | −0.20 | −0.22 | 0.09 | 0.30 | −0.81 |
| 10−10 | −0.13 | −0.21 | −0.23 | −0.25 | 0.04 | 0.36 | −0.41 |
| TYR | DXL-BOMD |
||||||
| SCF energy criteria[hartree] |
1 |
3 |
5 |
7 |
9 |
11 |
13 |
| 10−6 | 0.19 | 0.16 | 0.25 | 0.14 | 0.76 | 0.86 | −0.41 |
| 10−7 | −0.01 | 0.01 | 0.03 | −0.02 | 0.38 | 0.81 | −0.70 |
| 10−8 | −0.22 | 0.12 | −0.01 | −0.04 | 0.86 | 1.15 | −0.36 |
| 10−9 | −0.02 | 0.02 | −0.03 | −0.14 | 0.44 | 0.80 | −0.16 |
| 10−10 | −0.02 | −0.02 | 0.05 | 0.01 | 0.25 | 0.91 | 0.04 |
In addition, the total energy drift magnitude difference between these two extrapolation algorithms is shown in Table 6. Although the difference can be as large as −35.54 mKcal/mol ps−1 for 3rd order DXL-BOMD algorithm of glutamic acid molecule when using 10−6 hartree as SCF energy convergence criterion, most other difference values are relatively small in term of magnitude. This further confirms the similarity in performance between these two different choices of extended dynamical variables for the electronic degrees of freedom.
Table 6.
Total energy drift magnitude difference of amino acid molecules in microcanonical ensemble simulation using SCC-DFTB at 298 K with different DXL-BOMD algorithms for Fock matrix elements and for charges (|ΔEFock|−|ΔEcharge|). The number under DXL-BOMD is higher odd order term remained in DXL-BOMD algorithms. The energy drift is taken as the difference between the average energy of first 1000 steps and the final 1000 steps. The energy unit is 10−3 Kcal·mol−1 ps−1.
| ASN | DXL-BOMD |
||||||
|---|---|---|---|---|---|---|---|
| SCF energy criteria[hartree] | 1 | 3 | 5 | 7 | 9 | 11 | 13 |
| 10−6 | −5.23 | 1.29 | −0.55 | −0.92 | −1.14 | −1.62 | 0.39 |
| 10−7 | −0.06 | −0.11 | 0.02 | 0.31 | −0.01 | 0.26 | −0.47 |
| 10−8 | −0.16 | 0.26 | 0.12 | −0.19 | −0.14 | −0.19 | 0.57 |
| 10−9 | −0.14 | 0.00 | −0.66 | −0.38 | −0.36 | −0.07 | 0.06 |
| 10−10 | −0.14 | −0.10 | 0.05 | −0.06 | 0.26 | 0.65 | −0.12 |
| GLU | DXL-BOMD |
||||||
| SCF energy criteria[hartree] |
1 |
3 |
5 |
7 |
9 |
11 |
13 |
| 10−6 | −3.21 | 0.62 | 1.00 | −0.41 | −3.16 | −6.81 | 2.08 |
| 10−7 | −0.20 | 1.03 | 0.94 | −0.53 | 0.96 | −0.96 | 0.37 |
| 10−8 | −0.59 | −0.03 | 0.75 | −0.05 | −1.27 | −0.17 | −0.66 |
| 10−9 | 1.41 | 0.02 | −0.28 | −0.93 | −0.13 | −0.14 | −0.40 |
| 10−10 | 0.90 | −0.69 | −0.16 | 0.26 | 0.66 | 0.33 | 0.11 |
| LYS | DXL-BOMD |
||||||
| SCF energy criteria[hartree] |
1 |
3 |
5 |
7 |
9 |
11 |
13 |
| 10−6 | −35.54 | −1.63 | −0.34 | −2.68 | −7.59 | −18.25 | −5.87 |
| 10−7 | −4.76 | −0.13 | −0.40 | 0.65 | −1.61 | −0.69 | −6.59 |
| 10−8 | −0.01 | −0.35 | 0.11 | −1.79 | 1.60 | −1.13 | 0.03 |
| 10−9 | −0.54 | −0.25 | −1.40 | 0.57 | 0.88 | −0.16 | −0.02 |
| 10−10 | 2.34 | −0.87 | 1.72 | −0.73 | 0.35 | 0.68 | 1.83 |
| TYR | DXL-BOMD |
||||||
| SCF energy criteria[hartree] |
1 |
3 |
5 |
7 |
9 |
11 |
13 |
| 10−6 | −11.15 | −0.72 | −0.41 | 0.22 | −1.08 | −12.48 | −31.02 |
| 10−7 | −1.85 | 1.40 | −0.79 | −0.15 | 0.03 | −2.26 | −6.95 |
| 10−8 | −0.71 | −0.25 | 0.69 | −0.19 | 0.43 | 0.28 | 0.70 |
| 10−9 | −0.64 | −0.26 | −0.62 | 0.09 | 0.05 | 0.02 | −0.42 |
| 10−10 | 0.23 | −1.03 | −0.43 | 0.02 | −0.82 | 0.31 | 0.35 |
In summary, the DXL-BOMD method clearly outperforms the conventional approach using ZRC and PRC, both in terms of the average number of SCF iterations and the total energy drift rate. The reason for the excellent performance of DXL-BOMD is that the time reversibility of the auxiliary electronic variables (here, Fock matrix element and charges), is conserved to high orders while a dissipation term is added to counteract the noise introduced by the finite SCF convergence and other numerical errors. In the present cases, the performance using Fock matrix elements or charge is quite similar. It is found that 3rd, 5th and 7th order DXL-BOMD is better than other (even higher order) DXL-BOMD algorithms.
Liquid water
Water is ubiquitous in biological environment and its importance cannot be overstated. As liquid water has been studied both theoretically and experimentally,48, 50, 51, 52, 53 it is an important test case for the new DXL-BOMD algorithm. The results on liquid water system are complementary to those presented in Secs. 4A, 4B, where only gas-phase molecules are considered. Again, the emphasis is not on the accuracy of the SCC-DFTB results for water, per se, which has been studied by Maupin et al.,48 but rather on the comparison of the efficiency of the DXL-BOMD algorithm with that of the ZRC method.
Average temperature, energy drift and SCF iteration number
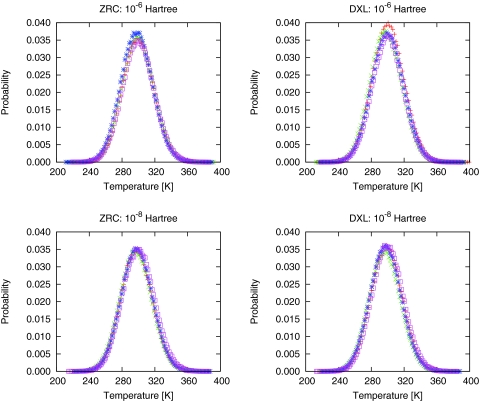
In Fig. 3, the temperature distribution for all trajectories are shown. For each algorithm with a specified SCF criterion, results from four different trajectories are presented. From the plots in Fig. 3, it is clear there is no appreciable difference in the temperature distribution between the trajectories using SCF convergence criteria of 10−6 or 10−8 hartree. In the previous study of water with SCC-DFTB,48 the SCF convergence criteria is 10−6 hartree. Also, there is also no appreciable difference between ZRC algorithm and the 5th order DXL-BOMD algorithm. The temperature has a normal distribution relative to 300 K for all trajectories, as expected in microcanonical ensemble simulation. Table 7 compares the results obtained for the ZRC and the DXL-BOMD algorithm with different convergence criteria. The mean average temperatures usually is within 1 K of the target temperature of 300 K. The standard deviations of the mean temperature values from four different trajectories indicates that the deviation is generally less than 2 K for different simulations under the same specified conditions.
Figure 3.
Temperature distribution of 32 water molecules in a periodic cubic box with side length of 9.862 Å during 300 ps microcanonical ensemble simulation using SCC-DFTB with time step of 1.0 fs. In each panel, there are results from four different trajectories. “ZRC” is for the algorithm using zero charge for every atom at every step; “DXL” for the algorithm using 5th order DXL-BOMD algorithm. SCF convergence criteria is shown on top of each panel.
Table 7.
Average temperature, average energy drift, average SCF iteration number, heat of vaporization, and diffusion coefficients calculated from Einstein relation of liquid water (32 water in 9.862 Å periodic cubic box) in microcanonical ensemble simulation using SCC-DFTB with 5th order DXL−BOMD algorithm and zero charge for initial charge guess, respectively. Results from two different SCF convergence criteria are shown. For each algorithm under a specified SCF convergence criteria, four different trajectories are carried out and summarized below.
| SCF criteria | Average | Average energy | Average SCF | Heat of vaporization | Diffusion coefficient | ||
|---|---|---|---|---|---|---|---|
| [a.u.] | Algorithm | Trajectory | temperature [K] | drift [Kcal/mol/ps] | iteration number | [Kcal/mol] | [A2]/ps |
| 1 | 300.6 | 0.012 | 9.44 | 4.16 | 1.02 | ||
| 2 | 300.1 | 0.015 | 9.44 | 4.17 | 1.04 | ||
| 10−6 | ZRC | 3 | 298.8 | 0.014 | 9.41 | 4.16 | 1.09 |
| 4 | 300.6 | 0.015 | 9.42 | 4.15 | 0.98 | ||
| average | 300.0 | 0.014 | 9.43 | 4.16 | 1.04 | ||
| |
|
standard deviation |
0.8 |
0.001 |
0.02 |
0.01 |
0.05 |
| 1 | 301.9 | −0.005 | 5.13 | 4.14 | 1.06 | ||
| 2 | 298.8 | 0.012 | 5.12 | 4.18 | 1.08 | ||
| 10−6 | DXL-BOMD | 3 | 300.9 | 0.003 | 5.11 | 4.15 | 1.06 |
| 4 | 301.1 | 0.014 | 5.07 | 4.13 | 1.11 | ||
| average | 300.6 | 0.006 | 5.11 | 4.15 | 1.08 | ||
| |
|
standard deviation |
1.3 |
0.009 |
0.03 |
0.02 |
0.03 |
| 1 | 298.7 | 0.013 | 11.93 | 4.17 | 1.03 | ||
| 2 | 297.9 | 0.018 | 11.93 | 4.22 | 0.93 | ||
| 10−8 | ZRC | 3 | 299.1 | 0.005 | 11.94 | 4.19 | 0.96 |
| 4 | 300.7 | 0.021 | 11.94 | 4.14 | 1.08 | ||
| average | 299.1 | 0.014 | 11.94 | 4.18 | 1.00 | ||
| |
|
standard deviation |
1.2 |
0.007 |
0.01 |
0.03 |
0.07 |
| 1 | 299.7 | 0.009 | 8.46 | 4.18 | 1.02 | ||
| 2 | 297.4 | 0.007 | 8.44 | 4.22 | 1.06 | ||
| 10−8 | DXL-BOMD | 3 | 298.4 | 0.006 | 8.40 | 4.16 | 1.07 |
| 4 | 301.1 | 0.013 | 8.38 | 4.14 | 1.06 | ||
| average | 299.1 | 0.009 | 8.42 | 4.17 | 1.05 | ||
| standard deviation | 1.6 | 0.003 | 0.04 | 0.03 | 0.02 |
In Table 7, the total energy drift is calculated as the energy difference between the average energy of the first picosecond and that of the last picosecond divided by the simulation time. Generally, the total energy drift is on the order of 10−2 kcal/mol ps−1. The magnitude of the energy drift is similar for ZRC and the 5th order DXL-BOMD algorithms. The drift is always small and very similar using the different convergence criteria. Most important, there is a significant difference for the number of SCF iterations required for the two algorithms for the same convergence criterion. About half the number of SCF iterations are required for calculations using the 5th order DXL-BOMD algorithm compared to those using ZRC algorithm for 10−6 hartree as the SCF convergence criterion. For the 10−8 hartree SCF convergence criterion, the reduction in SCF iteration number is somewhat less. The relatively efficiency will be further discussed in Sec. 4D.
Structure properties
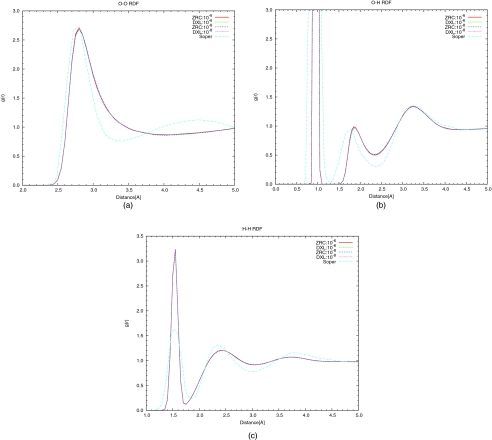
The radial distribution function (RDF) for (a) oxygen-oxygen, (b) oxygen-hydrogen and (c) hydrogen-hydrogen were calculated and compared to experimental results,53 which are plotted in Fig. 4, respectively. Results from only one trajectory with each algorithm and a specific SCF criterion are shown. As the size of the simulation box is only 9.862 Å, the RDF curves are only plotted up to 5.0 Å. Some features of these RDF curves are summarized in Table 8.
Figure 4.
Liquid water (32 water in a periodic cubic box with side length of 9.862 Å) radial distribution function for (a) oxygen-oxygen, (b) oxygen-hydrogen, and (c) hydrogen-hydrogen. “ZRC” is for the algorithm using zero charge for every atom at every step; “DXL” for 5th order DXL-BOMD algorithm. In each panel, the upper right legend shows SCF convergence criteria. In addition, the experimental data from Soper et al. (Ref. 53) is also plotted for comparison.
Table 8.
Radial distribution function features of liquid water (32 water in 9.862 Å periodic cubic box) in microcanonical ensemble simulation using SCC-DFTB with 5th order DXL-BOMD algorithm and zero charge for initial charge guess, respectively. These results are from those trajectories in Figure 4 and experimental values are from Soper et al. (Ref. 53).
| (a) O−O |
|
|
|
|
|---|---|---|---|---|
| SCF criteria | Algorithm | First maximum peak [A] | First minimum peak [A] | # O within first shell |
| 10−6 | ZRC | 2.80 | 4.05 | 9.03 |
| 10−6 | DXL-BOMD | 2.80 | 4.05 | 9.04 |
| 10−8 | ZRC | 2.80 | 4.05 | 9.04 |
| 10−8 | DXL-BOMD | 2.80 | 4.05 | 9.03 |
| Experiment |
2.75 |
3.41 |
4.76 |
|
| (b) O−H |
|
|
|
|
| SCF criteria | Algorithm | Second maximum peak [A] | Second minimum peak [A] | # H within second shell |
| 10−6 | ZRC | 1.85 | 2.35 | 1.74 |
| 10−6 | DXL-BOMD | 1.85 | 2.35 | 1.74 |
| 10−8 | ZRC | 1.85 | 2.35 | 1.74 |
| 10−8 | DXL-BOMD | 1.85 | 2.35 | 1.74 |
| Experiment |
1.75 |
2.36 |
1.93 |
|
| (c) H−H |
|
|
|
|
| SCF criteria | Algorithm | First maximum peak [A] | First minimum peak [A] | # H within first shell |
| 10−6 | ZRC | 1.55 | 1.75 | 1.03 |
| 10−6 | DXL-BOMD | 1.55 | 1.75 | 1.03 |
| 10−8 | ZRC | 1.55 | 1.75 | 1.03 |
| 10−8 | DXL-BOMD | 1.55 | 1.75 | 1.03 |
| Experiment | 1.54 | 1.85 | 1.02 | |
The RDF curves for oxygen-oxygen in Fig. 4a show that the results from all simulations are nearly identical. From the simulations, the first peak is at 2.80 Å, which is a slightly larger distance than the experimental value. Also, the peak is broader than the experimental one. Beyond the first peak, the calculated curves differ significantly from experiment. Such differences between the experimental results and simulation results have been observed previoulsy.47, 48 Since DFT results do reproduce the experimental O-O RDF curve,50, 54 the difference observed here reflects the deficiencies in the current implementation of SCC-DFTB. For O-H RDF curves in Fig. 4b, the difference between experimental values and simulation results is again significant. The second maximum from the simulations is located at 1.85 Å while the experimental value is 1.75 Å. According to Table 8, the number of non-bonded hydrogen atoms within the second shell of a reference O atom from the simulations is 1.74, while the corresponding number from experiment is 1.93. These differences have also been reported by Maupin et al.48 The H-H RDF curves in Fig. 4c also shows considerable differences between the simulation results and the experiments. Although the first maximum is located close to the experimental value, its magnitude is more than twice the experimental value. The numbers of hydrogen atom within the first solvation shell from the simulations is close to the number from experiment. (see Table 8)
From above results and earlier work, it is clear that SCC-DFTB does not accurately reproduce the experimental results for water. This fact could be due to the deficiency of the present formulation of SCC-DFTB or its parameterization scheme, or both. Although there have been some efforts to improve the original SCC-DFTB method by modifying the distance dependent γ functions,55 the resulting RDF curves are still considerably different from experimental ones.48 However, this does not invalidate the comparison between the ZRC and DXL-BOMD in the present paper.
Energetic and dynamic properties
In addition to studying the structural properties of the liquid water system, it is of interest to examine the energetic results of the SCC-DFTB method. As shown by previous studies,48, 52 the SCC-DFTB method underestimates the dimerization energy of water compared to the results at the MP2 level, which has been attributed to the structural differences between the dimers. Here, the heat of vaporization energy is calculated in accord with the approach of Maupin et al.48. In Table 7, the value of heat of vaporization energy of water from the different trajectories are listed. The difference between ZRC and DXL-BOMD algorithms is no larger than the difference between different trajectories using the same algorithm. Further, the difference obtained from calculations with the two SCF convergence criteria are indistinguishable from the difference using same SCF convergence criterion. These facts demonstrate the DXL-BOMD algorithm is as accurate as the ZRC algorithm for these properties.
Although the DXL-BOMD algorithm can well reproduce results using the ZRC algorithm, the predicted heat of vaporization from both methods is about 4.16 Kcal/mol as shown in Table 7. This value is close to the previous study,48 but both values are much smaller than the experimental value [10.50 Kcal/mol (Ref. 48)]. The difference is due to the underestimation of dimerization energy of water molecule mentioned above.
The diffusion coefficients in liquid water of oxygen calculated from the Einstein relation are also listed in Table 7. The results from ZRC algorithm and DXL-BOMD algorithm are very similar. The small difference in the oxygen diffusion coefficients from different algorithms and SCF convergence criteria again support the accuracy of the DXL-BOMD algorithm. The oxygen diffusion coefficients calculated here are slightly smaller than a previous study (1.11 ± 0.04 Å2/ps);48 this result is likely due to the larger simulation box size used in Ref. 47 according to the analysis by Dünweg and Kremer.56 However, in all cases, the calculated oxygen diffusion coefficients are much larger than the experimental value (0.23 Å2/ps).57 This difference between calculated coefficients and the experimental value is due to the fact that the stabilization energy of the water dimer is underestimated by the SCC-DFTB method, as the heat of vaporization.
Computation efficiency
Since the primary purpose of this paper is a comparison of the efficiency of the ZRC method and the DXL-BOMD method, we show in Table 9, 10 some timing results for a neutral tryptophan molecule and the liquid water system. These timing values clearly demonstrate the significant computational efficiency achieved by DXL-BOMD, as compared to ZRC algorithm.
Table 9.
Timing of SCC-DFTB MD calculations using ZRC and 5th order DXL-BOMD algorithm, respectively, of neutral tryptophan molecule (27 atoms in total). The SCF threshold value applied is 10−6 hartree. These calculations were done by a single processor of Intel Xeon 2.80GHz processor.
| Method | Number of MD steps | Total SCF iterations | Energy calculation time [s] | Gradient calculation time [s] |
|---|---|---|---|---|
| DXL-BOMD | 1000 | 5032 | 17.25 | 5.01 |
| ZRC | 1000 | 10360 | 35.56 | 4.99 |
Table 10.
Timing of SCC-DFTB MD calculations using ZRC and 5th order DXL-BOMD algorithm, respectively, of liquid water system (i.e., 32 water molecules in a 9.862 Å periodic cubic box). These calculations were done by a single processor of Opteron 1.993 GHz processor.
| SCF criteria | Number of | Total SCF | Energy calculation | Ewald component | Other Energy | Gradient calculation | |
|---|---|---|---|---|---|---|---|
| Method | [a.u.] | MD steps | iterations | time [s] | time [s] | component [s] | time [s] |
| DXL-BOMD | 10−6 | 500 | 2584 | 431.5 | 282.3 | 149.3 | 321.4 |
| ZRC | 10−6 | 500 | 4732 | 559.0 | 282.4 | 276.6 | 322.0 |
| ZRC | 10−4 | 500 | 3535 | 486.1 | 281.9 | 204.2 | 320.7 |
From Table 9, the reduction in the time of the energy calculations is directly proportional to the number of SCF iterations. This result is a consequence of the fact that matrix diagonalization for solving Roothaan equation dominates every SCF iteration in terms of computation time and thus reduction of the iteration number will proportionally reduce the whole computation time. The gradient (or force) computational time is close to the timing of one SCF iteration. Such a ratio (between gradient and one SCF iteration computation) is close to those of Hartree-Fock or DFT method calculations. Although the gradient calculations can be straightforwardly speed up using modern parallel technique due to the independence of forces on different atoms, the matrix diagonalization is hardly accelerated by either alternative schemes, e.g., density matrix constrained optimization, or parallelization. This indicates the importance of SCF iteration number reduction for gas phase molecule simulations in practice by DXL-BOMD.
The computational timings for liquid water systems are shown in Table 10. It is noted that for a convergence criterion of 10−6 hartree, about twice as many iterations are required for the ZRC algorithm than the DXL-BOMD algorithm. Interestingly, even if with a convergence criterion of 10−4 hartree for ZRC, reasonable values for the properties studied are obtained. However, with 10−4 hartree criterion, ZRC still requires significantly more iterations than DXL-BOMD (with 10−6 hartree) for convergence. In the liquid water simulations, the Ewald component calculations, which is independent of the SCF iterations (it is performed only once for each geometry), requires most of the computation time and is, of course, independent of the convergence criterion. This clearly indicates that for studying periodic systems, particle mesh Ewald method (PME), or a similar technique,58 should be implemented with SCF-DFTB to speed up the calculations. Table 10 also shows that the other energy component scale essentially with the value of SCF iterations. The other component performance resembles that shown in Table 9 for tryptophan. Thus, some speedup for these components is obtained with DXL-BOMD algorithm; the overall reduction in time would be more significant if PME were implemented and the SCF portion of the calculation becomes rate determining.
CONCLUSION
This paper has explored the time requirements of BOMD with a Lagrangian formulation including dissipation (DXL-BOMD) for the auxiliary variables. The use of SCC-DFTB has made possible simulations several hundred picoseconds in length, in contrast to previous studies using DFT, which were limited to 10 ps or less.29, 32 The results obtained for small molecules (i.e., the standard test system C2F4 and the amino acids), as well as a box of 32 water molecules, show that it leads to a significant reduction in the number of iterations required for convergence of the SCF, relative to a standard method. The dynamics stability of DXL-BOMD is better than that based on an initial guess from the previous step converged charge (PRC), as well as from the zero charge guess (ZRC). Interestingly, the 3rd, 5th, and 7th order DXL-BOMD algorithms behave better than 9th, 11th, and 13th order DXL-BOMD algorithms, mostly likely due to the better balance between the noise/error (from all possible sources) and the dissipative terms. It is also demonstrated that for the DXL-BOMD scheme used with SCC-DFTB, either Mulliken charges or Fock matrices can be propagated as good initial values for the SCF of the next molecular dynamics time step. Tests on a liquid water with 32 water molecules show that the DXL-BOMD algorithm require fewer SCF iterations to reproduce the structural properties and dynamical properties of liquid water system obtained from the ZRC algorithm. Overall, the DXL-BOMD algorithm is numerically more efficient (by up to a factor of two) than ZRC or PRC algorithms for obtaining a converged SCF in BOMD simulations. Such an improvement is significant, particularly for larger QM simulations, as well as for its extension to QM/MM molecular dynamics calculations of proteins and nucleic acids.
ACKNOWLEDGMENTS
We gratefully acknowledge helpful discussion with Dr. J. Pu, Dr. V. Ovchinnikov, and Dr. K. Nam at Harvard University. This work done at Harvard was supported in part by a grant from National Institutes of Health (Dr. Martin Karplus). The computations were run on the Odyssey cluster at Harvard University and on computers of the National Energy Research Scientific Computing Center (NERSC), which is supported by the Office of Science of the U.S. Department of Energy (DOE) under Contract No. DE-AC02-05CH11231. Support from the U.S. Department of Energy through the LANL LDRD/ER program for this work is acknowledged by Dr. Niklasson.
References
- Tuckerman M., J. Phys.: Condens. Matter 50, R1297 (2002); 10.1088/0953-8984/14/50/202 [DOI] [Google Scholar]; Senn H. M. and Thiel W., Top. Curr. Chem. 268, 173 (2007). 10.1007/978-3-540-38085-6 [DOI] [Google Scholar]
- Gao J., in Reviews in Computational Chemistry, edited by Lipkowitz K. B. and Boyd D. B. (VCH Publishers, New York, 1995), Vol. 7, pp. 119. [Google Scholar]
- Wang I. S. Y. and Karplus M., J. Am. Chem. Soc. 95, 8160 (1973). 10.1021/ja00805a033 [DOI] [Google Scholar]
- Leforestier C., J. Chem. Phys. 68, 4406 (1978); 10.1063/1.435520 [DOI] [Google Scholar]; Warshel A. and Karplus M., Chem. Phys. Lett. 32, 11 (1975). 10.1016/0009-2614(75)85157-8 [DOI] [Google Scholar]
- Car R. and Parrinello M., Phys. Rev. Lett. 55, 2471 (1985). 10.1103/PhysRevLett.55.2471 [DOI] [PubMed] [Google Scholar]
- Tangney P., J. Chem. Phys. 124, 044111 (2006); 10.1063/1.2162893 [DOI] [PubMed] [Google Scholar]; Tangney P. and Scandolo S., J. Chem. Phys. 116, 14 (2002); 10.1063/1.1423331 [DOI] [PubMed] [Google Scholar]; Pastore G., Smargiassi E., and Buda F., Phys. Rev. A 44, 6334 (1991). 10.1103/PhysRevA.44.6334 [DOI] [PubMed] [Google Scholar]
- Ong S. W., Tok E. S., and Kang H. C., Phys. Chem. Chem. Phys. 12, 14960 (2010). 10.1039/c0cp00411a [DOI] [PubMed] [Google Scholar]
- Herbert J. M. and Head-Gordon M., J. Chem. Phys. 121, 11542 (2004); 10.1063/1.1814934 [DOI] [PubMed] [Google Scholar]; Wathelet V., Champagne B., Mosley D. H., André J.-M., and Massidda S., Chem. Phys. Lett. 275, 506 (1997). 10.1016/S0009-2614(97)00753-7 [DOI] [Google Scholar]
- Li X., Tully J. C., Schlegel H. B., and Frisch M. J., J. Chem. Phys. 123, 084106 (2005). 10.1063/1.2008258 [DOI] [PubMed] [Google Scholar]
- Alonso J. L., Andrade X., Echenique P., Falceto F., Prada-Gracia D., and Rubio A., Phys. Rev. Lett. 101, 096403 (2008); 10.1103/PhysRevLett.101.096403 [DOI] [PubMed] [Google Scholar]; Andrade X., Castro A., Zueco D., Alonso J. L., Echenique P., Falceto F., and Rubio A., J. Chem. Theory Comput. 5, 728 (2009). 10.1021/ct800518j [DOI] [PubMed] [Google Scholar]
- Field M. J., Bash P. A., and Karplus M., J. Comput. Chem. 11, 700 (1990); 10.1002/jcc.540110605 [DOI] [Google Scholar]; Warshel A. and Levitt M., J. Mol. Biol. 103, 227 (1976); 10.1016/0022-2836(76)90311-9 [DOI] [PubMed] [Google Scholar]; Singh U. C. and Kollman P. A., J. Comput. Chem. 7, 718 (1986). 10.1002/jcc.540070604 [DOI] [Google Scholar]
- Bash P. A., Field M. J., Davenport R. C., Petsko G. A., Ringe D., and Karplus M., Biochemistry 30, 5826 (1991); 10.1021/bi00238a003 [DOI] [PubMed] [Google Scholar]; Bash P. A., Field M. J., and Karplus M., J. Am. Chem. Soc. 109, 8092 (1987). 10.1021/ja00260a028 [DOI] [Google Scholar]
- Kohn W. and Sham L. J., Phys. Rev. 140, A1133 (1965); 10.1103/PhysRev.140.A1133 [DOI] [Google Scholar]; Becke A. D., J. Chem. Phys. 98, 5648 (1993); 10.1063/1.464913 [DOI] [Google Scholar]; Hamprecht F. A., Cohen A. J., Tozer D. J., and Handy N. C., J. Chem. Phys. 109, 6264 (1998). 10.1063/1.477267 [DOI] [Google Scholar]
- Hartree D. R., The Calculation of Atomic Structure (Wiley, New York, 1957). [Google Scholar]
- Dewar M. J. S., Jie C., and Yu J., Tetrahedron 49, 5003 (1993); 10.1016/S0040-4020(01)81868-8 [DOI] [Google Scholar]; Dewar M. J. S. and Thiel W., J. Am. Chem. Soc. 99, 4899 (1977); 10.1021/ja00457a004 [DOI] [Google Scholar]; Dewar M. J. S. and Thiel W., J. Am. Chem. Soc. 99, 4907 (1977); 10.1021/ja00457a005 [DOI] [Google Scholar]; Dewar M. J. S., Zoebisch E., Healy E. F., and Stewart J. J. P., J. Am. Chem. Soc. 107, 3902 (1985). 10.1021/ja00299a024 [DOI] [Google Scholar]
- Stewart J. J. P., J. Comput. Chem. 10, 209 (1989); 10.1002/jcc.540100208 [DOI] [Google Scholar]; Rocha G. B., Freire R. O., Simas A. M., and Stewart J. J. P., J. Comput. Chem. 27, 1101 (2006); 10.1002/jcc.20425 [DOI] [PubMed] [Google Scholar]; Stewart J. J. P., J. Mol. Model 13, 1173 (2007). 10.1007/s00894-007-0233-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elstner M., Porezag D., Jungnickel G., Elsner J., Haugk M., Frauenheim T., Suhai S., and Seifert G., Phys. Rev. B 58, 7260 (1998); 10.1103/PhysRevB.58.7260 [DOI] [Google Scholar]; Porezag D., Frauenheim T., Kohler T., Seifert G., and Kaschner R., Phys. Rev. B 51, 12947 (1995). 10.1103/PhysRevB.51.12947 [DOI] [PubMed] [Google Scholar]
- Alfe D., Comput. Phys. Commun. 118, 31 (1999); 10.1016/S0010-4655(98)00195-7 [DOI] [Google Scholar]; Dai J. Y. and Yuan J. M., Epl 88, 20001 (2009). 10.1209/0295-5075/88/20001 [DOI] [Google Scholar]
- Atsumi T. and Nakai H., J. Chem. Phys. 128, 132 (2008). 10.1063/1.2839857 [DOI] [PubMed] [Google Scholar]
- Atsumi T. and Nakai H., Chem. Phys. Lett. 490, 102 (2010). 10.1016/j.cplett.2010.03.012 [DOI] [Google Scholar]
- Pulay P. and Fogarasi G., Chem. Phys. Lett. 386, 272 (2004). 10.1016/j.cplett.2004.01.069 [DOI] [Google Scholar]
- Herbert J. M. and Head-Gordon M., Phys. Chem. Chem. Phys. 7, 3269 (2005). 10.1039/b509494a [DOI] [PubMed] [Google Scholar]
- VandeVondele J., Krack M., Mohamed F., Parrinello M., Chassaing T., and Hutter J., Comput. Phys. Commun. 167, 103 (2005); 10.1016/j.cpc.2004.12.014 [DOI] [Google Scholar]; Kühne T. D., Krack M., Mohamed F. R., and Parrinello M., Phys. Rev. Lett. 98, 066401 (2007). 10.1103/PhysRevLett.98.066401 [DOI] [PubMed] [Google Scholar]
- Pulay P., Chem. Phys. Lett. 73, 393 (1980); 10.1016/0009-2614(80)80396-4 [DOI] [Google Scholar]; Pulay P., J. Comput. Chem. 3, 556 (1982). 10.1002/jcc.540030413 [DOI] [Google Scholar]
- Niklasson A. M. N., Tymczak C. J., and Challacombe M., Phys. Rev. Lett. 97, 123001 (2006). 10.1103/PhysRevLett.97.123001 [DOI] [PubMed] [Google Scholar]
- Niklasson A. M. N., Tymczak C. J., and Challacombe M., J. Chem. Phys. 126, 144103 (2007). 10.1063/1.2715556 [DOI] [PubMed] [Google Scholar]
- Niklasson A. M. N., Phys. Rev. Lett. 100, 123004 (2008). 10.1103/PhysRevLett.100.123004 [DOI] [PubMed] [Google Scholar]
- Frenkel D. and Smit B., Understanding Molecular Simulation from Algorithms to Applications (Academic, New York, 2002). [Google Scholar]
- Niklasson A. M. N., Steneteg P., Odell A., Bock N., Challacombe M., Tymczak C. J., Holmstrom E., Zheng G. S., and Weber V., J. Chem. Phys. 130, 214109 (2009). 10.1063/1.3148075 [DOI] [PubMed] [Google Scholar]
- Zwanzig R., Nonequilibrium Statistical Mechanics (Oxford University Press, New York, 2001). [Google Scholar]
- Kolafa J., J. Comput. Chem. 25, 7 (2004). 10.1002/jcc.10385 [DOI] [PubMed] [Google Scholar]
- Steneteg P., Abrikosov I. A., Weber V., and Niklasson A. M. N., Phys. Rev. B 82, 075110 (2010). 10.1103/PhysRevB.82.075110 [DOI] [Google Scholar]
- Gaus M., Cui Q., and Elstner M., J. Chem. Theory Comput. 7, 931 (2011). 10.1021/ct100684s [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cui Q., Elstner M., Kaxiras E., Frauenheim T., and Karplus M., J. Phys. Chem. B 105, 569 (2001). 10.1021/jp0029109 [DOI] [Google Scholar]
- Mulliken R. S., J. Chem. Phys. 23, 1841 (1955). 10.1063/1.1740589 [DOI] [Google Scholar]
- Perdew J. P., Burke K., and Ernzerhof M., Phys. Rev. Lett. 77, 3865 (1996). 10.1103/PhysRevLett.77.3865 [DOI] [PubMed] [Google Scholar]
- Zheng G., Irle S., and Morokuma K., Chem. Phys. Lett. 412, 210 (2005). 10.1016/j.cplett.2005.06.105 [DOI] [PubMed] [Google Scholar]
- Johnson D. D., Phys. Rev. B 38, 12807 (1988). 10.1103/PhysRevB.38.12807 [DOI] [PubMed] [Google Scholar]
- Nocedal J. and Wright S. J., Numerical Optimization (Springer, New York, 1999). [Google Scholar]
- Eyert V., J. Comput. Phys. 124, 271 (1996). 10.1006/jcph.1996.0059 [DOI] [Google Scholar]
- Nesbet R. K., Variational Principles and Methods in Theoretical Physics and Chemistry (University of Cambridge, New York, 2003). [Google Scholar]
- Chandler D., Introduction to Modern Statistical Mechanics (Oxford University Press, New York, 1987). [Google Scholar]
- A. D.MacKerellJr., Bashford D., Bellott R. L., R. L.DunbrackJr., Evanseck J. D., Field M. J., Fischer S., Gao J., Guo H., Ha S., Joseph-McCarthy D., Kuchnir L., Kuczera K., Lau F. T. K., Mattos C., Michnick S., Ngo T., Nguyen D. T., Prodhom B., W. E.ReiherIII, Roux B., Schlenkrich M., Smith J. C., Stote R., Straub J., Watanabe M., Wiorkiewicz-Kuczera J., Yin D., and Karplus M., J. Phys. Chem. B 102, 3586 (1998). 10.1021/jp973084f [DOI] [PubMed] [Google Scholar]
- Jorgensen W. L., Chandrasekhar J., Madura J. D., Impey R. W., and Klein M. L., J. Chem. Phys. 79, 926 (1983). 10.1063/1.445869 [DOI] [Google Scholar]
- Ryckaert J.-P., Ciccotti G., and Berendsen H. J. C., J. Comput. Phys. 23, 327 (1977). 10.1016/0021-9991(77)90098-5 [DOI] [Google Scholar]
- Feller S. E., Zhang Y., Pastor R. W., and Brooks B. R., J. Chem. Phys. 103, 4613 (1995). 10.1063/1.470648 [DOI] [Google Scholar]
- Hu H., Lu Z. Y., Elstner M., Hermans J., and Yang W. T., J. Phys. Chem. A 111, 5685 (2007). 10.1021/jp070308d [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maupin C. M., Aradi B., and Voth G. A., J. Phys. Chem. B 114, 6922 (2010). 10.1021/jp1010555 [DOI] [PubMed] [Google Scholar]
- Brooks B. R., Brooks C. L. I., Mackerell A. D. J., Nilsson L., Petrella R. J., Roux B., Won Y., Archontis G., Bartels C., Boresch S., Caflisch A., Caves L., Cui Q., Dinner A. R., Feig M., Fischer S., Gao J., Hodoscek M., Im W., Kuczera K., Lazaridis T., Ma J., Ovchinnikov V., Paci E., Pastor R. W., Post C. B., Pu J. Z., Schaefer M., Tidor B., Venable R. M., Woodcock H. L., Wu X., Yang W., York D. M., and Karplus M., J. Comp. Chem. 30, 70 (2009). 10.1002/jcc.21287 [DOI] [Google Scholar]
- Kühne T. D., Krack M., and Parrinello M., J. Chem. Theory Comput. 5, 235 (2009). 10.1021/ct800417q [DOI] [PubMed] [Google Scholar]
- Rao F., Garrett-Roe S., and Hamm P., J. Phys. Chem. B 114, 15598 (2010); 10.1021/jp1060792 [DOI] [PubMed] [Google Scholar]; Marx D., ChemPhysChem 7, 1848 (2006); 10.1002/cphc.200600128 [DOI] [PubMed] [Google Scholar]; Geissler P. L., Dellago C., Chandler D., Hutter J., and Parrinello M., Science 291, 2121 (2001); 10.1126/science.1056991 [DOI] [PubMed] [Google Scholar]; Laasonen K., Sprik M., Parrinello M., and Car R., J. Chem. Phys. 99, 9080 (1993); 10.1063/1.465574 [DOI] [Google Scholar]; Luzar A. and Chandler D., Nature (London) 379, 55 (1996); 10.1038/379055a0 [DOI] [Google Scholar]; Luzar A. and Chandler D., Phys. Rev. Lett. 76, 928 (1996); 10.1103/PhysRevLett.76.928 [DOI] [PubMed] [Google Scholar]; Schwegler E., Grossman J. C., Gygi F., and Galli G., J. Chem. Phys. 121, 5400 (2004); 10.1063/1.1782074 [DOI] [PubMed] [Google Scholar]; VandeVondele J., Mohamed F., Krack M., Hutter J., Sprik M., and Parrinello M., J. Chem. Phys. 122, 014515 (2005); 10.1063/1.1828433 [DOI] [PubMed] [Google Scholar]; Chen B., Ivanov I., Klein M., and Parrinello M., Phys. Rev. Lett. 91, 215503 (2003); 10.1103/PhysRevLett.91.215503 [DOI] [PubMed] [Google Scholar]; Kuo I. F. W., Mundy C. J., McGrath M. J., Siepmann J. I., VandeVondele J., Sprik M., Hutter J., Chen B., Klein M. L., Mohamed F., Krack M., and Parrinello M., J. Phys. Chem. B 108, 12990 (2004); 10.1021/jp047788i [DOI] [Google Scholar]; Lee H.-S. and Tuckerman M. E., J. Chem. Phys. 126, 164501 (2007). 10.1063/1.2718521 [DOI] [PubMed] [Google Scholar]
- Choi T. H. and Jordan K. D., J. Phys. Chem. B 114, 6932 (2010). 10.1021/jp912289e [DOI] [PubMed] [Google Scholar]
- Soper A. K., Chem. Phys. 258, 121 (2000). 10.1016/S0301-0104(00)00179-8 [DOI] [Google Scholar]
- Lee H.-S. and Tuckerman M. E., J. Chem. Phys. 125, 154507 (2006). 10.1063/1.2354158 [DOI] [PubMed] [Google Scholar]
- Elstner M., Theor. Chem. Acc. 116, 316 (2006). 10.1007/s00214-005-0066-0 [DOI] [Google Scholar]
- Yeh I.-C. and Hummer G., J. Phys. Chem. B 108, 15873 (2004); 10.1021/jp0477147 [DOI] [Google Scholar]; Dünweg B. and Kremer K., J. Chem. Phys. 99, 6983 (1993). 10.1063/1.465445 [DOI] [Google Scholar]
- Wu Y., Chen H., Wang F., Paesani F., and Voth G. A., J. Phys. Chem. B 112, 467 (2008). 10.1021/jp076658h [DOI] [PubMed] [Google Scholar]
- Darden T., York D., and Pedersen L., J. Chem. Phys. 98, 10089 (1993); 10.1063/1.464397 [DOI] [Google Scholar]; Essmann U., Perera L., Berkowitz M. L., Darden T., Lee H., and Pedersen L. G., J. Chem. Phys. 103, 8577 (1995). 10.1063/1.470117 [DOI] [Google Scholar]