The Capsule’s Contribution to Total Hip Construct Stability – A Finite Element Analysis

Abstract

Instability is a significant concern in total hip arthroplasty, particularly when there is structural compromise of the capsule due to pre-existing pathology or due to necessities of surgical approach. An experimentally grounded fiber-direction-based finite element model of the hip capsule was developed, and was integrated with an established three-dimensional model of impingement/dislocation. Model validity was established by close similarity to results from a cadaveric experiment in a servohydraulic hip simulator. Parametric computational runs explored effects of graded levels of capsule thickness, of regional detachment from the capsule’s femoral or acetabular insertions, of surgical incisions of capsule substance, and of capsule defect repairs. Depending strongly upon the specific site, localized capsule defects caused varying degrees of construct stability compromise, with several specific situations involving over 60% decrement in dislocation resistance. Construct stability was returned substantially toward intact-capsule levels following well conceived repairs, although the suture sites involved were often at substantial risk of failure. These parametric model results underscore the importance of retaining or robustly repairing capsular structures in total hip arthroplasty, in order to maximize overall construct stability.

INTRODUCTION

Dislocation is an incompletely understood and all-too-frequent complication of total hip arthroplasty (THA). In a recent report¹, instability was identified as having surpassed mechanical loosening as the most common cause for revision surgery. Because of the many confounding factors involved, clinical registries of dislocation have often been equivocal in terms of elucidating the relative importance of predisposing factors, even when involving patient populations that are unusually large by orthopaedic standards^2–4. However, one issue where there is near unanimity of opinion is that hips with mechanical compromise of the capsule are at heightened risk. This is manifest most directly in terms of the greatly increased incidence of dislocation in hips that have had a prior surgery⁵, particularly a previous THA⁴. Other corroborating evidence is the differential of dislocation rates among alternative surgical approaches^{6, 7} and the differential of dislocation rates without versus with capsule repair^8–10, especially when a posterior approach is used without complete soft tissue repair.

Abnormality of capsule function can be due to various factors (e.g., thickness anomaly, stiffening/scarring, substance tears, insertion detachment, and surgical incisions), most of which involve different technical considerations intra-operatively. Moreover, since some of the causes of capsule deficit that are amenable to surgical repair unfortunately involve trade-offs (especially additional exposure), intra-operative decision making would benefit from quantitative information linking defect site and severity with dislocation propensity. Because dislocation is fundamentally a biomechanical event, quantitative biomechanical data can aid in understanding which aspects of capsule compromise are most deleterious and the degree of construct stability improvement attainable by respective repair alternatives.

Most biomechanical work involving the influence of capsule status on dislocation propensity has come from physical experiments, involving either cadaver preparations^{11, 12} or mechanical surrogates^{13, 14}. While both approaches have their attractions, neither offers a platform conducive to systematic, clinically realistic study of multiple variables, due to limitations such as experimental unwieldiness, tissue deterioration, and inter-specimen variability. Computational simulations by contrast provide absolute reproducibility, allow study of a limitless range of variables, provide a wide range of outcome metrics, and are economical to manipulate parametrically once the necessary investment in model development has been made.

The present study builds upon earlier research with dislocation resistance of implant hardware per se^15–20 and preliminary work with capsule simulation²¹ to now include fiber-direction-dependence of capsule material properties. Parametric series were undertaken to determine the sensitivity to which resistance to dislocation depended upon capsule thickness, upon locations and extent of capsule detachment from bony insertions, and upon (surgical) longitudinal incisions at various sites. Trials were also run to assess stability improvements accompanying suture repairs, and the relative risk of failure of those suture repairs.

MATERIALS AND METHODS

Data for THA implant hardware representation in the FE model were imported from manufacturer-provided CAD files and pre-processed using an FE mesh preprocessor (TrueGrid v. 2.3, XYZ, Scientific Applications, Inc., Livermore, CA). Implant positioning was held constant at 35° of inclination and 20° anteversion for the acetabular component, and at 0° anteversion for the femoral component. A metal-on-metal bearing couple was chosen, with the head, neck, and liner (all CoCr) modeled as exhibiting linearly elastic behavior (modulus = 210 GPa, Poisson’s ratio = 0.3). For purposes of computational economy, the cup backing and the distal regions of the femoral component were represented as rigid. For the same reason, the bony surfaces into which the capsule inserted on the acetabulum and proximal femur were also assumed to be rigid.

The particular dislocation challenge considered was a sit-to-stand maneuver, commonly associated with posterior dislocation. Input hip rotations and contact forces were based on data from our previous laboratory opto-electronic motion studies of dislocation-prone maneuvers¹⁷. The sit-to-stand kinematic challenge began with the hip flexed in a seated position, continuing (unless dislocation occurred) to 110° of hip flexion, and then returning to full extension.

To map the orientation of capsule fibers, a fresh-frozen human cadaveric hemipelvis was obtained from a donor having no history of hip joint disorder. The specimen was examined radiographically and physically to verify the absence of pathology, and was then carefully dissected to remove all non-capsular soft tissue. Major families of fiber bundles were visually identified on the exposed intact capsule, and were demarcated by overlaying and suturing thin silicone rubber tubing that had been filled with aqueous barium contrast medium. The tubes were directed along the full longitudinal length of the capsule from the acetabular to the femoral attachment sites. The specimen was then scanned in a 64-detector CT scanner (Fig. 1A). Next, the capsule was dissected from the bony pelvis, and the full extent of the acetabular and femoral attachment sites were identified and similarly marked and scanned.

Fig. 1.

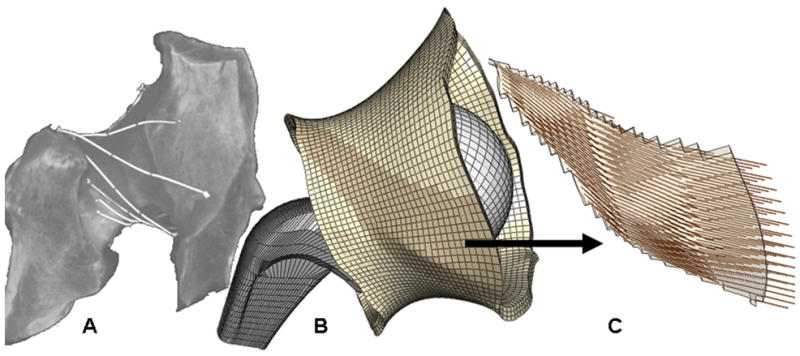
(A) CT dataset for a native (left) cadaver hip hemi-pelvis affixed with contrast-filled marking tubes to delineate capsule fiber directions. (B) Capsule representation in the corresponding FE model. (C) Fiber directions shown for a single fiber-direction family, approximately coincident with the ischiofemoral ligament (Size scales are different).

The CT scan datasets were segmented to define the inner and outer surfaces of the capsule, the marker tubes, and the acetabular and proximal femoral bony surfaces. After segmentation, these two CT data sets were co-registered to one other. This dataset was then further pre-processed using a series of rotations and translations to anatomically position the capsule with respect to a previously validated FE THA dislocation model²¹. The segmented marker tubes were converted to 3D curves, and were mathematically subjected to the same series of translations and rotations. These capsule surfaces and marker curves were then imported into TrueGrid, and were meshed entirely with hexahedral elements (Fig. 1B). Based on mesh convergence studies, the capsule was discretized into 9,744 hexahedral elements with an average element volume of ~4 mm³, providing a balance between accuracy and computational expense. To facilitate anatomic parametric studies, the capsule FE mesh was geometrically parsed into eight circumferential sectors. This allowed features such as surgical incisions, attachment releases, and suture repairs to be conveniently defined. Projection of the fiber-direction curves onto the inner and outer capsular surfaces provided a basis for identifying 27 different capsular material regions.

Anisotropic (fiber direction-dependent) representation of the capsule was implemented using the micromechanically based hyperelastic constitutive model originally introduced by Gasser et al.²², which is available within the material set library of Abaqus. Material coefficients for the capsule model were optimized such that the resulting load-displacement data from a simulated distraction matched physical load-displacement data²³ for a corresponding cadaveric capsule distraction experiment (Fig. 2). The fibers were modeled as having a distinct unidirectional distribution within each of the 27 distinct regions (Fig. 1C).

Fig. 2.

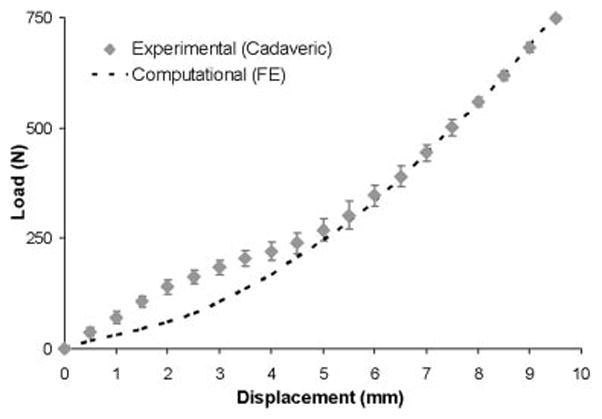
Comparison of load-displacement data, measured experimentally in a cadaver specimen, versus that best-fit for the computational model. The specimen and the model were identically loaded by distraction along the direction of the femoral neck axis.

Physical validation of the FE analysis was conducted using a novel transpelvic implantation of THA-replicating specialty hardware into a cadaveric hemipelvis (Fig. 3A–C). This transpelvic procedure allowed for investigation of the capsule’s contribution to construct stability, beginning from a baseline condition where the capsule’s normal anatomic integrity was fully preserved. A cadaveric hemipelvis implanted so as to replicate the THA’s intra-articular geometry was fixed to a purpose-built four degree-of-freedom servo-hydraulic hip simulator (Fig. 4). This simulator allowed for compound joint rotation (flex/extension, ab/adduction, and endo/exorotation) along with axial loading. The moment resisting dislocation was recorded during sit-to-stand challenge simulations. The measured resultant moment behavior compared favorably with that from an FE analysis simulating identical loading and motion inputs (Fig. 5). Excellent computational vs. experimental agreement was also achieved regarding the spatial and temporal occurrence of impingement.

Fig. 3.

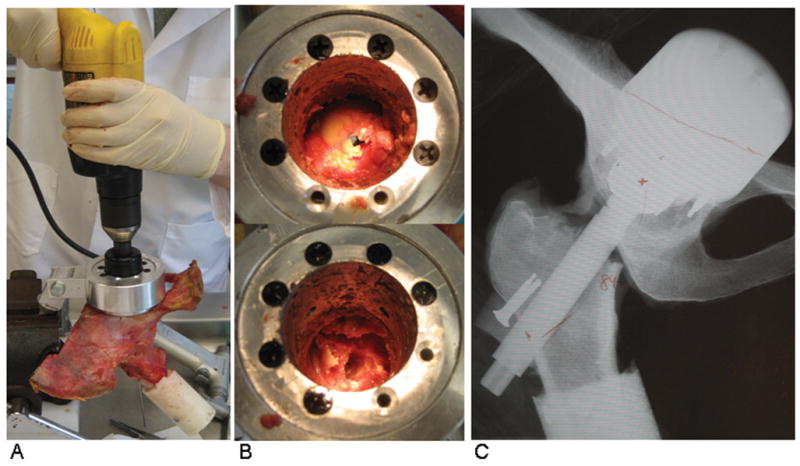
The transpelvic procedure allowed for implantation of THA hardware into a cadaveric hemipelvis without violating the capsular soft tissue integrity. (A) Access to the hip was gained by guiding a hole saw from the posterior pelvis into the joint. (B) The femoral head was exposed (top) and removed (bottom) through the access port. (C) THA-replicating hardware was implanted, and alignment was verified using coronal radiographs.

Fig. 4.

Servo-hydraulic hip simulator. This system independently prescribed flex/extension, endo/exorotation, ab/adduction, and joint loading magnitude.

Fig. 5.

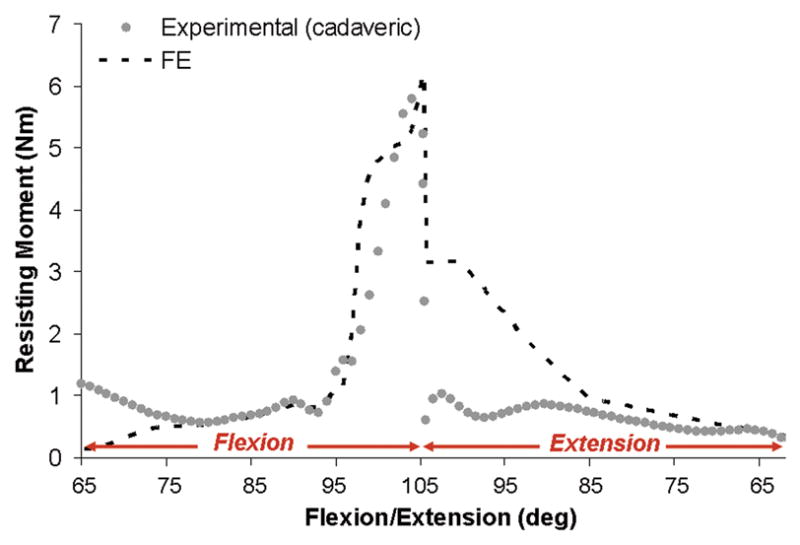
FE validation comparing resisting moment results for a sit-to-stand dislocation challenge for a cadaveric specimen implanted with THA equivalent hardware versus FE prediction using identical kinematic and kinetic profiles for the case of an uncompromised hip capsule. Reduced joint loading (nominally 10% of physiologic peak joint loads for this maneuver) was utilized to avoid risk of damaging the cadaver specimen.

A parametric framework was developed that allowed for modeling specific deviations from a baseline configuration of the capsule’s normal intact state (Fig. 6). To investigate plausible capsule thickness variations, 18 distinct capsule meshes were created, spanning published²⁴ ranges for male and female anatomy. Surgical incisions were simulated by defining surfaces imposed between specified adjacent circumferential sectors of the capsule (Fig. 6B). Surgical incision repairs were simulated by specifying that certain nodes across the incision became merged specified at equidistant spacings, effectively representing discrete “sutures” spaced equally along the incision (Fig. 6C). Bony attachment releases were simulated by removing the nodes associated with the corresponding anatomic insertion and freeing up all degrees of freedom at those locations. Attachment-site release repairs were simulated by selecting specific nodes across the thickness of the released section (again, equidistantly spaced), and returning them to insertion site boundary conditions.

Fig. 6.

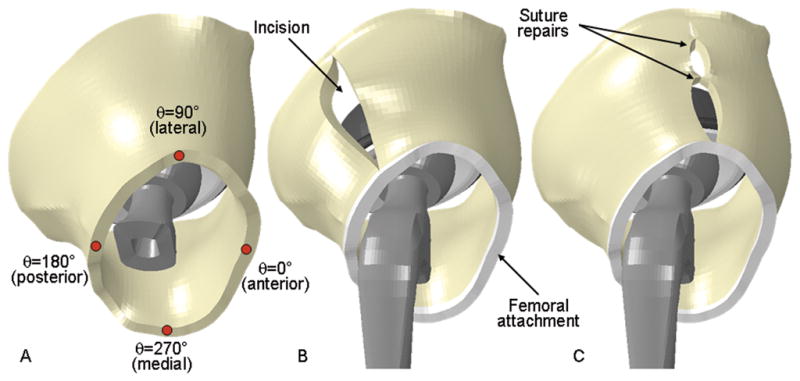
(A) Coordinate conventions for specifying circumferential location. The anterior-most aspect of the capsule was assigned a value of θ=0°, with θ increasing in a counter-clockwise fashion (for visual clarity, the femoral stem has been rendered transparent). (B) A single longitudinal incision is shown at a posterolateral location. (C) Repair of a laterally located incision with two sutures, equidistantly spaced.

Kinematic contact definitions were specified for all possible perturbations of implant, bone, and soft tissue engagement (Fig. 7). For all FE runs, the resultant moment that developed to resist dislocation (designated as the resisting moment) was tracked throughout the entire kinematic input sequence (Fig. 8). The area under the moment-rotation curve corresponds to the mechanical energy dissipated within the construct during the dislocation challenge. This energy value, determined for each parametric run by numerically integrating the area under spline curves fitted to each analysis’ motion-rotation data, provided a useful comparative metric of overall resistance to dislocation. One-hundred-nine FE simulations were run (Abaqus Explicit 6.9.3), including the baseline case of an intact normal capsule, 22 cases of capsule thickness variation, and 86 specific situations of defect or defect + repair.

Fig. 7.

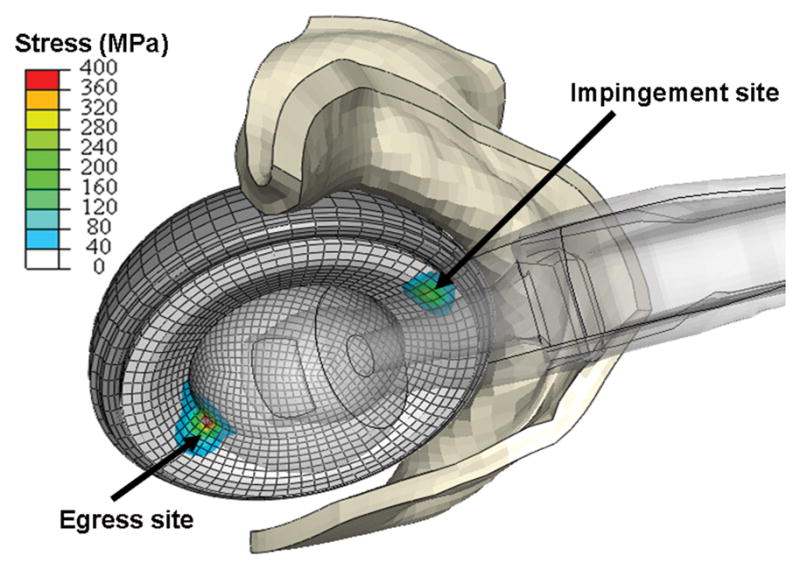
Contour plot of liner von Mises stresses developed during impingement/subluxation of a right hip at high flexion. Stress concentrations occurred at two distinct regions of the cup: the impingement site (anteriorly) and the egress site (posteriorly). For clarity, the femoral component is rendered translucent, and only the anterior half of the capsule is shown.

Fig. 8.

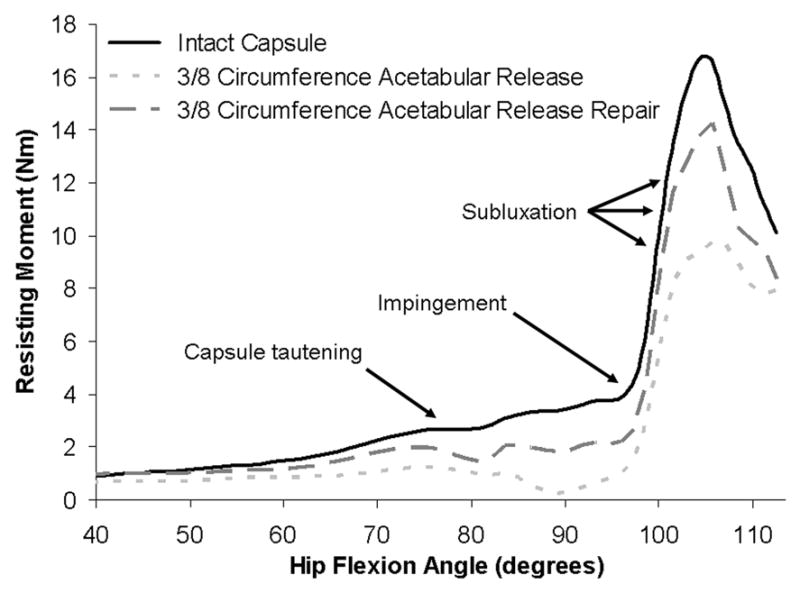
Resisting moment development for hip flexion during the sit-to-stand maneuver for the intact capsule and for the most stability-compromising capsule defect (3/8 acetabular insertion release) and its repair. For this most compromising case, the capsule provided virtually no resistance to dislocation, and the resisting moment was attributable to hardware interactions only. Repair of this defect returned construct stability to near baseline levels.

RESULTS

Variations in capsule thickness had substantial effects on construct stability (Fig. 9). For the thinnest capsule considered (1 mm), peak dislocation resistance reached only 53% of that for a (baseline) 3.5 mm capsule thickness, and reached only 31% of that for the thickest capsule modeled (6 mm). Population-wide, at the 25^th percentile vs. 75^th percentile of thickness for males and for females, the peak resisting moment values reached only 43 vs. 56% and 40 vs. 57%, respectively, compared to a 6 mm thick capsule.

Fig. 9.

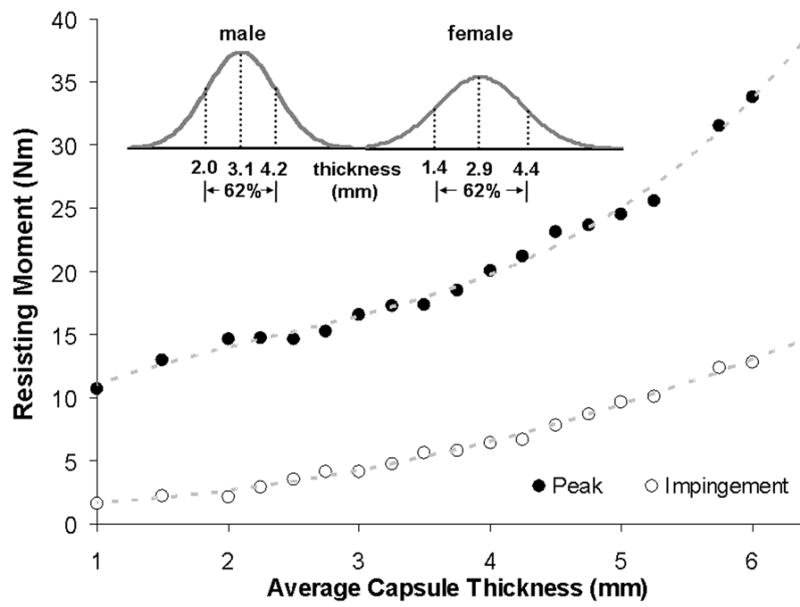
Resisting moment developed during hip flexion versus capsule thickness across the population-wide range (inset) of thicknesses. Moment values are reported both at incipient impingement and at the instant of maximum resistance to dislocation. Insert curves are replotted from the data of Dihlmann et al²⁴.

The effects of localized capsule detachments/releases at the femoral and acetabular insertion sites showed similarly strong dependence on the defect location (Fig. 10). Posterior-and posterolateral-aspect capsule insertion defects, along either the acetabular or femoral attachments, involved decreases in computed dislocation energy dissipation of >50% relative to intact-capsule levels. As can be appreciated conceptually from Fig. 7, posterior attachment defects effectively removed substantial fractions of capsule substance from being able to contribute to opposing dislocation in flexion-dominated maneuvers. Repairs of such defects returned peak resisting moment values to within 10 to 20% of baseline levels.

Fig. 10.

Relative (%) change in computed dislocation-resistance energy developed during hip flexion for simulated capsule acetabular insertion detachments (circle symbols) and femoral detachments (square symbols) as a function of circumferential position of detachment site. Construct stability compromise depended on both the site and extent of the detachment. Otherwise comparable-extent defects generally involved greater stability compromise for femoral attachment defects located on the medial aspect and for acetabular attachment defects located on the lateral aspect. Construct stability was consistently returned appreciably toward intact levels for suture repair (demonstrated by piecewise curves) of the most compromising detachments (posterolaterally located).

Unrepaired full-length longitudinal capsule incisions likewise were substantially compromised construct stability (Fig. 11), but again in a site-dependent manner. The most deleterious positions for longitudinal incisions tended to be located more laterally than was the case for acetabular insertion site defects, and more medially than was the case for femoral insertion site defects, presumably a consequence of the obliquity of directional fiber architecture. Another distinction was that the most severe levels of stability compromise for longitudinal incisions (~50% reductions from intact baseline) were less pronounced than those for extremum insertion defects (~60%), presumably because capsule material on either side of the incision could still participate in load transmission “in parallel”, whereas insertion defects represent “in series” disruptions of load transmission. Suture repairs of even worst-case longitudinal incisions successfully returned stability to within ~10% of baseline levels.

Fig. 11.

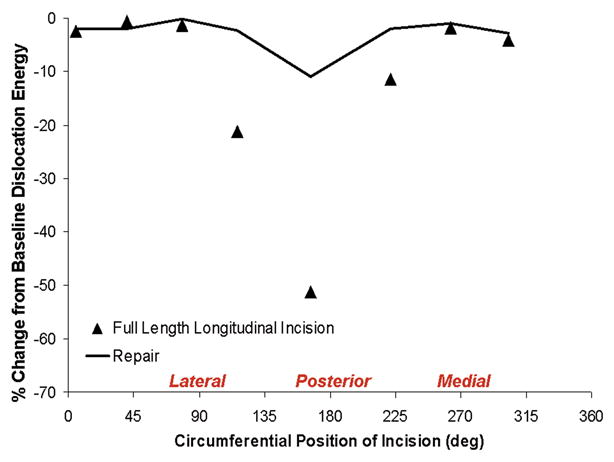
Relative (%) change in computed dislocation-resistance energy developed during hip flexion for unrepaired (symbols) and repaired (piecewise curves) longitudinal capsular incisions located at selected stations circumferentially. Assuming that suture failure or pull-out did not occur, appreciably improved stability (although not to intact-capsule levels) was obtained for the more compromising posteriorly located incisions.

Computed pull-apart forces for individual suture sites for various repair alternatives for various capsule defects are shown in Figs. 12 & 13. Many repair scenarios that would restore near-normal construct stability involved forces that approach or exceed the mechanical strength of sutured repair²⁵ (shaded band in Figs. 12 & 14). Multiple sutures per repair site substantially reduced per-suture tensile loads. However, the safety factor improvements achieved were not in direct proportion to the number of sutures employed (Fig. 14), as load allocation was sensitive to both suture number and suture location within a single repaired defect.

Fig. 12.

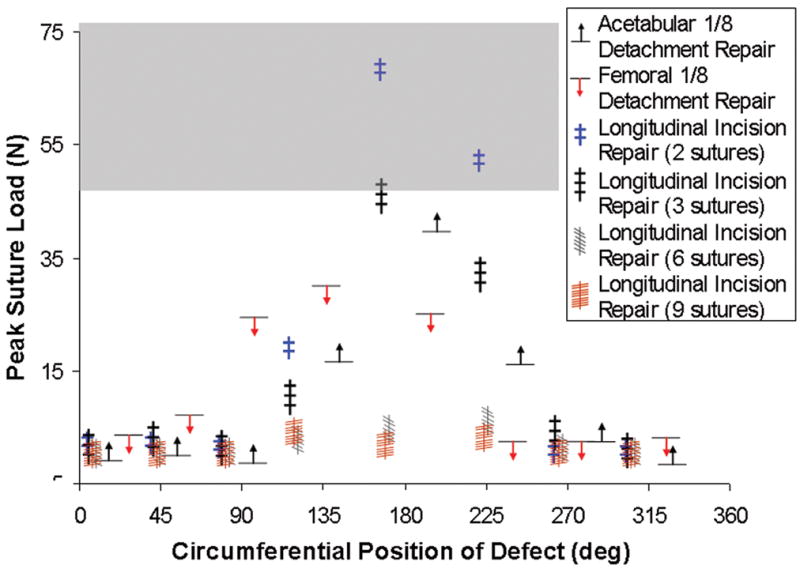
Peak tension developed at the suture site, for repairs of longitudinal slits with 2, 3, 6, or 9 sutures, and for single-site repairs of regional acetabular and femoral insertion detachments. For these model runs, suture material failure or suture pullout was assumed not to occur. For reference, the range of ultimate tensile strength for No. 1 and No. 2 suture materials reported in the literature²⁵ is shown in gray.

Fig. 13.

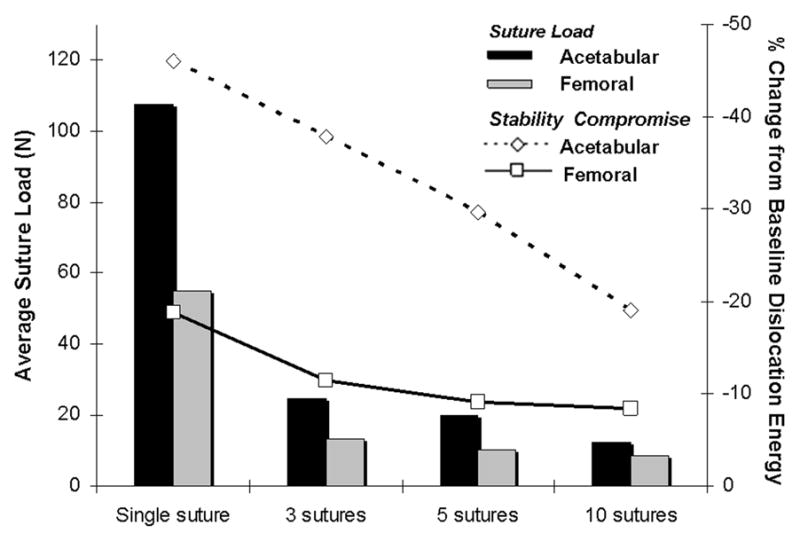
Per-suture tensile loads (bars) developed at simulated femoral and acetabular repair sites for a 3/8- circumference posteriorly centered capsule insertion release for single-suture versus averages for 3-, 5- and 10-suture repairs spaced equally along the defect. Deviations from baseline dislocation dissipation energy are shown (open symbols) for each repair.

Fig. 14.

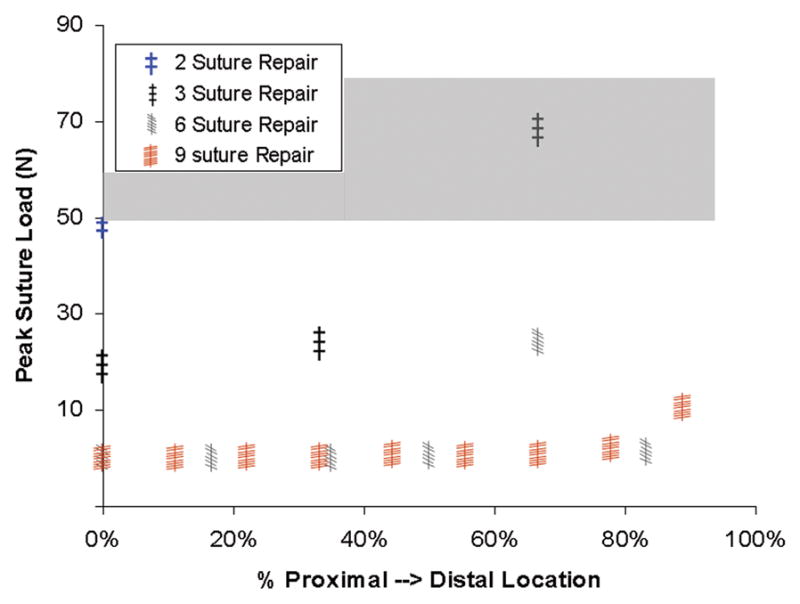
Peak suture tensile load for repair of a posterior longitudinal incision for 2-, 3-, 6- and 9-suture repairs as a function of suture location along the proximal-distal length of the incision. Significance of the gray band is the same as in Fig. 12.

DISCUSSION

Mechanical compromise of the capsule is empirically recognized as a leading factor associated with THA dislocation. Even so, the dramatic decreases of hip stability computed for the most adversely located capsule deficits in our study were sobering, and suggest that capsule compromise may in fact be the dominant predisposing consideration. The computed resisting moment reductions were far greater than those estimated in earlier hardware-only FE series for design variables such as head size, liner chamfer angle, neck bevel, or head center insert^{19, 20}. The present range of stability reductions also substantially exceeded previously-computed reductions associated with clinically plausible sub-optimal component orientations^{16, 17}.

This apparent dominance of capsule compromise as a factor affecting instability arguably merits further attention, particularly for identifying effective strategies for surgical repair of specific categories or locations of defects and deficiencies. The high tensile stresses at some of the suture repair sites are disconcertingly consistent with the high incidence of early failures of certain posterior structure repair procedures^{26, 27}. While suture failure in our model was predicted based on ultimate tensile stress of the suture material, this is certainly a conservative approach: surgical wound healing is a dynamic process and does not begin until the acute phase of resulting inflammation subsides²⁸. Insertion-site tendon degeneration persists for at least six weeks²⁹, suggesting that repair failure immediately post-op might occur due to suture pullout, not suture breakage. While our global-construct FE model is not ideal for addressing the local mechanics of suture rupture/pull-out, these global results clearly show that some repairs are much more challenged than others.

Although the present computational formulation represents a substantial step forward from cadaver/surrogate testing and from hardware-only FE analysis, several simplifications and limitations merit mention. First, although the capsule material model addressed prevailing anatomic fiber directionality and was grounded in earlier experimental work involving region-specific physical testing, the present embodiment involves only a single direction of fibers throughout the entire thickness of capsule at any given site. Obviously, a population of multiple fiber directions might exists at any given site, and fiber orientations probably vary through the thickness. Another limitation of our model is that only a single dislocation challenge maneuver was considered, whereas a broad variety of challenges ensue in activities of daily living¹⁷. We would emphasize, however, that capsule defect locations that are relatively benign for one particular dislocation-risk maneuver are not necessarily benign for others; “the chain is only as strong as its weakest link,” and that weakest link most certainly varies with activity.

In summary, we have provided novel mechanistic information regarding the sometimes dramatic degree to which capsule compromise can contribute to THA instability. Since most THA dislocations occur for flexion-dominated motion challenges such as we modeled, the present FE results help explain the lower dislocation rates documented in clinical series where the posterior capsular structures either have not been violated or have been robustly repaired. Furthermore, the present data reinforce the need to meticulously re-approximate and repair the posterior capsular structures to the greatest extent possible.