Independent Histogram Pursuit for Segmentation of Skin Lesions

Abstract

In this paper, an unsupervised algorithm, called the Independent Histogram Pursuit (IHP), for segmenting dermatological lesions is proposed. The algorithm estimates a set of linear combinations of image bands that enhance different structures embedded in the image. In particular, the first estimated combination enhances the contrast of the lesion to facilitate its segmentation. Given an N-band image, this first combination corresponds to a line in N dimensions, such that the separation between the two main modes of the histogram obtained by projecting the pixels onto this line, is maximized. The remaining combinations are estimated in a similar way under the constraint of being orthogonal to those already computed. The performance of the algorithm is tested on five different dermatological datasets. The results obtained on these datasets indicate the robustness of the algorithm and its suitability to deal with different types of dermatological lesions. The boundary detection precision using k-means segmentation was close to 97%. The proposed algorithm can be easily combined with the majority of classification algorithms.

I. Introduction

Nowadays, the lack of objective methods to evaluate and track the evolution of dermatological lesions is one of the main image processing problems in dermatology. During the last decade, image analysts have tried to provide a solution to this problem. Many research projects have been conducted to automatically and objectively evaluate the severity of the disease [1]–[3]. These studies have provided several measures to describe the lesion such as asymmetry coefficients, border information, color information, or differential structures [4]. In order to precisely estimate these indices, an accurate segmentation of the lesion is required. Some of the segmentation techniques that have been proposed include thresholding [5], region growing such as the JSEG algorithm [6], or gradient vector field (GVF) snakes [7] and watersheds [8].

The common feature of the majority of these algorithms is that their accuracy heavily depends on the color representation. The more contrast there is between the lesion and the normal skin in the chosen color space, the more accurate the segmentation will be. In order to obtain a color representation that enhances the contrast between the lesion and the normal skin, several works have been conducted to transform the original RGB image into a more suitable color space (in many cases standard and independent of the image). The most common and widely used color spaces are the CIE L*a*b* and CIE L*u*v*, described in [9]. These transformations have been shown to produce good segmentation results for some dermatological diagnoses [10]–[12].

These color spaces, being too general (i.e., independent of the image or problem), have a reduced applicability. In dermatological images, the selection of the color space depends on the type of diagnosis. It is unlikely that the same color space is optimal for different dermatological diagnoses or even for series of images of the same diagnosis acquired by different systems. Therefore, utilizing specific color spaces per case and designing algorithms bound to these color spaces makes most of the algorithms specific to a given set of diagnoses. Another disadvantage of these transformations is that they are limited to tri-chromatic band images, and they cannot be applied to the images collected by new imaging systems [13], [14]. To obtain a better segmentation of the lesion, these systems acquire a multitude of spectral bands, ranging from ultraviolet to near-infrared including the classical RGB. The latter stimulates a search for a transformation that is able to use the information provided by all the bands.

A possible approach to incorporate the information provided by the extra bands is to use features obtained by the principal component analysis (PCA) [15]. The shortcoming of this methodology is its reduced capacity to adapt itself to variation of the lesion in different patients. The principal component direction can vary considerably if the image has other structures such as hair or vessels. Moreover, it is not guaranteed that the component that enhances the lesion will always appear in the same position in the ordered set of all the components. To date, there is no general method that can be applied to the majority of dermatological datasets, and many studies are being conducted to improve the existing methods.

To compensate for the disadvantages of the described approaches, we propose here the adaptation of the Independent Histogram Pursuit (IHP) algorithm [16] for finding a suitable image-dependent linear transformation of an arbitrary multi-spectral color space to aid segmentation of dermatological images. The IHP algorithm is composed of two steps. During the first step, the algorithm finds a combination of spectral bands that enhances the contrast between healthy skin and lesion. This combination can be efficiently used to segment the lesion by any clustering or any classification method [17]. During the second step, the algorithm estimates the remaining N – 1 combinations that enhance less obvious structures of the image. These combinations can be utilized to diagnose the severity of the lesion. Note that in this formulation, the algorithm is independent of the chosen image representation, whether it is one of the standard color spaces or a multiband image.

II. Independent Histogram Pursuit

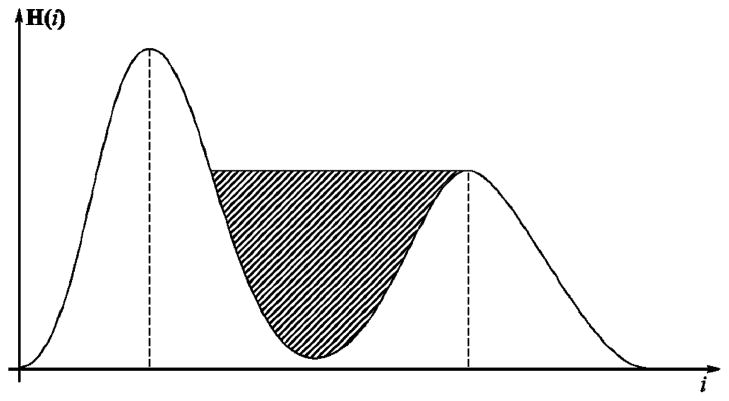
Let X be an m × n image with N bands. Then the (i,j)th pixel of this image can be considered as an N-vector ${\mathbf{x}}_{ij}={\left(x_{ij}^{(1)},\dots ,x_{ij}^{(N)}\right)}^T$. All the pixels x_ij of a given image constitute the input data. The IHP estimates a sequence of N orthogonal N-vectors, or components, that constitute a linear transformation of the original color space of the image. These orthogonal components are obtained based on the fact that a typical dermatological image consists of two large classes of pixels: the lesion and the normal skin. Therefore, the histogram of pixels projected onto the optimal component would have two large maximally separated modes (two groups of pixels). Based on this observation, the first component is computed so that the histogram of pixels, projected onto it, is bimodal and the concavity between the two modes has the maximum area (the hatched area in Fig. 1). During the second step, the remaining (N – 1) IHP components are estimated using the same criterion, requiring each component to be orthogonal to those previously estimated. Formally, the set of IHP components {u_k|k = 1,…, N} is estimated by solving the following optimization problem for each k:

$${\stackrel{\sim }{\mathbf{u}}}_k=\underset{\mathbf{z}\in {\mathfrak{R}}^N}{argmax}f[\{{\mathbf{z}}^T{\stackrel{\sim }{\mathbf{x}}}_{ij}\mid i=1,\dots ,m;j=1,\dots n\}]$$ (1)

$${\stackrel{\sim }{\mathbf{u}}}_k^T{\stackrel{\sim }{\mathbf{u}}}_l=0,\text{for}k>1\text{and}l=1,\dots ,k-1$$ (2)

where x̃_ij are the whitened pixels of x_ij [18]. Whitening is needed to eliminate the correlations in the data, which is a necessary condition to make estimated components independent. The function f [{z^Tx̃_ij}] on the right-hand side of (1) is defined as the area of the concavity between the two modes of the histogram of data x̃_ij projected onto z, as in Fig. 1. It is important to note that the histogram has to be smoothed in order to eliminate insignificant local extrema, we used 15 iterations of the mean filter of length 3 [19], but any alternative approach can be used. Then all the local maxima can be easily found by comparing the value of each bin with its two neighbors.

Fig. 1.

Sample bimodal histogram of pixels projected onto z during optimization. The hatched pattern indicates the area maximized by the algorithm.

The problem (1)–(2) is solved by genetic algorithms (GA) [20]. Since we are interested only in bimodal histograms, the population of GA is reduced only to those z that have exactly two maxima. Note that the first IHP component is estimated without any constraint. To introduce the orthogonality constraint for each subsequent component ũ_k (k > 1), all the candidate vectors, evaluated at every step of the genetic algorithm, are orthogonalized with respect to the already estimated ũ₁,…,ũ_k–1. The orthogonalization can be performed by any method, the simplest being the Gram–Schmidt algorithm [21].

Since the obtained set of IHP components Ũ = [ũ₁,…,ũ_N] describes projections for the whitened pixels, they have to be transformed back by the inverse of the whitening transformation.

III. Experimental Results

In our implementation, we used MATLAB Genetic Algorithm Toolbox.¹ The population size and the number of iterations were set to 100 and 200, respectively. The percentages of best chromosomes selected, crossovered and mutated were left at their default values (90%, 70%, and 50%, respectively). The real-valued chromosome encoding was used. The processing time for an 576 × 768 RGB image was 11 min on average, running on a Pentium IV 3-GHz processor.

To evaluate the performance of IHP, five databases have been used. The first database, introduced in Chen et al. [22], contains 100 RGB melanoma images with 70 malignant melanomas and 30 benign cases, mostly dysplastic nevi. We intend to show that, in contrast to standard color spaces, the IHP is able to find in an unsupervised manner an image-dependent projection well-suited for segmentation. We shall compare the lesion segmentation in the individual bands of the standard color spaces such as RGB, CIE L*a*b*, L*u*v*, and XYZ [22] with the segmentation in the images obtained by projecting the pixels onto the principal components and IHP components. In other words, the six above representations are computed for each image and k-means is applied to each component of each colorspace representation. The k-means has been chosen in order to guarantee that the accuracy of the segmentation is due to the properties of the projection and not of the classification algorithm. Table I shows the average segmentation accuracy with respect to the manual contour delineation provided by a dermatologist. The names in the table are made up of color space name and component in parenthesis. The numbers represent the average percentage of correctly classified pixels with the corresponding standard error. It can be seen that the largest correct classification rate is obtained using the first IHP component. Moreover, the fact that almost random classification is obtained using the second and the third component points out that most of the information needed to discriminate the lesion is concentrated in the first one.

TABLE I.

Lesion Segmentation by k-Means in Different Color Spaces on Chen’s [22] Database

Component	Error (%)	Component	Error (%)
Red	89.69±0.6	XYZ(X)	93.40±0.4
Green	94.23±0.4	XYZ(Y)	93.80±0.4
Blue	95.42±0.5	XYZ(Z)	95.30±0.5
Lab(L*)	92.52±0.4	Luv(L*)	92.52±0.4
Lab(a*)	91.92±0.5	Luv(u*)	86.70±1.1
Lab(b*)	94.24±0.5	Luv(v*)	83.67±1.3
IHP(l)	96.13±0.2	PCA(l)	94.83±0.3
IHP(2)	64.78±0.8	PCA(2)	88.84±0.9
IHP(3)	62.05±0.6	PCA(3)	73.52±0.8

It is worth noting that the results presented in Table I can still be improved by pre- and postprocessing. The preprocessing is a morphological hair removal [23], and the postprocessing is just the morphological closing and opening with a 5 × 5 square structuring element filled with ones. Since postprocessing is out of scope of this paper, the choice of the structuring element was purely empirical and therefore not necessarily optimal. The postprocessing is finished by hole filling and selection of the largest blob, which is assumed to be the lesion. This allows raising the segmentation precision to 97%.

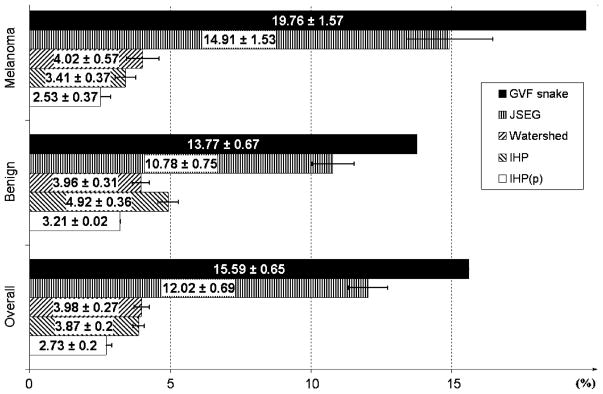
To compare the IHP to the existing lesion segmentation methods, we have chosen the JSEG [24], Watershed [8] and GVF snake [7] reported to be the best three techniques of the four tested by Chen [22]. The comparison is shown in Fig. 2, where “IHP(p)” stands for IHP with the pre- and postprocessing mentioned in the previous paragraph.

Fig. 2.

Mean segmentation errors of different segmentation algorithms on Chen’s [22] database.

To further evaluate the performance of the algorithm a second database has been chosen. This database is composed of 150 melanoma images and was introduced by Ganster [5]. In this case, the performance of our algorithm (k -means segmentation of pixels projected onto the first IHP component) is compared to the segmentation algorithm that has been reported to perform well on this database. This algorithm, proposed by Ganster [5], fuses the results of five different segmentation techniques. These techniques are the global thresholding in the blue component of the RGB image, three dynamic adaptive thresholds in the b component of the CIE-Lab model (mask sizes are 100 × 100, 150 × 150, and 200 × 200) and a 3-D color clustering with the X, Y, and Z and components of the CIE-XYZ color model. As can be seen from Table II, the performance of both algorithms is comparable. However, IHP is simpler, in the sense that it is just a linear combination of image bands, while Ganster’s algorithm combines five different segmentation techniques. Moreover, those techniques were performed in colorspaces empirically chosen for the database at hand, while our algorithm does not exhibit any such bias.

TABLE II.

Segmentation of Ganster’s Database [5] by Different Algorithms

Method	Mean Error(%)
Ganster’s Algorithm [5]	0.9625 ± 0.03
IHP	0.9631 ± 0.03

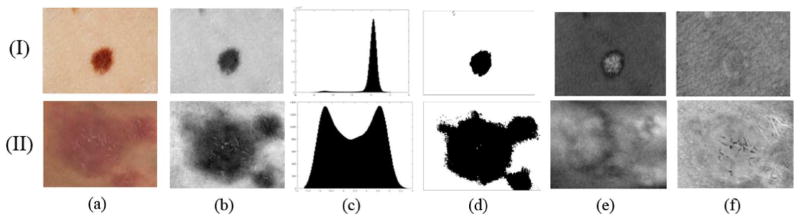
We tested our algorithm on one more melanoma dataset composed of 57 images. This dataset was introduced in Hintz–Madsen et al. [25]. The authors preprocessed the images with a 11 × 11 median filter to remove noise, and applied the Karhunen–Loeve transform to enhance the border of the lesion. After the images were preprocessed, a threshold was applied to segment the lesions. In our experiment, the images do not undergo any preprocessing other than hair removal. The algorithm performed very well, with correct segmentation of all images in the dataset. Due to the lack of manual segmentations in this dataset, the segmentation results were evaluated visually and the detected boundary always matched that of the lesion. An example of segmentation is shown in Fig. 3(I). The result of projecting the pixel intensities of the melanoma image in Fig. 3(I)(a) onto the first IHP component is displayed in Fig. 3(I)(b). The histogram of the projected pixels and the result of applying a k-mean algorithm to the projected data are displayed in Fig. 3(I)(c) and (d), respectively.

Fig. 3.

Results of applying the IHP to a melanoma image (row I) and a psoriasis image (row II). In columns: (a) RGB images. (b) Projection onto the first IHP component. (c) Histogram of the pixels projected onto the first IHP component. (d) Segmentation results. (e) Projections onto the second IHP component. (f) Projections onto the third IHP component.

To demonstrate that the IHP is not limited to melanoma or RGB images and that it can be also successfully applied to other dermatological images as well as multispectral images, two psoriasis datasets have been chosen. The first dataset is a 35-image subset of the database introduced in Delgado et al. [26]. The second dataset is composed of nine multispectral images [13]. Each image has nine bands ranging from ultraviolet to near-infrared. So far, dermatological studies based on digital images, have exclusively paid attention to tri-chromatic band images. Only a few works in spectroscopy have considered near-infrared images [14], [27]. Fig. 3(II) shows the segmentation results on one of the RGB psoriasis images. It can be seen that the IHP managed to find a contrast-enhancing combination.

The previous experiments were focused only on the properties of the first IHP component. Now we would like to demonstrate how the IHP can enhance substructures of a lesion, which might facilitate the diagnosis of a disease. Looking at Fig. 3 columns (e) and (f), it can be seen that the different substructures of the lesion have been enhanced. In particular, for the melanoma image the second IHP component enhances its border as seen in Fig. 3(I)(e). The image corresponding to the third component Fig. 3(I)(f) does not carry much information, and it can be easily verified that the corresponding histogram is unimodal Gaussian, which means that most of the information for segmentation is accounted for by the first two components. The fact that psoriasis is a more interpretable disease allows for a better evaluation of the performance of the IHP algorithm. It is known that psoriasis is characterized by the red area and the scales, which are clearly visible in Fig. 3(II)(e) and (f). The second IHP component also usually exhibits some other structures, such as vessels or hair.

IV. Conclusion

In this paper, we have proposed the IHP algorithm that estimates a linear multispectral color space transformation optimal for segmentation of dermatological lesions. Projecting the images onto the first IHP component facilitates unsupervised lesion segmentation on these images. The segmentation precision was close to 97% which could be increased by generic postprocessing. The proposed algorithm have been compared to an algorithm presented by Ganster [5]. The performance of both algorithms is comparable, but Ganster’s image representation was empirically chosen for his database. The method proposed here is independent of database and images, and the results can still be improved by using more sophisticated clustering methods. It remains to add that our approach can be applied irrespective of the color space of the image and the number of image bands.

Biographies

David Delgado Gómez received the M.Sc degree in mathematics from the Autonomous University of Madrid, Madrid, Spain, in 1999 and the Ph.D. degree in applied mathematics from the Technical University of Denmark, Lyngby, in 2005.

Currently, he is working as a Full-Time Professor in Universitat Pompeu Fabra, Barcelona, Spain, where he combines research and teaching. His research interests include applied multivariate statistical analysis, machine learning, and pattern recognition.

Constantine Butakoff was born in Uzhgorod, Ukraine, in 1977. He received the M.Sc. degree in mathematics from Uzhgorod National University in 1999. He is currently pursuing the Ph.D. degree at the University of Zaragoza, Zaragoza, Spain.

Since 1998, he has been working in the field of image processing and recognition. He is now a member of the Computational Imaging Lab, Universitat Pompeu Fabra, Barcelona.

Bjarne Kjær Ersboll received the M.Sc.Eng. and Ph.D. degrees in statistics and image analysis from the Technical University of Denmark, Lyngby, in 1983 and 1990, respectively.

He is currently an Associate Professor at the Department of Informatics and Mathematical Modeling, Technical University of Denmark. His research interests include applied multivariate statistical analysis of multidimensional digital imagery. He has worked on related problems from many domains: remote sensing, industry, and medical/biological. He has also organized or coorganized many international and national conferences and workshops on these topics

William Stoecker received the B.S. degree in mathematics from the California Institute of Technology (Caltech), Pasadena, in 1968, the M.S. degree in systems science from the University of California, Los Angeles (UCLA), in 1970, and the M.D. degree from the University of Missouri, Columbia, in 1977.

He is a practicing Dermatologist, Clinical Assistant Professor of Internal Medicine-Dermatology, at the University of Missouri, Columbia, where he is also Director of Dermatology Informatics and Adjunct Assistant Professor of Computer Science at the University of Missouri, Rolla. He is Chairman of the American Academy of Dermatology Task Force on Computer Data Base Development, which has developed diagnostic and therapeutic software for dermatologists. He is President of Stoecker and Associates, Rolla, which develops medical computer vision systems. His interests include artificial intelligence in medicine, computer vision in medicine, and diagnostic problems in dermatology.