Abstract
Purpose: This work seeks to develop exact confidence interval estimators for figures of merit that describe the performance of linear observers, and to demonstrate how these estimators can be used in the context of x-ray computed tomography (CT). The figures of merit are the receiver operating characteristic (ROC) curve and associated summary measures, such as the area under the ROC curve. Linear computerized observers are valuable for optimization of parameters associated with image reconstruction algorithms and data acquisition geometries. They provide a means to perform assessment of image quality with metrics that account not only for shift-variant resolution and nonstationary noise but that are also task-based.
Methods: We suppose that a linear observer with fixed template has been defined and focus on the problem of assessing the performance of this observer for the task of deciding if an unknown lesion is present at a specific location. We introduce a point estimator for the observer signal-to-noise ratio (SNR) and identify its sampling distribution. Then, we show that exact confidence intervals can be constructed from this distribution. The sampling distribution of our SNR estimator is identified under the following hypotheses: (i) the observer ratings are normally distributed for each class of images and (ii) the variance of the observer ratings is the same for each class of images. These assumptions are, for example, appropriate in CT for ratings produced by linear observers applied to low-contrast lesion detection tasks.
Results: Unlike existing approaches to the estimation of ROC confidence intervals, the new confidence intervals presented here have exactly known coverage probabilities when our data assumptions are satisfied. Furthermore, they are applicable to the most commonly used ROC summary measures, and they may be easily computed (a computer routine is supplied along with this article on the Medical Physics Website). The utility of our exact interval estimators is demonstrated through an image quality evaluation example using real x-ray CT images. Also, strong robustness is shown to potential deviations from the assumption that the ratings for the two classes of images have equal variance. Another aspect of our interval estimators is the fact that we can calculate their mean length exactly for fixed parameter values, which enables precise investigations of sampling effects. We demonstrate this aspect by exploring the potential reduction in statistical variability that can be gained by using additional images from one class, if such images are readily available. We find that when additional images from one class are used for an ROC study, the mean AUC confidence interval length for our estimator can decrease by as much as 35%.
Conclusions: We have shown that exact confidence intervals can be constructed for ROC curves and for ROC summary measures associated with fixed linear computerized observers applied to binary discrimination tasks at a known location. Although our intervals only apply under specific conditions, we believe that they form a valuable tool for the important problem of optimizing parameters associated with image reconstruction algorithms and data acquisition geometries, particularly in x-ray CT.
Keywords: image quality, ROC, CT
INTRODUCTION
The development of new reconstruction algorithms and data acquisition strategies often requires image quality assessment to optimize system parameters. A rigorous way to measure image quality is with a task-based approach.1 This approach requires the clear definition of (1) a task, (2) an observer, and (3) a meaningful figure of merit.1 Unfortunately, image quality assessment with human observers is not practical for purposes of system optimization. Indeed, because human observer studies are expensive and time-consuming, they are cumbersome for system optimization over a large set of possible system and signal parameters.2 To overcome this problem, the use of computerized observers has been advocated for image quality assessment for the purpose of system optimization.1 The results presented in this work are specifically intended for linear computerized observers; they should not be blindly applied to human observers (our assumptions are not likely to be met in this case).
Task-based assessments of image quality using linear computerized observers often involve binary classification. For example, studies of medical image quality frequently evaluate a task in which an observer attempts to discriminate between two classes of images: those images that contain a feature of interest (later called lesion, following customary usage) and those that do not. Observer performance for a binary classification task can be expressed using a receiver operating characteristic (ROC) curve, which plots the true positive fraction (TPF) as a function of false positive fraction (FPF).1 For purposes of simplification, the whole ROC curve is often reduced to a single number, called an ROC summary measure.1, 3 In practice, ROC curves and ROC summary measures must be estimated from observer rating data obtained experimentally. Consequently, they suffer from statistical variability that must be characterized in order to make inferences about observer performance.
One way that estimator variability may be summarized is through the use of confidence intervals. As opposed to point estimates, confidence intervals provide a probabilistic guarantee of covering the parameter of interest.4 Moreover, as observed in Ref. 5 a virtue of confidence intervals is that they convey more information than hypothesis testing (together with p-values) in two ways. First, confidence intervals communicate the amount of statistical precision involved in an experiment. Second, they communicate the relative size of an experimental effect, i.e., they show how significant experimentally observed differences are in terms of their magnitude. The importance of confidence intervals for ROC analysis of diagnostic image quality has been previously emphasized by Metz.6
Previous work that examined confidence intervals with application to ROC analysis has primarily focused on estimation of the area under the ROC curve (AUC), a widely used summary measure; see, e.g., Refs. 7, 9 for overviews of the literature on this topic. Also, confidence bands for the entire ROC curve have been investigated by.10, 11 The majority of the previously investigated ROC confidence intervals are based on either nonparametric or semiparametric estimation techniques. Such distribution-free methods have the advantage that they are broadly applicable because they make very weak assumptions regarding the distributions of the observer ratings; this makes them suitable for assessment of human observers. However, a drawback of the previously investigated interval and band estimators is a reliance on either asymptotic approximations or resampling techniques. Because these methods are not appropriate for small samples, they can yield confidence intervals with inaccurate coverage probabilities.8 By contrast, the coverage probabilities for the confidence intervals that we propose in this work are known exactly when our assumptions are satisfied.
In this work, we present fully parametric estimators that yield exact confidence intervals for ROC summary measures and exact confidence bands for ROC curves. Our new estimators are designed for continuous-valued observer ratings under the dual assumptions that (i) the observer ratings are normally distributed for each class of images and (ii) the variance of the observer ratings is the same for each class of images.
Although the aforementioned assumptions appear to be restrictive, they are generally satisfied for image evaluation tasks involving detection of small, low-contrast lesions with linear computerized observers. The reasons are as follows. First, most linear computerized observers compute each observer rating as a linear combination of a large number of image pixel values. Therefore, a general formulation of the central limit theorem12 implies that the ratings will tend to be normally distributed for each class of images. For x-ray computed tomography (CT), the normality of the observer ratings is further re-enforced by the near-normality of measured data13 and the linearity of reconstruction algorithms. Second, the absence or presence of a small, low-contrast lesion usually has little impact on the image covariance matrix, so that the variance of ratings produced by linear computerized observers is practically the same for each class of images. This second observation has been made by Barrett and Myers1(p. 1209) in the context of nuclear medicine. We carefully analyze its applicability for CT in Sec. 4.
After reviewing relevant background material, we present our new confidence interval estimators. Subsequently, we evaluate two aspects of the AUC interval estimator. The first aspect regards the statistical utility of using more images from one class than the other. Knowledge of this utility is important, as it is often possible to get more images from the class without a lesion; see e.g., Ref. 14. The second aspect regards the robustness of our estimator for application to rating data with unequal variances for the two classes. We examine cases that are likely to be extreme for linear computerized observers performing low-contrast lesion detection tasks with CT images. Finally, the paper illustrates the usefulness of our estimators in the context of image quality evaluation with real x-ray CT images.
PRELIMINARIES
This section introduces our notation and reviews important background material. First, we remind the reader of the definition of the noncentral t distribution. The remainder of the section reviews summary measures of observer performance.
Throughout the text, the probability density function (pdf) of a continuous random variable X, will be written as fX (x), and its cumulative distribution function (cdf) will be denoted as FX (x). If fX (x) and FX (x) depend on a parameter θ, then they will be written as fX(x;θ) and FX(x;θ), respectively. Similarly, if fX (x) and FX (x) depend on several parameters θ1,θ2,…,θm, then they will be written as fX(x;θ1,θ2,…,θm) and FX(x;θ1,θ2,…,θm), respectively.
We assume that the reader is familiar with the normal and χ2 probability distributions.4 If a random variable X is normally distributed with mean μ and variance σ2, this fact will be written as X~N(μ,σ2). Similarly, a χ2 distributed random variable Y with ν degrees of freedom is denoted by . For only the particular case of the standard normal distribution, N(0,1), we depart from the notation introduced above for the cdf and employ the usual notations Φ(x) and Φ-1(p) for the cdf and inverse cdf, respectively.
The noncentral t distribution
If X~N(0,1) and are independent random variables, then for any δ∈(-∞,∞), the ratio
| (1) |
has a noncentral t distribution with ν degrees of freedom and noncentrality parameter δ.15 In this case, we write . The mean of a noncentral t random variable is15(p. 513)
| (2) |
where B(x,y) is the Euler beta function. Expressions for the pdf, cdf, and higher moments of the noncentral t distribution may be found in Ref. 15.
ROC figures of merit
We consider assessment of linear computerized observer performance for a binary classification task in which the observer must discriminate between two classes of images, denoted as class 1 and class 2. For a detection task, these classes could correspond to normal and diseased conditions, respectively. Given an image, a linear computerized (model) observer1 computes a scalar, continuous-valued rating statistic y, as the inner product of a fixed (nonrandom) q×1 template, w, with the image, p, represented as a q×1 column vector, i.e., y = wTp. The observer then compares y to a threshold, c, to classify the image. If y>c, the observer decides the image is from class 2. Otherwise, the image is classified as belonging to class 1.
For each threshold, c, the observer’s performance is fully characterized by two quantities, called the true positive fraction (TPF) and the false positive fraction (FPF).1, 3 The TPF is the probability that the observer correctly classifies a class-2 image as belonging to class 2, whereas the FPF is the probability that the observer incorrectly classifies a class-1 image as belonging to class 2. Since each value of c results in a different TPF and FPF, observer performance over all thresholds is completely described by the curve of (FPF, TPF) values parameterized by c. This curve is called the receiver operating characteristic (ROC) curve.1, 3 To denote the TPF as a function of the FPF, we will write TPF(FPF).
Throughout this paper, we assume that y is normally distributed with equal variances for each class, i.e, y~N(μ1,σ2) and y~N(μ2,σ2) for images from classes 1 and 2, respectively. In this case, the ROC curve takes the form [Ref. 3 (p. 82), Result 4.7]
| (3) |
where
| (4) |
is the observer signal-to-noise ratio. The SNR is sometimes used as figure of merit, since it may be interpreted as a measure of the distance between the distributions of classes 1 and 2. It must be remembered, however, that the SNR is useful only when the variance is a good measure of the spread of the distribution for y (Ref. 1, p. 819); this is the case when y is normal under each class.
Another useful figure of merit for observer performance is the area under the ROC curve, denoted as AUC. The AUC generally falls in the range [0, 1], with larger values signifying greater discrimination ability, and values less than 0.5 indicating that, on average, the observer performs worse than guessing. The AUC may be interpreted as the average TPF, averaged over the entire range of FPF values.3 Under our distributional assumptions, the AUC may be calculated as1(p. 819),3(p. 84)
| (5) |
If only a restricted range of FPF values is considered relevant for observer performance, then the partial area under the ROC curve, defined as
| (6) |
may be used as a summary measure. Observe that under our assumptions for y, TPF at fixed FPF, AUC, and pAUC are strictly increasing functions of SNR only. We use this property in the next section to construct our confidence interval estimators.
It is well-known that the ROC curve is invariant under any strictly increasing transformation of y [Ref. 3 (p. 69), Result 4.1]. Therefore, AUC and pAUC are also invariant under any such transformation. Likewise, if SNR is defined from AUC via Eq. 5, then it too is invariant under any strictly increasing transformation of y. However, it is important to recognize that if SNR is computed using Eq. 4, then the resulting value is not invariant under any such transformation, since this relation depends on the first and second moments of y in each class. The confidence interval estimators that we propose in the next section each rely on a point estimate of SNR, motivated by Eq. 4. Therefore, our interval estimators are not invariant under arbitrary strictly increasing transformations of y. Nonetheless, they are invariant under any strictly increasing affine transformation of y, and we will see that they possess attractive properties.
The figures of merit discussed above are widely used and accepted summary measures for observer performance.1, 3 For additional examples of summary measures, see (Ref. 3, Sec. 4.3.3) and (Ref. 16).
CONSTRUCTION OF INTERVAL ESTIMATORS
Suppose that an observer rates n1 images from class 1 and n2 images from class 2. Denote these ratings for classes 1 and 2 as and , respectively. We wish to estimate confidence intervals for summary measures of observer performance from this finite sample of rating data. In this section, we introduce our estimators assuming that y~N(μ1,σ2) and y~N(μ2,σ2) for images from classes 1 and 2, respectively, where μ1, μ2, and σ2 are unknown. Each of our interval estimators is based on a point estimator for SNR, which is introduced first. For a clear presentation, all mathematical proofs are deferred to the appendices.
Point estimation of SNR
Let the sample mean and the sample variance for class k be and , respectively. Also, define a pooled estimator for σ2 as . With these definitions in place, we define an estimator of SNR as
| (7) |
with
| (8) |
where B(x,y) is the Euler beta function. The multiplicative factor γ is chosen to make the estimator unbiased. We have the following characterization of , which is proved in Appendix A.
Theorem 1. Suppose that y~N(μ1,σ2) for images from class 1 and that y~N(μ2,σ2) for images from class 2. Also, suppose that is computed from independent samples of y, denoted as and , corresponding to classes 1 and 2, respectively. then
-
(i)
-
(ii)
is the unique uniformly minimum variance unbiased (UMVU) estimator of SNR.
Confidence interval estimation
Given a random variable, X, with a distribution depending on a parameter θ, one may define a random interval estimate [θL(X),θU(X)] for θ. This interval is said to be a 1-α confidence interval for θ if P(θ∈[θL(X),θU(X)])=1-α for any value of θ.17
Our knowledge of the sampling distribution for implies the next theorem, which is proved in Appendix B. It allows us to compute confidence intervals for SNR with exact coverage probabilities.
Theorem 2. Suppose that the hypotheses of Theorem 1 are satisfied. Let α1,α2∈(0,1) be such that α1+α2=α for some α∈(0,1), and let with . then
-
(i)
For each observation t of T, there exist unique values δL(t) and δU(t) in (-∞,∞) satisfying FT(t;ν,δL(t))=1-α1 and FT(t;ν,δU(t))=α2, where FT(t;ν,δ) is the cdf of the noncentral t distribution with ν=n1+n2-2.
-
(i)
The random interval [δL(T)∕(γη),δU(T)∕(γη)] is an exact 1-α confidence interval for SNR.
Hence, we can calculate a 1-α confidence interval for SNR from a realization of by numerically solving the relations in Theorem 2(i) for δL and δU and then substituting these values into the expression of Theorem 2(ii). Above, if α1=0, then δL(t)=-∞ and if α2=0, then δU(t)=∞. In either of these cases, the confidence interval is said to be one-sided. Otherwise, the interval is said to be two-sided.17
The following corollary shows that we can also calculate exact confidence intervals for TPF(FPF), AUC, and pAUC(FPF0, FPF1). It follows from Theorem 2 and the strictly increasing transformation property of confidence intervals, which is stated and proved in Appendix B as Lemma 3.
Corollary 1. Suppose that the hypotheses of Theorem 2 are satisfied. Let SNRL(T)=δL(T)∕(γη) and SNRU(T)=δU(T)∕(γη). Then the random intervals
and
defined by substituting SNRL(T) and SNRU(T) for SNR in Eqs. 3, 5, 6 are exact 1-α confidence intervals for TPF(FPF), AUC, and pAUC(FPF0, FPF1), respectively.
A MATLAB® routine that calculates the confidence intervals for SNR, TPF, AUC, and pAUC is provided in along with the article on the Medical Physics Website. Note that because is invariant under strictly increasing affine transformations of y, it follows that our confidence intervals also share this invariance.
A confidence band for the entire ROC curve may be found from a confidence interval for SNR in the sense of the next theorem, which is proved in Appendix C. We denote the collection of points on the ROC curve as ΩROC={(FPF,TPF):FPF∈[0,1]}.
Theorem 3. Suppose that y~N(μ1,σ2) for images from class 1 and y~N(μ2,σ2) for images from class 2. Let [SNRL, SNRU] be a 1-α confidence interval for SNR, and define the set
where
Then is a 1-α confidence band for the ROC curve in the sense that, for any value of SNR, ΩROC is contained in with probability 1-α, i.e., .
Observe that the 1-α confidence band defined in the above theorem is equivalent to the union over all FPF values of 1-α confidence intervals for TPF. This construction of a simultaneous 1-α confidence band for the ROC curve is possible because our assumptions imply that the ROC curve is parameterized by only SNR. More generally, when the ROC curve is parameterized by more than one parameter (as in the binormal model3), the confidence band formed from the union of 1-α TPF intervals will have a coverage probability smaller than 1-α for the whole ROC curve simultaneously.10
PROPERTIES OF THE AUC CONFIDENCE INTERVALS
In this section, we examine two aspects of the previously introduced AUC confidence intervals. First, we explore the potential advantage offered by using additional images from class 1 if such images are readily available. Second, for situations relevant to CT image quality assessment, we evaluate the robustness of the proposed intervals to violation of the equal-variance assumption on the rating data.
Advantage gained by using additional images from one class
In some circumstances, it may be possible to obtain additional images from one class of images at low cost; see, e.g., Ref. 14. Therefore, it is desirable to examine the potential decrease in statistical variability that may be gained by using such extra images. Below, we consider the case when more images are available for class 1. However, due to the symmetric role of n1 and n2 in our confidence interval estimators, the same conclusions also hold when there are more images for class 2.
For our evaluations, we assessed the mean 95% AUC confidence interval length, defined as MCIL.95 = E[AUCU − AUCL] for fixed values of n1, n2, and AUC, where AUCU and AUCL are the upper and lower endpoints, respectively, of the 95% (α1=α2=0.025) confidence interval estimator for AUC. To compute this expected value, we numerically evaluated the integral
| (9) |
| (10) |
where η, ν, and δ are as given in Theorem 1(i). In Eq. 10, the pdf of , , was rewritten in terms of the noncentral t pdf, fT, using Theorem 1(i) and a standard result for the pdf of a monotonic transformation of a random variable [Ref. 4 (p. 51), Theorem 2.1.5].
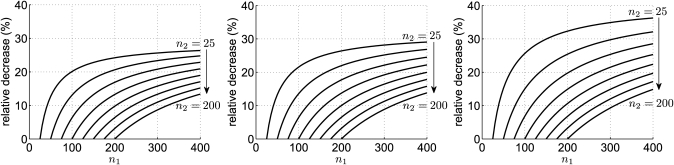
Figure 1 contains plots of the relative decrease in mean 95% AUC confidence interval length that is obtained by increasing n1 relative to n2. In these plots, the relative percentage decrease (RPD) in MCIL.95, relative to the n1 = n2 case, was calculated as
| (11) |
The plots in Fig. 1 indicate that the mean AUC confidence interval length can shrink by as much as 35% when n1 is increased relative to n2. In particular, the relative decrease is greatest for small values of n2 and for large values of AUC. Moreover, the plots illustrate that the advantage gained by increasing n1 relative to n2 flattens out for large values of n1.
Figure 1.
Percentage decrease of mean (95%) AUC confidence interval length, relative to the n1 = n2 case, plotted as a function of n1, with n2 and AUC held fixed. From top to bottom, the curves correspond to n2 values of 25, 50, 75, 100, 125, 150, 175, and 200, respectively. The plots are for AUC values of 0.6 (left), 0.75 (center), and 0.9 (right).
Applicability for CT image quality evaluation: Robustness to violation of the equal-variance assumption
The ROC confidence intervals introduced in Sec. 3 assume that the variance of the ratings is the same for each class of images, i.e., , where and are the rating variances for classes 1 and 2, respectively. As discussed in the introduction, this assumption should be a good approximation for linear computerized observers applied to tasks involving the detection of small, low-contrast lesions in CT images. We now take a closer look at the quality of the approximation in the context of CT image quality evaluation, and then we examine the coverage probability of the AUC interval estimator in extreme cases.
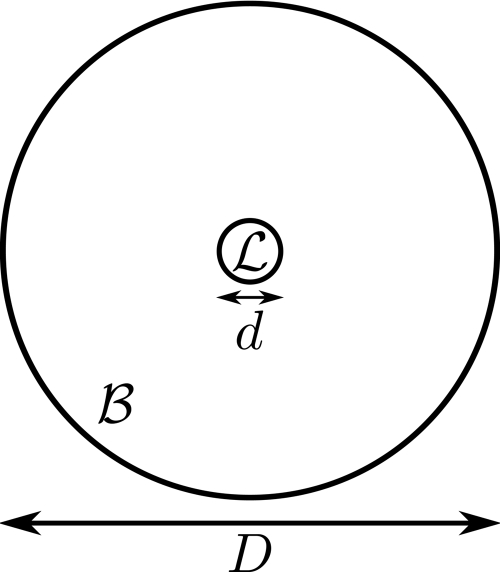
Consider a uniform circular cylinder B of diameter D, which may, or may not, contain a small spherical lesion L of diameter d at its center; see Fig. 2. Denote the linear x-ray attenuation coefficients for the cylinder and for the lesion as μB and μL, respectively. Assuming a conventional Poisson noise model and a monochromatic beam,18, 19 the variance of the measured CT data for a ray passing through the center of B when the lesion is not present is
| (12) |
where Ni is the number of photons entering the cylinder. When the lesion L is present, the variance of the measured CT data for a ray passing through the center of B becomes
| (13) |
where μW is the linear x-ray attenuation coefficient for water, and the lesion contrast C is defined in Hounsfield units as C=(μL-μB)1000∕μW. Forming the ratio of the above variances, we have
| (14) |
Hence, the ratio of the variances for rays passing through the lesion always falls between exp(-dCμW∕1000) and one. It is straightforward to see that this result is very general and is, for example, applicable to noncircularly symmetric background objects and arbitrarily located lesions. Now, suppose that image reconstruction is performed using the classical 2-D filtered backprojection (FBP) algorithm. Then, expressions given for the image variance and covariance in18, 19 show that the entry-wise ratio of the image covariance matrices for each class is, to a good approximation, bounded between exp(-dCμW∕1000) and one. Consequently, it follows that for linear computerized observers, the ratio of the rating variances, , is approximately bounded between exp(-dCμW∕1000) and one. The bound exp(-dCμW∕1000) is tabulated in Table TABLE I. for various lesion diameters, d, and contrasts, C, assuming a linear x-ray attenuation coefficient of μW=0.183cm-1 for water.
Figure 2.
Depiction of a small lesion embedded in a larger, uniform cylinder.
TABLE I.
Bounds on the variance ratio of the rating data, , for a lesion of diameter d mm with contrast C HU. (The other bound on is always 1).
| d(mm) | C(HU) | exp(-dCμW∕1000) |
|---|---|---|
| 1 | 100 | 0.9982 |
| 1 | –100 | 1.0018 |
| 5 | 500 | 0.9553 |
| 5 | 10 | 0.9991 |
| 5 | –10 | 1.0009 |
| 5 | –500 | 1.0468 |
| 10 | 50 | 0.9909 |
| 10 | –50 | 1.0092 |
| 15 | 50 | 0.9864 |
| 15 | –50 | 1.0138 |
| 20 | 100 | 0.9641 |
| 20 | 75 | 0.9729 |
| 20 | –75 | 1.0278 |
| 20 | –100 | 1.0373 |
Examining Table TABLE I., we see that for a large variety of lesion detection tasks, it is safe to assume that . Moreover, the values and correspond to extreme cases in which the lesion must either be very large or have a high contrast. In light of these results, we next examine the coverage probability of the AUC interval estimator when the equal-variance assumption is violated with either or . We consider two scenarios: (i) n1 = n2 and (ii) n1 = 2 n2.
For each choice of the parameters n1, n2, AUC, and , we performed 107 Monte Carlo trials to estimate the coverage probability of the 95% (α1=α2=.025) AUC confidence intervals. Without loss of generality, we assumed that the ratings for class 1 came from a standard normal distribution since our confidence interval estimators are invariant under strictly increasing affine transformations of the ratings. An individual trial was carried out by first randomly generating n1 values of y~N(0,1) and n2 values of y~N(μ,σ2), with and σ2=1∕κ. [The formula for μ was found using the AUC expression given in Ref. 1 (p. 819) for the general case when may not equal .] Then, a single interval estimate for AUC was calculated from the ratings using the steps described in Sec. 3. After running the trials, the coverage probability was estimated as the proportion of the 107 trials for which the estimated interval covered the true AUC value. In addition, 95% confidence intervals for the coverage probability were estimated using the Wilson score method advocated in (Ref. 20) for binomial proportions. In all cases, the Wilson score intervals indicated that the upper (respectively lower) bound of a conservative 95% confidence interval for the coverage probability may be obtained by adding 0.014% to (respectively subtracting 0.014% from) each point estimate expressed in percent.
Table TABLE II. contains the estimated coverage probabilities for the and cases in the n1 = n2 scenario. From this table, we see that for all AUC values and choices of n1 = n2, the coverage probabilities are very close to 95%. The estimated coverage probabilities in the unbalanced n1 = 2n2 scenario are shown in Table TABLE III. for the and cases. For all of the tested AUC values and choices of n1 = 2n2, the coverage probabilities for the case are conservative. On the other hand, the coverage probabilities for the case are all slightly less than 95% in the n1 = 2n2 scenario.
TABLE II.
Estimated coverage probabilities (in percent) for two-sided 95% AUC confidence intervals generated from normally distributed rating data with n1 = n2 = n. The tables correspond to variance ratios of and . In all cases, the upper and lower bounds of a conservative 95% confidence interval for the coverage probability may be obtained by adding and subtracting 0.014% to∕from each point estimate, respectively.
| AUC \ n | 25 | 50 | 75 | 100 |
|---|---|---|---|---|
| 0.52 | 95.00 | 95.00 | 95.00 | 94.99 |
| 0.55 | 95.00 | 95.01 | 95.00 | 94.99 |
| 0.60 | 94.99 | 95.00 | 94.99 | 95.00 |
| 0.70 | 94.99 | 95.00 | 95.00 | 95.01 |
| 0.80 | 95.00 | 95.00 | 95.00 | 95.01 |
| 0.90 | 94.99 | 94.99 | 95.00 | 95.01 |
| 0.95 | 94.99 | 94.99 | 94.99 | 94.99 |
| 0.98 | 95.00 | 95.00 | 95.01 | 95.00 |
| 0.52 | 95.01 | 95.00 | 95.00 | 95.01 |
| 0.55 | 95.00 | 95.01 | 95.00 | 95.00 |
| 0.60 | 94.99 | 95.01 | 94.99 | 95.00 |
| 0.70 | 94.99 | 95.00 | 95.01 | 95.00 |
| 0.80 | 95.00 | 95.00 | 95.00 | 95.00 |
| 0.90 | 94.99 | 95.01 | 95.00 | 95.00 |
| 0.95 | 94.99 | 95.00 | 94.99 | 95.00 |
| 0.98 | 95.00 | 95.01 | 95.01 | 94.99 |
TABLE III.
Estimated coverage probabilities (in percent) for two-sided 95% AUC confidence intervals generated from normally distributed rating data with n1 = 2n and n2 = n. The tables correspond to variance ratios of and ). In all cases, the upper and lower bounds of a conservative 95% confidence interval for the coverage probability may be obtained by adding and subtracting 0.014% to∕from each point estimate, respectively.
| AUC \ n | 25 | 50 | 75 | 100 |
|---|---|---|---|---|
| 0.52 | 94.81 | 94.80 | 94.81 | 94.81 |
| 0.55 | 94.80 | 94.80 | 94.80 | 94.81 |
| 0.60 | 94.81 | 94.81 | 94.81 | 94.81 |
| 0.70 | 94.81 | 94.81 | 94.82 | 94.80 |
| 0.80 | 94.83 | 94.84 | 94.83 | 94.82 |
| 0.90 | 94.87 | 94.85 | 94.86 | 94.85 |
| 0.95 | 94.90 | 94.88 | 94.86 | 94.86 |
| 0.98 | 94.90 | 94.92 | 94.90 | 94.88 |
| 0.52 | 95.19 | 95.18 | 95.19 | 95.19 |
| 0.55 | 95.18 | 95.18 | 95.18 | 95.19 |
| 0.60 | 95.18 | 95.18 | 95.18 | 95.19 |
| 0.70 | 95.17 | 95.16 | 95.17 | 95.15 |
| 0.80 | 95.14 | 95.14 | 95.14 | 95.12 |
| 0.90 | 95.10 | 95.09 | 95.10 | 95.08 |
| 0.95 | 95.08 | 95.05 | 95.04 | 95.04 |
| 0.98 | 95.02 | 95.04 | 95.02 | 95.01 |
Overall, these results indicate that our AUC interval estimators maintain accurate coverage probabilities even in the extreme cases and . They also exhibit a difference in behavior between having n1 = n2 or not—the error in coverage probability is smaller when n1 = n2. Also, when n1 is different from n2, the coverage probability may be conservative or not depending on the value of the variance ratio.
Last, note that although the evaluations in this section were performed only for AUC confidence intervals, the same conclusions hold for the SNR interval estimator discussed in (Sec. 3B), since SNR and AUC are related through a continuous, strictly increasing transformation that does not depend on .
APPLICATION TO TASK-BASED IMAGE QUALITY EVALUATION
We present here an example of how our estimators can be used in the context of task-based image quality evaluation. This example involves real x-ray computed tomography (CT) images but is not meant to recommend a specific methodology for assessment of image quality in CT. Specifically, our choices for the task and for the observer are not optimal for CT images. Furthermore, the example should not be taken as evidence in favor of one reconstruction strategy over another. Our purpose is simply to demonstrate the usefulness of the tools that we have developed in this paper for interval estimation of ROC summary measures and of ROC curves.
A Siemens SOMATOM® SensationTM 64 CT scanner was employed to repeatedly scan a thorax phantom 186 times over a circular source trajectory. The phantom consisted of a torso constructed by QRM (Möhrendorf, Germany)21 together with two different water bottles attached to the sides to simulate arms. A mean image of the whole phantom estimated from 186 reconstructions is shown in Fig. 3(left). The scans were executed in a thorax scan mode using a two-slice acquisition with a slice thickness of 1 mm and a rotation speed of 3 revolutions per second. The x-ray tube settings were 25 mAs and 120 kVp, and the data acquisition was performed with no tube current modulation to accentuate noise correlation in the image. The measurements for the first of the two slices over the 186 repeated scans constituted 186 fan-beam data sets that were used for the image quality evaluation.
Figure 3.
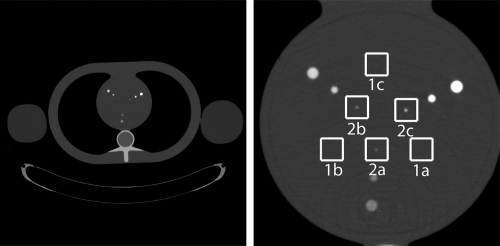
Mean images of the QRM phantom displayed with a grayscale window of [–200, 600] HU. Whole phantom (left) and reconstruction focused on the heart insert (right) with regions of interest marked with white boxes. ROI-1a, ROI-1b, and ROI-1c contain no lesion. ROI-2a, ROI-2b, and ROI-2c contain a low-contrast, and a medium-contrast, and high-contrast lesion, respectively.
The CT data was read using software supplied by Siemens and fed directly into our implementation of the classical filtered backprojection (FBP) algorithm for direct reconstruction from either short-scan or full-scan fan-beam data; see Ref. 19 for a description of the algorithm as we used it. The short-scan reconstructions were performed using only 230∘ of the source trajectory. The reconstructions were consistently performed on a grid of 550×550 square pixels, each of size 0.02×0.02 cm, that was centered on the heart insert, as shown in Fig. 3 (right).
For both short-scan and full-scan reconstructions, we considered a lesion detection task that amounts to determining whether or not a lesion is present at the center of a region-of-interest (ROI). To train and test an observer for this task, we identified six regions of interest (ROI) in the heart insert: three regions without lesions, labeled as ROI-1a, ROI-1b, and ROI-1c, and three regions with a lesion at their center, labeled as ROI-2a, ROI-2b, and ROI-2c; see Fig. 3(right). Each ROI when viewed as an image consists of 50×50 pixels. The lesion diameter in each of the lesion-present images is 1 mm, but the contrast varies. Specifically, the lesion contrast is 210 HU for ROI-2a, 452 HU for ROI-2b, and 997 HU for ROI-2c. In each case, the background value is 40 HU. We assumed that the images of the six ROIs obtained from one given CT data set are independent. This is justified by a previous study of direct fan-beam FBP reconstruction from simulated CT data, which indicated that correlations between image pixels are negligible over the distance (1–2 cm) that separates the ROIs.19 For examples of practical image quality studies that employ multiple ROIs in a similar fashion, see Refs. 2, 14.
For our observer, we used a trained channelized Hotelling observer (CHO), which is a popular type of linear computerized observer; for details, see Ref. 1. The CHO was implemented with 40 Gabor channels using the parameters given in Ref. 19. A specific template was built for each type of reconstruction (full-scan and short-scan). These two templates were each estimated (trained) using the first 50 CT data sets. The class-1 images used for the training were the images defined by ROI-1a, ROI-1b, and ROI-1c, pooled together, and the class-2 images used for the training were the images for ROI-2a, ROI-2b, and ROI-2c, pooled together. In total, 150 class-1 and 150 class-2 images were thus used to train the observer for each reconstruction type.
Once the observer was trained, we tested its performance on a lesion detection task. The class-1 images for this task were defined using only ROI-1a, and the class-2 images were defined using only ROI-2a. The observer performance for the detection task was estimated (tested) using the remaining 136 CT data sets in a fully paired design, i.e., the same CT data sets were used for the short-scan and full-scan testing. Hence, for each type of scan, n1 = 136 class-1 images and n2 = 136 class-2 images were used for testing the observer.
For both the short-scan and full-scan reconstructions, our two assumptions that (i) the observer ratings are normally distributed for each class of images, and (ii) the variance of the observer ratings is the same for each class of images, were further verified with hypothesis tests. The first assumption was checked by performing the Lilliefors normality test22 at the α=0.10 significance level, using the built-in matlab® function lillietest. In all cases, there was not enough evidence at the 0.10 significance level to reject the null hypothesis that the ratings for each class came from a normal distribution. The second assumption was checked by performing the two-sample F-test for equal variances at the α=0.10 significance level using the built-in matlab® function vartest2. For both types of reconstruction, there was not enough evidence at the 0.10 significance level to reject the null hypothesis that the ratings were normally distributed in each class with equal variances. The p-values for these tests are reported in Table TABLE IV.. Note that because all of the p-values are very large, they cast little doubt on the validity of the null hypothesis for each test.
TABLE IV.
Estimated p-values for the example. The p-values for the Lilliefors normality test and for the two-sample F-test of equal variances.
| Short-scan | Full-scan | |
|---|---|---|
| The p-values for the Lilliefors normality test | ||
| class 1 | 0.744 | 0.370 |
| class 2 | 0.905 | 0.544 |
| The p-values for the two-sample F-test of equal variances | ||
| 0.279 | 0.710 | |
We estimated the observer performance by first applying Eq. 7 with n1 = 136 and n2 = 136 to obtain the value of . Then, we applied the matlab® routine supplied along with the article on the Medical Physics Website with the following parameters: α1=α2=0.025, FPF0 = 0, FPF1 = 0.2 and a fine sampling of FPF values over the range [0,1].
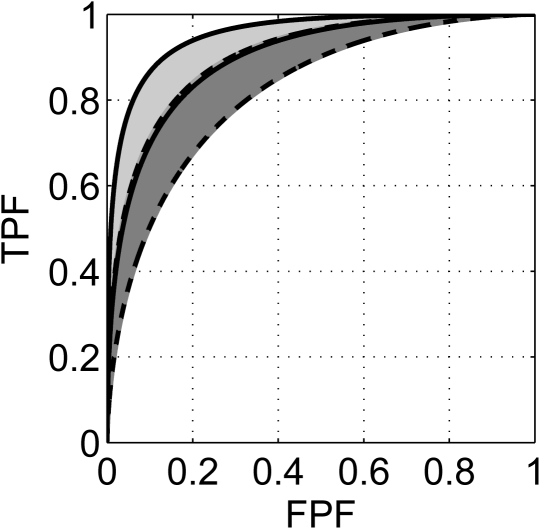
Table TABLE V. gives the estimated 95% confidence intervals for SNR, AUC, and pAUC corresponding to the short-scan and full-scan reconstructions, respectively. In addition, the estimated 95% confidence bands for the entire ROC curve are displayed in Fig. 4.
TABLE V.
Comparison of 95% confidence intervals estimated for observer performance on short-scan and full-scan reconstructions. The intervals were estimated from n1 = 136 class-1 ratings and n2 = 136 class-2 ratings.
| Short-scan | Full-scan | |
|---|---|---|
| SNR | [1.2939 1.8377] | [1.7982 2.3905] |
| AUC | [0.8199 0.9031] | [0.8982 0.9545] |
| pAUC(0, 0.2) | [0.0935 0.1320] | [0.1294 0.1634] |
Figure 4.
Ninety-five percent confidence bands for the ROC curves corresponding to observer performance on short-scan and full-scan reconstructions. The band for short-scan reconstruction is shown in dark gray, delimited by dashed lines and the band for full-scan reconstruction is shown in light gray, delimited by solid lines. Note that the bands slightly overlap.
Table TABLE V. indicates that the 95% confidence intervals for observer performance overlap for the short-scan and full-scan reconstructions, with the lower (respectively upper) interval bound for full-scan reconstruction being above that for short-scan reconstruction. Care has to be taken with the statistical interpretation of the results. To compare the results for the two reconstruction strategies against each other, recall that the testing used a fully paired design so that the 95% confidence interval (band) estimates obtained for each task are dependent. In this case, we can use the Bonferroni inequality to determine a lower bound on the joint coverage probability of the intervals for observer performance.23(p. 232) For arbitrary events A1, A2, …, An, the Bonferroni inequality takes the form [Ref. 4 (p. 13) Eq. (1.2.10), and Ref. 23]
| (15) |
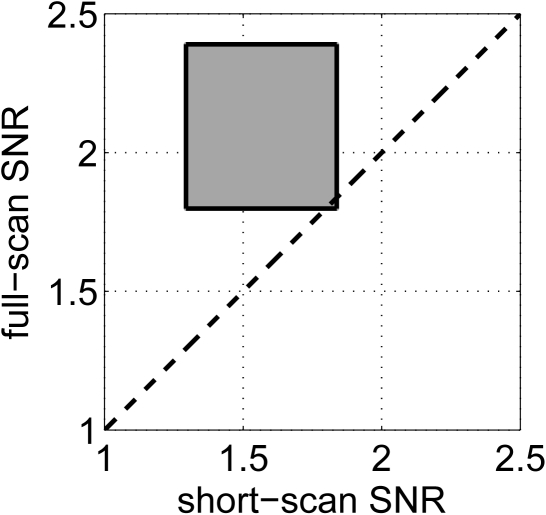
Suppose, for example, that we wish to compare the SNR values obtained for the short-scan and full-scan reconstruction strategies. Let SNRss and SNRfs be these two values, and let [Lss,Uss] and [Lfs,Ufs] be their 95% confidence intervals, respectively. Then by the Bonferroni inequality, the region [Lss,Uss]×[Lfs,Ufs] covers the pair (SNRss, SNRfs) with a probability of at least 0.95 + 0.95 – 1 = 0.90, i.e., with 90% confidence; see Fig. 6. Both the size and the position of the confidence region determine how the results should be interpreted. First, a smaller region covering a given pair of SNR values indicates a higher statistical precision. Second, if the confidence region does not intersect the line at 45° in the plane of possible values for (SNRss, SNRfs), then there is evidence that the two tasks correspond to dissimilar detection performance. Going back to the example, because the SNR confidence intervals overlap, the SNR confidence region intersects the 45° line, as shown in Fig. 5, and there is not enough evidence at the 90% confidence level to reject the hypothesis that SNRss = SNRfs. Likewise, the same conclusion can be made for the other figures of merit. Conversely, if the confidence region had instead not intersected the 45° line, there would have been evidence at the 90% confidence level to reject the hypothesis that SNRss = SNRfs. Moreover, note, from the large size of the confidence region, that our conclusion is drawn with a fairly poor statistical precision.
Figure 5.
Ninety percent confidence region for (SNRss, SNRfs).
DISCUSSION AND CONCLUSIONS
In this work, we proposed confidence interval estimators that may be used in ROC evaluations of task-based image quality studies employ in linear computerized observers defined with a fixed (nonrandom) template. All ratings provided by such an observer are linear combinations of image pixel values. A strength of the new interval estimators is that they have exactly known coverage probabilities. This property is particularly relevant for small sample sizes, since approximate confidence intervals have been found to be problematic in this case.8 The price of our approach is a reliance on two assumptions, which are usually satisfied by ratings produced by linear computerized observers performing lesion detection tasks involving small, low-contrast lesions at a known location: (i) the observer ratings are normally distributed for each class of images, and (ii) the variance of the observer ratings is the same for each class of images. For x-ray CT, the normality assumption on the ratings is commonly accepted, and we used Monte Carlo simulations to investigate the reliability of the proposed AUC confidence intervals when the equal-variance assumption is violated for the rating data. In cases that are extreme for CT, we observed that the AUC interval estimators maintain highly accurate coverage probabilities. In addition, we discovered that the error in coverage probability was very small (≤0.01%) when n1 = n2. When n1≠n2, we found that the error in coverage probability was about 0.2% in extreme cases, and that the confidence intervals may or may not be conservative, depending on the variance ratio of the ratings. These results demonstrate the practicality of our ROC confidence intervals for CT image quality evaluation.
When our assumptions for the observer ratings are strongly violated (which would be the case for human observer studies), the interval estimators introduced here are no longer appropriate. In this situation, it is preferable to use confidence intervals based on either nonparametric or semiparametric estimators, Ref. 3 (Chap. 5) which often rely on resampling techniques. Such approaches have the advantage that they do not require distributional assumptions on the observer ratings. However, construction of confidence intervals based on these estimators requires asymptotic assumptions that are violated for small samples.8
Note that our approach is equivalent to explicit utilization of a binormal model with a priori knowledge that the second binormal parameter (usually denoted as b) is equal to one. This knowledge was a critical component in our construction of confidence bands for the ROC curve with exactly known coverage probabilities. The ability to build such confidence bands is an attractive feature of our parametric approach. Another attractive feature is the ability to evaluate sample size effects without expensive Monte Carlo trials. As an example, we explored the potential decrease in statistical variability that can be gained by increasing the number of images from one class, which is an important issue, since it is often possible to get many additional class-1 images at low cost, as previously discussed in Ref. 14. Our results indicated that the mean AUC confidence interval length can shrink by as much as 35% when using this strategy.
Last, we illustrated the use of the new confidence interval estimators with an example involving a trained CHO applied to a lesion detection task with real x-ray CT images. This example demonstrated how different reconstruction methods can be compared with two-sided confidence intervals. Although it was not discussed in the example, our interval estimators can also be used to calculate one-sided confidence intervals, which occur when either α1 or α2 is zero.17 One-sided intervals are useful for inferences involving statements such as “The AUC for method 1 is higher than the AUC for method 2.” The matlab® routine supplied along with this article on the Medical Physics Website works for both two-sided and one-sided confidence intervals.
When designing an image evaluation study, it is sometimes possible to use the same data set for each scenario of interest. The design of the study is then called paired (as opposed to unpaired). The example we considered is compatible with pairing, and so we used a fully paired study design. Other comparisons, such as a study of the effect of different bowtie filters or dose-modulation strategies, would not allow pairing. In a paired situation, it is important to realize that the SNR estimates obtained for each reconstruction scenario are correlated and this must be taken into account when generating a joint confidence region for these estimates. We used the Bonferroni inequality to obtain a conservative rectangular confidence region. Another approach would have been to look for a nonrectangular confidence region. It is not clear that such a region can be found without assuming that the SNR estimates follow a joint multivariate normal distribution, which is only true for large sample sizes. In any case, such nonrectangular regions are difficult to visualize when more than two reconstruction scenarios have to be compared, unlike the rectangular Bonferroni-based regions. The interested reader will find a discussion on Bonferroni-based joint confidence regions and their attractive properties in Johnson and Wichern (Ref. 23, Sec. 5.4).
Because paired studies offer higher statistical power than unpaired studies, they should be considered whenever possible. The gain in statistical power results from two effects due to the pairing. First, more images are available to assess each scenario. Second, the pairing is likely to induce a positive correlation between the ratings associated to the scenarios under comparison. The Bonferroni-based confidence region approach makes full use of the first effect, but does not take advantage of large positive correlations in the ratings. One way to take advantage of large positive correlations between scenarios is to construct a nonrectangular confidence region, with the associated drawbacks discussed in the last paragraph. Another approach is to instead form a confidence interval for the difference of summary measures; see, e.g., Ref. 3 (Chap. 5). However, this approach typically requires an asymptotic normality assumption (which is not satisfied for small samples) to construct the confidence interval. In addition, the relative importance of an observed difference can be meaningfully interpreted only if the baseline is known, i.e, if the nominal value of one of the summary measures is known. As a concrete example, an observed gain in AUC value of 0.05 carries different meanings when the AUC value of the reference approach is 0.55 as opposed to 0.95; in the first case, the gain may seem marginal, whereas in the second case, it is as large as it could possibly be. For the example we used, the correlations between ratings can be shown to offer little benefit.
Finally, it should be emphasized that our choices for the task and for the observer in our image quality evaluation example were not optimal for image quality assessment in CT. There is large flexibility in the way that the task and the observer template may be defined. Investigation of more sophisticated tasks and observers suitable for CT images is an important topic for future research.
ACKNOWLEDGMENTS
This work was partially supported by NIH Grants R01 EB007236, R21 EB009168 and by a generous grant from the Ben B. and Iris M. Margolis Foundation. Its contents are solely the responsibility of the authors.
APPENDIX A: Proof of Theorem 1
Here, we prove Theorem 1, which characterizes when the rating data are normally distributed with equal variances for each class, i.e., and , for i = 1, 2,..., n1 and j = 1, 2,..., n2.
Part 1. Since and are independent, it follows that
| (A1) |
Also, since
| (A2) |
are independent, we have
| (A3) |
| (A4) |
where ν=n1+n2-2 and . The desired relation then follows from the definitions of η and .
Part 2. From Part 1 and the expression for the mean of a noncentral t random variable given in Eq. 2 , it is easy to see that is an unbiased estimator of SNR. The joint pdf of the rating data is
| (A5) |
After some algebra, one may show that
| (A6) |
for r = 1, 2. Using Eq. A6 and the definition of s2, we may rewrite Eq. A5 in the form
| (A7) |
By the Fisher–Neyman factorization theorem [Ref. 24, Theorem 6.5 (p. 35)] the statistic
| (A8) |
is sufficient. Moreover, because the expression in Eq. A7 has the form of a full rank exponential family,24(p. 23,24)W is a complete statistic [Ref. 24, Theorem 6.22 (p. 42)]. Since (i) W is a complete sufficient statistic, (ii) is an unbiased estimator of SNR, and (iii) , i.e., is a function of W only, the Lehmann–Scheffé theorem [Ref. 24, Theorem 1.11 (p. 88) and Ref. 25 (p. 164)] implies that is the unique UMVU estimator of SNR.
APPENDIX B: Proof of Theorem 2
Next, we prove Theorem 2 and Corollary 1, which enable us to calculate our ROC confidence intervals. For this task, we need the following lemmas.
Lemma 1. Suppose that . Then at arbitrary fixed values of t and ν, the cdf of T, FT(t;ν,δ), is a continuous, strictly decreasing function of δ.
Proof. Although this lemma seems like a property that should be well-known, we could not find any proof of it in the literature. One way to prove it is as follows.
From Ref. 15 (p. 514), the cdf for the noncentral t distribution may be written in the form
| (B1) |
Suppose that t and ν are fixed quantities and define h(δ)=FT(t;ν,δ). Making the change of variables in the inner integral of Eq. B1 yields
| (B2) |
By the combination of Tonelli’s theorem and Fubini’s theorem,26(Chap. 8) an interchange in the order of integration is justified, and the previous equation may be rewritten as
| (B3) |
where
| (B4) |
is an integrable function of y. The theorem on absolute continuity for the Lebesgue integral26(p. 141) applied to Eq. B3 implies that h(δ) is continuous. In addition, since g(y) is strictly positive, Eq. B3 indicates that h(δ) is a strictly decreasing function of δ.
Lemma 2. Let X be a continuous random variable with cdf, FX(x;θ), that is a strictly decreasing function of the parameter θ for each x. Also, let α1,α2∈(0,1) be such that α1+α2=α for some α∈(0,1). Suppose that, for each x in the sample space of X, the relations
may be solved for θL(x) and θU(x). Then the functions θL(x) and θU(x) are uniquely defined and the random interval [θL(X),θU(X)] is an exact 1-α confidence interval for θ.
Proof. See Ref. 4 [Theorem 9.2.12(p. 432)] for a proof and Ref. 17 (Sec. 11.4) for a complementary discussion.
Finally, we state a lemma that facilitates construction of a confidence interval for any parameter that is related to another through a strictly increasing transformation. It is a well-known property of confidence intervals that, as observed in Ref. 5, is rarely formalized.
Lemma 3. Let g(θ) be a continuous, strictly increasing function of θ. If [θL,θU] is a 1-α confidence interval for θ, then [g(θL),g(θU)] is a 1-α confidence interval for g(θ).
Proof. The assumptions on g imply that g−1 exists and is strictly increasing. Because both g and g−1 are strictly increasing functions, it follows that θ∈[θL,θU] if and only if g(θ)∈[g(θL),g(θU)], i.e., the two events are equivalent. Hence, P(g(θ)∈[g(θL),g(θU)])=P(θ∈[θL,θU])=1-α.
Combining the above results, it is straightforward to see that Theorem 2 follows from Theorem 1 and Lemmas 1, 2, and 3. Furthermore, it follows from our distributional assumptions that TPF, AUC, and pAUC are strictly increasing functions of SNR, and therefore, Theorem 2(ii) and Lemma 3 imply Corollary 1.
APPENDIX C: Proof of Theorem 3
Here, we prove Theorem 3, which enables estimation of a confidence band for the entire ROC curve from a confidence interval for SNR.
For any fixed value of FPF∈[0,1], define the function g(SNR) = TPF(FPF; SNR), where TPF is given by Eq. 3. Since g(SNR) is a continuous, strictly increasing function of SNR, its inverse, g−1(TPF), exists and is a strictly increasing function of TPF. Therefore, SNR∈[SNRL,SNRU] if and only if g(SNR)∈[g(SNRL),g(SNRU)]. Because this is true for any FPF∈[0,1], it follows that SNR∈[SNRL,SNRU] if and only if . Hence, for any value of SNR.
References
- Barrett H. H. and Myers K. J., Foundations of Image Science (John Wiley & Son, New York, 2004). [Google Scholar]
- Park S., Jennings R., Liu H., Badano A., and Myers K., “A statistical, task-based evaluation method for three-dimensional x-ray breast imaging systems using variable-background phantoms,” Med. Phys. 37(12), 6253–6270 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pepe M. S., The Statistical Evaluation of Medical Tests for Classification and Prediction (Oxford University Press, New York, 2003). [Google Scholar]
- Casella G. and Berger R. L., Statistical Inference, 2nd ed. (Duxbury, Belmont, CA, 2001). [Google Scholar]
- Steiger J. H. and Fouladi R. T., “Noncentrality interval estimation and the evaluation of statistical models,” in What if There Were No Significance Tests? edited by Harlow L. L., Mulaik S. A., and Steiger J. H. (Lawrence Erlbaum, Mahwah, NJ, 1997). [Google Scholar]
- Metz C. E., “Quantification of failure to demonstrate statistical significance: The usefulness of confidence intervals,” Invest. Radiol. 28(1), 59–63 (1993). 10.1097/00004424-199301000-00017 [DOI] [PubMed] [Google Scholar]
- Bamber D., “The area above the ordinal dominance graph and the area below the receiver operating characteristic graph,” J. Math. Psychol. 12, 387–415 (1975). 10.1016/0022-2496(75)90001-2 [DOI] [Google Scholar]
- Obuchowski N. A. and Lieber M. L., “Confidence intervals for the receiver operating characteristic area in studies with small samples,” Acad. Radiol. 5(8), 561–571 (1998). 10.1016/S1076-6332(98)80208-0 [DOI] [PubMed] [Google Scholar]
- Newcombe R. G., “Confidence intervals for an effect size measure based on the Mann-Whitney statistic. Part 2: Asymptotic methods and evaluation,” Stat. Med. 25, 559–573 (2006). 10.1002/sim.v25:4 [DOI] [PubMed] [Google Scholar]
- Ma G. and Hall W., “Confidence bands for receiver operating characteristic curves,” Med. Decis Making 13(3), 191–197 (1993). 10.1177/0272989X9301300304 [DOI] [PubMed] [Google Scholar]
- Macskassy S. A., Provost F., and Rosset S., “ROC confidence bands: An empirical evaluation,” in Proceedings of 22nd International Conference on Machine Learning Bonn, Germany, 2005, pp. 537–544.
- Godwin H. and Zaremba S., “A central limit theorem for partly dependent variables,” Ann. Math. Stat. 32(3), 677–686 (1961). 10.1214/aoms/1177704963 [DOI] [Google Scholar]
- Wang J., Lu H., Liang Z., Eremina D., Zhang G., Wang S., Chen J., and Manzione J., “An experimental study on the noise properties of x-ray CT sinogram data in Radon space,” Phys. Med. Biol. 53(12), 3327–3341 (2008). 10.1088/0031-9155/53/12/018 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gagne R. M., Gallas B. D., and Myers K. J., “Toward objective and quantitative evaluation of imaging systems using images of phantoms,” Med. Phys. 33(1), 83–95 (2006). 10.1118/1.2140117 [DOI] [PubMed] [Google Scholar]
- Johnson N. L., Kotz S., and Balakrishnan N., Continuous Univariate Distributions, 2nd ed. (John Wiley & Son, New York, 1995), Vol. 2. [Google Scholar]
- Lee W. C. and Hsiao C. K., “Alternative summary indices for the receiver operating characteristic curve,” Epidemiology 7(6), 605–611 (1996). [DOI] [PubMed] [Google Scholar]
- Bain L. J. and Engelhardt M., Introduction to Probability and Mathematical Statistics, 2nd ed. (Duxbury, 1992). [Google Scholar]
- Kak A. C. and Slaney M., Principles of Computerized Tomographic Imaging, Series. Classics in Applied Mathematics (SIAM, Philadelphia, PA, 2001), Vol. l3. [Google Scholar]
- Wunderlich A. and Noo F., “Image covariance and lesion detectability in direct fan-beam x-ray computed tomography,” Phys. Med. Biol 53(10), 2471–2493 (2008). 10.1088/0031-9155/53/10/002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Agresti A. and Coull B. A., “Approximate is better than “exact,” for interval estimation of binomial proportions,” Am. Stat. 52(2), 119–126 (1998). 10.2307/2685469 [DOI] [Google Scholar]
- QRM GmbH, http://www.qrm.de/. Last accessed May, 2011.
- Lilliefors H., “On the Kolmogorov-Smirnov test for normality with mean and variance unknown,” J. Am. Stat. Assoc. 62(318), 399–402 (1967). 10.2307/2283970 [DOI] [Google Scholar]
- Johnson R. A. and Wichern D. W., Applied Multivariate Statistical Analysis, 5th ed. (Prentice-Hall, Englewood Cliffs, NJ, 2002). [Google Scholar]
- Lehmann E. and Casella G., Theory of Point Estimation, 2nd ed. (Springer, New York, 1998). [Google Scholar]
- Poor H. V., An Introduction to Signal Detection and Estimation, 2nd ed. (Springer, New York, 1994). [Google Scholar]
- Jones F., Lebesgue Integration on Euclidean Space, Revised ed. (Jones and Bartlett, Sudbury, MA, 2001). [Google Scholar]