Two-dimensional and three-dimensional single-pixel and single-voxel speciation of Ni in Li-ion battery electrodes is accomplished combining full-field hard X-ray transmission microscopy and XANES imaging at tens of nanometers resolution.
Keywords: X-ray microscopy, synchrotron X-ray imaging, Li-ion battery, XANES
Abstract
The ability to probe morphology and phase distribution in complex systems at multiple length scales unravels the interplay of nano- and micrometer-scale factors at the origin of macroscopic behavior. While different electron- and X-ray-based imaging techniques can be combined with spectroscopy at high resolutions, owing to experimental time limitations the resulting fields of view are too small to be representative of a composite sample. Here a new X-ray imaging set-up is proposed, combining full-field transmission X-ray microscopy (TXM) with X-ray absorption near-edge structure (XANES) spectroscopy to follow two-dimensional and three-dimensional morphological and chemical changes in large volumes at high resolution (tens of nanometers). TXM XANES imaging offers chemical speciation at the nanoscale in thick samples (>20 µm) with minimal preparation requirements. Further, its high throughput allows the analysis of large areas (up to millimeters) in minutes to a few hours. Proof of concept is provided using battery electrodes, although its versatility will lead to impact in a number of diverse research fields.
1. Introduction
1.1. Background
Understanding nanoscale processes is critical towards understanding how materials operate. The vast majority of functional devices are composed of multiple phases in the form of hierarchical structures, and it is the interplay between the different components and their distribution that determines the final properties. Because these hierarchies are assembled at scales larger than a few nanometers, tools that can probe multiple levels of complexity are required to fully determine the parameters that control performance.
Imaging with high spatial resolutions can be achieved by the scanning of focused beams, and advances in both optics and source brightness have made available sub-micrometer probes such as soft X-ray scanning transmission X-ray microscopy (STXM) with sufficient flux for extraction of valuable information with reasonable exposures (de Smit et al., 2008 ▶; Macdonald et al., 2010 ▶; de Groot et al., 2010 ▶; Obst et al., 2009 ▶; Johansson et al., 2007 ▶; Hitchcock et al., 2003 ▶). The drawback of this scanning technique is that image build-up is performed pixel-by-pixel, with their dimensions being only a few tens of nanometers, thereby leading to prohibitive amounts of collection time to cover a field of view (FOV) of even just a few micrometers (Obst et al., 2009 ▶).
Electron microscopy, especially in transmission mode (Wang, 2003 ▶; Erni et al., 2009 ▶), can lead to a picture of chemical and structural diversity with even higher resolution. However, probing hierarchically structured materials using electron microscopy is difficult because the FOVs at the highest resolution and/or in tomographic three-dimensional mode (Bals et al., 2006 ▶) are, at best, of the order of a few hundreds of nanometers. In addition, because all these techniques work in vacuum, even when environmental chambers are employed, the design of experiments where measurements are performed during device operation (in situ) is challenging, especially if liquids are involved. Further, because electrons interact very strongly with matter and, hence, penetrate no more than a few tens of nanometers, only thin samples can be analyzed, which may be produced by ion-milling procedures that can induce irreversible alterations. In contrast, hard X-rays can penetrate through tens of micrometers of matter and are also sensitive to chemical and structural differences. Indeed, hard X-ray full-field transmission X-ray microscopy (TXM) has achieved resolutions as high as 40 nm (Chu et al., 2008 ▶) and 30 nm (Liu et al., 2011 ▶) with 15–30 µm FOV in a single exposure of a few minutes or even seconds, and even larger (up to millimeters) if multiple images are stitched together. Another unique capability of TXM is that the large depth of focus (tens of micrometers) enables the generation of three-dimensional images even for thick samples over the same large areas (Andrews et al., 2010 ▶).
Monitoring the modes of failure of functional materials during operation requires the ability to image changes at the chemical as well as the morphological level. Bulk X-ray absorption spectroscopy (XAS) measurements maintain sample integrity and can be used to follow the evolution of the redox states for a given material, even as it is being used in a device (McBreen, 2009 ▶; Singh et al., 2010 ▶). However, they only provide average chemical information over a relatively large volume. Electron microscopy coupled with electron energy-loss spectroscopy (EELS) can probe changes at the nanoscale after (and, in some limited instances, during) operation, but sample preparation requirements are incompatible with the analysis of architectures with complexity at the micrometer scale or larger. In consequence, as of today, there are no standard analytical techniques that are non-destructive and can enable multi-scale multi-dimensional chemical imaging of complex and large architectures. XANES TXM bridges this gap. It holds the promise of combining morphological imaging with chemical speciation (oxidation state and bonding) at nanoscale resolution, while gathering three-dimensional architectural visualization from much larger and thicker volumes than STXM or TEM (transmission electron microscopy). While XANES and hard X-ray full-field TXM are established techniques of their own, their combination and subsequent application to the study of large-scale (up to millimeters) complex systems at high resolutions (tens of nanometers) in three dimensions has so far been considered under development (Grunwaldt & Schroer, 2010 ▶). The capabilities of this unprecedented set-up are demonstrated here for the first time.
1.2. Overview of the three-dimensional XANES microscopy method
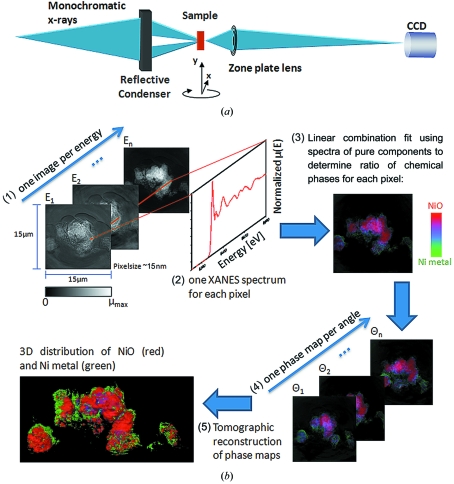
The concept of XANES microscopy is illustrated in Fig. 1 ▶. A series of single images is recorded upon sweeping the photon energy across the X-ray absorption edge of the element of interest (in this case Ni). Because zone plate focusing is energy dependent, zone plate refocusing is performed for each energy, and computationally challenging reference correction and image correlation are required. Refocusing introduces not only noticeable magnification changes between images recorded at different energies, but also misalignment of the imaged FOV owing to finite motor precision. Further misalignment owing to motor precision is caused by the need to move the sample to record a reference image at each energy value for background correction and photon flux normalization. While magnification correction can be easily implemented by rescaling images according to theoretical changes in magnification, image registration algorithms to correct misalignment must be fast, robust and provide sufficient precision to sustain the resolution of the microscope.
Figure 1.
Microscope set-up and principles of data processing for three-dimensional XANES microscopy. (a) A monochromatic X-ray beam is focused onto the sample using an elliptical capillary and the image is projected onto the detector (Peltier-cooled 2 K × 2 K pixel array Retiga CCD) by means of a micro-zone plate lens. The sample is mounted on an X, Y, Z, θ stage. Details can be found by Andrews et al. (2010 ▶). (b) (1) One image is acquired in absorption contrast at each energy in the XANES scan. (2) XANES are constructed from each pixel plotting normalized absorption versus energy. (3) XANES from each pixel is fit to create a chemical phase map. (4) One phase map is generated at each angle in the tomographic scan. (5) The set of phase maps is used for tomographic reconstruction to retrieve three-dimensional chemical speciation.
After this initial processing the intensity change of each pixel as a function of energy provides XANES spectra, which can be fit with known reference compounds using a least-squares method. The resulting combination of chemical phases for each pixel can be expressed in a two-dimensional color map. In turn, the collection of two-dimensional chemical maps at different sample-beam angles (Fig. 1 ▶) allows tomographic reconstruction with three-dimensional chemical speciation, thereby extending work in previous related reports where only three-dimensional elemental information was obtained for Ni distribution in fuel cell electrodes by difference mapping, or imaging above and below the absorption edge (Izzo et al., 2008 ▶; Grew et al., 2010 ▶), hence collecting data at significantly fewer energy values. Similarly, STXM difference mapping of Ca and C (Obst et al., 2009 ▶; Johansson et al., 2007 ▶) has been used for elemental mapping of Ca, and to distinguish between two chemically very different species of carbon. The addition of chemical speciation at this resolution on micrometer-scale (and up to millimeter-sized) structures within time scales of minutes (for two-dimensional mapping of a single FOV) to a few hours (single FOV three-dimensional mapping) is unique to the full-field XANES imaging method presented in this paper, and will provide needed insight into the nanoscale variability of large portions of composite systems. This method also eliminates the need for previous knowledge to select adequate energy values, particularly important if the species to be identified have close edge structures (e.g. more than one speciation state of a single element in the same structure) or if unknown species of the element are present. The possibility to identify unknown chemical phases in the sample is a major advantage of this method as this is only possible if a full XANES spectrum is provided for each pixel.
The design of algorithms for full-field XANES image data processing is a non-trivial task when the samples are composed of a random collection of particles without sharp edges, whose luminosity varies in an undefined way as the energy is changed. In addition, each two-dimensional image contains one million pixels (less after filtering), resulting in a very demanding need for computation time. The absence of a solution to this problem to date (Grunwaldt & Schroer, 2010 ▶) is the reason why chemical images from TXM have not been reported until now, and is one of the technical developments achieved in this work.
2. Experiment
2.1. Instrument
Measurements were performed at wiggler beamline 6-2 at the Stanford Synchrotron Radiation Lightsource (SSRL) at the SLAC National Accelerator Laboratory (California, USA) using an Xradia transmission X-ray microscope. This microscope is equipped with optics optimized for photon energies ranging from ∼5 to 14 keV, provides a spatial resolution as high as 30 nm and a single flat field of view of 15 µm × 15 µm or 30 µm × 30 µm, depending on the chosen magnification (10× or 20×). Depth of focus is ∼50 µm. More details about the instrument can be found by Andrews et al. (2010 ▶) and Liu et al. (2011 ▶).
2.2. Sample preparation
The Li-ion composite electrodes were films composed of NiO (99%, Alfa Aesar), acetylene black (Chevron Phillips Chemical Company) and polyvinylidene fluoride (PVDF; Kureha Corporation) in a weight ratio of 77:13:10, cast onto copper foil. Electrochemical cycling was carried out in a 2032 coin cell (Hohsen Corporation) with Li metal foil (>99.8%, Chemetall) as a counterelectrode. The separator was a polypropylene membrane (Celgard 2400) soaked in a 1 M LiPF6 solution in 1:2 (v/v) ethylene carbonate:dimethylcarbonate (DMC). The electrodes were cycled at C/5 rate (full reduction of NiO to Ni in 5 h), and subsequently recovered and washed with anhydrous DMC (≥99%; Sigma Aldrich) to eliminate electrolyte impurities. Finally, the electrodes were hot sealed into a polypropylene pouch to prevent contact with air during measurement. Samples were prepared at various states of charge and discharge as indicated in Fig. 3. All sample manipulation prior to transport to the beamline hutch was performed in a He-filled glove box (<2 p.p.m. O2).
2.3. Experimental parameters
Two-dimensional XANES images [5–30 s exposure time, pixel size 0.016–0.032 µm, depending on binning, image size 1024 × 1024 pixels (for binning of 2), FOV 16.4 µm × 16.4 µm] were collected from 8250 to 8600 eV (energy resolution of the beamline, ΔE/E = 10−4), in 154 steps with varying energy interval across the Ni K-edge at 8333 eV, with spectral sampling of 0.5 eV in the immediate edge region. The zone plate was adjusted to maintain focus, ∼3 µm eV−1. Reference images were recorded at each energy within 1–2 s of the sample image to account for changes in flux and small beam instabilities. The (fully automated) two-dimensional XANES measurement of a single FOV can be accomplished within several minutes to 1 h. Further time reduction can be achieved by limiting the number of energy points to the minimum necessary to discriminate different chemical phases, which, in turn, requires a priori knowledge of the chemical phases present in the sample. The two chemical phases present (NiO and Ni) were fit to XANES spectra (collected by the same method but averaged from a full FOV) of pure NiO (from pristine electrode sample P, which contains pure NiO) and pure Ni metal (obtained from fully reduced sample R2). The Ni metal XANES from sample R2 were almost identical to those from XANES imaging of 10 µm-thick Ni wire (also averaged from a full FOV).
Three-dimensional chemical imaging was performed from −67 to 67°, in 1° steps. Tomography was acquired at 13 distinct energy points, identified from the two-dimensional XANES to have significantly different absorption values for NiO and Ni. The (fully automated) measurement of three-dimensional XANES was accomplished within 17.5 h. XANES spectra acquired before and after this radiation exposure were consistent within 7%, which is less than the experimental error of 8% (determined from repetitive two-dimensional measurements), confirming no radiation damage to the sample.
2.4. Data analysis
The tri-color maps containing red (NiO), green (Ni) and blue from the two-dimensional chemical images obtained at each angle were reconstructed using algebraic reconstruction techniques applying an iterative method (Liu et al., 2007 ▶). After determining the amount of NiO or Ni present in each pixel based on the fraction from least-squares fitting, plus the relative concentration from the edge-jump map, the three-dimensional distribution of NiO (red) and Ni (green) were each reconstructed separately, and joined together for the final rendering of three-dimensional volume and slices. Rendering was accomplished using the AVIZO Fire software package. The blue component in the reconstructed figure was rendered as a cloud and contains all voxels showing 50% Ni and 50% NiO. This was done to highlight areas corresponding to the intermediate step of the phase transformation from NiO to Ni [see color bar in Fig. 1(b)-(3) ▶]. In the two-dimensional distribution maps for red, green and blue (NiO, Ni metal, 50:50 ratio) the edge-jump height (Ni concentration) was considered. However, in the three-dimensional rendering a threshold for concentration was used to define the isosurface.
All data processing for two-dimensional chemical maps, except for SIFT alignment of images (Vedaldi & Fulkerson, 2006 ▶), was performed using a self-developed code written in the MATLAB programming language. The chemical phase maps were generated in a seven-step process of (1) rescaling and image alignment, (2) filtering to remove spectra with low signal-to-noise ratios, (3) determination of edge energies, (4) construction of spectra for pure compounds, (5) least-squares fitting, (6) pixel rendering as red, green or blue based on speciation, and (7) correction for total Ni absorption per pixel.
2.4.1. Step 1: correction of magnification and misalignment
The magnification of the transmission X-ray microscope is energy dependent. Therefore, the images were rescaled (using bicubic interpolation) to the smallest FOV (lowest energy) using the theoretical magnification change calculated for each recorded energy. To correct for positioning errors of the motor stages of optics and sample, the images of each energy scan were aligned. For this alignment single-pixel precision is desirable because XANES spectra are generated for each pixel of the image set, and the final resolution of the result is therefore limited by the quality of the alignment. Two different alignment algorithms which should provide the demanded precision were tested: Fast-Fourier-Transform-based phase correlation, and scale invariant feature transform (SIFT) alignment (Vedaldi & Fulkerson, 2006 ▶). The results produced by these two methods showed no relevant differences, proving their applicability and robustness. After alignment, the XANES were obtained as the intensity value versus energy for each pixel, resulting in more than 1 million spectra (1024 × 1024 pixels) per image, and accordingly more for a three-dimensional reconstruction using one image per angle.
2.4.2. Step 2: determination of edge jump and noise filtering
Pixels with poor XANES signal-to-noise (S/N) ratios owing to weak absorption (e.g. areas with little or no sample) were filtered using the absorption-edge jump, defined as the difference between the average intensity value in the post-edge region (8408–8600 eV) and the average intensity value in the pre-edge region (8250–8322 eV). Pixels with edge jumps greater than four times their pre-edge standard deviation were removed (i.e. set to zero intensity). Relevant information about the samples is obtained during this step because the magnitude of the edge jump is proportional to the total Ni concentration. After filtering, background removal and normalization were performed on all spectra.
2.4.3. Step 3: determination of edge energy
The energy position of the Ni absorption edge was determined by linear interpolation for each of the filtered pixels as the energy where the absorption values of the XANES was half of the edge-jump intensity as defined in step 2. The edge position appears at higher energies for NiO than for Ni, and, therefore, a map of the edge jump provides initial information on the location of redox fronts.
2.4.4. Step 4: extract principle components from standard samples
The method described in step 3 was applied to the samples showing pure phases: NiO for sample P (the pristine electrode) and Ni for sample R2 (reduced to 0 V). All pixels showing the same edge energy were then pooled (clustered) to further increase the XANES S/N ratio. The XANES features of these spectra (Fig. 2d ▶) were found to be in excellent agreement with literature data (Boyanov & Segre, 2008 ▶) of bulk NiO and Ni, which, together with the good S/N ratios, validates the use of these spectra, representing start and end products of the Ni reduction process, as standards in step 5.
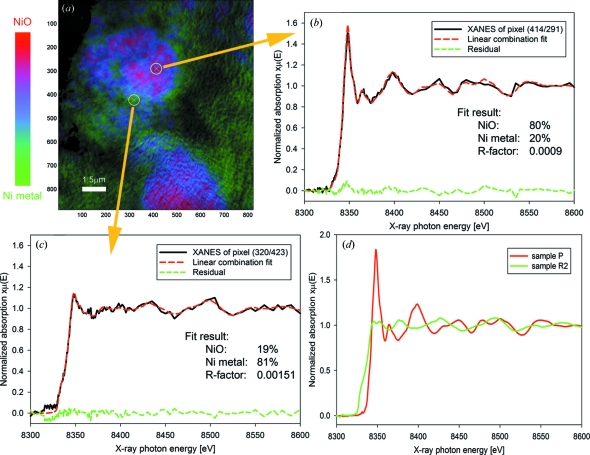
Figure 2.
(a) Chemical RGB phase map for Li-ion battery electrode sample R1 (red = NiO, green = Ni, blue = mixed states); (b), (c) XANES from two arbitrarily selected pixels with linear combination fit result, residual and quality of fit R-factor. (b) XANES showing 80% NiO, 20% Ni. (c) XANES showing 19% NiO and 81% Ni. (d) XANES for NiO and Ni standards: normalized absorption versus achieved energy for pristine electrode (pure NiO) and reduced electrode R2 (pure Ni).
2.4.5. Step 5: least-squares linear combination fitting
In this step all images recorded for all samples (including samples P and R2 to double check the robustness of the method) were processed by performing a least-squares linear combination (LC) fit of the standard Ni metal and NiO XANES (created in step 4) to the XANES of each pixel, providing the NiO to Ni metal ratio for each pixel. The quality of each LC fit was checked using the R-factor commonly used for XANES fitting and defined as
R-factors were found to be below 0.05 for almost all pixels, with higher values being found in regions of weak absorption (lower S/N ratios). However, because step 7 (below) accounts for such pixels using their intensity as a weighing function, no additional R-factor filter was applied.
2.4.6. Step 6
Pixel rendering as red, green or blue based on speciation is described above, and in §3.2 below.
2.4.7. Step 7: correction of pixel intensities
To account for absorption differences owing to higher or lower Ni concentration at each pixel, the height of the Ni edge jump, determined as described in step 2 above and further normalized to values between 0 and 1, was used to correct pixel intensities, therefore representing total Ni absorption in the final images.
3. Results
3.1. Two dimensional single-pixel XANES imaging of Li-ion battery electrodes
The power of the TXM XANES method is best illustrated for complex hierarchical structures such as those found in Li-ion battery electrodes. These electrodes are usually composites of the active material with carbon and a polymer binder to form a flexible film that is several tens of micrometers thick, in which homogeneity and porosity are the key for good electrical contact, electrolyte wetting and mechanical properties (Guy et al., 2004 ▶). Here we chose NiO, currently considered for the Li-ion battery anode because of its very high charge storage capability (Cabana et al., 2010 ▶), as a model system. In previous studies, electron microscopy data were used to prove that, in a Li battery, NiO reduces to Ni and Li2O through a reversible conversion reaction (Poizot et al., 2000 ▶; Varghese et al., 2008 ▶), resulting in only two Ni-containing phases in the system. In a representative two-dimensional chemical speciation map in which the electrode reaction is completed halfway (Fig. 2a ▶), the resulting ratio of the two phases is expressed for each pixel in a red (NiO) to green (Ni) scale RGB image. The existence of only these two phases was confirmed with separate XAS measurements (data not shown). The blue pixels in these maps highlight areas where both phases are present, and the blue color is purest for states with a 1:1 NiO:Ni ratio. The XANES spectra and fit results for two arbitrarily selected pixels from Fig. 2(a) ▶ are shown in Figs. 2(b) and 2(c) ▶; the R-factor, commonly used as a quality-of-fit parameter for XANES fitting (Ravel & Newville, 2005 ▶), is included. XANES spectra for pure NiO and Ni metal are shown in Fig. 2(d) ▶. This two-dimensional XANES method permits the production of spectra from single pixels (∼15 nm × 15 nm) and therefore for features down to 30 nm × 30 nm, the current spatial resolution of the microscope (Liu et al., 2011 ▶). With relatively short collection times (up to 30 min for a fully resolved XANES spectrum), two-dimensional XANES imaging is ideally suited for the probing of chemical changes within complex systems over large areas. In our work, each FOV is 15 µm × 15 µm, and several can be collected via mosaic imaging while keeping data collection times to minutes.
3.2. Chemical speciation of NiO and Ni in various states of charge
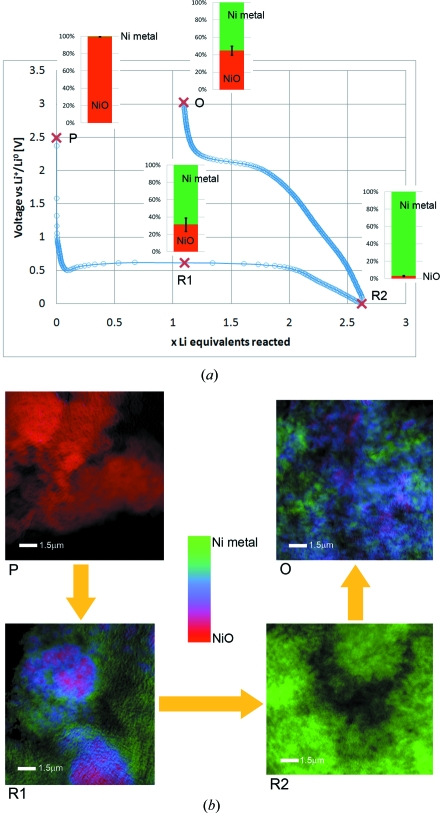
Two-dimensional and three-dimensional XANES microscopy can be used to identify nanoscale chemical and morphological changes that occur during the electrochemical reduction and re-oxidation of NiO. Chemical phase distribution was mapped in two and three dimensions from NiO electrodes in various states during the first cycle of operation in a Li battery, which is depicted in Fig. 3(a) ▶ as a voltage–charge (defined in Li, or electron, equivalents) trace. A set of two-dimensional chemically resolved maps show the distribution of NiO and Ni in several ex situ samples collected during the first discharge (reduction) and charge (oxidation) as well as changes in morphology (Fig. 3b ▶). The corresponding NiO:Ni ratios displayed next to each point in Fig. 3(a) ▶ were determined from these phase maps (Fig. 3b ▶) by XANES fitting and averaging of all non-zero values in each image recorded for corresponding samples (see §2.4.5). Error estimates for NiO:Ni ratios were derived as the standard deviation of average values calculated for multiple images recorded for different areas of the same sample. During discharge, pristine NiO (sample P) is progressively reduced to Ni and Li2O, the footprint being a long plateau at ∼620 mV. The XANES images show an obvious change in morphology as large NiO agglomerates are electrochemically ground into very small particles of either reduced Ni or NiO (sample R1). Previous studies of this reaction using TEM have shown that the metallic nickel particles can be less than 10 nm in size (Poizot et al., 2000 ▶; Varghese et al., 2008 ▶). After two Li equivalents have reacted, the reaction is considered complete and the additional charge is associated with Faradaic processes of electrolyte decomposition and/or to capacitive interfacial storage (Cabana et al., 2010 ▶). Accordingly, a sample at full discharge (R2) is composed solely of Ni nanoparticles and the initial texture is completely lost. When the polarization is reversed, the potential progressively increases and Ni is subsequently re-oxidized to NiO. Nonetheless, the reaction is not complete even at a very high potential of 3 V (sample O), where a mixture of Ni and NiO particles is still observed. This observation is consistent with the fact that only approximately 55% of the capacity at the end of discharge is recovered upon charge, which provides clear visual proof that this lack of reaction reversibility is one of the origins of the very large coulombic inefficiencies that are systematically observed for electrode materials that react through similar mechanisms (Cabana et al., 2010 ▶). It should be noted that the initial morphology (see sample P versus sample O) is not recovered upon re-formation of NiO and the texture remains fine-grained. Therefore, two-dimensional XANES microscopy provides valuable insight into the morphological as well as chemical changes that are introduced during this conversion reaction.
Figure 3.
(a) Trace of the first discharge/charge cycle of a NiO electrode in a Li battery, with bars indicating NiO/Ni ratios determined from the chemical phase maps of several ex situ samples, shown in (b). NiO/Ni ratios were determined for each phase map as the average over all pixels in the image. Multiple single FOV images (tiles of mosaic images, not shown) were included to determine error bars (N = 2, 6, 4 and 4 for samples P, R1, R2 and O, respectively). (b) Corresponding chemical RGB phase maps (red = NiO, green = Ni, blue = mixed states) for samples P (pristine electrode), R1 (partially reduced), R2 (fully reduced to Ni) and O (re-oxidized).
3.3. Three-dimensional XANES imaging
Within a two-dimensional transmission image, multiple particles through the full sample thickness contribute to the X-ray attenuation (and XANES) within a single pixel. With the addition of three-dimensional capability, both morphology and chemical speciation are obtained for a given large volume, avoiding overlap of contributions to the attenuation and providing the opportunity to probe the sample at different depths. Previous studies using methods such as Fourier shell correlation (Cardone et al., 2005 ▶) or Fourier ring correlation (Schneider et al., 2010 ▶) indicate that the final three-dimensional resolution is expected to be of the order of double the resolution achieved in two dimensions, or about 60–70 nm.
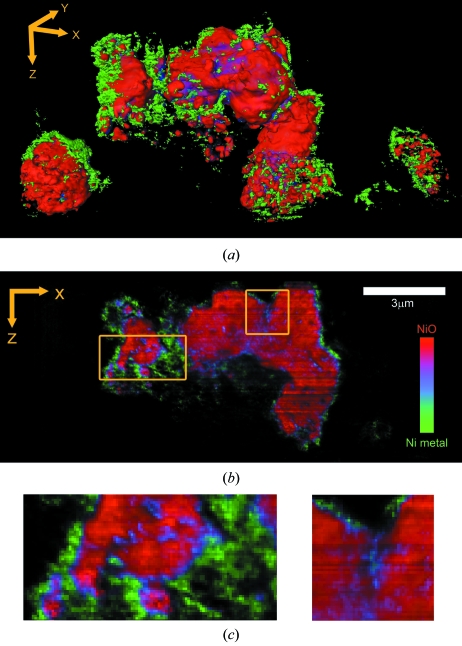
The three-dimensional capability of the XANES microscope is shown for sample R1. The measurement was performed for a large particle agglomerate (Fig. 4a ▶, center) and two smaller ones (lower left- and right-hand corner). (See also the supplementary video.1) A comparison of the different sized particles provides insight into the conversion of NiO to Ni during the discharge process. While the smallest particle (right) is homogeneously converted, the transformation of the larger particles is concentrated around the edges. More detailed insight into the chemical phase transformation that occurs during the electrochemical reduction of NiO by Li can be obtained by analyzing slices of single voxel thickness (Figs. 4b and 4c ▶). This feature is particularly useful when probing depth-dependent chemical and morphological characteristics in the sample. Some of the reconstructed slices clearly revealed that, while conversion to Ni is extensive at the surface of the larger agglomerate, it can also happen through cracks that go through the interior of the grain. This is particularly evident in the blue area of Fig. 4(c) ▶ (right-hand side). The large volume expansion that is associated with the reduction process introduces large strains in these confined spaces, and, hence, it appears to contribute to the process that breaks down large NiO grains and dramatically alters the morphology of the electrode. In fact, it is likely that the fine grains of NiO observed in the smallest particle are already the end result of such a process of electrochemical grinding. This observation also implies that pores between and within particles/agglomerates are large enough for the electrolyte to penetrate, and provides direct evidence of the critical role of open spaces within the composite architecture of a Li-ion battery electrode (Zheng et al., 2010 ▶).
Figure 4.
Reconstructed three-dimensional XANES tomography data of sample R1. (a) Perspective rendering of three-dimensional data set of electrode sample R1. (b) Single slice of the three-dimensional data set. (c) Selected areas from (b) are shown zoomed 3×.
4. Discussion
Because battery electrodes and other catalytic systems have hierarchical structures, e.g. the overall size of the different agglomerates ranges from 1 to 5 µm, and the open spaces are rather smaller, all these observations would not be possible without the high resolution and large FOV of the XANES microscope. At the same time, the size of these agglomerates is much larger than the limits of observation that can be achieved with STXM [typically 20 × 20 pixels (Beale et al., 2010 ▶), which are typically up to 3 µm (Obst et al., 2009 ▶)] or with electron tomography (Bals et al., 2006 ▶), typically a few tens of nanometers, because of the option to image relatively quickly over large single or multiple FOVs. Even if larger FOVs could be achieved with STXM, the scanning character of the probe, as opposed to the full field of XANES TXM, would lead to total collection times that would be orders of magnitude longer than we achieved during our work, making its application prohibitive. As an example, Obst et al. (2009 ▶) report collection times of several hours to collect 3 µm × 3 µm two-dimensional XANES images of cyanobacteria using STXM. As a consequence, chemical resolution in three-dimensional STXM imaging was achieved by selecting a limited number of energy values, thereby requiring previous knowledge of the system and reducing the capability to resolve species with close XANES signatures. In addition, sample preparation and thickness requirements for STXM, as well as the requirement that the order-sorting aperture be prohibitively close to the sample (Warwick et al., 1998 ▶), severely handicap the ability to analyze complex samples such as real battery electrodes, and the intricate porous architecture formed by the active material and the different additives has length scales that span to micrometers and even millimeters. Therefore, XANES microscopy is well placed to make an impact in our understanding of battery operation in the very near future.
In contrast, minimization of radiation damage, especially for biological samples, has been cited as an advantageous feature of STXM precisely because it relies on soft X-rays, illuminating only one small spot at a time (Johansson et al., 2007 ▶). In this work, XANES fits were consistent within 7% (less than the experimental error) for spectra collected before and after 12 h of imaging, with beam illuminating the full FOV. Photochemical effects can be further minimized by decreased acquisition times via the use of improved optics, and also by choosing fewer energy points for tomography for three-dimensional XANES. (A minimum of three energies would be required for the NiO/Ni system, and more would be required for more complex systems.) Hence, for inorganic materials such as those examined here, radiation damage is likely to be less of an issue.
The chemical information obtained using this technique can be combined with the characterization of morphology and porosity, making it an ideal means for investigating nanoscale reactions and phase transformations in complex systems. Further improvements can be envisaged in which the collection process is optimized to reduce the measurement time even further. These features certainly enable the design of experiments aimed at the evaluation of dynamic changes occurring in real time during a chemical reaction or the operation of a material, for instance, in a battery electrode, in which a full cycle of discharge/charge is normally completed within several hours. Indeed, in situ two-dimensional TXM imaging has already been used to track microstructural evolution in single particles or aggregates in a Sn electrode during electrochemical cycling (Chao et al., 2010 ▶), but the results did not include any chemical speciation. The large distance from the sample to the zone plate for TXM (∼26 mm) would facilitate rotation of an operating battery cell at the sample stage for in situ three-dimensional imaging. Combined with the possibility of short data collection times, three-dimensional chemical speciation of in situ reactions is certainly possible within the near future. Achievements in this direction are currently being actively pursued and certainly constitute the next frontier for this powerful technique.
5. Conclusions
The data presented in this paper clearly indicate the unique power of three-dimensional XANES microscopy for producing high-quality spectra for single voxels, down to 30 nm × 30 nm × 30 nm in a FOV of 15 µm × 15 µm × 15 µm or 30 µm × 30 µm × 30 µm. Because mosaics of different tomographic images can be collected and stitched together, the analyzed areas can easily be increased to hundreds of micrometers by hundreds of micrometers, e.g. 250 µm × 250 µm or larger. Broadly speaking, three-dimensional XANES microscopy is a unique tool that combines unprecedented spatial and energy resolution with large FOVs and fast acquisition in a virtually limitless variety of samples. It is certain to have an overarching impact, as we anticipate its use to monitor an array of phenomena in a variety of functional materials, in fields as diverse as energy storage, environmental science, biomedicine and archaeology.
Supplementary Material
Reconstructed three-dimensional XANES tomography data of electrode sample R1. DOI: 10.1107/S0909049511019364/ie5055sup1.mpg
Acknowledgments
We acknowledge Martin George and Sean Brennan of SSRL, and Jeff Gelb and others from Xradia for their assistance interfacing microscope software with optics motors for XANES imaging. JC acknowledges funding support for the 2D work on full electrodes by the Assistant Secretary for Energy Efficiency and Renewable Energy (Office of Vehicle Technologies of the US Department of Energy) under contract number DE-AC02-05CH11231, and for the 3D XANES microscopy as part of the Northeastern Center for Chemical Energy Storage, an Energy Frontier Research Center funded by the US Department of Energy (Office of Science, Office of Basic Energy Sciences) under award number DE-SC0001294. He is also thankful to Dr Marca M. Doeff (LBNL) for providing laboratory access. The transmission X-ray microscope at SSRL has been supported by the National Institutes of Health (NIH)/National Institute of Biomedical Imaging and Bioengineering (NIBIB) grant number 5R01EB004321. SSRL is supported by the Department of Energy, Office of Basic Energy Sciences.
Footnotes
Supplementary data for this paper are available from the IUCr electronic archives (Reference: IE5055). Services for accessing these data are described at the back of the journal.
References
- Andrews, J. C., Almeida, E., van der Meulen, M. C. H., Alwood, J. S., Lee, C., Liu, Y., Chen, J., Meirer, F., Feser, M., Gelb, J., Rudati, J., Tkachuk, A., Yun, W. & Pianetta, P. (2010). J. Microsc. Microanal. 16, 327–336. [DOI] [PMC free article] [PubMed]
- Bals, S., Van Tendeloo, G. & Kisielowski, C. (2006). Adv. Mater. 18, 892–895.
- Beale, A. M., Jacques, S. D. & Weckhuysen, B. M. (2010). Chem. Soc. Rev. 39, 4656–4672. [DOI] [PubMed]
- Boyanov, B. & Segre, C. (2008). Farrell Lytle Database, http://ixs.iit.edu/database/data/Farrel_Lytle_data.
- Cabana, J., Monconduit, L., Larcher, D. & Palacín, M. R. (2010). Adv. Mater. 22, E170–E192. [DOI] [PubMed]
- Cardone, G., Grünewald, K. & Steven, A. C. (2005). J. Struc. Biol. 151, 117–129. [DOI] [PubMed]
- Chao, S.-C., Yen, Y.-C., Song, Y.-F., Chen, Y.-M., Wu, H.-C. & Wu, N.-L. (2010). Electrochem. Commun. 12, 234–237.
- Chu, Y. S., Yi, J. M., De Carlo, F., Shen, Q., Lee, W. K., Wu, H. J., Wang, C. L., Wang, J. Y., Liu, C. J., Wang, C. H., Wu, S. R., Chien, C. C., Hwu, Y., Tkachuk, A., Yun, W., Feser, M., Liang, K. S., Yang, C. S., Je, J. H. & Margaritondo, G. (2008). Appl. Phys. Lett. 92, 103119.
- Erni, R., Rossell, M. D., Kisielowski, C. & Dahmen, U. (2009). Phys. Rev. Lett. 102, 027201. [DOI] [PubMed]
- Grew, K. N., Chu, Y. S., Yi, J., Peracchio, A. A., Izzo, J. R. Jr, De Carlo, F., Hwu, Y. & Chiu, W. K. S. (2010). J. Electrochem. Soc. 157, B783–B792.
- Groot, F. M. de, de Smit, E., van Schooneveld, M. M., Aramburo, L. R. & Weckhuysen, B. M. (2010). Chem. Phys. Chem. 11, 951–962. [DOI] [PubMed]
- Grunwaldt, J. D. & Schroer, C. G. (2010). Chem. Soc. Rev. 39, 4741–4753. [DOI] [PubMed]
- Guy, D., Lestriez, B. & Guyomard, D. (2004). Adv. Mater. 16, 553–557.
- Hitchcock, A. P., Araki, T., Ikeura-Sekiguchi, H., Iwata, N. & Tani, K. (2003). J. Phys. IV Fr. 104, 509–512.
- Izzo, J. R., Joshi, A. S., Peracchio, A. A., Grew, K. N., Chiu, W. K. S., Tkachuk, A. T., Wang, S. H. & Yun, W. (2008). J. Electrochem. Soc. 155, B504–B508.
- Johansson, G. A., Tyliszczak, T., Mitchell, G. E., Keefe, M. H. & Hitchcock, A. P. (2007). J. Synchrotron Rad. 14, 395–402. [DOI] [PubMed]
- Liu, Y., Andrews, J. C., Wang, J., Meirer, F., Zhu, P., Wu, Z. & Pianetta, P. (2011). Opt. Express, 19, 545. [DOI] [PMC free article] [PubMed]
- Liu, Y. J., Zhu, P. P., Chen, B., Wang, J. Y., Yuan, Q. X., Huang, W. X., Shu, H., Li, E. R., Liu, X. S., Zhang, K., Ming, H. & Wu, Z. Y. (2007). Phys. Med. Biol. 52, L5–L13. [DOI] [PubMed]
- McBreen, J. (2009). J. Solid State Electrochem. 13, 1051–1061.
- Macdonald, D., Rougieux, F., Mansoulie, Y., Tan, J. S., Paterson, D., Howard, D. L., de Jonge, M. D. & Ryan, C. G. (2010). Phys. Status Solidi A, 207, 1807–1810.
- Obst, M., Wang, J. & Hitchcock, A. P. (2009). Geobiology, 7, 577–591. [DOI] [PubMed]
- Poizot, P., Laruelle, S., Grugeon, S., Dupont, L. & Tarascon, J. M. (2000). Nature (London), 407, 496–499. [DOI] [PubMed]
- Ravel, B. & Newville, M. (2005). J. Synchrotron Rad. 12, 537–541. [DOI] [PubMed]
- Schneider, G., Guttmann, P., Heim, S., Rehbein, S., Mueller, F., Nagashima, K., Heymann, J. B., Müller, W. G. & McNally, J. G. (2010). Nat. Methods, 7, 985–987. [DOI] [PMC free article] [PubMed]
- Singh, J., Lamberti, C. & van Bokhoven, J. A. (2010). Chem. Soc. Rev. 39, 4754–4766. [DOI] [PubMed]
- Smit, E. de, Swart, I., Creemer, J. F., Hoveling, G. H., Gilles, M. K., Tyliszczak, T., Kooyman, P. J., Zandbergen, H. W., Morin, C., Weckhuysen, B. M. & de Groot, F. M. (2008). Nature (London), 456, 222–225. [DOI] [PubMed]
- Varghese, B., Reddy, M. V., Yanwu, Z., Lit, C. S., Hoong, T. C., Rao, G. V. S., Chowdari, B. V. R., Wee, A. T. S., Lim, C. T. & Sow, C. H. (2008). Chem. Mater. 20, 3360–3367.
- Vedaldi, A. & Fulkerson, B. (2006). SIFT for MATLAB, http://www.vlfeat.org/.
- Wang, Z. L. (2003). Adv. Mater. 15, 1497–1514.
- Warwick, T., Franck, K., Kortright, J. B., Meigs, G., Moronne, M., Myneni, S., Rotenberg, E., Seal, S., Steele, W. F., Ade, H., Garcia, A., Cerasari, S., Denlinger, J., Hayakawa, S., Hitchcock, A. P., Tyliszczak, T., Kikuma, J., Rightor, E. G., Shin, H.-J. & Tonner, B. P. (1998). Rev. Sci. Instrum. 69, 2964–2973.
- Zheng, H., Liu, G., Song, X., Ridgway, P., Xun, S. & Battaglia, V. S. (2010). J. Electrochem. Soc. 157, A1060–A1066.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Reconstructed three-dimensional XANES tomography data of electrode sample R1. DOI: 10.1107/S0909049511019364/ie5055sup1.mpg