A non-linear finite-element model of the newborn ear canal

Abstract

We present a three-dimensional non-linear finite-element model of a 22-day-old newborn ear canal. The geometry is based on a clinical X-ray CT scan. A non-linear hyperelastic constitutive law is applied to model large deformations. The Young’s modulus of the soft tissue is found to have a significant effect on the ear-canal volume change, which ranges from approximately 27% to 75% over the static-pressure range of ±3 kPa. The effects of Poisson’s ratio and of the ratio C₁₀:C₀₁ in the hyperelastic model are found to be small. The volume changes do not reach a plateau at high pressures, which implies that the newborn ear-canal wall would not be rigid in tympanometric measurements. The displacements and volume changes calculated from the model are compared with available experimental data.

I. INTRODUCTION

Children whose hearing loss is identified and corrected within six months of birth are likely to develop better language skills than children whose hearing loss is detected later (Yoshinaga-Itano et al., 1998). It is recommended that all infants be screened for hearing loss before the age of three months (NIDCD, 1993; Joint Committee on Infant Hearing, 2000).

Although hearing loss is one of the most frequently occurring disorders in newborns, early diagnosis is difficult. Auditory brain-stem response (ABR) screening tests and otoacoustic emissions (OAE) tests can provide objective hearing-loss assessments. Neither test, however, can distinguish conductive hearing loss, which in newborns is often transient, from sensorineural hearing loss. The two types of hearing loss require different medical approaches.

Tympanometry is a fast and simple hearing test routinely used in clinics for the evaluation of conductive hearing loss. Tympanometry involves the measurement of the acoustic admittance of the middle ear in the presence of a range of static pressures. In order to obtain an accurate result for the middle-ear admittance as seen from the tympanic membrane, the complex admittance measured at the probe tip must be adjusted to compensate for the complex admittance due to the ear-canal volume between the probe tip and the tympanic membrane. The accuracy of the middle-ear admittance estimate therefore relies on obtaining an accurate estimate of the admittance of the enclosed air volume.

Studies have shown that middle-ear admittance measurements differ significantly between newborns and adults, in both low-frequency (226 Hz) and higher-frequency (e.g., 1 kHz) tympanometry (Paradise et al., 1976; Holte et al., 1990, 1991; Keefe et al., 1993; Keefe and Levi, 1996; Shahnaz, 2002; Polka et al., 2002; Margolis et al., 2003; Margolis and Hunter, 1999). Holte et al. (1990) measured ear-canal wall movement in newborns of different ages and found that the diameter of the ear canal can change by up to 70% in response to high static pressures. Keefe et al. (1993) measured ear-canal reflectance over a wide frequency range. They concluded that significant differences between newborn and adult tympanograms are presumably due in part to the incomplete development of the newborn ear-canal wall and tympanic ring.

The outer ear and the middle ear in human newborns are not completely mature at birth, and various anatomical and physiological changes occur between birth and adulthood (Saunders et al., 1983; Eby and Nadol, 1986). The tympanic membrane and the ossicles have reached adult size at birth but the external auditory canal is much smaller than its adult size. In adults the tympanic membrane lies at about a 45-degree angle from the horizontal, while in newborns it is nearly horizontal. The tympanic ring is not completely developed until the age of two years (Saunders et al., 1983). Furthermore, in adults, the inner two thirds of the ear-canal wall are bony and the outer one third is composed of soft tissue; in newborns, the ear canal is surrounded almost entirely by soft tissue (McLellan and Webb, 1957). This lack of ossification presumably allows the external ear canal to change volume significantly in response to large static pressures.

Although the importance of obtaining accurate ear-canal volume-change measurements has been acknowledged, few studies have been conducted to date. Owing to ethical issues and procedural problems it is difficult to measure newborn ear-canal volume change experimentally. The finite-element method is an invaluable research and design tool as it can be used to simulate the behaviour of structures in conditions that cannot be achieved experimentally. Since the first finite-element model of the tympanic membrane was developed (Funnell and Laszlo, 1978), this method has been widely used to investigate the behaviour of both human and animal ears (e.g., Wada et al., 1992; Funnell, 1996; Funnell and Decraemer 1996; Koike et al., 2002; Gan et al., 2002, 2004; Elkhouri et al., 2006). To the best of our knowledge, no finite-element model of the newborn ear canal has been produced until now.

The purpose of this study is to use modelling to investigate newborn ear-canal volume changes under high static pressures. We present here a non-linear three-dimensional model of a healthy newborn ear canal. The geometry of the model is based on a clinical X-ray computed tomography (CT) scan of the ear of a 22-day-old newborn.

We chose a 22-day-old newborn ear canal for two reasons. First, during the first few days of a newborn’s life, the outer ear may contain debris and the middle-ear cavity may be filled with amniotic fluid (Eavey, 1993). Newborns are therefore likely to present with conductive hearing loss during the immediate postnatal period, followed by an improvement in hearing as the debris and fluid are cleared. Consequently, hearing-screening tests conducted shortly after birth may lead to high false-positive rates. Second, as part of its Early Hearing Detection and Intervention program (EHDI, 2003), the American Academy of Pediatrics (AAP) recommends that all infants be screened for hearing loss before the age of one month. For these reasons, a 22-day-old newborn is an appropriate study subject.

A hyperelastic constitutive law is applied to model soft tissue undergoing large deformations. Plausible ranges for material-property values are based on data from the literature. Model results are then compared with available experimental measurements.

II. MATERIALS AND METHODS

A. 3-D reconstruction

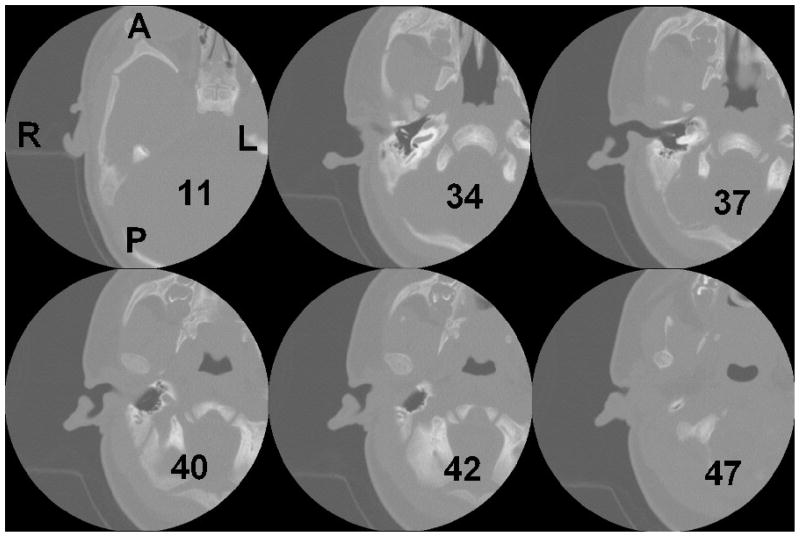
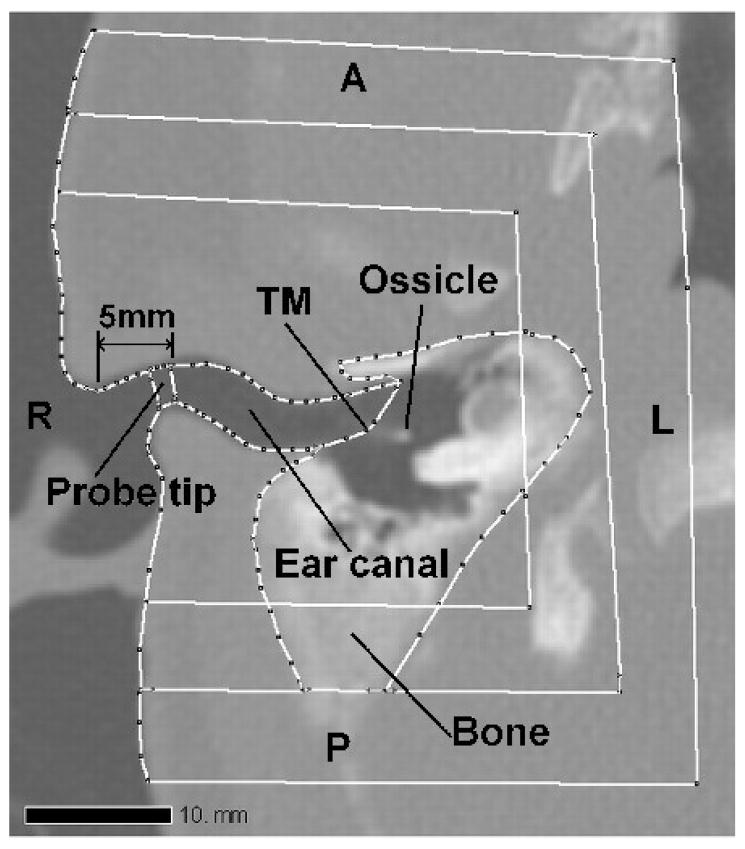
The geometry of the model is based on a clinical X-ray CT scan (GE LightSpeed16, Montréal Children’s Hospital) of the right ear of a 22-day-old newborn (study number A07-M69-02A, McGill University Institutional Review Board). The infant had a unilateral congenital atresia (absent external ear canal) on the left side. The external and middle ear on the right side was found to be entirely normal anatomically and exhibited normal hearing. The CT scan contained 47 horizontal slices, numbered from superior to inferior. The scan had 0.187-mm pixels and a slice spacing of 0.625 mm. The ear canal is present in slices 34 to 42. Figure 1 shows slices 11, 34, 37, 40, 42 and 47. The region surrounding the right ear canal in Figure 1 (slice 37) has been enlarged, segmented and labelled in Figure 2. Figure 2 includes the ear canal itself, the soft tissue surrounding the ear canal, the tympanic membrane, the ossicles, the temporal bones, and the simulated probe tip. Rather than including the entire head in the model, the anterior, posterior and medial surfaces were positioned so as to include the temporal bone and a generous amount of soft tissue. More details are given in section III A.

FIG. 1.

X-ray CT data for 22-day newborn. Slices 11, 34, 37, 40, 42 and 47 are shown. Slices 34 to 42 include the ear canal. A is anterior; P is posterior; R is right; L is left.

FIG. 2.

Slice 37, showing segmented structures. TM is tympanic membrane. The probe tip is positioned at 5 mm from the entrance of the ear canal. A is anterior; P is posterior; R is right; L is left. Three different sizes of models are shown; more details are given in Section III A.

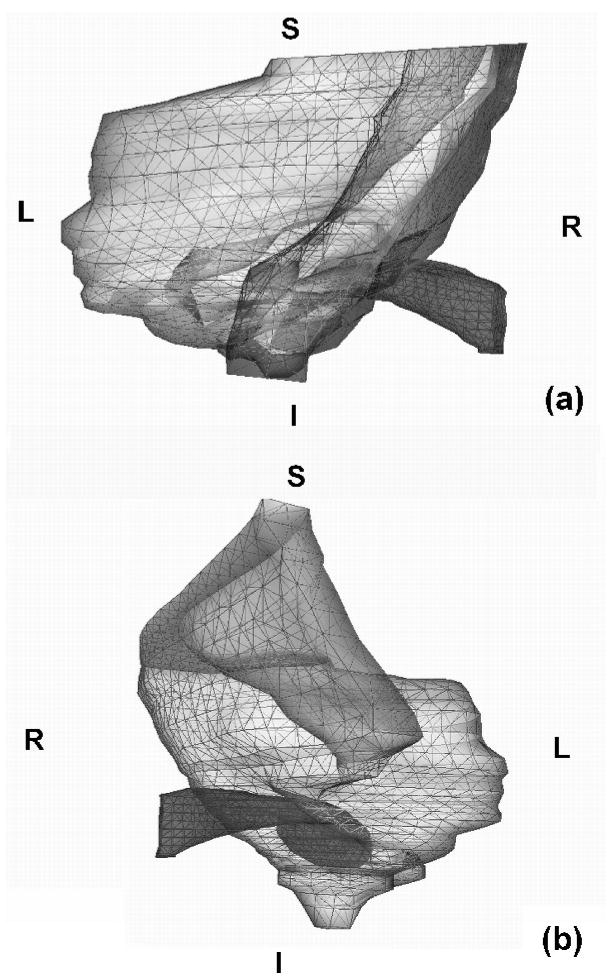
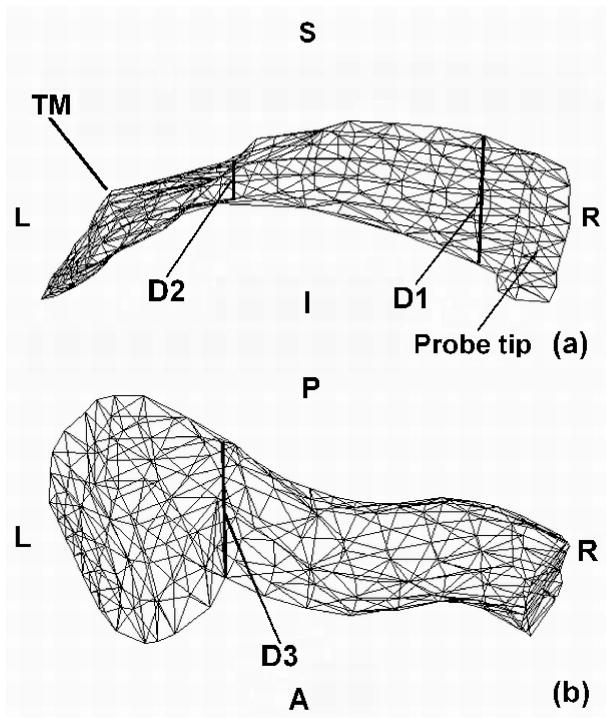
In this study we used 37 slices, from slice 11 to slice 47. From slice 11 to slice 33, every second slice was used; from 34 to 47, every slice was used. A locally developed program, Fie, was used to segment the cross-sections of the temporal bone and soft tissue, as shown in Figure 2. The contours were imported into a 3-D surface-triangulation program, Tr3, and the surface was generated by optimally connecting contours in adjacent slices. The surface model is shown in Figure 3. Both Fie and Tr3 are available at http://audilab.bmed.mcgill.ca/~funnell/AudiLab/sw/. Figure 3a is a posterior view of the ear canal and the temporal bone surface. Figure 3b is an antero-lateral view. In order to better display the relationships between the ear canal and the temporal bone, the soft tissue is not shown in Figure 3. It can be seen that there is more temporal bone superior to the ear canal. Figure 4 shows the enclosed ear-canal surface. The ear-canal superior wall is much shorter than the inferior wall, as seen in Figure 4a. The tympanic membrane terminates the canal wall in a very horizontal position. It may be considered to form part of the ear-canal wall for the innermost 8 mm or so of canal length. As shown in Figure 4b, the superior-inferior diameter (D1) is larger than the anterior-posterior diameter (D3), which agrees with the observations of McLellan and Webb (1957). Table I provides a summary of ear-canal and tympanic-membrane data from the literature for the adult ear and the newborn ear, and the corresponding data for the finite-element model.

FIG. 3.

Surface mesh of finite-element model. The ear canal and temporal bone surface are displayed; the soft tissue is not shown. (a) Posterior view. (b) Antero-lateral view. S is superior; I is inferior; R is right; L is left.

FIG. 4.

Ear-canal model. (a) Posterior view. (b) Inferior view. D1 (4.8mm) is the maximum diameter, in the superior-inferior direction; D2 (1.6mm) is the minimum diameter, in the superior-inferior direction; D3 (4.4mm) is the maximum diameter in the anterior-posterior direction. S is superior; I is inferior; P is posterior; A is anterior; R is right; L is left.

TABLE I.

Summary of adult and newborn ear canal and TM data

	Adult	Newborn (Published Data)	Data in the model
Ear Canal
Shape	S shape	Straight	Straight
Roof length (mm)	25–301,2	13–22.53	16
Floor length (mm)	25–301,2	17–22.53	22.5
Diameter (mm)	101	4.44	1.6–4.8
Bone	Inner 2/31	None	None
Soft tissue	Outer 1/31	Entire EAC	Entire EAC
TM
Diameter along the manubrium (mm)	8–101	Adult size1	8.7
Diameter perpendicular to the manubrium (mm)	7–91	Adult size1	8.3
Surface area (mm2)	55–851	Adult size1	67

¹Saunders et al., 1983

²Stinson and Lawton, 1989

³2-month old newborn measurement (McLellan and Webb, 1957)

⁴Average ear-canal diameter for 1-month-old newborn (Keefe et al., 1993)

A solid-element model with tetrahedral elements was generated from the triangulated surface using Gmsh (http://www.geuz.org/gmsh/) and imported into COMSOL^™ version 3.2 (http://www.comsol.com) for finite-element analysis.

B. Material properties

There are three types of cartilage in the human body: articular cartilage, elastic cartilage and fibrocartilage (Fung, 1993). Elastic cartilage is found in the wall of the external auditory canal (McLellan and Webb, 1957). Articular and elastic cartilage have a similar structure, both containing type II collagen, but elastic cartilage contains more elastic fibres and is therefore more flexible than articular cartilage (Fung, 1993). The Young’s modulus of elastic cartilage in adult is between 100 kPa and 1 MPa (Zhang et al., 1997; Liu et. al., 2004). The mechanical properties of cartilage are age-dependent. Williamson et al. (2001) found that the tensile Young’s modulus of bovine articular cartilage increased by an average of 275% from newborn to adult.

To the best of our knowledge, the stiffness of human newborn elastic cartilage has never been measured. In this study, we used three Young’s moduli: 30 kPa, 60 kPa and 90 kPa. The lowest value is close to the lowest stiffness of soft tissue such as fat (4.8 kPa, Wellman et al., 1999) and gland (17.5 kPa, Wellman et al., 1999) and 90 kPa is close to the lowest stiffness of cartilage in adult humans.

The ear-canal soft tissue is assumed to be homogeneous, isotropic and nearly incompressible. The Poisson’s ratio of elastic cartilage in newborns is taken to be 0.475. This value has been widely used in soft-tissue modelling (Torres-Moreno et al., 1999; Cheung et al., 2004; Chui et al., 2004). The soft tissue is also assumed to be hyperelastic, as discussed in Section II D.

C. Boundary conditions and load

In newborn tympanometric measurement, the volume change caused by high static pressures has two sources. The first is tympanic-membrane movement; the second is ear-canal wall movement. The ear canal and the middle ear are configured as a parallel acoustic system. The same uniform static pressure is applied to the ear-canal wall and to the tympanic membrane. The total volume change is equal to the sum of the contributions of these two components. In this study, we focus only on the contribution of ear-canal-wall movement to volume change. We thus assume that the tympanic membrane is rigid and the ossicles, ligaments, etc. are not taken into account. Given that the bones are also assumed to be rigid in this model, only their surface representation is needed. The probe tip is also assumed to be rigid and its position is taken to be 5 mm inside the ear canal (Keefe et al., 1993), as shown in Figure 2. All other parts of the model are free to move. Static pressure is applied to the ear-canal wall from the inside of the canal.

D. Hyperelastic finite-element method

While undergoing tympanometry procedures, the newborn ear-canal wall deforms significantly under the high static pressures. Accordingly, linear elasticity with the infinitesimal-deformation formulation is not appropriate to formulate the finite-element model. As a result, we used a hyperelastic finite-deformation formulation.

In finite-deformation theory, the deformation gradient F = ∂x/∂X is defined where X denotes a point in the reference configuration. The current position of the point is denoted by x = X + u where u is the displacement from the reference position to the current position. Using C =F^TF, the ‘strain invariants’ are defined as

$$I_1=\text{tr}(\mathbf{C})$$ (1)

and

$$I_2=\frac{1}{2}(I_1^2-\text{tr}(\mathbf{C}·\mathbf{C}))$$ (2)

where tr is the trace operator.

Various strain-energy functions can be applied to soft tissue, such as neo-Hooke, Mooney-Rivlin, Arruda-Boyce, etc. In this study we focus on the polynomial method, which is a generalization of the neo-Hooke and Mooney-Rivlin methods and which has been widely used to simulate large deformations in almost incompressible soft tissues such as skin, brain tissue, breast tissue and liver (e.g., Samani and Plewes, 2004; Cheung et al., 2004). A second-order polynomial strain-energy function can be written as

$$W=C_{10}(I_1-3)+C_{01}(I_2-3)+\frac{\kappa }{2}{(J-1)}^2$$ (3)

where W is the strain energy; C₁₀ and C₀₁ are material constants; κ is the bulk modulus; and J is the volume-change ratio. J is defined as

$$J=det\mathbf{F}$$ (4)

where det is the determinant operator.

Under small strains the Young’s modulus of the material, E, may be written as

$$E=6(C_{10}+C_{01})$$ (5)

Further details about the hyperelastic model can be found elsewhere (e.g., Holzapfel, 2000).

The ratio C₁₀:C₀₁ is here taken to be 1:1, which has been widely used for biological soft tissue (e.g., Mendis et al., 1995; Samani and Plewes, 2004).

E. Volume calculation

The air volume between the probe tip and the tympanic membrane can be calculated using the three-dimensional divergence theorem:

$${\iiint }_M\text{div}\mathbf{F}dV={\iint }_S\mathbf{F}·\mathbf{n}dS$$ (6)

where M is a solid volume with a closed boundary surface, S, whose unit normal vector is denoted by n. The divergence of F is defined as

$$\text{div}\mathbf{F}=\frac{\partial F_x}{\partial x}+\frac{\partial F_y}{\partial y}+\frac{\partial F_z}{\partial z}$$ (7)

By choosing F such that div F=1, we can easily obtain the ear-canal volume as

$$V={\iiint }_M\text{div}\mathbf{F}dV={\iint }_s\mathbf{F}·\mathbf{n}dA$$ (8)

There is an infinite number of choices for F that have div F=1. In our study, we simply choose F=(x,0,0). The air volume can therefore be computed by integration over the deformed surface of the corresponding closed volume. Further details can be found elsewhere (e.g., Matthews, 2000, p. 97).

III. RESULTS

A. Convergence tests

Convergence tests are used to investigate how many elements should be used in the model. The results of a finite-element simulation depend in part on the resolution of the finite-element mesh, that is, on the numbers and sizes of the elements used. In general, the greater the number of elements the more accurate the results, but also the longer the time required for the computations. Nonlinear simulations in particular can be very time-consuming.

In our convergence tests, the first step was to decide how much of the scan to incorporate in the x direction (from lateral to medial) and y direction (from posterior to anterior). The second step was to decide how many slices should be used in the model. For both step 1 and step 2, the surface models have a nominal mesh resolution of 18 elements per diameter. The last step was to decide what mesh resolution to use for the model. In the convergence tests the Young’s modulus is 60 kPa and the Poisson’s ratio is 0.475.

As shown in Figure 2, three different models are compared. The first one (small model) has a lateral-medial size of about 32 mm and an anterior-posterior size of about 28 mm. The second model (middle model) is about 36 mm by 39 mm. The third one (large model) is about 41 mm by 50 mm. All three models were generated based on slices 11 to 47.

The three models were compared based on the absolute values of the maximum displacements for both negative and positive pressures of 3 kPa, and on the ear-canal volume change for the same pressure. All three models have almost the same maximum displacements. The volume changes for model 1 were 6.7% larger than those of model 2 because model 1 contains less bone to constrain the wall motion, but models 2 and 3 differed by only about 1%. This implies that the middle model provides enough accuracy and it is the one used for the remaining simulations.

As mentioned earlier, the ear canal is present in slices 34 to 42. In order to investigate how many slices above and below the canal should be incorporated into the model, five different models were studied. Figure 5 illustrates the different configurations. Model 1 was composed of 20 slices, from slice 28 to slice 47. Model 2 included 5 more slices superiorly; it contains 25 slices, from 23 to 47. Model 3 included 5 more slices inferiorly. Since our CT scan did not include any slices inferior to slice 47, we created five artificial slices (numbered 48 to 52) by extrapolation and comparison with CT scans for newborns of about 3 months of age. The artificial slices included only soft tissue, the boundary conditions of which were made the same as those of the other soft tissue in the model. Model 3 was thus composed of 30 slices, from 23 to 52, slices 48 to 52 being artificial. Model 4 was based on model 3, the only difference being the incorporation of another 5 artificial slices inferiorly; the model thus contained 35 slices, from 23 to 57. Finally, model 5 was composed of 37 slices, from 11 to 47; no artificial slices were included in model 5.

FIG. 5.

Slices used in test models 1 to 5. Slices 48 to 57 are artificial slices, as discussed in the text. A is anterior; P is posterior; S is superior; I is inferior.

As before, the different models were compared based on the absolute values of the maximum displacements and on the ear-canal volume changes for both negative and positive pressures of 3 kPa. The maximum displacements were almost same; the differences were less than 2%. The volume changes for model 1 are up to 8.9% larger than those for the other models, presumably because it has fewer constraints due to the temporal bone superior to the canal, but the volume changes for models 2 to 5 are all within 1.3%. These results imply that our 37-slice dataset is sufficient even though there are not very many slices inferior to the ear canal. For the remainder of this paper we use model 5.

In order to decide what mesh resolution should be used, four different resolutions were compared. The initial surface models have nominal numbers of elements per diameter of 12, 15, 18 and 22 respectively. The resulting solid models have 9076, 12786, 19233 and 23674 tetrahedral elements respectively. As the mesh resolution increases, the maximum displacement of the entire model increases monotonically. The difference in maximum displacement between the 9076-element model and the 12786-element model was about 4%, and the difference between the 12786-element model and the 19233-element one was about 5%. The difference between the 19233-element model and the 23674-element one, however, was less than 1%, and the location of the maximum displacement changed by less than 1mm. The model with 19233 elements was selected for further simulations.

B. Sensitivity analysis

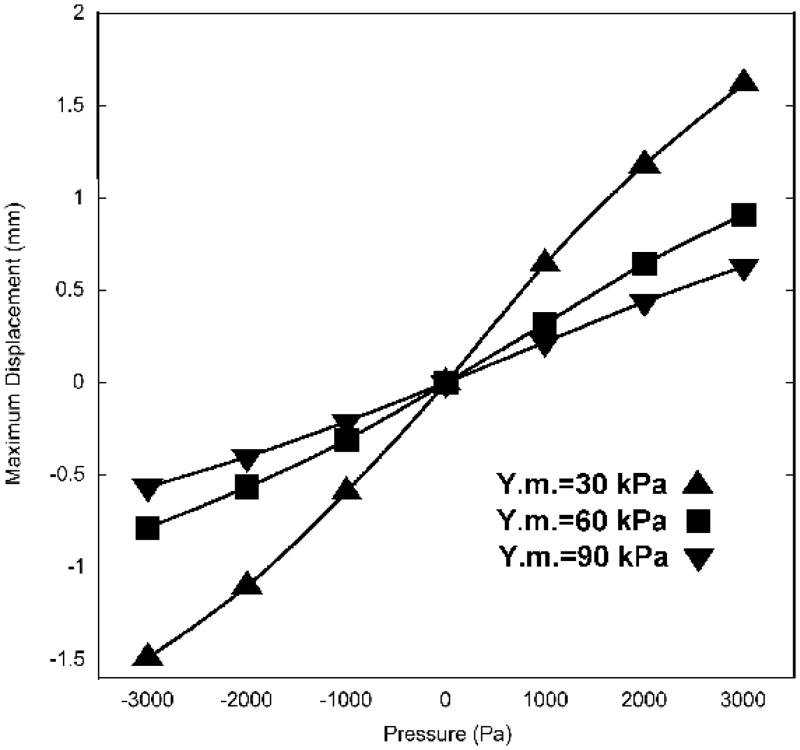
Sensitivity analysis is used to investigate the relative importance of model parameters. In this study we focus on the ear-canal volume change under high static pressures, and therefore the effects of parameters on ear-canal volume changes were investigated. Sensitivity was analyzed for Young’s modulus, Poisson’s ratio and the C₁₀:C₀₁ ratio. The Young’s modulus was found to have the greatest impact on the volume change. Figure 6 shows ear-canal volumes corresponding to different Young’s moduli for static pressures from −3 to +3 kPa. As Young’s modulus increases, the model canal-wall volume changes decrease significantly.

FIG. 6.

Calculated ear-canal volume for three different Young’s moduli (Y.m.). When pressure is 0, ear-canal volume is 150 mm³.

Values from 0.45 to 0.499 have been used in the literature for Poisson’s ratio for soft tissue (Li et al., 2001; Samani and Plewes, 2004). A value of 0.5 corresponds to incompressibility. Increasing Poisson’s ratio from 0.45 to 0.499, with a Young’s modulus of 60 kPa, resulted in a 1.5% reduction in volume change at +3 kPa, and a change of only 1.1% at −3 kPa. The model is thus insensitive to Poisson’s ratio, which is consistent with previous modelling (Funnell and Laszlo, 1978; Qi et al., 2004).

Three different ratios of C₁₀ to C₀₁ were studied, namely, 1:0, 1:1 and 0:1. The sum of C₁₀ and C₀₁ is kept constant at 10 kPa, corresponding to a small-strain Young’s modulus of 60 kPa as given by Equation 5. The volume changes occurring with the three combinations of C₁₀ and C₀₁ differ by less than 3% at +3 kPa and by even less at −3 kPa. The model is thus insensitive to the C₁₀:C₀₁ ratio when the sum of C₁₀ and C₀₁ remains constant. This is consistent with the results of Mendis (1995), who used a three-dimensional Mooney-Rivlin model for brain tissue and found that, when the deformation is under 30%, the different combinations of C₁₀ and C₀₁ had little effect on model displacements.

C. Model displacements and displacement patterns

The ear-canal wall of the model displays non-linear elastic behaviour leading to an S-shaped pressure-displacement relation under high static pressures, as shown in Figure 7. The displacement curves are very similar in shape to the volume curves shown in Figure 6. As the Young’s modulus increases, the maximum displacement decreases in approximately inverse proportion.

FIG. 7.

Maximum displacement of the entire model for three different Young’s moduli.

The smaller the Young’s modulus is and the larger the displacements are, the stronger the non-linearity is. When Young’s modulus is 90 kPa, the pressure-displacement relation becomes almost linear. When Young’s modulus is 30 kPa, the slopes of the curves decrease significantly as the pressure becomes either more negative or more positive, but the displacement curve does not reach a plateau by either −3 kPa or +3 kPa.

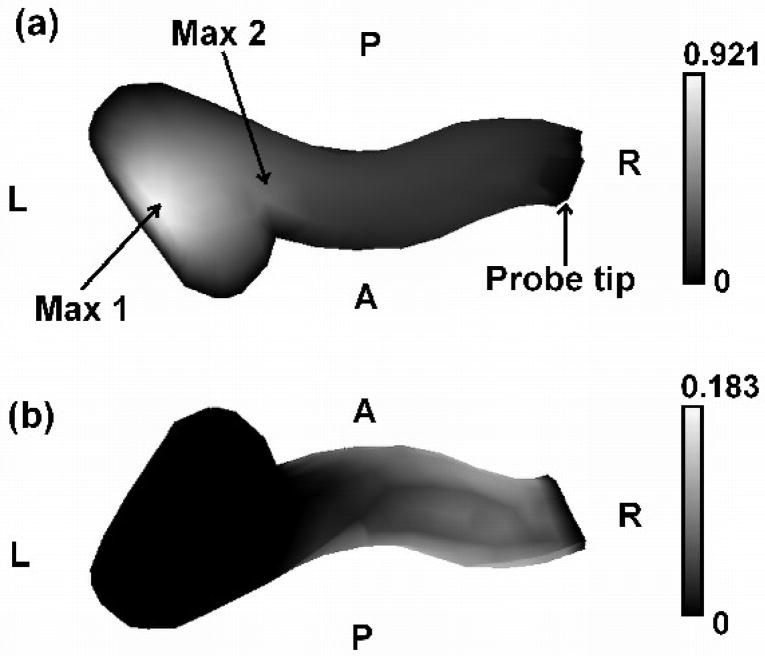
The maximum displacement of the entire model occurs on the medial inferior surface of the ear canal. The maximum is quite localized. Figure 8 shows the displacement patterns on the superior and inferior surfaces of the canal for a pressure of +3 kPa, when Young’s modulus is 60 kPa. The displacements of the inferior surface are bigger than those of the superior surface. This is because there is temporal bone around the top of the newborn ear-canal but the bone around the bottom has not completely developed, as shown in Figure 3.

FIG. 8.

Displacement pattern of ear-canal wall for static pressure of +3 kPa. (a) Ear-canal floor. Grey-scale is from 0 to 0.921 mm. (b) Ear-canal roof. Grey-scale is from 0 to 0.183 mm. Max 1, the maximum displacement of the entire model, is 0.921 mm. Max 2, the maximum displacement observable from the probe tip, is 0.452 mm. Since the tympanic membrane (TM) and the probe tip are assumed to be fixed, the corresponding displacements are zero. A is anterior; P is posterior; R is right; L is left.

D. Comparisons with experimental data

In this section we shall compare our simulation results with two sets of experimental data, maximum canal-wall displacement measurements (Holte et al., 1990) and tympanometry (Shahnaz, 2002; Polka et al., 2002).

1. Displacement measurements

Holte et al. (1990) measured the maximum displacements of ear-canal walls in newborns of different ages. Positive and negative pressures of 2.5 to 3 kPa were introduced by a syringe system. Displacements of the ear-canal wall and tympanic membrane were recorded by an otoscope with a videocassette recorder. The videotapes were reviewed, and ear-canal wall diameters at ambient pressure and at maximum static pressures were measured with a transparent ruler. The relative change in ear-canal wall diameter under maximum static pressure was expressed as a percentage of the resting diameter. For newborns aged from 11 to 22 days, the diameter change was 7.9% ±11.1% for the positive pressure, and −15.0% ± 22.1% for the negative pressure.

The maximum displacement in our model takes place on the medial inferior surface of the ear canal, which probably corresponds to a location beyond that which Holte et al. were able to observe. McLellan and Webb (1957) used an otoscope to examine 20 cleansed ear canals from 10 healthy full-term newborns. They concluded that the inferior wall ascends from the tympanic membrane, and from the external orifice of the canal, to a transverse ridge which divides the inferior wall into inner and outer portions. Unlike the outer portion, the inner portion of the inferior wall can hardly be seen with an otoscope. Since Holte et al. also used an otoscope in their experiments, it would have been difficult for them to observe the inner part of the inferior wall. We conclude, therefore, that their diameter-change measurements were taken lateral to the ridge. As shown in Figure 8, in our model the displacements of the canal wall are larger at the ridge than they are lateral to the ridge; we therefore assume that Holte et al. measured the diameter changes at the ridge. In our model the ridge is located 11 mm from the probe tip. We use the model displacements at this point for comparison with the measurements of Holte et al.

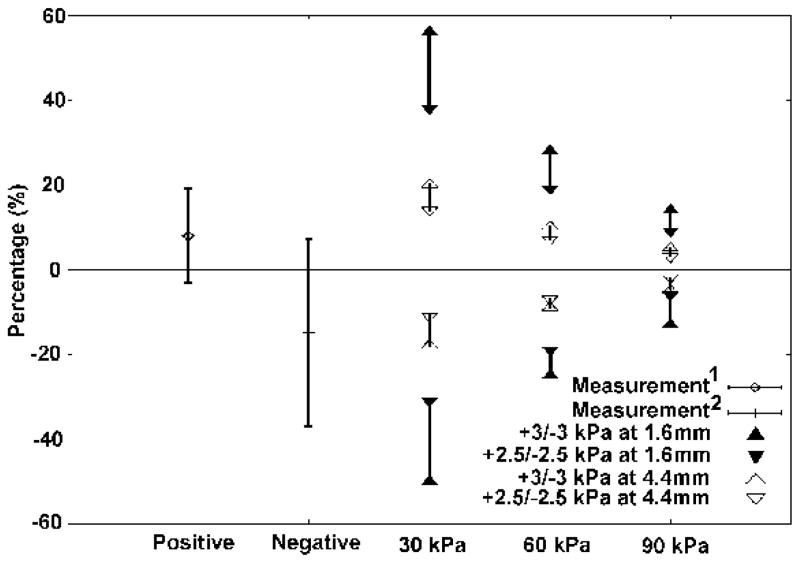
McLellan and Webb (1957) observed a sagittal cross section at the ridge which appeared oval in shape in 16 ears, with the longer diameter being anterior-posterior. In our model, the resting diameters at the transverse ridge are shown in Figure 4. The narrowest diameter (D2) at 11 mm is about 1.6 mm, and the widest diameter (D3) is about 4.4 mm. Since the resting diameters were not mentioned by Holte et al., we do not know if the narrowest or the widest diameter was applied when the ratios of ear-canal wall displacements to resting diameters were calculated. Thus, for our model, the ratio of displacement (at the 11-mm position) to diameter was calculated for both resting diameters (1.6 and 4.4 mm), and for both ±2.5 kPa and ±3 kPa. The results are shown in Figure 9 together with the experimental results of Holte et al. For positive pressures, when the narrowest resting diameter (1.6mm) is applied the results for the model with a Young’s modulus of 30 kPa are beyond the experimental range; when Young’s modulus is 60 kPa, the simulation results are partly within the experimental range; when Young’s modulus is 90 kPa, they are totally within the experimental range. For negative pressures, the simulation results with a Young’s modulus of 30 kPa are partly within the experimental range; for 60 and 90 kPa they are all within the experimental range. When the widest resting diameter (4.4mm) is applied, all of the simulation results are within the experimental range for both positive and negative pressures.

FIG. 9.

Comparison of experimental data (Holte et al., 1990) with simulation results. Positive = experimental data for pressures of +2.5 to +3 kPa; Negative = experimental data for pressures of −2.5 to −3 kPa. Triangles represent simulation results for Young’s moduli of 30, 60 and 90 kPa, respectively. Filled and open triangles indicate the use of 1.6 and 4.4 mm, respectively, as the denominator when computing percentage changes. Upward-pointing and downward pointing triangles indicate the use of ±3 kPa and ±2.5 kPa, respectively, as the pressure for the simulation results.

2. Tympanometry

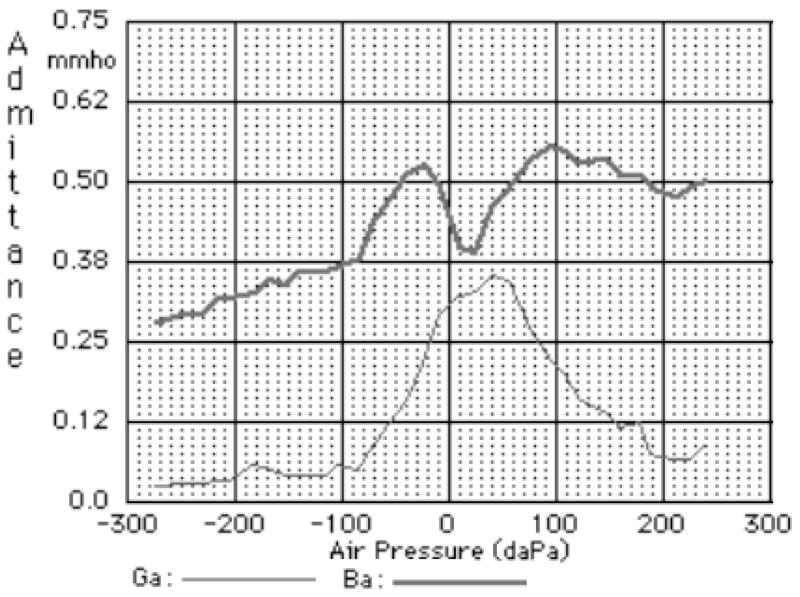
Polka et al. (2002) showed complete susceptance and conductance tympanograms for two 3-week-old infants measured at 226, 600, 800 and 1000 Hz. Both infants had normal hearing as measured by automated auditory brainstem response (ABR) screening. Figure 10 shows one of the 226-Hz measurements.

FIG. 10.

Susceptance and conductance tympanogram at 226 Hz for 3-week-old newborn (based on Polka et al., 2002).

For frequencies up to about 1 kHz, the adult ear canal can be modelled as a lumped acoustical element (e.g., Shanks and Lilly, 1981). This assumption is valid up to higher frequencies in the newborn canal because it is smaller than the adult canal. The susceptance measured at the probe tip includes the susceptance of the enclosed air volume (B_V), and the susceptances due to the vibration of the ear-canal wall (B_W) and tympanic membrane (B_TM) in response to the probe tone. Thus, the susceptances at the extreme positive pressure and negative pressure are given by

$$B^{+}=B_V^{+}+B_W^{+}+B_{TM}^{+}$$ (9)

and

$$B^{-}=B_V^{-}+B_W^{-}+B_{TM}^{-}$$ (10)

The difference between the two is given by

$$\mathrm{\Delta }B=B^{+}-B^{-}=[B_V^{+}-B_V^{-}]+[B_W^{+}-B_W^{-}]+[B_{TM}^{+}-B_{TM}^{-}]$$ (11)

Given the near symmetry of the non-linear response predicted by the model, as shown in Figure 7, it may be reasonable to assume that the vibrations at the extreme positive and negative pressures are similar. In that case their effects cancel and the susceptance change is mainly determined by the actual volume change due to the static displacement of the canal wall and tympanic membrane.

Table II shows the susceptance and conductance values at the extreme static pressures (−275 and +250 daPa, i.e., −2.75 and +2.5 kPa), and their differences, from the measurements of Polka et al. (2002). The fact that the conductance changes are very small for seven out of the eight measurements supports the assumption that the vibrations are similar at the extreme positive and negative pressures.

Table II.

Tympanometry results for two 3-week-old infants

Newborn 1
Frequency (Hz)	226	630	800	1000
B+ (mmho)	0.5	1	0.875	1
B− (mmho)	0.26	0.5	0.45	0.47
ΔB (mmho)	0.24	0.5	0.425	0.53
ΔV (mm3)	240	180	120	120
G+ (mmho)	0.05	0.5	0.8	1.1
G− (mmho)	0	0.6	0.7	0.6
ΔG (mmho)	0.05	−0.1	0.1	0.5
Newborn 2
Frequency (Hz)	226	630	800	1000
B+ (mmho)	0.3	1.01	1.45	1.8
B− (mmho)	0.25	0.5	0.8	1.1
ΔB (mmho)	0.05	0.51	0.65	0.7
ΔV (mm3)	50	183	183	158
G+ (mmho)	0.05	0.5	0.8	0.9
G− (mmho)	0.05	0.65	0.8	0.9
ΔG (mmho)	0	−0.15	0	0

Tympanometry data are from Polka et al. (2002). B⁺, B⁻, G⁺ and G⁻ are susceptance and conductance measurements at extreme positive and negative pressures. ΔB is the susceptance difference between extreme positive and negative pressures. ΔV is the equivalent-volume difference corresponding to ΔB. ΔG is the conductance difference between extreme positive and negative pressures.

The table also includes the equivalent-volume changes corresponding to the susceptance changes, computed using

$$\mathrm{\Delta }{V}_{eq}=\mathrm{\Delta }B\rho c^2/2\pi f$$ (12)

where ρ is the air density (1.2 kg/m³), c is the sound speed (343 m/s), and f is the frequency (cf. Shanks and Lilly, 1981).

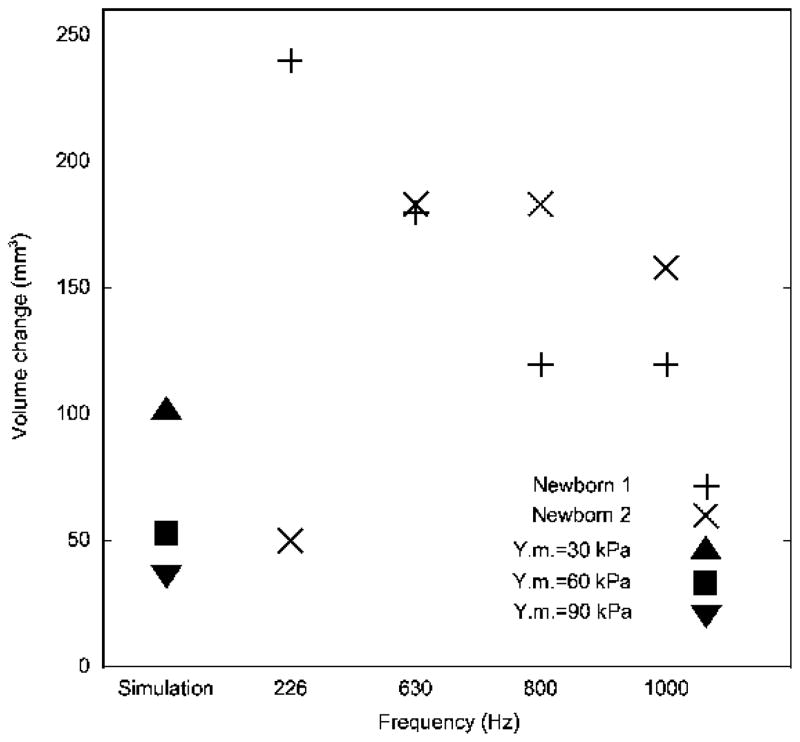
Figure 11 shows model volume changes obtained for different Young’s moduli, compared with the experimentally measured equivalent-volume changes from Table II. The volume changes obtained for the model are lower than those observed experimentally, which is consistent with the fact that the experimental equivalent-volume changes include contributions not only from ear-canal wall movement but also from tympanic-membrane movement.

FIG. 11.

Comparison of simulation results with equivalent-volume changes taken from tympanograms for two newborns. ▲, ■ and ▼ represent the volume changes from the simulation results for three different Young’s moduli. + and × represent the tympanogram-based equivalent-volume changes for 226, 630, 800 and 1000 Hz.

IV. DISCUSSION AND CONCLUSIONS

A non-linear hyperelastic model of the newborn ear canal is presented and compared with available experimental data.

For static pressures from −3 kPa to +3 kPa, the canal-wall displacements and volume changes are non-linear, with the degree of non-linearity increasing as the Young’s modulus decreases and the displacements increase. Our sensitivity analysis indicates that the Young’s modulus of the tissue in the ear-canal wall plays the most important role in determining volume changes. The effects of varying the Poisson’s ratio and the C₁₀:C₀₁ ratio are found to be small.

In our simulations, the displacements of the ear-canal wall are slightly larger under positive pressures than under negative pressures. In the measurements of Holte et al., however, the mean diameter changes were much bigger for negative pressures than for positive pressures. In the measurements, a large overlap exists between the percentage displacement changes for the positive pressures and those for the negative pressures, as shown in Figure 9. Possible reasons for the variability include individual differences between ears, age-related changes from 11 days to 22 days, and uncertainty in the applied pressures. It is not clear whether the displacements under the positive pressures and the negative pressures are significantly different or not.

The cross-section of the newborn ear canal is quite flattened; in our model, for example, the horizontal and vertical diameters are 1.6 mm and 4.4 mm, respectively, just lateral to the tympanic membrane. We do not know which diameter was used by Holte et al. in computing percentage changes. When the narrowest diameter was applied to our model results, the model with a Young’s modulus of 30 kPa produces diameter changes far above the experimental range under positive pressures. In Holte’s measurements, in a younger age group (1 to 11 days) the diameter changes may be up to 70%. This may indicate that Young’s modulus of the newborn ear-canal is 30 kPa for younger newborns, and between 60 and 90 kPa for older newborns. However, for a better comparison with the model, it would be desirable to be able to know where their measurements were made in the canal, and to know which diameter was used in the calculations.

In tympanometry a change of equivalent volume consists of two components. One component is the actual air-volume change caused by static pressures, which should be independent of frequency. The actual volume change is caused by the static displacement of both the ear-canal wall and the tympanic membrane. The other component is due to the vibration of the ear-canal wall and tympanic membrane in response to the probe tone. Assuming that the vibrations caused by the probe tone at the positive and negative extreme pressures cancel each other out, as discussed above, the difference between the experimental value and the simulation value may be taken to be the volume change caused by the static displacement of the newborn tympanic membrane. The average equivalent-volume change across all four frequencies in Table II and Figure 11 is 154 mm³. The equivalent-volume changes at 630, 800 and 1000 Hz seem to fit the pattern of frequency independence quite well, but the values at 226 Hz do not – one is too high and the other is too low. It is not clear why this is so. Dropping these two values and taking the average over the three higher frequencies yields an equivalent-volume change of 157 mm³, very close to the value obtained using all four frequencies. According to the simulation results, when the Young’s modulus of the ear-canal wall is 30, 60 and 90 kPa, the ear-canal volume change is 101, 53 and 37 mm³, respectively, from −2.75 kPa to 2.5 kPa. Subtracting these values from the average equivalent-volume change of 157 mm³ yields predicted volume changes caused by tympanic-membrane displacement of about 56, 104 and 120 mm³ respectively. No independent measurements of newborn tympanic-membrane volume displacements are available for comparison, and measurements in adult ears (e.g., Shanks and Lilly, 1981; Dirckx and Decraemer, 1992; Gaihede, 1999) may be quite different.

Shanks and Lilly (1981) measured adult ear-canal volume change over a static pressure range of ±4 kPa. They found a mean ear-canal volume change of 113 mm³ caused by the movement of the cartilaginous part of the wall of the ear canal and the movement of the probe tip. Our simulated volume changes for the newborn are mostly less than those measured by Shanks and Lilly for adult ears. This is reasonable because the diameter and length of the newborn ear canal are much less than those of the adult ear canal. We also do not take probe-tip and tympanic-membrane movements into account and our pressure range is ±3 kPa rather than ±4 kPa. If we compare the ratio of volume change to the original volume, the results of Shanks and Lilly (1981) correspond to an average ratio of about 16% in the range ±4 kPa in adult, while the ratio in newborn is from 27% (for a Young’s modulus of 90 kPa) to 75% (for a Young’s modulus of 30 kPa) in the range of ±3 kPa based on our model results.

The simulated ear-canal volume changes do not reach a plateau when the pressure is varied between −3 kPa and +3 kPa, which is consistent with the report by Shanks and Lilly (1981) that even at ±4 kPa the adult ear canal is not rigid if the probe tip is placed on the cartilaginous part of the ear canal. The failure of the model to reach a plateau is also consistent with the non-flat tails often found in susceptance tympanograms in newborns (Paradise et al., 1976; Holte et al., 1990).

As a first step in modelling the newborn ear-canal wall, we have taken into account only the hyperelastic properties of the ear canal. Further work is required to incorporate in the model the tympanic membrane and the middle ear, and the probe tone itself. Modelling of the response to the probe tone will require inclusion of inertial and damping effects which are not in the current model. The addition of viscoelastic effects would permit simulation of the effects of the timing and direction of the large quasi-static pressure changes used in tympanometry (Osguthorpe and Lam, 1981). It will also be important to obtain a better idea of the types of tissue present: X-ray data will need to be supplemented by data obtained from sources such as MRI and histology.