Abstract
The CN stretching vibrations of the guanidyl group in the arginine dipeptide sidechain are examined by two-dimensional infrared spectroscopy. In D2O, the spectra display two distinct diagonal peaks. These nearly degenerate modes undergo ultrafast energy transfer. The energy transfer rate was determined directly from the 2D-IR spectra to be 1/2.1 ps-1. The cross peaks in 2D-IR arising from the energy transfer provide a definitive identification of arginine in larger proteins. An example of arginine in the transmembrane protein M2, found in Influenza viruses, is given.
Keywords: Ultrafast 2D IR spectroscopy, arginine, photon-echo, population transfer, coherence transfer, energy transfer
Introduction
The infrared spectra of proteins and peptides provide valuable information on the backbone and side chain conformations and also on their environments, which makes it an invaluable tool for understanding the structural and dynamical properties of proteins. However, challenges arise when distinguishing residue specific information due to the overlapping transitions in the broad Amide I transitions in larger proteins and peptides. The infrared transitions of the amino acid side chains can provide a possible solution for understanding the local environment of specific sites in the peptide sequence. Different side chains have characteristic IR spectra which can serve as spectral markers of specific amino acids in proteins.1-6 Moreover, the knowledge and understanding of the infrared spectra of different amino acid side chains is often pivotal for interpreting secondary structures of proteins. Charged side chains like arginine and lysine are often involved in intra or inter molecular salt bridges that play a key role in the structure and function of proteins so they cannot simply be excluded by mutation without altering the essential properties. An example that will be discussed in the present paper is the transmembrane protein M2, found in Influenza viruses. It contains a highly conserved arginine residue, which has an interfering infrared spectrum but is involved in a salt bridge interaction with an aspartic acid in an adjacent helix, that is required to stabilize the transmembrane tetrameric structure.7
Two-dimensional infrared (2D-IR) spectroscopy is a unique tool, ideally suited to investigate the dynamics of protein vibrations.8,9 2D-IR methods have been applied to study a wide range of biological systems, from small peptides in solution to transmembrane channels; even to macroscopic fibrils.10-14 One of the key advantages of 2D-IR over conventional linear infrared experiments is that the coupling between different modes can be measured directly.15-20 The presence of cross-peaks in the 2DIR spectra is direct proof that two modes are interacting with each other. 2D-IR methods have used to investigate chemical exchange processes in equilibrium,10,21,22 wherein the system the system stochastically oscillates between two or more chemically distinct species. Cross peaks, which have signature time dependence, are also present in the event that energy transfer occurs between two modes.23-25 One of the most promising approaches for determining the structural dynamics of proteins at the residue level is the use of 13C=18O or 13C=16O isotope substitution at particular amide units.12,16,26-28 The isotopic shift for 13C=18O of ca. 60 cm-1 relocates the amide I vibrational mode with 13C=18O out of the spectral range of the 12C=16O transitions of the remaining backbone amides. This spectral isolation of the vibrational transition of one residue permits the design and implementation of 2D-IR experiments where the amide unit is used as a probe of the immediate environment. However, these isotopic substitutions do not always shift the amide out of the range of the side chain transitions, and hence the interpretations of structural dynamics can be made more difficult. Side chain transitions that appear in the amide I region include the antisymmetric CO2 - stretches of the carboxylate side chains of aspartic acid (aspartate) and glutamic acid (glutamate) and also the CN stretches of the guanidyl group of arginine.
IR results for side chain transitions
The Amide I mode has been used for structure and dynamics studies of proteins. As mentioned above, side chains of a number of amino acids appear in the same spectral region. Linear IR spectroscopy has systematically identified and assigned most of these sidechain transitions.1-6,29-31 Some side chain infrared spectra, such as Arg, Lys, Asp, and Glu show additional complexity due to them having pH dependent transitions.2 These transitions can shift in frequency depending on their protonation states causing the presence of one or even multiple peaks over a range of biological relevant pH's. Attempts to eliminate side chain absorptions in the linear spectra through subtraction methods have been suggested.5 Nevertheless, side chain transtions can also prove useful as potential vibrational spectral markers. For instance, Asp and Glu carboxylic groups have been suggested as a local probe of the hydrogen bonding status within a peptide system.30 Arginine has been shown to have two bands observed at 1586 and 1608 cm-1 due to the asymmetrical vibrations of the CN bonds of the guanidine group. Although these two overlapping bands are not always clearly observable,3 they have been well characterized in the linear infrared spectra.1,2,6 The interactions of these side chains with counterions and their involvement in salt bridge formation result in significant changes in the linear spectrum.3 The complications of the charged side chains is particularly apparent through 2D-IR studies on the transmembrane domain of the M2(M2TM) channel32 and the Villin Headpiece10 where the side chain bands can couple significantly with the amide I mode and mask isotope edited amide bands. Charged side chains have also been observed in 2D-IR studies of other large proteins.33 Only by characterizing the side chain transitions will it become possible to utilize them as intrinsic 2D-IR spectroscopic probes.10,34 As will be demonstrated here, 2D-IR spectroscopy can be utilized to characterize vibrational modes on the basis of their dynamics which adds a new dimension to the customary spectral location, bandwidth, cross section, and coupling.
Similarity of protonated arginine and guanidinium+
Recent 2DIR and ultrafast pump-probe experiments have measured energy transfer between two nearly degenerate modes of the guanidinium ion (Gdm+) in water.35,36 Isolated Gdm+ has D3 symmetry, with the C and three N atoms being on the plane perpendicular to the C3 axis. The IR spectrum of Gdm+ at ∼1600 cm-1 involves a degenerate vibration, having component transition dipoles oriented perpendicular to one another. In aqueous solution, the three-fold symmetry is slightly perturbed and the degeneracy is split by a few wavenumbers as the molecule adopts on average a lower symmetry configuration The solvent interactions induce picosecond timescale energy transfer between these nearly degenerate modes.35,36
The side chain of arginine consists of a guanidyl group, which presents us with a unique opportunity to identify and characterize the sidechain IR spectra of arginine because it differs from the Gdm+ system only by virtue of its broken symmetry caused by alkyl substitutions at one of the six N-H groups. The CN3 stretching modes of Gdm+ are no longer degenerate in arginine, but the amine substitution should only have a small effect on the degenerate normal mode. Therefore it is predicted on qualitative grounds that the fast energy transfer between the component states will not be significantly altered in arginine(Arg) compared to Gdm+. While linear infrared spectra can identify the two transitions of the split degeneracy, unequivocal assignments become difficult when overlapping transitions are present from other side chains as is typically encountered in proteins and peptides. 2D-IR spectroscopy has the key advantage of allowing direct observation of the ultrafast energy transfer between these modes, which should therefore serve as a unique spectral signature of arginine even in complex environments.
Experimental section
Peptide Synthesis
An arginine amino acid acetylated (Ac) at the N-terminus and methyl amindated (NHMe) at the C-terminus is subsequently referred to as the “ arginine dipeptide”. This dipeptide (Ac-Arg-CONHMe) was synthesized using standard Fmoc-protocols employing 3-(Methyl-Fmoc-amino)-methyl)-indol-1-yl) acetyl AM resin (EMD Chemicals, Inc.). After addition of the arginine residue, the peptide was acytelated using acetic anhydride. The peptide was purified to homogeneity by reverse-phase chromatography and characterized by mass-spectrometry. Following purification, the residual trifuoroacetic acid from peptide synthesis, which has a sharp mid-IR band centered at 1678 cm-1, was removed by multiple lyophilizations against a 0.1 DCl solution. The peptide was additionally exchanged in D2O and lyophilized. The peptide sample was prepared in D2O and titrated to a pH of 7.5. The synthesis of M2TM has been discussed in detail in a prior publication.32
Methods
A detailed description of the 2D-IR photon echo experiment and data processing has been discussed in detailed in earlier publications.16,37 Fourier-transform limited 75-80 fs pulses with a center frequency of 1600 cm-1 were used in the 2D-IR experiments. Three laser pulses each with an energy, ∼400 nJ, having wave vectors k1, k2, and k3, were incident to the sample to generate a signal in the direction ks= -k1+k2+k3 with the ordering 123 (rephasing) and 213 (nonrephasing). To obtain the absorptive spectra, the rephasing and nonrephasing 2D frequency spectra were properly phased and combined. To observe the dynamics of the spectra, the waiting time, T, between the second and third pulse, was varied from 0 to 3 ps. The signal was detected by heterodyning it with a local oscillator pulse that always preceded the signal pulse by a fixed interval of ∼1 ps. After appropriate Fourier transforms along the coherence, τ, and detection, t, axes, the 2D-IR spectra are plotted as ωτ vs. ωt. For polarization-dependent echo experiments the incident and local oscillator pulses passed through polarizers to produce either the same polarization for all pulses which measure the XXXX tensor signal, or perpendicular polarizations of (k1,k2) and (k3,ks) pulses corresponding to the XXYY tensor. FTIR spectra were recorded using a Nicolet 6700 spectrometer. A sample optical density of 0.1 (pathlength ∼25 μm) was used for all experiments.
Results
FTIR spectra
Figure 1 shows the linear FTIR spectrum of the arginine dipeptide in D2O at pH 7.5. The two modes from the sidechain guanidyl group are observed at 1587 cm-1 and 1610 cm-1, and labeled A1 and A2 respectively. Also shown in Figure 1 is the fit of the experimental spectrum to a sum of three Gaussian transitions which accounts for the two guanidyl modes and the Amide I transitions of the two CONH groups. The gaussian widths are 19 cm-1, 16 cm-1 and 32 cm-1 for the A1, A2 and the unresolved amide I mode pair respectively. The ratio of the integrated areas of the two guanidyl modes are found to be A1 : A2 =1.34 which establishes the ratio of the transition dipoles squared of the nearly degenerate components. This result is consistent with previous linear IR measurements on arginine in D2O.2
Figure 1.
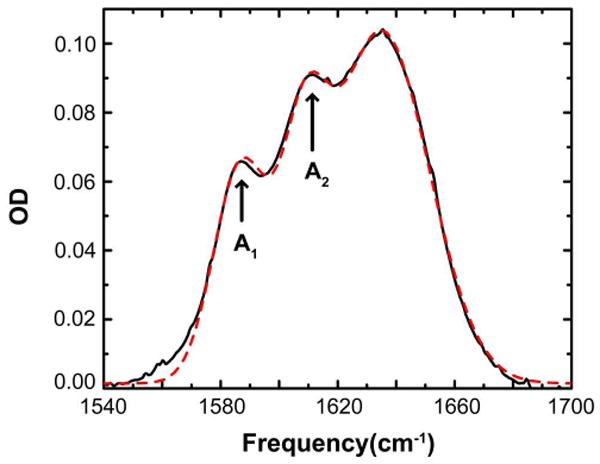
FTIR spectrum of arginine dipeptide (black). The fitted spectrum is plotted in red (dashed). The two guanidyl modes are labeled A1 and A2.
2D-IR Spectra
Figure 2 shows the 2DIR spectra of the arginine dipeptide in D2O for XXXX and XXYY polarization conditions at different values of the waiting time, T. The A1 and A2 arginine modes are peaked at {ωτ,ωt}={1587,1587 cm-1} and {ωτ,ωt}=. The backbone amide I mode, which appears as a single broad transition in the linear IR spectra, is split in the 2D-IR into two transitions, which very likely correspond to the two amide units present in the dipeptide.10,16,38 In Figure 2, these transitions are labeled as Am1 at {1631,1631 cm-1} and Am2 at {1642,1642 cm-1}. The 2D spectra in both polarizations are elongated along the diagonal at T=0 from the inhomogeneous broadening. The coupling between the putative nearly degenerate arginine modes is evidenced by the presence of a cross peak at {ωτ, ωt}={1587,1610 cm-1}, illustrated by the dotted circles in Figure 1B and 1E. With increasing waiting time, T, the spectra show increased relative signal strength in this cross peak region, a process which is strongly indicative of energy transfer between the two vibrations. The cross peak is more pronounced for the XXYY polarization, which is evident from comparison of spectra at equivalent waiting times for the two polarization conditions XXXX and XXYY. These observations are very similar to the results obtained for the guanidinium ion in water35,36 and strongly suggest that the 1587 cm-1 and 1610 cm-1 modes of arginine are also in dynamic equilibrium characterized by an ultrafast energy transfer process.
Figure 2.
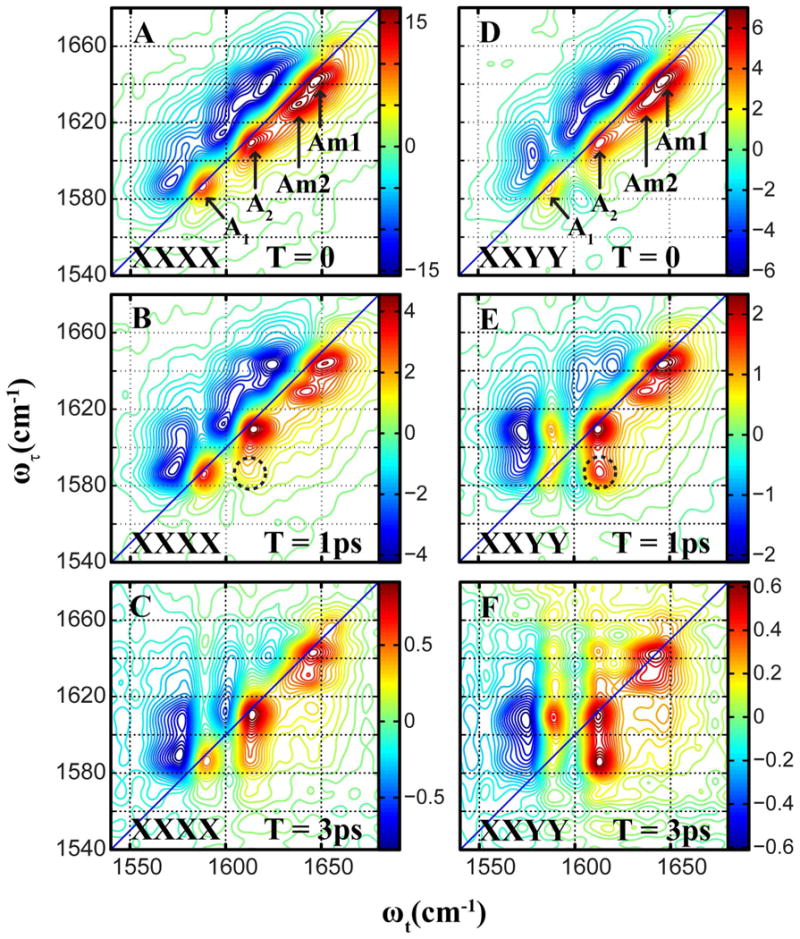
Absorptive 2D-IR spectra of arginine dipeptide in D2O for waiting times 0, 1ps and 3ps. The spectra for the XXXX polarization scheme are plotted on the left column, and those for the XXYY polarization scheme are plotted on the right column. The two Amide-I modes are labeled Am1 and Am2. The cross peak region is shown in dotted circles.
The timescale of the evolution of the cross peak signals (S12 implies excitation of mode 1 and probing that of 2) was characterized by the ratio of the integrated volumes (number of voxels within a given diameter in frequency space) at the cross peak and the diagonal peak as a function of the waiting time. Although both signals depend on the population relaxation, T1, their ratio is independent of this relaxation process, which then only causes the overall signal to decay during T. It is assumed that T1 is the same for both of the modes. Vibrational relaxation into the symmetric stretch(ss) transition may dominate the T1 relaxation pathways, but we assume such processes do not modify the discussion of the inter mode energy transfer. For an accurate estimate of the cross peak growth due to energy transfer, the absorptive spectra at T=0 were subtracted from those at longer waiting times, T>0. The resulting cross peak : diagonal peak ratios S12(T)/S22(T) subtracted from those at T=0 are shown in Figure 3 for the two polarization conditions, along with their fits to exponential growth functions. The characteristic exponential rate coefficient, ket, required to fit these data was determined to be 1/(2.1 ps). The details of the model used for the fits are discussed in detail later.
Figure 3.
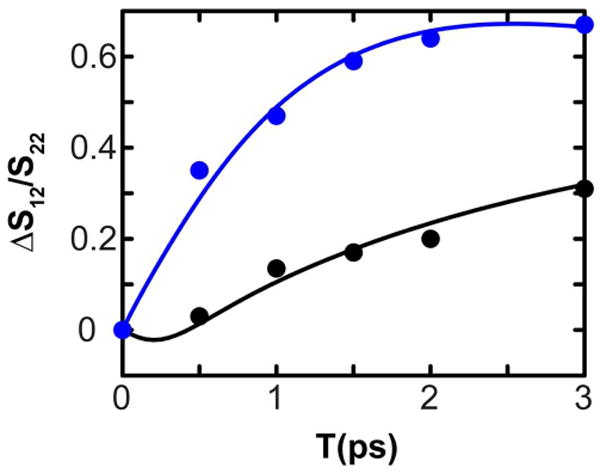
Cross peak : Diagonal peak evolution with T for XXXX (black) and XXYY (blue) polarization schemes of the guanidyl modes of arginine dipeptide. The filled circles are the experimentally obtained values, and the solid lines are the respective fits to the data. The S12/S22 value at T=0 was subtracted from each data point to give ΔS12/S22, according to equation 11.
Discussion
Theory of spectra
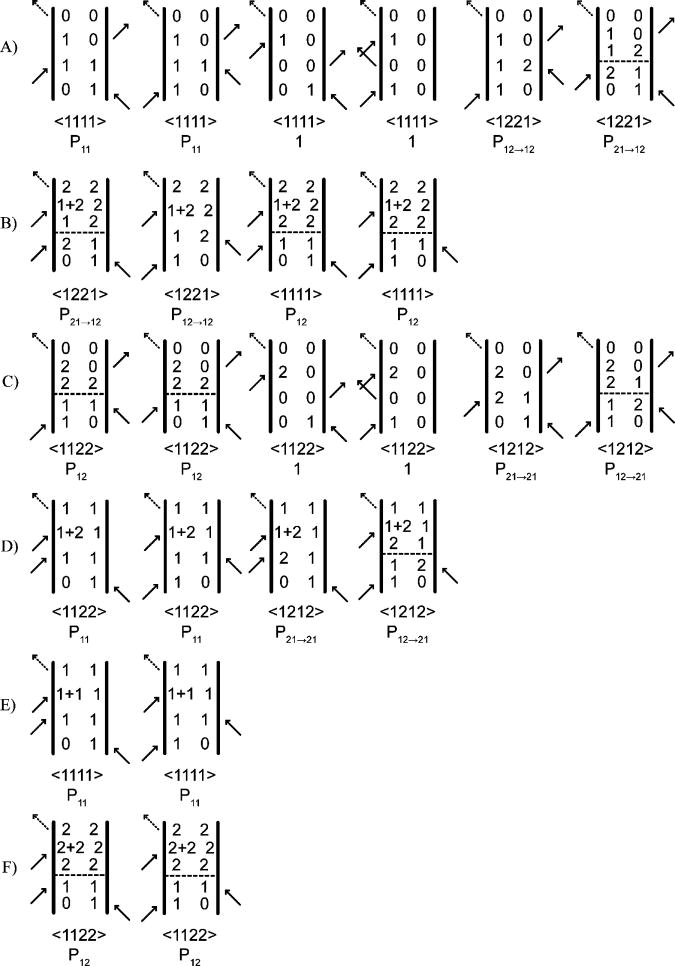
As discussed above, the protonated side chain of arginine can be regarded as a guanidinium ion with broken symmetry, where one of the six amine hydrogen atoms is linked to the alkyl portion of the arginine side chain. This substitution perturbs the threefold symmetry of the guanidyl moiety, which must split the degenerate CN stretching mode into two bands. It is well known that even in Gdm+, the three amine groups are not exactly equivalent because a small splitting of 10 cm-1 is observed in water,36 indicating that it does not have a three-fold axis of symmetry. The frequency splitting observed in the arginine dipeptide is 23cm-1. These splittings in protonated arginine and Gdm+ are both very small compared with the vibrational frequency and the individual vibrational transitions are partially overlapped. It is therefore reasonable to assume that the modes are well described by a weakly perturbed degenerate oscillator. Therefore we use a model having two harmonic one-quantum states, |1〉 = 10〉 and |2〉 = 01〉, which are the two nearly degenerate guanidyl eigenstates. The dipole moments corresponding to the transitions to these states from the ground state |00〉 are nearly perpendicular to one another for isolated Gdm+. For arginine, the perturbation to the symmetry caused by the amino acid moiety results in this angle deviating from 90°, as will be shown later. There are three two-quanta eigenstates involved in the 2D-IR spectra; |20〉, |02〉, and |11〉, corresponding to the overtones and a combination mode. The eigenenergies of these states are the averages of those in the water solution. The Liouville pathway diagrams considered in the model are shown in Figure 4. The energy transfer between the one quantum modes is taken into account by allowing spontaneous jumps from one state to the other during the waiting time T. Similarly, a coherence created by the second pulse may also transform to its conjugate during T. The transformations of the populations and the coherences are denoted in the diagrams by dotted lines. For degenerate vibrational modes, the Redfield matrix elements coupling the populations and coherences created by the interaction of the second pulse are zero.39 Thus, for the nearly degenerate modes of arginine, it is reasonable to approximate that the coupling between populations and coherences can be neglected. The populations and coherences then can be treated independently with separate master equations:
Figure 4.
Liouville pathways for two coupled oscillators for the echo signal emitted in the −k1+k2+k3 direction. Horizontal dashed lines imply a spontaneous coherence or population transfer in the corresponding time period. The diagrams are arranged according to their detection frequency on the ωt. axis. (A) ωt = ω1; (B) ωt = ω1 - δ; (C) ωt = ω2; (D) ωt = ω2 - δ; (E) ωt = ω1-Δ; and (F) ωt = ω2-Δ; where Δ is the diagonal and δ the mixed mode anharmonicity.
| (1) |
and
| (2) |
The rates for these processes, kii→jj and kij→ji, which are exactly equal for two degenerate modes, were assumed to be equal for the near degeneracy of the guanidyl modes36, and denoted as ket. γ is the coherence dephasing rate. Coherence transfers during the τ period are neglected because they involve fluctuations of the bath at the frequency of the fundamental transitions, and might be expected to be slower.36 Thus, each pathway involving the evolution of a population during T, as represented in Figure 4, has an associated conditional probability P that energy transfer between the modes will occur during the T evolution. Pii→jj (T) is the probability that if a molecule is put into a population state i at T=0 it will be found in the state j at time T, where i,j =1,2. The conditional probability factors can be calculated from equation 1 and they are:
| (3) |
Diagrams that involve the ground state bleaching during T are assumed to have a T-independent conditional probability distribution because if a molecule is in the ground state at T=0 then it will still be in the ground state at all T>0. Of course the v=1 populations of both states 1 and 2 are decreasing and the ground state population is growing with time constant T1, assumed equal for both excited states. Vibrational relaxation into states having spectra different from the ground state was neglected. Thus with this notation, the population in the ensemble of |i〉 at delay time T is aie−T/T1 (Pii + Pij) = aieT/T where the initial population at T=0 is ai. The pathways that involve the evolution of a coherence during T also need to be considered. The density operator of the sub-ensemble of the system in which the interaction with the second pulse has created a coherence that can be calculated from Equations 2 as:
| (4) |
where the coefficients are given by:
| (5) |
| (6) |
with .
According to this model, there are signals from the contributions to the electric polarizations from processes described by the 24 diagrams shown in Figure 4. If a slice of the 2D-IR spectrum is taken along ωτ = ω1 (where ω1 = 1587 cm-1 and ω2 = 1610 cm-1), these signals appear at 6 separate ωt frequencies: (A) ωt=ω1, (B) ωt= ω1 − δ, (C) ωt= ω2, (D) ωt=ω2−δ, (E) ωt = ω1 −Δ and (F) ωt = ω2 −Δ; where Δ is the diagonal anharmonicity assumed to be equal for the two modes; and δ is the mixed mode anharmonicity. The ωt frequencies and the kinetic probabilities associated of each pathway are shown in Figure 4. For modeling the S12 and S22 signals a vertical trace in the region ωt = ω1 was employed with the pathways involving Δ being neglected. For these conditions the signals measured in the experiments, which are the real parts of the double half-Fourier transforms of the responses, can be represented as follows:
| (7) |
where f(T) describes the dynamics of the system during T which includes an oscillatory term at the difference frequency of the two modes. S(τ,t,T) is the third order time domain signal and the primes and double primes indicate real and imaginary parts. The calculation of the volume under a peak involves integration over frequencies ωτ and ωt. The integrated signal (Sint) is:
| (8) |
Here we have set to zero the integral over all frequencies of the imaginary part of the spectral signal, S″(ωτ, ωt) The integrals of the real part of the signal over all frequencies were assumed to have the same value for all pathways. In practice we cannot integrate over “all frequencies” but the imaginary parts were nevertheless neglected in analyzing the data.
Polarization dependence
Each diagram corresponding to a pathway (ijkl) also is associated with an orientational average factor 〈iajakblb〈 where the two laboratory polarization conditions a,b used in the experiment were either a=b=X or a=X, b=Y. The expressions for the orientational factors for the XXXX and XXYY polarizations and their dependence on the rotational diffusion coefficient D for a spherical rotor have been tabulated previously.40 In the present model, the signal contribution from any diagram includes the kinetic and orientational factors along with a 2D spectral shape factor arising from the Fourier transform of the corresponding third-order response along τ and t. Every term includes a scalar transition dipole factor μiμjμkμl, which is always either or . Assuming that the spectral shape factors are the same for all the pathways, and δ is very small, we can write out an approximation to the ratio of the cross peak to the diagonal 2D-IR signals as in Equation 9. In the first line of equation the contribution from each diagram from Figure 4 is written down explicitly and the transition dipole factors are rationalized:
| (9) |
As T goes to infinity, . The orientational factors 〈iajakblb〉 are implicitly dependent on T.40 Therefore, limiting values of S12/S22 for a given polarization condition depend on the values of these factors as T → ∞, denoted by the subscript. If the mixed mode anharmonicity, δ, is not negligibly small, then the signal at {ωτ, ωt} = {ω1, ω2} becomes dominated by the pathways illustrated in row C, Figure 4. Similarly, the diagonal peak signal at {ωt = ω2} is dominated by the diagrams in row A, Figure 4. In that case, the ratio of the cross peak to the diagonal peak signal becomes
| (10) |
We define Δ(S12/S22) as the difference between the ratio at T and that at T=0 so that from Equation (10), this factor is given by:
| (11) |
For perpendicular transitions and in absence of any rotational diffusion, Δ(S12/S22) approaches 0.145 and 1.27 for XXXX and XXYY polarization conditions respectively, as T → ∞. The deviation of the experimental data from these values indicates that the guanidyl transitions are not perpendicularly polarized. This result is understood to arise from the perturbation by the alkyl substitution. The fits of Equation 11 to the experiments are shown in Figure 3. The fitted value of ket is 1/2.1 ps-1 which is close to 1/1.9 ps-1 obtained for guanidinium chloride in D2O.36 The square of the cosine of the angle between the two transition dipoles is also obtained from the fit and gives two possible angles of 66° or 114°; this suggests that the perturbation introduced by amino acid moiety is significant and rotates the transition dipoles by 24 ° from their perpendicular orientation expected for the threefold symmetry in the guanidinium ion. The rotational diffusion time is estimated from the fits to be very long at ca. 51 ps.
Ab Initio calculations on methyl guanidinium
The experiments reveal a strong similarity between protonated arginine and the IR spectra and their associated dynamics at equilibrium of the two nearly degenerate CN stretch components of Gdm+. For Gdm+ in D2O the free ion is slightly distorted from three fold symmetry, presumably because a distorted hydrogen bonded structure was more stable than the symmetric one in the D2O environment. Contrastingly, the alkyl substituted Gdm+ of the protonated arginine is chemically modified in such a manner that it is intrinsically asymmetric. In order to assess the consequences of such intrinsic asymmetry we have used computations to investigate the effects of methyl substitution on one of the Gdm+ amine groups. We expect that a substantial fraction of the asymmetry splitting in protonated arginine will be modeled by a methyl substitution. Therefore ab initio calculations were performed on methyl guanidinium (MGdm+): [CND5CH3]+ by means of Gaussian03 package and B3LYP Density Functional Theory (DFT) method with a basis of 6-31G. The computation shows vibrations at 1633 cm-1 and 1657 cm-1 that correlate with the degenerate modes of Gdm+ in the gas phase found with the same method at 1642 cm-1.The perturbation introduced by the methyl group splits the degeneracy of the two guanidyl modes by ∼20 cm-1, which is close to the experimental value. Computation of the transition dipole vectors (Figure 5) shows that the methyl perturbation causes the angle between the dipoles to change from 90° in Gdm+ to 99° in methyl guanidinium+. The angle estimated from experiment on the dipeptide is 114°. The computed infrared cross section of the higher frequency A2 mode is larger than that of A1; experimentally the opposite trend is seen. The nearly degenerate normal modes of the guanidyl group in MGdm+ are depicted in Figure 5, along with the degenerate modes of Gdm+.
Figure 5.
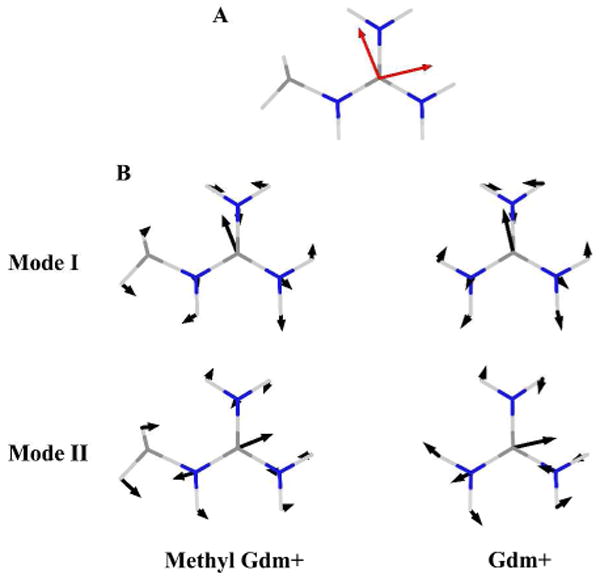
A: Transition dipole directions(red) of the nearly degenerate modes of methyl guanidinium. B: The nearly degenerate normal modes of methyl guanidinium (left) and the degenerate modes of Gdm+(right). The atomic displacements are indicated with blue arrows.
Detection of arginine in proteins by 2D-IR
The foregoing results show that the side chain of protonated arginine has a highly distinctive 2D-IR spectrum. Conventional spectroscopy shows that it has two bands but 2D-IR exposes through easily identifiable cross peaks that the arginine side chain bands are strongly coupled and in rapid equilibrium exchange with one another. The arginine pKa is high at ca. ∼11 and hence will display these dynamic properties characteristic of the protonated form at practically all biologically relevant pH values. The present experiments are carried out at pH 7.5, and the side chain is in its biologically ubiquitous protonated form. For transmembrane systems like the M2 channel discussed below, arginine is a highly conserved residue, necessary for the helix tetramer structure because of its ability to form a salt bridge with Asp44 of adjacent helices. Thus the background signals from Arg, which are in the same spectral range as isotopically labeled amide vibrations, cannot be avoided by employing mutants. Therefore it is very useful to have a method that can clearly identify these transitions and hence provide the parameters to quantitatively analyze its contributions to isotopically edited protein studies.
The arginine vibrations in the M2 channel
The M2 transmembrane protein is found in the Influenza viruses. The channel is activated at low pH to transport protons across the membrane to acidify the viral interior; a process that is vital to the replication of the Influenza A virus.7,41 The protein is a homo-tetramer consisting of N-terminal, transmembrane(TM), and cytoplasmic domains. The twenty five residue TM domain (M2TM), residues 22-46, forms four-helix bundles that conduct protons. All strains of M2 have a highly conserved arginine residue (Arg45), and crystal structures have suggested that this residue is involved in a trans-helix salt bridge interaction with Asp44.7 Thus M2 provides us with an opportunity to study the arginine band in a biological environment and also understand the effects of salt bridge interactions on the guanidyl modes and their energy transfer. Figure 6 shows the 2D-IR spectra of M2TM in DPC micelles at pH 6.2 at T values of 0 and 2ps for XXXX and XXYY polarization conditions. The two guanidyl modes appear at 1610 cm-1 and 1582 cm-1. The assignment of these modes among many nearby bands is made apparent by the rapid energy transfer between them, evidenced by the growth of cross peaks as clearly seen in the 2D-IR spectra. The cross peaks are more enhanced for the XXYY polarization scheme, similar to the dipeptide and Gdm+. Thus the energy transfer and polarization dependence of the 2D spectra unequivocally establish the assignment. Such assignments are crucial and the detailed knowledge of the sidechain modes of arginine is pivotal in analysis of spectra involving isotope labeled transitions, as has been shown elsewhere.32 Figure 7 shows the evolution of the S12/S22 signal with T for the XXXX and XXYY polarization conditions. The energy transfer rate obtained from the fit is ket = 1/1.8 ps-1. The angle between the dipoles is obtained to be 31° or 149°. These values are consistent with those obtained for the arginine dipeptide. The ratio of the transition dipoles could not be estimated accurately from the linear IR spectra, and was therefore allowed to vary for the fitting of the 2D-IR spectra. The fit yields . This value is similar to what was measured for the arginine dipeptide. This result implies that the nature of the perturbation to the guanidyl modes in the dipeptide and the tetrameric assembly in M2 must be quite similar. The rotational diffusion time was estimated to be longer than 100ps. Armed with these data for Arg45 of M2 we were able to eliminate its effect on the recent measurements of vibrational dynamics of isotopically substituted residues needed to describe the dynamics of water in the M2 channel.32
Figure 6.
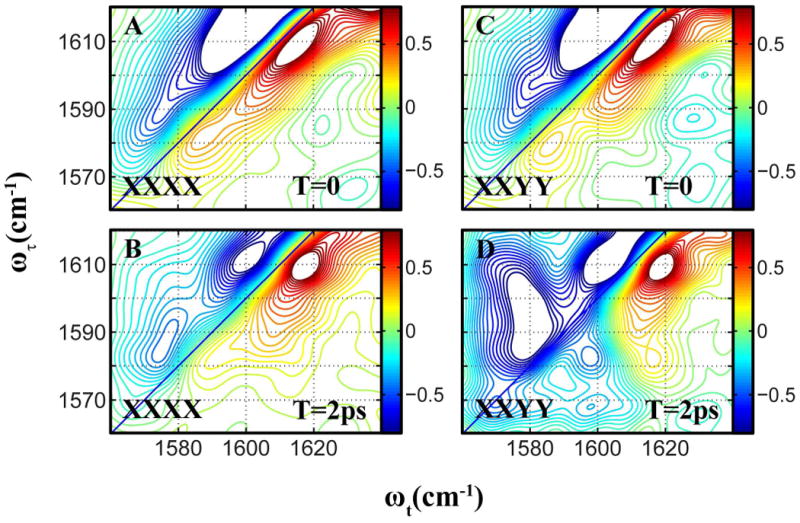
Absorptive 2D-IR spectra of the guanidyl modes of M2TM in DPC micelles at pH 6.2, for waiting times 0 and 2 ps. The spectra for the XXXX polarization condition are plotted on the left column, and those for the XXYY condition are plotted on the right column.
Figure 7.
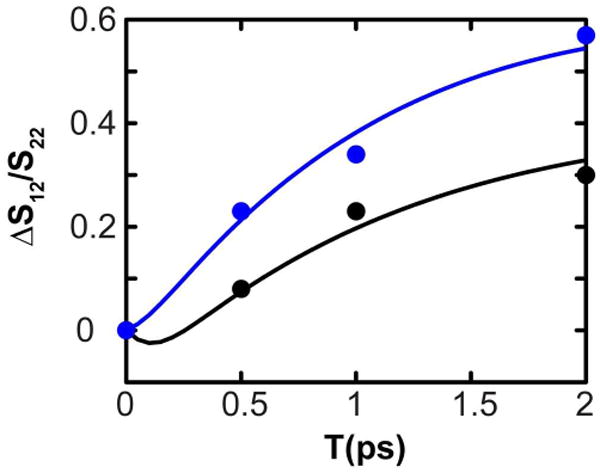
Cross peak : Diagonal peak evolution with T for XXXX (black) and XXYY (blue) polarization schemes for the guanidyl modes of M2TM. The filled circles are the experimentally obtained values, and the solid lines are the respective fits to the data. The value S12/S22 value at T=0 was subtracted from each data point to give ΔS12/S22.
Coupling of arginine side chain modes to the peptide backbone amides
The dipeptide 2D-IR spectra in Figure 6 show cross peaks between the arginine and the peptide amide modes. These peaks are particularly clear for the coupling of the higher frequency (A2) mode and the two amide (Am1 and Am2) modes. The cross peak signal at {ωτ, ωt} = {ωA2,ωAm1} is measured from the 2D spectra for both polarizations. For both XXXX and XXYY polarization schemes, the cross peak appears to have an oscillatory behavior on the T axis (data not shown). From Figure 4, it can be readily checked that the cross peak signal from two coupled modes has contributions from pathways that involve evolution of coherences during T; these pathways can cause an oscillatory time evolution of cross peak signals. Thus, while such oscillatory behavior is expected on the basis of a simple coupling mechanism, more complex processes, including energy transfer, can influence the time dependence of cross peak signals. The large coupling between the backbone amide I modes and the guanidyl vibrations suggests that the peptide is in a conformation where the side chain is oriented in a configuration where the amide and the guanidyl moieties are relatively close to one another.
Residual anharmonic coupling corresponding to a signal at T=0
There are cross peaks between the nearly degenerate modes at T=0. An estimate yields roughly the values 0.36 and 0.29 for S12/S22 for XXXX and XXYY polarization conditions at T=0. Equation 4 predicts that there should be residual cross peaks at T=0 having S12/S22 ratios of 0.45 and 1.4 at T=0. The predicted values for both XXXX and XXYY polarization conditions are markedly different from the experimentally measured ratios. It has been assumed that the signals from the positive diagonal and cross peaks can be regarded to be free of any significant interference with the anharmonically shifted negative peaks. However when Δ12 is small, spectral overlap of the positive and negative cross peaks reduces the ratio of the cross to diagonal peaks for different polarizations. In the limit Δ12 → 0, the cross peaks should cancel, leading to no cross peak signal. The presence of cross peaks between the two guanidyl modes at T=0 indicates that we are in the intermediate regime. Moreover, the cross peak at ωt = ω2 - Δ overlaps strongly with the diagonal peak at ωt = ω1 and the cross peak at ωt = ω2, likely leading to erroneous estimates of the positive cross peak intensity at ωt = ω2. Subtracting the ratio at T=0 from the ratio at other T's focuses the measurement on only the part of the signal that grows with T and errors in measuring the absolute values of the ratio have been largely avoided.
Conclusions
The CN stretching modes of the arginine side chain guanidyl moieties are examined by two-dimensional infrared spectroscopy in D2O. Arginine has a sidechain guanidyl group having the degenerate modes of the parent guanidinium (Gdm+) split into two transitions in the infrared spectrum. These modes have been characterized by the energy transfer directly observed in the time dependence of the 2D-IR spectra. The energy transfer rates between the two modes are 1/2.0 ps-1 and 1/1.8 ps-1 for the arginine dipeptide and Arg45 of the M2 protein, respectively, in close agreement with previous findings for Gdm+, where the energy transfer was shown to result from a reconfiguration of the H-bonded water molecules around the perimeter forcing significant variations of the NH2 geometries. The NH2 groups are bending out of plane and wagging in response to their interactions with the water molecules. The splitting of the degeneracy of the CN stretching mode is accomplished by the solvent interactions. Arginine, on the other hand, has an inherent break in the symmetry of the guanidimium side chain because of the alkyl substitution at one of the amine groups. However, the similarity of the energy transfer rates suggests the same mechanism of transfer operates in both cases. Identification by 2D IR of these modes is important for studies of biological systems that contain arginine side chains. By understanding these transitions, one can characterize more clearly the environment of the arginine and use it to examine dynamics in proteins. Furthermore a definitive assignment procedure for arginine residues can prove extremely valuable as an analytic tool in infrared studies of proteins.
Acknowledgments
The research was supported by NIH GM 12592 and NSF and instrumentation developed at the Research Resource (NIH RR01348). We thank Dr. Jade Qiu and Professor William F. DeGrado for the synthesis of the M2 peptides.
References
- 1.Barth A. Progress in Biophysics & Molecular Biology. 2000;74:141–173. doi: 10.1016/s0079-6107(00)00021-3. [DOI] [PubMed] [Google Scholar]
- 2.Chirgadze YN, Fedorov OV, Trushina NP. Biopolymers. 1975;14:679–694. doi: 10.1002/bip.1975.360140402. [DOI] [PubMed] [Google Scholar]
- 3.Hernandez B, Pfluger F, Derbel N, De Coninck J, Ghomi M. Journal of Physical Chemistry B. 2010;114:1077–1088. doi: 10.1021/jp909517r. [DOI] [PubMed] [Google Scholar]
- 4.Hernandez B, Pfluger F, Nsangou M, Ghomi M. Journal of Physical Chemistry B. 2009;113:3169–3178. doi: 10.1021/jp809204d. [DOI] [PubMed] [Google Scholar]
- 5.Rahmelow K, Hubner W, Ackermann T. Analytical Biochemistry. 1998;257:1–11. doi: 10.1006/abio.1997.2502. [DOI] [PubMed] [Google Scholar]
- 6.Venyaminov SY, Kalnin NN. Biopolymers. 1990;30:1243–1257. doi: 10.1002/bip.360301309. [DOI] [PubMed] [Google Scholar]
- 7.Stouffer AL, Acharya R, Salom D, Levine AS, Di Costanzo L, Soto CS, Tereshko V, Nanda V, Stayrook S, DeGrado WF. Nature. 2008;451:596–U513. doi: 10.1038/nature06528. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Ganim Z, Chung HS, Smith AW, Deflores LP, Jones KC, Tokmakoff A. Accounts of Chemical Research. 2008;41:432–441. doi: 10.1021/ar700188n. [DOI] [PubMed] [Google Scholar]
- 9.Kim YS, Hochstrasser RM. Journal of Physical Chemistry B. 2009;113:8231–8251. doi: 10.1021/jp8113978. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Bagchi S, Falvo C, Mukamel S, Hochstrasser RM. Journal of Physical Chemistry B. 2009;113:11260–11273. doi: 10.1021/jp900245s. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Fang C, Senes A, Cristian L, DeGrado WF, Hochstrasser RM. Proceedings of the National Academy of Sciences of the United States of America. 2006;103:16740–16745. doi: 10.1073/pnas.0608243103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Fang C, Wang J, Kim YS, Charnley AK, Barber-Armstrong W, Smith AB, Decatur SM, Hochstrasser RM. Journal of Physical Chemistry B. 2004;108:10415–10427. [Google Scholar]
- 13.Kim YS, Liu L, Axelsen PH, Hochstrasser RM. Proceedings of the National Academy of Sciences of the United States of America. 2008;105:7720–7725. doi: 10.1073/pnas.0802993105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Manor J, Mukherjee P, Lin YS, Leonov H, Skinner JL, Zanni MT, Arkin IT. Structure. 2009;17:247–254. doi: 10.1016/j.str.2008.12.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.DeFlores LP, Ganim Z, Nicodemus RA, Tokmakoff A. Journal of the American Chemical Society. 2009;131:3385–3391. doi: 10.1021/ja8094922. [DOI] [PubMed] [Google Scholar]
- 16.Kim YS, Wang JP, Hochstrasser RM. Journal of Physical Chemistry B. 2005;109:7511–7521. doi: 10.1021/jp044989d. [DOI] [PubMed] [Google Scholar]
- 17.Kurochkin DV, Naraharisetty SRG, Rubtsov IV. Journal of Physical Chemistry A. 2005;109:10799–10802. doi: 10.1021/jp055811+. [DOI] [PubMed] [Google Scholar]
- 18.Lim M, Hochstrasser RM. Journal of Chemical Physics. 2001;115:7629–7643. [Google Scholar]
- 19.Rubtsov IV, Wang JP, Hochstrasser RM. Proceedings of the National Academy of Sciences of the United States of America. 2003;100:5601–5606. doi: 10.1073/pnas.0931292100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Tucker MJ, Kim YS, Hochstrasser RM. Chemical Physics Letters. 2009;470:80–84. doi: 10.1016/j.cplett.2009.01.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Kim YS, Hochstrasser RM. Proceedings of the National Academy of Sciences of the United States of America. 2005;102:11185–11190. doi: 10.1073/pnas.0504865102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Ghosh A, Remorino A, Tucker MJ, Hochstrasser RM. Chemical Physics Letters. 2009;469:325–330. doi: 10.1016/j.cplett.2008.12.094. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Cahoon JF, Sawyer KR, Schlegel JP, Harris CB. Science. 2008;319:1820–1823. doi: 10.1126/science.1154041. [DOI] [PubMed] [Google Scholar]
- 24.Khalil M, Demirdoven N, Tokmakoff A. Journal of Chemical Physics. 2004;121:362–373. doi: 10.1063/1.1756870. [DOI] [PubMed] [Google Scholar]
- 25.Kurochkin DV, Naraharisetty SRG, Rubtsov IV. Proceedings of the National Academy of Sciences of the United States of America. 2007;104:14209–14214. doi: 10.1073/pnas.0700560104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Torres J, Kukol A, Goodman JM, Arkin IT. Biopolymers. 2001;59:396–401. doi: 10.1002/1097-0282(200111)59:6<396::AID-BIP1044>3.0.CO;2-Y. [DOI] [PubMed] [Google Scholar]
- 27.Fang C, Hochstrasser RM. Journal of Physical Chemistry B. 2005;109:18652–18663. doi: 10.1021/jp052525p. [DOI] [PubMed] [Google Scholar]
- 28.Hauser K, Krejtschi C, Huang R, Wu L, Keiderling TA. Journal of the American Chemical Society. 2008;130:2984–2992. doi: 10.1021/ja074215l. [DOI] [PubMed] [Google Scholar]
- 29.Kumar S, Rai SB. Indian Journal of Pure & Applied Physics. 2010;48:251–255. [Google Scholar]
- 30.Nie BN, Stutzman J, Xie AH. Biophysical Journal. 2005;88:2833–2847. doi: 10.1529/biophysj.104.047639. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Pfluger F, Hernandez B, Ghomi M. Journal of Physical Chemistry B. 2010;114:9072–9083. doi: 10.1021/jp103348y. [DOI] [PubMed] [Google Scholar]
- 32.Ghosh A, Qiu J, Degrado WF, Hochstrasser RM. Proceedings of the National Academy of Sciences of the United States of America. 2011 doi: 10.1073/pnas.1103027108. submitted. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.DeFlores LP, Tokmakoff A. Journal of the American Chemical Society. 2006;128:16520–16521. doi: 10.1021/ja067723o. [DOI] [PubMed] [Google Scholar]
- 34.Kuroda DG, Vorobyev DY, Hochstrasser RM. Journal of Chemical Physics. 2010;132 doi: 10.1063/1.3285265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Vorobyev DY, Kuo CH, Chen JX, Kuroda DG, Scott JN, Vanderkooi JM, Hochstrasser RM. Journal of Physical Chemistry B. 2009;113:15382–15391. doi: 10.1021/jp9069256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Vorobyev DY, Kuo CH, Kuroda DG, Scott JN, Vanderkooi JM, Hochstrasser RM. Journal of Physical Chemistry B. 2010;114:2944–2953. doi: 10.1021/jp909531s. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Kim YS, Hochstrasser RM. Journal of Physical Chemistry B. 2005;109:6884–6891. doi: 10.1021/jp0449511. [DOI] [PubMed] [Google Scholar]
- 38.Wang JP. Journal of Physical Chemistry B. 2008;112:4790–4800. doi: 10.1021/jp710641x. [DOI] [PubMed] [Google Scholar]
- 39.Redfield AG. Advances in Magnetic Resonance. 1966;1:1–32. [Google Scholar]
- 40.Hochstrasser RM. Chemical Physics. 2001;266:273–284. [Google Scholar]
- 41.Pinto LH, Lamb RA. J Biol Chem. 2006;281:8997–9000. doi: 10.1074/jbc.R500020200. [DOI] [PubMed] [Google Scholar]