A bidirectional interface growth model for cranial interosseous suture morphogenesis

Abstract

Interosseous sutures exhibit highly variable patterns of interdigitation and corrugation. Recent research has identified fundamental molecular mechanisms of suture formation, and computer models have been used to simulate suture morphogenesis. However, the role of bone strain in the development of complex sutures is largely unknown, and measuring suture morphologies beyond the evaluation of fractal dimensions remains a challenge. Here we propose a morphogenetic model of suture formation, which is based on the paradigm of Laplacian interface growth. Computer simulations of suture morphogenesis under various boundary conditions generate a wide variety of synthetic sutural forms. Their morphologies are quantified with a combination of Fourier analysis and principal components analysis, and compared with natural morphological variation in an ontogenetic sample of human interparietal suture lines. Morphometric analyses indicate that natural sutural shapes exhibit a complex distribution in morphospace. The distribution of synthetic sutures closely matches the natural distribution. In both natural and synthetic systems, sutural complexity increases during morphogenesis. Exploration of the parameter space of the simulation system indicates that variation in strain and/or morphogen sensitivity and viscosity of sutural tissue may be key factors in generating the large variability of natural suture complexity.

Introduction

The complex and corrugated shape of cranial interosseous sutures has long attracted the attention of morphologists. Sutures represent growth interfaces at which two osteogenic fronts meet and interact with each other (Rice, 2007a,b;). Cranial sutures act as bone growth sites, permitting expansion of the braincase and extension of the face (Opperman, 2000; Rice, 2007a,b;). Beyond their primary function as regions of bone growth sutures have been proposed to act as strain dissipators. Suture lines are often highly corrugated, thus providing large effective contact interfaces between adjacent bony elements, which might dissipate strain and reduce local peak strain (Sun et al. 2004). This hypothesis is corroborated by evidence from sheep, where male crania exposed to high peak strains during head-to-head confrontation with competitors exhibit more corrugated interosseous sutures than female crania (Jaslow, 1989). Similarly, patent sutures in adults of species generating high masticatory strain have been interpreted as strain dissipators (Rayfield, 2005). Also, there is experimental evidence that the morphogenesis of suture interdigitation directly depends on the presence of strain (Moss, 1961), and increases as a response to external forces (Rafferty & Herring, 1999; Sun et al. 2004; Byron, 2009). A recent morphometric study on human interparietal sutures provides further evidence for a direct correlation between sutural complexity and strain (Mann et al. 2009).

Various methods have been proposed to classify and/or quantify the shape of human cranial interosseous sutures (Hauser et al. 1991), and to use this information to infer sex and age at death of osteoarcheological specimens (Lovejoy et al. 1985; Meindl & Lovejoy, 1985; Mann et al. 1987; Meindl et al. 1990; Hershkovitz et al. 1997; Schiwy-Bochat, 2001; Lynnerup & Jacobsen, 2003; Skrzat & Walocha, 2003; Sahni et al. 2005; Wu et al. 2007; Wittwer-Backofen et al. 2008). Classification systems typically define different degrees of ‘corrugatedness’ of the suture line, while quantitative methods rely on fractal analysis. Estimated fractal dimensions D of interparietal suture lines vary between 1.0 (straight line) and about 1.30 (Hartwig, 1991; Long & Long, 1992; Skrzat & Walocha, 2003; Yu et al. 2003). However, while suture obliteration is clearly (although weakly) correlated with individual age (Meindl & Lovejoy, 1985; Meindl et al. 1990; Wittwer-Backofen et al. 2008; Harth et al. 2009), correlation between the fractal dimension of cranial sutures and individual age could not be confirmed (Lynnerup & Jacobsen, 2003; Yu et al. 2003), such that it appears that cranial suture complexity is only marginally useful for age determination of mature individuals (Hershkovitz et al. 1997). Nevertheless, the complexity of the interparietal suture increases during the first 10 years of life, as has been shown in a study using Fourier analysis (FA) to quantify suture line excursions from the midsagittal plane (Wu et al. 2007).

Techniques such as tissue culture and histochemistry have been used extensively to elucidate the molecular mechanisms of suture formation (Ogle et al. 2004; Morriss-Kay & Wilkie, 2005; Opperman & Rawlins, 2005; Miura et al. 2009). Also, non-invasive imaging techniques such as micro-computed tomography and synchrotron tomography are increasingly used to analyze the micromorphology of sutures (Skrzat et al. 2002; Reinholt et al. 2009; Corega et al. 2010; Harth et al. 2010; Regelsberger et al. 2010). Miura et al. (2009) integrated the current knowledge about the molecular basis of suture formation into a morphogenetic model, and showed that a reaction-diffusion (RD) model involving two classes of molecules is well suited to reproduce many of the characteristic features of convoluted suture lines. One important perspective offered by this study is that standard morphogenetic models provide valuable approximations of complex regulatory genomic networks governing pattern formation (Kondo & Miura, 2010).

Cranial suture biology has also become an important focus of clinically oriented research. Data on suture formation at different levels of organization are integrated to investigate how molecular (Kim et al. 1998; Ogle et al. 2004), cellular and biomechanical mechanisms act together to give rise to the wide variety of observed sutural forms (Opperman et al. 1999; Opperman, 2000; Henderson et al. 2004; Opperman & Rawlins, 2005; Byron, 2006; Vij & Mao, 2006), and how disruption of normal signaling pathways leads to congenital malformations of the head involving premature suture closure (Cohen, 2002; Connerney et al. 2006). Along another line of research, various biophysical, molecular and cellular models have been proposed to study suture formation by means of computer simulations. These models investigate the role of statistical fluctuations (Oota et al. 2006), biochemical/cellular mechanisms (Miura et al. 2009) and strain (Garcia-Ruiz et al. 1990).

Based on current empirical evidence, cranial suture morphogenesis thus appears as a multifactorial process, in which local mechanisms of tissue differentiation and surface growth lead to globally convoluted structures. Various questions, however, remain open. For example, while it has been shown that osteocytes are strain-sensitive and that bone growth is a strain-mediated process, the possible role of bone strain during suture morphogenesis and its implications for suture morphology have not yet been studied in detail. Specifically, it remains to be tested whether suture morphology reflects in vivo adaptation to strain, and whether it is functionally optimized for strain dissipation and mechanical stability. A second open question is how sutural form and form variability can be quantified comprehensively. Fractal geometry is a means to quantify scale-independent (hierarchical) properties of geometric structures. Suture lines have been shown to exhibit fractal properties such as hierarchically organized convolutions (‘convolutions within convolutions’), but only over a restricted range of scale (Gorsky & Skrzat, 2006). Also, the fractal dimension is a relatively coarse measurement of sutural shape, as lines with widely different morphologies can have similar fractal dimensions (Fig. 1a,b). Accordingly, new morphometric methods are required to quantify sutural morphology more accurately and comprehensively.

Fig. 1.

Fractals and fractal surface growth. (a, b) Diversity of structures with fractal dimension D=1.5. Wiener process (Brownian motion) paths (a) and Koch fractal (b). (c, d) Laplacian surface growth via DLA starting with a single cell (c) and a planar surface (d). The structure in (c) has fractal dimension D∼ 1.71 (Mandelbrot et al. 1995).

Aims and hypotheses

This paper combines modeling and morphometric analysis to investigate how suture growth is related to structure and function. First, we propose a new morphogenetic model of strain-mediated suture morphogenesis. The model is designed to be ‘minimal’ in the sense that it should generate the observed complexity and diversity of modern human neurocranial sutural morphologies with a minimum of model parameters. Computer simulations are then used to generate synthetic sutures, to explore the morphogenetic space (morphospace) of the model system, and to assess the diversity of morphologies that the model system can produce.

Second, we propose a new morphometric method, which combines FA with principal components analysis (PCA) to quantify suture morphology. The method is used to assess to what extent the model system reproduces key features of natural sutures, and to determine which regions of the theoretical morphospace are occupied by natural suture morphologies. These comparative data are then used to test hypotheses about the factors governing suture morphogenesis and variation in suture shape. Specifically, we test two hypotheses: the first proposes that suture complexity is correlated with developmental time (age) and with physiological properties of the suture tissue (Miura et al. 2009). The second proposes that variation in corrugatedness along the suture line is correlated with variation in strain patterns (Mann et al. 2009).

We focus on the formation and morphology of the interparietal (sagittal) suture in modern human crania. This suture line has been the subject of various morphogenetic and morphometric studies, and it is used as a standard model in clinical studies of cranial synostoses (Cohen, 2002; Rice, 2007b; Slater et al. 2008). From a modeling perspective, the anatomical and biomechanical context of interparietal suture formation is less complex than in other sutures. The interparietal suture is located in the cranial midplane and formed between homologous bones, thus representing bilateral (statistical) symmetry of growth directions and mechanical loading. Moreover, due to the large size and spheroid shape of the human cranial vault, midsagittal suture formation occurs in the absence of potentially confounding factors such as complex cranial vault geometry and/or muscle attachment sites in close proximity to the suture line. To further restrict the complexity of the model approach, the morphometric methods and morphogenetic models proposed here focus on the external (two-dimensional) morphology of the suture.

The sutural growth model

Interface growth is an active research area in physics, engineering sciences and biology. Various concepts and models are currently available to describe how interfaces between materials with different properties develop in time and space (Family & Vicsek, 1991; Dünweg et al. 2003). The growth model proposed by Garcia-Ruiz et al. (1990) establishes a link between ammonoid1 suture formation and a type of interface growth known from physics as ‘Saffman–Taylor growth’ or ‘viscous fingering’ (Saffman, 1986). Saffman–Taylor fingers are formed at the phase boundary between two liquid immiscible media with different viscosities (e.g. water and oil) when pressure is applied to inject the less viscous fluid into the more viscous one. During this process, local differences in pressure along the interface lead to instabilities in the form of finger-like extrusions of the expanding surface. The Saffman–Taylor model represents one specific case of a larger class of surface growth processes known as Laplacian systems, where the term ‘Laplacian’ refers to the basic growth equations governing these systems (see below). Laplacian models have been used to demonstrate basic similarities of a wide spectrum of surface growth phenomena in physical and biological systems. In all these systems, surface growth velocities depend on the local distribution of an external field, φ. This field may reflect quite diverse physical and/or chemical properties, such as a pressure potential in the case of viscous fingering, a temperature gradient during directional solidification, an electrostatic potential in dielectric breakdown phenomena such as lightning, electrolyte concentration in dendritic crystal growth, and a nutrient concentration in bacterial colonies growing on a Petri dish (Sander, 1986; Matsushita et al. 1993).

One key property of Laplacian growth systems is the spatiotemporal interdependence of large-scale and small-scale changes in the external field φ and in the growing surface. While local growth velocities at the interface depend on the local spatial properties of the field, these properties are determined by the overall geometry of the growing surface. This feedback system gives rise to ramified, fractal-like structures of the interface (Fig. 1c,d).

Suture formation as a bidirectional extension of Laplacian interface growth

Various studies indicate that suture formation is a strain-dependent process, in which bone growth and remodeling are controlled by the dura mater underlying the cranial vault bones, and in which the differential activity of osteoblasts and osteoclasts is relevant for the generation of the characteristic undulating patterns of the suture line (Yu et al. 1997; Levine et al. 1998; Henderson et al. 2004; Ogle et al. 2004; Opperman & Rawlins, 2005; Byron, 2006). It is thus sensible to model sutural growth as a process of bone deposition/resorption mediated by a strain field.

The standard Laplacian model describes growth at the surface of an incompressible phase S as a function of the spatiotemporal distribution of a field variable φ within the adjacent phase B (Fig. 2a). The system is set to the following boundary conditions:

(1)

indicating that strain is constant at locations far away from the interface (φ_B,far = 1; strain source), while strain is dissipated within S (φ_S = 0). Under these far-from-equilibrium conditions, the system obeys the steady-state diffusion equation or ‘Laplace equation’

(2)

Fig. 2.

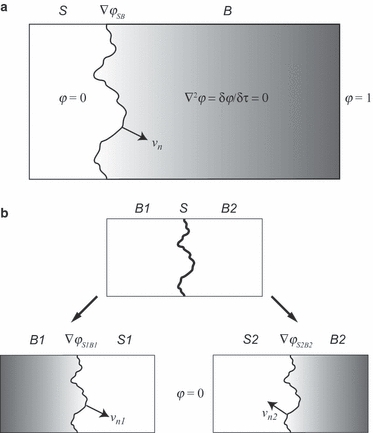
Laplacian models of interface growth. (a) Unidirectional model. Phase S grows with velocity v_n as a function of gradient ∇φ_SB at the S–B interface. Field distribution of φ within B obeys the Laplace equation; φ within S is zero. (b) Bidirectional model of bone growth at suture interface. The system is subdivided into complementary subsystems [S1, B1] and [S2, B2]. Bone deposition/resorption rates are evaluated as functions of strain gradients (∇φ_S1B1 and ∇φ_S2B2) on opposite sides of the suture line.

The left two terms correspond to the standard diffusion equation, in which the second spatial derivative of φ (the Laplacian term ∇²φ) equals its first temporal derivative (dφ/dt). Setting the diffusion equation to zero characterizes a strain field with zero net flux within B, implying that the strain gradient distribution does not change over time.

To account for the specific growth characteristics of sutural tissue, the basic Laplacian growth model needs to be modified and extended in several ways. Sutures develop when two expanding osteogenic fronts meet each other and form a common interface, which then continues to grow in either direction (Opperman & Rawlins, 2005). Before osteogenic fronts meet, they typically exhibit a ‘spiky’ surface, which arises from the outgrowth of bony spicules during intramembranous ossification. As soon as growth fronts have met, the morphology of the suture interface starts to differ in some key aspects from the growth fronts of isolated bones. Initially, the interface is relatively smooth, but then develops interdigitations with characteristic recurvations. Although direct experimental evidence is not yet available, it is sensible to assume that recurvations arise through a combination of bone deposition and resorption on either side of the suture line. This assumption is backed by the observation that the complexity of neurocranial interosseous sutures increases even after neurocranial expansion has been completed (see Fig. 5 below).

Fig. 5.

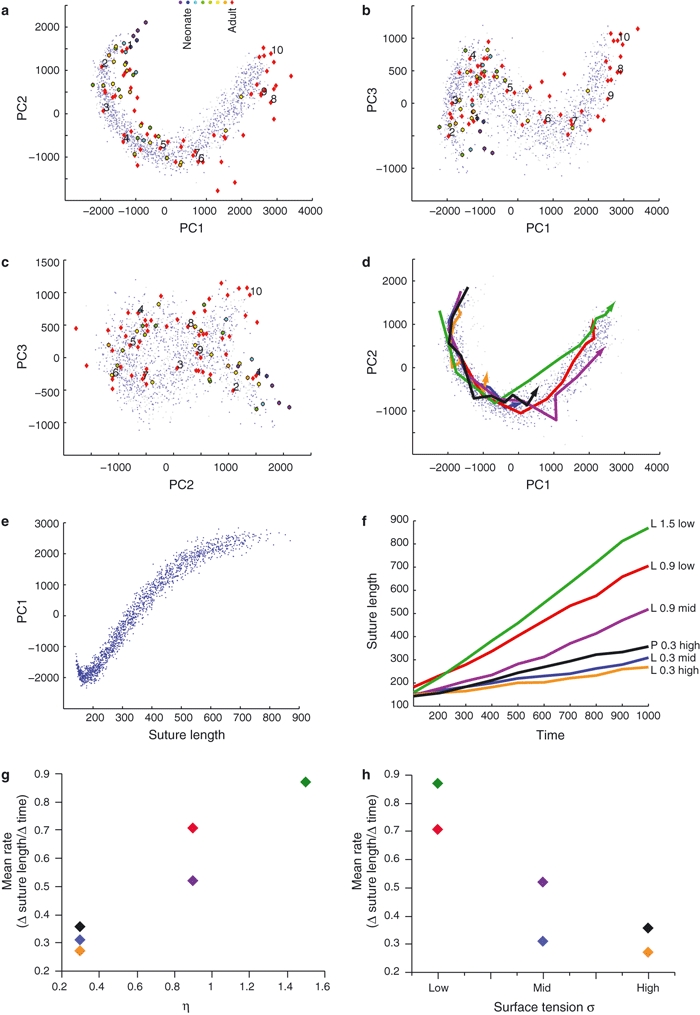
Principal components analysis (PCA) of synthetic and natural suture morphologies. (a–c) Distribution of morphologies in shape subspace defined by the first three PCs. Each gray/light blue dot represents the morphology of a synthetic suture grown according to L/P equations, respectively. Red diamonds represent adult natural sutures (numbering as in Fig. 3); color-filled circles represent immature natural sutures. (d) Growth trajectories of selected synthetic sutures (PC1–PC2 plot, as in a; morphometric data were acquired at time steps T = 100, 200, …, 1000). Note that morphogenesis occurs along largely similar curved trajectories, but at different developmental rates. (e) Suture length increases along PC1. (f) Time course of suture development (colors correspond to trajectories in d; L/P, Laplace/Poisson growth; η = 0.3, 0.9, 1.5; surface tension low, middle, high). (g, h) Sutural corrugation rate (measured as Δ suture length per Δ time) increases with exponent η (g), and decreases with surface tension (h) (colors as in d and f).

Our model thus postulates two effects: first, during neurocranial growth, deposition is more intense than resorption and leads to expansion of the braincase; and second, after completion of neurocranial growth, a balance is reached between deposition and resorption. Because we are interested here in suture morphology rather than neurocranial expansion, we focus on the net effects of deposition vs. resorption and observe how the shape of the sutural interface develops over time, assuming that the midsagittal plane remains stationary.

These considerations are incorporated into the following ‘bidirectional Laplacian interface growth model’. We define a thin strip of sutural tissue S that deposits and/or resorbs extracellular bone matrix on either side (B1 and B2; see Fig. 2b). Bone deposition/resorption is governed by the distribution of strain φ at the boundary between suture S and bone B. However, because bone matrix can be deposited and/or resorbed on either side of S, the model system is subdivided conceptually into two subsystems, [S1, B1] and [S2, B2], as illustrated in Fig. 2b. Each subsystem obeys standard Laplacian growth conditions

(3)

A key feature of the bidirectional Laplacian model is that the subsystems are coupled. Accordingly, deposition of B on one side of S results in resorption of B on the opposite side, such that the sutural interface S increases its intrinsic length (path length along the interface) through corrugation, but does not change its mean position, thickness and extrinsic length (distance between endpoints).

While the Laplacian growth equation defines the overall constraints of the sutural growth model, physiological parameters of the sutural tissue define local constraints. Extracellular bone deposition/resorption rate is modeled as a function f of the local gradient of φ at the interface between S and B

(4)

This function specifies how suture cells sense strain gradient ∇φ_SB and transform this information into bone deposition/resorption velocity v_n (velocity is a vector denoting rate and direction of deposition/resorption). The precise response function of strain receptors is not known; in a heuristic approach, we assume a non-linear relationship between the local strain gradient and bone deposition rates (the length of the velocity vector v_n). Specifically, we use the function

(5)

where c is a constant, and η is used to model non-linear dependence of bone deposition rates on strain. For η = 0, surface growth occurs independent of strain φ, which corresponds to a ‘Brownian’ growth model (also known as ‘Eden growth’; Eden, 1961). For a linear relationship between strain gradient and bone deposition/resorption rates (η = 1), the surface grows according to a process known as ‘diffusion-limited aggregation’ (DLA). Here, DLA can be thought of as ‘strain particles’ (or alternatively as morphogen molecules) diffusing from a source at infinity and triggering growth where they hit the suture line (Witten & Sander, 1981; Bogoyavlenskiy, 2001). For values of η≠ 1, surface growth is a non-linear function of the local strain gradient. The postulated local strain gradient ∇φ can be thought of as transient microstrain caused by masticatory forces, and/or inertial forces during head movement. This corresponds to the Laplacian assumption of a diffusion-limited process, which essentially implies a non-saturated system with low levels of φ.

The physical properties of the growing surface are specified with additional parameters (Vicsek, 1991). One is surface tension, which tends to suppress formation of features exhibiting high surface curvature, such as spines and small-scale branching patterns. In the present model, surface tension is used to model the viscosity of the osteogenic front, i.e. the strength with which cells adhere to each other. Furthermore, noise reduction techniques are used to control the smoothness of the resulting surface. An additional parameter is anisotropy, which implies a directional bias in surface growth probabilities. Because computer simulations are run on a square grid, some degree of growth anisotropy along grid lines can be expected. Implementation details are given below.

Generalization of the Laplacian model: Poisson growth

In the Laplacian growth model, the source of field φ is far away from the expanding phase S, and constant. As a generalization of Laplacian growth, Poisson growth models assume that the source of field φ is a general function of the location (x, y) outside phase S:

(6)

Here, we simulate the following condition:

(7)

In this model, strain source distribution is spatially homogeneous in B (φ_B = k), and S acts as a strain dissipator. Metaphorically, φ_B can be thought of as a homogeneous source of diffusing particles, which trigger growth where they hit the surface of S, and are then removed from the system (La Roche et al. 1991). Note that this modeling approach is similar to RD models of sutural growth, as proposed by Miura et al. (2009). The relevant aspect of the Poisson model is that the metaphorical ‘diffusing particles’ can be thought of as actual morphogen molecules, as an alternative to a strain field.

Computer simulations

Suture morphogenesis is simulated on a lattice with dimensions 512 × 128; x-coordinates range from 0 to 511 (along the suture's principal axis) and h-coordinates range from −63 to +64 (across the suture). The lattice has periodic boundary conditions in the x-direction. System [S1, B1] is initialized with half the pixels (h < 0) labeled as bone B1, the other half (h≥0) labeled as suture S1. System [S2, B2] is initialized as a mirror system (h < 0: suture S2; h≥0: bone B2).

Suture growth is then modeled by solving the steady-state diffusion equation (see Eqs 1 and 2) for each subsystem. In practical terms, the equation is solved for each ‘bone’ pixel at position (x = i, h = j) via the lattice form of the Laplace operator ∇²φ

(8)

with boundary conditions φ = 0 within S, and φ = 1 far from the suture (i.e. at h = 64 for B1, and h = −63 for B2). Iteration is performed until a convergence criterion ε is reached,

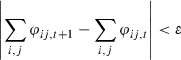(8a)

To achieve faster convergence, a multigrid approach is used, in which the above iteration is calculated on increasingly fine-grained grids, where the results of calculation for one grid are used for the initial values at the next level of grid scale. These calculations yield the distribution of φ_ij along the suture line (i.e. the S–B interface).

Growth velocity v_{i,j→i’,j’} at a suture site (i, j) towards a neighboring bone site (i’, j’) is a function of the gradient of φ between these two sites (Eq. 5). By definition, φ_i,j = 0 at the suture site, such that

(9)

Using Eq. 5, we thus write

(10)

Actual growth velocities are evaluated by further modification of the growth velocity vector through a linear surface tension function of the form

(11)

where K is the number of neighboring suture sites of suture site (i, j) in a 3 × 3 neighborhood, and a and b denote the coefficients of a linear regression equation. We then obtain

(12)

The v-values are normalized over the entire suture line, yielding a growth probability P_ij for each suture site (note that upon normalization the constant c in Eq. 10 becomes c = 1). One site is then chosen probabilistically, its position is updated, and the φ-field is re-evaluated according to Eq. 8. These calculations are performed alternately (in random order) for [S1, B1] and [S2, B2], such that bidirectional growth of the suture line occurs. Note that [S1, B1] and [S2, B2] are coupled via their common interface; any growth-mediated modification of the S1–B1 interface entails a corresponding modification of the S2–B2 interface.

Noise reduction is simulated by means of annealing, i.e. the position (i, j) of a recently added interface pixel is optionally changed to that of its nearest neighbor surrounded by the highest number of interface pixels. This procedure tends to smooth out surface peaks and indentations. The source code is available on request from the authors.

Data acquisition and analysis

Data on natural shape variation of human midsagittal sutures were collected from a sample of N = 17 immature (fetal to subadult) and N = 30 adult crania (a subsample of 10 adult suture lines is shown in Fig. 3). Each exocranial suture line was replicated with high-resolution dental casting material (President Putty, Coltene). Replicas were scanned with a conventional flatbed scanner, such that the spatial resolution of the digital image (1024 dpi, corresponding to ∼ 25 microns per pixel) was higher than the finest excursions of the suture line. Suture lines were then directly traced on the digital images using Photoshop (Adobe). Synthetic suture lines resulting from model simulations were extracted with the marching-squares algorithm (Hansen & Johnson, 2005).

Fig. 3.

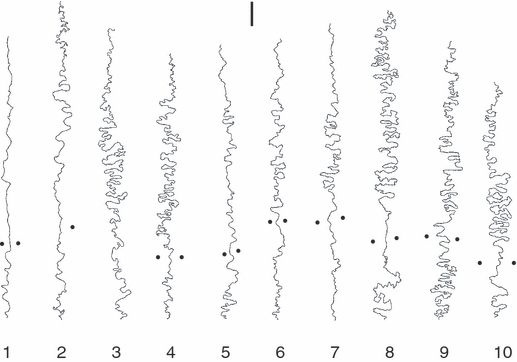
A set of 10 human interparietal sutures (bregma is on top, lambda on bottom; black dots indicate parietal foramina; scale bar is 1 cm).

Current methods used to quantify suture shape typically extract global (statistical) properties of the suture line, such as fractal dimension, and excursion from the midline (Gorsky & Skrzat, 2006; Wu et al. 2007). The method proposed here considers the actual shape (geometry) of the suture line. To this end, the suture line s is expressed in parametric form

with t ranging from t=0 (start) to t=1 (end). This can be thought of as moving along the suture line with a given step length Δt, while recording positions (x, y). This permits definition of surface curvature as

Curvature functions c_i(t) are computed for all specimens i of a sample (i=1 …N). Because suture lines vary considerably in individual shape, direct (point-to-point) comparisons of curvature characteristics are not possible. We thus use FA to calculate the Fourier-transforms F(c_i) of all functions c_i(t), and submit the transformed data to PCA. PCA is a dimension reduction technique, which serves as a means to extract the statistically most significant patterns of shape variation in the sample (Jolliffe, 1986).

Results

The properties of the suture growth models were explored by systematic variation of parameter values (Table 1). Computer simulations were run for up to 1000 time steps, and snapshots of the developing morphologies were taken at intervals of 100 time steps. Figure 4 illustrates the development of model sutures for various parameter settings. A comparison of model sutures with real sutures (Fig. 3 vs. Fig. 4) shows that a relatively restricted range of model parameters generates forms that are visually similar to biological morphologies. Figure 5a–c represents form variation of computer-generated and real sutures in morphospace. The first three principal components (PCs) shown in these graphs account for 19.4, 4.8 and 1.8% of the total shape variation in the sample (each point in morphospace corresponds to the morphology of one specific suture line). Computer-generated sutures develop along trajectories through morphospace, which track the transformation of initially straight lines into highly convoluted forms. All simulated developmental trajectories largely overlap in PC1–3 graphs and exhibit a horseshoe-shaped course characteristic of serial data (Kendall, 1970), irrespective of the particular parameter settings used to grow individual model sutures (Table 1). Considering that PCs are statistically independent factors of shape variation that account for the largest, second largest and successively smaller proportions of the total sample variance, the following picture emerges: 26% (PCs 1–3) of the shape variation of model sutures is due to developmental shape change (along developmental trajectories), while 74% (PCs 4 onward) is due to variation between individual suture lines (across developmental trajectories). The latter portion of variability does not exhibit significant correlations with specific model parameters.

Table 1.

Parameter settings used for computer simulations

Parameter	Range	See equation no.
Exponent η	0.0, 0.5, 1.0, 1.5, 2.0	5
Surface tension σ		11
Slope a	1, 2, 3, 4	11
Intercept b	1, 2, 3, 4	11
Poisson strain constant k	0, 1, 2	7

Fig. 4.

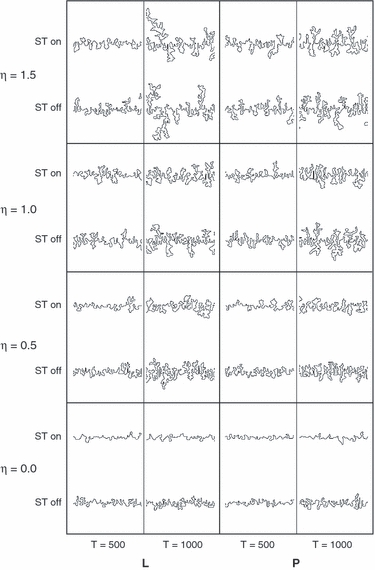
Morphological diversity of computer-generated suture lines. Morphologies are shown for a variety of parameter settings [L, Laplacian growth; P, Poisson growth; ST, surface tension (off: a = b=0; on: a = b=4); η: exponent of Eq. 5], and at time steps 500 and 1000. Note that morphologies similar to natural sutures are generated within a restricted parameter subspace.

While Fig. 5a–c shows that model sutures develop along largely similar trajectories through morphospace, Fig. 5d shows that individual model sutures differ in rates of development (rates are measured here as the increase in intrinsic suture length per unit time). Rates of development are positively correlated with exponent η, and negatively correlated with surface tension (Fig. 5g,h). In other words, high exponents η and/or low surface tension result in fast corrugation of the suture line. This results in more rapid advancement along developmental trajectories through morphospace (Fig. 5d), as well as in increased total suture length at any given time t.

Natural suture lines were analyzed with identical morphometric methods, such that their position in morphospace can be directly compared with the outcome of model simulations (Fig. 5a–c). The distribution pattern of natural sutures in morphospace largely coincides with the distribution of computer-generated sutures. Sutures of immature individuals group with early developmental stages of synthetic sutures, while highly convoluted natural sutures tend to group with late developmental stages in computer simulations. The natural sutures in our sample thus correspond to different morphogenetic states of corrugation of the model system. In Fig. 6 natural sutural complexity is graphed as a function of individual age and extrinsic suture length (i.e. parietal arc length). Complexity tends to increase during ontogeny, and continues to increase after cessation of neurocranial expansion. Because our data come from a cross-sectional ontogenetic sample, Fig. 6 also indicates that the range of complexity increases during ontogeny. In other words, all perinatal individuals exhibit sutures with a low degree of complexity, while adult individuals exhibit a wide spectrum from low to high complexity.

Fig. 6.

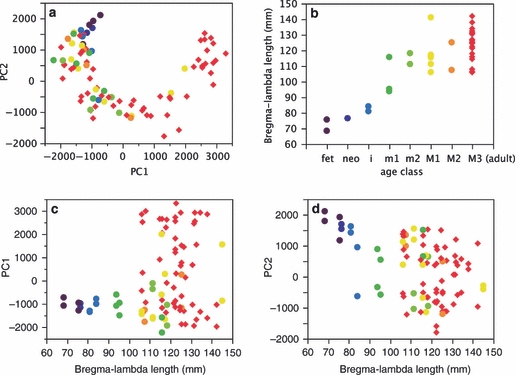
Development of complexity in natural sutures. (a) Graph of principal component (PC)2 vs. PC1 (data and color code as in Fig. 5a); (b) Extrinsic suture length (bregma–lambda arc length) vs. age class (fet, fetal; i/m1/m2, deciduous incisors/molars1/2 erupted; M1/M2/M3, permanent molars 1/2/3 erupted; neo, neonate). (c, d) PC1 and PC2 vs. bregma–lambda arc length. The range of suture complexity increases with dental age class and suture length.

In morphospace, natural suture shapes exhibit some offset relative to model trajectories (Fig. 5a). This indicates that while our model system captures the essential modes of sutural shape variation, natural sutures exhibit spatial characteristics not reproduced by the model system. Overall, morphometric comparison of model and real sutures supports the hypothesis that suture formation appears as a strain-mediated process. According to this hypothesis, variation in complexity between individual sutural shapes is due to: first, differences in ontogenetic stage; and second, differences in physiological properties of the suture tissue, such as strain response function (exponent η) and surface tension.

To further validate the model, we consider Eq. 5, which predicts that variation in convolutedness along the suture line should be correlated with variation in strain patterns. Natural sutures provide an ideal case to test this hypothesis. As evinced in Fig. 3, suture lines exhibit the lowest degree of convolution in the region between the parietal (obelic) foramina (Mann et al. 2009). We hypothesize that these foramina act as strain dissipators (φ = 0), which generate high local strain gradients and disturb the strain field in their immediate neighborhood. We performed computer simulations incorporating foramina-like ‘strain sinks’ representing locations where φ = 0. The resulting model shapes (Fig. 7) exhibit a substantial decrease in sutural complexity around foramina, similar to natural sutures.

Fig. 7.

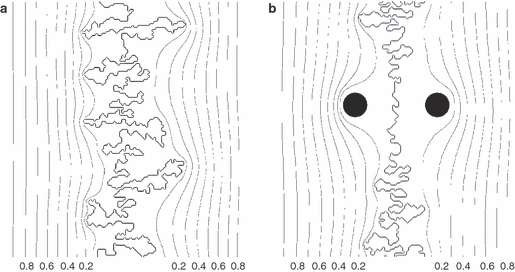
Simulation of normal suture development (a), and development in the vicinity of parietal foramina that act as ‘strain sinks’ (b). Both graphs show strain distribution around suture lines (strain isolines are drawn at intervals of Δφ = 0.1). Note decrease of suture complexity in the region of the foramina (black circles; strain φ = 0).

As an additional validation of the model system, we simulated the morphogenesis of sutures under classical Laplacian growth conditions, i.e. suture interfaces that grow in only one direction. Unidirectional suture growth can occasionally be observed in the human parieto-occipital (lambdoid) suture, when the occipital squama overgrows the parietal bones. Overgrowth is relatively rare in modern humans, but it seems to be the rule in the Neanderthals. Figure 8 shows the lambdoid suture of the type specimen of Homo neanderthalensis, and two simulations of unidirectional suture growth. The model sutures develop cauliflower-shaped outgrowths, which are similar to those observed in the natural suture. Unidirectional suture growth could indicate that the osteogenic fronts of the two adjacent bones forming the suture exhibit different gradient response characteristics.

Fig. 8.

Unidirectional suture growth. (a) Lambdoid (parieto-occipital) suture of the type specimen of Homo neanderthalensis. (b) Two simulated unidirectional sutures.

Discussion

The cranium is typically perceived as a highly constrained structure, which is composed of modules exhibiting consistent morphologies. However, it also comprises elements exhibiting ‘stochastic’ macroscopic morphologies, such as the paranasal sinuses and air cells (Zollikofer & Weissmann, 2008), and the interosseous sutures discussed here. The analysis of these structures is challenging and comprises three different tasks: first, understanding and modeling the basic mechanisms governing their development; second, devising morphometric methods to quantify their highly variable form; and third testing hypotheses about possible form-function relationships.

The morphogenetic model of suture formation proposed in this study is based on a standard approach typically used in physics to describe gradient-dependent growth of the interface in a two-phase system (Family & Vicsek, 1991). Compared with RD models, which emphasize the role of local interactions between two or more classes of reactants, Laplace/Poisson (LP) growth models emphasize the role of global ‘signals’ in the form of gradient fields mediating interface development. RD and LP models are not mutually exclusive, and have been combined to simulate interface growth under various conditions (Nagatani, 1990; De Wit & Homsy, 1999a,b; Lega & Passot, 2003; Gerard & De Wit, 2009). In the case of suture formation, applications of local and global growth models can be expected to optimally recreate sutural features at different levels of scale. A visual comparison of natural and model sutures (Figs 3 and 4) shows that LP models produce morphologies with considerable spatial inhomogeneity along and across the suture line, which is a typical feature of natural sutures. RD models, on the other hand, produce comparatively homogeneous patterns with characteristic ‘space-filling’ properties (largely equidistant spacing of neighboring loops of the interface). Natural sutures do exhibit space-filling features, but they are typically restricted to subregions of the entire suture line (fig. 8 in Miura et al. 2009). Furthermore, LP models recreate the formation of ‘island’ contours, i.e. sutural loops that are isolated from the main interface (Fig. 9). These features, which result from the fusion of neighboring meanders (loops) of the suture line, are often seen in natural sutures, but they do not seem to emerge from RD models. On the other hand, RD models recreate sutural sprouting, i.e. the formation of spike-like offshoots perpendicular to the main direction of the sutural interface (fig. 4 in Miura et al. 2009), a feature not seen in LP models.

Fig. 9.

Simulation of sutural ‘islands’ (isolated loops of the sutural interface). Laplacian growth with η = 0.5 (left), 1.0 (middle), 1.5 (right); time T=1000; low surface tension.

Laplace/Poisson models of suture formation permit establishment of hypothetical links between suture morphogenesis, the resulting form of the suture line, and its function as a strain absorber. According to our hypothesis, strain gradient sensitivity of the growing suture tissue implies higher probability of bone deposition at sites exhibiting higher strain gradients. As a consequence, bony peaks (where strain gradients are high) tend to grow more rapidly than valleys tend to fill up, and this process is reinforced by the symmetric organization of the system (peaks on one side are valleys on the other). Because growth at peak sites can occur into a wider range of directions than at other sites, peaks tend to ramify, resulting in a hierarchical (fractal) organization of sutural convolutions. The resulting increase in local complexity of the interface results in a high degree of sutural interdigitation. Also, total interface length (intrinsic length) increases (Fig. 5f). Together, these postulated mechanisms would thus lower local strain magnitudes while increasing the mechanical stability of the interface between the two bones involved in suture formation.

While Laplace and Poisson models capture essential properties of natural suture formation, it has to be kept in mind that model systems do not provide explanations of the actual molecular and mechanical processes governing suture formation. As mentioned, the field variable φ, which we hypothesize here to represent strain, could also be thought of as the concentration of a morphogen, which is released by sutural or adjacent tissue. Which of the two representations is closer to the actual morphogenetic process remains to be verified with experimental studies (for ease of argument, we will use ‘strain’ in the following discussion). Nevertheless, exploring the system's behavior, and comparing model with natural morphologies permits testing of several hypotheses about how general mechanisms of suture formation influence sutural complexity.

According to our model, sutural growth occurs via feedback between the geometry of the suture line and the geometry of the strain field: small (random) excursions of the sutural interface generate local maxima of the strain gradient, which in turn reinforce local surface growth. How this inherent dynamic instability of growing LP systems (the so-called ‘Saffman–Taylor instability’; Saffman, 1986) is transformed into suture convolutions depends on the model parameters specifying various properties of the suture tissue. One such property is surface tension, which effectively suppresses growth at surface peaks (Fig. 4). Another property is the response function of suture tissue to strain gradients. Values of exponent η < 1 result in proportionally lower responses to high strain gradients, while η> 1 results in proportionally higher responses. As can be seen from Fig. 4, interfaces generated with η≤ 1 correspond to the range of natural suture variation, while exponents η> 1 yield interfaces that are clearly different from natural sutures; these interfaces develop few but highly ramified, tree-like structures, which are reminiscent of axonal growth in neurons.

The hypothesis that sutural complexity is a function of mechanical loading and resultant strain has been studied experimentally, both at macroscopic and molecular levels (Moss, 1961; Jaslow, 1990; Jaslow & Biewener, 1995; Rafferty & Herring, 1999; Herring & Teng, 2000; Mao, 2002; Byron et al. 2004; Henderson et al. 2004; Sun et al. 2004; Sarasa-Renedo & Chiquet, 2005; Wang et al. 2006, 2010; Tholpady et al. 2007; Byron, 2009). These studies indicate that osteoblast activity is strain-mediated, and that sutural interdigitation is highest in animals experiencing high peak strain. Our model, which simulates osteoblast activity (bone deposition/resorption rate) as a function of local strain gradients (Eq. 5), is in good agreement with empirical data. The morphological complexity of model sutures clearly correlates with strain sensitivity (as measured by exponent η; Eqs 5 and 12). Also, simulation of ‘strain sinks’ results in reduced suture complexity (Fig. 7), which is in good agreement with the decrease of natural sutural complexity in the vicinity of parietal foramina (Fig. 3).

The role of strain as a hypothetical agent of suture formation has also been considered in the RD model proposed by Miura et al. (2009). Interestingly, simulation of RD-based suture morphogenesis under high mechanical loading conditions resulted in reduced interdigitation of the suture line, which stands in contrast with the basic tenet that stress increases bone growth. The LP growth models used here help to resolve this paradox: under LP conditions, the strain field (or morphogen concentration field) is modeled as a ‘diffusion-limited’ quantity, which implies that the system is not saturated and the field is inhomogeneous. High mechanical loads correspond to saturation, which implies equal distribution of strain. In the LP model, a spatially homogeneous strain field is equivalent to a situation where η = 0 (strain gradient insensitivity), which implies reduced suture interdigitation (see Fig. 4).

The possible influence of altered strain patterns on sutural morphologies has been discussed in the context of culturally mediated cranial vault deformation. It has been hypothesized that deformation alters cranial loading and associated strain patterns, which might entail changes in sutural complexity and favor the formation of interstitial ossicles (Anton et al. 1992; Wilczak & Ousley, 2009). None of these studies, however, found significant correlations between suture morphology and cranial deformation, and this was taken as evidence that deformation leads to only minor modification of cranial strain distribution patterns. LP models provide an alternative explanation: while Laplace models simulate directional (anisotropic) strain sources, Poisson models simulate isotropic strain sources. Interfaces grown according to Laplace and Poisson models, however, exhibit only minor morphological differences (Fig. 4), indicating that global differences in strain patterns (reflecting differences in loading patterns) have only little influence on the resulting sutural morphology. Also, the formation of sutural islands (Fig. 9), and probably of interstitial ossicles, seems to be independent of the overall loading regime.

Fractal dimensions D have been widely used to measure suture complexity, and to correlate complexity with age (Saito et al. 2002; Lynnerup & Jacobsen, 2003; Skrzat & Walocha, 2003; Yu et al. 2003; Byron, 2006; Wu et al. 2007; Miura et al. 2009). As mentioned, D is an adequate measure of overall complexity, but it does not contain specific shape information. The morphometric methods proposed here permit to quantify both complexity and shape of suture lines. FA provides a multidimensional measure of sutural convolutedness, and PCA represents a convenient means to reduce the high dimensionality of Fourier space. Together, these methods permit one to visualize and compare the distribution of model and natural sutures in morphospace: specific suture morphologies correspond to specific locations in morphospace, and shape change during suture development can be traced along well-defined trajectories through morphospace.

Because all model sutures follow a common basic trajectory, it is possible to discriminate between shape variation along and across the common developmental trajectory. Our data show that 26% of variation (represented by PC1–3) corresponds to the former type of variation. As shown in Fig. 5d–h, developmental rates along the trajectory vary considerably between simulations. Differences in developmental rates result from differences between simulated physiological and biomechanical properties of the model suture tissue. Specifically, a high exponent η of the strain response function (Eqs 5 and 12) and low surface tension σ (Eqs 11 and 12) yield high developmental rates and rapid corrugation. On the other hand, 74% of the total shape variation (represented by PC4 onwards) must be attributed to other mechanisms. Shape variation comprised in these higher-order PCs does not exhibit correlation with specific model parameters. Most likely, it reflects random variation caused by the inherently stochastic nature of Laplace and Poisson growth processes. In fact, replication of simulations with identical parameter settings yields considerable data scatter in higher-order PCs.

Our model also provides a tentative answer to the question why suture complexity is a poor indicator of individual age (Lynnerup & Jacobsen, 2003; Yu et al. 2003; Wu et al. 2007). Figure 6 shows that suture complexity does not increase linearly with increasing age; rather, it is the range of complexity that increases. During growth some sutures reach high levels of complexity, while others remain at a low level. Neurocranial growth is almost completed after the eruption of the first permanent molar (M1 in Fig. 6), such that any sample of individuals with age classes ≥ M1 tends to exhibit a wide spectrum of suture morphologies, ranging from low to high complexity. This effect is also seen in the analyses of Wu et al. (2007).

Insights gained from computer simulations can be used to interpret patterns of morphological variation in natural sutures in terms of morphogenetic processes. In morphospace, the distribution of natural suture morphologies largely coincides with the developmental trajectories of computer-generated sutures. This indicates that our model system replicates some fundamental properties of natural suture morphogenesis. Following the logic of the morphogenetic model system, we hypothesize that the growth-related increase in suture complexity reflects strain and/or morphogen gradient-dependent morphogenesis. We further hypothesize that adult variation in complexity reflects interindividual differences in suture tissue properties, such as sensitivity to the strain field (exponent η) and surface tension (expressed by σ), while in vivo loading history and actual duration of suture growth are less important factors. Similar arguments can be used to interpret within-suture variation in complexity: compared with synthetic sutures (Fig. 4), natural sutures exhibit conspicuous fluctuations in complexity, comprising relatively straight stretches as well as highly convoluted regions (Fig. 3). We hypothesize that these fluctuations reflect variation in tissue properties (η, σ) along the suture.

The morphogenetic model of suture formation proposed here used a minimum number of parameters to generate a wide spectrum of suture morphologies. Morphological variation in model sutures closely mimics the basic pattern of morphological variation in natural sutures. Which combination of morphogenetic parameters actually generates diversity in cranial interosseous sutures remains a question for further research. Also, it needs to be clarified to what extent these parameters are under genetic vs. environmental control. Overall, however, our study indicates that suture morphology largely depends on how suture tissue responds to local signals, which could come in the form of strain gradients and/or morphogen gradients.