Abstract
In the intensive care unit (ICU), prompt therapeutic intervention to hypotensive episodes (HEs) is a critical task. Advance alerts that can prospectively identify patients at risk of developing an HE in the next few hours would be of considerable clinical value. In this study, we developed an automated, artificial neural network HE predictor based on heart rate and blood pressure time series from the MIMIC II database. The gap between prediction time and the onset of the 30-minute target window was varied from 1 to 4 hours. A 30-minute observation window preceding the prediction time provided input information to the predictor. While individual gap sizes were evaluated independently, weighted posterior probabilities based on different gap sizes were also investigated. The results showed that prediction performance degraded as gap size increased and the weighting scheme induced negligible performance improvement. Despite low positive predictive values, the best mean area under ROC curve was 0.934.
1. Introduction
In the intensive care unit (ICU), persisting hypotension can result in end-organ damage. As a result, ICU clinicians must be vigilant to detect and treat hypotensive episodes (HEs) in a timely manner. However, this is challenging to achieve in a real ICU for several reasons. First, the amount of time that clinical staff can allocate per patient is generally limited. Second, ICU data is not only massive in size but also heterogeneous in nature due to their vastly different sources and suboptimal organization. In the stressful context of busy ICUs it clearly would be of considerable value to prospectively identify patients who are at increased risk of developing HEs in the next few hours, since it would facilitate efficient allocation of ICU resources and minimize the latency to appropriate therapy.
Continuous and quantitative analysis of complex medical data is a suitable task for a computer in comparison with a human clinician. In particular, multi-parameter time series of physiologic variables may contain subtle patterns that are a signature of impending frank hemodynamic instability, and such patterns are best identified and characterized by machine learning algorithms. Real-time pattern recognition may lead to advance alerts, and change ICU monitoring from “reactive” to “predictive” [1]. The importance of automated or semi-automated assistance in analyzing multimodal ICU data is increasingly recognized [2].
Following this rationale, the primary objective of this study was to develop and evaluate performance of an automated HE predictor based on heart rate and blood pressure time series.
2. Methods
2.1. Data compilation
We analyzed the heart rate (HR) and systolic, diastolic, and mean arterial blood pressure (ABP) time series from the adult patients in the Multi-parameter Intelligent Monitoring for Intensive Care (MIMIC) II database [3]. These time series were either minute-by-minute or second-by-second; the second-by-second time series were first made minute-by-minute by taking the median every minute. A total of 1,357 records, each corresponding to an ICU stay, were compiled for analysis. The median duration of the records was 90.9 hours with an interquartile range of 100.5 hours (Q1=49.2, Q3=149.8).
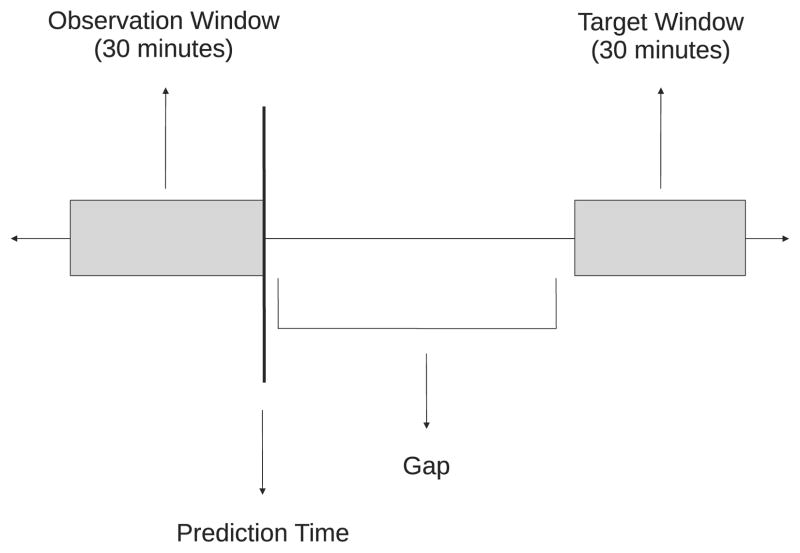
From each record, as many examples as possible were compiled. Each example was a 5.5 hour segment that included a 30 minute target window (the subject of prediction), a gap between prediction time and the onset of the target window, and a 30 minute observation window that preceded the prediction time. Only the information in the observation window was available to the predictor as input. Four gap sizes were investigated: 1, 2, 3, and 4 hours. This setup is graphically illustrated in Figure 1.
Figure 1.
A graphical illustration of the gap, observation, and target windows with respect to prediction time.
To compile examples, a 5.5 hour sliding window traversed each record by advancing 30 minutes at a time. A simple filter was utilized to discard examples with unsatisfactory time series quality. For both HR and ABP time series (in units of bpm and mmHg, respectively), the quality of a given data point was deemed satisfactory only if the amplitude was between 10 and 250 AND the absolute value of the rate of change was less than 20 per minute. Only the examples in which quality was satisfactory for at least 95% of the 5.5 hour window in ALL of the 4 time series (HR and 3 ABP) were included in the study. The reader should be aware that the rate of change threshold rejected paroxysmal arrhythmias.
Furthermore, the target window in each example was labeled either control or hypotensive. An HE was defined as a 30-minute target window in which mean ABP (MAP) was less than 60 mmHg and greater than 10 mmHg for at least 90% of the window. The threshold of 60 mmHg has often been used in previous hypotension studies (e.g., [4,5]). Any 30-minute target window that did not meet the HE definition was regarded as a control.
At the end of the data compilation step, 130,325 control and 3,953 hypotensive examples were compiled for subsequent feature extraction.
2.2. Feature extraction and dimensionality reduction
Features were extracted from the following 3 time series: HR, MAP, and pulse pressure (PP) (PP = SBP − DBP, where SBP and DBP are systolic and diastolic ABP, respectively). From each time series, the following features were extracted in the observation window: mean, median, standard deviation, variance, interquartile range, skewness, kurtosis, linear regression slope, and relative energies in different spectral bands determined by a 5-level discrete wavelet decomposition with the Meyer wavelet. In addition, the cross-correlations at zero lag of all 3 possible time series pairs were computed. These features were selected to quantify different aspects of hemodynamics such as the amplitude and variability of a particular physiologic variable. Each feature was subsequently normalized to be zero-mean and unit-variance. A total of 45 features comprised the feature space.
Feature space dimensionality was reduced via principal component analysis (PCA). In this study, PCA was conducted on training data and retained the principal components with the largest eigenvalues that captured approximately 90% of the total variance. Both training and test data were projected onto the same feature space defined by the selected principal components. Across different training data sets in cross-validation (to be discussed in the ensuing section), the reduced dimensionality ranged from 15 to 16.
2.3. Classification
According to the label assigned to each example (control or hypotensive), feed-forward, 3-layer artificial neural networks (ANNs) with one hidden layer of 20 hidden units were trained to perform binary classification. The log-sigmoid activation function was utilized in both the hidden and output layers. ANNs of this architecture are powerful nonlinear classifiers that can capture any continuous input-output mapping [6]. A 5-fold cross-validation was conducted to evaluate classification performance, and a random 20% partition of the training data was designated as the validation data for early stopping. Separate ANNs were trained for different gap sizes and cross-validation folds.
In order to balance the two groups in training data so that the classifier is prevented from favoring the majority group, a subset of the majority group (which was always the control group) was randomly sampled without replacement to match the size of the minority (hypotensive) group. This randomized sub-sampling was repeated 10 times. On the other hand, test data were left unbalanced to reflect the true prevalence of HEs. Further, the partition between training and test data was conducted with respect to records rather than individual examples. In other words, examples from the same record belonged exclusively to either training or test data.
The threshold on the posterior probability produced by the ANN was determined from the receiver operating characteristic (ROC) curve based on training data. The selection criterion for the threshold was the following:
| (1) |
where TS is the selected threshold and T is the threshold variable ranging from 0 to 1.
For performance evaluation, the area under ROC curve (AUC), accuracy, sensitivity, specificity, positive predictive value (PPV), and negative predictive value (NPV) were calculated. All these measures except AUC were dependent on Equation 1.
2.4. Weighted prediction
In addition to independent predictions from different gap sizes, posterior probabilities arising from different gap sizes for the same target window were combined in a weighted fashion as follows:
| (2) |
where PW is the weighted posterior probability, PI = [p1 p2 p3 p4] is a row vector containing independent posterior probabilities from different gap sizes (subscript equals gap size in hours), and W = [w1 w2 w3 w4]T is a column weight vector, the elements of which add up to unity. The following 3 weight vectors were investigated:
Above weight vectors were designed to investigate weighting smaller gap sizes more (W1), equal weights (W2), and ignoring 3 and 4 hour gaps (W3). For each weight vector, the threshold on the weighted posterior probability was again selected via Equation 1 based on training data.
3. Results
Tables 1 and 2 tabulate classification performance from independent gap sizes and weighted prediction, respectively. Table 1 clearly shows the general trend that overall performance degrades as gap size increases. Also, comparing Table 1 with Table 2, weighted prediction resulted in negligible improvement over the performance associated with 1 hour gap reported in Table 1 but outperformed predictions based on the larger gap sizes. However, the reader should note that a fair comparison between Tables 1 and 2 can only be made with respect to 1 hour gap, since the prediction time in the weighted scheme was 1 hour prior to target window onset.
Table 1.
Classification performance from individual gap sizes (mean±SD)
| Gap (h) | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| AUC | 0.921±0.008 | 0.901±0.010 | 0.887±0.015 | 0.872±0.019 |
| Accuracy | 0.873±0.008 | 0.842±0.014 | 0.835±0.017 | 0.810±0.019 |
| Sensitivity | 0.826±0.033 | 0.806±0.041 | 0.782±0.048 | 0.776±0.053 |
| Specificity | 0.875±0.009 | 0.844±0.015 | 0.837±0.018 | 0.811±0.021 |
| PPV | 0.159±0.014 | 0.129±0.013 | 0.121±0.014 | 0.105±0.012 |
| NPV | 0.994±0.001 | 0.994±0.001 | 0.993±0.001 | 0.992±0.002 |
Table 2.
Classification performance from weighted prediction (mean±SD)
| Weight Vector | W1 | W2 | W3 |
|---|---|---|---|
| AUC | 0.934±0.007 | 0.930±0.008 | 0.930±0.007 |
| Accuracy | 0.861±0.018 | 0.852±0.013 | 0.869±0.012 |
| Sensitivity | 0.851±0.038 | 0.851±0.036 | 0.839±0.033 |
| Specificity | 0.862±0.020 | 0.852±0.014 | 0.870±0.013 |
| PPV | 0.151±0.018 | 0.142±0.013 | 0.156±0.015 |
| NPV | 0.995±0.001 | 0.995±0.001 | 0.995±0.001 |
In Table 2, there is no meaningful difference in performance among the three weight vectors. It is also noticeable that W3 completely ignored predictions made at 3 and 4 hour gaps but still resulted in similar performance to W1 and W2.
In both Tables 1 and 2, sensitivity and specificity are roughly balanced. This shows the effect of the sub-sampling during ANN training, given that only approximately 3% of the data were hypotensive examples. However, there is a large discrepancy between PPV and NPV in both Tables 1 and 2, highlighted by very low PPVs.
4. Discussion and conclusions
We have demonstrated promising prediction performance with 1 hour gap. The fact that the reported results were based on such a large-scale, real-ICU data as the MIMIC II database assigns credibility to the results. Also, the data compilation and cross-validation in this study simulated continuous hemodynamic monitoring (every 30 minutes), which is a necessity for a real-time clinical decision support system (e.g., [7, 8]). Hence, similar prediction performance is expected from a clinical trial of the HE predictor developed in this study.
Intuitively, it is expected that prediction performance would decrease with increasing gap size, since predicting further into the future should be more challenging. In other words, the diminishing performance with increasing gap size suggests that the autocorrelations of the HR and ABP time series decay with increasing lag.
The fact that the weighted prediction scheme failed to meaningfully outperform the 1-hour gap predictor suggests that there is no advantage in consulting previous predictions. Although this study investigated only 3 specific weight vectors, this argument is corroborated by the observation that ignoring predictions at 3 and 4 hour gaps (W3) did not adversely affect performance. It is concluded that the voting mechanism based on serial predictions for the same target window does not increase predictive certainty.
The low PPVs are attributable to the prominent imbalance between the numbers of control and hypotensive examples, which reveals the true prevalence of HEs in the ICU. However, as mentioned in the Introduction section, this HE prediction algorithm was designed to serve as an HE risk stratifier that would simply identify patients who require more careful attention in the near future. In comparison with other clinical decision support systems that ask for immediate clinical attention by generating an alarm and suffer from the delay in human response associated with a low PPV [9], this risk management approach ensures minimal disruption to clinical staff even with such low PPVs.
One limitation of the binary classification approach in this study is the hard distinction between control and hypotensive examples according to an arbitrary (but reasonable) HE threshold of 60 mmHg. Classification results on borderline cases, such as near-hypotensive control examples in which the target windows contain MAP values consistently between 60 and 65 mmHg, could be debatable. This implies that certain misclassifications could be more tolerable than others from a clinical perspective.
A real-time implementation of the HE predictor described in this paper would be ready for a clinical trial, perhaps in silent mode. The clinical trial would give ICU clinicians an opportunity to evaluate the predictor and elucidate its clinical utility from their perspective.
Acknowledgments
This research work was funded by the US National Institute of Biomedical Imaging and Bioengineering (NIBIB) under grant number R01-EB001659. The content of this article is solely the responsibility of the authors and does not necessarily represent the official views of the NIBIB or the National Institutes of Health (NIH).
References
- 1.Morris AH. Decision support and safety of clinical environments. Quality and Safety in Health Care. 2002;11:69–75. doi: 10.1136/qhc.11.1.69. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Clifford GD, Long WJ, Moody GB, Szolovits P. Robust parameter extraction for decision support using multimodal intensive care data. Philosophical Transactions of the Royal Society A. 2009;367:411–429. doi: 10.1098/rsta.2008.0157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Saeed M, Lieu C, Raber G, Mark RG. MIMIC II: a massive temporal ICU patient database to support research in intelligent patient monitoring. Computers in Cardiology. 2002;29:641–644. [PubMed] [Google Scholar]
- 4.Redl-Wenzl EM, Armbruster C, Edelmann G, Fischl E, Kolacny M, Wechsler-Fordos A, Sporn P. The effects of norepinephrine on hemodynamics and renal function in severe septic shock states. Intensive Care Medicine. 1993;19:151–154. doi: 10.1007/BF01720530. [DOI] [PubMed] [Google Scholar]
- 5.Bernard J, Hommeril J, Passuti N, Pinaud M. Postoperative analgesia by intravenous clonidine. Anesthesiology. 1991;75:577–582. doi: 10.1097/00000542-199110000-00006. [DOI] [PubMed] [Google Scholar]
- 6.Funahashi K. On the approximate realization of continuous mappings by neural networks. Neural Networks. 1989;2:183–192. [Google Scholar]
- 7.McLachlan K, Jenkins A, O’Neal D. The role of continuous glucose monitoring in clinical decision making in diabetes in pregnancy. Obstetrical Gynecological Survey. 2007;62(10):643–644. doi: 10.1111/j.1479-828X.2007.00716.x. [DOI] [PubMed] [Google Scholar]
- 8.Vespa PM, Nenov V, Nuwer MR. Continuous EEG monitoring in the intensive care unit: early findings and clinical efficacy. Journal of Clinical Neurophysiology. 1999;16(1):1–13. doi: 10.1097/00004691-199901000-00001. [DOI] [PubMed] [Google Scholar]
- 9.Getty DJ, Swets JA, Pickett RM, Gonthier D. System operator response to warnings of danger: a laboratory investigation of the effects of the predictive value of a warning on human response time. Journal of Experimental Psychology. 1995;1(1):19–33. [Google Scholar]