A conserved RNA pseudoknot in a putative molecular switch domain of the 3′-untranslated region of coronaviruses is only marginally stable

Abstract

The 3′-untranslated region (UTR) of the group 2 coronavirus mouse hepatitis virus (MHV) genome contains a predicted bulged stem–loop (designated P0ab), a conserved cis-acting pseudoknot (PK), and a more distal stem–loop (designated P2). Base-pairing to create the pseudoknot-forming stem (P1^pk) is mutually exclusive with formation of stem P0a at the base of the bulged stem–loop; as a result, the two structures cannot be present simultaneously. Herein, we use thermodynamic methods to evaluate the ability of individual subdomains of the 3′ UTR to adopt a pseudoknotted conformation. We find that an RNA capable of forming only the predicted PK (58 nt; 3′ nucleotides 241–185) adopts the P2 stem–loop with little evidence for P1^pk pairing in 0.1 M KCl and the absence of Mg²⁺; as Mg²⁺ or 1 M KCl is added, a new thermal unfolding transition is induced and assignable to P1^pk pairing. The P1^pk helix is only marginally stable, ΔG₂₅ ≈ 1.2 ± 0.3 kcal/mol (5.0 mM Mg²⁺, 100 mM K⁺), and unfolded at 37°C. Similar findings characterize an RNA 5′ extended through the P0b helix only (89 nt; 294–185). In contrast, an RNA capable of forming either the P0a helix or the pseudoknot (97 nt; 301–185) forms no P1^pk helix. Thermal unfolding simulations are fully consistent with these experimental findings. These data reveal that the PK forms weakly and only when the competing double-hairpin structure cannot form; in the UTR RNA, the double hairpin is the predominant conformer under all solution conditions.

INTRODUCTION

RNA molecules fold into complex secondary and tertiary structures in order to carry out their biological functions. Some RNAs possess the additional capacity to adopt more than one conformation and can cycle between conformations as a function of solution conditions, ligand or protein binding, or intermolecular base-pairing with a second RNA (Fortner et al. 1994; LeCuyer and Crothers 1994; Abbink et al. 2005; Li et al. 2006). Riboswitches are a particularly dramatic example of conformational switching, where the direct binding of a small molecule metabolite can drive a global conformational change that results in the formation of one RNA conformation to the exclusion of others; when found in noncoding regions, riboswitches play a role in the regulation of the expression of downstream genes (Wakeman et al. 2007; Baird et al. 2010). Other RNA motifs often found in the 5′- or 3′-untranslated regions (UTRs) of viral RNAs are postulated to undergo conformational switching (Chen and Olsthoorn 2010; Hammond et al. 2010); however, how the conformational landscape is changed to accommodate a pair of mutually exclusive structures is often not well understood. RNA pseudoknotting, which defines a specific RNA topology, is often intimately associated with RNA conformational switching (Hammond et al. 2009; Kang et al. 2009; Klein et al. 2009; Rieder et al. 2009; Chen and Olsthoorn 2010). Here, we investigate the energetics that characterize a putative molecular switch in the 3′ UTR of the model animal coronavirus, mouse hepatitis virus (MHV) (Goebel et al. 2004a; Zust et al. 2008).

MHV is a group 2 coronavirus that has been studied extensively and represents a robust model system for the study of coronavirus replication and assembly. The causative agent of severe acute respiratory syndrome, SARS-CoV, is also a group 2 coronavirus; as such, MHV has emerged as an excellent model system with which to obtain insight into the replication of SARS-CoV (Anand et al. 2003; Masters 2006). Coronaviruses are enveloped, positive-sense RNA viruses that replicate intracytoplasmically through a membrane-bound replication complex (Gosert et al. 2002). During viral replication, genomic-length RNA as well as a nested set of coterminal subgenomic mRNAs (sg mRNA) are generated (Pasternak et al. 2006; Sawicki et al. 2007). The sg mRNAs are transcribed such that the 5′ and the 3′ ends of the transcript are exactly identical to the genomic-length 5′- and 3′-UTR counterparts. The mechanism of replication of the genomic RNA and the sg mRNA requires cis-acting secondary structural elements located in both the 5′ and 3′ UTRs (Li et al. 2008). These sequences are known to play essential roles in processes involving RNA synthesis, gene expression, translation, and virion assembly (for review, see Sola et al. 2011).

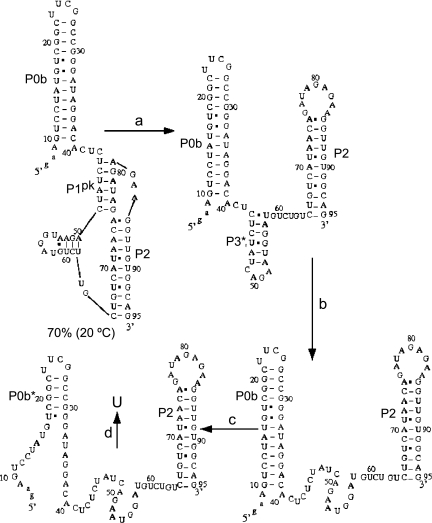
Both genomic RNA and sgRNA transcription initiate at the 3′ UTR; as such, this region is expected to harbor RNA structural elements involved in transcription initiation and replication. MHV, bovine CoV, and SARS-CoV contain common functional elements since chimeric MHV virions containing a BCoV or SARS-CoV 3′ UTR are infectious in cell culture (Hsue and Masters 1997; Goebel et al. 2004a,b). In MHV, the secondary structure of the 3′ UTR can be represented as depicted in Figure 1. Upstream of the poly(A) tail is a hypervariable (HVR) region (data not shown) whose sequence and predicted structure are not well conserved. The HVR has recently been shown to harbor second site suppressor mutations of crippling mutations in the 5′-UTR SL1 (Li et al. 2008) but can be deleted with minimal impact on replication in tissue culture cells (Goebel et al. 2007). The remaining elements located immediately after the N-encoding ORF are a bulged stem–loop and a pseudoknot that have been extensively studied using enzymatic probing and mutational replication analysis (Goebel et al. 2004a). More recent molecular genetic studies in MHV suggest additional base-pairing at the extreme 3′ end of the genome with loop L1 of the pseudoknot to create P4 and P5 helices (Fig. 1; Zust et al. 2008).

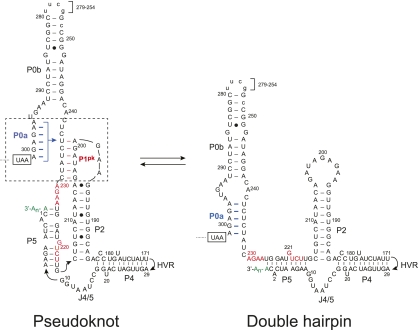
FIGURE 1.

Secondary structural representation of a proposed molecular switch model of the MHV 3′-UTR region consistent with functional studies (Goebel et al. 2004a; Zust et al. 2008). The psuedoknotted conformation is shown on the left, with the double hairpin conformation shown on the right. Formation of the P1^pk helix (left, red base pairs) is mutually exclusive with the formation of the P0a stem (right, highlighted in blue). Nucleotides are numbered 3′ to 5′ from the 3′ terminus of the genome (C1) to A301, encompassing the entire 3′ UTR in MHV. Nucleotides that form the short P3 helix in the L1 loop (²³⁰AGAA²²⁷, ²²¹GUCA²¹⁸) (see Fig. 2A) are highlighted in red. The termination codon of the N gene is boxed, and in the RNAs investigated here, an extended stem–loop on P0b (nucleotides 279–254) not required for viral replication (Goebel et al. 2004a) was replaced with a uucg tetraloop sequence. The hypervariable region (HVR, nucleotides 170–30) is not shown and is also dispensable for viral replication in cells (Goebel et al. 2007). A 97-nt RNA that contains the minimal components of the proposed molecular switch corresponds to nucleotides 301–185 (Goebel et al. 2004a).

A conserved feature of the 3′ UTR of nucleotides in the lower stem in the 5′-most hairpin P0a (Fig. 1) are also complementary to loop nucleotides in the downstream P2 stem forming a new stem we have designated P1^pk (Fig. 1, boxed region). As can be seen, Watson-Crick base-pairing between stem P0a and the alternate pseudoknot stem P1^pk are mutually exclusive and require that only one conformation be present at any one time (Goebel et al. 2004a). Extensive reverse genetics experiments support the presence and necessity of both conformations, supporting the idea that both helical stems must form at some point during the viral replication cycle (Goebel et al. 2004a,b, 2007). Since the two conformations are mutually exclusive, it has been proposed that this RNA element represents a molecular switch that could regulate differential initiation of RNA replication for either the full-length anti-genomic RNA or for the nested set of subgenomic mRNA (Fig. 1; Goebel et al. 2004a).

Here, we present RNA unfolding (thermodynamic) experiments designed to determine if both conformations are, in fact, capable of forming and to use the subsequently derived absolute stability (ΔG₂₅) to characterize the pseudoknot-forming stem, P1^pk, in the presence and absence of competition from the alternately folded P0a stem. To accomplish this, we have systematically characterized subdomain fragments excised from the minimal 97-nt UTR that corresponds to nucleotides 301–185 (Fig. 1). We show that the pseudoknot is only marginally thermodynamically stable and can only form in absence of competition from the P0a stem. The implications of these findings on the conformational switch model (Goebel et al. 2004a) are discussed.

RESULTS AND DISCUSSION

Thermal denaturation of the MHV PK RNA

The minimal MHV 3′-UTR fragment that contains all originally proposed components of the molecular switch (Goebel et al. 2004a) and lacks the P4 and P5 helices proposed later (Zust et al. 2008) is 97 nt and has been designated here as UTR (see Fig. 2C). Using this model of the UTR RNA, we characterized two RNA subdomain fragments denoted Δ8 UTR (89 nt) and PK (58 nt), to stabilize predicted substructures of the molecular switch (Fig. 2). Both Δ8 UTR and PK RNAs prevent the competing stem P0a from forming. Individual component helical domains P0b, P0ab, and P2 were also prepared to enable their folding assignments in more complex RNAs (see below). Mutant RNAs based on the UTR, Δ8 UTR, and PK constructs were designed to abrogate, stabilize, or otherwise alter base-pair compositions in either P1^pk or P2 stems as indicated (Fig. 2). In addition, loop L1 substitutions and deletion mutations were prepared in an effort to identify thermal unfolding transitions resulting from loop structures (the PK L1 U-loop in which all of the L1 loop nucleotides were converted to uridine residues) (see Fig. 2A) as well as investigate loop length and P1^pk pairing (PK L1 Δ4 in which 4 nt were deleted from the 3′ most sequence of L1 (see Fig. 2A).

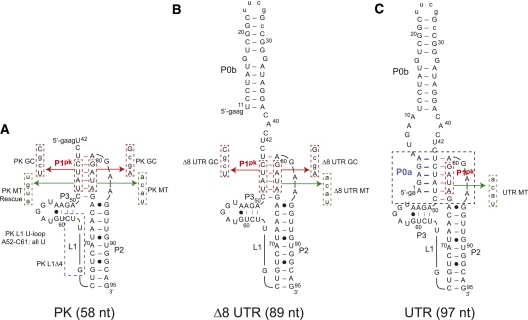
FIGURE 2.

Diagram of constructs used in thermodynamic analysis of a minimal MHV 3′-UTR RNA (residues 301–185) (Fig. 1). The competing lower stem, pseudoknotted stem, stem 2, and short 4-bp stem in loop L1 are designated P0a, P1^pk, P2, and P3, respectively. (A) PK RNA (residues 241–185 in Fig. 1; 42–95 here). Expanded sequences display the PK MT, which disrupts P1^pk pairing, and PK GC replaces two A-U base pairs with two G-C base pairs. In addition, loop L1 mutants are indicated as PK L1 U-loop and PK L1 Δ4 RNAs, which replace nucleotides 52–61 in L1 with uridines and deletes the 3′ 4 nt of L1, respectively. (B) Δ8 UTR RNA (residues 294–185 in Fig. 1; 11–95 here). Expanded sequences display the Δ8 UTR MT construct, which disrupts P1^pk pairing, and Δ8 UTR GC replaces two A-U base pairs with two G-C base pairs. (C) UTR RNA construct (residues 301–185 in Fig. 1; 1–95 here). The expanded sequence represents the mutations used in the UTR MT construct designed to eliminate P1^pk pairing. In all cases, two to four non-native nucleotides added at the 5′ end to facilitate in vitro transcription are shown in lowercase. Mutations in the body of each RNA are also shown in lowercase.

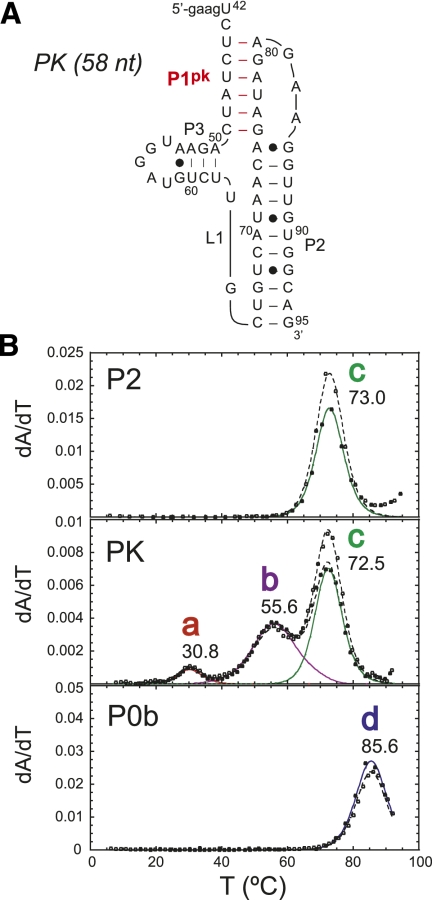
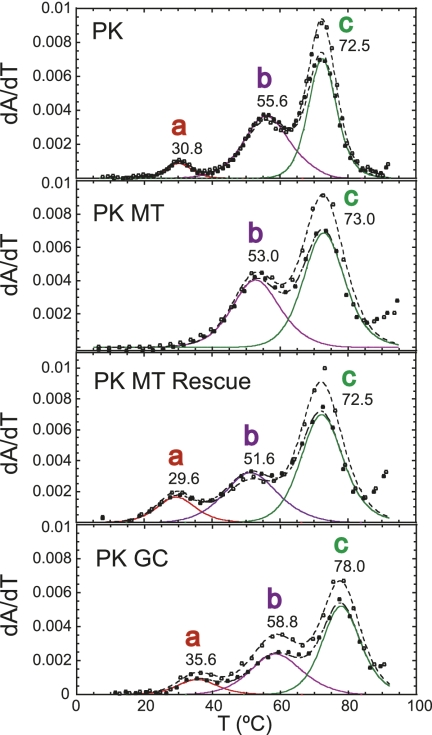
The thermal melting profiles are shown for PK RNA compared to that of the isolated P2 and P0b helical stems collected in 10 mM potassium phosphate buffer (pH 6.0), 100 mM KCl, and 5 mM MgCl₂ (Fig. 3). The PK RNA is characterized by three resolvable unfolding transitions, labeled as a (t_m = 30.8°C), b (t_m = 55.6°C), and c (t_m = 73.0°C). Individual melting profiles measured at 260 and 280 nm were simultaneously fit to a sequential two-state unfolding model that generates a t_m and van't Hoff ΔH (for fitted parameters, see Table 1) for each unfolding transition (Theimer and Giedroc 1999).

FIGURE 3.

Thermal melting profiles for PK RNA compared with P2 and P0b isolated stems. (A) Schematic of MHV PK RNA secondary structure and sequence. (B) Thermal melting profiles for P2, PK, and P0b RNAs. Solid curves represent fitted curves of each transition with 260-nm (closed circles) and 280-nm data (open circles). The solid unfolding curves are color coded: (red) transition a; (purple) transition b; (green) transition c; (blue) transition d, with the fitted t_m indicated for each two-state transition, with the parameters compiled in Table 1. Solution conditions were 10 mM phosphate buffer (pH 6.0), 100 mM KCl, and 5 mM Mg²⁺.

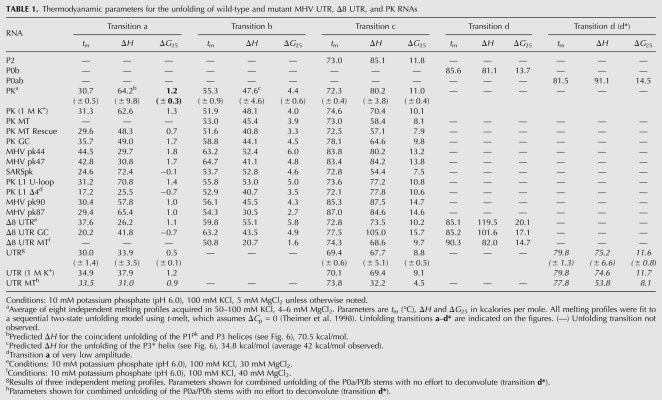
TABLE 1.

Thermodyanamic parameters for the unfolding of wild-type and mutant MHV UTR, Δ8 UTR, and PK RNAs

A comparison of thermal melts for PK and P2 RNAs allows the assignment of unfolding transition c to the unfolding of P2, given the close correspondence of thermodynamic parameters associated with the unfolding of this stem alone (Table 1). Additional support for this assignment comes from the characterization of MHV pk90 and MHV pk87 RNAs, in which compensatory A-U to G-C substitutions in P2 stabilize the P2 helix in a predictable fashion (Supplemental Fig. S2; Table 1). Additionally, the P0b stem (transition d) melts at a higher t_m compared with P2 and is obviously not found in the PK RNA unfolding profile. After assignment of transition c to P2, two transitions remain, labeled a and b, that must be reporting on some aspect of PK unfolding, and possibly P1^pk. To investigate this further, a series of mutant RNAs were characterized in an effort to specifically alter P1^pk base-pairing. The PK MT RNA introduces a 4-bp mismatch previously used (Williams et al. 1999) to disrupt the formation of P1^pk. Two additional RNAs were also analyzed. One, designated PK MT Rescue, incorporates the compensatory base-pairing mutations within the PK MT RNA to restore P1^pk pairing while the other replaces two A-U base pairs within the projected P1^pk stem with two G-C base pairs. This allows us to take advantage of distinct hyperchromic shifts associated for the unfolding of A-U base pairs versus G-C base pairs (Theimer and Giedroc 1999, 2000). A stack plot of thermal melting profiles for these RNAs is shown in Figure 4.

FIGURE 4.

Thermal melting profiles for wild-type and mutant PK RNAs designed to alter the stability of P1^pk (for sequences, see Fig. 2A) and plotted according to the conventions described in Figure 3. Thermodynamic parameters are compiled in Table 1. Solution conditions were 10 mM phosphate buffer (pH 6.0), 100 mM KCl, and 5 mM Mg²⁺.

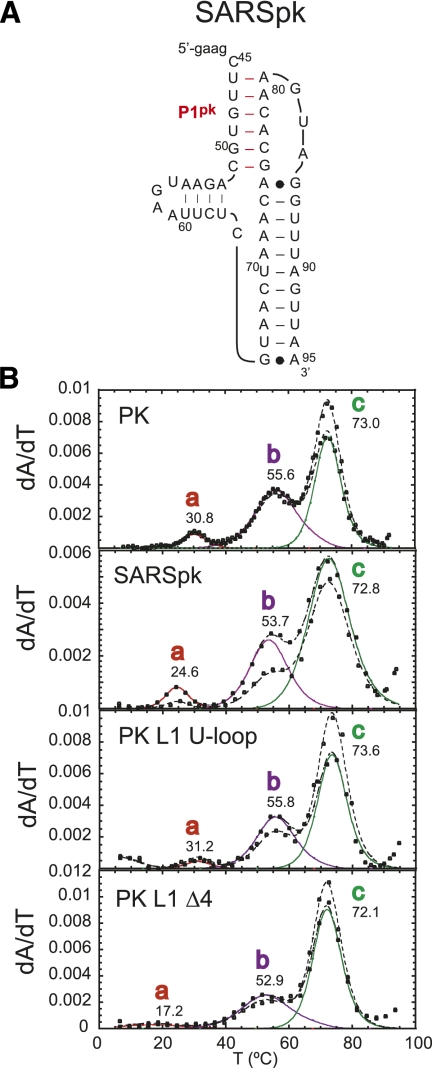
The thermal unfolding profile for PK MT results in two transitions that align with transitions b and c of the wild-type PK RNA, with transition a lost. Thermal unfolding of the PK MT Rescue RNA, which restores P1^pk base-pairing, contains all three transitions and aligns with transitions a, b, and c of the wild-type PK RNA. Finally, inspection of the PK GC RNA reveals the presence of all three transitions as well, with transitions a and b characterized by an increase in hyperchromicity at 280 nm as expected for a A-U to G-C replacement (Theimer et al. 1998). Results from all three RNAs unambiguously indicate that transition a is reporting on unfolding of the P1^pk helix. Transitions a and c are therefore assigned to unfolding of P1^pk and P2 stems, respectively. The genomes of SARS-CoV and other group 2 CoVs have previously been predicted to contain a pseudoknot similar to that of MHV within the 3′ UTR (Goebel et al. 2004b). The thermal unfolding profile of the SARSpk RNA (Fig. 5) indicates three unfolding transitions qualitatively similar to that observed in the MHV PK RNA including a b unfolding transition, consistent with this prediction.

FIGURE 5.

(A) Proposed secondary structure and sequence of the PK RNA from the 3′ UTR of SARS-CoV (SARSpk). (B) Thermal unfolding profiles of wild-type MHV PK and PK mutants L1 U-loop and L1 Δ4 (for schematic representations of these RNAs, see Fig. 2A), compared with SARSpk RNA. The SARSpk RNA may well follow a similar unfolding pathway as the MHV PK RNA. Thermal unfolding profiles are plotted and fitted according to the conventions used in Figure 3, with the thermodynamic parameters compiled in Table 1. Solution conditions were 10 mM phosphate buffer (pH 6.0), 100 mM KCl, and 5 mM Mg²⁺.

Simulations of the unfolding of the PK RNA

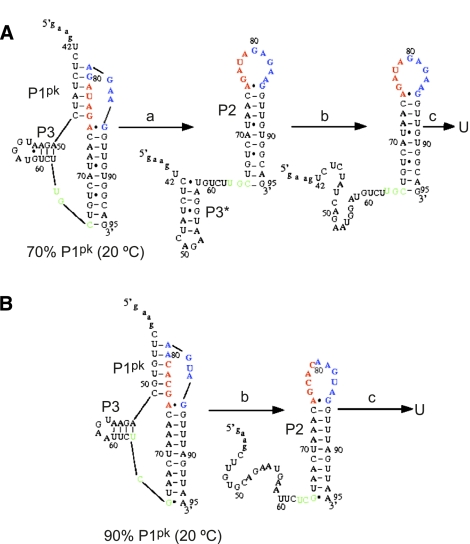
In previous work, we developed an algorithm that allows us to quickly compute the ensemble of conformers and simulate thermal unfolding curves from known thermodynamic parameters for secondary structure and calculated parameters for tertiary structural (loop–stem) interactions (Cao and Chen 2005, 2006, 2008, 2009; Cao et al. 2010). Remarkably good agreement between theory and experiment for simple H-type pseudoknots involved in ribosomal frameshifting was recently obtained (Cao et al. 2010). Here we use these methods to calculate the predominant conformers for the MHV and SARS-CoV PK RNAs (Fig. 6) at 20°C, 1 M NaCl, and determine how the conformational ensemble changes as a function of temperature. These data reveal that the P1^pk pseudoknotted conformation is the predominant conformer in each case, with the 5′ end of the long L1 loop (see Fig. 2) tied up in a 4-bp stem–loop, labeled P3 (Fig. 6A,B). Thermal unfolding simulations (Supplemental Fig. S3A,B) give rise to major transitions that qualitatively correlate with the experimentally observed a, b, and c transitions, respectively. These simulations suggest that transition a is actually reporting on the coincident unfolding of both P1^pk and P3 helices, while transition b in the MHV PK RNA melting profiles may correspond to the melting of a non-native stem–loop P3* that forms once P1^pk is disrupted (Fig. 6A). Predicted and experimental enthalpies of unfolding are consistent with these assignments (Table 1). These data taken collectively are therefore consistent with the three-transition unfolding model, PK → I → P2 → U, as defined by unfolding steps a, b, and c.

FIGURE 6.

The predicted structural changes associated with the unfolding transitions as shown in the melting curves of the MHV PK (A) and SARS-CoV PK (B) RNAs calculated at 1 M NaCl (see Supplemental Fig. S3A,B). Secondary structures of the predominant conformations (and % of total conformers at 20°C) of each RNA are shown, with those nucleotides in the P2 hairpin loop colored red and blue for clarity. The short 4-bp P3 helix is shown on the left of each conformer. Nucleotides shaded green define the 3′ end of the predicted long L1 loop (see Fig. 2A). For the MHV PK pseudoknot, transition a is associated with the unfolding of the pseudoknot structure. A misfolded hairpin-like structure (P3*) is found after unfolding of the pseudoknot. Transition b is associated with unfolding of the misfolded hairpin-like structure P3* (for details, see text).

Quantitative analysis of the PK RNA unfolding profiles reveals that transition a is characterized by a very low t_m, and analysis of this transition as a single two-state unfolding transition reveals ΔG₂₅ = 1.2 (± 0.3) kcal/mol, or only marginally stable under these conditions (Table 1), and nearly completely unfolded at 37°C. A number of compensatory base-pairing (A-U to G-C) mutations designed to stabilize the P1^pk helix, e.g., in the context of the PK GC (Fig. 4) and MHV pk44 and pk47 RNAs (Supplemental Fig. S2), do so, with ΔG₂₅ of 1.7–1.8 kcal/mol (Table 1).

Effect of loop L1 composition and length of P1^pk stability in the PK RNA

The effect of L1 loop length was investigated next by characterizing PK L1 Δ4 and PK L1 Δ8 RNAs. PK L1 Δ4 RNA deletes the 3′-most 4 nt in L1 and should abolish formation of the short P3 helix in L1, but will not affect formation of the non-native P3* helix whose unfolding is assigned to transition b (see Fig. 6A). Inspection of the PK L1 Δ4 RNA melting profile is consistent with this prediction (Fig. 5B). Although the PK L1 Δ4 RNA shows three unfolding transitions, transition a is significantly destabilized to t_m = 17°C, with little effect on the t_m of transition b; transition a is destabilized relative to the wild-type RNA (ΔΔG₂₅) by 1.7 kcal/mol (Table 1). Thermal unfolding of a PK L1 Δ8 RNA, which deletes the 3′-most 8 nt within L1, results in a complete absence of transition a with little effect on transition b or c (melts not shown). These data reveal that incremental deletions introduced into the long L1 loop are destabilizing to the pseudoknotted conformation.

We next evaluated the effect of the loop L1 sequence on pseudoknot stability by characterizing PK L1 U-loop RNA, which replaces all but five of the residues in L1 with uridines (nucleotides 52–61) (see Fig. 2A). This RNA is expected to eliminate non-native P3* pairing along the unfolding pathway (see Fig. 6A), but the formation of the short 4-bp P3 helix is possible since a G51-C61 base pair could be swapped for a G51-U61 noncanonical base pair and an A53-G55 noncanonical base pair swapped for the canonical A53-U55 base pair (see Fig. 2A). The thermal unfolding profiles of PK L1 U-loop RNA reveals three unfolding transitions with similar t_m values when compared with the wild-type PK (Fig. 5B; Table 1). The major difference between the PK L1 U-loop and the wild-type RNAs is a lower-amplitude a transition but one characterized by an apparent stability of the P1^pk helix (ΔG₂₅ = 1.4 kcal/mol) similar to the wild-type RNA, with ΔH_b and ΔG_25b for the b transition lower (Table 1).

Thermal denaturation of MHV Δ8 UTR RNA

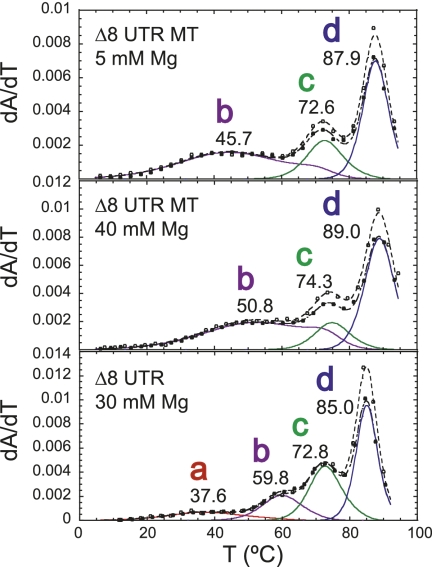
We next investigated pseudoknot unfolding within the context of the larger RNA without competition from the double-hairpin conformation. To do this, eight 5′ nucleotides of the UTR RNA were deleted to create Δ8 UTR (89 nt) (Fig. 2B). This RNA is unable to form P0a and thus cannot adopt the full double-hairpin conformation but leaves the predicted pseudoknot base-pairing unaffected.

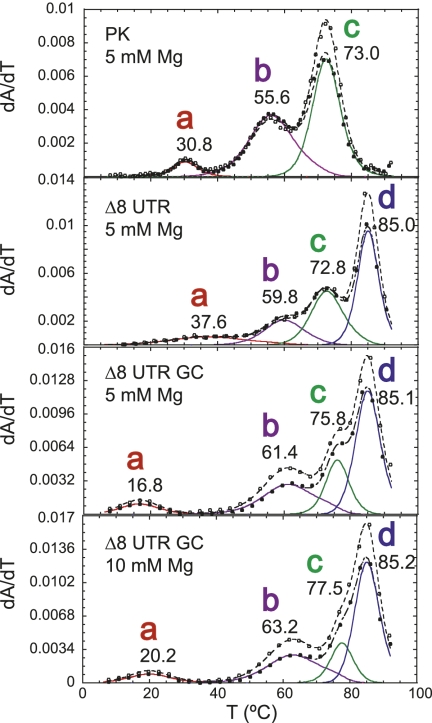
Examination of thermal melts obtained at 30 mM Mg²⁺ (pH 6.0) for the Δ8 UTR RNA reveals four unfolding transitions, labeled a–d (Fig. 7). Relative to the PK RNA, the Δ8 UTR RNA melting profile differs in that transition a is very broad and only appears under conditions of very high magnesium (see Supplemental Fig. S5). In addition, a high t_m unfolding transition labeled transition d is present that is tentatively assigned to unfolding of P0b (Fig. 7). Likewise, transition c can be identified as P2 unfolding. Transition b resembles the unfolding transition assigned to the unfolding of the non-native P3* helix (I) as observed for MHV PK unfolding (Fig. 6A).

FIGURE 7.

Thermal unfolding profiles of Δ8 UTR and P1^pk stabilizing mutant Δ8 UTR GC RNAs (for schematics, see Fig. 2B). Thermal unfolding spectra of PK, Δ8 UTR, and Δ8 UTR GC RNAs, the latter at two different Mg²⁺ concentrations, with thermodynamic parameters compiled in Table 1. Solution conditions were 10 mM phosphate buffer (pH 6.0) with the indicated Mg²⁺ concentration.

To investigate the unfolding transitions further, the same P1^pk stabilizing mutations were incorporated into the Δ8 UTR RNA. Resulting thermal melts of construct Δ8 UTR GC RNA (see Fig. 2B) reveal the same hyperchromic and t_m shifts observed for the PK RNA. Transitions a and b increase in 280-nm absorbance (see Fig. 7), and transitions a, b, and c are each characterized by an increase in t_m relative to the wild-type Δ8 UTR RNA (see Table 1). Interestingly, comparison of the thermal melts of the Δ8 UTR GC RNA with the PK GC RNA reveals that transition a is destabilized by 1.0 kcal/mol (100 mM KCl, 5 mM MgCl₂) (see Table 1). Taking into account the broad nature of transition a in the wild-type Δ8 UTR RNA under all solution conditions and the lower stability of the a transition in the two GC RNAs reveals that formation of the P0b stem, although not directly involved in P1^pk base-pairing, destabilizes the formation of the P1^pk helix in the context of Δ8 UTR RNA relative to the PK RNA.

Further investigation of P1^pk pairing was conducted within the Δ8 UTR RNA by analyzing the unfolding profile of an equivalent pseudoknot stem mutant analyzed to probe for P1^pk pairing. The Δ8 UTR MT RNA thermal melting profile is markedly perturbed relative to the Δ8 UTR RNA (Fig. 8). The melt consists of unfolding transitions readily assigned to P2 (transition c) and P0b (transition d) unfolding, and a featureless broad transition that remains unchanged even in the presence of high concentrations of magnesium. The nature of this transition is unknown but may reflect the unfolding of the I-state P3* helix in the L1 loop. In any case, transition a is absent in these melts, consistent with the disruption of pseudoknot pairing in the Δ8 UTR MT RNA.

FIGURE 8.

Thermal melting profiles for the Δ8 UTR MT RNA compared with wild-type Δ8 UTR RNA at high [Mg²⁺] (for schematics, see Fig. 2B). Profiles follow conventions used in Figure 3, with the thermodynamic parameters complied in Table 1. Transition a is very broad but observable in all melting profiles collected at [Mg²⁺] ≥ 10 mM, 0.1 M K⁺ (see Supplemental Fig. S5). Solution conditions were 10 mM phosphate buffer (pH 6.0) with the indicated Mg²⁺ concentrations.

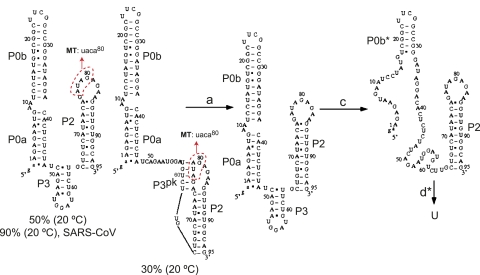
Simulations of the unfolding profile of the Δ8 UTR RNA are largely consistent with these experimental conclusions (Fig. 9; Supplemental Fig. S3). The starting conformational ensemble (20°C, 1 M NaCl) is predicted to contain ∼70% of the P1^pk pseudoknot, which after unfolding in transition a (see Supplemental Fig. S3) adopts a non-native P3* helix, which then is predicted to unfold as transition b. In the simulations, transitions c and d are predicted to correspond to the unfolding of the P0a stem, followed by most of P0b (P0b*) and P2 in the last unfolding step.

FIGURE 9.

The predicted structural changes associated with the melting curve of the 89-nt Δ8 UTR at 1 M NaCl. At room temperature, the native structure contains a native pseudoknot structure P1^pk. Transition a is associated with the unfolding of the native pseudoknot. Transition b is associated with unfolding of the misfolded hairpin structure P3* in loop L1. At high temperature, the transition c corresponds to partial unfolding of the P0b stem, and transition d is associated with unfolding of the P2 stem and the rest P0b stem.

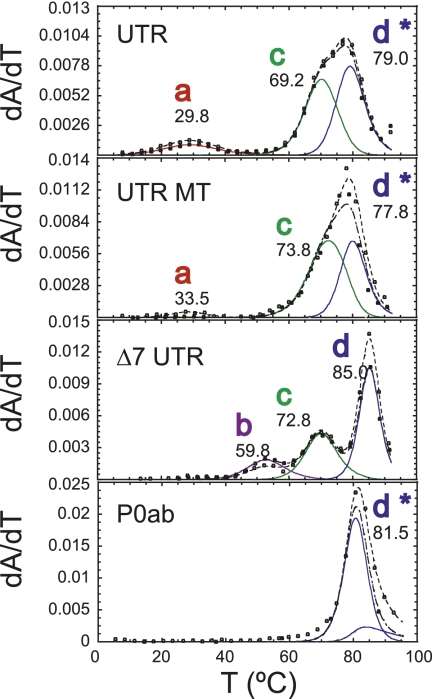
Thermal denaturation of the UTR RNA

We next investigated the unfolding profiles of an intact UTR molecule denoted as UTR (97 nt) (see Fig. 2A) that allows the formation of the two mutually exclusive competing stems P0a and P1^pk. These thermal unfolding profiles reveal three unfolding transitions labeled as transitions a, c, and d* (Fig. 10). To deconvolute this unfolding pattern, we compared it to those obtained for an RNA that abolishes P1^pk pairing, UTR MT, as well as an RNA containing the full bulged stem–loop, P0ab RNA (see Fig. 10). Unfolding of the P0ab RNA was modeled as a single unfolding transition labeled d* for identification purposes only (no attempt was made to extract independent thermodynamic parameters for P0a). Addition of the P0a stem reduced the apparent t_m of the P0b helix, and this is reflected in the thermal melt of UTR RNA and has a t_m of ∼80°C versus 85°C for the P0b helix (Fig. 3). Transition c corresponds to P2 unfolding and is found precisely at previously determined t_m values. Comparison of the UTR and the UTR MT RNA reveal that the broad transition labeled a (t_m = 39°C) cannot be reporting on P1^pk pairing since it is found in both melting profiles, although its intensity is lower in the UTR MT RNA (Fig. 10). An interesting feature of both the UTR and UTR MT melting profiles is that transition b assigned to the unfolding of the loop L1 P3* helix so prominent in the PK and Δ8 UTR RNA melts, is completely absent.

FIGURE 10.

Thermal melting profiles of the UTR and UTR MT RNAs (for schematics, see Fig. 2C) compared with the Δ8 UTR and component P0ab RNAs under the same solution conditions. The thermodynamic parameters are compiled in Table 1. Note that under these conditions of 5 mM Mg²⁺, the pseudoknot is not obviously present in the Δ8 UTR RNA (for details, see text). Solution conditions were 10 mM phosphate buffer (pH 6.0), 100 mM KCl, and 5 mM Mg²⁺.

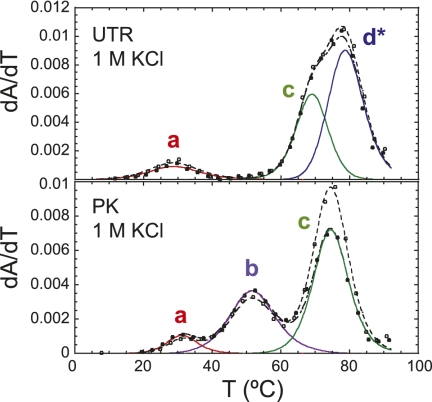
We next carried out simulations of the UTR RNA conformational ensemble as a function of temperature as described above in an effort to understand the nature of the fully folded state (20°C, 1 M NaCl), and what the individual unfolding transitions (a–d) may be reporting on. As found for the PK RNA, the calculated melting profile (Supplemental Fig. S3C) is quite similar to the experimental melting curve measured in 1 M KCl (Fig. 11), with the major conformers shown in cartoon form along the unfolding coordinate illustrated in Figure 12. Thus, although all three RNAs are stabilized by the incremental addition of MgCl₂ to varying degrees (Supplemental Fig. S5), a high concentration of monovalent salt is sufficient to capture the major observable features of the experimental melting profiles in each RNA (Fig. 11); this is consistent with Mg²⁺ functioning in a nonspecific manner (Theimer and Giedroc 2000). The major conclusion is that these simulations reveal that the native P1^pk helix is completely absent, with 50% of the molecules predicted to adopt the double-hairpin conformation with a short P3 in between (P0a/P0b, P3, P2), and 30% of the molecules predicted to adopt a non-native P3^pk pseudoknotted conformation. These simulations would seem to leave open the assignment of transition a in the UTR RNA thermal melts (Figs. 10, 11), although it may in part be reporting on the unfolding of the P3^pk helix in the minor conformer (an analogous 5-bp P3^pk helix can form in the UTR MT RNA by flipping mutant u77 out and pairing a78 with U60, c79 with G59 and a80 with U58) (Fig. 12). In any case, both conformers preclude formation of the P3* helix, consistent with the lack of unfolding transition b in the melts (Figs. 10, 11). Transitions c and d* then report on unfolding of the P0a and P3 helices, followed by P0b* and P2 helices as discussed above for the Δ8 UTR RNA.

FIGURE 11.

Thermal unfolding profiles of PK and UTR RNAs in the presence of 10 mM phosphate buffer (pH 6.0), 1 M KCl. These profiles are very similar to those obtained in the presence of 5 mM Mg²⁺, 0.1 M KCl (cf. Figs. 10 and 3, respectively) and mimic the conditions of the calculated melting curves at 1 M NaCl (Supplemental Fig. S3), on which the simulations of the conformational ensemble are based (in Figs. 6 and 12, respectively). The thermodynamic parameters are given in Table 1.

FIGURE 12.

The predicted structural changes associated with thermal unfolding of the 97-nt MHV UTR RNA calculated at 1 M NaCl. The two predominant conformations are shown with the percent of all conformations indicated at 20°C. The two conformers differ only in the disposition of nucleotides 78–82; in the major conformer these nucleotides pair to form the short stem–loop P3 contained entirely in loop L1. In the right conformer, these nucleotides pair with nucleotides 75–79 in the P2 loop to form a non-native pseudoknot, P3^pk. In no case do nucleotides 41–49 of P0a pair with nucleotides in the P2 loop, as found for the PK RNA simulations (see Fig. 6). Simulations with the 92-nt SARS-CoV UTR RNA give rise to 90% of the conformations on the left, with no P1^pk pseudoknot present. For the MHV UTR RNA, transition a is found to correspond to unfolding of the pseudoknot P3^pk helix in the minor conformer, while b-transition unfolding is not present in either the simulated or experimental melts. Transition c corresponds to unfolding of the P0a stem and part of the P0b stem, and transition d is associated with unfolding of the P2 stem and the remainder of the P0b stem (denoted P0b*). The 4-nt substitution to create the UTR MT RNA is shown schematically on both major native-state conformers (circles in red).

CONCLUSIONS

In this study, we have carried out a thermodynamic investigation of a minimal MHV 3′-UTR molecular switch that lacks recently proposed P4 and P5 helices (Fig. 1) using a strategy that divides this RNA into three RNA constructs: PK, Δ8 UTR, and UTR RNAs. Quantitative analysis of the thermal unfolding profiles obtained for each RNA in conjunction with calculations of the conformational ensemble as a function of temperature leads to a self-consistent picture of the behavior of this molecular switch. The major conclusion is that the pseudoknotted stem P1^pk is weakly stable at 25°C (ΔG₂₅ = 1.2 kcal/mol in 5 mM Mg²⁺ 100 mM K⁺) and fully unfolded at 37°C under these conditions, even in the context of the PK RNA. This stability is lower than might have been anticipated. P1^pk can form a maximum of 8 bp based on complementarity (Goebel et al. 2004a) leaving a 2-nt L2, while our simulations suggest a 6-bp stem (Fig. 6); the projected stability of P1^pk is therefore expected to range from 5 to 9 kcal/mol. This suggests that the P1^pk stem is not fully folded and/or is strongly destabilized by surrounding structural elements. In fact, this modest stability is consistent with what is known about the structure/stability requirements for loop versus stem lengths as in the classic H-type pseudoknots (Pleij et al. 1985). In a standard H-type pseudoknot topology, loop L1 will cross the deep major groove of stem 2 while loop L2 will cross the wide minor groove of stem 1. To span a pseudoknot stem 1 (here P1^pk) of 6 bp, a loop length of 6–8 nt will be required to maintain coaxial stacking of the P1^pk and P2 helices (Pleij et al. 1985), which is stabilizing. More detailed structural studies are required to determine the structural disposition of the P1^pk and P2 helices in the intact UTR.

The pseudoknot is destabilized further in the context of the Δ8 UTR RNA by ≈1.0 kcal/mol (Table 1) and simply does not form at all in the context of the intact MHV UTR fragment. The long loop L1 appears capable of adopting or incorporating a number of other helical elements, e.g., P3, P3*, and P3^pk, some of which can only form after the native P1^pk helix is disrupted at low temperature. The sequence and length of the L1 loop are conserved in all group 2 coronaviruses in a way that maintains P3 pairing, disruption of which significantly influences PK stability. In fact, a 6-nt insertion in loop L1, 3′ to A53 in the P3 stem–loop (see Supplemental Fig. S4), was found to be lethal to MHV and was proposed to abrogate a key RNA–RNA interaction with another region of the genome (Goebel et al. 2004a).

It is of interest to discuss our findings with a minimal 97-nt RNA in the context of a recently proposed model for the full-length MHV 3′ UTR elucidated on the basis of second site revertants of the original 6-nt insertion in loop L1 P3 stem–loop (Zust et al. 2008). This model posits that most of the pseudoknot loop L1 is base-paired with the extreme 3′ end of the genome to form the P5 helix (see Fig. 1), which includes the first adenosine residue of the poly(A) tail (Zust et al. 2008). If this is the case, this would prevent the formation of the P3 helix in L1. Sequences immediately 3′ to the P2 helix are also paired to form P4 and combine to make a three-helix junction in the context of the pseudoknot that is predicted to be conserved in all coronaviral 3′ UTRs, including SARS-CoV (see Fig. 1; Zust et al. 2008). Although there is as yet no direct structural support for this model, mutants designed to disrupt base-pairing are generally consistent with this secondary structure model (J Leibowitz, unpubl.). Interestingly, second site suppressors of the original L1 insertion mutants were also found in the coding region of the nsp9 gene, and this led Masters and coworkers to postulate that the pseudoknot domain functions prominently in the initiation of both replication and transcription by a primase–replicase complex (Zust et al. 2008). For example, as the 3′ end of the genome is copied by the primase–replicase, this allows loop L1 to become single stranded, which the investigators speculate might ultimately drive formation of the pseudoknot.

Our thermodynamic findings obtained on the minimal construct would appear to argue exactly the opposite. They suggest that pseudoknot formation with a largely single-stranded L1 loop is unlikely to occur in the absence of host or virally encoded proteins that stabilize the pseudoknot against the far more stable double-hairpin conformation. In fact, inspection of the full-length minimal UTR model involving P4 and P5 helices suggests that the pseudoknot could be stabilized by the P5 helix since this would allow the UTR to adopt a double-pseudoknotted conformation that is quite common in large RNAs, albeit with distinct topologies (Ferre-D'Amare et al. 1998; Hammond et al. 2010). In particular, the 3′ UTRs of a number of plant viruses, including turnip yellow mosaic virus (TYMV) and tobacco mosaic virus (TMV), contain one (Kolk et al. 1998) or more pseudoknots; in TMV, the double pseudoknot folds but appears dynamic and not tightly packed (Hammond et al. 2009). In any case, any structure that is formed in the 3′ UTR will have to be unfolded to allow for passage by the RNA-dependent RNA polymerase complex. As P5 becomes unpaired as a result of minus strand synthesis to create the L1 loop, our thermodynamic studies suggest that this would favor formation of the double-hairpin architecture (see Fig. 1). Studies designed to further investigate the conformational states accessible to a full-length 3′-UTR RNA using single-molecule fluorescence methods would yield considerable insight into the dynamics of this putative molecular switch, and may ultimately provide a means to investigate primer synthesis by nsp8–nsp12 in real time in vitro (Imbert et al. 2006; te Velthuis et al. 2010), as well as identify proteins or small molecules as potential antiviral agents that stabilize the poorly stable pseudoknotted conformation.

MATERIALS AND METHODS

RNA preparation

RNA constructs were prepared using runoff transcription from synthetic double-stranded DNA templates or blunt-end-digested plasmids. Both SP6 and T7 RNA polymerases were used depending on the construct. Transcription conditions for individual templates were concentration-optimized for the concentrations of nucleotides (2–10 mM), RNA polymerase (2–6 μL of a stock solution), and MgCl₂ (10–20 mM) prior to large-scale synthesis. All transcription reactions contained 5 μM template, 0.05 mg/mL 8000 MW polyethylene glycol, 4 units/mL inorganic pyrophosphatase, and 1× transcription buffer (40 mM Tris-HCl at pH 8.0, 5 mM dithiothreitol, 1 mM spermidine, 50 μg/mL bovine serum albumin). Reactions were incubated for 8 h at 40°C for SP6 and 37°C for T7 and quenched with a 1/10 volume of 0.5 M ethylenediamine tetraacetic acid (EDTA; pH 8.0) and precipitated with absolute ethanol stored overnight at −80°C. Centrifuged RNA pellet was resuspended in a solution of 7 M urea and 50 mM EDTA. Crude RNA was purified using denaturing polyacrylamide gel electrophoresis (PAGE) using 20% (19:1 bis-acrylamide:acrylamide), 7 M urea, and 1× Tris:borate:EDTA (TBE) acrylamide gels run at 250 V for 8–14 h depending on the size of the RNA. Gel bands were visualized using UV shadowing and electroeluted in a 1× TBE solution using an S&S electroeluter. Recovered RNAs were buffer-exchanged repeatedly using Millipore Amicon Ultra centrifugal filter devices. Final buffer conditions consisted of 10 mM phosphate (pH 6.0) with varying amounts of monovalent KCl and magnesium. Annealing conditions consisted of heating RNA for 3 min at 95°C and then slow cooling for 45 min at room temperature.

Thermal denaturation methods and data analysis

A Cary 1 spectrophotometer operating in the double-beam mode equipped with a six-cell block and temperature controller was used to monitor RNA unfolding simultaneously at 260 nm and 280 nm. RNA samples ranging from 2 to 15 μM strand concentration (typically 2–4 μM) in a total volume of 600 μL were prepared on ice, heated for 10 to 15 min to 65°C, slow-cooled on the bench, loaded into capped 10-mm pathlength cuvettes at room temperature, and allowed to equilibrate for 30 to 60 min at 5.0°C. The temperature was ramped between 5°C and 95°C in increments of 0.3°C/min with a data point collected every 0.3°C. Cary 1 text files collected in transmittance mode at 260 and 280 nm were converted to absorbance, subjected to smoothing (window ≈4°C), and normalized against the absorbance value for the temperature at which the value of the derivative was largest. The melting profile was obtained by taking the first derivative of the absorbance with respect to the temperature (∂A/∂T). Low- and high-temperature baseline offsets were manually adjusted by visual inspection of the derivative data and subtracted before fitting as described previously (Laing and Draper 1994; Theimer and Giedroc 1999). Both sets of derivative data (∂A₂₆₀/∂T and ∂A₂₈₀/∂T) were subjected to a simultaneous nonlinear least-squares fit to a multiple sequential interacting two-state transition model that optimizes ΔH_i and t_m,i for the unfolding of each i-th unfolding transition (Laing and Draper 1994) implemented by the algorithm t-melt, ΔC_p^o = 0 (Theimer and Giedroc 1999, 2000). The unfolding entropies were obtained from ΔS = ΔH/t_m, while ΔG₂₅ = ΔH − 298.15*ΔS. Typical uncertainties in ΔG₂₅ were 5%–15% of the fitted mean values as a result of propagation of the errors in ΔH and t_m (see Table 1 for representative uncertainties in ΔG₂₅, ΔH, and t_m from multiple melting profiles). Thermodynamic parameters were not systematically dependent on RNA concentration and thus are consistent with unimolecular unfolding in all cases.

Theoretical predictions for RNA structures and folding pathways

Folding pathways and structural changes are predicted from the partition function. The partition function Q is the sum over all the possible conformations

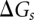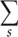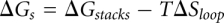where is the free energy of a given structure s. In our calculation, the conformational sum includes all the possible nonpseudoknotted secondary structures and pseudoknotted structures. The free energy for each given structure is determined from . Here 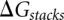is the total free energy of all the base stacks in the structure as determined from the Turner rules (Serra and Turner 1995) and 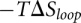is the loop free energy as determined from the Vfold model (Cao and Chen 2005, 2006, 2009; Chen 2008; Cao et al. 2010). Loop formation is allowed in the helical stems for a pseudoknot (Cao and Chen 2009). However, loop–stem tertiary interactions are neglected in the predictions for the melting curves of MHV and SARS-CoV PKs. Structures are determined from the base-pairing probability. For each pair of nucleotides i and j, the probability 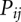for i and j to form a base pair is computed from the conditional partition function 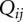: 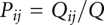. Here 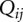is the partition function for all the conformations that contain the (i, j) pair. We compute 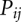for all the possible (i, j) pairs and predict the stable (populous) state at temperature T as structures comprised of large- 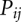base pairs. The change of the stable structures with temperature gives the equilibrium folding/unfolding pathway.

SUPPLEMENTAL MATERIAL

Supplemental material is available for this article.