Abstract
Hyperactivation in mammalian sperm is characterized by highly asymmetrical waveforms and an increase in the amplitude of flagellar bends. It is important for the sperm to be able to achieve hyperactivated motility in order to reach and fertilize the egg. Calcium (Ca2+) dynamics are known to play a large role in the initiation and maintenance of hyperactivated motility. Here we present an integrative model that couples the CatSper channel mediated Ca2+ dynamics of hyperactivation to a mechanical model of an idealized sperm flagellum in a 3-d viscous, incompressible fluid. The mechanical forces are due to passive stiffness properties and active bending moments that are a function of the local Ca2+ concentration along the length of the flagellum. By including an asymmetry in bending moments to reflect an asymmetry in the axoneme’s response to Ca2+, we capture the transition from activated motility to hyperactivated motility. We examine the effects of elastic properties of the flagellum and the Ca2+ dynamics on the overall swimming patterns. The swimming velocities of the model flagellum compare well with data for hyperactivated mouse sperm.
Keywords: regularized Stokeslets, calcium dynamics, fluid-structure interaction, CatSper channels
1. Introduction
The propulsion of sperm, through an undulatory motion of the flagellum, is vital for fertilization. Sperm exhibit different types of motility in response to varying environments and chemical cues [1–4]. Activated motility is characterized by symmetrical flagellar bending that is associated with highly linear trajectories [5]. Hyperactivation is a motility pattern of mammalian sperm that is characterized by highly asymmetrical flagellar bending, leading to nonlinear trajectories, including swimming in circles. There is evidence that hyperactivation is key in enabling the sperm to swim effectively through oviductal mucus, escape from the sperm reservoir, penetrate the cumulus matrix, and penetrate the zona pellucida of the oocyte [6–11]. Initiation and maintenance of hyperactivated motility is associated with a change in calcium (Ca2+) concentration in the flagellum [6–8, 12, 13].
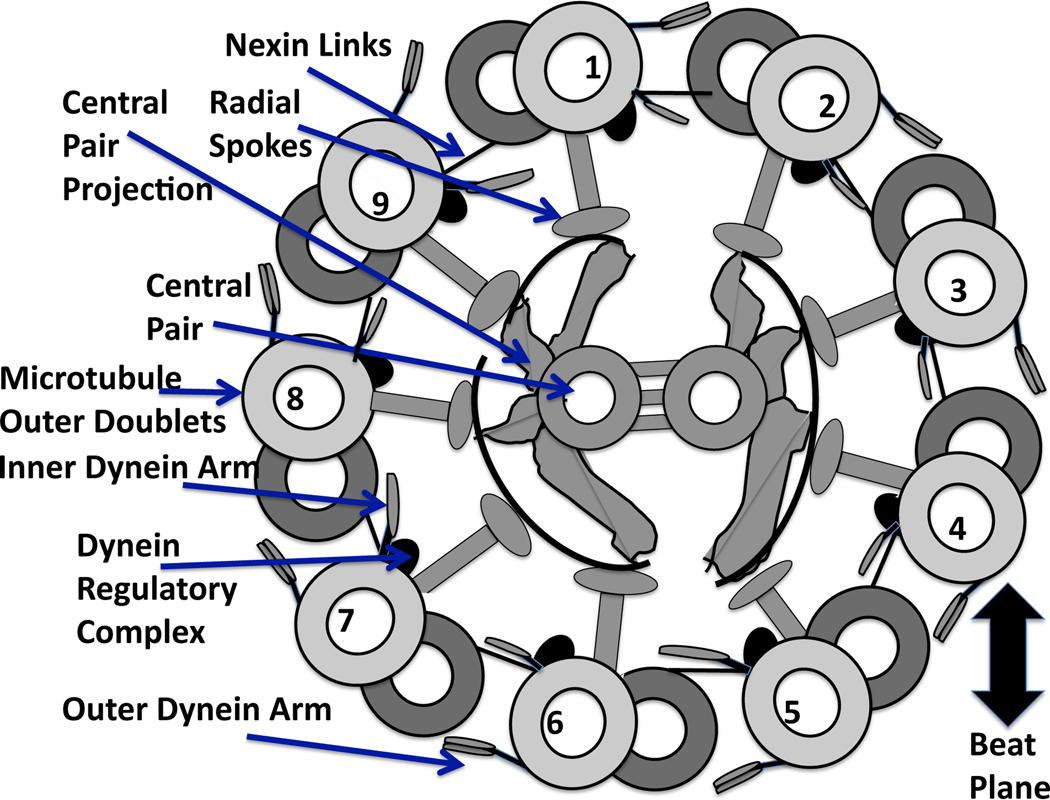
In order to transition from symmetrical to asymmetrical beating, there must be some change in the axoneme, the core of the flagellum. There are many passive and active elements of the axoneme, as well as sites where signaling molecules can bind and cause conformational changes that affect force generation [14]. The ultrastructure of the axoneme, whose cross section is shown in Fig. 1, consists of a central pair of microtubules surrounded by 9 microtubule doublets. Inner and outer rows of dyneins, chemo-mechanical ATPases, emanate from each doublet and face the adjacent doublet at regularly spaced intervals [11]. Passive structures include the nexin links which connect the adjacent pairs of doublets and the radial spokes.
Fig. 1.
Diagram of a cross section of the “9+2” axoneme, recreated from [93], and viewed from base toward tip. Each of the internal structures of the flagellum are labeled with arrows. The central pair are positioned perpendicular to the beat plane, which is defined by dyneins on doublets 1–4 bending the axoneme in one direction, followed by the deactivation of these dyneins and the activation of the opposite group of dyneins on doublets 6–9 [14, 56].
Bending of the axoneme is due to the action of dynein motors causing local sliding of microtubule doublets relative to one another. This sliding is converted to bending by the restraining influence of the other passive structures, including the nexin links [15–17]. Currently, there are many hypotheses for the mechanisms that provide the switching point for activation and deactivation of dyneins [11]. While bending is due to the local sliding of microtubules, the overall flagellar waveform arises from the coupled nonlinear system that consists of chemical signaling, active force generation, passive elastic forces, and external fluid dynamics [18, 19].
The length of mammalian sperm is on the order of 100 microns; typical human and bull sperm are approximately 60 µm in length, while rat and hamster sperm are approximately 150–200 µm in length [20]. Due to the small length scales, mammalian sperm swim at low Reynolds number, Re ~ 10−4–10−2, where viscous forces dominate. Classic fluid dynamic analyses of flagellar swimming due to prescribed kinematics has made use of the linear Stokes equations in this Reynolds number regime (for example [21–25]). More recently, fluid dynamic studies relevant to sperm motility have addressed the effect of surfaces [26, 27], viscoelasticity [28, 29], and effects of head shape [30, 31].
Recognizing that a ciliary or flagellar waveform emerges from the coupling of fluid dynamics to passive and active forces along the axoneme, recent models that capture various elements of the full fluid-structure interaction have been developed (for example [32–36]). Some of these models prescribe a preferred curvature along the flagellum, but the extent to which this curvature is achieved depends upon the elastic properties of the filament as well as the viscous forces of the surrounding fluid [28, 36]. Other mechanical models are more detailed, and include discrete representations of dynein motors, microtubules, and nexin links [34, 35].
In this manuscript, we present the first model of flagellar hydrodynamics that couples Ca2+ dynamics along the moving flagellum, viscous fluid mechanics, and the elastic properties of the flagellum. We use our previous Ca2+ model derived for mouse sperm that accounts for Ca2+ influx through CatSper channels and an internal Ca2+ store [37]. A time-dependent, preferred curvature that depends upon the evolving Ca2+ concentration is modeled. Forces due to the bending moments induced by this curvature model, along with passive elastic forces, are coupled to a viscous fluid. The waveform of the flagellum is not preset, but emerges from the coupling of the biochemistry, mechanics, and hydrodynamics. By including a slight asymmetry in the curvature model that reflects a hypothesized asymmetry in the axoneme’s response to Ca2+, we observe the transition from activated motility to hyperactivated motility as a result of Ca2+ influx through CatSper channels.
2. Model development
Since mammalian sperm swim at a Reynolds number that is approximately zero, we assume that the fluid flow is governed by the incompressible Stokes equations:
| (1a) |
| (1b) |
| (1c) |
| (1d) |
where p is the pressure (Pascals, kg m−1 s−2), u is the fluid velocity (m s−1), μ is the kinematic viscosity of the fluid (kg m−1 s−1), and f is a force density that represents the force of the flagellum on the fluid (kg m−2 s−2 or N m−3). The centerline of this cylindrical sperm flagellum is modeled as a neutrally-buoyant elastic filament, Γ, that is immersed in the fluid and its position is X(s, t), where s is a Lagrangian parameter that we initialize as arclength. Note that g is a force per unit length that is concentrated along the length of the filament, and ϕδ (m−3) is a cutoff function, or regularized delta function where:
| (2) |
and δ is the regularization parameter. We will discuss in §5 how this formulation naturally gives rise to the method of regularized Stokeslets [38, 39], which allows us to numerically solve the coupled system. Eq. (1d) states that the velocity of a material point on the flagellar centerline coincides with the fluid velocity evaluated at that point. In order to focus on the effect of Ca2+ dynamics on motility, we ignore the presence of the sperm head and we constrain the flagellar centerline to beat within a fixed plane.
2.1. Forces
The filament Γ is taken to be a generalized Euler elastica [28, 36, 40] whose energy E (Nm) is given by:
| (3) |
| (4) |
where ℰtens and ℰbend are the tensile and bending energy densities, respectively. The integration is taken over the filament Γ and ‖ · ‖ is the Euclidean norm. The shear angle, Θ(s, t), is the angle formed by the tangent to the curve X(s, t) and the base of the flagellum. We define the (signed) curvature to be the rate of change of the shear angle with respect to arclength, ∂Θ/∂s. In our model, a preferred curvature, ζ(s, t), will be a function of the local Ca2+ concentration along the filament. Here, S1 (Nm) and S2 (Nm2) are the tensile and bending stiffness constants, respectively. As will be discussed in §2.2, we will vary S1 along the length of the flagellum and we will fix the value of S2 to isolate the effects of the Ca2+ dynamics on the bending energy of the filament.
The energy E is non-negative, translation and rotation invariant, and achieves its minimum when ‖dX=ds‖ = 1 and when the signed curvature, ∂Θ/∂s, along the filament is ζ(s, t). The force per unit length, g is derived from this energy:
| (5) |
2.2. Passive stiffness of mammalian sperm
In mammalian sperm, the connecting piece near the head serves as the basal anchor for the flagellum and outer dense fibers [41, 42]. It has been well established that the diameter of the outer dense fibers decrease from the connecting piece to the tip of the tail in mammalian sperm [43], which should affect the magnitude of the passive stiffness. Lindemann proposed to model the passive stiffness along the length of the bull sperm flagellum as:
| (6) |
where IE(x) is the stiffness at a given location x along the flagellum, IoE is the stiffness constant determined from experiments and models that did not take into account the tapering of the flagellum, and L is the length of the flagellum where x = 0 and x = L correspond to the tip and base of the flagellum, respectively [44]. Lindemann has also used a linear taper (proximal to distal) in the stiffness to successfully model bull sperm flagellar waveforms with the geometric clutch hypothesis [45]. Recent experiments of bull [46] and rat [47] sperm have disabled dynein arms and measured the passive stiffness along the length of the flagellum, and it has been found to taper from the base to the tip. In our model, we choose to study the varying passive stiffness properties along the length of the mammalian sperm flagellum by varying the tensile stiffness parameter S1 in Eq. (4). Here we will examine three cases for S1: a flagellum whose tensile stiffness is constant along its length, one whose tensile stiffness tapers linearly proximal to distal, and one with a fourth-order taper proximal to distal. Note that S2, the bending stiffness, can also vary along the length of the flagellum, but we choose to keep it fixed in order to isolate the effects of Ca2+ dynamics on the bending energy of the filament.
2.3. Calcium-dependent curvature model
It has been well established that there exists a Ca2+ dependence on flagellar curvature and amplitude in mammalian sperm [2, 48, 49]. In demembranated sperm experiments, increasing levels of Ca2+ cause increased asymmetry in the flagellar waveform at relevant biological concentrations [48, 49], where asymmetry has been found to be associated with the bend ending early in one direction (reverse bend) and growing in the other direction (principal bend) [49]. Also, if Ca2+ is increased to very high concentrations, sperm motility is inhibited [50, 51]. The ions Ni2+ and Cd2+ bind to Ca2+ binding sites and selectively block dyneins on one side of the flagellum or the other [52, 53]. This indicates that the sensitivitiy to divalent cations, such as Ca2+, varies on the two sides of the flagellum.
There are many possible ways for the change in Ca2+ concentration to affect the waveform. One mode of action is for Ca2+ to bind directly to a subset of dynein arms, altering the probability of dyneins attaching to the corresponding microtubule doublet [54]. The second mode of action is for Ca2+ to bind to a receptor such as calmodulin (CaM) which then activates kinases, such as CaMKIIβ, that phosphorylate a protein associated with the axonemal structure, resulting in a modification of the waveform [10, 51]. Lindemann has hypothesized that Ca2+-induced mechanical changes such as changing the spoke length, nexin length or elasticity, or changing the elasticity or tensile strength of the spoke – central pair axis, would alter the switch point of the beat, and ultimately change the amplitude and wave propagation characteristics of the flagellum [54].
The exact mechanism of how Ca2+ modifies the waveform is not known, but most of the current hypotheses assume that Ca2+ binding causes a change in the force generation, which, in turn, causes a change in the sliding distance that results in a change in the amplitude of the waveform. Here, we model hyperactivated sperm motility by choosing a preferred curvature function, ζ(s, t) (change in shear angle with respect to the material parameter s), in Eq. (4), as a function of the local Ca2+ concentration. Because high speed imaging (e.g. [55]) has shown that the flagellum exhibits a propagating wave of curvature, we choose an idealized sine wave as the preferred shape. The preferred (signed) curvature function corresponding to a simple sine wave with x(s, t) = s and y(s, t) = b sin(κs − ωt) is:
| (7) |
for small amplitudes, b. The sine wave travels to the right with speed ω/κ and period 2π/ω, and has been used in previous models of sperm motility [28, 36, 40]. To reflect the dependence of local dynein force generation on Ca2+, we express the amplitude b = b(s, t) in Eq. (7) in terms of a modified Hill equation,
| (8) |
that depends on the Ca2+ concentration, Ca (µM), along the length of the flagellum. The parameter VA (m) is a maximum amplitude and kA (µM) is a coefficient for receptor activation.
It has been proposed that some mammalian flagella, including rat, exhibit mostly planar beating due to the alternating activation of dyneins on microtubule doublets 1–4 and then doublets 6–9, bending the axoneme in one direction and then the other [14, 56]. In our model, we assume that Ca2+ affects the bending moments in these two directions differently. We can differentiate between the two bend directions of our flagellar centerline X(s, t) by monitoring the sign of ζ ~ ∂Θ/∂s that identifies whether the bend is concave up or concave down with respect to arclength, a material coordinate. This allows us to designate a principal bend direction versus a reverse bend direction. We assume VA is constant and we choose
| (9a) |
in order to account for an asymmetry in the model. We regard the parameter kA as the Ca2+ concentration where half of the binding sites are occupied, and, choosing kA,1 ≠ kA,2 is equivalent to assuming there exists a difference in the number of Ca2+ binding sites on one side of the flagellum versus the other, or assuming different Ca2+ binding affinities on each side of the flagellum.
3. CatSper mediated calcium dynamics model
CatSper channels, located on the plasma membrane of the principal piece of the flagellum, are Ca2+ channels that are sperm specific and required for hyperactivated motility [6, 7, 12, 57, 58]. (Refer to Fig. 2 for a depiction of the regions of the flagellum.) Recent experiments have also shown that CatSper channels are necessary for sperm to ascend beyond the oviductal reservoir [59] and to penetrate the zona pellucida of the oocyte [6, 7]. The relative intracellular Ca2+ concentration, [Ca2+]in, was recorded in mouse sperm after the application of a cell permeable cyclic adenosine monophosphate (cAMP) analog in experiments by Xia et al. [58]. The [Ca2+]in first started to increase in the principal piece, the location of the CatSper channels, and was followed by an increase in [Ca2+]in along the length of the flagellum, with a sustained increase in the head region. After the initial increase in [Ca2+]in, Ca2+ clearance mechanisms brought the [Ca2+]in back down to the basal, resting level. Xia et al. [58] completed two additional experiments to assess the role of the CatSper channels. When the cAMP analog was applied to sperm from CatSper null mutants, no significant increase in [Ca2+]in was observed. After the application of ionomycin, which facilitates the transport of Ca2+ across the plasma membrane, there was an immediate increase in the [Ca2+]in in all regions of the sperm. Xia et al. hypothesized that the cAMP analog facilitates the opening of the CatSper channels, causing Ca2+ influx in the principal piece through the CatSper channels, initiating a tail to head propagation of Ca2+[58].
Fig. 2.
Sperm geometry of a rodent sperm showing the head, neck, and the flagellum, which is made up of the principal piece, midpiece, and end piece. The redundant nuclear envelope (RNE) is an IP3 gated Ca2+ store at the base of the flagellum located in the neck and has been identified in several species of mammalian sperm [13, 63]. The CatSper channels are a sperm specific Ca2+ channel located along the principal piece and are required for hyperactivation [57, 59].
We developed a 1-d reaction diffusion model to describe the CatSper mediated Ca2+ dynamics associated with hyperactivation along a flat, stationary flagellar centerline [37]. This model was based on the experimental results of Xia et al. [58]. In order to account for the sustained increase in Ca2+ concentration in the head observed in the experiments, it was was necessary to include the release of Ca2+ from an internal store in the model. Since this 1-d model will be used as a starting point, we will describe it below.
We track two chemical signaling molecules: Ca2+ and inositol 1,4,5-trisphosphate (IP3), that are governed by the reaction diffusion equations for t > 0 and 0 < s < L:
| (10a) |
| (10b) |
where Ca(s, t) is the Ca2+ concentration (µM), I(s, t) is the IP3 concentration (µM), DCa and DI are the effective Ca2+ and IP3 diffusion coefficients (µm2 s−1), respectively, and J(s, t) are the effective Ca2+ fluxes (µM s−1). Ca2+ release from the redundant nuclear envelope (RNE), a Ca2+ store in the neck, is assumed to be IP3 gated, therefore, JRNE,out depends on the local Ca2+ and IP3 concentrations. Note that each of these fluxes are space and time dependent. The Ca2+ fluxes due to the RNE are localized to the neck. The PMCA, leak, and CatSper fluxes are localized to the principal piece (PP) of the flagellum. We note that internal structures of the flagellum, such as the microtubules, and Ca2+ buffering will cause the diffusion coefficient to vary. As a first approximation, we assume that the diffusion coefficient is constant and assume that the Ca2+ buffers are fast, immobile, and unsaturated [37, 60, 61].
In the experiments of Xia et al. [58], the cAMP analog, 8-Br-cAMP was applied to the medium where it then diffused into the cytosol of the sperm and underwent enzymatic conversion to cAMP. The opening of CatSper channels is facilitated by cAMP [62] and is modeled as follows:
| (11a) |
| (11b) |
| (11c) |
where the Ca2+ flux through the CatSper channels, JCAT (µM s−1), is proportional to the fraction of open CatSper channels, 𝕆(t), and the Ca2+ concentration in the surrounding medium, CaEXT (µM). Note that kCAT, υ1, υ2, and adeg are all rate constants that are defined in Olson et al. [37]. The fraction of open CatSper channels along the principal piece, 0 ≤ 𝕆 ≤ 1, depends on the local cAMP concentration, A(t) (µM). We assume the cAMP is being degraded throughout the cytosol of the flagellum following first order degradation kinetics. In Eq. (10a), the flux out through the PMCA, JPMCA, is modeled using a Hill function and the leak flux into the cytosol, JPP,leak, is modeled using a constant leak flux.
The last two Ca2+ fluxes are due to the redundant nuclear envelope (RNE), a Ca2+ store located at the base of the flagellum in the neck. The RNE is found in a variety of mammalian sperm [13, 63] and immunolabeling has verified the presence of type I inositol 1,4,5-trisphosphate (IP3) receptors on the RNE [63]. Due to the sustained increase in Ca2+ in the neck and head regions, it is assumed that Ca2+ is released from the RNE through an IP3 gated channel and is modeled as follows:
| (12) |
where VRNE is the Ca2+ flux when all IP3 receptors are open and activated on the RNE membrane (µM s−1) and VRNE,leak is the Ca2+ leak across the RNE membrane (µM s−1). It is assumed that the Ca2+ concentration in the RNE is large enough to sustain this flux out of the RNE. For this model, VRNE,leak is assumed to be constant. The probability of the IP3 receptor being open, PrIP3R is modeled in a phenomonological manner where we assume that the IP3 receptor has three binding domains, one for IP3 and two for Ca2+ [37, 64]. The last flux term JRNE,in is a flux term for the pumping of excess Ca2+ back into the RNE and is modeled using a Hill function.
We assume that production of IP3 is in the neck, the location of the RNE, and is modeled as a Hill equation,
| (13) |
where kP (µM) is the Ca2+ threshold concentration for IP3 synthesis and υS (s−1) is the maximal rate of IP3 production. The degradation of IP3, IP3deg, is assumed to follow first order degradation kinetics.
The framework of the Ca2+ model summarized here is based on standard Ca2+ models in other cell types [37]. The initial conditions are based on the experimental setup of Xia et al. [58], and no flux boundary conditions were prescribed. It was assumed that there was a uniform density of channels in each of the specified locations. Parameters from previous experiments with sperm were used when possible and other parameters were determined by balancing leak fluxes and using experimental values for other cell types [37]. In this simple 1-d model, keeping track of two signaling molecules, Ca2+ and IP3, gave good agreement with the qualitative trends of the Ca2+ concentration observed in the experiments [37, 58].
We now extend this model to capture the time and space dependent Ca2+ and IP3 concentration on a stretching and deforming interface, a swimming flagellum. The two reaction-diffusion equations, (10a)–(10b), will be rewritten in terms of the moving filament X(s, t) and will account for changes in material surface elements due to stretching and compression:
| (14a) |
| (14b) |
where JCk corresponds to the Ca2+ fluxes and JIk refers to IP3 synthesis and degradation. We account for local stretching and compression of the immersed interface in order to accurately account for the Ca2+ and IP3 concentrations. These equations, derived in [65, 66], ensure that mass is conserved on a moving interface when each of the fluxes are equal to zero. Note that the CatSper channels are maintained at a constant density and they act as a local source of Ca2+ influx into the cytosol. This Ca2+ influx through the CatSper channels is independent of the local fluid velocity and stretching of the flagellum.
4. Non-dimensional model
We nondimensionalize the model using the scales and parameters in Table 1. The nondimensional variables for the incompressible Stokes equations are defined as follows:
| (15) |
where the characteristic scales are based on mouse sperm. We set the length scale as ℒ =100 µm, roughly the length of a mouse sperm flagellum [20]. The beat frequency of hyperactivated sperm is ~ 10 Hz; we set the time scale (𝒯) and velocity scale (𝒱) accordingly [67, 68]. The characteristic force and pressure scales are ℱ and 𝒫, respectively. The Stokes equations, using the nondimensional variables in Eq. (15), simplify to:
| (16a) |
| (16b) |
where ū, p̄, and f̄ are the nondimensional velocity, pressure, and force density, respectively. The forces given in Eq. (1c) are also appropriately nondimensionalized.
Table 1.
Parameters and characteristic scales.
| Parameter/ Scale |
Description | Values |
|---|---|---|
| ℒ | length scale | ~1×10−4m (100 µm), mouse sperm [20] |
| 𝒯 | time scale | 0.1 s (beat frequency of hyperactivated mouse sperm ~10 Hz [67, 68]) |
| 𝒱 | velocity scale (wavespeed) | ℒ · 10 Hz = 1×10−3m s−1 (1000 µm s−1) |
| μ | viscosity | for water 1 × 10−3 kg m−1 s−1 |
| ℱ | force scale | μ · 𝒱 · ℒ = 1 × 10−10 N |
| 𝒫 | pressure scale | (μ𝒱)/ℒ=0.01 Pascals, kg m−1 s−2 |
| 𝒞 | concentration scale | 1 µM |
| PeC | Ca2+ Peclet number | (ℒ𝒱)/DCa ~ 5000 |
| PeI | IP3 Peclet number | (ℒ𝒱)/DI ~ 333 |
Since the forces are coupled to the Ca2+ concentration through the preferred curvature function, we nondimensionalize the system of reaction diffusion equations on the deforming interface. We define the following nondimensional variables for the Ca2+ model in Eqs. (14a)–(14b):
| (17) |
where 𝒞 is a characteristic concentration, set to 1 µM. When we rewrite Eqs. (14a)–(14b) using the nondimensional variables in Eqs. (15) and (17), we get:
| (18a) |
| (18b) |
where Ca̅ and Ī are the nondimensional Ca2+ and IP3 concentrations, respectively. The Peclet numbers, PeC and PeI, are nondimensional measures of the relative importance of advection to diffusion. Note that each of the flux terms are appropriately nondimensionalized and the preferred curvature function is appropriately rewritten to be a function of the nondimensional Ca2+ concentration. For notational simplicity, all parameters and variables in the following sections are nondimensional unless specifically stated otherwise, and the bars are omitted.
5. Numerical methods and parameters
A Stokeslet is the velocity field due to a point force go exerted at Xo, in an unbounded 3-d fluid and is given by:
| (19) |
where r = ‖x − Xo‖. Note that this solution is singular at x = Xo, which motivates the use of numerical methods that regularize this singularity.
5.1. Regularized Stokeslets
The method of regularized Stokeslets is a Lagrangian method for computing Stokes flow due to a distribution of forces [38, 39]. This method has been used to investigate the hydrodynamics of sperm swimming near surfaces [30], flagellar bundling of bacteria [69], and the forward progression of a rigid helical tube of nonzero thickness as a model of spirochete motility [39]. We use the method of regularized Stokeslets in 3-d, to solve the nondimensional Stokes equations. The flagellar centerline is represented by Xk for k = 1, 2,…, M and the force density is:
| (20) |
where ϕδ is the radially symmetric smooth approximation to a 3-d delta distribution given in Eq. (2). Note that ϕδ satisfies ∫ ϕδ(x − Xk)dx = 1. The flagellar centerline, as in [30], acts as a distribution of regularized point forces, and inherits a virtual radius that we take as the regularization parameter δ. This regularization parameter gives the extent of the region about the centerline where the force is applied. The regularized Stokeslet formulation treats the immersed flagellum as part of the fluid domain (all of ℝ3) where smoothed forces are distributed. This is in contrast to Lighthill’s slender body theory approximation [24], where the fluid domain is the exterior of the cylindrical flagellum, whose centerline supports singular forces. In this model, we do not enforce boundary conditions sharply on the surface of a cylindrical tube by including higher order singularities, as in slender body theory [24]. However, Gillies et. al [30] have shown that the near-field velocity error for the ‘smeared’ flagellum is small. Requiring that the fluid velocity decays at infinity, the unique solution to the Stokes equations (16a)–(16b) in all of ℝ3 due to the smoothed forces in Eq. (20) is:
| (21) |
This velocity is an exact solution of the Stokes equations and is everywhere incompressible. Note that, while the flow is three-dimensional, we restrict the motion of the flagellar centerline to a fixed plane.
5.2. Numerical algorithm
The details of the numerical time integration are outlined below. Note that denotes a variable • at the nth time step at the kth point on the flagellar centerline and k = 1, 2,…, M.
Given Xn, Can, and In:
Evaluate the fluid velocity at the flagellar centerline, using Eq. (21)
Use a 4th order Runge–Kutta method to update the locations of the flagellar centerline,
Solve for using a Crank-Nicolson scheme to discretize the reaction-diffusion equations, (18a)–(18b) (outlined in [65])
5.3. Parameters, initial conditions, and boundary conditions
A mouse sperm flagellum has a length of ~100 µm and a radius of 1 µm [20]. In the nondimensional model, the flagellar length is set to 1 and accordingly, the regularization parameter is set to δ = 0.01. The flagellar centerline is discretized using M = 100 points. The flagellum is divided into the following regions: end piece s = 0−0.07, principal piece s = 0.07−0.73, midpiece s = 0.73−0.9, neck s = 0.9 − 0.92, and the head s = 0.92 − 1. The time step is Δt = 5 × 10−7, representing 2×106 time steps per beat period.
The parameters that govern the Ca2+ and IP3 dynamics are given in Olson et al. [37]. As described previously, we assume a constant, effective diffusion coefficient for the Ca2+ and IP3 that is an order of magnitude slower than diffusion in water to account for barriers to diffusion and buffering [37]. We prescribe no flux boundary conditions for the Ca2+ and IP3 concentrations at the ends of the flagellar centerline. The Ca2+ concentration in the external fluid is assumed to be constant and at a nondimensional concentration of 2000 and the Ca2+ concentration within the cytosol of the flagellum is initialized at 0.1. In all of the simulations, the cAMP was applied at t = 1 nondimensional time, initiating the CatSper mediated Ca2+ dynamics.
Since the nondimensional Ca2+ concentration varies between ~0.1–1, we choose to vary kA, the nondimensional concentration where half of the receptors are bound by Ca2+, in this range. The nondimensional maximum amplitude, VA, is chosen to be 0.45 (unless stated otherwise), which corresponds to a dimensional amplitude of 45 µm. The exact flagellar bend amplitude of mouse sperm is difficult to measure due to the high degree of asymmetry in the bending. The amplitude of lateral head displacement (ALH) is often reported as an indicator of how the flagellar amplitude is changing. In mouse sperm, hyperactivated sperm have an ALH of ~ 18 µm [2], which is smaller than the amplitude in the flagellum. The flagellum is initialized as a sine wave and we prescribe nondimensional wavenumber κ = 2π and angular frequency ω = −2π throughout the simulations.
5.4. Calculation of flexural rigidity
The stiffness parameters chosen should reflect the material properties of mammlian sperm. In order to estimate the flexural rigidity of our elastic model flagellum, we follow the procedure of Lim and Peskin [70]. The flagellum is initialized as an arc of a circle with curvature K. The total elastic energy in the system stored is calculated using Eq. (4) for the given initialized curve with the preferred curvature ζ(s, t) set to 0. That is, we are thinking of the flagellum as an elastic beam that wants to be flat with zero curvature and we are bending it in a series of preset curvatures. The energy E that we are calculating for the generalized Euler elastica is computed for the various curvatures. For a homogeneous elastic beam, the energy is:
| (23) |
where Y is the flexural rigidity, K is curvature, and L is the length of the beam. The flexural rigidity is defined as the product of the Young’s modulus and the second moment of the area. We calculate the energy E for several values of curvature using constant stiffness coefficients S1 = 75 and S2 = 0.075. From these calculations, we determine that the flexural rigidity is Y = 1.485 × 10−15 Nm. In order to compare this with experimental results of a 3-d flagellum, we need to multiply by a length scale to achieve a flexural rigidity with the proper units of Nm2. We choose to multiply by the dimensional length scale of the regularization parameter, δ ·ℒ, since this is giving a width to the flagellum and we obtain a macroscopic flexural rigidity of 1.485×10−21 Nm2. From previous experiments, the apparent stiffness along the length of the flagellum for bull sperm was found to be ~4–27 ×10−21 Nm2 [46] and was in the range of 1–10×10−19 Nm2 for rat sperm (demembranated and dynein arms disabled) [47]. Therefore, the flexural rigidity of our model flagellum is of the order of the flexural rigidity measured for mammalian sperm.
We choose to fix the bending stiffness at S2 = 0.075 for all simulations to isolate the effect of Ca2+ dynamics on the bending energy As mentioned in §2.2, we wish to study different cases for the passive tensile stiffness S1. We study the case of a constant tensile coefficient using S1 = 75. We also explore a taper in passive tensile stiffness from the base of the flagellum to the tip using a linear taper (S1 = 25 − 125) and a 4th order taper (S1 = 25 − 125). Note that these tensile stiffness coefficients are nondimensional. Since most of the model parameters are based off of mouse sperm, we do not try to precisely match the spatial variation reported for passive stiffness in rat [47] and bull sperm [46].
6. Computational results of integrative model
6.1. CatSper mediated Ca2+ dynamics and emergent waveforms
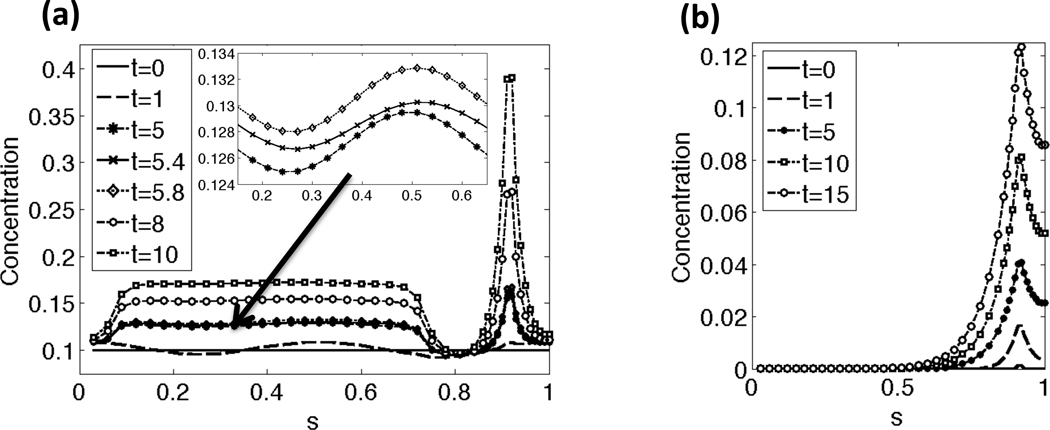
Representative results of the CatSper mediated Ca2+ dynamics along the beating flagellum with a constant tensile stiffness S1 are shown in Fig. 3(a)–(b). The initial nondimensional Ca2+ concentration is set to 0.1 along the length of the flagellum and there is assumed to be a constant, high concentration of Ca2+ in the external fluid. As seen in Fig. 3(a), application of cAMP at t = 1 allows Ca2+ to enter the principal piece through the CatSper channels. The inset zooms in on the Ca2+ concentration at t = 5, 5.4, and 5.8. Note that the Ca2+ concentration has small oscillations in concentration due to the flagellar undulations, which cause local stretching and compression of the flagellar centerline, accounted for in Eqs. (18a)–(18b). In Fig. 3(b), the IP3 concentration initially starts at 0 along the length of the flagellum, and is being synthesized locally at the RNE, the Ca2+ store, in the neck. Once the IP3 reaches a threshold concentration, Ca2+ is released from the RNE as seen in Fig. 3(a). At later time points, the Ca2+ concentration reaches a maximum of about 1, the CatSper channels close, and Ca2+ clearance mechanisms pump Ca2+ out of the principal piece to the surrounding fluid and sequester Ca2+ back into the RNE (results not shown). This allows for Ca2+ and IP3 to return to their resting or initial concentrations.
Fig. 3.
Concentration along the length of the flagellum for a few time points: (a) Ca2+ concentration, (b) IP3 concentration. In (a), the Ca2+ concentrations starts at a resting level and then increases in the principal pieces as the CatSper channels open. When the Ca2+ and IP3 concentration reach a threshold concentration, the RNE in the neck releases additional Ca2+. The arrow and inset zooms in on the Ca2+ concentrations in the principal piece at time points t = 5, 5.4, and 5.8. Note that the Ca2+ concentration has small oscillations in concentration due to the local stretching and compression of the flagellum, as accounted for in the left hand side of Eq. (18a). Note that the sperm is divided into the following regions: end piece s = 0 − 0.07, principal piece s =0.07–0.73, midpiece s = 0.73−0.9, neck s = 0.9−0.92, and the head s = 0.92−1. This simulation had a constant tensile stiffness S1 and kA=0.3 if ζ(s, t) > 0 and kA = 0.5 if ζ(s, t) < 0.
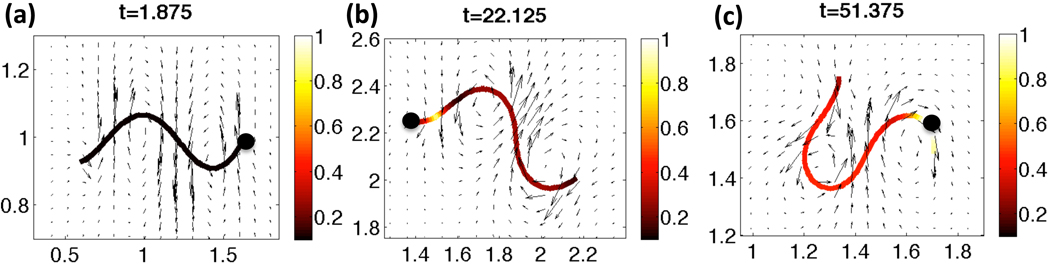
Fig. 4 shows snapshots of the velocities in the fixed plane of the flagellar centerline and the Ca2+ concentration along the flagellum for a representative simulation with a constant tensile stiffness S1. The flagellum is initialized as a sine wave with the prescribed nondimensional wavenumber κ = 2π and amplitude as given by the nondimensional Ca2+ concentration and maximum amplitude VA. The Ca2+ concentration initially starts at a resting level of 0.1 and increases in the principal piece at nondimensional time t = 1 when the cAMP is applied and CatSper channels subsequently open. By time t =22.125, shown in Fig. 4(b), there is Ca2+ release from the RNE, the Ca2+ store in the neck. The evolving Ca2+ concentration along the length of the flagellum is coupled to the preferred amplitude of the waveform through Eq. (8). As time progresses to t = 51.75 in Fig. 4(c), the higher concentrations of Ca2+ are observed along with a highly asymmetrical waveform with increased amplitude.
Fig. 4.
Velocity vectors for the local fluid velocity depicted in the fixed plane of the beating flagellum. The Ca2+ concentration along the length of the flagellum is shown for (a) t =1.875, (b) t =22.125, (c) t =51.375 nondimensional time. The solid black circle denotes the head side of the flagellum. This simulation had a constant tensile stiffness S1, and kA=0.3 if ζ(s, t) > 0 and kA = 0.5 if ζ(s, t) < 0.
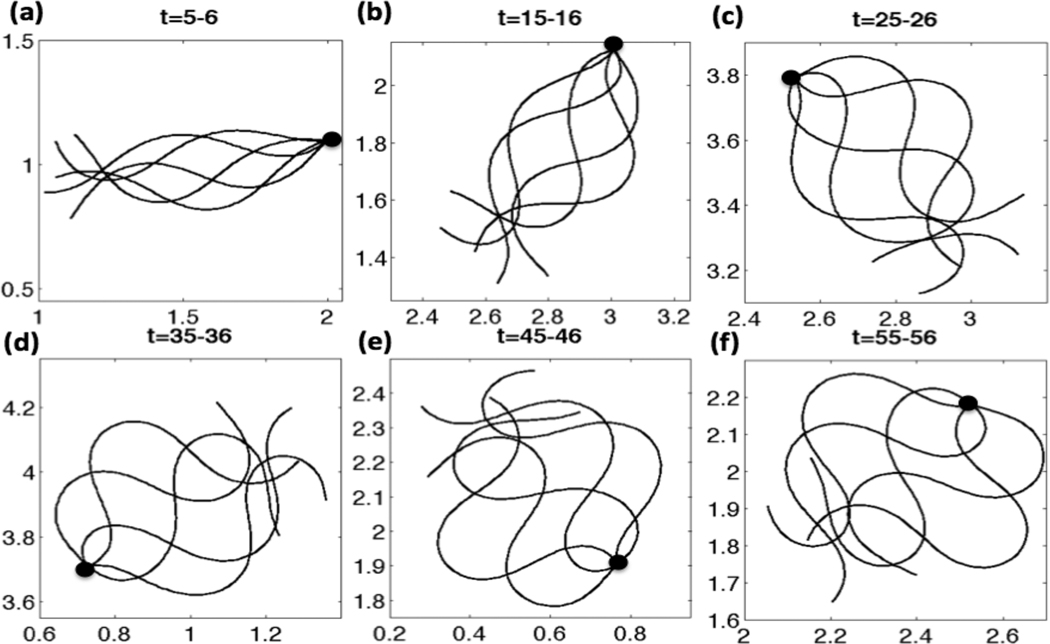
The Ca2+ concentration evolves in time and depends on the local configuration of the flagellum as well as the local IP3 concentration. In turn, the emergent waveform is driven by the preferred curvature function. In Fig. 5, flagellar waveforms over the given nondimensional time period are shown and the first material point of the flagellar centerlines is superimposed for simulations with a linear taper in the tensile stiffness S1. Initially, the waveforms resemble sine waves of constant amplitude, as seen at earlier time points in Fig. 5(a). The Ca2+ concentration is increasing due to the CatSper channels opening and the resulting Ca2+ release from the RNE. This causes the amplitude of the sine wave to increase largely in the principal piece as time increases. Since we also include an asymmetry in the model, the amplitude is slightly larger in one direction (the principal bend). The sperm flagellum initially swims to the right, but then its trajectory assumes a counter-clockwise, circular path. In Fig. 5(f), the overlaid emergent waveforms are qualitatively similar to those obtained by Carlson et al. for hyperactivated mouse sperm [62].
Fig. 5.
Emergent waveforms overlayed for CatSper mediated Ca2+ dynamics, for nondimensional times (a) t =5–6, (b) t =15–16, (c) t =25–26, (d) t =35–36, (e) t =45–46, (f) t =55–56. Simulations are with a linear taper of tensile stiffness, S1 = 25 − 125, VA = 0.45, κ = 2π, ω = −2π, ε = 0.01, S2 = 0.075, kA=0.3 if Ck(t) > 0 and kA = 0.5 if Ck(t) < 0.
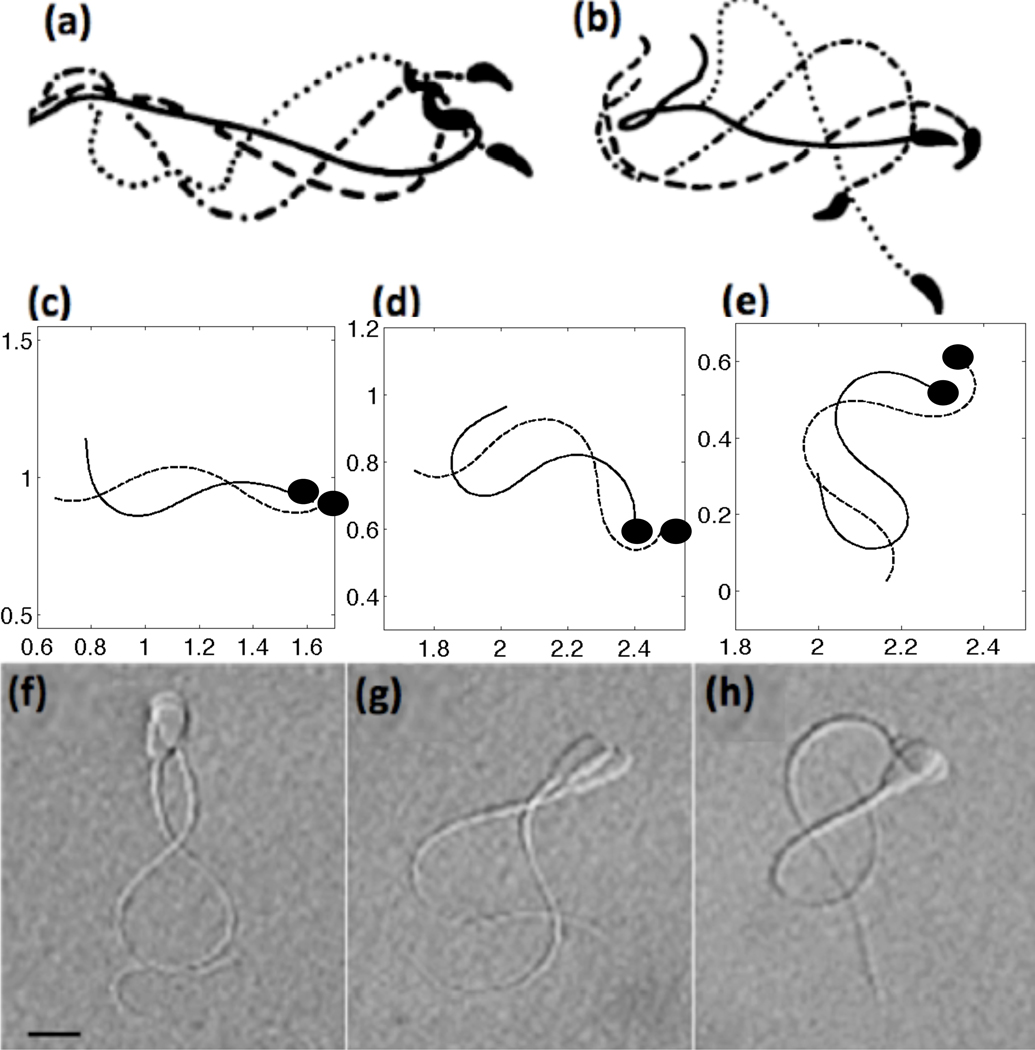
In Fig. 6, we compare our simulated tracings of flagella to the experimental tracings and micrographs of Suarez et al. [71, 72]. The top row depicts tracings of mouse sperm, the middle row are the results of the computational model including CatSper mediated Ca2+ dynamics, and the bottom row shows micrographs of bull sperm. Each frame shows tracings that are approximately one-fourth of a beat apart. When the Ca2+ concentration is low and fairly uniform, our simulated model with a 4th order taper in tensile stiffness S1 has waveforms similar to that of mouse activated motility (compare Fig. 6(a) and (c)). As the Ca2+ concentration increases via the CatSper mediated Ca2+ influx, the waveform is modified to be asymmetric and has a larger bend amplitude (Fig. 6(d)). When the Ca2+ reaches its maximal concentration in Fig. 6(e), we see that the fully hyperactivated waveform is qualitatively similar to hyperactivated mouse sperm in Fig. 6(b). Coupling the Ca2+ dynamics to the preferred curvature, we observe that the emergent flagellar waveforms have an asymmetry that is evolving throughout the simulations. We also compare our simulated results to bull sperm, shown in the bottom row. Even though bull sperm are approximately half of the length of mouse sperm, they exhibit the same asymmetrical beating in the hyperactivated state.
Fig. 6.
Top row: tracings of flagellar bending patterns of (a) activated and (b) hyperactivated motility of mouse sperm where the four tracings cover one full beat, reproduced with permission from [72]. Middle row: simulated results of computational model including CatSper mediated Ca2+ dynamics showing (c) activated (t = 5 nondimensional), (d) hyperactivated (t = 35), (e) and fully hyperactivated motility (t = 75) where the tracings are 1/4 of a beat apart with the dashed line the later time point. For these simulations, a 4th order taper of tensile stiffness S1 was used and kA=0.3 if ζ(s, t) > 0 and kA = 0.5 if ζ(s, t) < 0. The solid black circle denotes the head side of the flagellum. Bottom row: in comparison, images of bull sperm swimming patterns (~ 50 µm in length) for (f) activated, (g) hyperactivated, (h) and fully hyperactivated motility where each of the images are approximately 1/4 of a beat apart, reproduced with permission from [71]
6.2. Effect of Ca2+ dynamics on trajectories and swimming speeds
Often, three types of motility are defined: progressive forward motility or activated motility, a transitional motility, and hyperactivated motility. Progressive motility is characterized by highly linear forward trajectories and a symmetrical waveform. Hyperactivated motility occurs when the flagellum develops an asymmetrical waveform, characterized by highly nonlinear and often times circular trajectories. In general, hyperactivated motility is associated with a decrease in beat frequency and an increase in the bend angle of the most proximal bend [73, 74]. In order to assess our model for capturing these types of motility, we look at trajectories of the last immersed boundary point at the end of the flagellum over the course of a simulation.
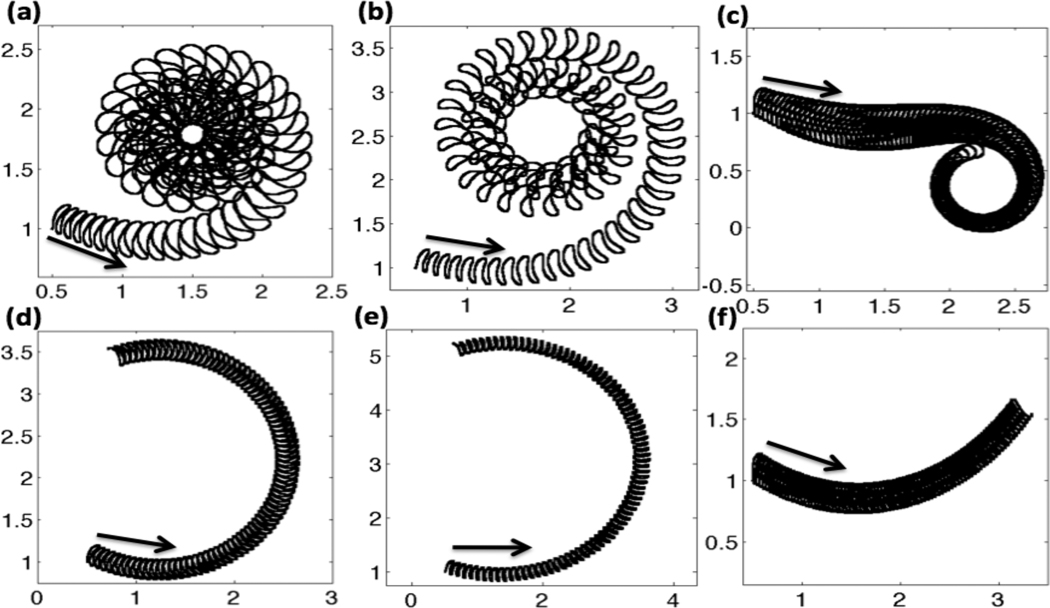
In Fig. 7, trajectories of the flagellum are shown for the three passive tensile stiffness coefficients S1, grouped by column. The top row accounts for the full model, where the CatSper mediated Ca2+ dynamics of hyperactivation is used. The bottom row assumes there is an asymmetry, but there is a constant Ca2+ concentration along the length of the flagellum. The first column, graphs Fig. 7(a) and (d) are for the case of constant tensile stiffness S1 along the length of the flagellum. In Fig. 7(a), the hyperactivated Ca2+ dynamics are included and the tail starts off with a low amplitude undulation. As the Ca2+ concentration increases, the tail maps out a larger amplitude trajectory and starts to move in a counter clockwise circle. The radius of the circle the sperm is swimming decreases at first as the Ca2+ concentration is increasing. After this transitional motility, the sperm is fully hyperactivated and the sperm then swims at a circle of a fairly constant radius as the Ca2+ receptors saturate in the Hill function for the target amplitude. In comparison, Fig. 7(d) shows the same simulation assuming a basal or resting level of Ca2+ throughout the entire simulation. For the same length of time, accounting for asymmetry with a constant Ca2+ concentration gives a circular counter clockwise path with the tail having the same amplitude as time progresses. In Fig. 7(d), a full circular rotation is not observed in the same amount of time that the hyperactivated Ca2+ model can swim in a circular path several times.
Fig. 7.
Trajectories of the last immersed boundary point at the end of the flagellum for nondimensional time t =0–85. Top row: with CatSper mediated Ca2+ dynamics, (a) constant S1, (b) linear taper of S1, (c) fourth order taper of S1. Bottom row: no CatSper mediated Ca2+ dynamics, i.e. with constant resting level of Ca2+ concentration, (d) constant S1, (e) linear taper of S1, (f) fourth order taper of S1. Arrows denote initial starting location and initial direction. All simulations are with kA=0.3 if ζ(s, t) > 0 and kA = 0.5 if ζ(s, t) < 0.
A linear taper in tensile stiffness S1 from head to tail is used in Fig. 7 (b) and (e). In these simulations, the radius of the circular path is larger than in Fig. 7(a) and (d), where a constant tensile stiffness S1 was used. When the CatSper mediated Ca2+ dynamics are included in Fig. 7(b), we see that the trajectory of the tail is changing as the Ca2+ increases, with the tail having a larger amplitude than the constant tensile stiffness S1 in 7(a). When the tensile stiffness S1 is constant or tapers off linearly, 7(a) and (b), we start with activated motility, have a small transition period before the flagellum assumes the circular trajectory associated with hyperactivated motility. As we change the tensile stiffness S1 to a 4th order taper, we see some interesting results. In Fig. 7(c), we can see a longer transition region. The sperm initially starts swimming in a linear trajectory, which would be classified as forward progressive motility or activated motility. In the cases of constant and linear taper of S1, the sperm always progressed in a counter-clockwise fashion, whereas in the case of the 4th order stiffness taper of S1, the sperm is able to swim in a counter-clockwise or clockwise fashion after a transitional period. Since the principal piece or last two-thirds of the flagellum have a much smaller passive stiffness in the tapered cases, the flagellum is able to bend a larger amount, causing complex flagellar waveforms that are very different from a simple sine wave (refer to Fig. 6(d)–(e)). Since this is a fully coupled system, a change in the tensile stiffness coefficient S1 has an effect on the emergent waveform, that then interacts with the viscous fluid. As time progresses, we can see large differences in the trajectories of the sperm with different stiffness distributions of S1 due to small differences in the realized waveforms. It is noted that when no asymmetry is included, the trajectories of all sperm are linear, with or without CatSper mediated Ca2+ dynamics.
In order to analyze the results from this computational model, we characterize swimming speeds, trajectories, and other metrics using methods similar to those used by experimentalists. In many laboratories, sperm motility is analyzed using computer-aided sperm analysis (CASA). Using CASA, images are obtained of swimming sperm at a rate of 25–60 Hz. These images are then analyzed by the computer software to identify and follow the sperm and to determine the kinematics [75–77]. The following metrics are used to characterize and identify hyperactivated motility [75]:
VCL = curvilinear velocity, the total distance the sperm head covers in a given observation period (usually the max of VCL, VSL, V AP)
VSL = straight line velocity, the straight line distance between the first and last points of a given trajectory over a given observation period
V AP = average path velocity, the distance the sperm has traveled in the average path direction of movement in a given observation period, i.e. to determine the average path direction, we have to create an averaged smooth path first by interpolation and then find the distance of that curve over a given observation period
LIN = linearity = (VSL=VCL)· 100
Since these metrics are reported in the literature to distinguish hyperactivated motility, they serve as a benchmark comparison between theory and experiment
In general, most of the experimental data calculations are performed by tracking the center of the sperm head, as it is easiest to follow. Therefore, all of the velocity and linearity results from our computations track a material point near the head of the flagellar centerline. In order to compare our nondimensional computer simulated model to experimental results, we return to dimensional units.
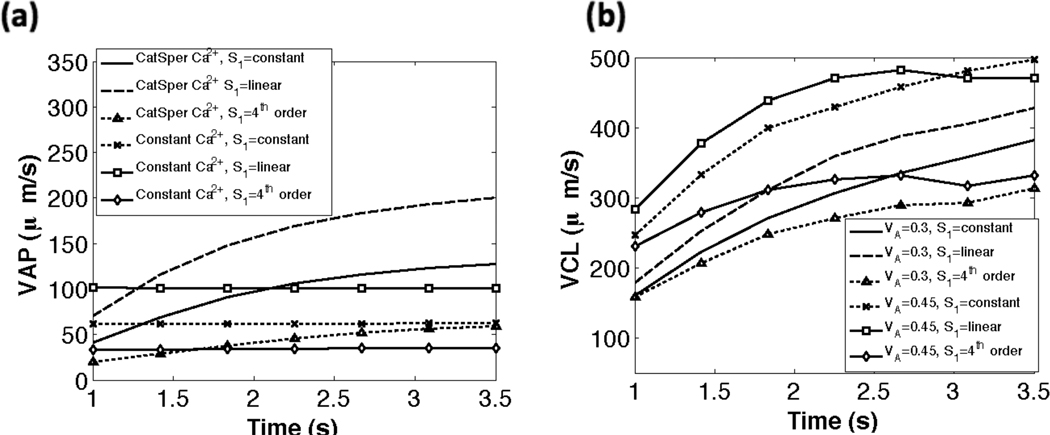
In Fig. 8(a), we compare the swimming speeds for different tensile stiffnesses (S1) and model parameters. The calculations are done at 30 Hz, i.e. we determine the velocities based on sampling 30 times per second. For a given set of parameters, the swimming speeds vary for the three cases of tensile stiffness coefficients used. As shown in Fig. 8, when the CatSper mediated Ca2+ dynamics are included, the sperm starts off with an initial average path velocity V AP of 25–75 µm s−1, which increases initially and then levels off to a V AP of 60 − 200 µm s−1. We can think of the increasing region as the transitional motility and the maximal velocity as the hyperactivated V AP. As shown in Table 2, the experimentally measured average path velocity V AP for hyperactivated mouse sperm is approximately 155 µm s−1. Fig. 8(a), indicates that simulations that do not account for Ca2+ dynamics resulted in fairly constant V AP values that are considerably lower than those observed experimentally. It is interesting to note that the case of a linear taper in tensile stiffness S1 had the highest average path velocity V AP. In Fig. 8(b), the results for the curvilinear velocity VCL are shown for the different stiffness cases and two values of VA, the maximal amplitude. As expected, a smaller maximal amplitude results in a smaller curvilinear velocity VCL for all passive stiffness coefficients. As with the average path velocity V AP, we observe that the linear taper in tensile stiffness S1 has the highest VCL. The curvilinear velocity VCL in our simulations are also in line with experimental data; experiments have reported mouse VCL at approximately 393 µm s−1 [2].
Fig. 8.
Comparison of swimming speeds (µm s−1) vs dimensional time (s). (a) average path velocity (VAP) for the three tensile stiffness coefficients S1 with CatSper mediated Ca2+ dynamics and with constant Ca2+. (b) curvilinear velocity (VCL) for the three tensile stiffness coefficients S1 using VA=0.3 and VA=0.45. For all simulations kA=0.3 if ζ(s, t) > 0 and kA = 0.5 if ζ(s, t) < 0.
Table 2.
Experimental values for swimming speeds of activated and hyperactivated (HA) mouse sperm. VCL is the curvilinear velocity, VSL is the straight line velocity, and V AP is the average path velocity.
The linearity, a ratio of the straight line velocity to the curvilinear velocity, decreases from activated to hyperactivated motility as the flagellum switches from linear to circular trajectories. In Table 3, the linearities are reported for the three tensile stiffness coefficients S1 used in the model along with experimental values for mouse sperm. We stay within the range of experimental values of linearity for mouse data and we note that the case of the 4th order taper in tensile stiffness S1 exhibited the lowest linearity values.
Table 3.
Experimental and computational values for linearity of sperm trajectories (LIN, %). Linearity is defined as the ratio of the straight line velocity and curvilinear velocity multiplied by 100. S1 is the nondimensional tensile stiffness parameter.
| Value | |
|---|---|
| 65.9 | fresh (activated, mouse) [72] |
| 37.6 | HA (mouse) [72] |
| 54 ± 12 | forward progressive (human) [90] |
| 30 ± 10 | transition (human) [76, 90, 91] |
| 11 ± 7 | HA (human) [5, 77, 90–92] |
| 31.39 | Constant S1 and CatSper/Constant Ca2+ |
| 44.13 | Linear taper of S1 and CatSper Ca2+ |
| 15.5 | 4th order taper of S1 and CatSper Ca2+ |
In comparison to CASA values for velocities and linearity, results from our computational model are within the range of experimental results for mouse sperm. We note that all of the velocity and linearity calculations were highly sensitive to the frequency of sampling per dimensional time when the results are post-processed. To be consistent, all velocities were taken at a sampling frequency of 30 Hz after t=1 s dimensional time. When the results were post-processed at a sampling rate of 60 Hz, the results varied greatly with the curvilinear velocity VCL having the largest variation. Since VCL is calculated as the total distance the sperm head covers in an observation period [75], the distance covered per observation period increased at the higher sampling frequency. All of the calculations also varied slightly based on the location that they were sampled. Since CASA results are generally taken from the center of the head, our results may not be consistent since we do not accurately account for head morphology.
7. Discussion
The details of how Ca2+ affects the dynein-microtuble force generation is not known. There are several possible Ca2+ binding sites that could initiate a chain of events to alter the flagellar beat. One candidate is calmodulin (CaM), a Ca2+ receptor that has been localized to the principal piece of the flagellum [78]. CaM is a plausible place for the Ca2+ to act since CaM inhibitors have been observed to reduce percentages of activated and hyperactivated sperm [79], decrease the swimming speed of sperm [4, 80], and alter the beat patterns [49, 81]. After Ca2+ binds to CaM, kinases such as CaMKIV and CaMKIIα may be activated, which could cause a conformational change to alter the waveform. CaM kinases have been identified in the flagella of human [82] and bovine sperm [83] and, in the presence of CaMKII inhibitors, hyperactivation was inhibited [82]. Asymmetry of the waveform could be due to an asymmetric distribution of calmodulin along the flagellum.
In this model, we differentiate between two ‘sides’ of the flagellum by designating a principal bend direction and a reverse bend direction, that correspond to the sign of the preferred curvature. For each side of the flagellum, we define the parameter kA as the number of available Ca2+ receptors. By choosing a slightly different value of kA on each side, we achieve asymmetric flagellar beatforms. The asymmetry in waveform is minimal at early simulation times, but increases as the Ca2+ dynamics evolve. Here, the preferred amplitude was chosen to be a continuous function of Ca2+, but this can easily be modified so that the preferred amplitude responds differently to values of Ca2+ beyond a specified threshold.
Different flagellar bend directions are easily identified in mouse sperm because of their hook-shaped head. Recent experiments by Chang and Suarez have shown that mouse sperm can achieve asymmetric bends in both the pro-hook and anti-hook direction [84]. Mouse sperm incubated under capacitating conditions, once hyperactivated, exhibit pro-hook bends. In contrast, capacitated mouse sperm that are treated with thimerisol exhibit pronounced anti-hook bends [84]. It has been shown that thimerisol induces Ca2+ release from internal stores [2]. The change in bend direction could, therefore, be due to different time courses of Ca2+ evolution. In the pro-hook case, Ca2+ first enters the flagellum through the CatSper channels on the principal piece, but in the anti-hook case, Ca2+ first enters the flagellum through the internal stores near the head. We remark that our simple model does not require a change in the origin of the influx of Ca2+ along the flagellum to change principal bend direction. This change in principal bend direction can be achieved just by altering the binding affinities for Ca2+ on either side of the flagellum.
The preferred curvature of our model flagellum is driven by the evolving Ca2+ dynamics. In the current model we do not include any Ca2+ dependence on preferred wavelength or beat frequency. In fact, the flagellar beat frequency does decrease when sperm switch from activated to hyperactivated motility [73, 74]. We hope to examine the sensitivity of the emergent waveforms and swimming progression to the choice of parameters in the CatSper mediated Ca2+ dynamics model and the Ca2+ parameters in the target amplitude function [37]. Moreover, this model does not take into account the internal structure of the axoneme, but phenomonologically expresses the coupling of Ca2+ to a preferred curvature. We plan to extend this model to one that includes discrete representations of dynein motors [35], whose activation kinetics depends upon the evolving Ca2+ dynamics, and may be governed by mechanisms such as curvature control [15–17], the geometric clutch hypothesis [85, 86], or dynein cross bridge cycle models [87–89].
8. Conclusions
Calcium dynamics play a large role in initiation and maintenance of hyperactivated motility, which is vital for mammalian spermatozoa to reach and fertilize the egg. We have presented a model that couples CatSper mediated Ca2+ dynamics to a simple mechanical model of an actuated, elastic flagellum that is, in turn, coupled to a viscous, incompressible fluid. While the flagellar model is structurally simple, we use 3-d Stokes equations to describe the fluid dynamics, and accurately account for the diffusion and fluxes of Ca2+ and IP3 on a moving interface. The simplicity of the flagellar model, along with the use of the grid-free method of regularized Stokeslets, provides an efficient computational framework that allows us to resolve the fast time scale of a single flagellar beat - and to simulate many such beats to capture the much longer time scale of the Ca2+ dynamics.
We have investigated how these flagellar waveforms give rise to the nonlinear trajectories characteristic of hyperactivated sperm. In particular, this model elucidates the importance of CatSper mediated Ca2+ dynamics in generating hyperactivated flagellar motion. When preferred curvature was specified as a function of asymmetry in Ca2+ binding affinities, but not Ca2+ dynamics, the resulting waveforms are not characteristic of hyperactivation. However, adding the Ca2+ dynamics to drive the preferred curvature did give rise to emergent waveforms and trajectories that closely match experimental data for hyperactivated motility. In addition, this model shows that motility properties are dependent upon the distribution of tensile stiffness along the flagellum. We view this model as a starting point to investigate the biochemistry and mechanics of sperm hyperactivation and there are many avenues yet to explore.
Highlights.
Presented a model that couples CatSper mediated calcium dynamics to a simple mechanical model of an actuated, elastic flagellum that is, in turn, coupled to a viscous, incompressible fluid.
We use 3-d Stokes equations to describe the fluid dynamics, and accurately account for the diffusion and fluxes of calcium and inositol-1,4,5 trisphosphate on a moving interface.
The model elucidates the importance of CatSper mediated calcium dynamics in generating hyperactivated motility and the dependence of motility on the passive tensile stiffness along the flagellum.
A hypothesized asymmetry in calcium binding affinities on each side of the flagellum is included and is important in the model to achieve flagellar waveforms characteristic of hyperactivated motility.
Investigate in the model how emergent flagellar waveforms give rise to nonlinear trajectories characteristic of hyperactivated motility, swimming velocity compares well with the experimental data.
Acknowledgements
The work of S. Olson and L. Fauci was supported, in part, by NSF DMS 0652775. The work of S. Suarez was supported, in part, by NIH 1RO3HD062471-01, NSF MCB-0421855, and USDA CSREES NRICGP 2004-35203-14952. The authors would like to thank R. Cortez for helpful discussions.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Suarez S, Katz D, Overstreet J. Movement characteristics and acrosomal status of rabbit spermatozoa at the site and time of fertilization. Biol Reprod. 1983;29:1277–1287. doi: 10.1095/biolreprod29.5.1277. [DOI] [PubMed] [Google Scholar]
- 2.Marquez B, Ignotz G, Suarez S. Contributions of extracellular and intracellular Ca2+ regulation of sperm motility: release of intracellular stores can hyperactivate CatSper1 and CatSper2 null sperm. Dev Biol. 2007;303:S1214–S1221. doi: 10.1016/j.ydbio.2006.11.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Ho H, Granish K, Suarez S. Hyperactivated motility of bull sperm is triggered at the axoneme by Ca2+ and not cAMP. Dev Biol. 2002;250:208–217. doi: 10.1006/dbio.2002.0797. [DOI] [PubMed] [Google Scholar]
- 4.White D, Aitken R. Relationship between calcium, cyclic AMP, ATP, and intracellular pH and the capacity of hamster spermatozoa to express hyperactivated motility. Gamete Res. 1989;22:163–177. doi: 10.1002/mrd.1120220205. [DOI] [PubMed] [Google Scholar]
- 5.Burkman L. Discrimination between nonhyperactivated and classical hyperactivated motility patterns in human sperm using computerized analysis. Fertil Steril. 1991;55:363–371. [PubMed] [Google Scholar]
- 6.Quill T, Sugden S, Rossi K, Doolittle L, Hammer R, Garbers D. Hyperactivated sperm motility driven by CatSper2 is required for fertilization. Proc Natl Acad Sci USA. 2003;100:14869–14874. doi: 10.1073/pnas.2136654100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Ren D, Navarro B, Perez G, Jackson A, Hsu S, Shi Q, Tilly J, Clapham D. A sperm ion channel required for sperm motility and male fertility. Nature. 2001;413:603–609. doi: 10.1038/35098027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Stauss C, Votta T, Suarez S. Sperm motility hyperactivation facilitates penetration of the hamster zona pellucida. Biol Reprod. 1995;53:1280–1285. doi: 10.1095/biolreprod53.6.1280. [DOI] [PubMed] [Google Scholar]
- 9.Ho H, Suarez S. Hyperactivation of mammalian spermatozoa: function and regulation. Reproduction. 2001;122:519–526. doi: 10.1530/rep.0.1220519. [DOI] [PubMed] [Google Scholar]
- 10.Suarez S. Control of hyperactivation in sperm. Hum Reprod Update. 2008;14:647–658. doi: 10.1093/humupd/dmn029. [DOI] [PubMed] [Google Scholar]
- 11.Woolley D. Flagellar oscillation: a commentary on proposed mechanisms. Biol Rev. 2010;85:453–470. doi: 10.1111/j.1469-185X.2009.00110.x. [DOI] [PubMed] [Google Scholar]
- 12.Carlson A, Quill T, Westenbroek R, Schuch S, Hille B, Babcock D. Identical phenotypes of CatSper1 and CatSper2 null sperm. Int J Biol Chem. 2005;280:32238–32244. doi: 10.1074/jbc.M501430200. [DOI] [PubMed] [Google Scholar]
- 13.Ho H, Suarez S. An inositol 1,4,5-trisphosphate receptor-gated intracellular Ca2+ store is involved in regulating sperm hyperactivated motility. Biol Reprod. 2001;65:1606–1615. doi: 10.1095/biolreprod65.5.1606. [DOI] [PubMed] [Google Scholar]
- 14.Lindemann C, Lesich K. Flagellar and ciliary beating: the proven and the possible. J Cell Science. 2010;123:519–528. doi: 10.1242/jcs.051326. [DOI] [PubMed] [Google Scholar]
- 15.Brokaw C. Bend propagation by a sliding filament model for flagella. J Exp Biol. 1971;55:289–304. doi: 10.1242/jeb.55.2.289. [DOI] [PubMed] [Google Scholar]
- 16.Brokaw C. Flagellar movement: a sliding filament model. Science. 1972;178:455–462. doi: 10.1126/science.178.4060.455. [DOI] [PubMed] [Google Scholar]
- 17.Brokaw C. Computer simulation of flagellar movement: I. Demonstration of stable bend propagation and bend initiation by the sliding filament model. Biophys J. 1972;12:564–568. doi: 10.1016/S0006-3495(72)86104-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Gaffney E, Gadelha H, Smith D, Blake J, Kirkman-Brown J. Mammalian sperm motility: observation and thoery. Annu Rev Fluid Mech. 2001;43:501–528. [Google Scholar]
- 19.Fauci L, Dillon R. Biofluidmechanics of reproduction. Annu Rev Fluid Mech. 2006;38:371–394. [Google Scholar]
- 20.Cummins J, Woodall P. On mammalian sperm dimensions. J Reprod Fert. 1985;75:153–175. doi: 10.1530/jrf.0.0750153. [DOI] [PubMed] [Google Scholar]
- 21.Brennen C, Winet H. Fluid mechanics of propulsion by cilia and flagella. Ann Rev Fluid Mech. 1977;9:339–398. [Google Scholar]
- 22.Gray J, Hancock G. The propulsion of sea-urchin spermatozoa. J Exp Biol. 1955;32:802–814. [Google Scholar]
- 23.Higdon J. A hydrodynamic analysis of flagellar propulsion. J Fluid Mech. 1979;90:685–711. [Google Scholar]
- 24.Lighthill J. Flagellar hydrodynamics. SIAM Rev. 1976;18:161–230. [Google Scholar]
- 25.Phan-Thien N, Tran-Cong T, Ramia M. A boundary element analysis of flagellar propulsion. J Fluid Mech. 1987;185:533–549. [Google Scholar]
- 26.Elgeti J, Kaupp U, Gompper G. Hydrodynamics of sperm cells near surfaces. Biophys J. 2010;99:1018–1026. doi: 10.1016/j.bpj.2010.05.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Smith D, Gaffney E, Blake J, Kirkman-Brown J. Human sperm accumulation near surfaces: a simulation study. J Fluid Mech. 2009;621:289–320. [Google Scholar]
- 28.Teran J, Fauci L, Shelley M. Viscoelastic fluid response can increase the speed of a free swimmer. Phys Rev Lett. 2010;104:038101–038104. doi: 10.1103/PhysRevLett.104.038101. [DOI] [PubMed] [Google Scholar]
- 29.Lauga E. Propulsion in a viscoelastic fluid. Phys Fluids. 2007;19:083104. [Google Scholar]
- 30.Gillies E, Cannon R, Green R, Pacey A. Hydrodynamic propulsion of human sperm. J Fluid Mech. 2009;625:445–474. [Google Scholar]
- 31.Gadelha H, Gaffney E, Smith D, Kirkman-Brown J. Nonlinear instability in flagellar dynamics: a novel modulation mechanism in sperm migration? J Roy Soc Int. 2010;7:1689–1697. doi: 10.1098/rsif.2010.0136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Gueron S, Levit-Gurevich K. Computation of the internal forces in cilia: Application to ciliary motion, the effects of viscosity, and cilia interactions. Biophys J. 1998;74:1658–1676. doi: 10.1016/S0006-3495(98)77879-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Fu H, Powers T, Wolgemuth C. Theory of swimming filaments in viscoelastic media. Phys Rev Lett. 2007;99:258101–258105. doi: 10.1103/PhysRevLett.99.258101. [DOI] [PubMed] [Google Scholar]
- 34.Dillon R, Fauci L. An integrative model of internal axoneme mechanics and external fluid dynamics in ciliary beating. J Theor Biol. 2000;207:415–430. doi: 10.1006/jtbi.2000.2182. [DOI] [PubMed] [Google Scholar]
- 35.Dillon R, Fauci L, Omoto C. Mathematical modeling of axoneme mechanics and fluid dynamics in ciliary and sperm motility. Dyn Contin Discret I. 2003;10:745. [Google Scholar]
- 36.Fauci L, McDonald A. Sperm motility in the presence of boundaries. Bull Math Biol. 1995;57:679–699. doi: 10.1007/BF02461846. [DOI] [PubMed] [Google Scholar]
- 37.Olson S, Suarez S, Fauci L. A model of CatSper channel mediated calcium dynamics in mammalian spermatozoa. Bull Math Bio. 2010;72:1925–1946. doi: 10.1007/s11538-010-9516-5. [DOI] [PubMed] [Google Scholar]
- 38.Cortez R. The method of regularized Stokeslets. SIAM J Sci Comput. 2001;23:1204–1225. [Google Scholar]
- 39.Cortez R, Fauci L, Medovikov A. The method of regularized Stokeslets in three dimensions: Analysis, validation, and application to helical swimming. Phys Fluids. 2005;17 0315041–14. [Google Scholar]
- 40.Fauci L, Peskin C. A computational model of aquatic animal locomotion. J Comp Phys. 1988;77:85–108. [Google Scholar]
- 41.Fawcett D, Phillips D. The fine structure and development of the neck region of the mammalian spermatozoan. Anat Rec. 1969;165:153–184. doi: 10.1002/ar.1091650204. [DOI] [PubMed] [Google Scholar]
- 42.Hamasaki M, Wakimoto M, Maehara T, Matsuo H. Three-dimensional structures of the neck region of the hamster spermatozoa in the caudal epididymis. Arch Histol Cytol. 1994;57:59–65. doi: 10.1679/aohc.57.59. [DOI] [PubMed] [Google Scholar]
- 43.Telkka A, Fawcett D, Christensen A. Further observations on the structure of the mammalian sperm tail. Anat Rec. 1961;141:231–245. doi: 10.1002/ar.1091410308. [DOI] [PubMed] [Google Scholar]
- 44.Lindemann C. The stiffness of the flagella of impaled bull sperm. Biophys J. 1973;13:437–448. doi: 10.1016/S0006-3495(73)85997-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Lindemann C. Functional significance of the outer dense fibres of mammalian sperm examined by computer simulations with geometric clutch model. Cell Motil Cytoskeleton. 1996;34:258–270. doi: 10.1002/(SICI)1097-0169(1996)34:4<258::AID-CM1>3.0.CO;2-4. [DOI] [PubMed] [Google Scholar]
- 46.Lesich K, Pelle D, Lindemann C. Insights into the mechanism of ADP action of flagellar motility derived from studies of bull sperm. Biophys J. 2008;95:472–482. doi: 10.1529/biophysj.107.127951. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Schmitz-Lesich K, Lindemann C. Direct measurement of the passive stiffness of rat sperm and implications to the mechanism of the calcium response. Cell Motil Cytoskel. 2004;59:169–179. doi: 10.1002/cm.20033. [DOI] [PubMed] [Google Scholar]
- 48.Lindemann C, Goltz J. Calcium regulation of flagellar curvature and swimming pattern in triton X-100 extracted rat sperm. Cell Motil Cytoskel. 1988;10:420–431. doi: 10.1002/cm.970100309. [DOI] [PubMed] [Google Scholar]
- 49.Tash J, Means A. Regulation of protein phosphorylation and motility of sperm by cyclic adenosine monophosphate and calcium. Biol Reprod. 1982;26:745–763. doi: 10.1095/biolreprod26.4.745. [DOI] [PubMed] [Google Scholar]
- 50.Tash J, Means A. Ca2+ regulation of sperm axonemal motility. Method Enzymol. 1987;139:808–823. doi: 10.1016/0076-6879(87)39128-1. [DOI] [PubMed] [Google Scholar]
- 51.Tash J, Krinks M, Patel J, Means R, Klee C, Means A. Identification, characterization, and functional correlation of calmodulin-dependent protein phosphatase in sperm. J Cell Biol. 1988;106:1625–1633. doi: 10.1083/jcb.106.5.1625. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Kanous K, Casey C, Lindemann C. Inhibition of microtubule sliding by Ni2+ and Cd2+: evidence for a differential response of certain microtubule pairs within the bovine sperm axoneme. Cell Motil Cytoskel. 1993;26:66–76. doi: 10.1002/cm.970260107. [DOI] [PubMed] [Google Scholar]
- 53.Lindemann C, Walker J, Kanous K. Ni2+ inhibition induces asymmetry in axonemal functioning and bend initiation of bull sperm. Cell Motil Cytoskel. 1995;30:8–16. doi: 10.1002/cm.970300103. [DOI] [PubMed] [Google Scholar]
- 54.Lindemann C, Kanous K. Geometric clutch hypothesis of axonemal function: key issues and testable predictions. Cell Motil Cytoskel. 1995;31:1–8. doi: 10.1002/cm.970310102. [DOI] [PubMed] [Google Scholar]
- 55.Smith D, Gaffney E, Gadelha H, Kapur N, Kirkman-Brown J. Bend propagation in the flagella of migrating human sperm, and its modulation by viscosity. Cell Motil Cytoskel. 2009;66:220–236. doi: 10.1002/cm.20345. [DOI] [PubMed] [Google Scholar]
- 56.Lindemann C, Orlando A, Kanous K. The flagellar beat of rat sperm is organized by the interaction of two functionally distinct populations of dynein bridges with a stable central axonemal partition. J Cell Sci. 1992;102:249–260. doi: 10.1242/jcs.102.2.249. [DOI] [PubMed] [Google Scholar]
- 57.Qi H, Moran M, Navarro B, Chong J, Krapivinsky G, Krapivinsky L, Kirichok Y, Ramsey I, Quill T, Clapham D. All four CatSper ion channel proteins are required for male fertility and sperm cell hyperactivated motility. Proc Natl Acad Sci USA. 2007;104:1219–1223. doi: 10.1073/pnas.0610286104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Xia J, Reigada D, Mitchell C, Ren D. CATSPER channel-mediated Ca2+ entry into mouse sperm triggers a tail-to-head propagation. Biol Reprod. 2007;7:551–559. doi: 10.1095/biolreprod.107.061358. [DOI] [PubMed] [Google Scholar]
- 59.Ho K, Wolff C, Suarez S. CatSper-null mutant spermatozoa are unable to ascend beyond the oviductal reservoir. Reprod, Fertility, and Development. 2009;21:345–350. doi: 10.1071/rd08183. [DOI] [PubMed] [Google Scholar]
- 60.Sneyd J, Tsaneva-Atanasova K, Bruce J, Straub S, Giovannucci D. Yule, A model of calcium waves in pancreatic and parotid acinar cells. Biophys J. 2003;85:1392–1405. doi: 10.1016/S0006-3495(03)74572-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Wagner J, Keizer J. Effects of rapid buffers on ca2+ on diffusion and ca2+ oscillations. Biophys J. 1994;67:447–456. doi: 10.1016/S0006-3495(94)80500-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Carlson A, Westenbroek R, Quill T, Ren D, Claphan D, Hille B, Garbers D, Babcock D. CatSper1 required for evoked Ca2+ entry and control of flagellar function in sperm. Proc Natl Acad Sci USA. 2003;100:14864–14868. doi: 10.1073/pnas.2536658100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Ho H, Suarez S. Characterization of the intracellular calcium store at the base of the sperm flagellum that regulates hyperactivated motility. Biol Reprod. 2003;68:1590–1596. doi: 10.1095/biolreprod.102.011320. [DOI] [PubMed] [Google Scholar]
- 64.Sneyd J, Wetton B, Charles A, Sanderson M. Intercellular calcium waves mediated by diffusion of inositol trisphosphate - a two-dimensional model. Am J Physiol Cell Physiol. 1995;268:C1537–C1545. doi: 10.1152/ajpcell.1995.268.6.C1537. [DOI] [PubMed] [Google Scholar]
- 65.Lai M, Tseng Y, Huang H. An immersed boundary method for interfacial flows with insoluble surfactant. J Comp Phys. 2008;227:7279–7293. [Google Scholar]
- 66.Stone H. A simple derivation of the time-dependent convective-diffusion equation for surfactant transport along a deforming interface. Phys Fluids A. 1990;2:111–112. [Google Scholar]
- 67.Wolf D, Hagopian S, Ishijima S. Changes in sperm plasma membrane lipid diffusibility after hyperactivation during in vitro capacitation in the mouse. J Cell Biol. 1986;102:1372–1377. doi: 10.1083/jcb.102.4.1372. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Mukai C, Okuno M. Glycolysis plays a major role for adenosine triphosphate supplementation in mouse sperm flagellar movement. Biol Reprod. 2004;71:540–547. doi: 10.1095/biolreprod.103.026054. [DOI] [PubMed] [Google Scholar]
- 69.Flores H, Lobaton E, Mendez-Diez S, Tlupova S, Cortez R. A study of bacterial flagellar bundling. Bull Math Bio. 2005;65:137–168. doi: 10.1016/j.bulm.2004.06.006. [DOI] [PubMed] [Google Scholar]
- 70.Lim S, Peskin C. Simulations of the whirling instability by the immersed boundary method. SIAM J Comp Sci. 2004;25:2066–2083. [Google Scholar]
- 71.Marquez B, Suarez S. Different signaling pathways in bovine sperm regulate capacitation and hyperactivation. Biol Reprod. 2004;70:1626–1633. doi: 10.1095/biolreprod.103.026476. [DOI] [PubMed] [Google Scholar]
- 72.Suarez S, Dai X. Hyperactivation enhances mouse sperm capacity for penetrating viscoelastic media. Biol Reprod. 1992;46:686–691. doi: 10.1095/biolreprod46.4.686. [DOI] [PubMed] [Google Scholar]
- 73.Suarez S, Katz D, Owen D, Andrew J, Powell R. Evidence for the function of hyperactivated motility in sperm. Biol Reprod. 1991;44:375–381. doi: 10.1095/biolreprod44.2.375. [DOI] [PubMed] [Google Scholar]
- 74.Ohmuro J, Ishijima S. Hyperactivation is the mode conversion from constant-curvature beating to constant-frequency beating under a constant rate of microtubule sliding. Molecular Reproduction and Development. 2006;73:1412–1421. doi: 10.1002/mrd.20521. [DOI] [PubMed] [Google Scholar]
- 75.Mortimer S. CASA– practical aspects. Journal of Andrology. 2000;21:515–524. [PubMed] [Google Scholar]
- 76.Zhu J, Pacey A, Barratt C, Cooke I. Computer assisted measurement of hyperactivation in human sperm: differences between European and American versions of the Hamilton-Thorn motility analyser. Hum Reprod. 1994;9:835–839. doi: 10.1093/oxfordjournals.humrep.a138527. [DOI] [PubMed] [Google Scholar]
- 77.Grunert J, De Geyter C, Nieschlag E. Objective identification of hyperactivated human sperm by computerized sperm motion analysis with the Hamilton-Thorn sperm motility analyser. Hum Reprod. 1990;5:593–599. doi: 10.1093/oxfordjournals.humrep.a137151. [DOI] [PubMed] [Google Scholar]
- 78.Schlingmann K, Michaut M, Mcelwee J, Wolff C, Travis A, Turner R. Calmodulin and CaMKII in the sperm principal piece: evidence for a motility-related calcium/calmodulin pathway. J Androl. 2007;28:706–716. doi: 10.2164/jandrol.106.001669. [DOI] [PubMed] [Google Scholar]
- 79.Si Y, Olds-Clarke P. Evidence for the involvement of calmodulin in mouse sperm capacitation. Biol Reprod. 2000;62:1231–1239. doi: 10.1095/biolreprod62.5.1231. [DOI] [PubMed] [Google Scholar]
- 80.Ahmad K, Bracho G, Wolf D, Tash J. Regulation of human sperm motility and hyperactivation components by calcium, calmodulin, and protein phosphatases. Arch Androl. 1995;35:187–208. doi: 10.3109/01485019508987871. [DOI] [PubMed] [Google Scholar]
- 81.Aoki F, Sakai S, Kohmoto K. Regulation of flagellar bending by cAMP and Ca2+ in hamster sperm. Mol Reprod Dev. 1999;53:77–83. doi: 10.1002/(SICI)1098-2795(199905)53:1<77::AID-MRD9>3.0.CO;2-C. [DOI] [PubMed] [Google Scholar]
- 82.Ignotz G, Suarez S. Calcium/calmodulin and calmodulin kinase II stimulate hyperactivation in demembranated bovine sperm. Biol Reprod. 2005;73:519–526. doi: 10.1095/biolreprod.105.040733. [DOI] [PubMed] [Google Scholar]
- 83.Marin-Briggiler C, Jha K, Chertihin O, Buffone M, Herr J, MH V-L, Visconti P. Evidence of the presence of calcium/calmodulin-dependent protein kinase IV in human sperm and its involvement in motility regulation. J Cell Science. 2005;118:2013–2022. doi: 10.1242/jcs.02326. [DOI] [PubMed] [Google Scholar]
- 84.Chang H, Suarez S. Rethinking the relationship between hyperactivation and chemotaxis in mammalian sperm. Biol Reprod. 2010 doi: 10.1095/biolreprod.109.083113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Lindemann C. A geometric clutch hypothesis to explain oscillations of the axoneme of cilia and flagella. J Theor Biol. 1994;168:175–189. [Google Scholar]
- 86.Lindemann C. A model of flagellar and ciliary functioning which uses the forces transverse to the axoneme as the regulator of dynein activation. Cell Motil Cytoskel. 1994;29:141–154. doi: 10.1002/cm.970290206. [DOI] [PubMed] [Google Scholar]
- 87.Sugino K, Naitoh H. Simulated cross-bridge patterns corresponding to ciliary beating in Paramecium. Nature. 1982;295:609–611. [Google Scholar]
- 88.Murase M, Shimizu H. A model of flagellar movement based on cooperative dynamics of dyneintubulin cross bridges. J Theor Biol. 1986;119:409–433. doi: 10.1016/s0022-5193(86)80192-8. [DOI] [PubMed] [Google Scholar]
- 89.Camelet S, Julicher F, Prost J. Self-organized beating and swimming of internally driven filaments. Phys Rev Lett. 1999;82:1590–1593. [Google Scholar]
- 90.Sukcharoen N, Keith J, Irvine D, Aitken R. Definition of the optimal criteria for identifying hyperactivated human spermatozoa at 25 Hz using in-vitro fertilization as a functional end-point. Hum Reprod. 1995;10:2928–2937. doi: 10.1093/oxfordjournals.humrep.a135822. [DOI] [PubMed] [Google Scholar]
- 91.Robertson L, Wolfe D, Tash J. Temporal changes in motility parameters related to acrosomal status: identification and characterization of populations of hyperactivated human sperm. Biol Reprod. 1988;39:797–805. doi: 10.1095/biolreprod39.4.797. [DOI] [PubMed] [Google Scholar]
- 92.Mortimer S, Mortimer D. Kinematics of human sperm incubated under capacitating conditions. J Androl. 1990;11:195–203. [PubMed] [Google Scholar]
- 93.Lindemann C. The geometric clutch as a working hypothesis for future research on cilia and flagella. Ann NY Acad Sci. 2007;1101:477–493. doi: 10.1196/annals.1389.024. [DOI] [PubMed] [Google Scholar]