Abstract
Selective genotyping can increase power in quantitative trait association. One example of selective genotyping is two-tail extreme selection, but simple linear regression analysis gives a biased genetic effect estimate. Here, we present a simple correction for the bias.
Keywords: Bias correction, Linear regression, Selective genotyping, QTL association, Extreme selection
Selective genotyping can increase the power in the association studies of quantitative trait loci (QTL) (Chen et al. 2005; Huang and Lin 2007; Xiong et al. 2002; Kwan et al. 2009; Slatkin 1999; Van Gestel et al. 2000; Xing and Xing 2009). By genotyping only individuals with extreme phenotypes, genetic information is enriched compared to random genotyping of the same number of individuals. Examples of selective genotyping include one-tail extreme selection, two-tail extreme selection and extreme-concordant and -discordant design (Abecasis et al. 2001). Tang (Tang 2010) proved that the three score tests based on the prospective (Xiong et al. 2002), retrospective (Wallace et al. 2006) and conditional (Huang and Lin 2007) likelihoods, were all equivalent in QTL association under selective genotyping, but Huang and Lin (Huang and Lin 2007) showed that the prospective test, which is a linear regression of phenotype on the number of risk alleles at a QTL, gives a biased QTL effect estimate under two-tail extreme selection. Here, we present a simple bias correction and validate the results through simulations.
In a population sample, the direct regression of phenotype on genotype can be written as,
 |
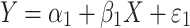1 |
where Y and X are respectively the phenotype and QTL genotype before selection. The regression estimator,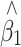 
, is of our primary interest but is biased in a two-tail extreme selected sample (Huang and Lin 2007). Since the selection (S) on Y is conditionally independent of genotype (X) given Y, i.e., P(X|Y,S) = P(X|Y), the selection on Y should not, in theory, affect the reverse regression estimator, 
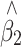, in
 |
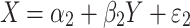2 |
and
 |
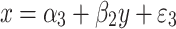3 |
where y and x are respectively, the phenotype and QTL genotype after selection. DeMets and Halperin (DeMets and Halperin 1977) showed that an unbiased estimator of β 1 of the same problem in a non-genetic (statistical) context can be given by,
 |
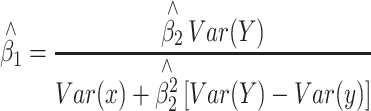4 |
Since the reverse linear regression in Eq. 3 is valid in selected samples, instead of reusing the DeMets and Halperin’s derivation of the standard error (SE), we come up with a simpler formula, which is
 |
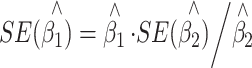5 |
To validate our results, we simulated a population of 5,000 individuals, containing a QTL under different scenarios: minor allele frequencies (MAF) of 10, 25 and 50%, and phenotype variance explained of none and 5%. Different proportions of individuals were sampled (25 and 50%) at various ratios (1:1, 2:1 and 4:1) from the two tails of the trait distribution. After 1,000 simulations, the average bias in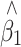 
before and after correction, and average SE and empirical standard deviation (SD) of 
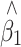after correction are shown in Table 1 and a plot of the beta distributions for one of the extreme cases is provided in Fig. 1. A bias was seen in the raw 
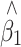under the alternative, but this disappeared after the adjustment. Also, the adjusted SE reflected accurately the true variation of the adjusted estimator.
Table 1.
The average bias, SE and empirical SD of the adjusted QTL effect estimate (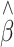
) in linear regression for association studies of QTL under two-tail extreme selection
| MAF (%) | % Sampled. | U/L ratioa | β = 0.00 | β = 0.05 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Bias before adjustment | Bias after adjustment | Average SE | Empirical SD | Bias before adjustment | Bias after adjustment | Average SE | Empirical SD | |||
| 10 | 25 | 1:1 | −0.001 | 0.000 | 0.039 | 0.040 | 0.094 | 0.000 | 0.037 | 0.037 |
| 2:1 | −0.007 | −0.002 | 0.041 | 0.039 | 0.083 | 0.000 | 0.039 | 0.040 | ||
| 4:1 | 0.002 | 0.001 | 0.046 | 0.047 | 0.056 | 0.000 | 0.044 | 0.046 | ||
| 10 | 50 | 1:1 | −0.002 | −0.001 | 0.035 | 0.036 | 0.042 | −0.001 | 0.033 | 0.033 |
| 2:1 | 0.001 | 0.000 | 0.036 | 0.036 | 0.039 | 0.001 | 0.034 | 0.034 | ||
| 4:1 | −0.001 | −0.001 | 0.039 | 0.039 | 0.025 | 0.001 | 0.037 | 0.038 | ||
| 25 | 25 | 1:1 | −0.001 | 0.000 | 0.027 | 0.028 | 0.094 | 0.000 | 0.026 | 0.026 |
| 2:1 | −0.002 | −0.001 | 0.028 | 0.029 | 0.081 | −0.001 | 0.027 | 0.029 | ||
| 4:1 | −0.003 | −0.001 | 0.032 | 0.032 | 0.063 | 0.003 | 0.030 | 0.031 | ||
| 25 | 50 | 1:1 | 0.001 | 0.000 | 0.024 | 0.023 | 0.044 | 0.001 | 0.023 | 0.023 |
| 2:1 | 0.001 | 0.000 | 0.025 | 0.024 | 0.040 | 0.002 | 0.024 | 0.024 | ||
| 4:1 | 0.001 | 0.001 | 0.027 | 0.027 | 0.026 | 0.002 | 0.026 | 0.026 | ||
| 50 | 25 | 1:1 | −0.001 | 0.000 | 0.024 | 0.023 | 0.094 | 0.000 | 0.022 | 0.023 |
| 2:1 | −0.001 | 0.000 | 0.025 | 0.024 | 0.084 | 0.001 | 0.023 | 0.023 | ||
| 4:1 | −0.004 | −0.002 | 0.027 | 0.028 | 0.057 | 0.001 | 0.026 | 0.027 | ||
| 50 | 50 | 1:1 | 0.000 | 0.000 | 0.021 | 0.020 | 0.042 | 0.000 | 0.020 | 0.020 |
| 2:1 | 0.000 | 0.000 | 0.021 | 0.021 | 0.037 | 0.000 | 0.020 | 0.020 | ||
| 4:1 | −0.001 | −0.001 | 0.023 | 0.024 | 0.023 | 0.000 | 0.022 | 0.022 | ||
aSample size ratio in the upper versus lower tail of the trait distribution
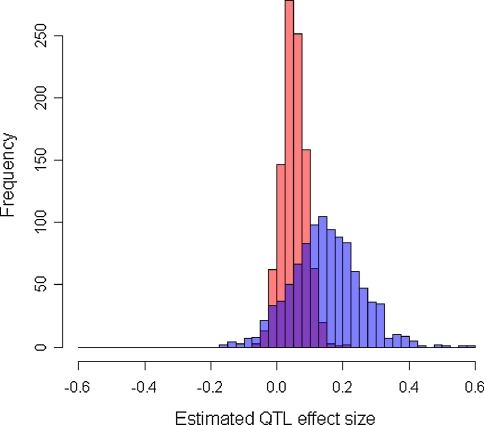
Fig. 1.
Distributions of the estimated QTL effect size before (blue) and after (red) adjustment in linear regression for association studies of QTL under two-tail extreme selection The case shown is when a quarter of the individuals were sampled at 1:1 ratio from the two tails of the trait distribution from a population of 5,000 individuals, each containing a QTL that had MAF of 10% and explained 5% of the trait variation. The means (SEs) of the estimated QTL effect size (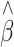
) from linear regression are, respectively, 0.144 (0.105) and 0.050 (0.036) before and after adjustment (Color figure online)
Next, to see whether the adjustment can be applied to a more complicated model, we repeated the above simulation for two unlinked QTLs with or without epistasis and fitted the regression model below to test for epistasis:
 |
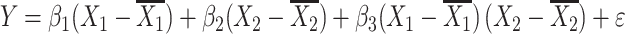6 |
where Y is the phenotype before selection, X 1 and X 2 are the genotypes for the two QTLs. Epistasis is inferred when β 3 differs significantly from zero. Since mean-centering of X 1 and X 2 alleviates collinearity between the main effects and the epistatic term (Aiken et al. 1991; Jaccard et al. 1990), we can model the regression as three independent regressions:
 |
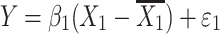7 |
 |
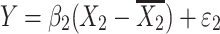8 |
 |
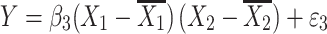9 |
and β 3 in Eq. 9 was estimated as in Eq. 4. The results are shown in Table 2. In most cases, the adjustment worked well. But caution must be taken when more genotyping are carried out in one tail of the distribution than the other because the adjustment might give an epistasis estimator with a small bias in the presence of main effects under the null hypothesis.
Table 2.
The average bias, SE and empirical SD of the adjusted epistatic effect estimate (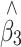
) in linear regression for association studies of QTL under two-tail extreme selection
| QTL1 MAF (%) | QTL2 MAF (%) | % Sampled. | U/L ratioa | β 3 = 0.00 | β 3 = 0.05 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Β 1 = β 2 = 0.00 | β 1 = β 2 = 0.05 | β 1 = β 2 = 0.00 | β 1 = β 2 = 0.05 | ||||||||
| Bias | SE (emp. SD) | Bias | SE (emp. SD) | Bias | SE (emp. SD) | Bias | SE (emp. SD) | ||||
| 10 | 10 | 25 | 1:1 | −0.001 | 0.093 (0.091) | 0.001 | 0.084 (0.083) | 0.001 | 0.089 (0.088) | 0.003 | 0.079 (0.081) |
| 2:1 | 0.003 | 0.097 (0.098) | −0.002 | 0.089 (0.092) | 0.002 | 0.091 (0.088) | 0.001 | 0.084 (0.089) | |||
| 4:1 | 0.000 | 0.109 (0.110) | −0.006 | 0.101 (0.111) | 0.001 | 0.102 (0.099) | −0.001 | 0.095 (0.102) | |||
| 10 | 10 | 50 | 1:1 | 0.001 | 0.082 (0.082) | 0.003 | 0.074 (0.073) | −0.002 | 0.078 (0.078) | 0.002 | 0.070 (0.071) |
| 2:1 | −0.002 | 0.085 (0.086) | 0.003 | 0.077 (0.080) | 0.000 | 0.080 (0.079) | 0.001 | 0.072 (0.074) | |||
| 4:1 | −0.002 | 0.092 (0.093) | −0.001 | 0.084 (0.092) | −0.001 | 0.087 (0.087) | 0.002 | 0.079 (0.082) | |||
| 10 | 25 | 25 | 1:1 | 0.001 | 0.064 (0.066) | 0.001 | 0.058 (0.059) | 0.001 | 0.061 (0.062) | 0.000 | 0.055 (0.056) |
| 2:1 | 0.001 | 0.067 (0.067) | −0.001 | 0.061(0.064) | −0.001 | 0.063 (0.064) | 0.001 | 0.058 (0.059) | |||
| 4:1 | 0.000 | 0.075 (0.075) | −0.004 | 0.069 (0.074) | 0.001 | 0.071 (0.069) | −0.001 | 0.065 (0.070) | |||
| 10 | 25 | 50 | 1:1 | 0.001 | 0.057 (0.057) | 0.002 | 0.051 (0.051) | 0.000 | 0.054 (0.054) | 0.000 | 0.048 (0.048) |
| 2:1 | 0.000 | 0.058 (0.058) | −0.001 | 0.053 (0.053) | 0.000 | 0.055 (0.055) | −0.001 | 0.050 (0.051) | |||
| 4:1 | 0.001 | 0.064 (0.063) | −0.003 | 0.058 (0.061) | −0.001 | 0.060 (0.059) | −0.001 | 0.055 (0.058) | |||
| 10 | 50 | 25 | 1:1 | 0.000 | 0.056 (0.056) | 0.000 | 0.050 (0.050) | 0.000 | 0.053 (0.053) | −0.002 | 0.047 (0.047) |
| 2:1 | −0.001 | 0.058 (0.058) | −0.002 | 0.053 (0.055) | −0.001 | 0.055 (0.053) | −0.002 | 0.050 (0.052) | |||
| 4:1 | 0.001 | 0.065 (0.065) | −0.005 | 0.060 (0.062) | 0.001 | 0.062 (0.061) | −0.003 | 0.056 (0.059) | |||
| 10 | 50 | 50 | 1:1 | 0.001 | 0.049 (0.048) | 0.000 | 0.044 (0.044) | −0.002 | 0.047 (0.047) | 0.001 | 0.042 (0.042) |
| 2:1 | −0.001 | 0.051 (0.051) | 0.000 | 0.046 (0.046) | −0.001 | 0.048 (0.048) | −0.002 | 0.043 (0.044) | |||
| 4:1 | 0.000 | 0.055 (0.056) | −0.003 | 0.050 (0.051) | 0.001 | 0.052 (0.052) | −0.001 | 0.047 (0.049) | |||
| 25 | 25 | 25 | 1:1 | 0.000 | 0.044 (0.045) | 0.001 | 0.040 (0.039) | 0.000 | 0.042 (0.042) | −0.001 | 0.038 (0.037) |
| 2:1 | 0.001 | 0.046 (0.046) | −0.002 | 0.042 (0.043) | 0.001 | 0.044 (0.043) | −0.003 | 0.040 (0.040) | |||
| 4:1 | 0.001 | 0.052 (0.051) | −0.004 | 0.048 (0.051) | 0.000 | 0.049 (0.049) | −0.003 | 0.045 (0.046) | |||
| 25 | 25 | 50 | 1:1 | 0.001 | 0.039 (0.039) | −0.001 | 0.035 (0.036) | 0.000 | 0.037 (0.037) | 0.000 | 0.033 (0.033) |
| 2:1 | 0.001 | 0.040 (0.040) | −0.002 | 0.037 (0.038) | 0.000 | 0.038 (0.039) | −0.001 | 0.035 (0.035) | |||
| 4:1 | 0.000 | 0.044 (0.045) | −0.004 | 0.040 (0.042) | 0.000 | 0.042 (0.041) | −0.001 | 0.038 (0.039) | |||
| 25 | 50 | 25 | 1:1 | 0.001 | 0.039 (0.038) | 0.001 | 0.035 (0.034) | 0.001 | 0.037 (0.036) | 0.000 | 0.033 (0.033) |
| 2:1 | −0.001 | 0.040 (0.041) | −0.004 | 0.036 (0.037) | −0.001 | 0.038 (0.038) | −0.002 | 0.034 (0.035) | |||
| 4:1 | 0.000 | 0.045 (0.045) | −0.005 | 0.041 (0.043) | 0.000 | 0.043 (0.044) | −0.003 | 0.039 (0.040) | |||
| 25 | 50 | 50 | 1:1 | 0.000 | 0.034 (0.034) | 0.000 | 0.031 (0.031) | −0.001 | 0.032 (0.033) | 0.000 | 0.029 (0.029) |
| 2:1 | −0.001 | 0.093 (0.091) | −0.002 | 0.032 (0.032) | 0.001 | 0.033 (0.033) | −0.001 | 0.030 (0.030) | |||
| 4:1 | 0.003 | 0.097 (0.098) | −0.003 | 0.035 (0.036) | 0.000 | 0.036 (0.037) | −0.003 | 0.033 (0.033) | |||
| 50 | 50 | 25 | 1:1 | 0.001 | 0.033 (0.034) | −0.001 | 0.030 (0.031) | −0.001 | 0.032 (0.031) | −0.001 | 0.028 (0.028) |
| 2:1 | 0.000 | 0.035 (0.035) | −0.002 | 0.031 (0.031) | 0.000 | 0.033 (0.034) | −0.003 | 0.030 (0.029) | |||
| 4:1 | 0.000 | 0.039 (0.039) | −0.005 | 0.035 (0.035) | 0.001 | 0.037 (0.037) | −0.006 | 0.033 (0.034) | |||
| 50 | 50 | 50 | 1:1 | 0.000 | 0.029 (0.030) | 0.000 | 0.026 (0.027) | 0.000 | 0.028 (0.028) | 0.000 | 0.025 (0.025) |
| 2:1 | 0.000 | 0.030 (0.030) | −0.001 | 0.027 (0.027) | −0.001 | 0.029 (0.029) | −0.002 | 0.026 (0.026) | |||
| 4:1 | −0.001 | 0.033 (0.033) | −0.004 | 0.030 (0.030) | −0.001 | 0.031 (0.031) | −0.003 | 0.028 (0.028) | |||
aSample size ratio in the upper versus lower tail of the trait distribution
We showed that the bias in QTL effect estimate in linear regression for association under two-tail extreme selection can be corrected easily. Bearing this in mind, researchers may use linear regression, which is simple and implemented in most statistical packages, in QTL association under selective genotyping.
Acknowledgments
This work was funded by Hong Kong Research Grants Council GRF HKU 774707, and The University of Hong Kong Strategic Research Theme on Genomics, and the European Community’s Seventh Framework Programme under grant agreement No. HEALTH-F2-2010-241909 (Project EU-GEI).
Open Access
This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
Footnotes
Edited by Sarah Medland.
References
- Abecasis GR, Cookson WOC, Cardon LR. The power to detect linkage disequilibrium with quantitative traits in selected samples. Am J Hum Genet. 2001;68(6):1463–1474. doi: 10.1086/320590. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aiken LS, West SG, Reno RR. Multiple regression: testing and interpreting interactions Inc. Thousand Oaks: Sage Publications; 1991. [Google Scholar]
- Chen Z, Zheng G, Ghosh K, Li Z. Linkage disequilibrium mapping of quantitative-trait loci by selective genotyping. Am J Hum Genet. 2005;77(4):661–669. doi: 10.1086/491658. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DeMets D, Halperin M. Estimation of a simple regression coefficient in samples arising from a sub-sampling procedure. Biometrics. 1977;33(1):47–56. doi: 10.2307/2529302. [DOI] [Google Scholar]
- Huang B, Lin D. Efficient association mapping of quantitative trait loci with selective genotyping. Am J Hum Genet. 2007;80(3):567–576. doi: 10.1086/512727. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jaccard J, Wan CK, Turrisi R. The detection and interpretation of interaction effects between continuous variables in multiple regression. Multivar Behav Res. 1990;25(4):467–478. doi: 10.1207/s15327906mbr2504_4. [DOI] [PubMed] [Google Scholar]
- Kwan JSH, Cherny SS, Kung AWC, Sham PC. Novel sib pair selection strategy increases power in quantitative association analysis. Behav Genet. 2009;39(5):571–579. doi: 10.1007/s10519-009-9284-x. [DOI] [PubMed] [Google Scholar]
- Slatkin M. Disequilibrium mapping of a quantitative-trait locus in an expanding population. Am J Hum Genet. 1999;64(6):1765–1773. doi: 10.1086/302413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang Y. Equivalence of three score tests for association mapping of quantitative trait loci under selective genotyping. Genet Epidemiol. 2010;34(5):522–527. doi: 10.1002/gepi.20498. [DOI] [PubMed] [Google Scholar]
- Van Gestel S, Houwing-Duistermaat JJ, Adolfsson R, van Duijn CM, Van Broeckhoven C. Power of selective genotyping in genetic association analyses of quantitative traits. Behav Genet. 2000;30(2):141–146. doi: 10.1023/A:1001907321955. [DOI] [PubMed] [Google Scholar]
- Wallace C, Chapman JM, Clayton DG. Improved power offered by a score test for linkage disequilibrium mapping of quantitative-trait loci by selective genotyping. Am J Hum Genet. 2006;78(3):498–504. doi: 10.1086/500562. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xing C, Xing G. Power of selective genotyping in genome-wide association studies of quantitative traits. BMC Proc. 2009;3:S23. doi: 10.1186/1753-6561-3-s7-s23. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xiong M, Fan R, Jin L. Linkage disequilibrium mapping of quantitative trait loci under truncation selection. Hum Hered. 2002;53:158–172. doi: 10.1159/000064978. [DOI] [PubMed] [Google Scholar]