Abstract
This study examined the use of frontal analysis and high-performance affinity chromatography for detecting heterogeneous binding in biomolecular interactions, using the binding of acetohexamide with human serum albumin (HSA) as a model. It was found through the use of this model system and chromatographic theory that double-reciprocal plots could be used more easily than traditional isotherms for the initial detection of binding site heterogeneity. The deviations from linearity that were seen in double-reciprocal plots as a result of heterogeneity were a function of the analyte concentration, the relative affinities of the binding sites in the system and the amount of each type of site that was present. The size of these deviations was determined and compared under various conditions. Plots were also generated to show what experimental conditions would be needed to observe these deviations for general heterogeneous systems or for cases in which some preliminary information was available on the extent of binding heterogeneity. The methods developed in this work for the detection of binding heterogeneity are not limited to drug interactions with HSA but could be applied to other types of drug-protein binding or to additional biological systems with heterogeneous binding.
Keywords: Frontal analysis, High-performance affinity chromatography, Heterogeneous binding, Human serum albumin, Acetohexamide, Drug-protein binding
1. Introduction
Frontal analysis is often used in affinity chromatography to characterize the properties of a column and to obtain measurements of binding affinity and activity for immobilized ligands. This approach, sometimes referred to as frontal affinity chromatography (FAC) has been used to examine various biomolecular interactions [1-6]. The combination of frontal analysis with high-performance affinity chromatography (HPAC; also known as high-performance liquid affinity chromatography, or HPLAC) has been of particular interest in recent years because of the high precision, speed and ease of automation of this method [1,2,4,5,7-10]. Frontal analysis is carried out by continuously applying to a column a solution with a known concentration of an analyte. The column contains an immobilized ligand (e.g., a protein or other type of biomolecule) that can bind to the analyte. As the binding sites on the ligand and in column become saturated by analyte, the amount of analyte that elutes from the column will increase and form a characteristic breakthrough curve. The position of this curve can then be used to obtain information on both the association equilibrium constants and the number of binding sites for the analyte on the immobilized ligand and in the column [1-10].
Many previous applications of frontal analysis in affinity chromatography have used this approach to examine ligands that have a single type of binding site for an analyte (e.g., see reviews in Refs. [1-5]). However, there have been several recent studies that have also used this method to study multi-site systems with heterogeneous interactions [11-16]. Some sources of these multi-site interactions can be examined and measured through the use of control experiments, such as the binding of an applied solute to a support in the absence of an immobilized ligand [11-15]. Other types of heterogeneity may be inherent to the interaction of the analyte with the immobilized ligand. For example, this type of situation may be produced by natural heterogeneity of the ligand, as may occur during the modification of proteins through glycosylation, glycation or phosphorylation [1,11]. In other cases, the ligands may have several, non-equivalent binding sites for the analyte or multiple binding sites plus various levels of ligand modification [1,13-15].
The goal of this study is to examine methods for the detection of binding heterogeneity in HPAC columns when using frontal analysis. Particular emphasis will be given to the use of double-reciprocal plots for data analysis, although traditional binding isotherms will also be considered. These methods of analysis will be examined and compared by using the binding of acetohexamide with human serum albumin (HSA) as a model system. This model has been recently examined by HPAC and frontal analysis and is known to involve multi-site interactions [12]. Chromatographic theory will be used to examine the use of double-reciprocal plots in detecting binding heterogeneity, as well as to determine the experimental conditions that are needed for such detection. The expected result is an improved set of tools for the identification and study of heterogeneous binding by frontal analysis and HPAC, which can then be employed in the analysis of other biological systems.
2. Theory
Frontal analysis data for a system that follows a one-site binding model can be analyzed according to either the adsorption isotherm shown in eq. (1) or the double-reciprocal form of this isotherm that is shown in eq. (2) [1,4].
| (1) |
| (2) |
In these equations, mLapp is the apparent moles of analyte required to saturate the column and to reach the mean breakthrough point in a frontal analysis curve at a given analyte concentration [A]. The term mLtot is the total binding capacity, in moles, of the column for the analyte, and Ka is the association equilibrium constant for the analyte with the immobilized ligand (i.e., the immobilized binding agent). Eq. (1) predicts that a non-linear response will occur when a plot is made of mLapp vs. [A]. When a plot of 1/mLapp vs. 1/[A] is made according to eq. (2), a linear response should result if one-site binding is taking place between the analyte and immobilized ligand. If deviations from linearity are seen at high analyte concentrations (i.e., low 1/[A] values), more than one type of binding site must be present for the analyte [1,4,11].
Similar equations to eq. (1) and (2) can be written to describe the results in frontal analysis experiments for systems that have heterogeneous interactions and multiple binding sites. Examples of such relationships are shown in eqs. (3) and (4) for a two-site binding model [11].
| (3) |
| (4) |
In these equations, Ka1 is the association equilibrium constant for an analyte at its binding site with the highest affinity (L1), and Ka2 is the association equilibrium constant for the binding site with the lowest affinity (L2). The values mL1 and mL2 in eq. (3) represent the moles of these high- and low-affinity binding sites, respectively. The term β, as used in eq. (4), is a dimensionless parameter that is defined as the ratio of the association equilibrium constant for any given type of site versus the association equilibrium constant for the highest affinity site in the population (e.g., β2 = Ka2/Ka1, where 0 < Ka2 < Ka1, and β1 = Ka1/Ka1 = 1). Similarly, the term α in eq. (4) is a dimensionless parameter that is equal to the mole fraction of all the binding regions that make up a given group of sites. For instance, α1 = mL1/mLtot and α2 = mL2/mLtot for a two-site system, where 1 = α1 + α2 and α2 = 1 - α1 [11].
A double-reciprocal plot of 1/mLapp vs. 1/[A] that is made according to eq. (4) for frontal analysis data would be expected to be non-linear for a two-site system when examined over a broad range of analyte concentrations. However, it has been demonstrated previously that this type of plot does approach linear behavior at low analyte concentrations, or high values for 1/[A]. This relationship is given by eq. (5) for a two-site system [11].
| (5) |
Similar linear relationships to eqs. (4) and (5) can be written for any n-site heterogeneous system as long as each binding site interacts independently with the analyte [11]. The general forms of these relationships are provided in eqs. (6) and (7), in which the summations or products are over the interval of i or j = 1 to n.
| (6) |
| (7) |
As these last two equations indicate, an n-site system will again give curvature in a plot of 1/mLapp versus [A] when examined over a broad range of concentrations, but this plot will approach a linear response at low concentrations of the analyte and high values of 1/[A] [11].
In this study, modified forms of eqs. (4) and (5), and of the more general expressions in eqs. (6) and (7), will be used to examine the effects of binding heterogeneity in frontal analysis.
| (8) |
| (9) |
For the rearranged forms of eqs. (4) and (5) that are given in eqs. (8) and (9), all terms are now expressed through the use of dimensionlesss parameters. These parameters include the terms α1 and β2, as discussed previously. Eqs. (8) and (9) also include the term 1/(Ka1[A]), which represents the independent variable, and the ratio mLtot/mLapp, which can be used as the dependent variable. These terms and equations will be used later in this study to generate universal plots for describing the effects of binding heterogeneity over a broad range of experimental conditions.
3. Experimental
3.1. Reagents
The acetohexamide and HSA (Cohn fraction V, essentially fatty acid free) were obtained from Sigma-Aldrich (St. Louis, MO, USA). The Nucleosil Si-300 (7 μm diameter, 300 Å pore size) was from Macherey-Nagel (Düren, Germany). All aqueous solutions were made using water obtained from a NANOpure system (Barnstead, Dubuque, IA, USA). Solutions used in the chromatographic studies were filtered prior to use through 0.20 μm GNWP nylon membranes from Millipore (Billerica, MA, USA).
3.2. Apparatus
The chromatographic system included a DG-2080-53 three-solvent degasser, two PU-2080 HPLC pumps, a UV-2075 absorbance detector, a CO-2060 column oven, and a AS-2055 autosampler from Jasco (Tokyo, Japan) plus a Rheodyne Advantage PF 6-port valve (Cotati, CA, USA). These system components were controlled by using EZChrom Elite software v3.2.1 (Scientific Software, Pleasanton, CA, USA) and Jasco LC Net hardware. In-house programs written in Labview 5.1 (National Instruments, Austin, TX, USA) were used to determine the breakthrough times during the frontal analysis experiments.
3.3. Chromatographic Methods
The HSA support and control support were both prepared by the Schiff base method and using Nucleosil Si-300 silica, as described previously [9,12], but with no protein being added to the control support during the immobilization step. The final amount of immobilized protein on the HSA support was determined in triplicate by a protein assay to be 38 (± 3) mg/g silica [12]. The HSA support and control support were downward slurry packed into separate 2.0 cm × 2.1 mm ID stainless steel columns at 3000 psi (20.7 MPa) using pH 7.4, 0.067 M potassium phosphate buffer as the packing solution. These columns were stored in the same pH 7.4 buffer at 4 °C and showed no significant changes in their binding properties throughout this study [12].
All solutions of acetohexamide were prepared in pH 7.4, 0.067 M potassium phosphate buffer and were degassed under vacuum for at least 15 min prior to use. A flow rate of 0.5 ml/min was used for sample application and injection. The application of either the pH 7.4, 0.067 M phosphate buffer or the desired drug solution during frontal analysis was accomplished by alternating between these solutions through the use of a six-port valve. The acetohexamide solutions consisted of up to fifteen different concentrations of acetohexamide ranging from 1 to 1000 μM. Although acetohexamide is a weak acid, all of these solutions had a pH within 0.05 units of pH 7.4 even at the highest drug concentrations that were used in this study. The frontal analysis curves were monitored at 248 nm for 1-20 μM acetohexamide and at 315 nm for 30-1000 μM acetohexamide; multiple detection wavelengths were used to ensure that a linear change in signal with concentration was present for each acetohexamide sample. All acetohexamide solutions were applied in triplicate to both the HSA column and the control column. Breakthrough times were determined using the equal area method [17]. All results were corrected for non-specific binding to the support by subtracting the values for the control column from those measured on the HSA column at each given concentration of the analyte, as has been employed in previous studies of acetohexamide and related drugs by HPAC [12-14]. Although the same equations as given in Section 2 could be used to examine the combined effects of analyte interactions with an immobilized ligand and a support [11], the use of a control column to correct for nonspecific binding to the support made it possible in this report to instead focus directly on the detection of heterogeneity for analyte-ligand interactions [12-14].
Linear regression of the frontal analysis data was performed by using Excel 2003 (Microsoft, Redmond, WA, USA) and non-linear regression was carried out by using DataFit 8.1.69 (Oakdale Engineering, PA, USA). Calculations for studying the deviations predicted in frontal analysis plots as a result of binding site heterogeneity were performed by using Mathematica (Wolfram Research, Champaign, IL, USA). The surface figures and contour plots used in analyzing the calculated results were generated by using Origin 8.0 (Originlab, Northampton, MS, USA).
4. Results and Discussion
4.1. Reciprocal Plots versus Binding Isotherms for Detecting Heterogeneous Binding
Early work in this study used experimental data that were obtained for the binding of acetohexamide with HSA to compare the effects of binding site heterogeneity on various types of frontal analysis plots. This particular system has been found in prior work to fit a model based two general groups of binding sites on HSA [12]. The first group of sites consists of two high affinity sites (i.e., Sudlow sites I and II) with an average association constant of 1.3 (± 0.2) × 105 M-1 at pH 7.4 and 37°C. The second group consists of at least five weaker sites with an average association equilibrium constant of 3.5 (± 0.3) × 102 M-1 at pH 7.4 and 37°C.
Figure 1(a) shows how this heterogeneity affected the use of typical binding isotherms to describe such a system. The binding isotherm for the acetohexamide/HSA system was found in previous experiments that used a broad range of drug concentrations (n = 15, 1-1000 μM) to give a good fit to a two-site model [12]. Similar results were obtained in Figure 1(a) when using eq. (3) and a smaller data set obtained over a narrower concentration range (n = 10, 1-50 μM). A one-site model based on eq. (1) also gave reasonable agreement with the experimental results over most of the binding isotherm, but this fit did deviate from the data at intermediate or high acetohexamide concentrations (e.g., see points at 20 and 50 μM). The use of an even smaller data set made it difficult to discriminate between one-site and two-site models for this system. Plots such as those shown in Figure 1(a) have often been used for detecting heterogeneous binding and for determining the association equilibrium constants and the number of sites that are involved in multi-site interactions in affinity columns [4,12-16]. However, this method does require the utilization of a sufficiently broad range of concentrations and a suitable number of data points to detect heterogeneous binding.
Figure 1.
Frontal analysis data for the binding of acetohexamide to HSA, as examined according to (a) standard binding isotherms, as described by eqs. (1) and (3), or (b) by using a double-reciprocal plot. In (a), the dashed line shows the fit for a single site model according to eq. (1) and the solid line shows the fit for a two-site model according to eq. (3). In (b), the solid line shows the linear fit that was obtained to the five points to upper right of this graph. Each point represents the mean of triplicate measurements.
An alternative approach that has been proposed for the initial detection of binding heterogeneity in frontal analysis data is to use double-reciprocal plots [12-14]. According to eqs. (5) and (7), such a plot should approach a linear relationship at low analyte concentrations (or high values of 1/[A]) for any system that has heterogeneous, independent binding sites. At high analyte concentrations (or low values of 1/[A]), eqs. (4) and (6) predict that deviations from a linear response will then occur. It is the absence or presence of these deviations from linearity that can then be used to determine whether a system follows a single-site model or if multiple binding sites are present for the analyte in a column [4,12-14]. An example of a double-reciprocal plot is shown in Figure 1(b) for the interactions of acetohexamide with HSA. This plot was prepared using the same data as in Figure 1(a). Figure 1(b) shows that a linear range is present at high values of 1/[Acetohexamide], as predicted by eqs. (5) and (7). In addition, negative deviations from this linear range appear at lower values of 1/[Acetohexamide], indicating more than one type of binding region is present for acetohexamide on HSA [4,11,12].
An important difference in Figures 1(a) and 1(b) is that a much smaller number of experiments were needed in Figure 1(b) to detect binding heterogeneity. For instance, the binding isotherms in Figure 1(a) required measurements over at least ten measurements spanning from 1-50 μM to differentiate between one- and two-site models. However, moving beyond the five highest values of 1/[Acetohexamide] in Figure 1(b) gave deviations from linearity over the next four lower values of 5.7%, 9.5%, 15%, and 21%, respectively. These deviations were much larger than the precision of the results over this concentration range (i.e., standard error of the mean, ±0.02-0.2% for triplicate measurements) and were larger than the average residual of ±1.1% for the upper five points about the best-fit line. The size of these deviations meant that data over as little as six concentrations spanning from only 1-7.5 μM acetohexamide could be used to detect binding heterogeneity in this example. These results demonstrated that the use of a double-reciprocal plot instead of a traditional isotherm required much fewer experiments and a significantly smaller amount of drug for the detection of binding heterogeneity. A similar conclusion was reached when using data from additional reports that have examined the binding of other drugs with HSA or with modified forms of this protein [12-15].
4.2. Conditions Leading to Deviations from Binding Site Heterogeneity
Eqs. (8) and (9) have been used previously to examine the effects of binding heterogeneity on the apparent association equilibrium constants and binding capacities that are obtained from the linear regions of double-reciprocal frontal analysis plots [11]. In this current study, eqs. (8) and (9) were instead used to examine the ability of double-reciprocal plots to detect binding heterogeneity. As discussed in Section 2, a linear response for these plots should be seen for a heterogeneous system when relatively small analyte concentrations, or high values of 1/(Ka1[A]), are employed [11-14]. However, deviations from this linearity would be expected at low values of 1/(Ka1[A]) and high analyte concentrations. Several factors are known to affect the linearity or curvature of such plots [11]. For instance, the greatest amount of curvature and deviations from linearity would be expected at high analyte concentrations and in systems for which there is a large difference in affinities (i.e., a small value of β2 in a two-site system) and/or a small population of the highest affinities sites (i.e., a small value of α1 in a two-site system). These general observations agree with the results shown in Figure 1(b) for the acetohexamide/HSA system, which represent data over a tested range of 1/(Ka1 [A]) = 0.08-7.7. In this case, deviations from linearity are noted at 1/(Ka1 [A]) ≈ 1.0 for a system with estimated values of α1 = 0.2 and β2 = 0.003 for a two-site model, as based on data from Ref. [12].
The next phase of this research looked at the size of the deviations from linearity in double-reciprocal plots that were obtained for systems with various degrees of binding heterogeneity. One way this was done was by making surface plots of the deviations that were measured for two-site systems at a given concentration of applied analyte, as represented by the term 1/(Ka1 [A]). These plots were prepared as a function of both the relative amount of each type of site (α1) and the relative affinities of these sites (β2). Both of these latter two parameters were allowed to vary in value from zero to one (i.e., a range which represented all possible combinations of these terms for a two-site system) [11]. A typical surface plot that was generated by this approach is shown in Figure 2 for the situation in which 1/(Ka1[A]) = 0.05. The relative deviation from linearity was calculated in this plot and in all following graphs by using eq. (10).
| (10) |
This equation was used to find the difference between the actual response of the curve, as predicted by eq. (8), and the response of the linear region, as described by eq. (9), with this difference then being divided by the linear response predicted by eq. (9). The use of eq. (10) and this approach gave a relative deviation at any given value of 1/(Ka1[A]) that could range in size from 0 to 1.0 (or 0 to 100%). This value was then used to indicate the relative deviation from linearity that occurred under any set of conditions for a two-site system.
Figure 2.
Surface plot showing the relative deviation from a linear response in the value of mLtot/mLapp for a double-reciprocal frontal analysis plot, as predicted by eq. (10) for two-site systems in which 1/(Ka1[A]) = 0.05 and as a function of both the mole fraction of the highest affinity site (α1) and the ratio of the association equilibrium constants for the low versus high affinity sites (β2).
Figure 2 indicates that the greatest deviations from a linear response for a double-reciprocal plot occurred as the values of α1 and β2 decreased. The same trends were noted for surface plots that were made for other values of 1/(Ka1[A]), but the size of the deviations did decrease as 1/(Ka1[A]) was increased. Different behavior was seen as α1 or β2 approached zero and dropped below 0.1-0.2. Under these conditions, a decrease in deviations was seen; this behavior reflected the fact that a value for α1 or β2 of zero would represent a one-site model, which should always follow a linear response according to eq. (2).
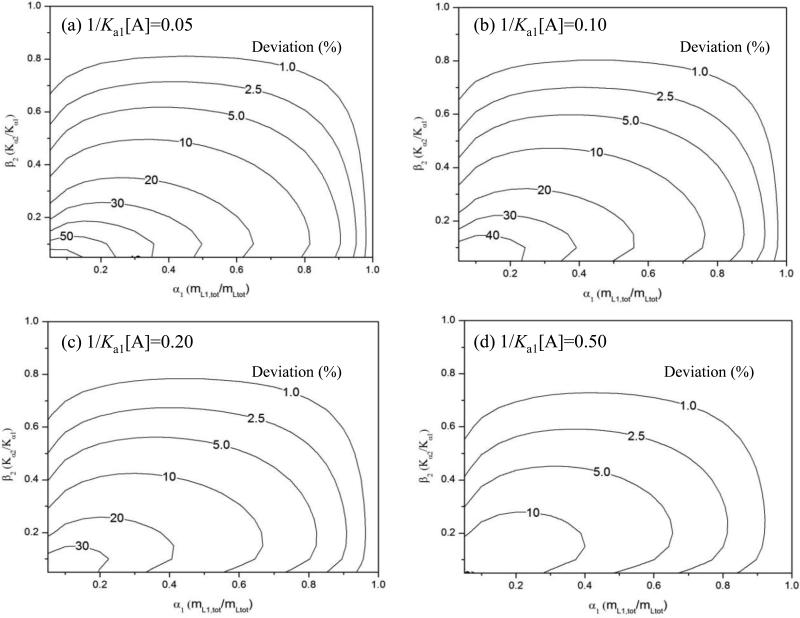
Figure 3 shows contour plots that were prepared from surface plots like Figure 2. These contour plots were made for several values of 1/(Ka1[A]) and were used to show the relative deviation from linearity that would be expected for a two-site system as the values of α1 and β2 were varied. The general trends in Figure 3 agree with those described for Figure 2, in which deviations from linearity tended to increase as the terms α1, β2, or 1/(Ka1[A]) were decreased. With the contour plots it was possible to determine which combinations of these parameters would create a given size of deviation from linearity. As an example, Figure 3(a) shows that heterogeneous systems with α1 ≤ 0.95 and β2 ≤ 0.80 at 1/(Ka1[A]) = 0.05 would generally have at least a 1% deviation from a linear response. At the same value of 1/(Ka1[A]), systems with α1 ≤ 0.8-0.9 and β2 ≤ 0.5-0.6 tended to have at least a 5% deviation from a linear response.
Figure 3.
Contour plots showing the relative deviation from a linear response in the value of mLtot/mLapp for a double-reciprocal frontal analysis plot, as predicted by eq. (10) for two-site systems at various values of 1/(Ka1[A]) and as a function of the mole fraction of the highest affinity site (α1) and the ratio of affinities (β2) for the binding sites in the column. These contour plots were generated by using surface plots like the one shown in Figure 2. These plots are for 1/(Ka1[A]) values of (a) 0.05, (b) 0.10, (c) 0.20 or (d) 0.50 and have contours that range from 1.0% deviation to 10-60% deviation.
4.3. Extent of Deviations Due to Binding Site Heterogeneity
By integrating the areas within each contour of plots like those in Figure 3, it was possible to determine the fraction of all heterogeneous systems that produced a given deviation from linearity at a particular value for 1/(Ka1[A]). For instance, 72.2% of all the two-site systems in Figure 3(a) gave a deviation from a linear response that was at least 1%; 59.7% produced a deviation of at least 2.5%; 47.5% gave a deviation of at least 5%; and 33.2% gave a deviation of at least 10%. The corresponding number of two-site systems at the same levels of deviation became smaller as 1/(Ka1[A]) was increased, as illustrated in Figures 3(b)-(d). As an example, for 1/(Ka1[A]) = 0.50 in Figure 3(b), 58.6% of the results now had a deviation from linearity of at least 1%; 39.7% had a deviation of at least 2.5%; 23.0% had a deviation of at least 5%; and 7.9% had a deviation of at least 10%.
Figure 4 summarizes the integrated results for contour plots that were prepared for a wide range of 1/(Ka1[A]) values. In Figure 4, the value given on the y-axis shows the percent of all two-site cases that produce a deviation from linearity that is greater than or equal to the amount of deviation that is listed on the x-axis. One way this plot can be used is to determine the likelihood of detecting heterogeneous binding at a given level of deviation from linearity and at a given value for 1/(Ka1[A]). For instance, a series of frontal analysis studies that use analyte concentrations up to Ka1[A] = 5 (or down to 1/(Ka1[A]) = 0.2) would detect 22.4% of all two-site systems when using up to a 10% deviation from linearity, 38.4% of these systems when using a 5% deviation, 52.7% when using a 2.5% deviation, and 67.7% when using a 1% deviation.
Figure 4.
Percent of all two-site cases expected to have a particular minimum deviation from a linear response for a double-reciprocal frontal analysis plot when using various values for 1/(Ka1[A]). These values were found by integrating the results of contour plots like those shown in Figure 3.
Figure 4 shows that increasing the value of Ka1[A], or decreasing 1/Ka1[A], typically makes it easier to detect heterogeneous binding when using double-reciprocal plots. As an example, if the analyte concentration was changed from Ka1[A] = 5 (or 1/(Ka1[A]) = 0.2), as used in the previous paragraph, to Ka1[A] = 50 (or 1/(Ka1[A]) = 0.02), these new conditions would make it possible to identify 35.7% of all two-site systems when using a 10% deviation from linearity, 49.4% at a 5% deviation, 61.1% at a 2.5% deviation, and 73.1% at a 1% deviation. However, it should be noted that the detection of heterogeneity does not improve to any significant amount once the value of 1/(Ka1[A]) has been extended below 0.02. Figure 4 shows that a further change in 1/(Ka1[A]) beyond this point produces only a minor increase in the detected cases of heterogeneity. Fortunately, Figure 4 also indicates that it is possible to increase the detection of heterogeneity at any value of 1/(Ka1[A]) by adjusting other experimental conditions (e.g., the number of replicates and/or the precision of the frontal analysis system) to allow smaller deviations from a linear response to be monitored.
4.4. Conditions Required to Detect Binding Site Heterogeneity
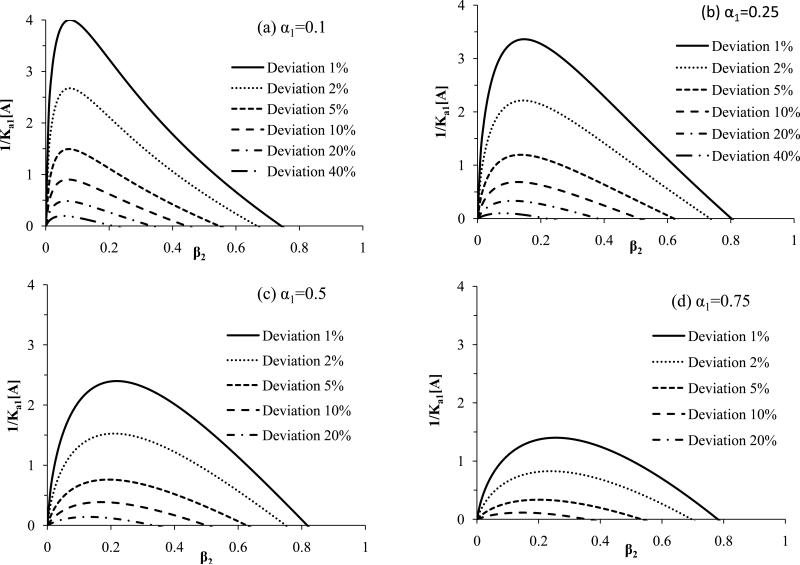
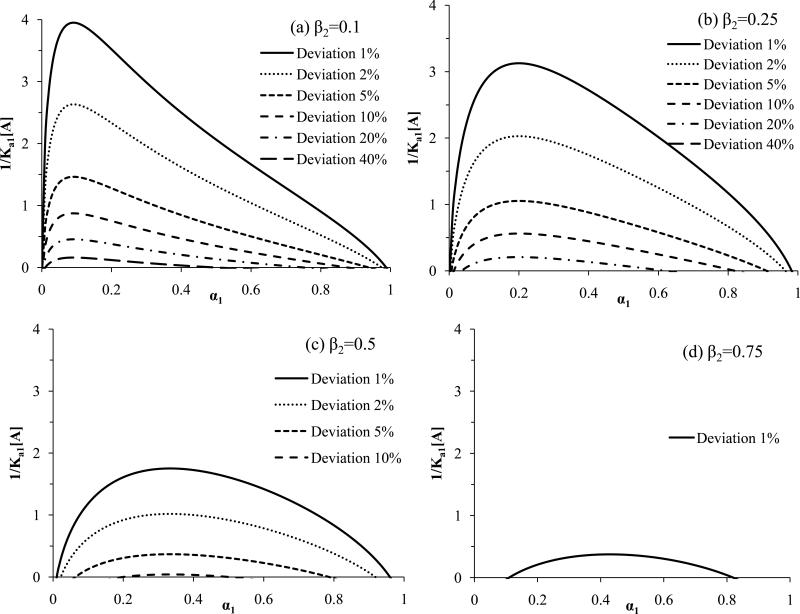
The results in Figure 4 show the values of 1/(Ka1[A]) that are needed to detect a given deviation from linearity for all possible combinations of heterogeneity in two-site systems. An alternative way of examining such systems is to use eq. (10) to determine the value of 1/(Ka1[A]) that is needed to detect a given level of deviation for linearity in a particular two-site system. This approach is demonstrated in Figure 5 for specific values of α1 as the term β2 is allowed to vary; a related plot is given in Figure 6 in which β2 is held at specific values and α1 is now varied. As predicted by Figures 2-3, the results in Figure 5 and 6 show that it is easiest to detect binding heterogeneity as α1 or β2 decreases until a value of roughly 0.1-0.2 for β2 or α1 has been reached. This greater ease of detection at relatively low α1 or β2 values is reflected by the larger 1/(Ka1[A]) values that can be used under these conditions to detect a given level of deviation from linearity.
Figure 5.
Minimum values of 1/(Ka1[A]) that can be used in frontal analysis experiments to produce a given deviation from linearity in double-reciprocal plots for two-site systems at various ratios for the affinities of the binding sites (β2) and at specific values for the mole fraction of the highest affinity site (α1), where α1 is equal to (a) 0.1, (b) 0.25, (c) 0.50 or (d) 0.75). These results were generated by using eq. (10).
Figure 6.
Minimum values of 1/(Ka1[A]) that can be used in frontal analysis experiments to produce a given deviation from linearity in double-reciprocal plots for two-site systems at various mole fractions of the highest affinity site (α1) and at specific ratios of the affinities for the binding sites (β2), where β2 is equal to (a) 0.1, (b) 0.25, (c) 0.50 or (d) 0.75). These results were generated by using eq. (10).
Figures 5 and 6 should be useful in cases in which some preliminary information is available on the possible heterogeneity of a binding system. In such a case, these plots can be employed to determine which conditions are needed to detect heterogeneity by means of double-reciprocal frontal analysis plots. For instance, suppose an immobilized protein is suspected to have two independent binding sites for an analyte (i.e., α1 = 0.5). In this situation, Figure 5(c) provides the minimum values of 1/(Ka1[A]) that are needed to detect such a system at a given deviation from a linear response (e.g., a minimum of 1/(Ka1[A]) = 1.0 is needed to detect a 2% deviation at β2 ≈ 0.05-0.45). The use of this more specific information for selecting the experimental conditions will, in turn, increase the likelihood of detecting such a heterogeneous system when using a double-reciprocal plot.
Another application of Figures 5-6 is to indicate which heterogeneous systems can or cannot be detected under a particular set of experimental conditions. The same plots can then be used to show how the experimental conditions should be changed to make the detection of additional systems more feasible. This can again be illustrated by using Figure 5(c) and two-site systems in which α1 = 0.5. In this situation, the use of analyte concentrations that produce a minimum value for 1/(Ka1[A]) = 1.0 will allow heterogeneity to be detected in systems with β2 = 0.05-0.45 when using a deviation of 2% or greater from linearity. However, the same conditions will not allow heterogeneity to be detected at 2% deviations if β2 < 0.05 or β2 > 0.45. Decreasing the value of 1/(Ka1[A]) by two-fold to 0.5 at α1 = 0.5 will expand the range of two-site systems that can be identified to include β2 ≈ 0.02-0.60 when using a 2% deviation from linearity. Improving the precision of the measurements so that a 1% deviation from linearity can be monitored will expand this range to β2 ≈ 0.01-0.75. Similar adjustments can be made based on Figure 5 and 6 to detect other types of two-site systems.
4.5. Effects of Higher Levels of Binding Site Heterogeneity
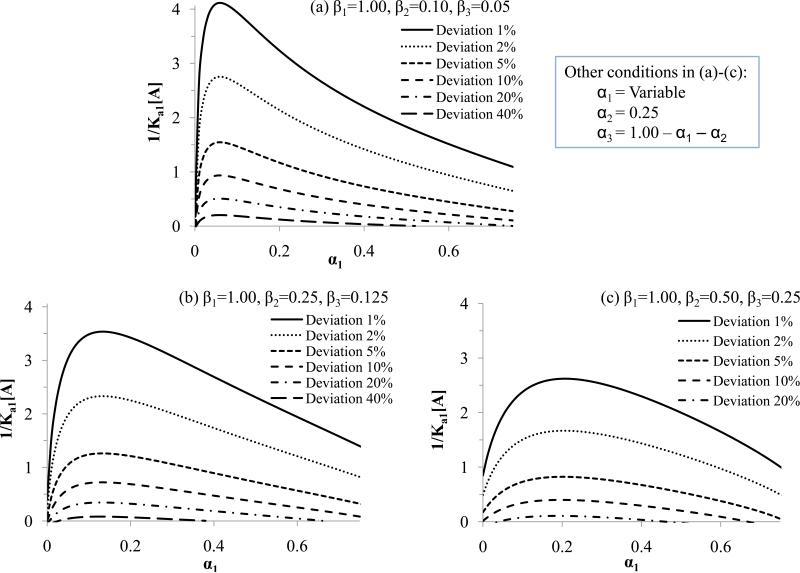
By using eqs. (6)-(7) and expressions equivalent to eqs. (8)-(10), similar plots to those already given for a two-site model could be prepared for systems with any number of binding sites. Figures 7 and 8 contain examples of such plots for a three-site system. In Figure 7, the relative affinities of the sites were varied but with the second and third lowest affinity sites always differing by two-fold in their association equilibrium constants. The relative amount of the intermediate binding site (i.e., as represented by the mole fraction α2) was held constant at 0.25 for the sake of this illustration, while the mole fractions of the highest and lowest affinity sites (as described by α1 and α3) were varied. These conditions were comparable to those used for a two-site system in Figure 6 (with α3 = 0 and β3 = 0), making it possible to directly compare the effects of heterogeneity in Figures 6 and 7 for two-site and three-site models.
Figure 7.
Minimum values of 1/(Ka1[A]) that can be used in frontal analysis experiments to produce a given deviation from linearity in double-reciprocal plots for three-site systems at various combinations of affinities and various mole fractions of the highest affinity site (α1) when the mole fraction for the second highest affinity site (α2) is equal to 0.25. The mole fraction of the lowest affinity site (α3) was calculated by using α3 = 1 - α1 - α2; the x-axis extends in this case up to 0.75, which is the maximum allowed value for α1 if α2 is equal to 0.25. The affinities for the binding sites that were used in these calculations were (a) β1 = 1.00, β2 = 0.10, and β3 = 0.05; (b) β1 = 1.00, β2 = 0.25, and β3 = 0.125; and (c) β1 = 1.00, β2 = 0.50, and β3 = 0.25. These results were generated by using a modified form of eq. (10) that was based on eqs. (6)-(7) and developed for a three-site system.
Figure 8.
Minimum values of 1/(Ka1[A]) that can be used in frontal analysis experiments to produce a given deviation from linearity in double-reciprocal plots for three-site systems at various mole fractions of the highest affinity sites (α1) and second highest affinity site (α2) and at relative affinities of β1 = 1.00, β2 = 0.50, and β3 = 0.25. The values of α2 used in generating these plots were (a) 0.10, (b) 0.25, and (c) 0.50. The mole fraction of the lowest affinity site (α3) was calculated by using α3 = 1 - α1 - α2; the x-axis extends in each plot up to a value of 1 - α2, which is the maximum allowed value for α1. These results were generated by using a modified form of eq. (10) that was based on eqs. (6)-(7) and developed for a three-site system.
Figures 6 and 7 show similar patterns in the values of 1/(Ka1[A]) that were needed to detect a given level of deviation from linearity in double-reciprocal plots. In both the two- and three-site systems, the deviations due to heterogeneity increased as α1 was decreased until a value for α1 of about 0.1-0.2 had been reached. The similarity of the results in Figures 6 and 7 indicated that the plots generated for two-site systems in the previous sections can be useful in the initial selection of conditions for the detection of binding heterogeneity in higher order systems. However, the introduction of a third, lower affinity site did create a slight increase in the range of conditions that could be used to detect binding site heterogeneity. This difference was represented by the higher maximum values of 1/(Ka1[A]) that were obtained at each given level of deviation in Figures 6 and 7. This difference indicated that higher-order binding systems can be easier to detect by double-reciprocal plots than two-site systems for at least some combinations of binding sites.
Figure 8 shows how the changes in the relative amount of the second highest affinity site affected the detection of heterogeneity in a three-site system. As the amount of this intermediate affinity site was decreased, a broader range of 1/(Ka1[A]) values could be used to detect heterogeneity at any given level of deviation. This trend is comparable to the one noted earlier for a two-site system, in which a decrease in the relative amount of the highest affinity site tended to produce larger deviations in double-reciprocal plots due to heterogeneity. This trend occurs until the amount of these higher affinity sites becomes so small that the low affinity sites become dominant and the system approaches a simpler binding model in its behavior.
5. Conclusion
This study examined the use of frontal analysis and HPAC for detecting heterogeneous binding in biomolecular systems, such as those involved in multi-site drug-protein interactions. An emphasis was placed on the use of double-reciprocal plots for detecting systems with binding heterogeneity. Chromatographic theory was utilized to determine the effects that heterogeneous binding would have on double-reciprocal plots and to predict the types of deviations from linearity that would be expected in these plots for various two-site systems. This approach was illustrated by using the binding of acetohexamide with HSA as a model system. A comparison of traditional binding isotherms with double-reciprocal plots indicated that the latter could be used more easily for the initial detection of binding heterogeneity and required less analyte for such an application. These features make this approach attractive as a screening method for examining solute-protein interactions prior to more detailed binding studies [1-4].
It was shown in this report that the deviations from linearity that are seen in double-reciprocal plots are a function of the applied concentration of the analyte, as represented by the unitless term 1/(Ka1[A]). These deviations are also dependent on the relative affinities of the binding sites in the system, as represented by the term β2, and the relative amount of each type of binding site, as represented by the term α1. The greatest deviations due to binding heterogeneity tended to occur at low analyte concentrations and as the values of β2 or α1 decreased to approximately 0.1-0.2. Plots were generated to determine the experimental conditions that would be needed to observe deviations from linearity for either general two-site systems or systems for which some preliminary estimate of either β2 or α1 was available. The results of this study should not only be useful in examining the binding of drugs such as acetohexamide with HSA, but should also be valuable in the use of frontal analysis to study the binding of other biological systems that are suspected to have heterogeneous binding [1-4,8,9,15].
Acknowledgements
This research was supported by the National Institutes of Health under grant R01 DK069629 and was conducted in facilities that were renovated under grant RR015468.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Schiel JE, Joseph KS, Hage DS. In: Advances in Chromatography. Grushka E, Grinberg N, editors. Vol. 48. CRC Press; Boca Raton, FL: 2010. Chap. 4. [PubMed] [Google Scholar]
- 2.Schreimer DS. Anal. Chem. 2004;76:440–448A. doi: 10.1021/ac041684m. [DOI] [PubMed] [Google Scholar]
- 3.Chaiken IM, editor. Analytical Affinity Chromatography. CRC Press; Boca Raton, FL: 1987. [Google Scholar]
- 4.Chen J, Hage DS. In: Handbook of Affinity Chromatography. 2nd Ed. Hage DS, editor. CRC Press; Taylor & Francis/Boca Raton, FL: 2006. Chap. 22. [Google Scholar]
- 5.Hage DS, Tweed SA. J. Chromatogr. B. 1997;699:499. doi: 10.1016/s0378-4347(97)00178-3. [DOI] [PubMed] [Google Scholar]
- 6.Kasai KI, Ishii SI. J. Biochem. 1975;653:78. doi: 10.1093/oxfordjournals.jbchem.a131025. [DOI] [PubMed] [Google Scholar]
- 7.Ohlson S, Hansson S, Larsson P-O, Mosbach K. FEBS Lett. 1978;93:5. doi: 10.1016/0014-5793(78)80792-3. [DOI] [PubMed] [Google Scholar]
- 8.Patel S, Wainer IW, Lough WJ. In: Handbook of Affinity Chromatography. 2nd Ed. Hage DS, editor. CRC Press; Taylor & Francis/Boca Raton, FL: 2006. Chap. 24. [Google Scholar]
- 9.Loun B, Hage DS. J. Chromatogr. 1992;579:225. [PubMed] [Google Scholar]
- 10.Schriemer DC, Bundle DR, Li L, Hindsgaul O. Angewandte Chemie Int. Ed. 1998;37:3383. doi: 10.1002/(SICI)1521-3773(19981231)37:24<3383::AID-ANIE3383>3.0.CO;2-C. [DOI] [PubMed] [Google Scholar]
- 11.Tweed SA, Loun B, Hage DS. Anal. Chem. 1997;69:4790. doi: 10.1021/ac970565m. [DOI] [PubMed] [Google Scholar]
- 12.Joseph KS, Hage DS. J. Chromatogr. B. 2010;878:1590. doi: 10.1016/j.jchromb.2010.04.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Joseph KS, Anguizola J, Hage DS. J. Pharm. Biomed. Anal. 2011;54:426. doi: 10.1016/j.jpba.2010.09.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Joseph KS, Anguizola J, Jackson AJ, Hage DS. J. Chromatogr. B. 2010;878:2775. doi: 10.1016/j.jchromb.2010.08.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Chen S, Sobansky M, Hage DS. Anal. Biochem. 2010;397:107. doi: 10.1016/j.ab.2009.10.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Zacharis CK, Kalaitzantonakis EA, Podgornik A, Theodoridis G. J. Chromatogr. A. 2007;1144:126. doi: 10.1016/j.chroma.2006.12.081. [DOI] [PubMed] [Google Scholar]
- 17.Hage DS. J. Chromatogr. B. 2002;768:3. doi: 10.1016/s0378-4347(01)00482-0. [DOI] [PubMed] [Google Scholar]