A collisional perspective on quadrupedal gait dynamics

Abstract

The analysis of terrestrial locomotion over the past half century has focused largely on strategies of mechanical energy recovery used during walking and running. In contrast, we describe the underlying mechanics of legged locomotion as a collision-like interaction that redirects the centre of mass (CoM). We introduce the collision angle, determined by the angle between the CoM force and velocity vectors, and show by computing the collision fraction, a ratio of actual to potential collision, that the quadrupedal walk and gallop employ collision-reduction strategies while the trot permits greater collisions. We provide the first experimental evidence that a collision-based approach can differentiate quadrupedal gaits and quantify interspecific differences. Furthermore, we show that this approach explains the physical basis of a commonly used locomotion metric, the mechanical cost of transport. Collision angle and collision fraction provide a unifying analysis of legged locomotion which can be applied broadly across animal size, leg number and gait.

1. Introduction

Walking and running gaits of animals have long captured the human imagination, as exemplified by the historic works of Da Vinci, Borelli and Muybridge. Beginning with Marie [1] and formalized by Hildebrand [2] gaits have been described in terms of temporal parameters such as duty factors and the phase relationships between limbs. However, these are only proximate definitions because they fail to characterize the fundamental mechanical interaction between the animal's centre of mass (CoM) and the supporting environment. In contrast, the broadly influential ‘two basic mechanisms’ [3] evaluate walking and running animals as mechanical systems that reduce locomotor cost through energy recovery strategies. In walking, CoM mechanical energy remains relatively constant as kinetic and potential energies are exchanged in a pendular manner, such that the CoM vaults over the support limb at mid-stance and falls forward into the next step. This exchange is unavailable during running because the CoM reaches its lowest point at mid-stance when kinetic energy is also low. Running gaits are, therefore, thought to employ a spring-mass mechanism, where interactions between the CoM and the ground allow storage and return of elastic strain energy in relatively compliant legs. By embracing these two basic mechanisms of energy recovery, the analysis of locomotor mechanics has required a priori assumptions of which mechanism is used in a given gait. Our collision-based analysis allows for these two mechanisms, and possibly others, but does not require the expectation of a given recovery mechanism. Instead, it reveals fundamental strategies that reduce the mechanical cost of moving the CoM in any gait regardless of energy recovery mechanisms that may or may not be employed.

In steady speed locomotion, the limbs act primarily as struts that divert the path of the CoM in a collision-like interaction with the supporting substrate. Dynamic collisions, such as two balls colliding, exert forces abruptly, whereas the compliant legs of animals distribute forces over the duration of a step and over multiple steps within a stride. Nonetheless, the principles that govern redirection of colliding objects can also be applied to redirection of the CoM during locomotion. Our approach considers each instance of temporally distributed single or multiple foot contacts as a dynamic collision. No collision occurs, and hence no work is done on the CoM, when force and velocity vectors are perpendicular, as in a rolling wheel. But legged locomotion requires discrete footfalls that preclude a consistent perpendicular relationship of these two vectors. The intermittent foot contacts of legged locomotion result in relatively abrupt, collision-like changes in CoM direction that require mechanical work. Theoretical [4–8] and experimental studies in humans [9,10] provide a nascent understanding of collision mechanics in legged locomotion. These previous approaches apply a collision-based perspective to the CoM velocity vector and, in one case, leg impulse vectors [9]—whereas we determine the collision from the dynamically changing relationship between instantaneous CoM velocity and force vectors. Considering each instance of a stride, we apply a collision-based analysis to compare the CoM dynamics of goats and dogs across the three typical quadrupedal gaits—walk, trot and gallop. This approach bridges collision theory to experimental biomechanics and provides a way of quantifying collision reduction, a dynamic strategy that decreases the mechanical cost of locomotion.

2. Methods

As a measure of the collision-like interaction of the animal and its supporting substrate, we introduce the collision angle, which is determined by the angle between the CoM force and velocity vectors as their orientations change throughout the stride. Because the analysis uses three-dimensional vectors, this approach can be applied to sprawled as well as upright locomotion—allowing comparisons of animals as different as cockroaches and horses. Multi-legged animals use a diversity of gaits with the potential for more complex footfall patterns than bipedal striders, offering a greater range of collision strategies. In this study, three-dimensional collision angles were determined in dogs and goats during walking, trotting and galloping.

2.1. Subjects

Four dogs and four goats walked, trotted and galloped on a runway instrumented with force platforms and a motion capture system. Four trials were collected from each subject at each gait. The dogs and goats had a mean body mass of 30 and 31 kg, respectively, and a mean leg length of 0.42 and 0.39 m. These experiments were approved by Harvard University IACUC in Protocol 23-15.

2.2. Force measurement

A series of four force platforms was used to measure the total three-dimensional force exerted by all of the limbs throughout a stride. A pair of Kistler type 9286AA force platforms mounted with epoxy foot mouldings onto separate 3.2 cm thick granite slabs and a pair of AMTI BP400600HF force platforms bolted onto separate 2.5 cm thick steel base plates were set lengthwise into a trench in an indoor runway. Force data were sampled at 2400 Hz for 5 s, using a manual pre-trigger from the motion capture system. Data acquisition from the Kistler force platforms used a BioWare type 2812A1-3 A/D system (DAS1602/16 A/D board) operated using BioWare v. 3.0 software (Kistler Instruments Corp.). Data acquisition from the AMTI force platforms used two AMTI MSA-6 strain gage amplifiers with a National Instruments DAQCard 6036E and LabView v. 7.1 software.

2.3. Motion analysis

A Qualisys three-dimensional infrared system (four ProReflex MCUs) and Qualisys Track Manager v. 1.6 software were used for motion capture. Retroreflective polystyrene hemispheres (covered with 3M 7610WS High Gain Sheeting) were used to mark the dorsal spine at the ‘girth’ (posterior to the scapulae one-third the distance between limb girdles) and the thorax ventral to this point mid-way down the thorax on each side. The three-dimensional positions of these markers were recorded at 240 Hz. Three-dimensional motion capture was used to measure the initial CoM velocity. Thereafter, velocities throughout the stride were determined by integration of CoM accelerations from the force platforms.

2.4. Centre of mass power

The dot product of the total ground reaction force vector F and the CoM velocity vector V yields the instantaneous mechanical power of the limbs on the CoM F · V. Arampatzis et al. [11] showed substantially reduced variability in power at higher velocities using the dot product when compared with a commonly used method for determining CoM mechanical power (e.g. [3,12,13]). Other investigators have used the dot product of individual limb force on CoM velocity to determine the work expended by the limbs against one another, as well as on the CoM—referred to as the individual limbs method [14]. This is important in human walking, where the limbs do work against one another during simultaneous heel-strike and toe-off of the step transition. As the present method uses the total force of all limbs, summation of the work done by individual limbs could be greater than the mechanical work measured here, but not less. It is technically more difficult to isolate individual limb forces in the various gaits of multi-legged animals; hence, a combined limbs method is a more practical starting point in a broad survey of species and gaits.

2.5. Collision angle

The instantaneous collision angle ϕ is the angle between F and V, shifted by π/2 (equation 6). This phase shift allows ϕ to increase as the collision increases. The collision angle is computed by taking the absolute value of F · V, dividing by the magnitudes of F and V, and then taking the arcsine. The absolute value of F · V is taken because it is the deviation of these two vectors, independent of sign, that determines a collision. Instantaneous collision angles are determined throughout all contact periods of the stride. The overall collision angle Φ for a given stride can be determined by force and velocity-averaging ϕ over the stride period (equation 7). In a similar fashion, the stride velocity angle with respect to the horizontal Λ and the stride force angle with respect to the vertical Θ can be determined from instantaneous velocity and force angles, λ and θ (table 1 and figure 1a). Figure 1a is a simple planar illustration of force, velocity and collision angles representing isolated instances of two hypothetical strides. The use of weighted averages to determine Φ, Λ and Θ accounts for the variable magnitudes of the force and velocity vectors throughout the stride. For example, instantaneous force angles that occur at very low force during initial foot placement are weighted less, while instantaneous force angles that occur near maximum force of the stride are weighted more in accordance with their greater effect on CoM dynamics. The same reasoning applies to the weighted averaging of instantaneous collision angles and instantaneous velocity angles, although the magnitude of velocity fluctuates much less than force magnitude because the velocity vector is dominated by the forward component throughout the stride.

Table 1.

Parameters of a collision-based analysis.

Force vector (N)	F
velocity vector (m s−1)	V
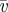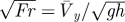dimensionless velocity (the square-root of Froude number), where h is the CoM height, g is the acceleration of gravity on the Earth and is the average forward velocity		equation 1
instantaneous force angle, where unit vector a is normal to the substrate and upward	θ = arccos (|F · a| / |F|)	equation 2
force angle determined by force-averaging over the stride period	Θ = ∑|F|θ/∑|F|	equation 3
instantaneous velocity angle, where unit vector b is parallel to the substrate and in the direction of travel	λ = arccos (|V · b| / |V|)	equation 4
velocity angle determined by velocity averaging over the stride period	Λ = ∑|V|λ/∑|V|	equation 5
instantaneous collision angle determined from the dot product of force on velocity. The arcsine represents a phase shift of π/2 to define an angle of zero when F⊥V so that ϕ is directly proportional to the collision. ϕ is undefined when F is 0 during flight periods	ϕ = arcsin (|F · V| / |F||V|)	equation 6
collision angle determined by force and velocity averaging over the stride period	Φ = ∑|F||V1ϕ/∑|F||V|	equation 7
mechanical cost of motion is equivalent to Φ when the small angle approximation (sin ϕ ≅ ϕ) of equation 6 is substituted into equation 7	CoMotmech = ∑|F ·V| / ∑|F||V|	equation 8
for small vertical and lateral oscillations		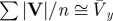equation 9
for small fore-aft and lateral forces, where m is body mass	∑|F|/n ≅ mg	equation 10
average CoM mechanical power is the summation of the absolute values of instantaneous power over the stride period divided by the number of samples	∑|F · V|/n	equation 11
mechanical cost of transport is equivalent to mechanical cost of motion when the conditions of equations 9 and 10 are met		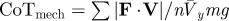equation 12
impulse angle over the stride period, where I is the impulse vector and unit vector a is normal to the substrate and upward	Ω = arccos (|I · a|/|I|)	equation 13

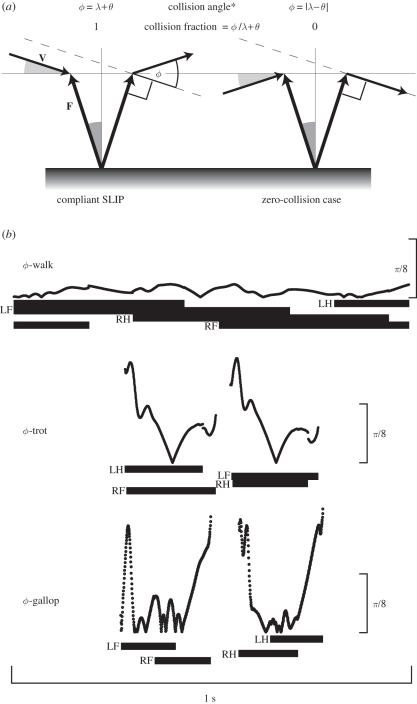
Figure 1.

(a) Planar illustrations of collision-based mechanics showing instantaneous angles. The force angle θ (equation 2; dark grey) is the magnitude of the angle between the force vector F and the vertical axis, and the velocity angle λ (equation 4; light grey) is the magnitude of the angle between the velocity vector V and the horizontal axis in the direction of travel. Collision angle ϕ is determined from the dot product of the force and velocity vectors (equation 6). The asterisk denotes trigonometric two-dimensional solutions to ϕ as these special cases are provided in an online supplement but only the equations of table 1 are used in our analysis. In these examples of compliant SLIP and idealized zero-collision cases, the magnitudes of all force and velocity angles are the same but their collision fractions represent opposite extremes. (b) Plots of instantaneous collision angle ϕ (in radians) versus time are drawn to the same scale for walking, trotting and galloping sample data from a dog. Footfall patterns are represented as horizontal bars beneath each plot with footfalls labelled as left hind (LH), left fore (LF), right hind (RH) or right fore (RF).

2.6. Collision fraction

A small Φ may be owing to a small Λ or Θ, a more nearly perpendicular orientation of F and V, or any combination of these. Collision reduction occurs when Φ is reduced by a more nearly perpendicular orientation of F and V throughout the stride and is quantified by the collision fraction. The collision fraction is the actual collision relative to potential collision, calculated as the quotient of stride collision angle and the sum of stride velocity and force angles: Φ/(Λ + Θ). Collision fraction is one in the case of a compliant spring-loaded inverted pendulum (SLIP), where braking force yields a non-perpendicular angle with downward velocity and propulsive force yields a non-perpendicular angle with upward velocity (figure 1a). This occurs whenever F and V are rotated in opposite directions from the vertical and horizontal axes. Whenever F and V are rotated in the same direction, collisions are reduced and the instantaneous collision fraction will be less than 1. In fact, collision fraction is 0 in an idealized case where F and V remain perpendicular throughout the stride (figure 1a). In order to connect a geometrical representation to our analysis, angles and collision fractions are illustrated at specific instances in figure 1a (lowercase symbols), whereas stride variables (uppercase symbols) are reported in the following results.

2.7. Statistics

The generalized linear model (JMP v. 8.0) included effects of species, gait, impulse angle (equation 13) and the interaction of impulse angle and gait. The last three effects were nested within species and were found to be highly significant (p < 0.001), except in the case of the velocity angle, where impulse angle and impulse angle × gait were non-significant (p > 0.05). In the relationship between CoT_mech and Φ for the complete dataset, the regression coefficient was determined by multiple regression of CoT_mech on Φ and impulse angle to account for any net braking or propulsion during the stride.

3. Results and discussion

As shown together with individual foot contacts in figure 1b, plots of instantaneous collision angle ϕ versus time reveal distinctly different patterns for walking, trotting and galloping. While examining these temporal patterns is not the focus of this report, they are provided to show the mapping of ϕ onto footfall diagrams. These plots illustrate that ϕ remains small throughout the walking stride and during most of the galloping stride—providing the basis of collision reduction, as we will show statistically in the following whole-stride analysis. In contrast, during trotting ϕ only approaches zero momentarily at mid-contact, when force is nearly vertical and velocity is nearly horizontal as the path of the CoM transitions from forward-downward to forward-upward—a pattern consistent with compliant SLIP mechanics (figure 1a).

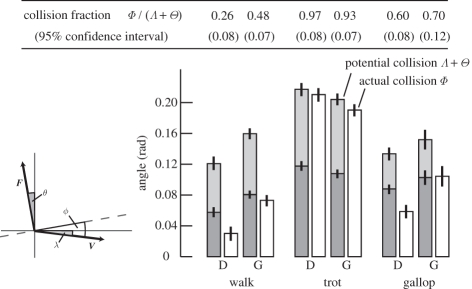
Our stride results indicate that goats and dogs employ collision-reduction strategies during walking and galloping but not during trotting. The collision angle Φ is two to seven times greater during trotting than during walking or galloping (p < 0.05; figure 2). Not only is Φ greatest during trotting, but collision fractions above 0.9 indicate little to no collision reduction—the actual collision Φ is almost equal to the potential collision Λ + Θ during trotting (figure 2). In contrast, Φ is substantially less than Λ + Θ during walking and galloping. Collision fractions of 0.2–0.5 during walking represent pronounced collision reduction (a defining feature of this gait) and collision fractions of 0.6–0.7 during galloping represent moderate collision reduction. Walking, trotting and galloping collision fractions are significantly different from one another in all cases (p < 0.05; figure 2). Interspecific differences in Φ are significant in all gaits (p < 0.05, figure 2). Φ is lower in dogs than goats during walking and galloping but that pattern is reversed during trotting. Collision fraction is significantly lower in dogs during walking but interspecific differences in collision fraction during trotting and galloping are non-significant (p > 0.05).

Figure 2.

Stride force (Θ, dark grey), velocity (Λ, light grey) and collision (Φ, unfilled regions) angles for all three gaits of dogs (D) and goats (G) were determined according to the equations of table 1. (A planar representation of instantaneous collision angles is provided for reference.) Vertical lines indicate 95% confidence intervals of each angle. Collision fraction is given by Φ/Λ + Θ, representing the actual/potential collision. Smaller collision fractions indicate more collision reduction. All angles are steady speed values predicted by the generalized linear model at an impulse angle of zero (no net horizontal acceleration of the CoM). Mean forward velocities of each gait, normalized according to equation 1, were 0.62 (walk), 1.42 (trot) and 2.72 (gallop).

The relatively large collision angles and collision fractions during trotting are consistent with the compliant SLIP model represented in figure 1a. Given the greater Φ during trotting, one might also expect a greater metabolic cost of transport. However, at the preferred speed of each gait, metabolic cost is remarkably similar for walking, trotting and galloping of horses [15] and presumably this holds for other quadrupeds, as should be verified using future studies. A comparable metabolic cost of trotting may be partially explained by elastic storage and return of mechanical energy in muscle–tendon systems of the limb (e.g. [16,17]). This is in good agreement with the leg compression and re-extension characterizing a compliant SLIP model [18–21]. A somewhat greater Φ might be permitted in a compliant SLIP mechanism because mechanical energy can be stored elastically and returned later in the trotting step. In animals with suitably compliant legs and structures capable of storing elastic strain energy, such as long tendons, this may explain why trotting allows greater collision angles and shows little to no collision reduction. Although a collision-based approach characterizes the mechanics that could favour elastic energy storage, direct in vivo muscle–tendon measurements and/or detailed musculoskeletal models are needed to demonstrate elastic energy storage and return.

Collision angle Φ is closely related to the mechanical cost of transport CoT_mech (equation 12), a commonly used, dimensionless metric of locomotor mechanical cost. CoT_mech is the CoM mechanical work expended to move a unit body weight a unit distance in the direction of travel [3] and depends only upon the average CoM mechanical power (equation 11), body weight and mean forward velocity during the stride. To explain the link between Φ and CoT_mech, we introduce the mechanical cost of motion CoMot_mech (equation 8), the dimensionless cost to move the CoM along its actual three-dimensional path (rather than just its forward translation). Neither the traditional metric CoT_mech nor CoMot_mech include non-CoM work, such as the mechanical work expended to move body segments relative to each other. Substituting the small angle approximation of equation 6 into equation 7 shows that Φ is approximately equal to CoMot_mech when ϕ is less than about 0.3 rad.

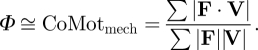3.1

If the CoM path is only moderately undulating, then the magnitude of the three-dimensional velocity vector is approximately the mean forward velocity (equation 9) and the magnitude of the three-dimensional force vector is approximately body weight (equation 10); hence,

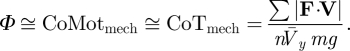3.2

These relationships reveal the physical basis of CoT_mech, whereas the dimensionless expression of CoT_mech was originally determined simply by dimensional analysis [22,23]. The mechanical cost of moving the CoM can now be conceptualized in light of the collision angle, which is the reason that mechanical work is required in the first place.

Our experimental results from goats and dogs show approximate equivalence of Φ and CoT_mech in walking, trotting and galloping: CoT_mech=1.00Φ + 0.003. The regression coefficient is neither significantly different from 1, nor is the intercept significantly different from 0 (p > 0.05; §2.7). Given the general conditions of equations 9 and 10, this result is expected for most animals with upright limb posture, such as goats and dogs. These conditions may be violated in lateral undulating gaits of sprawled runners, or gaits such as pronking (four-limb bouncing as a display of vigour) with extreme vertical CoM motion. If the three-dimensional CoM path is substantially undulating, CoT_mech will be greater than CoMot_mech because CoT_mech takes into account only the forward progression of the CoM.

In addition to facilitating the study of comparative, developmental or pathological locomotion, the collision angle and collision fraction can be applied to the mechanics of legged machines. As long as force and velocity vectors can be measured, the interaction of a robot's CoM with the environment can be analysed in exactly the same way as that of a dog or goat. Given that legged robots generally require an order of magnitude more CoM mechanical energy to move their body weight a given distance than do their biological counterparts [24], quantifying the collision-based mechanics responsible for this elevated mechanical cost of transport can lead to improved economy. One of the few comparisons available considers CoT_mech in walking humans (0.05), passive dynamic bipedal walking robots (0.055–0.07) and a humanoid bipedal robot (Honda ASIMO, approx. 1.6) that typifies the economical disparity between conventional robotic and biological systems [23]. Our ability to analyse and interpret the overall collision mechanics and discrete collision events throughout the stride will help determine the source of mechanical cost and lead to the development of economical-legged machines.

It is clear that galloping and especially walking show collision reduction along with a decreased Φ compared with trotting. Accordingly, CoT_mech is lower in walking and galloping than in trotting but all three gaits might ultimately have a similar metabolic cost of transport if passive springs are used to store and return elastic strain energy during trotting and to some extent during galloping. It should also be noted that myriad other factors such as cycling of the legs [25], individual limb work during stance [10,14], musculoskeletal transmissions and muscle contractile dynamics can influence the metabolic cost of transport. Nonetheless, differences in Φ and, therefore, CoT_mech between dogs and goats suggest that dogs walk and gallop more economically than goats because they are expending less mechanical energy in their interactions with the environment. In future studies, metabolic data can tell us if Φ and CoT_mech do in fact represent differences in the overall economy, and mechanical simulations or detailed musculoskeletal modelling may tell us why. A fundamental understanding of animals' interactions with their environments provided by the collision angle and collision fraction will help us identify and interpret functional similarities and differences in the expansive diversity of terrestrial walkers and runners.

We have demonstrated significant differences in Φ between gaits and between two mammals of similar size; yet, few studies have compared CoT_mech at a gait-specific or interspecific level. Prior experimental work has focused on the size invariance of CoT_mech in animals spanning five orders of magnitude from 1 g arthropods to 100 kg mammals [26], supporting the [22] prediction that CoT_mech should be independent of body mass. For example, an empirical equation based upon a large comparative dataset predicts a CoT_mech of approximately 0.11 across five orders of magnitude in body size [26,27]. This result is on par with our findings and falls between our gait-specific values of Φ (figure 2). Without a collision-based analysis, however, collision reduction could not be evaluated previously. The collision angle and collision fraction can now be used to uncover fundamental patterns across size, species, and gait, providing a common context for understanding locomotion.