Abstract
Flagella-generated fluid stirring has been suggested to enhance nutrient uptake for sufficiently large micro-organisms, and to have played a role in evolutionary transitions to multicellularity. A corollary to this predicted size-dependent benefit is a propensity for phenotypic plasticity in the flow-generating mechanism to appear in large species under nutrient deprivation. We examined four species of volvocalean algae whose radii and flow speeds differ greatly, with Péclet numbers (Pe) separated by several orders of magnitude. Populations of unicellular Chlamydomonas reinhardtii and one- to eight-celled Gonium pectorale (Pe ∼ 0.1–1) and multicellular Volvox carteri and Volvox barberi (Pe ∼ 100) were grown in diluted and undiluted media. For C. reinhardtii and G. pectorale, decreasing the nutrient concentration resulted in smaller cells, but had no effect on flagellar length and propulsion force. In contrast, these conditions induced Volvox colonies to grow larger and increase their flagellar length, separating the somatic cells further. Detailed studies on V. carteri found that the opposing effects of increasing beating force and flagellar spacing balance, so the fluid speed across the colony surface remains unchanged between nutrient conditions. These results lend further support to the hypothesized link between the Péclet number, nutrient uptake and the evolution of biological complexity in the Volvocales.
Keywords: phenotypic plasticity, evolution, Volvox, flagella, fluid dynamics, nutrient uptake
1. Introduction
A fundamental subject in evolutionary biology is the evolutionary transition from unicellular organisms to multicellular ones, and the accompanying cellular differentiation and specialization [1,2]. Not surprisingly for micro-organisms living in an aqueous environment, many of the important factors are physical, involving diffusion and mixing, for the exchange of molecular species with the environment is one of the most basic factors of life. Progress on this important evolutionary issue therefore involves not only studies of molecular and genetic aspects of multicellular life, but also the introduction of techniques from transport theory to address the allometric scaling of metabolic activity with size [3].
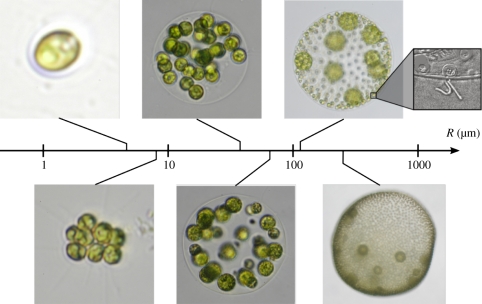
At least since the work of Weismann [4], it has been recognized that a particularly interesting class of organisms to study for insights into the origins of multicellularity is composed of the alga Volvox and its relatives. Volvocalean green algae are motile micro-organisms consisting of biflagellated cells. They range from the unicellular Chlamydomonas to colonies made of cells with no cellular differentiation, such as Gonium (one to eight cells), Eudorina (4–64 cells) and Pleodorina (16–256 cells), to the multicellular Volvox comprising 500–50 000 cells with specialization in reproductive and vegetative functions, i.e. germ–soma separation (figure 1; [6–8]). In the multicellular forms, each of the Chlamydomonas-like somatic cells is found at the surface of the extracellular matrix (ECM), with its two flagella oriented outwards, while the germ cells lose their flagella and grow on the inside of the colony (figure 1). The somatic cells may be connected through cytoplasmic bridges, as in Volvox barberi, or unconnected, as in Volvox carteri. Germ–soma separation in Volvox species such as V. carteri and V. barberi has evolved independently from different ancestors [9–13]. In short, Volvocales comprise a group of closely related lineages with different degrees of cell specialization which seem to represent ‘alternative stable states’ [14] that reflect clearly the stages of the transition to multicellularity and cellular differentiation.
Figure 1.
A selection of the volvocalean green algae, arranged according to organism radius R (after [5]). In order of increasing size, they are unicellular C. reinhardtii, undifferentiated G. pectorale and Eudorina elegans, followed by the soma-differentiated Pleodorina californica and germ–soma differentiated V. carteri and V. barberi. When two cell types can be recognized, the smaller are the somatic cells, the larger are the germ cells or daughter colonies.
Volvocales are found in quiet, standing waters of transient vernal puddles or in permanent lakes when thermal stirring stops and the lake becomes stratified [6,15]. Because they are negatively buoyant, these organisms need flagellar beating to avoid sinking and to reach light and nutrients [7,8]. In addition to providing motility, flagella may also be important for generating advective flows that can increase nutrient uptake. If the Volvocales were to rely on diffusion alone to acquire nutrients from a quiescent fluid environment, the total rate of uptake would scale linearly with organism size. In contrast, the metabolic needs of Volvocales that form spheroids grow at least quadratically [5], implying that there is a bottleneck organism size beyond which diffusion alone is insufficient to feed the cells. This theoretical work, together with the empirical evidence given by Solari et al. [16], supports the idea that advective flows are important for enhancing nutrient uptake in the larger Volvocales. Changes in the flagellar apparatus between unicellular species and species that form colonies [17] also indicate that the demands on the flagella change with organism size. The emerging hypothesis is therefore that, for larger Volvocales, the collective beating of flagella not only yields motility, but also improves the molecular transport of nutrients, waste products and chemical messengers.
To quantify this hypothesis, we note that the Volvocales, along with most other micro-organisms, live in a world of Reynolds number Re ≪ 1 [18,19]. In this ‘Stokes flow’ regime, motion is dominated by viscosity, fluid flows are linear and time reversible and nutrient transport is usually dominated by diffusion. However, on the surface of a Volvox colony, the collective beating of many closely spaced flagella can lead to fluid flows of sufficiently high speeds that nutrient transport by advection may replace diffusion as the most important mechanism. The relative importance of these transport processes can be quantified by first defining a typical fluid velocity U, length scale L and diffusion constant D (D ∼ 2 × 10−5 cm2 s−1 for O2 is typical for small molecules). Then, a dimensionless ratio of the time scale for diffusion (tdiff = L2/D) and advection (tadv = L/U), known as the Péclet number (Pe = tdiff/tadv = UL/D), serves to characterize the relative importance of the two processes. If Pe < 1, diffusion is faster than the transport of molecules by advection via the flowing medium, indicating that an organism does not need to invest in flagellar beating to increase nutrient uptake. If however Pe > 1, advection through collectively generated flows may be important. For Volvox colonies, the flagellar beating leads to Pe ≫ 1, while for the unicellular Chlamydomonas Pe ∼ 0.1 [16]. Self-generated flows (figure 2), produced by hundreds or thousands of somatic cells arrayed on the surface of Volvox, may thus free these large spherical colonies from the constraints of diffusion-limited nutrient uptake, facilitating the transition to multicellularity and germ–soma differentiation.
Figure 2.

Volvox carteri held by a micropipette, with streamlines superimposed. Streamlines were obtained from a map of the flow field by particle imaging velocimetry. The flows, driven solely by the somatic cells' flagella at the surfaces of the colonies, extend outward by several colony diameters. The magnitude of the velocities near the colony can reach several hundred micrometres per second, and the regular, smooth flow from anterior to posterior can lead to enhanced acquisition and discharge of metabolites (as compared with diffusion in a quiescent environment), which is likely to be crucial for metabolism and productivity. Scale bar, 200 µm.
If the larger Volvocales have come to depend upon fluid flow generated by beating flagella for enhanced nutrient uptake, it stands to reason that conditions of nutrient deprivation might trigger changes in the motility apparatus to mitigate such an environmental stress. On the other hand, for much smaller organisms like Chlamydomonas and Gonium, such effects would not be expected. This type of response would be an example of phenotypic plasticity, defined as the production of multiple phenotypes from a single genotype, depending on environmental conditions [20]. Phenotypic alterations in responses to biotic and abiotic factors have been well documented in a wide variety of organisms (e.g. for plants, see [20]). For example, when food is scarce, planktotrophic echinoderm larvae (plutei) produce longer food-gathering structures than when food is abundant [21].
Here we report evidence in favour of the hypothesis of Péclet-number-dependent phenotypic plasticity. This evidence was obtained by growing populations of four Volvocales species of very different size (Chlamydomonas reinhardtii and Gonium pectorale representing the low-Pe species, and germ–soma differentiated V. carteri and V. barberi representing the high-Pe species) in diluted and normal media. Standard microscopy and high-speed imaging were used to determine any phenotypic responses of the flagella and of the overall organism morphology. We found that the two Volvox species make an investment into increasing collective flagellar beating during nutrient deprivation, whereas under those same conditions C. reinhardtii and G. pectorale do not.
2. Material and methods
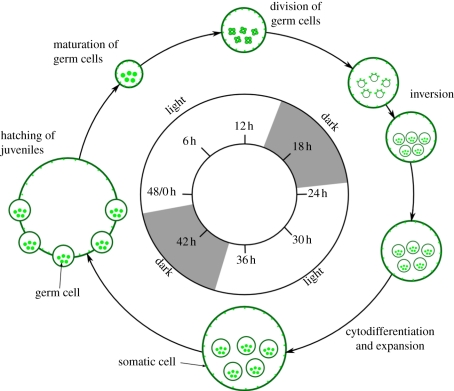
Populations of V. carteri f. nagariensis EVE strain (kindly provided by D. L. Kirk), V. barberi (Carolina Supplies, cat. no. 152660), C. reinhardtii (UTEX 89) and G. pectorale (UTEX LB826) were synchronized in test tubes with 20 ml of standard Volvox medium (SVM; [22]), and illuminated by homogeneous cool white light [approx. 1000 foot candles; fc (1fc = 10.764 lux)] in a daily cycle of 16 h of light (at 28°C) and 8 h of darkness (at 26°C). Under these conditions, the asexual life cycle of C. reinhardtii and G. pectorale has a 24 h generation time; cells grow during the light period, perform multiple divisions in the dark and daughter cells and colonies (for Gonium) are released when light returns. The asexual life cycle of V. barberi and V. carteri takes 48 h under these conditions, and is shown for V. carteri in figure 3.
Figure 3.
Life cycle of V. carteri (after [6]). When synchronized, V. carteri completes one asexual life cycle in 48 h. Colonies hatch 2 h into the light period and germ cells continue to grow until they begin multiple divisions towards the end of the light period. The divisions take approximately 7 h, and are followed by the inversion process that forms the daughter colonies inside the mother colony before the beginning of the next light period. The daughter colonies grow inside the mother colony for 24 h and hatch the next day.
To check for phenotypic plasticity, individuals were grown in two different nutrient concentrations as follows. From a synchronized population, just after individuals hatched (3, 6, 2 and 2 h into the light period for V. carteri, V. barberi, C. reinhardtii and G. pectorale, respectively), individuals were harvested by slow centrifugation, transferred to distilled water, centrifuged again and randomly separated into two subpopulations: one placed in full-strength SVM and the other in a 10−1 dilution of SVM. For each species and for both nutrient treatments, the organism concentration was adjusted to approximately 104 cells ml−1. The organism concentrations were therefore 104 C. reinhardtii cells ml−1, approximately 1400 G. pectorale colonies ml−1 (colonies had on average seven cells), five V. carteri spheroids ml−1 (organisms had on average 2000 cells) and two V. barberi spheroids ml−1 (organisms had on average 5000 cells). Measurements were performed after the organisms were grown in the diluted and undiluted SVM for 8 h. During these 8 h, and the ensuing measurement period, all species were in their growth phase. During the experiments, cellular division did not take place in any species, except in V. barberi. In contrast to the other species, in which the reproductive cells grow about 2n-fold in size and then undergo a rapid series of n synchronous divisions (the ‘palintomic’ ancestral developmental programme), the reproductive cells of V. barberi have a derived developmental programme and perform binary fission to produce daughter colonies [13,23,24].
In all experiments, digital images were taken at high magnification and analysed with image processing software (MetaMorph, Universal Imaging Corp., PA, USA) to measure flagellar lengths, diameters of cells and Volvox spheroids and the number and diameter of reproductive and somatic cells. Cell and spheroid diameters were measured by taking the mean of two orthogonal diameters. The number of somatic cells per unit area on the surface of a Volvox spheroid was calculated by taking the mean somatic cell concentration from two opposite sides of the spheroid. A multiple linear regression (MLR) analysis was performed (JMP software; SAS Institute, Cary, NC, USA) using indicator variables to account for the nominal factors. Continuous variables were used to account for factors such as flagellar length and colony cell number.
2.1. Initial experiments on the phenotypic plasticity of the organism and flagellar sizes
Measurements were performed at two times (t1 and t2) in the life cycle of the organisms: t1 = just before the organisms were harvested (as detailed above), and t2 = 8 h later on the same day. For these measurements, Lugol solution was used to fix 1 ml samples of all organisms, except V. barberi. Samples of V. barberi were fixed with formalin instead of Lugol solution because the Lugol solution made their flagellar curl. Spheroid size, cell size and flagellar length were measured for 10 individuals for each nutrient treatment and species. For G. pectorale, measurements were averaged from two cells in each colony; for Volvox species, measurements were averaged on two germ cells and five somatic cells in each colony. The experiments were repeated three times, yielding for each species data on n = 30 organisms at t1 and n = 60 organisms between the two nutrient treatments at t2.
2.2. Experiments for propulsion force measurement of C. reinhardtii and G. pectorale
To check for differences in propulsion force between the nutrient treatments, upward swimming Vup and sedimentation Vsed speeds were measured as detailed in Solari et al. [8] using the apparatus developed by Drescher et al. [25]. The growth conditions were as described in §2.1, but with a lower light intensity (approx. 600 fc) as the cultures for these experiments were grown in a different country and a different diurnal chamber that did not allow a higher light intensity. For each experiment, we measured Vup and Vsed of 30 individuals and the radius R of 15 individuals. As described in Solari et al. [8], the propulsion force Fp exerted by an individual swimming vertically upward at velocity Vup is balanced by the sum of the drag force and gravity, Fp = 6πηR(Vup + Vsed). By using the population average of Vup, Vsed and R in this equation, we obtain the population average of Fp for the two treatments. The experiments were repeated four times, yielding for each species data on n = 8 populations between the two nutrient treatments at t2.
2.3. Detailed experiments on the phenotypic plasticity of V. carteri
Flagellar lengths, beating frequencies and flagella-driven flow speeds of V. carteri were measured in vivo, while holding the spheroid in place by micropipette aspiration [16], as shown in figure 2. Spheroid sizes, cell sizes and flagellar lengths were measured as described in §2.1, but only at t2. The growth conditions were as described in §2.1, but with a lower light intensity (approx. 600 fc) as in §2.2. Measurements were performed in the 2 h period beginning at t2. This period was further divided into four sub periods of 30 min; in each sub period, measurements on five spheroids from the same nutrient treatment were performed, and the sub periods of measurements from each treatment were alternated (e.g. A/B/A/B or B/A/B/A). Flagella-driven flows around V. carteri were visualized with 1 µm micro-spheres (Invitrogen Corp., CA, USA), recorded with a high-speed camera (Phantom v. 5.1, Vision Research, NJ, USA) and measured using particle image velocimetry (FlowManager, Dantec Dynamics, Skovlunde, Denmark). For the measurements of the flow speed, a V. carteri spheroid was caught such that the micropipette aspiration point was approximately on the equator. The micropipette was then rotated until the Volvox anterior–posterior axis was in the focal plane. The flow speed was read out at the Volvox equator on the side opposite the aspiration point, just above the spheroid surface (10 µm above the flagellar tips), as the flow speed reaches a maximum there. This maximum speed U can be related mathematically to the force the flagella generate [5]. Flagellar beating frequencies were determined by averaging across 10 beating periods, and averaging across five somatic cells around the Volvox equator. The experiment was repeated four times, yielding data on n = 80 V. carteri colonies between the two nutrient treatments.
For each Volvox colony, the measured peak fluid speed U was used to estimate the total force F that all flagella exert on the fluid. Using a mathematical model, Short et al. [5] found that F = 64ηRU/3, where R is the Volvox radius and η is the viscosity of water. Taking into account that the flagellar force is applied to the fluid from the surface of a sphere, the net forward thrust can be shown to be Fp = πF/4 [26]. The measured colony, somatic and germ cell radii, and the calculated Fp, were then used to estimate the upward swimming speed Vup for each colony. As described in detail in Solari et al. [8], Vup = (Fp − gΔM)/6πηR, where g is the acceleration of gravity and ΔM is the difference in mass between the cells and the displaced water, assuming that the ECM is approximately neutrally buoyant (measured cell densities were taken from [27]).
3. Results and discussion
Table 1 gives results from the initial experiments on phenotypic differences in populations that were grown in normal and diluted media, at a light intensity of 1000 fc. Table 2 contains the results from the more detailed experiments on V. carteri, in which populations were grown at 600 fc. It also contains the swimming and sedimentation speeds, as well as the thrust force calculations of C. reinhardtii and G. pectorale. Figure 4 illustrates the effects of the nutrient deprivation on V. carteri. Details of the MLR models that were used to quantify phenotypic alterations are given in tables 3 and 4.
Table 1.
Data from populations grown at a light intensity of 1000 fc, i.e. experiment described in §2.1, in the format average ± s.e. The number of organisms n that make up an average value is n = 30 in each case. The times t1 and t2 at which measurements were conducted are 1–2 h after hatching and 8 h later, respectively. The difference between treatments is given in absolute terms as the difference between the measurements in normal and diluted media at t2, as obtained with an MLR model. The statistical p-value was obtained from the MLR model. A § marks statistically non-significant differences between treatments. Details of the MLR model used here are given in table 3. The symbols used are cell radius rC, and flagellar length l, and Volvox spheroid radius R, germ cell radius rG, somatic cell radius rS and somatic cell concentration C. The average cell number of a G. pectorale colony was 7.0 ± 0.28. The average total number of somatic cells of a V. carteri colony was 1970 ± 56, and the average number of germ cells was 11.9 ± 0.2. The average total number of somatic cells of a V. barberi colony was 4975 ± 336, and the average number of germ cells was 13.9 ± 0.5.
| t1: normal medium | t2: normal medium | t2: diluted medium | difference between treatments |
|||
|---|---|---|---|---|---|---|
| absolute | (%) | p-value | ||||
| C. reinhardtii | ||||||
| rC (µm) | 3.43 ± 0.07 | 5.24 ± 0.20 | 4.73 ± 0.16 | −0.36 ± 0.18 | −6.9±3.4 | 0.0431 |
| l (µm) | 10.4 ± 0.33 | 9.07 ± 0.40 | 9.11 ± 0.34 | § | § | 0.7362 |
| G. pectorale | ||||||
| rC (µm) | 4.66 ± 0.11 | 5.51 ± 0.15 | 5.03 ± 0.16 | −0.34 ± 0.16 | −6.2±2.9 | 0.0204 |
| l (µm) | 17.17 ± 1.29 | 17.75 ± 0.67 | 19.06 ± 0.49 | § | § | 0.4140 |
| V. carteri | ||||||
| R (µm) | 155 ± 3.9 | 204 ± 3.9 | 222 ± 4.0 | 14.6 ± 4.86 | 7.2 ± 2.4 | 0.0031 |
| rG (µm) | 24.1 ± 0.76 | 30.1 ± 0.40 | 29.3 ± 0.34 | −1.16 ± 0.63 | −3.9 ± 2.1 | 0.0691 |
| rS (µm) | 4.04 ± 0.09 | 4.89 ± 0.09 | 4.37 ± 0.07 | −0.46 ± 0.09 | −9.4 ± 1.8 | <0.0001 |
| l (µm) | 14.9 ± 0.71 | 18.2 ± 0.50 | 20.45 ± 0.46 | 2.14 ± 0.68 | 11.7 ± 3.7 | 0.0021 |
| C (cells/103 µm2) | 6.91 ± 0.49 | 3.68 ± 0.29 | 3.17 ± 0.18 | −0.65 ± 0.33 | −17.7 ± 9.1 | 0.0552 |
| V. barberi | ||||||
| R (µm) | 217 ± 5.4 | 279 ± 12.4 | 326 ± 7.2 | 59.1 ± 11.0 | 21.1 ± 3.9 | <0.0001 |
| rG (µm) | 14.0 ± 1.17 | 27.3 ± 1.21 | 29.7 ± 1.68 | § | § | |
| rS (µm) | 5.19 ± 0.22 | 7.02 ± 0.17 | 6.86 ± 0.10 | −0.77 ± 0.41 | −11.0 ± 5.8 | 0.0712 |
| l (µm) | 22.9 ± 0.54 | 28.6 ± 1.96 | 39.0 ± 2.17 | 9.93 ± 2.56 | 34.7 ± 9.0 | 0.0006 |
| C (cells/103 µm2) | 9.08 ± 1.01 | 5.42 ± 0.31 | 3.22 ± 0.31 | −1.20 ± 0.57 | −22.1 ± 10.5 | 0.0341 |
Table 2.
Data from C. reinhardtii, G. pectorale and V. carteri populations grown at a light intensity of 600 fc, i.e. experiments described in §§2.2 and 2.3. The format and notation are as in table 1. Additional symbols are the flagellar beating frequency f, the peak flow speed at the equator U (described in §2), the net force that all flagella exert on the fluid F, the propulsion force Fp, the upward swimming speed Vup and the sedimentation speed Vsed. For each measurement on V. carteri, n = 40 colonies were used. For measurements on C. reinhardtii and G. pectorale, n = 120 individuals were used for Vup and Vsed, and n = 4 populations for Fp. Details of the MLR model used here are given in table 4. The average number of somatic cells of a V. carteri colony was 1557 ± 50, and the average number of germ cells was 10.0 ± 0.2. In these experiments, the average number of cells in G. pectorale colonies was 4.1 ± 0.19.
| t2: normal medium | t2: diluted medium | difference between treatments |
|||
|---|---|---|---|---|---|
| absolute | (%) | p-value | |||
| C. reinhardtii | |||||
| Vsed (µm s−1) | 6.5 ± 0.24 | 3.7 ± 0.14 | −2.75 ± 0.27 | −42.3 ± 4.2 | <0.0001 |
| Vup (µm s−1) | 43 ± 1.9 | 54 ± 2.6 | 11.41 ± 3.32 | 26.5 ± 7.7 | 0.0007 |
| Fp (pN) | 5.59±0.57 | 5.13 ± 0.39 | § | § | 0.5367 |
| G. pectorale | |||||
| Vsed (µm s−1) | 10.0 ± 0.39 | 8.9 ± 0.37 | −1.11 ± 0.54 | −11.1 ± 5.4 | 0.0400 |
| Vup (µm s−1) | 33 ± 1.3 | 37 ± 1.1 | 4.21 ± 1.76 | 12.8 ± 5.3 | 0.0176 |
| Fp (pN) | 8.89 ± 0.93 | 9.06 ± 0.60 | § | § | 0.8847 |
| V. carteri | |||||
| R (µm) | 144 ± 3.5 | 174 ± 3.9 | 27.2 ± 3.32 | 18.9 ± 2.3 | <0.0001 |
| rG (µm) | 26.7 ± 0.56 | 27.1 ± 0.53 | § | § | 0.6384 |
| rS (µm) | 4.63 ± 0.06 | 4.40 ± 0.05 | −0.25 ± 0.07 | −5.4 ± 1.5 | <0.0001 |
| l (µm) | 17.49 ± 0.19 | 19.49 ± 0.26 | 0.93 ± 0.25 | 5.3 ± 1.4 | <0.0001 |
| C (cells/103 µm2) | 8.93 ± 0.44 | 6.21 ± 0.29 | −2.57 ± 0.34 | −28.8 ± 4.0 | <0.0001 |
| f (Hz) | 27.4 ± 0.27 | 26.3 ± 0.36 | 0.66 ± 0.45 | 2.4 ± 1.6 | 0.1521 |
| U (µm s−1) | 436 ± 11.2 | 435 ± 9.5 | § | § | 0.4232 |
| F (pN) | 1932 ± 63.6 | 2157 ± 55.4 | 211 ± 51 | 10.9 ± 2.6 | <0.0001 |
| Vup (µm s−1) | 274 ± 14.5 | 300 ± 12.3 | 26 ± 14.4 | 9.5 ± 5.3 | 0.0718 |
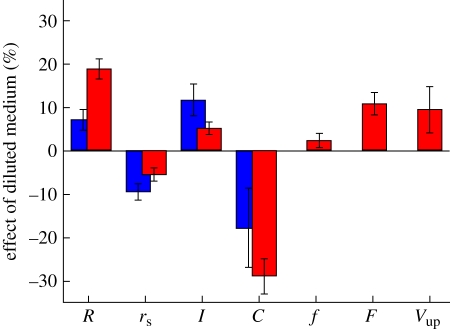
Figure 4.
Bar chart showing the percentage changes of properties of V. carteri colonies grown in diluted medium, with respect to those grown in normal medium. The two colours indicate results from the different experiments: table 1 in blue (1000 fc), and table 2 in red (600 fc). Error bars show the standard error. The symbols used are the spheroid radius R, somatic cell radius rS, flagellar length l, somatic cell concentration C, flagellar frequency f, net force of flagella on the fluid F, and the upward swimming speed Vup.
Table 3.
Model results for the MLR analysis of experiments conducted with populations grown at a light intensity of 1000 fc, i.e. experiment described in §2.1. The notation is as in table 1. Additional symbols are the total number of flagellated cells in colonies NS, the change Δ of the measured quantity over 8 h in normal medium and Δ + δ in diluted medium. Data analysis takes the form d = d0 + Σi aivi + Σi biNS,i, with dummy indicator variables vi = 0, 1 to take account of nominal factors such as the medium treatment, and a, b and d0 are parameters of the model. A § marks statistically non-significant terms. Differences between replicated experiments were taken into account as a nominal factor and are not reported. In G. pectorale, we found that colonies with more cells had smaller cells with longer flagella regardless of treatment. In Volvox, we found that colonies with a larger number of flagellated cells NS had a larger radius R and a larger cell concentration per unit area C. In V. barberi colonies with more cells, somatic cells were smaller. Because V. barberi germ cells perform binary fission, it was not possible to measure the germ cell size accurately.
| d0 | Δ | δ | NS | r2 | F-ratio | |
|---|---|---|---|---|---|---|
| C. reinhardtii | ||||||
| rC (µm) | 3.43 ± 0.12 | 1.46 ± 0.18 | −0.36 ± 0.18 | — | 0.58 | 29 |
| l (µm) | 10.18 ± 0.28 | −1.50 ± 0.39 | § | — | 0.43 | 16 |
| G. pectorale | ||||||
| rC (µm) | 5.58 ± 0.44 | 0.82 ± 0.25 | −0.34 ± 0.16 | −0.14 ± 0.06 | 0.45 | 21 |
| l (µm) | § | § | § | 0.57 ± 0.25 | 0.17 | 5 |
| V. carteri | ||||||
| R (µm) | 126 ± 8.1 | 46 ± 5.4 | 14.6 ± 4.86 | 0.013 ± 0.003 | 0.65 | 41 |
| rG (µm) | 23.2 ± 0.53 | 6.1 ± 0.70 | −1.16 ± 0.63 | § | 0.53 | 29 |
| rS (µm) | 3.81 ± 0.08 | 0.79 ± 0.10 | −0.46 ± 0.09 | § | 0.58 | 34 |
| l (µm) | 14.28 ± 0.58 | 3.03 ± 0.77 | 2.14 ± 0.68 | § | 0.48 | 23 |
| C (cells/103 µm2) | 3.07 ± 0.56 | −2.88 ± 0.37 | −0.65 ± 0.33 | 0.021 ± 0.0002 | 0.69 | 48 |
| V. barberi | ||||||
| R (µm) | 170 ± 15.0 | 60 ± 10.5 | 59.1 ± 11.0 | 0.009 ± 0.002 | 0.82 | 74 |
| rS (µm) | 6.11 ± 0.28 | 1.88 ± 0.20 | −0.39 ± 0.21 | −0.0003 ± 0.0001 | 0.82 | 109 |
| l (µm) | 24.80 ± 3.51 | 5.80 ± 2.46 | 9.93 ± 2.56 | § | 0.63 | 22 |
| C (cells/103 µm2) | 4.99 ± 0.93 | −3.85 ± 0.65 | −1.20 ± 0.57 | 0.0008 ± 0.0002 | 0.81 | 65 |
Table 4.
Model results for the MLR analysis (as explained in table 3) of experiments described in §§2.2 and 2.3 conducted with populations of V. carteri, C. reinhardtii and G. pectorale grown at a light intensity of 600 fc. The notation is as in table 3. For V. carteri, the continuous variable T ranges from 1 to 4 to account for the four intervals of 30 min where data were recorded. A § marks statistically non-significant terms. As in the previous analysis, an increase in NS increases R and C. Moreover, we found that colonies with more cells had smaller rS, larger U and larger F. In the 2 h measurement window, the colony spheroid, germ cells and flagella continued growing and the cell concentration continued decreasing significantly with time. Interestingly, the flagellar length l was significantly smaller when the cell concentration was large, regardless of treatment. The flagellar beating frequency f was found to be lower when the flagellar length was larger.
| d0 | δ | NS (10−3) | T | C | l | r2 | F-ratio | |
|---|---|---|---|---|---|---|---|---|
| C. reinhardtii | ||||||||
| rC (µm) | 5.90 ± 0.11 | −1.25 ± 0.16 | — | — | — | — | 0.42 | 19 |
| Vsed (µm s−1) | 7.18 ± 0.35 | −2.75 ± 0.27 | — | — | — | — | 0.32 | 56 |
| Vup (µm s−1) | 42.8 ± 2.45 | 11.41 ± 3.32 | — | — | — | — | 0.05 | 12 |
| G. pectorale | ||||||||
| rC (µm) | 6.61 ± 0.18 | −0.31 ± 0.14 | −220 ± 30 | — | — | — | 0.31 | 11 |
| Vsed (µm s−1) | 11.0 ± 0.39 | −1.11 ± 0.54 | § | — | — | — | 0.02 | 4 |
| Vup (µm s−1) | 32.5 ± 1.35 | 4.21 ± 1.76 | § | — | — | — | 0.02 | 6 |
| V. carteri | ||||||||
| R (µm) | 112 ± 7.6 | 27.2 ± 3.32 | 16 ± 4 | 5.29 ± 1.49 | — | — | 0.75 | 37 |
| rG (µm) | 26.0 ± 0.70 | § | § | 0.40 ± 0.26 | — | — | 0.35 | 10 |
| rS (µm) | 5.13 ± 0.14 | −0.25 ± 0.07 | −0.27 ± 0.09 | § | — | — | 0.41 | 10 |
| l (µm) | 19.18 ± 0.59 | 0.93 ± 0.25 | § | 0.44 ± 0.10 | −0.32 ± 0.05 | — | 0.67 | 25 |
| C (cells per 103 µm2) | 4.23 ± 0.77 | −2.57 ± 0.34 | 4 ± 0.4 | −0.48 ± 0.15 | — | — | 0.70 | 29 |
| f (Hz) | 39.3 ± 2.45 | 0.66 ± 0.45 | § | § | — | −0.70 ± 0.14 | 0.26 | 13 |
| U (µm s−1) | 368 ± 21 | § | 68 ± 11 | −10.1 ± 4.23 | — | — | 0.58 | 20 |
| F (pN) | 1249 ± 105 | 211 ± 51 | 443 ± 64 | § | — | — | 0.68 | 31 |
| Vup (µm s−1) | 274 ± 10.2 | 26 ± 14.4 | § | § | — | — | 0.46 | 16 |
For C. reinhardtii and G. pectorale, the only evident phenotypic alteration was that cells grown in diluted medium were smaller than those grown in normal medium (table 1); there was no difference in flagellar length between treatments. This reduction in cell size upon nutrient deprivation is not surprising, as nutrient uptake in these organisms is dominated by diffusion (the relevant Péclet number is Pe ∼ 0.1), implying that C. reinhardtii and G. pectorale can take no measures to oppose starvation if the growth medium is low in nutrients. The swimming and sedimentation speeds and swimming force calculations confirm these results: C. reinhardtii and G. pectorale have significantly higher swimming speeds and lower sedimentation speeds in diluted media owing to the decrease in cell size, but there is no difference in propulsion force between the treatments.
In contrast, V. carteri and V. barberi displayed intriguing phenotypic changes when grown for a short period in a low-nutrient medium. Regardless of treatment, V. barberi has a higher cell concentration per unit area and longer flagella than V. carteri (table 1). The initial experiments (table 1) showed that colonies grown in diluted media had smaller somatic cells with longer flagella and larger spheroids for both species, the latter owing to an increased amount of ECM. We investigated in more detail the phenotypic alterations of V. carteri (table 2), by using equipment that allowed measurements of the peak fluid speed U, the flagellar beating frequency f and the force exerted by the flagella on the fluid F. Because in these more detailed experiments colonies were grown with lower light intensity (approx. 600 fc instead of approx. 1000 fc), they had fewer cells, and reached a smaller spheroid, cell and flagellar size than in the initial experiments. However, the data from the more detailed experiments had a better statistical significance and qualitatively confirm the results from the initial experiments (see comparison in figure 4). It is worth noting that these experiments showed that, regardless of nutrient treatment, colonies with lower cell concentration have longer flagella, and that colonies with longer flagella have a lower beating frequency (table 4). Further, results from these more detailed experiments showed that there was no difference in fluid speed U between treatments, even though the biflagellated somatic cells were more sparsely spaced in the diluted medium owing to the larger spheroid size under those conditions. As there is only very weak evidence for a small increase in flagellar beating frequency upon dilution (table 2), the fact that the flow speed U remains constant despite the increased cell separation implies that the increase in flagellar length provides the necessarily increased beating force F. Also, weak evidence from the detailed experiments on V. carteri suggests that the upward swimming speed (estimated Vup) increased for colonies grown in the diluted medium (table 2 and figure 4). In the diluted medium, colonies have smaller somatic cells (i.e. lower negative gravitational force) and longer flagella (i.e. larger swimming force). These benefits seem to outweigh the increase in drag owing to the larger spheroid of colonies grown in diluted medium.
A plausible interpretation of the results showing that Volvox colonies, when grown in a diluted medium, make investments into collective properties, such as a larger spheroid radius R and maintaining a high fluid speed U, is that these changes tend to increase the rate of nutrient uptake and thereby help compensate for the environmental change. There are two key physical aspects that must be considered in estimating the rate of nutrient uptake to a spherical organism like Volvox. The first is the fact that the absorbing somatic cells cover only a fraction of the total colony surface, and it is not obvious a priori how even the purely diffusive rate of uptake would depend on the somatic cell size and the overall colony radius in a geometry with such patchy absorbers. However, this is precisely the problem considered some time ago in the context of chemoreception [28]. There it was found that the absorption rate J to a sphere of radius R whose surface is covered by n absorbing discs, each of radius rS, is Jmax nrS/(nrS + πR), where Jmax = 4πDC∞R is the rate associated with a sphere whose entire surface is a perfect absorber. When the number of discs tends to infinity the rate sensibly approaches Jmax, but the key point is that it can be very close to this asymptotic value even for moderate coverage of the surface. (The first detailed discussion of this kind of effect was given by Jeffreys [29] in the context of evaporation from the stomata on leaves.) Expressing the result as J = 4πDC∞R/(1+ πR/nrS), and using the values typical of Volvox (n = 1000, R = 250 µm, rS = 5 µm), the ratio πR/nrS ∼ 0.16 and thus J/Jmax = 0.86, only slightly depressed from the asymptotic value. We conclude from this that the surface coverage of somatic cells in Volvox is sufficiently large that not only is the diffusive rate of absorption well approximated by that of a sphere absorbing over its entire surface, but even quite substantial increases in the colony radius still leave it in that regime, so the purely diffusive absorption rate actually increases with colony radius at fixed somatic cell number. This would not be the case for very small NrS (πR/NrS ≫ 1), for then the rate is simply proportional to NrS and independent of the colony radius R. Using the typical values of R and rS above, this would require n ≪ 150.
The second issue to consider is how the presence of a fluid flow past the colony surface might affect the results described above. While there has been no detailed mathematical analysis of this particular problem, we may draw some conclusions based on the typical flow rates and diffusivities. The key physical feature that results in the diffusive flux in the absence of flow being so close to the fully absorbing sphere value is the very large number of encounters that a diffusing molecule makes with the sphere when it is in the vicinity of the surface [28]. It follows then that advection parallel to the surface would not significantly alter this effect (in fact it may even enhance it) provided the time spent near the surface during advection is not severely curtailed. In the case of Volvox the time scale for advection along the colony surface is several seconds, and in that time a molecule would typically diffuse a distance (2Dt)1/2 ∼ 40 µm, a distance large compared with the somatic cell size and comparable to if not greater than the intersomatic cell spacing. Thus, as the molecules are swept over the surface, they indeed have sufficient time to find an absorbing somatic cell.
The arguments advanced above suggest that nutrient uptake for an organism like Volvox can be estimated on the basis of a fully absorbing sphere. Attention then turns to the rate of uptake at high Péclet numbers. For a Volvox spheroid, Pe = 2RU/D, as the typical length scale over which the self-generated flow changes is 2R [5]. Increasing R and maintaining a high U may thus be seen as a strategy for Volvox to maintain, or even increase, the high Pe. Such a strategy is beneficial for the colony, as the rate of nutrient uptake by a ciliated spherical micro-organism through its surface is predicted to be proportional to R Pe1/2 [5,30]. Qualitatively, this Pe dependence of the nutrient uptake rate can be understood by noting that the high flow speeds create a fluid-dynamical boundary layer above the spheroid surface across which there is a steep nutrient concentration gradient, which leads to an enhanced diffusive transport across the boundary layer onto the organism surface. This strong dependence on Péclet number for large organisms should be contrasted with that for small organisms. A variety of calculations [5,30] suggest that, for organisms with a small Péclet number, the correction to the diffusive uptake owing to fluid flow is linear in Pe. Thus, an organism in the regime Pe < 1 will in general make only a small change to its uptake rate by a fractional change in Pe, whereas a comparable change in Pe for Pe ≫ 1 can produce a much larger change in uptake, proportional to Pe1/2. Even though Volvox is a colonial organism without a central nervous system, the phenotypic plasticity it displays suggests ‘awareness’ of the benefits associated with collective behaviour. The self-generated fluid flows are thus not only important for self-propulsion and phototaxis [31], but also for nutrient uptake.
The efforts of Volvox to counteract an impending decrease in nutrient uptake, if grown in low-nutrient medium, have a positive effect on the growth of the germ cells (which later turn into the daughter colonies; figure 3) in V. carteri. In the initial experiments, there was statistically weak evidence for a small dependence of the germ cell radii rG on the nutrient treatment (table 1), but there was no statistically significant dependence of rG on the nutrient treatment in the more detailed experiments (table 2). These results suggest that, in the investigated time window of the Volvox life cycle, colonies can maintain (almost) equal germ cell growth rates in normal and 10−1 diluted media.
4. Conclusion
We found evidence that growth in low-nutrient medium induces phenotypic plasticity that mitigates the effect of nutrient limitation in large Volvocales (V. carteri and V. barberi), and a lack of such plasticity in small Volvocales (C. reinhardtii and G. pectorale). The changes in phenotype induced by growing Volvox in a diluted medium were investments into advective fluid flows, and into an increase in colony radius. Such investments point to the important role of advection in enhancing nutrient uptake for the germ cells that grow inside the Volvox colony, consistent with recent theory [5] and experiments [16] which suggested a link between the Péclet number and the evolution to larger organism sizes and germ–soma differentiation in the Volvocales. Although this work provides further evidence for the importance of advection in nutrient uptake for large multicellular micro-organisms, direct measurement of the advection dependence of the rate of nutrient uptake or metabolic activity still require further study. Likewise, further studies are needed to understand the control of collective flagellar beating and the connection between flagellar beating frequency, length and spacing.
Acknowledgements
We are grateful to Matt Herron for a critical reading of the manuscript and many detailed suggestions, and thank J.-W. van de Meent, T. J. Pedley and I. Tuval for discussions. This work was supported in part by NSF grants DEB-0075296 (C.A.S., R.E.M.) and PHY-0551742 (S.G., J.O.K., R.E.G.), the Engineering and Biological Systems programme of the BBSRC and the Schlumberger Chair Fund.
References
- 1.Grosberg R. K., Strathmann R. R. 2007. The evolution of multicellularity: a minor mayor transition? Annu. Rev. Ecol. Evol. Syst. 38, 621–654 10.1146/annurev.ecolsys.36.102403.114735 (doi:10.1146/annurev.ecolsys.36.102403.114735) [DOI] [Google Scholar]
- 2.Smith J. M., Szathmáry E. 1995. The major transitions in evolution. Oxford, UK: Oxford University Press [Google Scholar]
- 3.Niklas K. J. 1994. Plant allometry. Chicago, IL: University of Chicago Press [Google Scholar]
- 4.Weismann A. 1891. Essays upon heredity and kindred biological problems. Oxford, UK: Clarendon Press [Google Scholar]
- 5.Short M. B., Solari C. A., Ganguly S., Powers T. R., Kessler J. O., Goldstein R. E. 2006. Flows driven by flagella of multicellular organisms enhance long-range molecular transport. Proc. Natl Acad. Sci. USA 103, 8315–8319 10.1073/pnas.0600566103 (doi:10.1073/pnas.0600566103) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Kirk D. L. 1998. Volvox: molecular-genetic origins of multicellularity and cellular differentiation. Cambridge, UK: Cambridge University Press [Google Scholar]
- 7.Koufopanou V. 1994. The evolution of soma in the Volvocales. Am. Nat. 143, 907–931 10.1086/285639 (doi:10.1086/285639) [DOI] [Google Scholar]
- 8.Solari C. A., Kessler J. O., Michod R. E. 2006. A hydrodynamics approach to the evolution of multicellularity: flagellar motility and the evolution of germ–soma differentiation in volvocalean green algae. Am. Nat. 167, 537–554 10.1086/501031 (doi:10.1086/501031) [DOI] [PubMed] [Google Scholar]
- 9.Coleman A. W. 1999. Phylogenetic analysis of ‘Volvocacae’ for comparative genetic studies. Proc. Natl Acad. Sci. USA 96, 13 892–13 897 10.1073/pnas.96.24.13892 (doi:10.1073/pnas.96.24.13892) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Herron M. D., Michod R. E. 2008. Evolution of complexity in the volvocine algae: transitions in individuality through Darwin's eye. Evolution 62, 436–451 10.1111/j.1558-5646.2007.00304.x (doi:10.1111/j.1558-5646.2007.00304.x) [DOI] [PubMed] [Google Scholar]
- 11.Nozaki H., Ohta N., Takano H., Watanabe M. M. 1999. Reexamination of phylogenetic relationships within the colonial Volvocales (Chlorophyta): an analysis of atpB and rbcL gene sequences. J. Phycol. 35, 104–112 10.1046/j.1529-8817.1999.3510104.x (doi:10.1046/j.1529-8817.1999.3510104.x) [DOI] [Google Scholar]
- 12.Nozaki H. 2003. Origin and evolution of the genera Pleodorina and Volvox (Volvocales). Biologia 58, 425–431 [Google Scholar]
- 13.Nozaki H., Ott F. D., Coleman A. W. 2006. Morphology, molecular phylogeny and taxonomy of two new species of Pleodorina (Volvoceae, Chlorophyceae). J. Phycol. 42, 1072–1080 10.1111/j.1529-8817.2006.00255.x (doi:10.1111/j.1529-8817.2006.00255.x) [DOI] [Google Scholar]
- 14.Larson A., Kirk M. M., Kirk D. L. 1992. Molecular phylogeny of the volvocine flagellates. Mol. Biol. Evol. 9, 85–105 [DOI] [PubMed] [Google Scholar]
- 15.Reynolds C. S. 1984. The ecology of freshwater phytoplankton. Cambridge, UK: Cambridge University Press [Google Scholar]
- 16.Solari C. A., Ganguly S., Kessler J. O., Michod R. E., Goldstein R. E. 2006. Multicellularity and the functional interdependence of motility and molecular transport. Proc. Natl Acad. Sci. USA 103, 1353–1358 10.1073/pnas.0503810103 (doi:10.1073/pnas.0503810103) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Hoops H. J. 1997. Motility in the colonial and multicellular Volvocales: structure, function, and evolution. Protoplasma 199, 99–112 10.1007/BF01294499 (doi:10.1007/BF01294499) [DOI] [Google Scholar]
- 18.Guyon E., Hulin J. P., Petit L., Mitescu C. D. 2001. Physical hydrodynamics. New York, NY: Oxford University Press [Google Scholar]
- 19.Purcell E. M. 1977. Life at low Reynolds number. Am. J. Phys. 45, 3–11 10.1119/1.10903 (doi:10.1119/1.10903) [DOI] [Google Scholar]
- 20.Sultan S. E. 2000. Phenotypic plasticity for plant development, function and life history. Trends Plant Sci. 5, 537–542 10.1016/51360-1385(00)01797-0 (doi:10.1016/51360-1385(00)01797-0) [DOI] [PubMed] [Google Scholar]
- 21.Miner B. G. 2005. Evolution of feeding structure plasticity in marine invertebrate larvae: a possible trade-off between arm length and stomach size. J. Exp. Mar. Biol. Ecol. 315, 117–125 10.1016/j.jembe.2004.09.011 (doi:10.1016/j.jembe.2004.09.011) [DOI] [Google Scholar]
- 22.Kirk D. L., Kirk M. M. 1983. Protein synthetic patterns during the asexual life cycle of Volvox carteri. Dev. Biol. 96, 493–506 10.1016/0012-1606(83)90186-0 (doi:10.1016/0012-1606(83)90186-0) [DOI] [PubMed] [Google Scholar]
- 23.Desnitski A. G. 1995. A review on the evolution of development in Volvox: morphological and physiological aspects. Eur. J. Protistol. 31, 241–247 [Google Scholar]
- 24.Solari C. A., Michod R. E., Goldstein R. E. 2008. Volvox barberi, the fastest swimmer of the Volvocales (Chlorophyceae). J. Phycol. 44, 1395–1398 10.1111/j.1529-8817.2008.00603.x (doi:10.1111/j.1529-8817.2008.00603.x) [DOI] [PubMed] [Google Scholar]
- 25.Drescher K., Leptos K. C., Goldstein R. E. 2009. How to track protists in three dimensions. Rev. Sci. Instrum. 80, 014301. 10.1063/1.3053242 (doi:10.1063/1.3053242) [DOI] [PubMed] [Google Scholar]
- 26.Drescher K., Leptos K. C., Tuval I., Ishikawa T., Pedley T. J., Goldstein R. E. 2009. Dancing Volvox: hydrodynamic bound states of swimming algae. Phys. Rev. Lett. 102, 168101. 10.1103/PhysRevLett.102.168101 (doi:10.1103/PhysRevLett.102.168101) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Solari C. A. 2005. A hydrodynamics approach to the evolution of multicellularity: flagellar motility and the evolution of germ–soma differentiation in volvocalean green algae. PhD thesis, University of Arizona, USA; [DOI] [PubMed] [Google Scholar]
- 28.Berg H. C., Purcell E. M. 1977. Physics of chemoreception. Biophys. J. 20, 193–219 10.1016/S0006-3495(77)85544-6 (doi:10.1016/S0006-3495(77)85544-6) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Jeffreys H. 1918. Some problems of evaporation. Phil. Mag. 35, 423–441 [Google Scholar]
- 30.Magar V., Goto T., Pedley T. J. 2003. Nutrient uptake by a self-propelled steady squirmer. Q. J. Mechanics Appl. Math. 56, 65–91 10.1093/qjmam/56.1.65 (doi:10.1093/qjmam/56.1.65) [DOI] [Google Scholar]
- 31.Drescher K., Goldstein R. E., Tuval I. 2010. Fidelity of adaptive phototaxis. Proc. Natl Acad. Sci. USA 107, 11 171–11 176 10.1073/pnas.1000901107 (doi:10.1073/pnas.1000901107) [DOI] [PMC free article] [PubMed] [Google Scholar]