Quantification and Compensation of Eddy-Current-Induced Magnetic Field Gradients

Abstract

Two robust techniques for quantification and compensation of eddy-current-induced magnetic-field gradients and static magnetic-field shifts (ΔB₀) in MRI systems are described. Purpose-built 1-D or 6-point phantoms are employed. Both procedures involve measuring the effects of a prior magnetic-field-gradient test pulse on the phantom’s free induction decay (FID). Phantom-specific analysis of the resulting FID data produces estimates of the time-dependent, eddy-current-induced magnetic field gradient(s) and ΔB₀ shift. Using Bayesian methods, the time dependencies of the eddy-current-induced decays are modeled as sums of exponentially decaying components, each defined by an amplitude and time constant. These amplitudes and time constants are employed to adjust the scanner’s gradient pre-emphasis unit and eliminate undesirable eddy-current effects. Measurement with the six-point sample phantom allows for simultaneous, direct estimation of both on-axis and cross-term eddy-current-induced gradients. The two methods are demonstrated and validated on several MRI systems with actively-shielded gradient coil sets.

Introduction

Eddy currents induced in MRI systems by the application of pulsed magnetic-field gradients result in undesired, time varying, magnetic-field gradients, G_ζ(t), and magnetic-field shifts, ΔB_o(t). These gradients and field shifts produce artifacts that are most pronounced in localized spectroscopy and diffusion-weighted EPI experiments. In localized spectroscopy, eddy currents result in broadened resonances and distorted lineshapes [1]. This can be especially problematic for very short echo-time experiments [2]. In the most severe cases, eddy currents can completely prevent the acquisition of localized MRS measurements [3]. For pulsed-field-gradient, spin-echo diffusion experiments, long-lived eddy currents induced by the application of diffusion-encoding gradients can result in spuriously high diffusion values [4].

In diffusion-weighted EPI, eddy-current-induced gradients and field shifts reveal themselves as distinctive geometric distortions in the resulting images. Image shearing artifacts (eddy-current-induced gradients in the read-out direction), image scaling artifacts (eddy-current-induced gradients in the phase-encode direction) and bulk-position shifts (homogeneous static field shifts) can all be nearly completely removed via data post-processing [5]. Further, the development of diffusion-weighting schemes designed to cancel eddy currents [6–8] have reduced the necessity of post-processing image correction, although post-processing is still routinely employed. Nevertheless, such post facto data correction schemes and eddy-current-suppressing pulse sequences benefit from strategies that address the genesis of eddy-current formation, e.g., eddy-current “pre-emphasis compensation” via modulation of gradient switching (on/off) dynamics – the subject of this report.

The unwanted, persistent eddy currents in MRI systems can be categorized into three basic types. A gradient pulse applied in one direction, the ŷ-direction for example, may induce a time-dependent eddy current within conducting structures (components of the magnet, gradient set, or RF coil) that results in a ŷ-direction magnetic field gradient, G_y,ζ(t), which acts in opposition to the applied time-dependent gradient. This is referred to as an on-axis or diagonal eddy-current-induced gradient term. In principle, a gradient pulse G_y(t) may also produce cross terms – an eddy-current-induced gradient along another axis, G_x,ζ(t) for example. The third eddy-current response category is a time-dependent homogeneous field shift, ΔB₀(t). This latter type of eddy-current-induced effect may arise from a spatial offset between the gradient isocenter and the center point of the eddy-current-carrying structures (which give rise to the undesirable eddy-current gradients) along the axis of the applied gradient pulse [9]. In other cases, the ΔB₀(t) shift may result from a bona fide homogeneous field shift, for instance, if the eddy-current-carrying structure is the magnet bore tube.

The amplitudes of the eddy currents induced in conducting structures of the MRI magnet (e.g., bore tube, magnet dewar, heat shield) are strongly dependent upon the relative sizes of the gradient set and eddy-current-carrying structures. Prior to the introduction of actively-shielded gradient-coil technology [10–12], mutual inductance between the gradient coil and peripheral conducting structures in the magnet led to crippling eddy-current-induced gradients and field shifts in systems without eddy-current compensation (e.g., eddy-current gradients with amplitudes up to 50% of the intended pulsed-gradient magnitude [13–15]). In modern imaging systems, a reduction of eddy-current amplitudes of more than an order of magnitude is achievable with active shielding of the gradient-coil assembly. As a result, uncompensated eddy-current gradient amplitudes are typically < 1% of the pulsed-gradient amplitude [2,16].

The residual eddy currents in an MRI system with actively-shielded gradients can be further reduced (10-fold or more) by pre-emphasis adjustments of the gradient waveform [2,13,14,16–18]. Newer MRI scanners are equipped with gradient pre-emphasis units that typically allow for the specification of at least three independent, exponential components (each defined by an amplitude and time constant) for each possible eddy-current-induced effect (diagonal and cross-term gradients, as well as time-dependent field shifts).

Numerous techniques have been described for the quantitative measurement of MR system eddy-current-induced gradients with the aim of obtaining optimal gradient pre-emphasis parameters [2,3,13–15,17–20]. Phase-mapping techniques [2,20] are elegant and do not require precise placement or repeated repositioning of the eddy-current-sensitive phantom sample. A phase-mapping approach geared specifically toward eddy-current correction in diffusion-weighted, spin-echo EPI has been reported [21]. A conceptually simple method involves moving a small point-sample to multiple positions (at least two different positions along each axis) and monitoring the temporal frequency response of the MR signal after a long gradient test pulse [9,14,15]. However, this method requires repeated measurements at multiple positions and delay times, making acquisition of a full set of measurements tedious. Alternatively, the position-dependent frequency behavior from multiple, point-like samples and an array of microcoils can be used to map the field without requiring sample repositioning [22–23]. The point-like sample approach has more recently been applied to monitor arbitrary gradient-waveform performance [24] and extended using a highly-doped, disk-like 1-D sample [25]. (Note that the 1-D method developed in this report uses a non-doped, extended, rod-like, 1-D sample.) The choice of measurement method is often one of convenience and/or operator preference.

In this report, we describe two robust and efficient techniques for quantitative measurement of eddy-current-induced gradients and field shifts in MRI systems. In addition to the scanner itself, a volume RF coil and an eddy-current-sensitive, purpose-built phantom sample are the only hardware required. Both measurements use a simple test procedure consisting of a single, long-duration gradient pulse followed by a variable delay time, a broadband RF excitation pulse, and sampling of the free induction decay (FID). Modeling of the FID allows extraction of the time varying residual (eddy-current-induced) gradient amplitudes and field shifts. The time evolution of the eddy-current-induced gradient amplitudes and field shifts are then modeled using Bayesian probability theory methods [26–28] to produce estimates of component amplitudes and time constants. After determining scaling factors that describe the response of the MRI scanner’s gradient pre-emphasis unit, the amplitudes and time constants characterizing the gradient and field shift time-dependencies are used to suppress the undesirable eddy-current behavior of the MRI magnet/gradient system.

It is worth noting that the design of eddy-current compensation units typically incorporates the assumption that the eddy-current-induced magnetic field gradients are spatially constant at any instant in time (i.e., the eddy-current-induced magnetic field varies as a linear function of spatial coordinates) and can be modeled as sums of exponentially decaying (in time) components. As a result, there is no option to employ other functional basis sets. Thus, the principal challenge is to obtain high quality data characterizing the MRI system’s eddy-current-induced magnetic-field gradients and then properly model the data as sums of exponential components (i.e., estimate the amplitudes and time constants).

Rather than aiming for sequence-specific eddy-current correction parameters, the measurement techniques described in this report are intended to eliminate global, MRI system-specific eddy-current gradients and field shifts for the varied applications employed by users of our MR facility. The two novel measurement methods described have different advantages and limitations, but are both simple and straightforward to implement as part of a routine, periodic QA testing procedure. (Note that many of the eddy-current measurement, data analysis, and correction procedures used by instrument vendors are proprietary and not always accessible to the end user, making it difficult to incorporate them into QA testing procedures.)

Theoretical Background

One-Dimensional Sample Measurement: Description of FID Signal Decay

The time-domain signal from an arbitrary, macroscopic sample of uniform density and possessing a single resonance (e.g, water) in a pulse-and-acquire experiment is described by an equation of the form

$$\text{S}(\text{t})={\text{S}}_{\text{o}}·{\text{e}}^{-{\text{R}}_2·\text{t}}·\underset{{\text{V}}_{\text{o}}}{\int }\rho (\overrightarrow{\text{r}})·{\text{e}}^{-\text{i}·\omega (\overrightarrow{\text{r}})·\text{t}}·\text{d}\overrightarrow{\text{r}}.$$ [Eq. 1]

When the magnetic field throughout the sample volume, V_o, is perfectly homogeneous, ω(r⃗)=γ · B_o=ω_o (ignoring chemical shift), and the resulting FID exhibits pure exponential decay with rate constant R₂. The situation becomes considerably more complex in the presence of magnetic-field inhomogeneities across the sample volume or within a magnetically non-homogeneous sample [29].

For the special case of a magnetically homogeneous, one-dimensional (1-D) sample of length L, in the presence of a static magnetic-field gradient G⃗(r⃗) that is collinear with the sample, the free-induction decay following a short, broadband RF pulse [i.e., Δν_RF ≫ (γ/2π)·G·L] is described by the well-known sinc function,

$$\text{S}(\text{t})={\text{S}}_{\text{o}}·{\text{e}}^{-{\text{R}}_2·\text{t}}·\frac{sin(\gamma ·\text{G}·\text{L}·\text{t}/2)}{\gamma ·\text{G}·\text{L}·\text{t}/2}.$$ [Eq. 2]

In practice, it is not possible to perfectly shim the magnetic field across the length of a finite sample. Thus, the frequency as a function of position (z) in the 1-D sample is more accurately described by

$$\omega (\text{z})={\omega }_{\text{o}}+({\text{G}}_{\zeta }+{\text{G}}_{\text{bg}})·\text{z}+\text{O}({\text{z}}^2),$$ [Eq. 3]

where G_ζ is either an eddy-current-induced gradient or an intentionally applied gradient. G_bg is the unavoidable static background gradient due to imperfect shimming of the sample. For simplicity, we ignore higher order, spatially non-linear terms, O(z²). In this case, the time-domain signal is still described by Eq. 2, but with G = G_ζ + G_bg. In most MRI applications, the applied imaging gradients, G_ζ, are much larger than the background field gradients. As a result, the G_bg term can usually be ignored. For the 1-D eddy-current measurements developed here, the background gradients may be comparable to or even larger than the eddy-current-induced gradients G_ζ(t).

The effects of signal damping due to T₂ relaxation (e^−R₂·t) and signal scaling due to transmit/receive hardware and pulse-sequence parameters (S_o) can be eliminated by normalizing the FID acquired in the presence of G_ζ + G_bg with the time-domain signal acquired when only G_bg is present. The resulting normalized time-domain signal is then

$$\frac{{\text{S}}_{+}[\text{t},({\text{G}}_{\zeta }+{\text{G}}_{\text{bg}})]}{\text{S}[\text{t},{\text{G}}_{\text{bg}}]}=\left(\frac{{\text{G}}_{\text{bg}}}{{\text{G}}_{\text{bg}}+{\text{G}}_{\zeta }}\right)·csc\left[\frac{1}{2}·\gamma ·{\text{G}}_{\text{bg}}·\text{L}·\text{t}\right]·sin\left[\frac{1}{2}·\gamma ·({\text{G}}_{\text{bg}}+{\text{G}}_{\zeta })·\text{L}·\text{t}\right].$$ [Eq. 4]

In Eq. 4, we have used the notation S₊[t,(G_ζ + G_bg)] to make it explicit that the polarity of the test gradient pulse is positive. If analysis is limited to a very early, narrow time window of data points in the normalized FID signal, over which the decaying eddy-current-induced gradient is nearly constant, the result of Eq. 4 can be approximated by a Taylor-Series expansion to second order around t = 0 (the center of the broadband RF excitation pulse),

$$\frac{{\text{S}}_{+}[\text{t},({\text{G}}_{\zeta }+{\text{G}}_{\text{bg}})]}{\text{S}[\text{t},{\text{G}}_{\text{bg}}]}\approx 1-\frac{1}{24}·{\gamma }^2·{\text{G}}_{\zeta }·(2{\text{G}}_{\text{bg}}+{\text{G}}_{\zeta })·{\text{L}}^2·{\text{t}}^2.$$ [Eq. 5]

After fitting the normalized time-domain signal to the function

$$\frac{{\text{S}}_{+}[\text{t},({\text{G}}_{\zeta }+{\text{G}}_{\text{bg}})]}{\text{S}[\text{t},{\text{G}}_{\text{bg}}]}=1-{\alpha }_{+}·{\text{t}}^2,$$ [Eq. 6]

it is straightforward to estimate G_ζ from the fitting parameter α₊ if G_bg is known.

If, however, G_bg is unknown, the amplitudes of eddy-current-induced gradients, G_ζ, can still be estimated by assuming that they are equal and opposite for test gradients of opposite polarities. In this situation, the background gradients remain unaltered and, in the presence of eddy currents following a test gradient pulse of negative polarity, the normalized signal is approximated by

$$\frac{{\text{S}}_{-}[\text{t},({\text{G}}_{\zeta }+{\text{G}}_{\text{bg}})]}{\text{S}[\text{t},{\text{G}}_{\text{bg}}]}\approx 1-\frac{1}{24}·{\gamma }^2·(-{\text{G}}_{\xi })·(2{\text{G}}_{\text{bg}}-{\text{G}}_{\zeta })·{\text{L}}^2·{\text{t}}^2.$$ [Eq. 7]

In analogy to Eq. 6, the normalized FID data can then be fit with a single parameter, α₋:

$$\frac{{\text{S}}_{-}[\text{t},({\text{G}}_{\zeta }+{\text{G}}_{\text{bg}})]}{\text{S}[\text{t},{\text{G}}_{\text{bg}}]}=1-{\alpha }_{-}·{\text{t}}^2.$$ [Eq. 8]

By adding α₋ and α₊, the background gradient can be eliminated, since

$${\alpha }_{+}+{\alpha }_{-}=\frac{1}{12}·{\gamma }^2·{\text{G}}_{\zeta }^2·{\text{L}}^2$$ [Eq. 9]

The normalized, time-domain data are most expeditiously fit to a fourth-order polynomial (even orders only) with respect to time, but the eddy-current amplitude is derived from treatment of the second-order coefficients, as per Eq. 9.

In situations where the eddy-current-induced gradient is large enough, it can be estimated directly from the first null (t₀) in the FID data. To a high degree of accuracy, the bandwidth of frequencies contained within a time-domain sinc envelope (symmetric about t = 0) is given by [30]

$$\mathrm{\Delta }v=\frac{1}{{\text{t}}_{\text{o}}}=\frac{\gamma }{2\pi }·({\text{G}}_{\zeta }+{\text{G}}_{\text{bg}})·\text{L}.$$ [Eq. 10]

Six-Point Sample Measurement

The phantom for the six-point (3-D) sample measurement consists of six ¹H-containing solvents in spherical bulbs approximating point samples. These point samples are positioned symmetrically about the origin along the principal coordinate axes (x, y, z) as depicted in Fig. 1. The point-sample solvents each have a ¹H NMR spectrum consisting of a single resonance with a chemical shift that is well-separated from those of the other five solvents (Table 1) [31–32].

Figure 1.

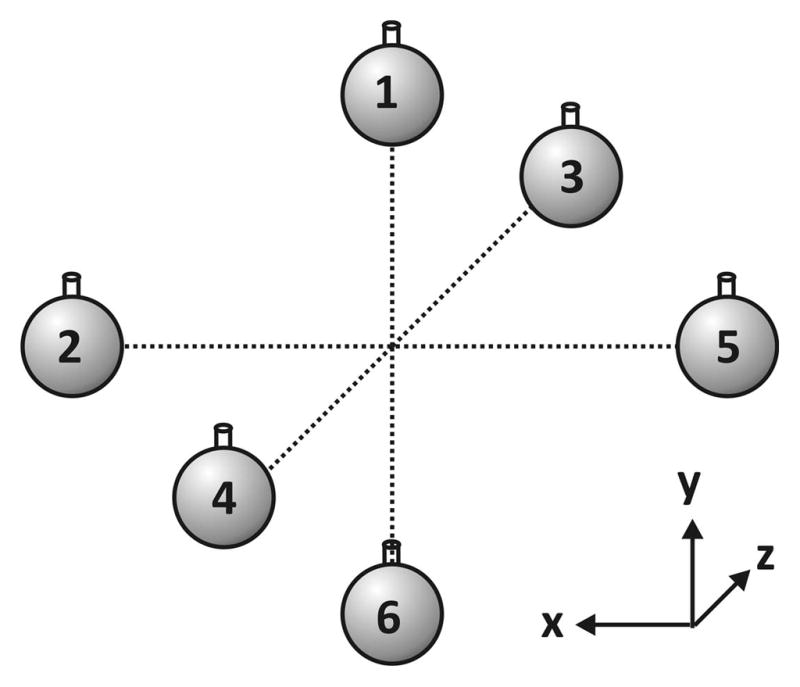
Geometry of the Six-Point-Sample (3-D) Phantom. The time-dependent frequency shift between a pair of point solvents aligned along a given principal axis is used to monitor the time-dependent, eddy-current-induced gradients in that direction.

Table 1.

¹H NMR Chemical Shifts of the Solvents in the Six-Point Sample Phantom.

Solvent	Chemical Shift (ppm)
Hexamethyldisilane, (CH3)6Si2	0.04
Cyclohexane, C6H12	1.43
Acetone, C3H6O	2.09
1,4-Dioxane, C4H8O2	3.71
Water, H2O	4.79
Benzene, C6H6	7.15

As an example, the resonance frequency of a given point-sample solvent (e.g., solvent #3), with chemical shielding constant, σ₃, in the presence of (i) static background magnetic-field gradient, G_bg, (ii) time-varying, eddy-current-induced field gradient along the z-axis, G_z,ζ(t), and (iii) spatially-homogeneous, time-dependent field shift, ΔB₀(t), is

$$\nu ({\text{z}}_3,\text{t})=\frac{\gamma }{2\pi }·(1-{\sigma }_3)·\left[{\text{B}}_{\text{o}}+\mathrm{\Delta }{\text{B}}_{\text{o}}(\text{t})+({\text{G}}_{\text{z},\zeta }(\text{t})+{\text{G}}_{\text{bg}})·{\text{z}}_3\right].$$ [Eq. 11]

The time-independent frequency shifts due to chemical shielding and background gradients can be collected into a single term, ν(z₃),

$$\nu (z_3)=\frac{\gamma }{2\pi }·(1-{\sigma }_3)·\left[{\text{B}}_{\text{o}}+{\text{G}}_{\text{bg}}·{\text{z}}_3\right].$$ [Eq. 12]

The eddy-current-induced gradient along a principal coordinate axis (e.g., z), as detected at two points (e.g., point-sample solvents 3 and 4, positioned at z₃ and z₄, respectively), is easily determined, since the difference in frequencies between samples 3 and 4 is given by

$$\mathrm{\Delta }\nu ({\text{z}}_3,{\text{z}}_4,\text{t})\cong \nu ({\text{z}}_4)-\nu ({\text{z}}_3)+\frac{\gamma }{2\pi }·{\text{G}}_{\zeta ,\text{z}}(\text{t})·({\text{z}}_4-{\text{z}}_3).$$ [Eq. 13]

In Eq. 13, the effect of the chemical shieldings, σ₃ and σ₄, on the eddy-current-induced frequency shift has been ignored since their effect is vanishingly small in this case (σ₃ ~ σ₄ ≪ 1).

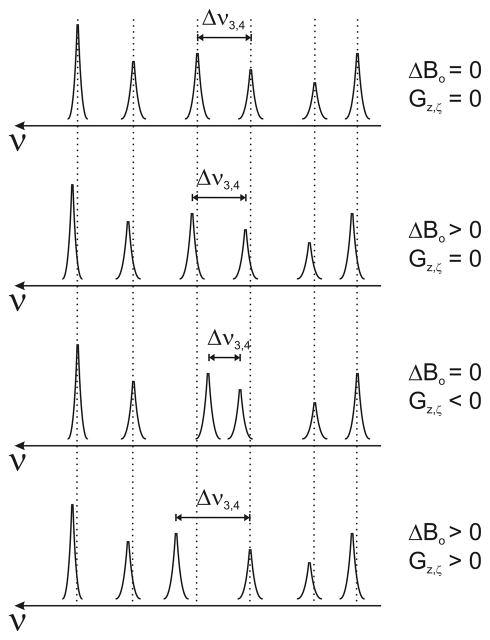
An implicit assumption in this treatment is that the field variation due to each time-dependent, eddy-current-induced gradient is linear in the spatial coordinate. Based on this assumption, the amplitudes of the eddy-current-induced gradients along all three Cartesian axes can be determined simultaneously from a single spectral measurement, as shown schematically in Fig. 2. The spectral measurements must be made by acquiring a highly truncated FID so as to quantify the eddy-current-induced gradient amplitudes at a well-defined delay time following the tailing edge of the applied gradient pulse. The practical limitations this imposes on the temporal resolution of the eddy-current decay and the minimum required spectral-acquisition times for spectral frequency estimates are described below.

Figure 2.

Schematic representation of the spectral response from the six-point (3-D) phantom in the presence of eddy-current-induced gradients and ΔB_o-field shifts.

Experimental

Eddy-current-induced gradient amplitudes were measured on each of three Agilent/Varian small-animal MRI scanners with Agilent/Magnex actively-shielded gradient assemblies and super conducting magnets (two @ 4.7 T and one @ 11.74 T). The relevant hardware characteristics of the MRI systems are listed in Table 2. We use the abbreviations System #1, #2 and #3 throughout. For measurements in the two 4.7-T scanners (Systems #1 and #2), the same 73-mm diameter linear Litz volume coil was used (Doty Scientific, Inc.). A 38-mm Doty quadrature Litzcage coil was used for measurements in the 11.74-T scanner (System #3).

Table 2.

Hardware Characteristics of the Three Small-Animal MRI Scanners.

Hardware Component	System #1	System #2	System #3
Magnet	4.7 T, Oxford Mk I (i.d., 40.0 cm)	4.7 T, Oxford Mk II (i.d., 33.0 cm)	11.7 T, Magnex (i.d., 26.0 cm)
MRI Console	Varian DirectDrive™ System	Varian DirectDrive™ System	Varian UnityINOVA™ system
Gradient Coil i.d.a	21 cm	12 cm	8 cm
Gmax	28 G/cm	58 G/cm	120 G/cm
trise (0 – Gmax)	650 μs	270 μs	298 μs
Imax	300 A	300 A	200 A
slew rate (dG/dt)	0.043 G/cm·μs	0.215 G/cm·μs	0.403 G/cm·μs
RF Coil	linear Litz volume coil, 73 mm i.d.	linear Litz volume coil, 73 mm i.d.	quadrature Litzcage coil, 38 mm i.d.

^aAll of these gradient sets were manufactured by Magnex Scientific (now a part of Agilent Technologies) and are water-cooled, actively-shielded, high-duty type coils.

Pulse Sequence

The pulse sequence used to produce and measure eddy-current-induced gradients and field shifts consisted of a long-duration (2.5 – 3 s) gradient pulse followed by a variable delay time, δ, and a broad-band RF excitation pulse. The gradient pulse ramp-down (tailing edge) was set to the maximum gradient linear slew rate for the system (Table 2). Gradient-pulse durations were chosen to be at least five-fold longer than the time constant of the slowest-decaying eddy-current component. Thus, the eddy-current effects all originate from the tailing edge of the long-duration gradient pulse. Limitations on the amplitude of the long test gradient pulses are imposed by circuit breakers (which nominally trip at current thresholds of 70 A r.m.s.) in the gradient-filter boxes of these MRI systems.

1-D Phantom Construction

The 1-D phantom consisted of a length of 3-mm, thin-wall (2.42 mm, i.d.) NMR tube (Wilmad LabGlass) filled with deionized water. To reduce B_o inhomogeneities arising from the finite length of the sample (end effects), p-phenylene sulfide susceptibility plugs (Doty Scientific, Inc.) were placed at the ends of the column of liquid. The length, L, of the 1-D sample was primarily limited by the volume of the RF volume coils. The eddy-current-measurement sensitivity is roughly proportional to L² (e.g., Eq. 9). However, the desire for increased sensitivity must be balanced against the need for uniform coil receptivity across the sample (implicit in Eq. 2) and the desire for optimal shimming over the spatial dimensions of the sample. The length of the column of water in the phantom ranged from 2 – 4.5 cm; its precise length was determined from MR images. The capped 1-D sample was held in a foam or plastic holder which was used to align it with the MRI magnet’s x-, y- or z-axes. Typical linewidths after manual shimming were 2 – 5 Hz.

Six-Point (3-D) Phantom Construction

The ¹H-containing solvents of the six-point phantom were placed in 18 μL spherical glass bulbs (Wilmad LabGlass). The collection of spherical bulbs was held in a plexiglass tube, machined with six small holes to accommodate the necks of the spherical bulbs and to align the bulbs in an octahedral geometry (Fig. 1). The phantom was positioned with the six samples symmetrically placed about the gradient isocenter. Field homogeneity adjustments for the six-sample measurement were most easily made by shimming on a large-volume, doped-water phantom centered within the RF coil. After shimming, the large-volume phantom was replaced with the six-point, 3-D phantom and the RF coil returned to the same position within the magnet with no further adjustment of field homogeneity. The six resonances in the resulting spectra were clearly resolved. The distances between point-sample solvents in the phantom, aligned along a given axis, were determined in a series of imaging experiments. The distance measurements were always made in the phase-encode direction of the images to avoid chemical shift artifacts. For this measurement method, sensitivity is improved with increasing separation between the point samples, but these dimensions are limited by the size of the RF coil.

Data Acquisition and FID modeling (1-D sample measurement)

FID measurements with the 1-D sample were made either in the absence of a long-duration gradient pulse or at variable delays after a gradient pulse of positive or negative polarity. After discarding the first 500 μs – 1.5 ms of each FID (25 kHz band width), the subsequent 2-ms FID window (50 time-domain data points) was employed in the analysis. (Note that the first 500 μs – 1.5 ms of each FID was dominated by a rapidly-decaying signal component due to ¹H-containing polymeric materials in the sample holder and/or RF coil. The 1-D phantom consists of a volume of < 1 mL. Under these conditions, the relative amplitude of the contaminating ¹H signal originating from the RF coil form and sample holder is non-negligible.) The individual FIDs (2 ms, 50 data points) were modeled, as described in the Theoretical Background section, using code running in Matlab (The Mathworks, Inc.). Briefly, the Varian binary FID data were imported into Matlab. The very early 2-ms sample of the discrete, magnitude FID, acquired in the absence of eddy-current-induced gradients and field shifts, was fit to a fourth-order polynomial. The resulting fit-function values at each time-domain data point were used to normalize the magnitude FIDs acquired in the presence of eddy-current-induced gradients (Eq. 4). The resulting normalized, magnitude FID was then fit with a polynomial, containing terms of order t⁰, t² and t⁴. Addition of the second-order coefficients from positive and negative test-gradient polarities (Eq. 9) allows for estimation of the eddy-current-induced gradient. Eddy-current-induced ΔB_o shifts were determined, after eliminating eddy-current-induced residual gradients, from the rate of phase accumulation of the time-domain FID compared to that in the absence of a gradient test pulse:

$$\mathrm{\Delta }{\nu }_{\text{o}}=\left(\frac{1}{2\pi }\right)·\left[{\left(\frac{\text{d}\phi }{\text{dt}}\right)}_{\zeta }-{\left(\frac{\text{d}\phi }{\text{dt}}\right)}_{{\text{G}}_{\text{test}}=0}\right].$$ [Eq. 14]

The signal phase was estimated in the usual manner from the time-domain signal, S(t):

$$\phi (\text{t})={tan}^{-1}\left(\frac{Im[\text{S}(\text{t})]}{Re[\text{S}(\text{t})]}\right).$$ [Eq. 15]

Data Acquisition and FID modeling (six-point, 3-D sample method)

Parameters employed for the six-point sample, 3-D measurement were: acquisition time = 8 ms, sweep width = 83 kHz (667 complex data points). To avoid the relatively large amplitude, short-T₂^* signal component arising from the sample holder and RF coil, the receiver was gated off for 500–750 μs after the broadband RF excitation pulse. A Bayesian analysis software suite [33,34] was used to model the time-domain FID data as a set of six exponentially-decaying sinusoids with independent phases and decay rates. Ideally, the frequencies of the six sinusoids should be estimated at specific instances in time following application of the gradient pulse. However, it is well appreciated that uncertainty in frequency estimates scales inversely with data-acquisition period, with shorter periods leading to greater uncertainty. Thus, there is an unavoidable tradeoff between accurate time-evolution registration and accurate frequency estimation. Fortunately, Bayesian estimation of resonance-frequency is quite accurate provided the data acquisition period (i.e., time-domain truncation) is not too short [35]. It was determined empirically that data collected in the absence of time-varying eddy currents with acquisition times less than 8 ms led to frequency estimates for the six resonances that deviated unacceptably from those determined by analysis of non-truncated FIDs. Thus, the data acquisition period was set to 8 ms.

The full set of FIDs, acquired following different delay times, δ, and different test-gradient directions, was batch processed with the Bayes Analyze module of the Bayesian software suite [33]. Software written in Matlab was used to read in the Bayesian-estimated resonance frequencies from the set of spectra to compute the associated directional gradient amplitudes and average ΔB_o shifts from each spectrum. Finally, the gradient amplitudes and ΔB_o shifts were formatted into ascii files and used as input for the Bayesian Exponential Analysis package (see below).

Bayesian Modeling of the Time-Dependent, Eddy-Current-Induced Gradients

The time-dependent, eddy-current-induced magnetic-field gradient amplitude and ΔB_o-shift data gathered via either the 1-D or six-point (3-D) sample measurements were modeled as a sum of exponentially decaying components, each with independent amplitudes and time-constants:

$${\text{G}}_{\text{i},\zeta }(\text{t})={\text{G}}_{\text{j},\text{test}}·\left[\sum _{\text{k}}{\text{A}}_{\text{k}}·{\text{e}}^{-\text{t}/{\tau }_{\text{k}}}\right]$$ [Eq. 15]

and

$$\mathrm{\Delta }{\text{B}}_{\text{o}}(\text{t})={\text{G}}_{\text{j},\text{test}}·\left[\sum _{\ell }{\text{A}}_{\ell }·{\text{e}}^{-\text{t}/{\tau }_{\ell }}\right].$$ [Eq. 16]

The Bayesian software suite’s exponential analysis package [26–28] was employed for model selection and parameter estimation.

Gradient Pre-emphasis

Eddy-current-induced gradient amplitudes and time constants, estimated from Bayesian exponential modeling, were applied by the MRI system’s pre-emphasis unit to suppress eddy-current-induced gradients. Eddy-current/pre-emphasis amplitude scaling factors were determined using the approach outlined by de Graaf [3].

Eddy current compensation efficacy

Single-shot, spin-echo EPI images were acquired using System #2 (Table 2) from a phantom sample of PEG 400 (polyethylene glycol, mol. wt._ave = 400 g/mol) without and with very heavy (b ~ 534,000 s/mm²) diffusion weighting. The diffusion-weighting scheme consisted of a pair of trapezoidal diffusion-weighting gradients. Thus, data were acquired without the benefit of eddy-current-minimizing diffusion-weighting schemes [6–8].

Results

The residual eddy-current-gradient amplitudes in the three small-animal MRI systems (hardware details as listed in Table 2) are presented in Table 3. The time-varying, eddy-current-induced gradient and ΔB_o shift components were characterized according to the time constant of the decay as fast (τ < 2 ms), intermediate (2 ms < τ < 100 ms) or slow (τ > 100 ms). Prior to pre-emphasis correction, the fast-decaying components of the eddy-current-induced gradients had the largest amplitudes in all three MRI systems.

Table 3.

Eddy-Current Amplitudes and Time Constants Determined from 1D Sample Measurement.^a

Gradients		System #1		System #2		System#3
		τ (ms)	Amplitude (%)	τ (ms)	Amplitude (%)	τ (ms)	Amplitude (%)
z → z	fast	0.8 ± 0.1	0.54 ± 0.06	1.89 ± 0.07	0.41 ± 0.03	2.1 ± 0.2	0.026 ± 0.001
	intermediate	6.0 ± 1.3	0.14 ± 0.02	43 ± 8	0.023 ± 0.002	60 ± 11	0.0089 ± 0.0005
	slow	254 ± 8	0.356 ± 0.004	585 ± 259	0.010 ± 0.002	---	---
y → y	fast	0.29 ± 0.07 0.65 ± 0.11	0.35 ± 0.17 0.15 ± 0.04	0.80 ± 0.09	0.21 ± 0.03	0.9 ± 0.1	0.09 ± 0.02
	intermediate	13 ± 2	0.052 ± 0.002	11.4 ± 2.8	0.016 ± 0.002	53 ± 8	0.052 ± 0.008
	slow	210 ± 8	0.150 ± 0.003	314 ± 180	0.0117 ± 0.0009	481 ± 302	0.016 ± 0.008
x → x	fast	---	---	0.89 ± 0.06	0.19 ± 0.02	---	---
	intermediate	---	---	---	---	60 ± 5	0.0294 ± 0.0004
	slow	---	---	---	---	---	---
y → x	fast	---	---	1.5 ± 0.3	0.018 ± 0.002	---	---
z → x	fast	---	---	1.6 ± 0.2	0.037 ± 0.003	---	---
z → y	fast	0.9 ± 0.2	0.04 ± 0.01	---	---	---	---
	slow	293 ± 75	0.017 ± 0.001	---	---	---	---
Bo shifts		τ (ms)	Amplitude (mG/G/cm)	τ (ms)	Amplitude (mG/G/cm)	τ (ms)	Amplitude (mG/G/cm)
z → Bo	fast	2.1 ± 0.1	0.59 ± 0.02	---	---	1.9 ± 1.2	0.18 ± 0.07
	intermediate	205 ± 16	−1.7 ± 0.4	---	---	52 ± 9.9	0.16 ± 0.02
	slow	434 ± 69	1.1 ± 0.4	113 ± 31	0.136 ± 0.005	---	---
y → Bo	fast	1.4 ± 0.3	−0.36 ± 0.02			---	---
	intermediate	14 ± 2	0.75 ± 0.02	13 ± 1	0.117 ± 0.002	56 ± 15	0.089 ± 0.002
	slow	109 ± 6	2.0 ± 0.1	321 ± 36	−0.085 ± 0.005	---	---
x → Bo	intermediate	115.8 ± 0.5	−0.911 ± 0.002	27 ± 4	0.38 ± 0.05	16 ± 5	0.19 ± 0.05
	slow	---	---	210 ± 44	0.26 ± 0.05	94 ± 15	0.35 ± 0.05

^avalues reported as mean ± SD as estimated by Bayesian multi-exponential analysis. Residual gradient amplitudes are reported as a percentage of the test gradient magnitude. B_o shifts (in mG) are normalized by the amplitude of the gradient test pulse in G/cm and are reported in units of mG/G/cm.

In most cases, the expected general trend toward larger eddy-current-induced gradient amplitude with an increasing ratio of gradient assembly-to-magnet bore diameters (d_grad/d_magnet) was observed. Figure 3 is a graphical depiction of this trend, wherein the size of eddy-current-induced gradients (quantified as the sum of the amplitudes of each time-decaying component in Table 3 across all three Cartesian axes) is plotted vs. d_grad/d_magnet. The importance of this factor dominates differences in gradient slew rates, which varied by an order of magnitude across the three MRI systems (Table 2). In the worst case, the z →z gradient interaction in System #1, the sum of diagonal residual gradient amplitudes was ~ 1% of the pulsed gradient’s amplitude. In all three systems, the smallest diagonal (on-axis) eddy-current gradients were observed for pulsed gradients applied along the x-direction (parallel to the laboratory floor). Surprisingly, in the system with the largest d_grad/d_magnet ratio (System #1), diagonal x → x eddy currents were completely absent.

Figure 3.

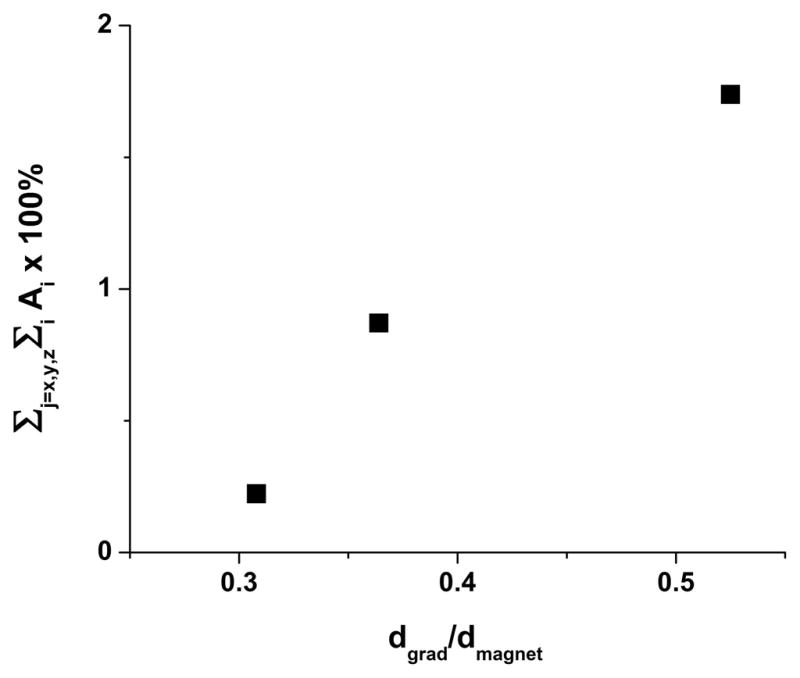
Prior to eddy-current compensation, a general trend toward higher eddy-current-induced gradients with greater d_grad/d_magnet is observed for the sample of MRI systems in this study. The quantity d_grad represents the gradient i.d., while d_magnet is the magnet bore diameter. For purposes of this plot, overall eddy-currents are represented as a sum of all of the on-axis (x → x, y → y, z → z) eddy-current decay components shown in Table 3 (e.g., in terms of Eq. 15, Σ_{j = x,y,z} Σ_i A_i ×100%).

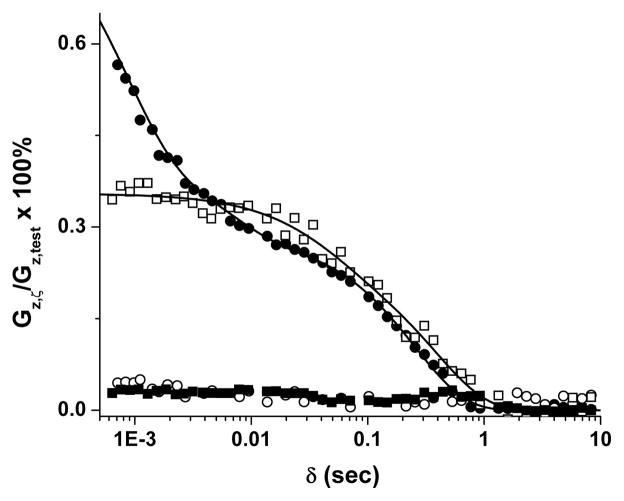
From inspection of the data in Fig. 4 and other plots (not shown), it is clear that the 1-D sample measurement captures information about short-lived decay components that is not detectable via the six-point (3-D) sample method. Presumably, this limitation of the six-point sample method is a result of the relatively long (8 ms) acquisition time required for accurate estimation of spectral frequencies. For the 1-D measurement a very early 2-ms window of the FID (50 data points) is fit to the Taylor Series model. For data in which the delay time (δ) between the end of the gradient pulse and the center of the broadband RF excitation pulse was larger than 5 ms, the eddy-current gradient-decay profiles measured by the 1-D and 3-D techniques were nearly superimposable. Small systematic differences in the results produced by the two techniques exist in the intermediate-to-long time range. Consider, for example, the data shown in Fig. 4. Here, for δ > 5 ms, the residual gradient observed via the six-point (3-D) sample method is consistently larger, by a few hundredths of a percent, than that determined by the 1-D sample measurement. Similar deviations in residual gradient amplitude between the two techniques were also observed in other data sets.

Figure 4.

Measured diagonal, z → z, eddy-current-induced gradients ([G_z,ζ/G_z,test] × 100%) in MRI system #1 (see Table 2 for system specifications) vs. delay time, δ, between the falling edge of the gradient test-pulse and the start of the FID acquisition. For the six-point sample (3-D) measurement (□), the gradient parameters were 2.5 s duration, 1 G/cm gradient amplitude; for the 1-D sample measurement (●), the gradient parameters were 2.5 s duration, 6 G/cm gradient pulse. After compensation, negligible eddy-current gradients remained as evidenced by results from the six-point sample measurement (■) and 1-D sample measurement (○) after properly setting the gradient pre-emphasis.

Based on scatter in the δ > 3 s data, the estimated residual gradient limit of detection is on the order of 0.6 mG/cm for both of the techniques described here. (Efforts to improve this limit of detection via greater signal averaging were not explored.) After setting the correct gradient pre-emphasis parameters, the MRI system residual eddy-current-induced gradients were reduced to nearly the noise level in the measurement (< 1 mG/cm). System eddy-current pre-emphasis parameters appeared to be highly reproducible between repeated measurements made days, or even weeks, apart.

Figure 5, shows single-shot, spin-echo EPI diffusion images obtained without and with (b ~ 534,000 s/mm²) diffusion weighting. Note that there is no detectible distortion in the heavily diffusion-weighted image, which was acquired without the benefit of eddy-current minimizing diffusion-weighting schemes [6–8].

Figure 5.

Single-shot EPI images of a sample of PEG 400 (polyethylene glycol, mol. wt._ave = 400 g/mol) contained within a 5 cc syringe. In addition to the PEG 400 liquid, the lumen of the syringe contains the ×-shaped piston taken from another identical 5 cc syringe. Both images were acquired at 4.7 T with system #2 (after proper eddy-current compensation) from a 2-mm thick slice with a 14 × 14 mm² (64 × 64) field-of-view using a spin-echo preparation (TE = 97 ms). Left. Image acquired without diffusion weighting (b = 0). Right. Heavily diffusion-weighted (b = 534,000 s/mm²) image of the sample employing a pair of trapezoidal gradient pulses on either side of the spin-echo refocusing pulse (G = 40 G/cm, δ = 25 ms, Δ = 33.2 ms, applied simultaneously along all three Cartesian axes).

Discussion

In addition to attenuating unwanted eddy-current-induced gradients by more than an order of magnitude, the introduction of actively-shielded gradient assemblies also greatly simplifies the data analysis required for non-iterative calculation of appropriate gradient pre-emphasis parameters. Two separate papers appearing in 1990 [14,17] pointed out that for elimination of eddy currents, an MRI system’s temporal response to gradient pulses required: (i) Laplace transformation of the time-dependent system response, (ii) solution for the required input current (I(s) in Laplace transform space), and (iii) inverse Laplace transformation (back into the time domain) to determine the required input current, I(t). This was necessary because the gradient pre-emphasis process itself produced eddy currents. In MRI scanners with actively-shielded gradient assemblies, however, the magnitudes of the eddy currents produced by the uncompensated gradient waveforms themselves are sufficiently small that the eddy currents can be treated as a small perturbation. In systems with very nearly linear response, once the eddy currents have been quantitatively measured, their amplitudes and time constants can be used directly for gradient waveform pre-emphasis [2–16].

This simpler approach of measuring the MRI systems’ eddy-current-induced gradient response and using the resulting residual gradient amplitudes and time constants for gradient pre-emphasis was essentially the one used herein. An important caveat is that the scaling relationship between the MRI system’s pre-emphasis unit and the measured eddy-current amplitudes must be measured. We followed the straightforward procedure outlined by de Graaf [3] for determining the eddy-current/pre-emphasis amplitude scaling factors. In two of our small-animal MRI systems (Systems #1 and #2 with newer Agilent/Varian DirectDrive^™ consoles) the scaling factors for eddy-current-induced gradient corrections were unity. In the third (System #3 with an older Varian INOVA console), the gradient scale factors were on the order of ~ 0.5, but differed for the three axes (x, y, and z). Also, the scaling factors for proper ΔB₀ pre-emphasis differed amongst the three gradient channels (x, y and z) on all three consoles. Presumably, this effect arises from subtle differences in the amplification/attenuation of each of the gradient-waveform channels as they feed into the ΔB₀ pre-emphasis unit. Lastly, except for very short-lived pre-emphases (τ < 2 ms), the scaling factors for a given gradient pre-emphasis channel were consistent across a range of time constants. With the exception of the fast-decaying components, eddy-current estimation and correction can be performed in a single step. For the short-lived components, the pre-emphasis amplitudes required were up to three times as large as their initial estimates. This likely arises from the difficulty of accurately estimating the amplitude of the fast components when the first 500 μs – 1.5 ms of FID data was discarded, coupled with finite delays for gradient turn-off and RF pulses.

The six-point (3-D) sample method offers the convenience of determining the residual gradients along all three axes simultaneously in one measurement. However, very short-lived, eddy-current-induced gradients (τ < 2 ms) are not detected by the six-point sample method. This limitation arises because accurate frequency estimation is compromised by severely truncated FID data [35]. In some circumstances, this limitation may be of very little or no consequence. For instance, in a 7.0 T clinical, head-only, 68.0-cm bore MRI system, the shortest-lived eddy currents decayed with a time constant of 43 ms [2–16]. Except for localized spectroscopy data acquired with sub-millisecond echo times [36], it is the long-lived eddy-current-induced gradient components that lead to measurement artifacts. Indeed, it has been suggested that correcting only the long-lived eddy-current behavior may be sufficient for most diffusion-weighted spin-echo EPI measurements [21]. Certainly, the long-lived components, whose effects integrate over time, have the opportunity to contribute more to signal phase evolution than short-lived, fast-decaying components.

The data available from this study do not directly address the cause of the systematic differences in eddy-current-induced gradients quantified by the 1-D and six-sample (3-D) measurements. We speculate that they are related to higher-order residual gradients, whose presence has been demonstrated previously [20]. Inaccuracy in determining the distance between point samples in the six-point (3-D) phantom is another possible contributing factor. The fundamental difference between the two methods is that while the 1-D sample measurement is based on a 1-D Fourier transform of the position-dependent phase accumulated across the entire length of a 1-D phantom, the six-point sample technique is based on the resonance frequency difference at two discrete positions, defining a line, along the residual gradient axis. Depending on the details of the residual-gradient profile, the differences in sign and amplitude of the measured gradients will be sensitive to the exact placement of each pair of point solvents along a given axis for the six-point sample phantom. However, these differences appear to be quite small – on the order of at most a few hundredths of a percent.

The measurement techniques and analyses described herein allow for straightforward and nearly complete elimination of eddy-current effects in MRI scanners. With the exception of the fastest-decaying eddy-current components (τ < 2 ms), the procedures require only a single measurement. The size of the non-ideality of the gradient response in the three different small-animal MRI scanners in our lab is small, but, as expected, depends primarily on the ratio of gradient-assembly to magnet-bore diameters.

While the focus of the current paper is on applications of the measurements in MRI systems, one could imagine using slightly adapted phantoms for measureming eddy currents in high-resolution NMR systems equipped with pulsed gradients, for which eddy currents can also be problematic. Indeed, diffusion-weighting schemes designed to offer some degree of eddy-current cancellation have been found to be beneficial in high-resolution NMR spectrometers [37]. The two methods developed in this paper for measurement of residual eddy current-induced gradients could be adapted for use in high-resolution NMR instruments. A 1-D sample (a short capillary tube) could be used for z-axis measurements (along the magnet bore) and an array of 4 capillaries held within a larger NMR tube used to quantify x and y components (a 2-D adaptation of the 6-point sample method described herein). Once acquired, the eddy current parameters could be used for setting gradient pre-emphases on high-resolution, pulsed-gradient NMR spectrqometers.